三角函数的图象与性质
- 格式：pdf
- 大小：139.08 KB
- 文档页数：7
下载文档原格式
合集下载
三角函数的图象与性质
1增至－ 1.
21
－1增至1.
π 3
三、余弦函数的单调性 1
-2π x -π -π y y=cosx (xR) O … π 0 1 2π …
2
？？
3π
4π
-1
…
2
x
π －1
…
cosx －1
0
0
增区间为[－π [， －0] π+2kπ，2kπ]，(k∈z) ，其值从 －1增至1.
今后所说的周期，如果不加特别说明，一般都是指函数的最 小的正周期. 说明: ①当函数对于自变量的一切值每增加或减少一个定值， 函数值就重复出现时，这个函数就叫做周期函数.
②设f(x)是定义在实数集 D上的函数，若存在一个 常数T( T≠0)， 具有下列性质: (1)对于任何的 x∈D，有(x±T)∈D； (2)对于任何的 x∈D，有f(x+T)=f(x)成立，则f(x)叫做周期函数. ③若函数f(x)不是当x取定义域内的“每一个值”时，都有 f(x+T)= f(x)成立，则T就不是f(x)周期. 17
(1) {x|x=
2
+2k， k z}；
(2) {x|x=6k， k z}；
25
例4 求下列函数y=sin(2x+ )的单调区间： 3 解 (1)令z=2x + ，函数y=sinz的单调增区间为: 3 [ 2k， 2k ]，（k z） 2 2 3 函数y=sinz的单调增区间为: [ 2k， 2k ]，（k z） 2 2 5 2 k 2 x 2 k ， 得 k x k , 2 3 2 12 12 3 7 2 k 2 x 2 k ， k x k， 2 3 2 12 12 12 k， k ](k z). 所以单调增区间为: [ 5 12 7 k， k ](k z). 单调减区间为: [
21
－1增至1.
π 3
三、余弦函数的单调性 1
-2π x -π -π y y=cosx (xR) O … π 0 1 2π …
2
？？
3π
4π
-1
…
2
x
π －1
…
cosx －1
0
0
增区间为[－π [， －0] π+2kπ，2kπ]，(k∈z) ，其值从 －1增至1.
今后所说的周期，如果不加特别说明，一般都是指函数的最 小的正周期. 说明: ①当函数对于自变量的一切值每增加或减少一个定值， 函数值就重复出现时，这个函数就叫做周期函数.
②设f(x)是定义在实数集 D上的函数，若存在一个 常数T( T≠0)， 具有下列性质: (1)对于任何的 x∈D，有(x±T)∈D； (2)对于任何的 x∈D，有f(x+T)=f(x)成立，则f(x)叫做周期函数. ③若函数f(x)不是当x取定义域内的“每一个值”时，都有 f(x+T)= f(x)成立，则T就不是f(x)周期. 17
(1) {x|x=
2
+2k， k z}；
(2) {x|x=6k， k z}；
25
例4 求下列函数y=sin(2x+ )的单调区间： 3 解 (1)令z=2x + ，函数y=sinz的单调增区间为: 3 [ 2k， 2k ]，（k z） 2 2 3 函数y=sinz的单调增区间为: [ 2k， 2k ]，（k z） 2 2 5 2 k 2 x 2 k ， 得 k x k , 2 3 2 12 12 3 7 2 k 2 x 2 k ， k x k， 2 3 2 12 12 12 k， k ](k z). 所以单调增区间为: [ 5 12 7 k， k ](k z). 单调减区间为: [
三角函数的图象与性质 (共44张PPT)
(
)
3 3 A.－2，2 3 3 3 3 C. － ， 2 2
解析： 当 故
π π 1 π π 5π x∈0，2 时， 2x－ ∈－ 6， 6 ， sin2x－6 ∈－2，1， 6
上是减函数 － π ， 0 C．在[0，π]上是增函数，在
)
π π π π D．在2，π和－π，－2上是增函数，在－2，2 上是减函数
3．(2015· 皖南八校模拟)函数 f(x)＝cos 2x＋2sin x 的最大值与最小值 的和是 A．－2 3 C．－ 2
4．求函数 y＝cos x＋sin
2
π x|x|≤4 的最大值与最小值．
π 2 2 解：令 t＝sin x，∵|x|≤ ，∴t∈－ ， . 4 2 2
∴y＝－t
2
1 2 5 ＋t＋1＝－t－2 ＋ ， 4
1－ 2 1 5 2 ∴当 t＝ 时，ymax＝ ，当 t＝－ 时，ymin＝ . 2 4 2 2 ∴函数 y＝cos x＋sin
sin 2x＞0， 解析：由 2 9－x ≥0，
π kπ＜x＜kπ＋ ，k∈Z， 2 得 －3≤x≤3.
π π ∴－3≤x＜－ 或 0＜x＜ . 2 2 ∴函数 y＝lg(sin 2x)＋ 9－x
2
π π 的定义域为－3，2 ∪0，2 .
2
π 1－ 5 x通法]
1．三角函数定义域的求法 求三角函数定义域实际上是构造简单的三角不等式(组)，常借 助三角函数线或三角函数图象来求解．
2．三角函数值域的不同求法 (1)利用 sin x 和 cos x 的值域直接求；
三角函数的图像与性质课件
1
0 -1
y
y=-cosx x [0,2 ]
1
●
o
●
3●
2
x
2
2
-1 ●
●
思考：
1、函数y=1+sinx的图象与函数y=sinx的图象有什么关系？ 2、函数y=-cosx的图象与函数y=cosx的图象有什么关系？
y 2
1
o
2
-1
y
1
o
2
-1
y=1+sinx x[0, 2 ]
3
2
x
2
y=sinx x[0, 2 ]
解：(1)函数的定义域为 R，
且
f(x)
＝
cos(
π 2
＋
2x)
＝
－
sin
2x.∵f( －x) ＝－
sin(－2x)＝sin 2x＝－f(x)，∴函数 f(x)＝cos(2x
＋52π)是奇函数．(2)函数的定义域为 R，
且 f(－x)＝sin[cos(－x)]＝sin(cos x)＝f(x)，
∴函数 f(x)＝sin(cos x)是偶函数．
【名师点评】 判断函数奇偶性时，必须先检查定义 域是否是关于原点的对称区间．如果是，再验证f(－x) 是否等于－f(x)或f(x)，进而判断函数的奇偶性；如果 不是，则该函数必为非奇非偶函数．
跟踪训练
3．判断下列函数的奇偶性．
(1)f(x)＝cos(2x＋52π)；
(2)f(x)＝sin(cos x)．
(2)y= - cosx， x [0, 2 ]
解：(1)按五个关键点列表
x
0
2
3
2
2
sinx 0 1 0 -1 0
三角函数的图象与性质知识点汇总
三角函数的图象与性质一、知识网络三、知识要点（一）三角函数的性质1、定义域与值域2、奇偶性（1）基本函数的奇偶性奇函数：y＝sinx，y＝tanx；偶函数：y＝cosx.（2）型三角函数的奇偶性（ⅰ）g（x）＝（x∈R）g（x）为偶函数由此得；同理，为奇函数 .（ⅱ）为偶函数；为奇函数.3、周期性（1）基本公式（ⅰ）基本三角函数的周期y＝sinx，y＝cosx的周期为；y＝tanx，y＝cotx的周期为 .（ⅱ）型三角函数的周期的周期为；的周期为 .（2）认知（ⅰ）型函数的周期的周期为；的周期为 .（ⅱ）的周期的周期为；的周期为 .均同它们不加绝对值时的周期相同，即对y＝的解析式施加绝对值后，该函数的周期不变.注意这一点与（ⅰ）的区别.（ⅱ）若函数为型两位函数之和，则探求周期适于“最小公倍数法”.（ⅲ）探求其它“杂”三角函数的周期，基本策略是试验――猜想――证明.（3）特殊情形研究（ⅰ）y＝tanx－cotx的最小正周期为；（ⅱ）的最小正周期为；（ⅲ）y＝sin4x＋cos4x的最小正周期为 .由此领悟“最小公倍数法”的适用类型，以防施错对象.4、单调性（1）基本三角函数的单调区间（族）依从三角函数图象识证“三部曲”：①选周期：在原点附近选取那个包含全部锐角，单调区间完整，并且最好关于原点对称的一个周期；②写特解：在所选周期内写出函数的增区间（或减区间）；③获通解：在②中所得特解区间两端加上有关函数的最小正周期的整数倍，即得这一函数的增区间族（或减区间族）循着上述三部曲，便可得出课本中规范的三角函数的单调区间族.揭示：上述“三部曲”也适合于寻求简单三角不等式的解集或探求三角函数的定义域.（2）y＝型三角函数的单调区间此类三角函数单调区间的寻求“三部曲”为①换元、分解：令u＝，将所给函数分解为内、外两层：y＝f（u），u＝；②套用公式：根据对复合函数单调性的认知，确定出f（u）的单调性，而后利用（1）中公式写出关于u的不等式；③还原、结论：将u＝代入②中u的不等式，解出x的取值范围，并用集合或区间形成结论.（二）三角函数的图象1、对称轴与对称中心（1）基本三角函数图象的对称性（ⅰ）正弦曲线y＝sinx的对称轴为；正弦曲线y＝sinx的对称中心为（，0） .（ⅱ）余弦曲线y＝cosx的对称轴为；余弦曲线y＝cosx的对称中心（ⅲ）正切曲线y＝tanx的对称中心为；正切曲线y＝tanx无对称轴.认知：①两弦函数的共性：x＝为两弦函数f（x）对称轴为最大值或最小值；（，0）为两弦函数f（x）对称中心＝0.②正切函数的个性：（，0）为正切函数f（x）的对称中心＝0或不存在.（2）型三角函数的对称性（服从上述认知）（ⅰ）对于g（x）＝或g（x）＝的图象x＝为g（x）对称轴为最值（最大值或最小值）；（，0）为两弦函数g（x）对称中心＝0.（ⅱ）对于g（x）＝的图象（，0）为两弦函数g（x）的对称中心＝0或不存在.2、基本变换（1）对称变换（2）振幅变换（纵向伸缩）（3）周期变换（横向伸缩）（4）相位变换（左右平移）（5）上、下平移3、y＝的图象（1）五点作图法（2）对于A，T，，的认知与寻求：①A：图像上最高点（或最低点）到平衡位置的距离；2A：图像上最高点与最低点在y轴上投影间的距离.②：图象的相邻对称轴（或对称中心）间的距离；：图象的对称轴与相邻对称中心间的距离.：由T＝得出. ③：解法一：运用“代点法”求解，以图象的最高点（或最低点）坐标代入为上策，若以图象与x轴交点坐标代入函数式求，则须注意检验，以防所得值为增根；解法二：逆用“五点作图法”的过程（参见经典例题）.四、经典例题例1、求下列函数的值域：（1）（2）（3）（4）（5）（6）分析：对于形如（1）（2）（3）的函数求值域，基本策略是（ⅰ）化归为的值域；（ⅱ）转化为sinx（或cosx）的二次函数；对于（4）（5）（6）之类含有绝对值的函数求值域，基本策略则是（ⅰ）在适当的条件下考察y2；（ⅱ）转化为分段函数来处理；（ⅲ）运用其周期性、奇偶性或函数图象对称性转化.解：（1）∵∴，即所求函数的值域为 .（2）由∴∴注意到这里x∈R，，∴∴所求函数的值域为[－1，1].（3）这里令sinx＋cosx＝t则有且由于是有∵∴因此，所求函数的值域为 .（4）注意到这里y>0，且∵∴即所求函数的值域为 .（5）注意到所给函数为偶函数，又当∴此时同理，当亦有 . ∴所求函数的值域为 .（6）令则易见f（x）为偶函数，且∴是f（x）的一个正周期. ①只需求出f（x）在一个周期上的取值范围.当x∈[0， ]时，又注意到，∴x＝为f（x）图象的一条对称轴②∴只需求出f（x）在[0， ]上的最大值.而在[0， ]上，递增. ③亦递增④∴由③④得f（x）在[0， ]上单调递增.∴即⑤于是由①、②、⑤得所求函数的值域为 .点评：解（1）（2）运用的是基本化归方法；解（3）运用的是求解关于sinx＋cosx 与sinxcosx的函数值域的特定方法；解（4）借助平方转化；解（5）（6）则是利用函数性质化繁为简，化暗为明.这一点在解（6）时表现得淋漓尽致.例2、求下列函数的周期：（1）；（2）；（3）；（4）；（5）分析：与求值域的情形相似，求三角函数的周期，首选是将所给函数化为＋k的形式，而后运用已知公式.对于含有绝对值的三角函数，在不能利用已有认知的情况下，设法转化为分段函数来处理.解：（1）＝＝∴所求最小正周期 .（2）＝＝＝∴所求周期 .（3）＝＝＝ .注意到的最小正周期为，故所求函数的周期为 .（4）注意到3sinx及-sinx的周期为2，又sinx≥0（或sinx<0）的解区间重复出现的最小正周期为2 . ∴所求函数的周期为2 .（5）注意到sin2x的最小正周期，又sinx≥0（或sinx<0）的解区间重复出现的最小正周期，这里的最小公倍数为 . ∴所求函数的周期 .点评：对于（5），令则由知，是f（x）的一个正周期.①又∴不是f（x）的最小正周期. ②于是由①②知，f（x）的最小正周期为 .在一般情况下，探求上述一类分段函数的周期，仅考虑各段函数的最小正周期的最小公倍数是不够的，还要考虑各分支中的条件区间重复出现的最小正周期.双方结合，方可能获得正确结果.请大家研究的最小正周期，并总结自己的有关感悟与经验.例3、已知函数的部分图象，（1）求的值；（2）求函数图象的对称轴方程和对称中心坐标.解：（1）令，则由题意得f（0）＝1∵∴注意到函数图象在所给长度为一个周期的区间的右端点横坐标为，故逆用“五点作图法”得：由此解得∴所求， .（2）由（1）得令，解得，∴函数f（x）图象的对称轴方程为；令解得，∴函数f（x）图象的对称中心坐标为 .点评：前事不忘，后事之师.回顾运用“五点作图法”作出所给三角函数在一个周期内图象的列表、描点过程，便可从中悟出所给函数图象上的五个关键点横坐标满足的等式：例4、（1）函数的单调递增区间为。
第14讲 三角函数图象与性质
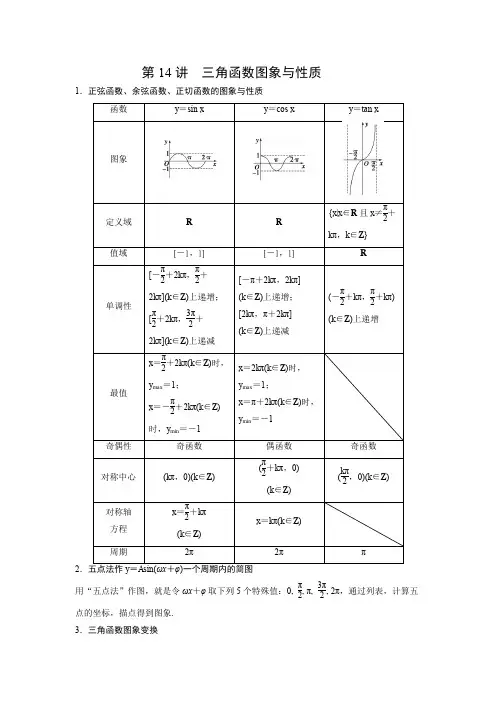
第14讲三角函数图象与性质1．正弦函数、余弦函数、正切函数的图象与性质π2．用“五点法”作图，就是令ωx＋φ取下列5个特殊值：0, π2, π,3π2, 2π，通过列表，计算五点的坐标，描点得到图象. 3．三角函数图象变换[玩转典例]题型一 三角函数的定义域和值域例1 （1）求函数f (x )＝lg sin x ＋16－x 2的定义域． (2)y ＝lg(3－tan x )．例2 求下列函数的最大值和最小值和值域． (1)f (x )＝sin ⎝⎛⎭⎫2x －π6，x ∈⎣⎡⎦⎤0，π2； (2)f (x )＝－2cos 2x ＋2sin x ＋3，x ∈⎣⎡⎦⎤π6，5π6.[玩转跟踪]1. 求函数y ＝tan x ＋1＋lg(1－tan x )的定义域．2.求函数y ＝ log 21sin x－1的定义域．3.函数y ＝－tan 2x ＋4tan x ＋1，x ∈⎣⎡⎦⎤－π4，π4的值域为____________．题型二 三角函数的单调性例3 求函数y ＝3cos ⎝⎛⎭⎫π3－x 2的单调递增区间．[玩转跟踪]1.求函数y ＝12log cos ⎝⎛⎭⎫π3－x 2的单调递增区间．2.求函数y ＝tan ⎝⎛⎭⎫2x －π3的单调区间．题型三 三角函数的周期性对称性和奇偶性 例4 已知函数y ＝2cos ⎝⎛⎭⎫2x ＋2π3. (1)在该函数的对称轴中，求离y 轴距离最近的那条对称轴的方程；(2)把该函数的图象向右平移φ个单位长度后，图象关于原点对称，求φ的最小正值．[玩转跟踪]1．把函数y ＝cos ⎝⎛⎭⎫x ＋4π3的图象向右平移φ个单位长度，正好关于y 轴对称，求φ的最小正值．2.已知函数f (x )＝sin ⎝⎛⎭⎫2ωx －π3(ω>0)的最小正周期为π，则函数f (x )的图象的一条对称轴方程是( )3.在函数①y ＝cos|2x |；②y ＝|cos x |；③y ＝cos ⎝⎛⎭⎫2x ＋π6；④y ＝tan ⎝⎛⎭⎫2x －π4中，最小正周期为π的所有函数为( ) A ．①②③ B ．①③④ C ．②④D ．①③题型四 三角函数的图像变换例5 把函数y ＝sin x (x ∈R )的图象上所有的点向左平移π3个单位长度，再把所得图象上所有点的横坐标缩短到原来的12(纵坐标不变)，得到的图象所表示的函数是( )A ．y ＝sin ⎝⎛⎭⎫2x －π3，x ∈R B ．y ＝sin ⎝⎛⎭⎫x 2＋π6，x ∈R C ．y ＝sin ⎝⎛⎭⎫2x ＋π3，x ∈R D ．y ＝sin ⎝⎛⎭⎫2x ＋2π3，x ∈R [玩转跟踪]1．把函数y ＝f (x )的图象上的各点向右平移π6个单位，再把横坐标伸长到原来的2倍，再把纵坐标缩短到原来的23倍，所得图象的解析式是y ＝2sin ⎝⎛⎭⎫12x ＋π3，求f (x )的解析式．题型五 由图象求函数y ＝A sin(ωx ＋φ)的解析式例6 如图是函数y ＝A sin(ωx ＋φ)⎝⎛⎭⎫A ＞0，ω＞0，|φ|＜π2的图象，求A ，ω，φ的值，并确定其函数解析式．[玩转跟踪]1.函数y ＝A sin(ωx ＋φ)的部分图象如图所示，则( )A ．y ＝2sin ⎝⎛⎭⎫2x －π6B ．y ＝2sin ⎝⎛⎭⎫2x －π3 C ．y ＝2sin ⎝⎛⎭⎫x ＋π6 D ．y ＝2sin ⎝⎛⎭⎫x ＋π3 类型六 函数y ＝A sin(ωx ＋φ)性质的应用例7 已知函数y ＝A sin(ωx ＋φ)⎝⎛⎭⎫A >0，ω>0，|φ|<π2的图象过点P ⎝⎛⎭⎫π12，0，图象上与P 点最近的一个最高点的坐标为⎝⎛⎭⎫π3，5. (1)求函数解析式； (2)指出函数的增区间； (3)求使y ≤0的x 的取值范围．[玩转跟踪]1.设函数f (x )＝sin(2x ＋φ)(－π＜φ＜0)，函数y ＝f (x )的图象的一条对称轴是直线x ＝π8.(1)求φ的值；(2)求函数y ＝f (x )的单调区间及最值．[玩转练习]1．下列函数中，最小正周期为4π的是( ) A ．y ＝sin x B ．y ＝cos x C ．y ＝sin x2D ．y ＝cos 2x2．已知函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π4(x ∈R ，ω＞0)的最小正周期为π，为了得到函数g (x )＝cos ωx 的图象，只需将y ＝f (x )的图象上所有的点( ) A ．向左平移π8个单位长度B ．向右平移π8个单位长度C ．向左平移π4个单位长度D ．向右平移π4个单位长度3．函数y ＝|sin x |的一个单调递增区间是( ) A.⎝⎛⎭⎫－π4，π4 B.⎝⎛⎭⎫π4，3π4 C.⎝⎛⎭⎫π，3π2 D.⎝⎛⎭⎫3π2，2π4．若f (x )＝tan ⎝⎛⎭⎫x ＋π4，则( ) A ．f (0)>f (－1)>f (1) B ．f (0)>f (1)>f (－1) C ．f (1)>f (0)>f (－1) D ．f (－1)>f (0)>f (1)5.函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0)的部分图象如图，则其解析式为( )A ．f (x )＝2sin ⎝⎛⎭⎫x ＋π4 B ．f (x )＝sin ⎝⎛⎭⎫2x ＋π4 C ．f (x )＝2sin ⎝⎛⎭⎫2x ＋π4 D ．f (x )＝2sin ⎝⎛⎭⎫2x －π46．当x ∈⎣⎡⎦⎤π6，7π6时，函数y ＝3－sin x －2cos 2x 的最小值是________，最大值是________． 7．函数f (x )＝2cos ⎝⎛⎭⎫2x －π4的单调递减区间是________． 8.设偶函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0,0<φ<π)的部分图象如图所示，△KLM 为等腰直角三角形，∠KML ＝90°，|KL |＝1，则f ⎝⎛⎭⎫16的值为________．9.已知函数f (x )＝A sin(ωx ＋φ)＋B ⎝⎛⎭⎫A >0，ω>0，|φ|<π2的最小正周期为T ，且在一个周期内的图象如图所示．(1)求函数f (x )的解析式；(2)若函数g (x )＝f (mx )＋1(m >0)的图象关于点M ⎝⎛⎭⎫4π3，0对称，且在区间⎣⎡⎦⎤0，π2上不是单调函数，求m 的取值所构成的集合．10．已知函数f (x )＝sin(2x ＋φ)，其中φ为实数，且|φ|<π.若f (x )≤⎪⎪⎪⎪f ⎝⎛⎭⎫π6对x ∈R 恒成立．且f ⎝⎛⎭⎫π2>f (π)，求f (x )的单调递增区间．。
第五章 第四节 三角函数的图象与性质 课件(共63张PPT)
，解
得 ω＝32 .
法二：由题意，得 f(x)max＝fπ3
2．(必修 4P35 例 2 改编)若函数 y＝2sin 2x－1 的最小正周期为 T，最大
值为 A，则( )
A．T＝π，A＝1
B．T＝2π，A＝1
C．T＝π，A＝2
D．T＝2π，A＝2
A [T＝22π ＝π，A＝2－1＝1.]
3．(必修 4P40 练习 T4 改编)下列关于函数 y＝4cos x，x∈[－π，π]的单 调性的叙述，正确的是( )
求三角函数单调区间的两种方法 (1)代换法：就是将比较复杂的三角函数含自变量的代数式整体当作一个 角 u(或 t)，利用复合函数的单调性列不等式求解．(如本例(1)) (2)图象法：画出三角函数的正、余弦曲线，结合图象求它的单调区间． [注意] 要注意求函数 y＝A sin (ωx＋φ)的单调区间时 ω 的符号，若 ω<0， 那么一定先借助诱导公式将 ω 化为正数．同时切莫漏掉考虑函数自身的定义 域．
又当 x∈[0，π2
]时，f(x)∈[－
2 2
，1]，所以π2
≤ω2π
－π4
≤5π4
，解得
3 2
≤ω≤3，故选 B.
π
π
π
优解：当 ω＝2 时，f(x)＝sin (2x－ 4 ).因为 x∈[0，2 ]，所以 2x－ 4 ∈
π [－ 4
，3π4
π ]，所以 sin (2x－ 4
)∈[－
2 2
，1]，满足题意，故排除 A，C，
B．[kπ，kπ＋π2 ](k∈Z)
C．[kπ＋π6 ，kπ＋23π ](k∈Z)
D．[kπ－π2 ，kπ](k∈Z)
(2)函数 y＝tan x 在－π2，32π 上的单调减区间为__________．
§4.3 三角函数的图象与性质
于点（ ｘ０ ，０） 中心对称．
( ) 设 ｆ（ ｘ） ＝
４ｃｏｓ
ωｘ－
π ６
ｓｉｎ ωｘ － ｃｏｓ （ ２ωｘ ＋ π） ， 其 中 ω
＞０．
（１）求函数 ｙ ＝ ｆ（ｘ）的值域；
[ ] （２）若 ｆ（ｘ）在区间
－ ３２π，
π ２
上为增函数，求 ω 的最大值．
( ) 解析 （１）ｆ（ｘ）＝ ４
．
（２） （２０１９ 成都七中 １ 月月考，１４） 如图为一弹簧振子作简 谐运动的图象，横轴表示振动的时间，纵轴表示振动的位移，则 这个振子振动的一个函数解析式是 ．
解析
（ １） 由
Ｔ ４
＝
１１ １２
π－
２ ３
π＝
π ４
，得
Ｔ
＝
π，
∵
Ｔ＝
２π ，∴
ω
ω ＝ ２，∴
ｆ（ ｘ） ＝
对称性
对称轴：ｘ ＝ ｋπ＋
π ２
（ ｋ∈Ｚ） ；
对称中心：（ ｋπ，０） （ ｋ∈Ｚ）
周期
２π
单调性
单调增区间：
[ ] ２ｋπ－
π ２
，２ｋπ＋
π ２
（ ｋ∈Ｚ） ；
单调减区间：
[ ] ２ｋπ＋
π ２
，２ｋπ＋
３π ２
（ ｋ∈Ｚ）
奇偶性
奇函数
［ －１，１］
对称轴：ｘ ＝ ｋπ（ ｋ∈Ｚ） ；
( ) 对称中心：
换，设
ｚ
＝
ωｘ＋φ，由
ｚ
取
０，
π ２
３π ，π， ，２π
２
来求出相
应的
ｘ，通过列
表、计算得出五点坐标，描点连线后得出图象．
高中数学三角函数图像和性质
高中数学
三角函数的图象和性质
知识点
一.正弦函数：
1.正弦函数的图象:
2.
定义域为
；值域为•
(1)
当且仅当
时，取得最大值1；
⑵
当且仅当
时，取得最小值1
3.单调性：
在闭区间上都是增函数，其值从1增大到1；
在闭区间上都是减函数，其值从1减小到1.
4.奇偶性：.
5.周期性：最小正周期是，周期是
6.对称性：对称轴是，对称中心是.
r
rK，
(1)将正切函数y tanx在区间(亍'上的图象向左、右扩展，就可以得到正切函y tanx,(x R, x-k , k Z)的图象，我们把它叫做正切曲线.正切曲线是由被互相平行的直线x
(k Z)所隔开的无数多支曲线组成的.这些平行直线x=(k Z)叫做正切曲线各支的
⑵结合正切曲线的特征，类比正弦、余弦函数的“五点法”作图，也可用三点两线作图法作出正切函数
6.对称性：对称轴是，对称中心是.
题型一 正弦，余弦函数的图象和性质
【例1】求函数y=g+sinx的定义域
函数y=2sin(4x+^)的对称轴方程为
3
【过关练习】
1•求函数y 3sin x2的值域以及取得最值时x的值
2.判断函数y=xsin( x)的奇偶性
3.求函数y1sinx的单调区间
二.余弦函数：
1.余弦函数的Βιβλιοθήκη 象:2.定义域为值域为
(1)当且仅当
时，取得最大值1；
(2)当且仅当
时，取得最小值1.
3.单调性：
在闭区间
上都是增函数，其值从
1增加到1；
在闭区间
上都是减函数，其值从
三角函数的图象和性质
知识点
一.正弦函数：
1.正弦函数的图象:
2.
定义域为
；值域为•
(1)
当且仅当
时，取得最大值1；
⑵
当且仅当
时，取得最小值1
3.单调性：
在闭区间上都是增函数，其值从1增大到1；
在闭区间上都是减函数，其值从1减小到1.
4.奇偶性：.
5.周期性：最小正周期是，周期是
6.对称性：对称轴是，对称中心是.
r
rK，
(1)将正切函数y tanx在区间(亍'上的图象向左、右扩展，就可以得到正切函y tanx,(x R, x-k , k Z)的图象，我们把它叫做正切曲线.正切曲线是由被互相平行的直线x
(k Z)所隔开的无数多支曲线组成的.这些平行直线x=(k Z)叫做正切曲线各支的
⑵结合正切曲线的特征，类比正弦、余弦函数的“五点法”作图，也可用三点两线作图法作出正切函数
6.对称性：对称轴是，对称中心是.
题型一 正弦，余弦函数的图象和性质
【例1】求函数y=g+sinx的定义域
函数y=2sin(4x+^)的对称轴方程为
3
【过关练习】
1•求函数y 3sin x2的值域以及取得最值时x的值
2.判断函数y=xsin( x)的奇偶性
3.求函数y1sinx的单调区间
二.余弦函数：
1.余弦函数的Βιβλιοθήκη 象:2.定义域为值域为
(1)当且仅当
时，取得最大值1；
(2)当且仅当
时，取得最小值1.
3.单调性：
在闭区间
上都是增函数，其值从
1增加到1；
在闭区间
上都是减函数，其值从
三角函数图象与性质
5、已知下图是函数
y A sin( x ) 的图象
2
1 –1
(1)求 、 的值；
(2)求函数图象的对称轴方程.
y
11 12
O
x
–2 2 0 6 ⑴ y 2sin(2 x ) 6 11 2 6 12
注意：当0<x<1,arcsinx,arccosx表示一个锐角， 而-1<x<0时，arcsinx表示一个锐角的负值，arccosx表示 一个钝角,两者不要混淆。 x>0时arctanx表示一个锐角。 x<0时arctanx表示一个锐角负值。
注意: 在给出三角函数值求角时,需注意反三角表 示的角的范围 对于不满足反三角范围的角,我们利用诱导公 式,对角 k 的整数倍,(整数倍需注意) 练习册:P43 P44 3 5
内容提要
函数图像变换
向上(b>0)或向下(b<0) 移︱b︱单位 向左(φ>0)或向右(φ<0)移︱ φ︱单位 y=f(x)+b图象
y=f(x+φ)图象
y=f(x)图象
点的纵坐标变为原来的A倍 y=Af(x)图象 横坐标不变 点的横坐标变为原来的1/ω倍 y=f(ωx)图象 纵坐标不变
3、求y=Asin(ωx+φ)+K 的解析式的方法
⑷函数的图象可以由函数 y 2 sin 2 x, x R的图象经过怎 样的变换得到。
解：y sin 2 x 2 sin x cos x 3 cos 2 x 1 sin 2 x 2 cos 2 x
1 sin 2 x cos 2 x 1 2 2 sin( 2 x ) 4 ⑶ 当2 x 2k , 即x k (k Z )时, y最大值 2 2 4 2 8 ⑷ y 2 sin 2 x 图象向左平移 8 个单位 y 2 sin( 2 x ) 4 图象向上平移2个单位 y 2 2 sin( 2 x ) 4
7.3三角函数的图像和性质课件高中数学苏教版必修第一册
当且仅当x=+2kπ(k∈Z)时,取 当且仅当x=2kπ(k∈Z)时,取得最
最值
得最大值1;当且仅当x=-+2kπ 大值1;当且仅当x=2kπ+π(k∈Z)
(k∈Z)时,取得最小值-1
时,取得最小值-1
奇偶性 奇函数
偶函数
对称轴 x=kπ+,k∈Z
x=kπ,k∈Z
对称
中心
(kπ,0),k∈Z
,k∈Z
3
π
π
kπ- ≤x≤kπ+ (k∈Z).
6
3
π
π
所以原函数的减区间是[kπ-6,kπ+3](k∈Z).
π
π
(2)y=2sin 4 - =-2sin - 4 .
π
令 z=x- ,则 y=-2sin z,求 y=-2sin z 的减区间,即求 2sin z 的增区间.
4
π
π
所以- +2kπ≤z≤ +2kπ,k∈Z,
(k∈Z)上都是增函数,其值由-1 (k∈Z)上都是增函数,其值由-1
单调性 增大到1;在每一个闭区间
增大到1;在每一个闭区间
[2kπ+,2kπ+] (k∈Z)上都是减函 [2kπ,2kπ+π] (k∈Z) 上都是减函
数,其值由1减小到-1
数,其值由1减小到-1
函数
正弦函数y=sin x
余弦函数 y=cos x
反思感悟与三角函数有关的函数的值域(或最值)的求解思路
1.求形如y=asin x+b的函数的最值或值域时,可利用正弦函数的有界性
(-1≤sin x≤1)求解.
2.对于形如y=Asin(ωx+φ)+k(Aω≠0)的函数,当定义域为R时,值域为
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三角函数的图象与性质
——正弦函数、余弦函数的性质
【教学目标】
1．理解正、余弦函数的定义域、值域、最值、周期性、奇偶性的意义；
2．会求简单函数的定义域、值域、最小正周期和单调区间；
3．掌握正弦函数的周期及求法。
(n )si y A x ωϕ＝＋
【教学重点】
正、余弦函数的性质。
【教学难点】
正、余弦函数性质的理解与应用。
【教学过程】
一、讲解新课：
（1）定义域：
正弦函数、余弦函数的定义域都是实数集［或］，
R (,)-∞+∞分别记作：
sin y x x ∈R
＝，cos ,y x x =∈R
（2）值域
，1sin 1x ≤≤--1cos 1
x ≤≤也就是说，正弦函数、余弦函数的值域都是。
[
]-1,1其中正弦函数，sin y x =x ∈R
（1）当且仅当，时，取得最大值1。
x 2k 2π
π=+k ∈Z （2）当且仅当，时，取得最小值。
x 2k 2π
π=+k ∈Z 1-
而余弦函数，cos y x ＝x ∈R
当且仅当，时，取得最大值1，时，取得最小值。
2x k π=k ∈Z (21)x k π=+k ∈Z 1-（3）周期性
由，()知：
sin(2)sin x k x π+=cos(2)cos x k x π+=k ∈Z 正弦函数值、余弦函数值是按照一定规律不断重复地取得的。
一般地，对于函数，如果存在一个非零常数，使得当取定义域内的每一个值()f x T x 时，都有，那么函数f(x)就叫做周期函数，非零常数叫做这个函数的周()()f x T f x +=T 期。
由此可知，，，…，，，…(且)都是这两个函数的周期。
2π4π2π-4π-2k πk ∈Z 0k ≠对于一个周期函数
，如果在它所有的周期中存在一个最小的正数，那么这个最小正()f x 数就叫做
的最小正周期。
()f x 注意：
1．周期函数定义域，则必有，且若则定义域无上界；则定义域x ∈M x T M +∈0T ＞0T ＜无下界；
2．“每一个值”只要有一个反例，则就不为周期函数（如）
()f x ()()00¹f x t f x +3．往往是多值的（如，，，…，，，…都是周期）周期中最T sin y x =2π4π2π-4π-T 小的正数叫做的最小正周期（有些周期函数没有最小正周期）
()f x 根据上述定义，可知：正弦函数、余弦函数都是周期函数，(且)都是它的2k πk ∈Z 0k ≠周期，最小正周期是2π
（4）奇偶性
由sin()sin x x
-=-可知：为奇函数
()cos x cosx -＝sin y x =为偶函数
cos y x =∴正弦曲线关于原点O 对称，余弦曲线关于y 轴对称
（5）单调性
从，的图象上可看出：
sin y x =3,22x ππ⎡⎤∈-⎢⎥⎣⎦当
时，曲线逐渐上升，的值由增大到1。
,22x ππ⎡⎤∈-⎢⎥⎣⎦sin x 1-当
时，曲线逐渐下降，的值由1减小到。
3x ,22ππ⎡⎤∈⎢⎥⎣⎦sin x 1-结合上述周期性可知：
正弦函数在每一个闭区间上都是增函数，其值从增大到1；
2,222k k ππππ⎡⎤-++⎢⎥⎣⎦()k ∈Z 1-在每一个闭区间上都是减函数，其值从1减小到。
32,2()22k k k ππππ⎡⎤++∈⎢⎥⎣⎦Z 1-余弦函数在每一个闭区间上都是增函数，其值从增加到1；在每一[(2k 1),2k ](k )ππ-∈Z 1-个闭区间上都是减函数，其值从1减小到。
[2,(21)]()k k k ππ+∈Z 1-二、讲解范例：
例1：
求使下列函数取得最大值的自变量的集合，并说出最大值是什么。
x （1），；
cos 1y x =+x ∈R （2），。
sin 2y x =x ∈R 解：（1）使函数，取得最大值的x 的集合，就是使函数，cos 1y x =+x ∈R cos y x =x ∈R 取得最大值的的集合。
x {|2,}x x k k π=∈Z 函数，的最大值是。
cos 1y x =+x ∈R 112=＋（2）令，那么必须并且只需，且使函数，取得最大值的2 z x =x ∈R z ∈R y sin z ＝z ∈R z 的集合是|2,2z z k k ππ⎧⎫=+∈⎨⎬⎩
⎭Z 由，
222x z k π
π==+
得4x k π
π
=+即使函数，取得最大值的x 的集合是。
sin 2y x ＝x ∈R |,4x x k k ππ⎧⎫=+∈⎨⎬⎩
⎭Z 函数，的最大值是1。
sin 2y x ＝x ∈R 例2求下列函数的定义域：
（1） （2）1
n 1si x y =+y =解：（1）由，得1sin 0x +≠sin -1
x ≠即
32()2x k k Z ππ≠+∈∴原函数的定义域为3|2,2x x k k ππ⎧⎫≠+∈⎨⎬⎩
⎭Z （2）由得cos 0x ≥22()
22k x k k π
π
ππ-++∈Z ∴原函数的定义域为2,2()22k k k ππππ⎡⎤-++∈⎢⎥⎣
⎦Z 例3求函数的单调区间
cos y x =-
解：由的图象可知：
cos y x =-单调增区间为[2,(21)]()
k k k ππ+∈Z 单调减区间为[(21),2]()
k k k ππ-∈Z 例4求下列三角函数的周期：1．
2． 3．sin 3y x π⎛⎫=+ ⎪⎝⎭y cos 2x =3sin 25x y π⎛⎫=+ ⎪⎝⎭解：1．令而 即：3z x π
=+sin(2)sin z z π+=(2)()
f z f z π+=(2)33f x f x πππ⎡⎤⎛⎫++=+ ⎪⎢⎥⎣⎦⎝
⎭
∴周期2T π
=2．令2z x
=∴()cos 2cos cos(2)cos(22)cos[2()]f x x z z x x πππ===+=+=+即：()()
f x f x π+=∴周期T π
=3．令则25x z π=+4()3sin 3sin(2)3sin 23sin (4)2525x x f x z z f x ππππππ+⎛⎫⎛⎫==+=++=+=+ ⎪ ⎪⎝⎭⎝
⎭∴周期
4T π=三、课堂练习：
1．求下列函数的周期：
（1）
（2） （3）sin 22cos 346y x x ππ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭sin y x =cos 2cos 21y x x x =+-解：（1）
最小正周期1sin 24y x π⎛⎫=+ ⎪⎝⎭1T π=最小正周期22cos 36y x π⎛⎫=- ⎪⎝⎭22T 3
π=∴为，的最小公倍数∴T 1T 2T 2πT π
=（2）T π
=
（3）∴2cos 2y x x =+T π
=2． 直接写出下列函数的定义域、值域：
（1）（2）1
1sin x y +=y =解：（1）当时函数有意义，值域：x 2k 2ππ≠-k ∈Z 1,2
⎡⎤+∞⎢⎥⎣⎦
（2）
()时有意义，值域3x 2k ,2k 22ππππ⎡⎤∈++⎢⎥⎣⎦k ∈Z 3．求下列函数的最值：
（1）
（2）（3）y=sin 314y x π⎛⎫=+- ⎪⎝⎭sin 24sin 5y x x =-+x x cos 3cos 3+-解：（1）当
即 x= ()时3242x k ππ
π+=+1232ππ+k k ∈Z max 0y =当即 ()时3242x k π
π
π+=-234k x ππ-=k ∈Z min 2
y =-（2）()sin 221y x =-+∴当 时22x k π
π=-k ∈Z max 10y =当 时22x k π
π=-k ∈Z min 2
y =（3）当 时1
3c 1os x y +=-+2x k ππ=+k ∈Z max 2
y =当 时
2x k π=k ∈Z 1
min 2y =4．函数的最大值为2，最小值为，求，的值。
sin y k x b =+4-k b 解：当时0k ＞⎩⎨⎧-==⇒⎩⎨⎧-=+-=+1
342b k b k b k 当时（矛盾舍去）∴ 0k ＜⎩⎨⎧-==⇒⎩
⎨⎧-=+=+-1342b k b k b k 3k =1b =-5．求下列函数的定义域：
（1）2）（3）y =()lg 2si n 1y x =++y =解：（1） ∵∴
3cos 12cos 20x x --≥co 112s x ≤≤
∴定义域为： 223()3k k k ππππ⎡-⎤∈⎢⎥⎣
+⎦Z （2）7122sin 662()1cos 22233k x k x k x k x k ππππππ
ππ⎧⎧-<<+>-⎪⎪⎪⎪⇒∈⎨⎨⎪⎪≥-≤≤+⎪
⎪⎩⎩Z 22()63k x k k π
πππ⇒-<≤+
∈Z ∴定义域为：
(2,2)63k k k π
πππ-+∈Z （3）∵
()cos sin 0x ≥∴22()
22k x k k π
π
ππ-≤≤+∈Z ∵1sin 1
x ≤≤∴
x R ∈1y ≤≤。