第二课时 利用导数研究函数的极值、最值

第二课时利用导数研究函数的极值、最值考点一利用导数求函数的极值多维探究角度1根据函数图象判断极值【例1－1】设函数f(x)在R上可导，其导函数为f′(x)，且函数y＝(1－x)f′(x)的图象如图所示，则下列结论中一定成立的是()A.函数f(x)有极大值f(2)和极小值f(1)B.函数f(x)有极大值f(－2)和极小值f(1)C.函数f(x)有极大值f(2)和极小值f(－2)D.函数f(x)有极大值f(－2)和极小值f(2)解析由题图可知，当x<－2时，f′(x)>0；当－2<x<1时，f′(x)<0；当1<x<2时，f′(x)<0；当x>2时，f′(x)>0.由此可以得到函数f(x)在x＝－2处取得极大值，在x＝2处取得极小值.答案 D规律方法由图象判断函数y＝f(x)的极值，要抓住两点：(1)由y＝f′(x)的图象与x 轴的交点，可得函数y＝f(x)的可能极值点；(2)由导函数y＝f′(x)的图象可以看出y ＝f′(x)的值的正负，从而可得函数y＝f(x)的单调性.两者结合可得极值点.角度2已知函数求极值【例1－2】已知函数f(x)＝ln x－ax(a∈R).(1)当a＝12时，求f(x)的极值；(2)讨论函数f(x)在定义域内极值点的个数.解(1)当a＝12时，f(x)＝ln x－12x，函数的定义域为(0，＋∞)且f′(x)＝1x－12＝2－x2x，令f′(x)＝0，得x＝2，于是当x变化时，f′(x)，f(x)的变化情况如下表.x (0，2) 2 (2，＋∞)f ′(x ) ＋0 － f (x )ln 2－1故f (x )极大值(2)由(1)知，函数的定义域为(0，＋∞)， f ′(x )＝1x －a ＝1－ax x .当a ≤0时，f ′(x )>0在(0，＋∞)上恒成立，则函数在(0，＋∞)上单调递增，此时函数在定义域上无极值点； 当a >0时，若x ∈⎝ ⎛⎭⎪⎫0，1a ，则f ′(x )>0，若x ∈⎝ ⎛⎭⎪⎫1a ，＋∞，则f ′(x )<0，故函数在x ＝1a 处有极大值.综上可知，当a ≤0时，函数f (x )无极值点， 当a >0时，函数y ＝f (x )有一个极大值点，且为x ＝1a . 规律方法 运用导数求导函数f (x )极值的一般步骤：(1)确定函数的定义域；(2)求导数f ′(x )；(3)解方程f ′(x )＝0，求出函数定义域内的所有根；(4)列表检验f ′(x )在f ′(x )＝0的根x 0左右两侧值的符号；(5)求出极值. 【训练1】 (1)(角度1)已知函数f (x )的定义域为(a ，b )，导函数f ′(x )在(a ，b )上的图象如图所示，则函数f (x )在(a ，b )上的极大值点的个数为( ) A.1B.2C.3D.4解析 由函数极值的定义和导函数的图象可知，f ′(x )在(a ，b )上与x 轴的交点个数为4，但是在原点附近的导数值恒大于零，故x ＝0不是函数f (x )的极值点.其余的3个交点都是极值点，其中有2个点满足其附近的导数值左正右负，故极大值点有2个.答案 B(2)(角度2)(2019·江苏卷节选)设函数f (x )＝(x －a )(x －b )(x －c )，a ，b ，c ∈R ，f ′(x )为f (x )的导函数.(ⅰ)若a ＝b ＝c ，f (4)＝8，求a 的值；(ⅱ)若a ≠b ，b ＝c ，且f (x )和f ′(x )的零点均在集合{－3，1，3}中，求f (x )的极小值. 解 (ⅰ)因为a ＝b ＝c ，所以f (x )＝(x －a )(x －b )(x －c )＝(x －a )3. 因为f (4)＝8，所以(4－a )3＝8，解得a ＝2.(ⅱ)因为b ＝c ，所以f (x )＝(x －a )(x －b )2＝x 3－(a ＋2b )x 2＋b (2a ＋b )x －ab 2，从而f ′(x )＝3(x －b )·⎝ ⎛⎭⎪⎫x －2a ＋b 3. 令f ′(x )＝0，得x ＝b 或x ＝2a ＋b3.令f (x )＝0，得x ＝a 或x ＝b . 因为a ，b ，2a ＋b3都在集合{－3，1，3}中，且a ≠b ，所以2a ＋b3＝1，a ＝3，b ＝－3.此时，f (x )＝(x －3)(x ＋3)2，f ′(x )＝3(x ＋3)(x －1). 令f ′(x )＝0，得x ＝－3或x ＝1. 当x 变化时，f ′(x )变化如下表：考点二 已知函数的极值求参数【例2】 (2018·北京卷)设函数f (x )＝[ax 2－(4a ＋1)x ＋4a ＋3]e x . (1)若曲线y ＝f (x )在点(1，f (1))处的切线与x 轴平行，求a ； (2)若f (x )在x ＝2处取得极小值，求a 的取值范围. 解 (1)因为f (x )＝[ax 2－(4a ＋1)x ＋4a ＋3]e x ，所以f ′(x )＝[ax 2－(2a ＋1)x ＋2]e x . f ′(1)＝(1－a )e.由题设知f ′(1)＝0，即(1－a )e ＝0，解得a ＝1. 此时f (1)＝3e ≠0. 所以a 的值为1.(2)f ′(x )＝[ax 2－(2a ＋1)x ＋2]e x ＝(ax －1)(x －2)e x . 若a >12，则当x ∈⎝ ⎛⎭⎪⎫1a ，2时，f ′(x )<0；当x ∈(2，＋∞)时，f ′(x )>0. 所以f (x )在x ＝2处取得极小值.若a ≤12，则当x ∈(0，2)时，x －2<0，ax －1≤12x －1<0， 所以f ′(x )>0.所以2不是f (x )的极小值点. 综上可知，a 的取值范围是⎝ ⎛⎭⎪⎫12，＋∞.规律方法 1.已知函数极值，确定函数解析式中的参数时，要注意：根据极值点的导数为0和极值这两个条件列方程组，利用待定系数法求解.2.导数值为0不是此点为极值点的充要条件，所以用待定系数法求解后必须检验. 【训练2】 (2020·滨州模拟)已知x ＝1是f (x )＝[x 2－(a ＋3)x ＋2a ＋3]e x 的极小值点，则实数a 的取值范围是( ) A.(1，＋∞)B.(－1，＋∞)C.(－∞，－1)D.(－∞，1)解析 f ′(x )＝[x 2－(a ＋1)x ＋a ]e x ＝(x －a )(x －1)e x . 令f ′(x )＝0，得(x －a )(x －1)e x ＝0. 设g (x )＝(x －1)(x －a ).(1)当a ＝1时，g (x )≥0，f ′(x )≥0，f (x )没有极值. (2)当a >1时，若x >a 或x <1时，g (x )>0，f ′(x )>0； 若1<x <a 时，g (x )<0，则f ′(x )<0.∴x ＝1是函数f (x )的极大值点，不合题意. (3)当a <1时，若x >1或x <a ，f ′(x )>0， 若a <x <1时，f ′(x )<0.所以x ＝1是f (x )的极小值点，满足题意. 综上所述，实数a 的取值范围是(－∞，1). 答案 D考点三 利用导数求函数的最值典例迁移【例3】 (2019·全国Ⅲ卷)已知函数f (x )＝2x 3－ax 2＋2. (1)讨论f (x )的单调性；(2)(经典母题)当0<a <3时，记f (x )在区间[0，1]的最大值为M ，最小值为m ，求M －m 的取值范围.解 (1)f (x )的定义域为R ，f ′(x )＝6x 2－2ax ＝2x (3x －a ). 令f ′(x )＝0，得x ＝0或x ＝a 3.若a >0，则当x ∈(－∞，0)∪⎝ ⎛⎭⎪⎫a 3，＋∞时，f ′(x )>0，当x ∈⎝ ⎛⎭⎪⎫0，a 3时，f ′(x )<0，故f (x )在(－∞，0)，⎝ ⎛⎭⎪⎫a 3，＋∞单调递增，在⎝ ⎛⎭⎪⎫0，a 3单调递减； 若a ＝0，则f (x )在(－∞，＋∞)单调递增；若a <0，则当x ∈⎝ ⎛⎭⎪⎫－∞，a 3∪(0，＋∞)时，f ′(x )>0，当x ∈⎝ ⎛⎭⎪⎫a 3，0时，f ′(x )<0，故f (x )在⎝ ⎛⎭⎪⎫－∞，a 3，(0，＋∞)单调递增，在⎝ ⎛⎭⎪⎫a 3，0单调递减.(2)当0<a <3时，由(1)知，f (x )在⎝ ⎛⎭⎪⎫0，a 3单调递减，在⎝ ⎛⎭⎪⎫a 3，1单调递增，所以f (x )在[0，1]的最小值为f ⎝ ⎛⎭⎪⎫a 3＝－a 327＋2，最大值为f (0)＝2或f (1)＝4－a .于是m ＝－a 327＋2，M ＝⎩⎨⎧4－a ，0<a <2，2，2≤a <3.所以M －m ＝⎩⎪⎨⎪⎧2－a ＋a 327，0<a <2，a 327，2≤a <3.①当0<a <2时，可知y ＝2－a ＋a 327单调递减， 所以M －m 的取值范围是⎝ ⎛⎭⎪⎫827，2.②当2≤a <3时，y ＝a 327单调递增， 所以M －m 的取值范围是⎣⎢⎡⎭⎪⎫827，1.综上，M －m 的取值范围是⎣⎢⎡⎭⎪⎫827，2.【迁移】 把本例(2)改为“是否存在正实数a ，使得f (x )在[0，1]上的最小值为－2，且最大值为2？若存在，求出实数a 的值；若不存在，说明理由.” 解 假设存在正实数a ，使得f (x )min ＝－2，且f (x )max ＝2. ①若a ≥3时，由例题(1)知，f (x )在[0，1]上是减函数， 当x ∈[0，1]时，f (x )max ＝f (0)＝2，f (x )min ＝f (1)＝4－a . 由题意，必有4－a ＝－2，则a ＝6.②若0<a <3时，由例题第(2)问知，f (x )在[0，1]的最小值f ⎝ ⎛⎭⎪⎫a 3＝2－a 327，最大值为2或4－a .由2－a 327＝－2，得a ＝334>3，与0<a <3矛盾.综上，存在正数a ＝6时，f (x )在[0，1]的最小值为－2，最大值为2. 规律方法 1.利用导数求函数f (x )在[a ，b ]上的最值的一般步骤：(1)求函数在(a ，b )内的极值；(2)求函数在区间端点处的函数值f (a )，f (b )；(3)将函数f (x )的各极值与f (a )，f (b )比较，其中较大的一个为最大值，较小的一个为最小值.2.研究含参数的最值，必要时要进行分类讨论.如本例迁移中，分类讨论的标准是单调区间的端点与0，1的大小关系，从而确定函数在[0，1]上的最值. 【训练3】 已知函数f (x )＝ax ＋ln x ，其中a 为常数. (1)当a ＝－1时，求f (x )的最大值；(2)若f (x )在区间(0，e]上的最大值为－3，求a 的值. 解 (1)易知f (x )的定义域为(0，＋∞)，当a ＝－1时，f (x )＝－x ＋ln x ，f ′(x )＝－1＋1x ＝1－xx ， 令f ′(x )＝0，得x ＝1.当0<x <1时，f ′(x )>0；当x >1时，f ′(x )<0.∴f (x )在(0，1)上是增函数，在(1，＋∞)上是减函数. ∴f (x )max ＝f (1)＝－1.∴当a ＝－1时，函数f (x )在(0，＋∞)上的最大值为－1. (2)f ′(x )＝a ＋1x ，x ∈(0，e]，1x ∈⎣⎢⎡⎭⎪⎫1e ，＋∞.①若a ≥－1e ，则f ′(x )≥0，从而f (x )在(0，e]上是增函数， ∴f (x )max ＝f (e)＝a e ＋1≥0，不合题意.②若a <－1e ，令f ′(x )>0得a ＋1x >0，结合x ∈(0，e]，解得0<x <－1a ； 令f ′(x )<0得a ＋1x <0，结合x ∈(0，e]，解得－1a <x ≤e. 从而f (x )在⎝ ⎛⎭⎪⎫0，－1a 上为增函数，在⎝ ⎛⎦⎥⎤－1a ，e 上为减函数，∴f (x )max ＝f ⎝ ⎛⎭⎪⎫－1a ＝－1＋ln ⎝ ⎛⎭⎪⎫－1a .令－1＋ln ⎝ ⎛⎭⎪⎫－1a ＝－3，得ln ⎝ ⎛⎭⎪⎫－1a ＝－2，即a ＝－e 2.∵－e 2<－1e ，∴a ＝－e 2为所求. 故实数a 的值为－e 2.A 级 基础巩固一、选择题1.函数y ＝x e x 的最小值是( ) A.－1B.－eC.－1eD.不存在解析 因为y ＝x e x ，所以y ′＝e x ＋x e x ＝(1＋x )e x ，当x >－1时，y ′>0；当x <－1时，y ′<0，所以当x ＝－1时，函数取得最小值，且y min ＝－1e . 答案 C2.(2020·德州模拟)设函数f (x )在R 上可导，其导函数为f ′(x )，且函数f (x )在x ＝－2处取得极小值，则函数y ＝x ·f ′(x )的图象可能是( )解析 ∵函数f (x )在R 上可导，其导函数为f ′(x )， 且函数f (x )在x ＝－2处取得极小值，当x >－2时，f ′(x )>0；当x ＝－2时，f ′(x )＝0； 当x <－2时，f ′(x )<0.∴当x >0时，xf ′(x )>0；当－2<x <0时，xf ′(x )<0； 当x ＝－2或0时，xf ′(x )＝0；当x <－2时，xf ′(x )>0. 因此y ＝xf ′(x )的图象应为选项C. 答案 C3.(2017·全国Ⅱ卷)若x ＝－2是函数f (x )＝(x 2＋ax －1)·e x －1的极值点，则f (x )的极小值为( ) A.－1B.－2e －3C.5e －3D.1解析 f ′(x )＝[x 2＋(a ＋2)x ＋a －1]·e x －1，则f ′(－2)＝[4－2(a ＋2)＋a －1]·e －3＝0⇒a ＝－1， 则f (x )＝(x 2－x －1)·e x －1，f ′(x )＝(x 2＋x －2)·e x －1， 又e x －1>0恒成立，令f ′(x )＝0，得x ＝－2或x ＝1， 当x <－2或x >1时，f ′(x )>0；当－2<x <1时，f ′(x )<0， 所以x ＝1是函数f (x )的极小值点， 则f (x )极小值为f (1)＝－1. 答案 A4.(2020·湘潭模拟)已知函数f (x )＝2e f ′(e)ln x －x e (e 是自然对数的底数)，则f (x )的极大值为( ) A.2e －1B.－1eC.1D.2ln 2解析 由题意知f ′(x )＝2e f ′（e ）x －1e ，∴f ′(e)＝2e f ′（e ）e －1e ，f ′(e)＝1e ， ∴f ′(x )＝2x －1e ，令f ′(x )＝0，得x ＝2e.∴f (x )在(0，2e)上递增，在(2e ，＋∞)上递减， ∴f (x )的极大值为f (2e)＝2ln(2e)－2＝2ln 2. 答案 D5.若函数f (x )＝12x 2＋(a －1)x －a ln x 存在唯一的极值，且此极值不小于1，则a 的取值范围为( ) A.⎣⎢⎡⎭⎪⎫32，2B.⎣⎢⎡⎭⎪⎫32，＋∞C.⎣⎢⎡⎭⎪⎫0，32D.(－1，0)∪⎣⎢⎡⎭⎪⎫32，＋∞解析 对函数求导f ′(x )＝x －1＋a ⎝ ⎛⎭⎪⎫1－1x ＝（x ＋a ）（x －1）x ，令f ′(x )＝0，解得x＝1或x ＝－a .因为函数f (x )＝12x 2＋(a －1)x －a ln x 存在唯一的极值，所以x ＝1，此时a ≥0.所以当x ∈(0，1)时，f ′(x )<0，函数f (x )单调递减；当x ∈(1，＋∞)时，f ′(x )>0，函数f (x )单调递增，所以f (x )的极小值为f (1)＝12＋a －1＝a －12，故f (1)≥1，即a －12≥1，解得a ≥32. 答案 B 二、填空题6.若商品的年利润y (万元)与年产量x (百万件)的函数关系式为y ＝－x 3＋27x ＋123(x >0)，则获得最大利润时的年产量为________百万件.解析 y ′＝－3x 2＋27＝－3(x ＋3)(x －3)，当0<x <3时，y ′>0；当x >3时，y ′<0. 故当x ＝3时，该商品的年利润最大. 答案 37.(2020·安徽江南十校联考)已知x ＝1是函数f (x )＝(x 2＋ax )e x 的一个极值点，则曲线y ＝f (x )在点(0，f (0))处的切线斜率为________. 解析 由f (x )＝(x 2＋ax )e x ，得f ′(x )＝(x 2＋ax ＋2x ＋a )e x ， 因为x ＝1是函数f (x )＝(x 2＋ax )e x 的一个极值点， 所以f ′(1)＝(3＋2a )e ＝0，解得a ＝－32. ∴f ′(x )＝⎝ ⎛⎭⎪⎫x 2＋12x －32e x ，所以f ′(0)＝－32.所以曲线f (x )在点(0，f (0))处的切线斜率为－32. 答案 －328.(2020·昆明诊断)直线y ＝b 分别与直线y ＝2x ＋1和曲线y ＝ln x 相交于点A ，B ，则|AB |的最小值为________.解析 设两个交点分别为A ⎝ ⎛⎭⎪⎫b －12，b，B (e b ，b )， 则|AB |＝e b－b －12.令g (x )＝e x－x －12，则g ′(x )＝e x －12.由g ′(x )＝0，得x ＝－ln 2.所以g (x )在区间(－∞，－ln 2)单调递减，在区间(－ln 2，＋∞)上单调递增， ∴g (x )min ＝g (－ln 2)＝1＋ln 22. 答案 1＋ln 22 三、解答题9.已知函数f (x )＝e x cos x －x .(1)求曲线y ＝f (x )在点(0，f (0))处的切线方程； (2)求函数f (x )在区间⎣⎢⎡⎦⎥⎤0，π2上的最大值和最小值.解 (1)因为f (x )＝e x cos x －x ，所以f ′(x )＝e x (cos x －sin x )－1，f ′(0)＝0. 又因为f (0)＝1，所以曲线y ＝f (x )在点(0，f (0))处的切线方程为y ＝1. (2)设h (x )＝e x (cos x －sin x )－1则h ′(x )＝e x (cos x －sin x －sin x －cos x )＝－2e x sin x . 当x ∈⎝ ⎛⎭⎪⎫0，π2时，h ′(x )<0，所以h (x )在区间⎣⎢⎡⎦⎥⎤0，π2上单调递减，所以对任意x ∈⎝ ⎛⎦⎥⎤0，π2有h (x )<h (0)＝0，即f ′(x )<0，所以函数f (x )在区间⎣⎢⎡⎦⎥⎤0，π2上单调递减，因此f (x )在区间⎣⎢⎡⎦⎥⎤0，π2上的最大值为f (0)＝1，最小值为f ⎝ ⎛⎭⎪⎫π2＝－π2. 10.(2020·武汉质检)已知函数f (x )＝⎩⎨⎧－x 3＋x 2，x <1，a ln x ，x ≥1.(1)求f (x )在区间(－∞，1)上的极小值和极大值点； (2)求f (x )在[－1，e](e 为自然对数的底数)上的最大值. 解 (1)当x <1时，f ′(x )＝－3x 2＋2x ＝－x (3x －2)， 令f ′(x )＝0，解得x ＝0或x ＝23.当x 变化时，f ′(x )，f (x )的变化情况如下表：函数f (x )的极大值点为x ＝23.(2)①当－1≤x <1时，由(1)知，函数f (x )在[－1，0]和⎣⎢⎡⎭⎪⎫23，1上单调递减，在⎣⎢⎡⎦⎥⎤0，23上单调递增.因为f (－1)＝2，f ⎝ ⎛⎭⎪⎫23＝427，f (0)＝0，所以f (x )在[－1，1)上的最大值为2. ②当1≤x ≤e 时，f (x )＝a ln x ， 当a ≤0时，f (x )≤0：当a >0时，f (x )在[1，e]上单调递增， 则f (x )在[1，e]上的最大值为f (e)＝a .故当a ≥2时，f (x )在[－1，e]上的最大值为a ； 当a <2时，f (x )在[－1，e]上的最大值为2.B 级 能力提升11.若函数y ＝f (x )存在n －1(n ∈N *)个极值点，则称y ＝f (x )为n 折函数，例如f (x )＝x 2为2折函数.已知函数f (x )＝(x ＋1)e x －x (x ＋2)2，则f (x )为( ) A.2折函数 B.3折函数 C.4折函数D.5折函数解析 f ′(x )＝(x ＋2)e x －(x ＋2)(3x ＋2) ＝(x ＋2)(e x －3x －2)，令f ′(x )＝0，得x ＝－2或e x ＝3x ＋2. 易知x ＝－2是f (x )的一个极值点，又e x ＝3x ＋2，结合函数图象，y ＝e x 与y ＝3x ＋2有两个交点. 又e －2≠3×(－2)＋2＝－4.所以函数y ＝f (x )有3个极值点，则f (x )为4折函数. 答案 C12.(2020·石家庄检测)若函数f (x )＝(1－x )(x 2＋ax ＋b )的图象关于点(－2，0)对称，x 1，x 2分别是f (x )的极大值点与极小值点，则x 2－x 1＝( ) A.－ 3B.2 3C.－2 3D. 3解析 不妨假设点(－2，0)在f (x )图象上， 则f (－2)＝3(4－2a ＋b )＝0，因为函数图象关于点(－2，0)对称，且f (1)＝0， 所以f (－5)＝0，即f (－5)＝6(25－5a ＋b )＝0， 联立⎩⎪⎨⎪⎧b －2a ＋4＝0，b －5a ＋25＝0，解得⎩⎪⎨⎪⎧b ＝10，a ＝7.故f (x )＝(1－x )(x 2＋7x ＋10)＝－x 3－6x 2－3x ＋10， 则f ′(x )＝－3x 2－12x －3＝－3(x 2＋4x ＋1)， 由于x 1，x 2分别是f (x )的极大值点与极小值点.∴x1，x2是f′(x)的零点，则x1＋x2＝－4，x1x2＝1.从而x1<0，x2<0，且x1>x2.因此x2－x1＝－（x1＋x2）2－4x1x2＝－2 3.答案 C13.传说中孙悟空的“如意金箍棒”是由“定海神针”变形得来的.这定海神针在变形时永远保持为圆柱体，其底面半径原为12 cm且以每秒1 cm等速率缩短，而长度以每秒20 cm等速率增长.已知神针的底面半径只能从12 cm缩到4 cm，且知在这段变形过程中，当底面半径为10 cm时其体积最大.假设孙悟空将神针体积最小时定形成金箍棒，则此时金箍棒的底面半径为________ cm.解析设神针原来的长度为a cm，t秒时神针的体积为V(t) cm3，则V(t)＝π(12－t)2·(a＋20t)，其中0≤t≤8，所以V′(t)＝[－2(12－t)(a＋20t)＋(12－t)2·20]π.因为当底面半径为10 cm时其体积最大，所以10＝12－t，解得t＝2，此时V′(2)＝0，解得a＝60，所以V(t)＝π(12－t)2·(60＋20t)，其中0≤t≤8.V′(t)＝60π(12－t)(2－t)，当t∈(0，2)时，V′(t)>0，当t∈(2，8)时，V′(t)<0，从而V(t)在(0，2)上单调递增，在(2，8)上单调递减，V(0)＝8 640π，V(8)＝3 520π，所以当t＝8时，V(t)有最小值3 520π，此时金箍棒的底面半径为4 cm.答案 414.(2019·北京卷)已知函数f(x)＝14x3－x2＋x.(1)求曲线y＝f(x)的斜率为1的切线方程；(2)当x∈[－2，4]时，求证：x－6≤f(x)≤x.(3)设F(x)＝|f(x)－(x＋a)|(a∈R)，记F(x)在区间[－2，4]上的最大值为M(a).当M(a)最小时，求a的值.(1)解由f(x)＝14x3－x2＋x，得f′(x)＝34x2－2x＋1.令f′(x)＝1，即34x2－2x＋1＝1，得x＝0或x＝83.又f (0)＝0，f ⎝ ⎛⎭⎪⎫83＝827，所以曲线y ＝f (x )的斜率为1的切线方程是y ＝x 与y －827＝x －83，即y ＝x 与y ＝x －6427.(2)证明 令g (x )＝f (x )－x ，x ∈[－2，4]. 由g (x )＝14x 3－x 2得g ′(x )＝34x 2－2x . 令g ′(x )＝0得x ＝0或x ＝83.当x 变化时，g ′(x )，g (x )的变化情况如下：故－6≤g (x )≤0，即x －6≤f (x )≤x . (3)解 由第(2)问知，当a <－3时，M (a )≥F (0)＝|g (0)－a |＝－a >3； 当a >－3时，M (a )≥F (－2)＝|g (－2)－a |＝6＋a >3； 当a ＝－3时，M (a )＝3； 综上，当M (a )最小时，a ＝－3.C 级 创新猜想15.(多选题)对于函数f (x )＝xe x ，下列说法正确的有( ) A.f (x )在x ＝1处取得极大值1e B.f (x )有两个不同的零点 C.f (4)＜f (π)＜f (3) D.πe 2＞2e π解析 由函数f (x )＝xe x ，可得函数f (x )的导数为f ′(x )＝1－x e x .当x ＞1时，f ′(x )＜0，f (x )单调递减；当x ＜1时，f ′(x )＞0，f (x )单调递增.可得函数f (x )在x ＝1处取得极大值1e ，且为最大值，所以A 正确；因为f (x )在(－∞，1)上单调递增，在(1，＋∞)上单调递减，且f (0)＝0，当x ＞0时，f (x )＞0恒成立，所以函数f (x )只有一个零点，所以B 错误；由f (x )在(1，＋∞)上单调递减，且4＞π＞3＞1，可得f (4)＜f (π)＜f (3)，所以C 正确；由f (x )在(1，＋∞)上单调递减，且π＞2＞1，可得πe π＜2e 2，即πe 2＜2e π，所以D 错误.故选AC. 答案 AC16.(多填题)设函数f (x )＝⎩⎨⎧x 3－3x ，x ≤a ，－2x ，x >a .(1)若a ＝0，则f (x )的最大值为________；(2)若f (x )无最大值，则实数a 的取值范围是________.解析 (1)若a ＝0，则f (x )＝⎩⎪⎨⎪⎧x 3－3x ，x ≤0，－2x ，x >0.当x >0时，f (x )＝－2x <0；当x ≤0时，f ′(x )＝3x 2－3＝3(x －1)(x ＋1)， 当x <－1时，f ′(x )>0，f (x )是增函数； 当－1<x <0时，f ′(x )<0，f (x )是减函数， ∴f (x )≤f (－1)＝2.∴f (x )的最大值为2.(2)在同一平面直角坐标系中画出y ＝－2x 和y ＝x 3－3x 的图象，如图所示，当a <－1时，f (x )无最大值； 当－1≤a ≤2时，f (x )max ＝2； 当a >2时，f (x )max ＝a 3－3a .综上，当a∈(－∞，－1)时，f(x)无最大值.答案(1)2(2)(－∞，－1)。

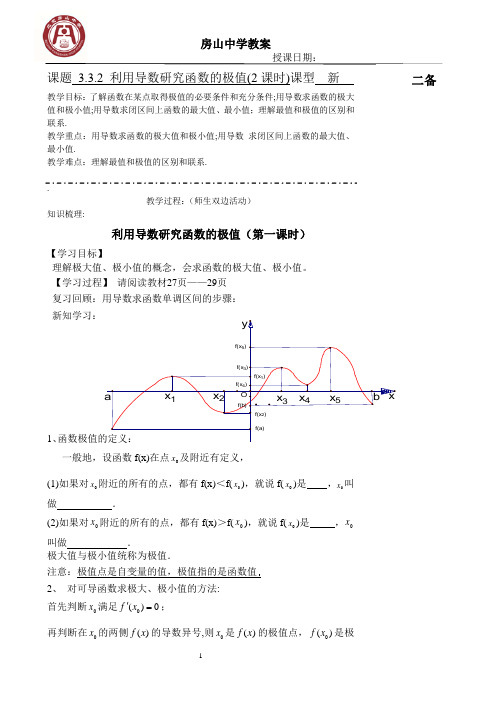
f(x 2)f(x 4)f(x 5)f(x 3)f(x 1)f(b)f(a)x 5x 4x 3x 2x 1b a xOy课题 3.3.2 利用导数研究函数的极值(2课时)课型 新 教学目标：了解函数在某点取得极值的必要条件和充分条件;用导数求函数的极大值和极小值;用导数求闭区间上函数的最大值、最小值；理解最值和极值的区别和联系.教学重点：用导数求函数的极大值和极小值;用导数 求闭区间上函数的最大值、最小值.教学难点：理解最值和极值的区别和联系. .教学过程：（师生双边活动）知识梳理:利用导数研究函数的极值（第一课时）【学习目标】理解极大值、极小值的概念，会求函数的极大值、极小值。

【学习过程】 请阅读教材27页——29页 复习回顾：用导数求函数单调区间的步骤： 新知学习：1、函数极值的定义：一般地，设函数f(x)在点0x 及附近有定义，(1)如果对0x 附近的所有的点，都有f(x)＜f(0x )，就说f(0x )是 ，0x 叫做．(2)如果对0x 附近的所有的点，都有f(x)＞f(0x )，就说f(0x )是 ，0x 叫做 ．极大值与极小值统称为极值．注意：极值点是自变量的值，极值指的是函数值2、 对可导函数求极大、极小值的方法: 首先判断0x 满足0()0f x '=；再判断在0x 的两侧()f x 的导数异号,则0x 是()f x 的极值点，0()f x 是极二备值.(1)如果()f x '在0x 两侧满足“左正右负”，则0x x =是()f x 的 ，0()f x 是 ；(2)如果()f x '在0x 两侧满足“左负右正”，则0x x =是()f x 的 ，0()f x 是例1、已知函数y=13x 3－4x+4(1)求函数的单调区间；(2)求函数的极值，并画出大致图像.例2、求函数34()13f x x x =-++的极值。

归纳：求可导函数f(x)的极值的步骤:(1)确定函数的定义域， (2)求导数f ′(x)，(3)求方程f ′(x)=0的根，(4)列表，判断各区间导数的符号，确定极值.例3、已知函数32()f x ax bx cx =++在点0x 处取得极大值5， 其导函数()y f x '=的图象经过点(1,0)，(2,0)，如图所示， 求 (1) 0x 的值(2)a ，b ，c 的值.xo12 yf(x 2)f(x 4)f(x 5)f(x 3)f(x 1)f(b)f(a)x 5x 4x 3x 2x 1b a xO y练习1：函数f （x ）是（a ，b ）上的可导函数，下列是关于f （x ）的极值的几种说法，判断它们的正误：（1）函数的极值点一定在区间的内部，区间的端点不能成为极值点。

利用导数研究函数的极值和最值问题１．利用导数研究函数的极值的一般步骤：（１）确定函数的定义域．（２）求)(x f '．（３）①若求极值，则先求方程 0)(='x f 的全部实根，再检验)(x f '在方程根的左右两侧值的符号，求出极值．（当根中有参数时，要注意讨论根是否在定义域内）②若已知极值大小或存在情况，则转化为已知方程 0)(='x f 的根的大小或存在情况，从而求解．２．求连续函数)(x f y =在[]b a , 上的最大值与最小值的步骤：（１）求函数 )(x f y =在()b a ,内的极值；（２）将函数 )(x f y =的各极值与端点处的函数值 )(a f ， )(b f 比较，其中最大的一个是最大值，最小的一个是最小值.例1.(2018北京,18,13分)设函数()[]x e a x a ax x f 3414)(2+++-=. (1)若曲线)(x f y =在点()()1,1f 处的切线与x 轴平行,求a ;(2)若)(x f 在2=x 处取得极小值,求a 的取值范围.解析 (1)因为()[]x e a x a ax x f 3414)(2+++-=, 所以()[]x e x a ax x f 212)(2++-='，()e a f -='1)1(. 由题设知f '(1)=0,即()01=-e a ,解得1=a .此时03)1(≠=e f .所以a 的值为1.(2)由(1)得()[]()()x x e x ax e x a ax x f 21212)(2--=++-='. 若21>a ,则当⎪⎭⎫ ⎝⎛∈2,1a x 时0)(<'x f ; 当()+∞∈,2x 时,0)(>'x f .所以)(x f 在2=x 处取得极小值. 若21<a ,则()2,0∈x 时,02<-x ,01211<-≤-x ax ,所以0)(>'x f , 所以2不是)(x f 的极小值点.综上可知,a 的取值范围是⎪⎭⎫ ⎝⎛∞+，21。

利用导数研究函数的极值最值导数是研究函数的极值、最值的重要工具之一、通过计算函数的导数，我们可以找到函数的临界点，进而确定函数的极值和最值。

极值是函数在定义域内取得的最大值或最小值。

极大值是函数在其中一点上取得的最大值，极小值是函数在其中一点上取得的最小值。

首先，我们可以通过计算函数的导数来找到函数的临界点。

临界点是函数导数等于0的点，也包括导数不存在的点。

然后，通过进一步的分析，可以确定临界点中的极值点。

假设函数f(x)在区间[a,b]上连续且可导。

首先，我们需要计算函数f(x)的导数f'(x)。

然后，我们找出导数f'(x)等于0的点，这些点就是函数f(x)的临界点。

接下来，我们进一步分析导数f'(x)的符号。

在临界点两侧，如果导数f'(x)由正变负，则表明在该点上函数f(x)取得极大值；如果导数f'(x)由负变正，则表明在该点上函数f(x)取得极小值。

当然，也可能存在导数f'(x)不存在的点，这些点也是函数的临界点。

最值是函数在定义域内取得的最大值或最小值。

最大值是函数在定义域内所有点上取得的最大值，最小值是函数在定义域内所有点上取得的最小值。

通过求解函数的导数，我们可以找到函数的临界点。

然后，通过分析函数在临界点、定义域的边界点和导数不存在的点上的取值，可以确定函数的最值。

当函数在闭区间[a,b]上连续时，最大值和最小值一定在定义域的边界点上或者在临界点上取得。

因此，在求解函数最值时，我们需要计算函数在闭区间的端点上的取值，并将其和临界点上的取值相比较。

需要注意的是，导数仅能帮助我们找到函数的临界点，但临界点未必都是极值点。

为了判断极值点是否为极大值或极小值，我们还需要进行二阶导数测试。

如果二阶导数大于0，则表示该点为极小值；如果二阶导数小于0，则表示该点为极大值；如果二阶导数等于0，则需要进行其他方法的分析。

总之，利用导数研究函数的极值、最值是一种有效的方法。

导数及其应用 利用导数研究函数的极值最值 课件 理 ppt xx年xx月xx日contents •导数及其应用•利用导数研究函数的极值最值•课件制作技巧•案例分析•导数的进一步学习与拓展目录01导数及其应用1导数的定义23导数是函数在某一点的变化率，它描述了函数在某一点的斜率。

导数的定义导数的几何意义是函数在某一点的切线斜率。

导数的几何意义导数的物理意义是速度的变化率，即物体运动的速度在某一时刻的变化率。

导数的物理意义导数的计算根据导数的定义，通过求极限来计算导数。

定义法公式法表格法图像法利用导数的运算法则和公式来计算导数。

利用导数表来计算导数。

利用函数图像来估计导数。

最优问题导数可以帮助我们找到最优解，例如在经济学、工程学等领域中，利用导数可以找到最优的成本、价格、利润等。

导数在实际问题中的应用运动问题导数可以描述物体的运动状态，例如速度、加速度等，利用导数可以解决运动问题，例如计算轨迹、碰撞时间等。

物理问题导数可以描述物理现象的变化规律，例如温度、压力、电流等，利用导数可以解决物理问题，例如计算热传导、弹性力学等。

02利用导数研究函数的极值最值极值的定义：设函数$f(x)$在点$x_{0}$的附近有定义。

若在$x_{0}$的左侧$f(x)$单调递增。

在$x_{0}$的右侧$f(x)$单调递减定义法：判断导数由正变负的点，这些点为可能极值点，再检验这些点两侧的导数值，确定是否为极值点。

表格法：通过列表计算函数在各点的导数值，并判断其正负，从而得到极值点。

极值的判定方法极值的概念及判定方法最值的定义及求法最值的定义：函数在某区间内取得最大（小）值的点称为最值点。

对于连续函数，还可以利用介值定理求解最值。

最值的求法利用定义法或表格法求极值点，然后比较极值与端点函数值的大小关系，从而得到最值。

1导数在极值最值问题中的综合应用23导数在极值最值问题中的应用非常广泛，例如在经济、物理、工程等领域都有应用。