巧思妙解题

一元一次方程之巧思妙解
解一元一次方程的通常步骤是去分母、去括号、移项、合并同类项、把系数化为1.但是对于有些具备特殊性的一元一次方程，我们完全可以打破常规，灵活、巧妙地变通解题步骤，避繁就简，使解题过程简捷明了. 下面介绍几种技巧，供同学们参考.
一、巧去括号
分析：如果按例1使括号前的系数依次相乘，解题过程会变得非常复杂.这时要充分利用方程特点，将方程两边同乘以或除以某数，是括号前的系数变成1，从而去掉括号.
解：方程两边同乘以3，去掉大括号，然后
二、巧拆项
分析：观察方程的特点，可先将每个含有分母的多项式拆开，分类合并，可简化过程.
分析：观察各项未知数的系数和常数
三、巧换元
分析：将（x-1）看成一个整体，用换元法，可大大简化运算.
四、巧用分式的基本性质
分析：若直接去分母较繁，观察本题可先用分数的基本性质，使化分数和去分母一次到位，从而避免了繁杂的运算.
五、巧分组通分
分析：观察四个分母的数字特点，采用移项后分组通分，即将分母是21和14的两项放在一组，另外两项成一组，可巧解方程.
分析：注意到左边的第一项和右边的第二项中的分母有公约数3，左边的第二项和右边的第一项中的分母有公约数4，移项局部通分，可简化解题过程.。

巧思妙解
在“图形变换”这一单元里，我们利用旋转图形，绘制出了很多很美的图案，让我们赏心悦目。

其实，在解决一些比较难的题时，利用旋转的知识，将图形进行变换，会使很复杂的题，变得非常容易。

【趣题点击】
用一张斜边长为29的红色直角三角形纸片，
一张斜边长为49的蓝色直角三角形纸片，
一张黄色的正方形纸片，如图所示拼成一个
直角三角形。

问红、蓝两张三角形纸片面积
之和是多少
【解题锦囊】
这道题乍一看好像缺少条件，每个三角形只告诉一个条件是绝对不能求出它的面积的。

但是，只要我们认真分析这道题的问题，它为什么要我们求蓝色与红色的和呢？是不是蓝色的面积与红色的面积有什么联系？想想它为什么要告诉我们黄色的是正方形，于是，我们很快就能找到
蓝色的与红色的它们的联系，就是它们分别有一
条直角边是一样长的。

然后，利用我们学过的旋
转知识，将红色的三角形绕A 点旋转，如右图，
这时，蓝色与红色三角形的面积之和就是一个大
三角形了，它的面积是：29×49÷2＝710.5
知道了利用旋转解题很重要吧。

那就试试。

两个边长为2cm 的正方形，其中一个的顶点在另一个的中心上如下图，求这两个正方形不重合部分的面积和。

（提示：图中两个阴影部分的面积相等。

）
49 29。

方法点击巧联想 妙解题江苏 孙洲一、由角平分线联想到距离相等例1 如图1，在△ABC 中，∠BCA 的平分线与AB 边的垂直平分线DG 相交于点D ，DE ⊥AC ，DF ⊥BC ，垂足分别为E ，F ，求证：AE=BF .图1分析：由DC 是∠BCA 的平分线，可得DE=DF.要证AE=BF ，只需连接AD ，BD ，根据线段垂直平分线的性质定理得到AD=BD ，证明Rt △ADE ≌Rt △BDF ．证明：如图1，连接AD ，BD.因为CD 平分∠BCA ，DE ⊥AC ，DF ⊥BC ，所以DE=DF .因为DG 是AB 的垂直平分线，所以DA=DB.在Rt △ADE 和Rt △BDF 中，DA=DB ，DE=DF ，所以Rt △ADE ≌Rt △BDF .所以AE=BF .二、由距离相等联想到角平分线例2 如图2，在△ABC 中，∠ACB=60°，D 为AC 的中点，延长BC 至E ，使CE=CD ，以DE 为边作等边三角形EDF ，连接AF ，求证：AF ∥BC.F E DC BA图2分析：由∠ACB=60°，CE=CD ，根据三角形内角和定理的推论及等腰三角形的性质求出∠CED=∠CDE=30°.再结合等边三角形的性质得到FD ⊥AC ，FE ⊥CE.由已知FD=FE ，则联想到CF 是∠ACE 的平分线.连接CF ，得∠FCA=60°.要使AF ∥BC ，只需∠FAC=60°.由FD 垂直平分AC ，根据线段垂直平分线的性质及等腰三角形的性质得到∠FAC=∠FCA= 60°.证明：连接CF.因为∠ACB=60°，CE=CD ，所以CED=∠CDE=30°.因为△EDF 是等边三角形，所以DE=EF=DF ，∠FDE=∠DEF=∠EFD=60°.所以∠CDF=∠CEF=90°，即FD ⊥AC ，FE ⊥CE.所以CF 平分∠ACE.所以∠DCF=21∠ACE=21（180°-∠ACB ）=60°. 因为D 为AC 的中点，所以AD=CD.又FD ⊥AC ，所以FA=FC.所以∠FAD=∠FCD=60°.所以∠FAC=∠ACB.所以AF ∥BC.。

第十一届海门之窗杯“巧思妙解”玩数学竞赛四年级试题含答案work Information Technology Company.2020YEAR第十一届海门之窗杯“巧思妙解”玩数学竞赛四年级模拟试题准考证号码姓名得分指导老师一、填空题：(每空3分，12小空，共36分）1.按规律填上适当的数。

5，2，8，4，12，8，17，16，（），（）。

2.几个同学交流自己家的门牌号，前六位同学家的门牌号分别是301，402，607，113，736，223。

小梅发现她家的门牌号与前面每个门牌号恰好在同一数位有一个相同的数字。

你知道小梅家的门牌号是（）。

3. 在一个减法算式里，被减数、减数与差的和是180，而差比减数少8.如果被减数不变，减数减少16，差应变（）。

4.小明在计算两位数乘两位数时，把一个因数的个位数6错写成9，结果得936，实际应为864。

这两个因数各是（）和（）。

5.小刚五次考试的平均成绩为93分（满分为100分），那么他每次考试的分数不得低于（）分。

6. 小明做错题时，把被减数百位上的3错写成8，把减数十位上的9错写成6，这样算得的差是806.正确答案是（）。

7. 一个等差数列的第5项是21，第8项是63，那么它的第14项是（）。

8.如图，已知大正方形的边长为4，小正方形的边长为3，那么阴影部分的面积为（）。

9.二进制数10110改写为十进制数为（）。

10.在四年级的100个学生中，68人订阅了《小学生数学报》，76人订阅了《小学生语文报》，其中仅订《小学生数学报》的有10人，则这100个学生中仅订《小学生语文报》的有（）人。

二、选择题：(每小题3分，5小题，共15分）1. 有两袋糖，一袋有71粒，另一袋有39粒，每次从多的一袋中拿出4粒放入少的一袋里，拿（）次才能使两袋糖数目同样多。

A. 36B.8C. 6D.42. 有一位工人把长18米的圆钢锯成了3米长的小段，锯断一次需4分钟，共需要（）分钟。

第15届“海门之窗网”杯小学生巧思妙解玩数学模拟卷一年级试卷姓名 准考证号 得分一、填空题。

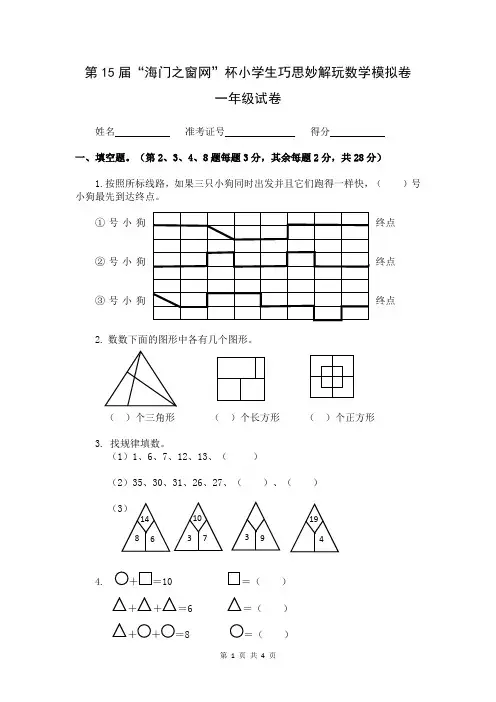
（第2、3、4、8题每题3分，其余每题2分，共28分）1.按照所标线路，如果三只小狗同时出发并且它们跑得一样快，（ ）号小狗最先到达终点。

①号小狗 终点 ②号小狗 终点 ③号小狗 终点2. 数数下面的图形中各有几个图形。

（ ）个三角形 （ ）个长方形 （ ）个正方形3. 找规律填数。

（1）1、6、7、12、13、（ ）（2）35、30、31、26、27、（ ）、（ ）（3）4. ＋＝10 ＝（ ）＋＋＝6 ＝（ ）＋＋＝8 ＝（ ）1943 9 10 3 7 14 8 61 1 ? 5.傍晚小红在灯下做作业时突然停电了，小红拉了五下开关，爸爸回来后又拉了三下开关。

等来电以后，小红房间的灯是（ ）的。

（填写“亮”或“不亮”）。

6.时钟在2点钟敲2下，2秒敲完；4点钟敲4下，（ ）秒敲完。

7. 如图，每个正方体的六个面上分别写着1～6这六个数字，并且任意两个相对的面上所写的两个数字之和都等于7，相连的两个数字之和都等于8。

图中打“？”的这个面上所写的数字是（ ）。

8. 在所给的数之间，填上“＋”“－”或“（ ）”，使等式成立。

（1）8 3 4 ＝ 9（2）4 4 4 4 ＝ 0（3）7 2 1 ＝ 89.小明的文具盒中有铅笔4支，钢笔3支，至少拿出（ ）支就能确保有2支是一样的。

10.把1、2、3、4、5、6、7、8这八个数分别填入□里（每个数只能用一次），使等式成立。

11. 公园到城堡有两条路，从城堡到森林动物园有四条路，从公园经过城堡到森林动物园有（ ）种不同的走法。

12. 鸡、兔关在同一个笼子里，共有10个头，28条腿，笼子里有（ ）只鸡，（ ）只兔。

二、实践与探索。

(每题6分，共24分)13. 只移动一根火柴棒，使下面算式成立。

（1）移动后的算式是（ ）⑥ 森林动物园 公园 ⑤ ① ④ ② 城堡 ③（2） 移动后的算式是（ ）14.把1、2、3、4、5、6、7这七个数填在右图的七个Ο里（每个数只能用一次），使每条直线上三个数相加的和都等于12。

小学二年级数学应用题（巧思妙解）1、一群小朋友在游乐场里划船，原有28人，走里5人又来了17人，现在有多少人？2、仓库里有一些水泥，用去26包，又运来45包，现在仓库里有水泥93包。

仓库里原来有多少包？3、一辆公交车里原有27人，到站点后下去6人，又上来13人，现在车上有多少人？4、广场上插的红旗比黄旗多22面，红旗再添14面，黄旗再添18面，现在哪种旗多？多多少面？5、公园里原来的杨树比柳树少13科，今年植树节那天，又栽了18棵杨树和15棵柳树，现在杨树和柳树哪个多？多多少棵？6、水果店原来苹果比梨树多7筐，又运来12筐和一些苹果，现在苹果还比梨多4筐，又运来了多少筐苹果？7、有三根铁丝，第一根比第二根长10厘米，第二根比第三根短5厘米，已知第三根长15厘米，三根铁丝一共长多少米？8、有一个书架，中层有书32本，比下层少10本比上层多7本，三层一共有书多少本？9、二年级一班有学生54人，比二年级二班多3人，比二年级三班少4人，三个班一共有多少人？10、一瓶水，连瓶重121克，倒掉一半水后连瓶重71克，瓶重多少克？水重多少克？11、一筐香蕉，连筐重25千克，卖出一半香蕉后连筐重13千克。

筐重多少千克？香蕉重多少千克？12、一桶油连桶重42千克，用去一半油后，连桶重23克。

油重多少千克？桶重多少千克？13、小树苗艺术团原有60人，今年暑期有15名同学毕业了，又有13名同学新加入了艺术团，小树苗艺术团现在有多少人？14、一桶水，连桶重36千克，用去一半后，连桶重20千克，满桶水重多少千克？15、操场上有8面黄旗，红旗比黄旗多6面，有多少面红旗？绿旗比黄旗和红旗的总数少2面，有绿旗多少面? 16、商场里有42个红皮球和25个花皮球。

早上有6个人买去19个皮球，现在商店里有多少个皮球？17、菜场原来青菜比萝卜多7筐，后又运来12筐萝卜和9筐青菜，现在青菜多还是萝卜多？多几筐？18、幼儿园有水果糖30块，还有一些奶糖。

小学二年级数学应用题（巧思妙解）1、一群小朋友在游乐场里划船，原有28人，走里5人又来了17人，现在有多少人？2、仓库里有一些水泥，用去26包，又运来45包，现在仓库里有水泥93包。

仓库里原来有多少包？3、一辆公交车里原有27人，到站点后下去6人，又上来13人，现在车上有多少人？4、广场上插的红旗比黄旗多22面，红旗再添14面，黄旗再添18面，现在哪种旗多？多多少面？5、公园里原来的杨树比柳树少13科，今年植树节那天，又栽了18棵杨树和15棵柳树，现在杨树和柳树哪个多？多多少棵？6、水果店原来苹果比梨树多7筐，又运来12筐和一些苹果，现在苹果还比梨多4筐，又运来了多少筐苹果？7、有三根铁丝，第一根比第二根长10厘米，第二根比第三根短5厘米，已知第三根长15厘米，三根铁丝一共长多少米？8、有一个书架，中层有书32本，比下层少10本比上层多7本，三层一共有书多少本？9、二年级一班有学生54人，比二年级二班多3人，比二年级三班少4人，三个班一共有多少人？10、一瓶水，连瓶重121克，倒掉一半水后连瓶重71克，瓶重多少克？水重多少克？11、一筐香蕉，连筐重25千克，卖出一半香蕉后连筐重13千克。

筐重多少千克？香蕉重多少千克？12、一桶油连桶重42千克，用去一半油后，连桶重23克。

油重多少千克？桶重多少千克？13、小树苗艺术团原有60人，今年暑期有15名同学毕业了，又有13名同学新加入了艺术团，小树苗艺术团现在有多少人？14、一桶水，连桶重36千克，用去一半后，连桶重20千克，满桶水重多少千克？15、操场上有8面黄旗，红旗比黄旗多6面，有多少面红旗？绿旗比黄旗和红旗的总数少2面，有绿旗多少面? 16、商场里有42个红皮球和25个花皮球。

早上有6个人买去19个皮球，现在商店里有多少个皮球？17、菜场原来青菜比萝卜多7筐，后又运来12筐萝卜和9筐青菜，现在青菜多还是萝卜多？多几筐？18、幼儿园有水果糖30块，还有一些奶糖。

巧思妙解2011年高考数学题（江苏卷）杨洪林1.（题18）如图，在平面直角坐标系x O y中，M、N分别是椭圆的顶点，过坐标原点的直线交椭圆于P、A两点，其中P在第一象限.过P作x轴的垂线，垂足为C，连接AC，并延长交椭圆于点B，设直线PA的斜率为k.（1）当直线PA平分线段MN时，求k的值；（2）当k= 2时，求点P到直线AB的距离d；（3）对任意k ＞0，求证：PA⊥PB.【参考答案】（1）…….（2）…….（3）解法一将直线PA的方程y= kx代入，解得x=±.记μ=，则P（μ,μk）, A（-μ, -μk）,于是C（μ,0）.故直线AB的斜率为=，其方程为.代入椭圆方程得（2 + k2）x2 -2μk2x–μ2（3k2 + 2）= 0, 解得x =或x = - μ .因此B（, ），于是直线PB的斜率k1 === -.因此k1 k= - 1，所以PA ⊥ PB.解法二设P（x1, y1）,B（x2, y2）,则x1＞0, x2＞0, x1≠x2，A（-x1,-y1）,C（x1,0）.设直线PB、AB的斜率分别为k1、k2，因为C在AB上，所以k2 ===.从而k1k+1=2k1k2+1 = 2··+ 1 =+ 1= = = 0. 因此k1k = - 1，所以PA ⊥ PB.·巧思·①利用三角形中位线定理，便知OD∥PB（D为AB的中点），“证明PA ⊥PB”就转化为“证明OA ⊥OD”。

②将点A、B的坐标设为对称式（关于中点D对称），便得两个对称的等式，从而又得一个简单的关系式。

③利用所得的简单关系式和A、B、C三点共线的条件（k= k BC），必可得到k OA·k OD = -1AB（条件都已用到）。

·妙解·设AB的中点D（a,b），A（a+ m,b+ n），B（a - m,b - n），则C（-a -m,0），OD ∥PB.且（a + m）2 + 2（b + n）2= 4 =（a - m）2 +2（b - n）2am + 2bn = 0.k PA = = 2 k AC = 2 k AB = = - = - = -PA⊥PB.【评注】①“对称美”是数学美之一，设立“对称式”求解问题也是数学研究中经常采用的手法之一。

好的，以下是一些具有巧思妙解的题目：
1. 有一道数学题，要求解一个复杂方程，但是经过反复尝试，
都无法得到正确的答案。

后来，他发现了一种巧妙的方法，可以快
速准确地解决这个问题。

请问，这个巧妙的方法是什么？
答案：这个巧妙的方法是利用数学中的“对数”和“指数”之
间的关系，将方程转化为一个容易求解的形式。

具体来说，他可能
使用了“换底公式”或者“自然对数”等工具，将方程变形为一种
更易于求解的形式。

2. 有一道物理题，要求计算一个物体的重量。

但是题目中只给
出了物体的质量和重力加速度，而且物体处于一个非惯性系中。

请问，如何利用这些信息计算物体的重量？
答案：在非惯性系中，物体的重量会受到额外的力作用。

这个
额外的力等于物体质量乘以非惯性系的加速度乘积。

因此，要计算
物体的重量，可以先计算出非惯性系的加速度，然后再将其乘上物
体的质量即可。

3. 有一道化学题，要求从一种混合物中分离出一种特定的化学
成分。

但是混合物中的其他成分会对这种化学成分产生干扰。

请问，如何利用化学知识快速分离出这种化学成分？
答案：可以利用化学中的“萃取”方法，将混合物中的特定成
分萃取出来。

具体来说，可以选择一种与目标成分不相互作用的溶剂，将混合物中的目标成分萃取出来，然后再将其分离出来。

以上题目都具有巧思妙解的特性，需要运用所学的知识进行深
入思考和灵活运用才能得到正确答案。

巧思妙解我的求法，妙广东省佛冈县第一小学六（4）班徐俊杰指导老师：黄秀银同学们，通过圆柱体积的学习，你们都知道圆柱的体积计算公式是：圆柱的体积=底面积高，用字母表示：V柱= S底h。

其实，除了这一计算公式外，圆柱的体积还有另一种求法。

我们先来回忆一下，把圆柱转化成我们所学过的立体图形，体积公式的推导过程是：首先把圆柱的底面分成许多相等的扇形（例如分成16份如图1），然后把圆柱切开，拼成一个近似的长方体（如图2，分成的扇形越多，拼成的立体图形就越接于近长方体），这个长方体的底面积等于圆柱的底面积，高就是圆柱的高。

因为长方体的体积=底面积高，所以圆柱的体积计算公式是：圆柱的体积=底面积高，用字母表示是：V柱= S底h。

我将拼成的近似长方体的立体图形由竖放变成横放（如图3），由此我就会发现了：这个长方体的底面积等于圆柱侧面积的一半，高等于圆柱的底面半径，所以圆柱体积的另一种计算公式是：圆柱的体积=圆柱侧面积的底面半径，用字母表示是：V柱=s侧r。

例如：一个圆柱的底面半径是5厘米，侧面积是62.8 平方厘一般解法：运用公式V柱= S底h进行计算。

圆柱的底面周长是：3.14 3 2=31.4（厘米）圆柱的高是：62.8 31.4=2（厘米）圆柱的体积是：3.14 52 2=157（立方厘米）巧妙解法：运用公式V柱=s侧r进行计算。

圆柱的体积是： 62.8 5=157（立方厘米）从上面的例子可以看出，用这两个公式算出的结果是一样的，两者相比，第二种解法非常巧妙。

不过，在实际解题时，我们应该根据题中所给出的具体条件，灵活地选择解题方法。

同学们，刚才所讲的求圆柱体积的新方法你一定学会了吧！那就快来动手试试看！练习：一个圆柱的底面直径是6厘米，侧面积是150.72 平方巧算圆的面积王家鹏一个正方形的面积是10平方米，在它的里面画一个最大的圆，求圆的面积。

图 1 图2方法一：如图1，在学了圆的面积S＝πr2以后，我知道了求圆面积的一般方法，即：先求r，再求S。

课程探讨数学思想，是指现实世界的空间形式和数量关系反映到人们的意识之中，经过思维活动而产生的结果，是对数学事实与理论经过概括后产生的本质认识。

在小学数学课堂教学的实践中，数学思想不仅能指导教师深入理解教材，进行高效的教学设计，更能帮我们巧妙地解决一些数学难题。

一、利用对应思想解决数学问题对应是人们对两个集合元素之间联系的一种思想方法。

这种思想方法是在两个事物之间建立起来的一种关系，即对应关系，从而揭示事物之间的联系。

运用对应思想可以让一些数学问题的数量关系变得简洁、明了。

例如：幼儿园教师把一箱饼干分给小班和中班的小朋友，平均每人分得6块；如果只分给中班的小朋友，平均每人可以多分4块。

如果只分给小班的小朋友，平均每人分得多少块？这是一道盈亏类型的题目，解决这道问题的常用思路：这箱饼干分给小班和中班的小朋友，平均每人分得6块；如果只分给中班的小朋友，平均每人可以多分4块。

说明中班的人数是小班人数的6÷4=1.5倍，因此，这箱饼干全分给小班的小朋友，每位小朋友可以多分6×1.5=9（块），一共可以分到6+9=15（块）。

但在实际的教学过程中，五年级的学生并不能很好地理解这种教学思路。

因此，在教学本道题目的时候，我就利用对应的思想来解决这道题目，收到了良好的教学效果。

“把这箱饼干分给小班和中班的小朋友，平均每人分得6块；如果只分给中班的小朋友，平均每人可以多分4块。

”通过对这句话的分析和理解，我们可以知道，如果只分给中班的小朋友，那么中班小朋友每人手中的6块饼干可以不用考虑，只考虑把小班小朋友的饼干重新分配给中班就可以。

认真观察，我们可以发现小班2个小朋友手中的饼干是6×2=12（块），这12块刚好分给中班的3个小朋友。

这样小班的2个小朋友和中班的3个小朋友之间就建立起一种对应关系。

因此，如果这箱饼干只分给小班的小朋友，每人就可以多分6×3÷2=9（块），每人共分6+9=15（块）。

◎相辉【题目】有红、黑两种颜色的笔，其中红颜色的笔的23等于黑颜色的笔的23，红颜色的笔比黑颜色的笔多21支。

两种颜色的笔各有多少支？思路一：转化成比。

根据红颜色的笔的23等于黑颜色的笔的23，可以推出红颜色的笔和黑颜色的笔的支数比是25∶24，说明红颜色的笔有这样的25份，黑颜色的笔就有这样的24份，红颜色的笔比黑颜色的笔多21支就是（25-24）份。

解：23∶23=25∶24……红颜色的笔和黑颜色的笔的比21÷）=21（支）21×25=525（支）21×24=504（支）答：红颜色的笔有525支，黑颜色的笔有504支。

思路二：列方程解答。

根据红颜色的笔的23等于黑颜色的笔的23，可以找出数量关系式：红颜色的笔的支数×23=黑颜色的笔的支数×2 3。

4 55 64 55 65 64545564556解：设黑颜色的笔有x 支，红颜色的笔就有（x +21）支。

2323x +21）2323852323x =504x +21=504+21=525答：红颜色的笔有525支，黑颜色的笔有504支。

思路三：根据分数乘、除法的意义进行解答。

已知“红颜色的笔的23颜色的笔的23”，可以把黑颜色的笔的支数看作单位“1”的量，红颜色的笔的支数就占黑颜色的笔的23÷23=23，21支就是黑颜色的笔的（23），根据黑颜色的笔的支数×（23）=21（支），可以求出黑颜色的笔的支数。

解：2323=2321÷（23-1）=504（支）504×23（支）答：红颜色的笔有525支，黑颜色的笔有504支。

【挑战自我】甲、乙两仓库共存粮950吨，如果23放入乙仓库，这时乙仓库存粮的23正好等于甲仓库存粮的。

甲、乙两仓库原来各存粮多少吨？扫描二维码获取更多资源564556451308454556452524564538143523842524252425242524252456。