2018 撷秀中学 中考专题练习9

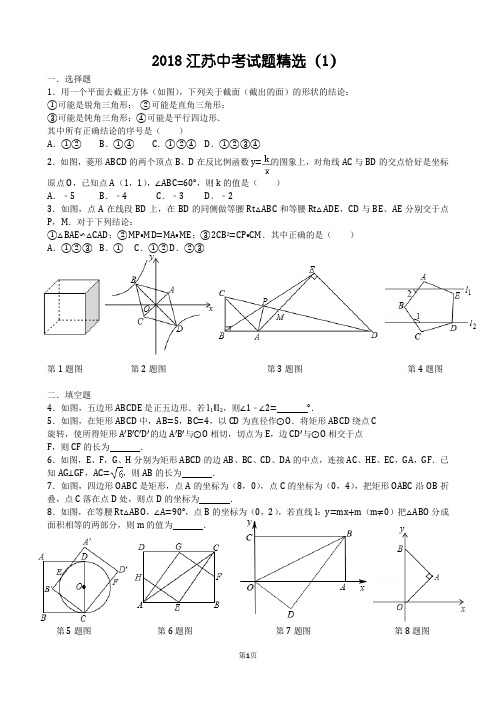
2018江苏中考试题精选（1）一．选择题1．用一个平面去截正方体（如图），下列关于截面（截出的面）的形状的结论：①可能是锐角三角形；②可能是直角三角形；③可能是钝角三角形；④可能是平行四边形．其中所有正确结论的序号是（）A．①②B．①④C．①②④D．①②③④2．如图，菱形ABCD的两个顶点B、D在反比例函数y=的图象上，对角线AC与BD的交点恰好是坐标原点O，已知点A（1，1），∠ABC=60°，则k的值是（）A．﹣5B．﹣4C．﹣3 D．﹣23．如图，点A在线段BD上，在BD的同侧做等腰Rt△ABC和等腰Rt△ADE，CD与BE、AE分别交于点P，M．对于下列结论：①△BAE∽△CAD；②MP•MD=MA•ME；③2CB2=CP•CM．其中正确的是（）A．①②③B．①C．①②D．②③第1题图第2题图第3题图第4题图二．填空题4．如图，五边形ABCDE是正五边形．若l1∥l2，则∠1﹣∠2=°．5．如图，在矩形ABCD中，AB=5，BC=4，以CD为直径作⊙O．将矩形ABCD绕点C旋转，使所得矩形A′B′C′D′的边A′B′与⊙O相切，切点为E，边CD′与⊙O相交于点F，则CF的长为．6．如图，E、F，G、H分别为矩形ABCD的边AB、BC、CD、DA的中点，连接AC、HE、EC，GA，GF．已知AG⊥GF，AC=，则AB的长为．7．如图，四边形OABC是矩形，点A的坐标为（8，0），点C的坐标为（0，4），把矩形OABC沿OB折叠，点C落在点D处，则点D的坐标为．8．如图，在等腰Rt△ABO，∠A=90°，点B的坐标为（0，2），若直线l：y=mx+m（m≠0）把△ABO分成面积相等的两部分，则m的值为．第5题图第6题图第7题图第8题图三．解答题9．结果如此巧合!下面是小颖对一道题目的解答．题目：如图，Rt△ABC的内切圆与斜边AB相切于点D，AD=3，BD=4，求△ABC的面积．解：设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x．根据切线长定理，得AE=AD=3，BF=BD=4，CF=CE=x．根据勾股定理，得（x+3）2+（x+4）2=（3+4）2．整理，得x2+7x=12．所以S△ABC=AC•BC=（x+3）（x+4）=（x2+7x+12）=×（12+12）=12．小颖发现12恰好就是3×4，即△ABC的面积等于AD与BD的积．这仅仅是巧合吗？请你帮她完成下面的探索．已知：△ABC的内切圆与AB相切于点D，AD=m，BD=n．可以一般化吗？（1）若∠C=90°，求证：△ABC的面积等于mn．倒过来思考呢？（2）若AC•BC=2mn，求证∠C=90°．改变一下条件……（3）若∠C=60°，用m、n表示△ABC的面积．10．如图1，图形ABCD是由两个二次函数y1=kx2+m（k＜0）与y2=ax2+b（a＞0）的部分图象围成的封闭图形．已知A（1，0）、B（0，1）、D（0，﹣3）．（1）直接写出这两个二次函数的表达式；（2）判断图形ABCD是否存在内接正方形（正方形的四个顶点在图形ABCD上），并说明理由；（3）如图2，连接BC，CD，AD，在坐标平面内，求使得△BDC与△ADE相似（其中点C与点E是对应顶点）的点E的坐标11．在数学兴趣小组活动中，小亮进行数学探究活动．△ABC是边长为2的等边形，E是AC上一点，小亮以BE为边向BE的右侧作等边三角形BEF，连接CF．（1）如图1，当点E在线段AC上时，EF、BC相交于点D，小亮发现有两个三角形全等，请你找出来，并证明．（2）当点E在线段上运动时，点F也随着运动，若四边形ABFC的面积为，求AE的长．（3）如图2，当点E在AC的延长线上运动时，CF、BE相交于点D，请你探求△ECD的面积S1与△DBF的面积S2之间的数量关系．并说明理由．（4）如图2，当△ECD的面积S1=时，求AE的长．12．问题呈现如图1，在边长为1的正方形网格中，连接格点D，N和E，C，DN和EC相交于点P，求tan∠CPN的值．方法归纳求一个锐角的三角函数值，我们往往需要找出（或构造出）一个直角三角形．观察发现问题中∠CPN不在直角三角形中，我们常常利用网格画平行线等方法解决此类问题，比如连接格点M，N，可得MN∥EC，则∠DNM=∠CPN，连接DM，那么∠CPN就变换到Rt△DMN中．问题解决（1）直接写出图1中tan∠CPN的值为；（2）如图2，在边长为1的正方形网格中，AN与CM相交于点P，求cos∠CPN的值；思维拓展（3）如图3，AB⊥BC，AB=4BC，点M在AB上，且AM=BC，延长CB到N，使BN=2BC，连接AN交CM 的延长线于点P，用上述方法构造网格求∠CPN的度数．13．如图1，四边形OABC是矩形，点A的坐标为（3，0），点C的坐标为（0，6），点P从点O出发，沿OA以每秒1个单位长度的速度向点A出发，同时点Q从点A出发，沿AB以每秒2个单位长度的速度向点B运动，当点P与点A重合时运动停止．设运动时间为t秒．（1）当t=2时，线段PQ的中点坐标为；（2）当△CBQ与△PAQ相似时，求t的值；（3）当t=1时，抛物线y=x2+bx+c经过P，Q两点，与y轴交于点M，抛物线的顶点为K，如图2所示，问该抛物线上是否存在点D，使∠MQD=∠MKQ？若存在，求出所有满足条件的D的坐标；若不存在，说明理由．江苏中考试题精选参考答案与试题解析一．选择题（共3小题）1．用一个平面去截正方体（如图），下列关于截面（截出的面）的形状的结论：①可能是锐角三角形；②可能是直角三角形；③可能是钝角三角形；④可能是平行四边形．其中所有正确结论的序号是（）A．①②B．①④C．①②④D．①②③④【解答】解：用平面去截正方体，得的截面可能为三角形、四边形、五边形、六边形，而三角形只能是锐角三角形，不能是直角三角形和钝角三角形．故选：B．2．如图，菱形ABCD的两个顶点B、D在反比例函数y=的图象上，对角线AC与BD的交点恰好是坐标原点O，已知点A（1，1），∠ABC=60°，则k的值是（）A．﹣5B．﹣4C．﹣3D．﹣2【解答】解：∵四边形ABCD是菱形，∴BA=BC，AC⊥BD，∵∠ABC=60°，∴△ABC是等边三角形，∵点A（1，1），∴OA=，∴BO=，∵直线AC的解析式为y=x，∴直线BD的解析式为y=﹣x，∵OB=，∴点B的坐标为（，），∵点B在反比例函数y=的图象上，∴，解得，k=﹣3，故选：C．3．如图，点A在线段BD上，在BD的同侧做等腰Rt△ABC和等腰Rt△ADE，CD与BE、AE分别交于点P，M．对于下列结论：①△BAE∽△CAD；②MP•MD=MA•ME；③2CB2=CP•CM．其中正确的是（）A．①②③B．①C．①②D．②③【解答】解：由已知：AC=AB，AD=AE∴∵∠BAC=∠EAD∴∠BAE=∠CAD∴△BAE∽△CAD所以①正确∵△BAE∽△CAD∴∠BEA=∠CDA∵∠PME=∠AMD∴△PME∽△AMD∴∴MP•MD=MA•ME所以②正确∵∠BEA=∠CDA∠PME=∠AMD∴P、E、D、A四点共圆∴∠APD=∠EAD=90°∵∠CAE=180°﹣∠BAC﹣∠EAD=90°∴△CAP∽△CMA∴AC2=CP•CM∵AC=AB∴2CB2=CP•CM所以③正确故选：A．二．填空题（共5小题）4．如图，五边形ABCDE是正五边形．若l1∥l2，则∠1﹣∠2=72°．【解答】解：过B点作BF∥l1，∵五边形ABCDE是正五边形，∴∠ABC=108°，∵BF∥l1，l1∥l2，∴BF∥l2，∴∠3=180°﹣∠1，∠4=∠2，∴180°﹣∠1+∠2=∠ABC=108°，∴∠1﹣∠2=72°．故答案为：72．5．如图，在矩形ABCD中，AB=5，BC=4，以CD为直径作⊙O．将矩形ABCD绕点C 旋转，使所得矩形A′B′C′D′的边A′B′与⊙O相切，切点为E，边CD′与⊙O相交于点F，则CF的长为4．【解答】解：连接OE，延长EO交CD于点G，作OH⊥B′C于点H，则∠OEB′=∠OHB′=90°，∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′，∴∠B′=∠B′CD′=90°，AB=CD=5、BC=B′C=4，∴四边形OEB′H和四边形EB′CG都是矩形，OE=OD=OC=2.5，∴B′H=OE=2.5，∴CH=B′C﹣B′H=1.5，∴CG=B′E=OH===2，∵四边形EB′CG是矩形，∴∠OGC=90°，即OG⊥CD′，∴CF=2CG=4，6．如图，E、F，G、H分别为矩形ABCD的边AB、BC、CD、DA的中点，连接AC、HE、EC，GA，GF．已知AG⊥GF，AC=，则AB的长为2．【解答】解：如图，连接BD．∵四边形ABCD是矩形，∴∠ADC=∠DCB=90°，AC=BD=，∵CG=DG，CF=FB，∴GF=BD=，∵AG⊥FG，∴∠AGF=90°，∴∠DAG+∠AGD=90°，∠AGD+∠CGF=90°，∴∠DAG=∠CGF，∴△ADG∽△GCF，设CF=BF=a，CG=DG=b，∴=，∴=，∴b2=2a2，∵a＞0．b＞0，∴b=a，在Rt△GCF中，3a2=，∴a=，∴AB=2b=2．故答案为2．7．如图，四边形OABC是矩形，点A的坐标为（8，0），点C的坐标为（0，4），把矩形OABC沿OB折叠，点C落在点D处，则点D的坐标为（，﹣）．【解答】解：由折叠得：∠CBO=∠DBO，∵矩形ABCO，∴BC∥OA，∴∠CBO=∠BOA，∴∠DBO=∠BOA，∴BE=OE，在△ODE和△BAE中，，∴△ODE≌△BAE（AAS），∴AE=DE，设DE=AE=x，则有OE=BE=8﹣x，在Rt△ODE中，根据勾股定理得：42+（8﹣x）2=x2，解得：x=5，即OE=5，DE=3，过D作DF⊥OA，∵S△OED=OD•DE=OE•DF，∴DF=，OF==，则D（，﹣）．故答案为：（，﹣）8．如图，在等腰Rt△ABO，∠A=90°，点B的坐标为（0，2），若直线l：y=mx+m（m≠0）把△ABO分成面积相等的两部分，则m的值为．【解答】解：∵y=mx+m=m（x+1），∴函数y=mx+m一定过点（﹣1，0），当x=0时，y=m，∴点C的坐标为（0，m），由题意可得，直线AB的解析式为y=﹣x+2，，得，∵直线l：y=mx+m（m≠0）把△ABO分成面积相等的两部分，∴，解得，m=或m=（舍去），故答案为：．三．解答题（共5小题）9．结果如此巧合!下面是小颖对一道题目的解答．题目：如图，Rt△ABC的内切圆与斜边AB相切于点D，AD=3，BD=4，求△ABC的面积．解：设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x．根据切线长定理，得AE=AD=3，BF=BD=4，CF=CE=x．根据勾股定理，得（x+3）2+（x+4）2=（3+4）2．整理，得x2+7x=12．所以S△ABC=AC•BC=（x+3）（x+4）=（x2+7x+12）=×（12+12）=12．小颖发现12恰好就是3×4，即△ABC的面积等于AD与BD的积．这仅仅是巧合吗？请你帮她完成下面的探索．已知：△ABC的内切圆与AB相切于点D，AD=m，BD=n．可以一般化吗？（1）若∠C=90°，求证：△ABC的面积等于mn．倒过来思考呢？（2）若AC•BC=2mn，求证∠C=90°．改变一下条件……（3）若∠C=60°，用m、n表示△ABC的面积．【解答】解：设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x，根据切线长定理，得：AE=AD=m、BF=BD=n、CF=CE=x，（1）如图1，在Rt△ABC中，根据勾股定理，得：（x+m）2+（x+n）2=（m+n）2，整理，得：x2+（m+n）x=mn，所以S△ABC=AC•BC=（x+m）（x+n）=[x2+（m+n）x+mn]=（mn+mn）=mn，（2）由AC•BC=2mn，得：（x+m）（x+n）=2mn，整理，得：x2+（m+n）x=mn，∴AC2+BC2=（x+m）2+（x+n）2=2[x2+（m+n）x]+m2+n2=2mn+m2+n2=（m+n）2=AB2，根据勾股定理逆定理可得∠C=90°；（3）如图2，过点A作AG⊥BC于点G，在Rt△ACG中，AG=AC•sin60°=（x+m），CG=AC•cos60°=（x+m），∴BG=BC﹣CG=（x+n）﹣（x+m），在Rt△ABG中，根据勾股定理可得：[（x+m）]2+[（x+n）﹣（x+m）]2=（m+n）2，整理，得：x2+（m+n）x=3mn，∴S△ABC=BC•AG=×（x+n）•（x+m）=[x2+（m+n）x+mn]=×（3mn+mn）=mn．10．如图1，图形ABCD是由两个二次函数y1=kx2+m（k＜0）与y2=ax2+b（a＞0）的部分图象围成的封闭图形．已知A（1，0）、B（0，1）、D（0，﹣3）．（1）直接写出这两个二次函数的表达式；（2）判断图形ABCD是否存在内接正方形（正方形的四个顶点在图形ABCD上），并说明理由；（3）如图2，连接BC，CD，AD，在坐标平面内，求使得△BDC与△ADE相似（其中点C与点E是对应顶点）的点E的坐标【解答】解：（1）∵点A（1，0），B（0，1）在二次函数y1=kx2+m（k＜0）的图象上，∴，∴，∴二次函数解析式为y1=﹣x2+1，∵点A（1，0），D（0，﹣3）在二次函数y2=ax2+b（a＞0）的图象上，∴，∴，∴二次函数y2=3x2﹣3；（2）设M（m，﹣m2+1）为第一象限内的图形ABCD上一点，M'（m，3m2﹣3）为第四象限的图形上一点，∴MM'=（1﹣m2）﹣（3m2﹣3）=4﹣4m2，由抛物线的对称性知，若有内接正方形，∴2m=4﹣4m2，∴m=或m=（舍），∵0＜＜1，∴存在内接正方形，此时其边长为；（3）在Rt△AOD中，OA=1，OD=3，∴AD==，同理：CD=，在Rt△BOC中，OB=OC=1，∴BC==，①如图1，当△DBC∽△DAE时，∵∠CDB=∠ADO，∴在y轴上存在E，由，∴，∴DE=，∵D（0，﹣3），∴E（0，﹣），由对称性知，在直线DA右侧还存在一点E'使得△DBC∽△DAE'，连接EE'交DA于F点，作E'M⊥OD于M，连接E'D，∵E，E'关于DA对称，∴DF垂直平分线EE'，∴△DEF∽△DAO，∴，∴，∴DF=，EF=，∵S△DEE'=DE•E'M=EF×DF=，∴E'M=，∵DE'=DE=，在Rt△DE'M中，DM==2，∴OM=1，∴E'（，﹣1），②如图2，当△DBC∽△ADE时，有∠BDC=∠DAE，，∴，∴AE=，当E在直线AD左侧时，设AE交y轴于P，作EQ⊥AC于Q，∵∠BDC=∠DAE=∠ODA，∴PD=PA，设PD=n，∴PO=3﹣n，PA=n，在Rt△AOP中，PA2=OA2+OP2，∴n2=（3﹣n）2+1，∴n=，∴PA=，PO=，∵AE=，∴PE=，在AEQ中，OP∥EQ，∴，∴OQ=，∵，∴QE=2，∴E（﹣，﹣2），当E'在直线DA右侧时，根据勾股定理得，AE==，∴AE'=∵∠DAE'=∠BDC，∠BDC=∠BDA，∴∠BDA=∠DAE'，∴AE'∥OD，∴E'（1，﹣），综上，使得△BDC与△ADE相似（其中点C与E是对应顶点）的点E的坐标有4个，即：（0，﹣）或（，﹣1）或（1，﹣）或（﹣，﹣2）．11．在数学兴趣小组活动中，小亮进行数学探究活动．△ABC是边长为2的等边形，E是AC上一点，小亮以BE为边向BE的右侧作等边三角形BEF，连接CF．（1）如图1，当点E在线段AC上时，EF、BC相交于点D，小亮发现有两个三角形全等，请你找出来，并证明．（2）当点E在线段上运动时，点F也随着运动，若四边形ABFC的面积为，求AE的长．（3）如图2，当点E在AC的延长线上运动时，CF、BE相交于点D，请你探求△ECD的面积S1与△DBF的面积S2之间的数量关系．并说明理由．（4）如图2，当△ECD的面积S1=时，求AE的长．【解答】解：（1）结论：△ABE≌△CBF．理由：如图1中，∴∵△ABC，△BEF都是等边三角形，∴BA=BC，BE=BF，∠ABC=∠EBF，∴∠ABE=∠CBF，∴△ABE≌△CBF．（2）如图1中，∵△ABE≌△CBF，∴S△ABE=S△BCF，∴S四边形BECF=S△BEC+s△BCF=S△BCE+S△ABE=S△ABC=，∵S四边形ABCF=，∴S△ABE=，∴•AE•AB•siin60°=，∴AE=．（3）结论：S2﹣S1=．理由：如图2中，∵∵△ABC，△BEF都是等边三角形，∴BA=BC，BE=BF，∠ABC=∠EBF，∴∠ABE=∠CBF，∴△ABE≌△CBF，∴S△ABE=S△BCF，∵S△BCF﹣S△BCE=S2﹣S1，∴S2﹣S1=S△ABE﹣S△BCE=S△ABC=．（4）由（3）可知：S△BDF﹣S△ECD=，∵S△ECD=，∴S△BDF=，∵△ABE≌△CBF，∴AE=CF，∠BAE=∠BCF=60°，∴∠ABC=∠DCB，∴CF∥AB，则△BDF的BF边上的高为，可得DF=，设CE=x，则2+x=CD+DF=CD+，∴CD=x﹣，∵CD∥AB，∴=，即=，化简得：3x2﹣x﹣2=0，解得x=1或﹣（舍弃），∴CE=1，AE=3．12．问题呈现如图1，在边长为1的正方形网格中，连接格点D，N和E，C，DN和EC相交于点P，求tan∠CPN的值．方法归纳求一个锐角的三角函数值，我们往往需要找出（或构造出）一个直角三角形．观察发现问题中∠CPN不在直角三角形中，我们常常利用网格画平行线等方法解决此类问题，比如连接格点M，N，可得MN∥EC，则∠DNM=∠CPN，连接DM，那么∠CPN就变换到Rt△DMN中．问题解决（1）直接写出图1中tan∠CPN的值为2；（2）如图2，在边长为1的正方形网格中，AN与CM相交于点P，求cos∠CPN的值；思维拓展（3）如图3，AB⊥BC，AB=4BC，点M在AB上，且AM=BC，延长CB到N，使BN=2BC，连接AN交CM 的延长线于点P，用上述方法构造网格求∠CPN的度数．【解答】解：（1）如图1中，∵EC∥MN，∴∠CPN=∠DNM，∴tan∠CPN=tan∠DNM，∵∠DMN=90°，∴tan∠CPN=tan∠DNM===2，故答案为2．（2）如图2中，取格点D，连接CD，DM．∵CD∥AN，∴∠CPN=∠DCM，∵△DCM是等腰直角三角形，∴∠DCM=∠D=45°，∴cos∠CPN=cos∠DCM=．（3）如图3中，如图取格点M，连接AN、MN．∵PC∥MN，∴∠CPN=∠ANM，∵AM=MN，∠AMN=90°，∴∠ANM=∠MAN=45°，∴∠CPN=45°．13．如图1，四边形OABC是矩形，点A的坐标为（3，0），点C的坐标为（0，6），点P从点O出发，沿OA以每秒1个单位长度的速度向点A出发，同时点Q从点A出发，沿AB以每秒2个单位长度的速度向点B运动，当点P与点A重合时运动停止．设运动时间为t秒．（1）当t=2时，线段PQ的中点坐标为（，2）；（2）当△CBQ与△PAQ相似时，求t的值；（3）当t=1时，抛物线y=x2+bx+c经过P，Q两点，与y轴交于点M，抛物线的顶点为K，如图2所示，问该抛物线上是否存在点D，使∠MQD=∠MKQ？若存在，求出所有满足条件的D的坐标；若不存在，说明理由．【解答】解：（1）如图1，∵点A的坐标为（3，0），∴OA=3，当t=2时，OP=t=2，AQ=2t=4，∴P（2，0），Q（3，4），∴线段PQ的中点坐标为：（，），即（，2）；故答案为：（，2）；（2）如图1，∵当点P与点A重合时运动停止，且△PAQ可以构成三角形，∴0＜t＜3，∵四边形OABC是矩形，∴∠B=∠PAQ=90°∴当△CBQ与△PAQ相似时，存在两种情况：①当△PAQ∽△QBC时，，∴，4t2﹣15t+9=0，（t﹣3）（t﹣）=0，t1=3（舍），t2=，②当△PAQ∽△CBQ时，，∴，t2﹣9t+9=0，t=，∵＞7，∴x=不符合题意，舍去，综上所述，当△CBQ与△PAQ相似时，t的值是或；（3）当t=1时，P（1，0），Q（3，2），把P（1，0），Q（3，2）代入抛物线y=x2+bx+c中得：，解得：，∴抛物线：y=x2﹣3x+2=（x﹣）2﹣，∴顶点k（，﹣），∵Q（3，2），M（0，2），∴MQ∥x轴，作抛物线对称轴，交MQ于E，∴KM=KQ，KE⊥MQ，∴∠MKE=∠QKE=∠MKQ，如图2，∠MQD=∠MKQ=∠QKE，设DQ交y轴于H，∵∠HMQ=∠QEK=90°，∴△KEQ∽△QMH，∴，∴，∴MH=2，∴H（0，4），易得HQ的解析式为：y=﹣x+4，则，x2﹣3x+2=﹣x+4，解得：x1=3（舍），x2=﹣，∴D（﹣，）；同理，在M的下方，y轴上存在点H，如图3，使∠HQM=∠MKQ=∠QKE，由对称性得：H（0，0），易得OQ的解析式：y=x，则，x2﹣3x+2=x，解得：x1=3（舍），x2=，∴D（，）；综上所述，点D的坐标为：D（﹣，）或（，）．。

中考必备化学图像题 pH的变化图像技巧全解及练习题(含答案)一、化学图像题 pH的变化图像（稀释或中和）CaCl的混合溶液,向其中逐滴加入过量某物质X,溶液的pH随滴1．现有一定质量的盐酸和2CaCl溶液.NaCl溶液均为中性)｡则X可能是（）入X的量的变化关系如下图所示(已知2CaCO固体A．水B．澄清石灰水C．纯碱溶液D．3【来源】2017年江苏省徐州市泉山区撷秀中学中考三模化学试题【答案】C【解析】【分析】【详解】已知氯化钙溶液呈中性，盐酸呈酸性，盐酸与氯化钙的混合溶液呈酸性，pH值小于7，则有：A、向盐酸与氯化钙的混合溶液中加水，酸性溶液不断稀释，pH值无限的接近7，不会等于和大于7，A选项物质的加入与图中pH值的变化关系不对应，不符合题意；B、向盐酸与氯化钙的混合溶液中加澄清石灰水，氢氧化钙与盐酸反应生成氯化钙和水，氢氧化钙溶液呈碱性，溶液的pH值由小于7逐渐增加，氢氧化钙与盐酸恰好完全时pH值等于7，继续加入，立即大于7，并逐渐增加，B选项物质的加入与图中pH值的变化关系不对应，不符合题意；C、向盐酸与氯化钙的混合溶液中加纯碱溶液，盐酸先与碳酸钠反应生成氯化钠、二氧化碳和水，氯化钠溶液呈中性，盐酸反应完之后氯化钙与碳酸钠反应生成碳酸钙沉淀和氯化钠。

随着碳酸钠溶液的加入，混合液的pH值由小于7逐渐增加，盐酸恰好完全反应时等于7，碳酸钠和氯化钙的反应过程中维持等于7，氯化钙完全反应后，pH大于7，C选项物质的加入与图中pH值的变化关系对应，符合题意；D、向盐酸与氯化钙的混合溶液中加碳酸钙固体，盐酸与碳酸钙反应生成氯化钙、二氧化碳和水，碳酸钙难溶于水，随着碳酸钙的加入，混合液的pH值由小于7逐渐增加，盐酸恰好完全反应时等于7，最后维持等于7，不会继续增加，D选项物质的加入与图中pH值的变化关系不对应，不符合题意。

故选C。

2．下列图像与对应叙述相符合的是A．向一定量的锌粒中加入稀盐酸B．向 pH=3 的溶液中加水C．一定量的镁条在密闭容器里与氧气反应D．向含少量盐酸的氯化钙溶液中加入碳酸钾溶液【来源】湖南省邵阳市邵阳县2018届九年级初中毕业学业模拟考试化学试题【答案】D【解析】【分析】【详解】A、向一定量的锌粒中加入稀盐酸生成的氢气的量不能一直增加，选项A错误；B、向 pH=3的溶液中加水，最终溶液的pH不可能大于7，选项B错误；C、一定量的镁条在密闭容器里与氧气反应，固体的质量增加，选项C错误；D、向含少量盐酸的氯化钙溶液中加入碳酸钾溶液，碳酸钾先和稀盐酸反应，没有沉淀生成，反应一段时间后，稀盐酸反应完，碳酸钾和氯化钙反应，有沉淀生成，当氯化钙反应完后，沉淀的质量不再增加，选项D正确。

2017--2018学年度第一学期第二次月考九年级英语试卷第I卷(90分)一、听力理解。

（共20小题；1-10题每题1分，11-20题每题2分，共30分）一）听对话，回答问题。

本部分共有10小题，每小题你将听到一段对话，每段对话听两遍。

在听每段对话前，你将有5秒钟时间阅读题目，听完后你将有5秒钟时间选择你认为最合适的备选答案。

1. What are they talking about?A. B. C.2. Which instrument is used in the music?A. B. C.3. What program does the boy dislike?A. B. C.4. How did the man often communicate with his friends in the past?A. B. C.5. How does the girl think about rock music?A. Exciting.B. Noisy.C. Peaceful.6. How much time does the girl spend watching TV every week?A. One hour.B. Less than one hour.C. About one hour and a half.7. How many days did Daisy stay in the United States?A. 2 days.B. 5 days.C. 7 days.8. How much does the yellow shirt cost?A. 12 dollars.B. 13 dollars.C. 20 dollars.9. What was out of control and caused the accident?A. A bus.B. A car.C. A truck.10. Where was Deny yesterday?A. At home.B. In the park.C. At work.二）听对话和短文，回答问题，听两遍。

江苏省徐州市撷秀中学2024-2025学年数学九上开学统考模拟试题题号一二三四五总分得分批阅人A 卷（100分）一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、（4分）如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD 、正方形EFGH 、正方形MNKT 的面积分别为S 1、S 2、S 3.若S 1+S 2+S 3=15，则S 2的值是()A ．3B ．154C ．5D ．1522、（4分）我校男子足球队22名队员的年龄如下表所示：这些队员年龄的众数和中位数分别是（）年龄/岁141516171819人数213673A ．18，17B ．17，18C ．18，17.5D ．17.5，183、（4分）要判断甲、乙两队舞蹈队的身高哪队比较整齐，通常需要比较这两队舞蹈队身高的（）A ．方差B ．中位数C ．众数D ．平均数4、（4分）某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所用的时间与原计划生产450台机器所用的时间相同．若设原计划平均每天生产x 台机器，则可列方程为()A ．600x ＝45050x +B ．600x ＝45050x -C ．60050x +＝450xD ．60050x -＝450x 5、（4分）如图,在ABC ∆中，5AB AC ==，D 是BC 上的点,DE ∥AB 交AC 于点E ，DF ∥AC 交AB 于点F ，那么四边形AFDE 的周长是（）A ．5B ．10C ．15D ．206、（4分）如图，在等边△ABC 中，点P 从A 点出发，沿着A →B →C 的路线运动，△ACP 的面积为S ，运动时间为t ，则S 与t 的图像是（）A ．B ．C ．D ．7、（4分）对四边形ABCD 加条件，使之成为平行四边形，下面的添加不正确的是（）A ．AB=CD ，AB ∥CD B ．AB ∥CD ，AD=BCC ．AB=CD ，AD=BC D ．AC 与BD 相互平分8、（4分）下列二次根式是最简二次根式的是（）A ．BCD ．二、填空题（本大题共5个小题，每小题4分，共20分）9、（4分）若□ABCD 中，∠A =50°，则∠C =_______°．10、（4分）若ab ＜0可化简为_____.11、（4分）若0,k >0x >，则关于函数y kx =的结论：①y 随x 的增大而增大；②y 随x 的增大而减小；③y 恒为正值；④y 恒为负值.正确的是________.（直接写出正确结论的序号）12、（4分）已知关于x 的分式方程111x k k x x +-=+-的解为负数，则k 的取值范围是.13、（4分）如图，平行四边形ABCD 的对角线相交于点O ，且AD CD ≠，过点O 作OM AC ⊥，交AD 于点M .若3,AB CDM =∆的周长为9，则BC =______．三、解答题（本大题共5个小题，共48分）14、（12分）如图①，在平面直角坐标系中，直线1l ：162y x =-+分别与x 轴、y 轴交于点B 、C ，且与直线2l ：12y x =交于点A ，以线段AC 为边在直线1l 的下方作正方形ACDE ，此时点D 恰好落在x 轴上．（1）求出,,A B C 三点的坐标．（2）求直线CD 的函数表达式．（3）在（2）的条件下，点P 是射线CD 上的一个动点，在平面内是否存在点Q ，使得以O 、C 、P 、Q 为顶点的四边形是菱形？若存在，直接写出点P 的坐标；若不存在，请说明理由．15、（8分）已知：四边形ABCD ，E ，F ，G，H 是各边的中点．（1）求证：四边形EFGH 是平行四边形；（2）假如四边形ABCD 是一个矩形，猜想四边形EFGH 是什么图形？并证明你的猜想．16、（8分）甲、乙两位运动员在相同条件下各射靶10次，毎次射靶的成绩情况如图.(1)请填写下表:(2)请你从平均数和方差相结合对甲、乙两名运动员6次射靶成绩进行分析:平均数方差中位数命中9环以上的次数(包括9环)甲7 1.21乙 5.47.5(3)教练根据两人的成绩最后选择乙去参加比赛，你能不能说出教练让乙去比赛的理由?(至少说出两条理由)17、（10分）如图，在直角坐标系中，每个小方格都是边长为1的正方形，ABC 的顶点均在格点上，点A 的坐标是()3,1--．()1先将ABC 沿y 轴正方向向上平移3个单位长度，再沿x 轴负方向向左平移1个单位长度得到111A B C △，画出111A B C △，点1C 坐标是________；()2将111A B C △绕点1B 逆时针旋转90，得到212A B C ，画出212A B C ，并求出点2C 的坐标是________；()3我们发现点C 、2C 关于某点中心对称，对称中心的坐标是________．18、（10分）我市某火龙果基地销售火龙果，该基地对需要送货且购买量在2000kg ～5000kg （含2000kg 和5000kg ）的客户有两种销售方案（客户只能选择其中一种方案）：方案A ：每千克6.8元，由基地免费送货；方案B ：每千克6元，客户需支付运费2000元.（1）请分别写出按方案A ，方案B 购买这种火龙果的应付款y （元）与购买数量x （kg ）之间的函数表达式；（2）求购买量在什么范围时，选择方案A 比方案B 付款少？（3）某水果批发商计划用30000元，选用这两种方案中的一种，购买尽可能多的这种火龙果，他应选择哪种方案？B 卷（50分）一、填空题（本大题共5个小题，每小题4分，共20分）19、（4分）当x ＝2018时，22111x x x x ----的值为____．20、（4分）如图，以Rt ABC ∆的两条直角边分别向外作等腰直角三角形．若斜边5AB =，则图中阴影部分的面积为_____．21、（4分）如图，ABC ∆的中位线5DE cm =，把ABC ∆沿DE 折叠，使点A 落在边BC 上的点F 处，若A 、F 两点之间的距离是8cm ，则ABC ∆的面积为______2cm ；22、（4分）已知2019x y +=，20202019-=x y ，则22x y -的值为___________．23、（4分）我市在旧城改造中，计划在市内一块如下图所示的三角形空地上种植草皮以美化环境，已知这种草皮每平方米售价a 元，则购买这种草皮至少需要______元.二、解答题（本大题共3个小题，共30分）24、（8分）解方程()21450x x +-=；()()()23222x x x -=-.25、（10分）如图，一次函数y =2x +4的图象分别与x 轴，y 轴教育点A 、点B 、点C 为x 轴一动点。

江苏省徐州市撷秀中学2016届九年级数学10月段考试题一、选择题（本大题共8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填在答题卡相应位置上）1．方程x2=4x的解是（）A．0 B．4 C．0或﹣4 D．0或42．导学案课前预习要求设计4幅既是轴对称又是中心对称的图案，小明设计完成了下列4幅图案，其中符合要求的个数是（）A．1个B．2个C．3个D．4个3．方程3x2+4x﹣2=0的根的情况是（）A．两个不相等的实数根B．两个相等的实数根C．没有实数根D．无法确定4．已知⊙O的半径是6cm，点O到同一平面内直线l的距离为5cm，则直线l与⊙O的位置关系是（）A．相交 B．相切 C．相离 D．无法判断5．如图，四边形ABCD是圆内接四边形，E是BC延长线上一点，若∠BAD=105°，则∠DCE的大小是（）A．115°B．105°C．100°D．95°6．如图，⊙O的半径为5，弦AB的长为8，点M在线段AB（包括端点A，B）上移动，则OM的取值范围是（）A．3≤OM≤5 B．3≤OM＜5 C．4≤OM≤5 D．4≤OM＜57．下列说法中，不正确的是（）A．过圆心的弦是圆的直径B．等弧的长度一定相等C．周长相等的两个圆是等圆D．同一条弦所对的两条弧一定是等弧8．如图，AD、BC是⊙O的两条互相垂直的直径，点P从点O出发，沿O→C→D→O的路线匀速运动，设∠APB=y（单位：度），那么y与点P运动的时间x（单位：秒）的关系图是（）A．B．C．D．二、填空题（本大题共10小题，每小题3分，共30分，不需写出解答过程，请把答案填写在答题卡相应位置上）9．方程3x（x﹣1）=2（x+2）化成一般形式为．10．请你写出一个有一根为1的一元二次方程：．（答案不唯一）11．如图，点A，B，C都在圆O上，若∠C=34°，则∠AOB的度数为．12．如图，C是以AB为直径的⊙O上一点，已知AB=5，BC=3，则圆心O到弦BC的距离是．13．如图，AB是⊙O的直径，点C在AB的延长线上，CD切⊙O于点D，连接AD．若∠A=25°，则∠C= 度．14．若直角三角形的两直角边长分别为6，8，则这个三角形的外接圆直径是．15．某药品原价每盒25元，经过两次连续降价后，售价每盒16元．则该药品平均每次降价的百分数是．16．若x=1是关于x的一元二次方程x2+3mx+n=0的解，则6m+2n= ．17．直角三角形的两直角边是3：4，而斜边的长是15cm，那么这个三角形的面积是．18．如图，每个正方形由边长为1的正方形组成，正方形中黑色、白色小正方形的排列规律如图所示，在边长为n（n≥1）的正方形中，设黑色小正方形的个数为P1，白色小正方形的个数为P2，当偶数n= 时，P2=5P1．三、解答题（本大题共8小题，共计86分．请在答题卡指定区域内作答，解答时应写出证明过程或演算步骤）19．（1）计算：（1﹣）0+|﹣|﹣（﹣1）2015+（）﹣1（2）解方程：（x+4）2=5（x+4）20．如图，在单位长度为1的正方形网格中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格图中进行下列操作：（1）利用网格线确定该圆弧所在圆的圆心D点的位置，并写出D点的坐标为；（2）利用网格线过C点画出⊙D的切线．21．已知关于x的方程mx2+x+1=0，试按要求解答下列问题：（1）当该方程有一根为1时，试确定m的值；（2）当该方程有两个不相等的实数根时，试确定m的取值范围．22．如图，学校准备修建一个面积为48m2的矩形花园．它的一边靠墙，其余三边利用长20m的围栏．已知墙长9m，问围成矩形的长和宽各是多少？23．小明在研究由矩形纸片折叠等边三角形之后，经过探究，他用圆形纸片也折叠出了等边三角形，以下是他的折叠过程：第一步：将圆形纸片沿直径AM对折，然后打开；第二步：将纸片沿折痕BC 翻折使点M落在圆心I处，然后打开，连接AB、AC．（1）在图③中BC与IM的位置关系是；（2）小明折叠出的△ABC是等边三角形吗？请你说明理由．24．某工厂现有80台机器，每台机器平均每天生产300件产品，现准备增加一批同类机器以提高生产总量，在试生产中发现，由于其它生产条件没变，因此每增加一台机器，每台机器平均每天将少生产4件产品．问应增加多少台机器，才可以使每天的生产总量达到22000件？25．阅读新知：移项且合并同类项之后，只含有偶次项的四次方程称作双二次方程．其一般形式为ax4+bx2+c=0（a≠0），一般通过换元法解之，具体解法是设 x2=y，则原四次方程化为一元二次方程：ay2+by+c=0，解出y之后代入x2=y，从而求出x的值．例如解：4x4﹣8y2+3=0解：设x2=y，则原方程可化为：4y2﹣8y+3=0∵a=4，b=﹣8，c=3∴b2﹣4ac=﹣（﹣8）2﹣4×4×3=16＞0∴y==∴y1=，∴y2=∴当y1=时，x2=∴x1=，x2=﹣；当y1=时，x2=∴x3=，x4=﹣小试牛刀：请你解双二次方程：x4﹣2x2﹣8=0归纳提高：思考以上解题方法，试判断双二次方程的根的情况，下列说法正确的是（选出所有的正确答案）①当b2﹣4ac≥0时，原方程一定有实数根；②当b2﹣4ac＜0时，原方程一定没有实数根；③当b2﹣4ac≥0，并且换元之后的一元二次方程有两个正实数根时，原方程有4个实数根，换元之后的一元二次方程有一个正实数根一个负实数根时，原方程有2个实数根；④原方程无实数根时，一定有b2﹣4ac＜0．26．如图，在平面直角坐标系中，面积为16cm2的正方形AOBC的边OA、OB分别在y轴、x轴上，点P在x轴上自左向右运动，连接PA，将PA绕点P顺时针旋转90°到PD，连接DB，设PO=xcm．（1）OA= cm；（2）在点P运动的过程中，△PDB的面积可以达到正方形面积的吗？若能，请求出x的值；若不能，请说明理由．（3）连接AB，当点P在OB边上（不含点O、B）运动时，以点A为圆心、以AB为半径的圆与△PDB 的边DB相切吗，为什么？江苏省徐州市撷秀中学2016届九年级上学期段考数学试卷（10月份）参考答案与试题解析一、选择题（本大题共8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填在答题卡相应位置上）1．方程x2=4x的解是（）A．0 B．4 C．0或﹣4 D．0或4【考点】解一元二次方程-因式分解法．【分析】先移项，然后利用“提取公因式法”将方程的左边转化为两个因式的积的形式．【解答】解：由原方程，得x2﹣4x=0，提取公因式，得x（x﹣4）=0，所以x=0或x﹣4=0，解得，x=0或x=4．故选D．【点评】本题考查了解一元二次方程﹣﹣因式分解法．解一元二次方程常用的方法有直接开平方法，配方法，公式法，因式分解法，要根据方程的特点灵活选用合适的方法．2．导学案课前预习要求设计4幅既是轴对称又是中心对称的图案，小明设计完成了下列4幅图案，其中符合要求的个数是（）A．1个B．2个C．3个D．4个【考点】中心对称图形；轴对称图形．【专题】应用题．【分析】根据轴对称图形与中心对称图形的定义，对每个图形分析、解答．【解答】解：第一、二、三个图形既是轴对称图形又是中心对称图形；第四个图形是轴对称图形，不是中心对称图形．故选C．【点评】本题主要考查了轴对称图形和中心对称图形，熟记轴对称图形和中心对称图形的定义，是解答本题的基础．3．方程3x2+4x﹣2=0的根的情况是（）A．两个不相等的实数根B．两个相等的实数根C．没有实数根D．无法确定【考点】根的判别式．【分析】首先求出方程的判别式，然后根据一元二次根与判别式的关系，可以判断方程的根的情况．【解答】解：∵方程3x2+4x﹣2=0中，△=42﹣4×3×（﹣2）=40＞0，∴方程有两个不相等的实数根．故选A．【点评】本题考查了一元二次方程根的情况与判别式△的关系：（1）△＞0⇔方程有两个不相等的实数根；（2）△=0⇔方程有两个相等的实数根；（3）△＜0⇔方程没有实数根．4．已知⊙O的半径是6cm，点O到同一平面内直线l的距离为5cm，则直线l与⊙O的位置关系是（）A．相交 B．相切 C．相离 D．无法判断【考点】直线与圆的位置关系．【分析】设圆的半径为r，点O到直线l的距离为d，若d＜r，则直线与圆相交；若d=r，则直线与圆相切；若d＞r，则直线与圆相离，从而得出答案．【解答】解：设圆的半径为r，点O到直线l的距离为d，∵d=5，r=6，∴d＜r，∴直线l与圆相交．故选：A．【点评】本题考查的是直线与圆的位置关系，解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定．5．如图，四边形ABCD是圆内接四边形，E是BC延长线上一点，若∠BAD=105°，则∠DCE的大小是（）A．115°B．105°C．100°D．95°【考点】圆内接四边形的性质．【专题】计算题．【分析】根据圆内接四边形的对角互补得到∠BAD+∠BCD=180°，而∠BCD与∠DEC为邻补角，得到∠DCE=∠BAD=105°．【解答】解：∵四边形ABCD是圆内接四边形，∴∠BAD+∠BCD=180°，而∠BCD+∠DCE=180°，∴∠DCE=∠BAD，而∠BAD=105°，∴∠DCE=105°．故选B．【点评】本题考查了圆内接四边形的性质：圆内接四边形的对角互补．也考查了邻补角的定义以及等角的补角相等．6．如图，⊙O的半径为5，弦AB的长为8，点M在线段AB（包括端点A，B）上移动，则OM的取值范围是（）A．3≤OM≤5 B．3≤OM＜5 C．4≤OM≤5 D．4≤OM＜5【考点】垂径定理；勾股定理．【专题】压轴题．【分析】当M与A或B重合时，达到最大值；当OM⊥AB时，为最小．【解答】解：当M与A或B重合时，达到最大值，即圆的半径5；当OM⊥AB时，为最小值==3．故OM的取值范围是：3≤OM≤5．故选A．【点评】本题考查的是勾股定理和最值．本题容易出现错误的地方是对点M的运动状态不清楚，无法判断什么时候会为最大值，什么时候为最小值．7．下列说法中，不正确的是（）A．过圆心的弦是圆的直径B．等弧的长度一定相等C．周长相等的两个圆是等圆D．同一条弦所对的两条弧一定是等弧【考点】圆的认识．【分析】根据直径定义、弧长和圆周长的计算公式，以及圆心角定理可得答案．【解答】解：A、过圆心的弦是圆的直径，说法正确；B、等弧的长度一定相等，说法正确；C、周长相等的两个圆是等圆，说法正确；D、同一条弦所对的两条弧一定是等弧，说法错误，应是在同圆或等圆中，同一条弦所对的两条弧一定是等弧；故选：D．【点评】此题主要考查了圆的认识，关键是掌握有关定义和定理．8．如图，AD、BC是⊙O的两条互相垂直的直径，点P从点O出发，沿O→C→D→O的路线匀速运动，设∠APB=y（单位：度），那么y与点P运动的时间x（单位：秒）的关系图是（）A．B．C．D．【考点】动点问题的函数图象．【分析】根据图示，分三种情况：（1）当点P沿O→C运动时；（2）当点P沿C→D运动时；（3）当点P沿D→O运动时；分别判断出y的取值情况，进而判断出y与点P运动的时间x（单位：秒）的关系图是哪个即可．【解答】解：（1）当点P沿O→C运动时，当点P在点O的位置时，y=90°，当点P在点C的位置时，∵OA=OC，∴y=45°，∴y由90°逐渐减小到45°；（2）当点P沿C→D运动时，根据圆周角定理，可得y=90°÷2=45°；（3）当点P沿D→O运动时，当点P在点D的位置时，y=45°，当点P在点0的位置时，y=90°，∴y由45°逐渐增加到90°．故选：D．【点评】（1）此题主要考查了动点问题的函数图象，解答此类问题的关键是通过看图获取信息，并能解决生活中的实际问题，用图象解决问题时，要理清图象的含义即学会识图．（2）此题还考查了圆周角定理的应用，要熟练掌握，解答此题的关键是要明确：在同圆或等圆中，同弧或等弧所对的圆周角相等；相等的圆周角所对的弧也相等．二、填空题（本大题共10小题，每小题3分，共30分，不需写出解答过程，请把答案填写在答题卡相应位置上）9．方程3x（x﹣1）=2（x+2）化成一般形式为3x2﹣5x﹣4=0 ．【考点】解一元二次方程-因式分解法．【分析】根据单项式乘以多项式的运算，移项、合并同类项，整理即可得解．【解答】解：3x（x﹣1）=2（x+2），3x2﹣3x=2x+4，3x2﹣3x﹣2x﹣4=0，3x2﹣5x﹣4=0．故答案为：3x2﹣5x﹣4=0．【点评】本题考查了一元二次方程的一般形式：ax2+bx+c=0（a，b，c是常数且a≠0），去括号的过程中要注意符号的变化，不要漏乘，移项要变号．10．请你写出一个有一根为1的一元二次方程：x2=1 ．（答案不唯一）【考点】一元二次方程的解．【专题】开放型．【分析】可以用因式分解法写出原始方程，然后化为一般形式即可．【解答】解：根据题意x=1得方程式x2=1．故本题答案不唯一，如x2=1等．【点评】本题属于开放性试题，主要考查一元二次方程的概念的理解与掌握．可以用因式分解法写出原始方程，然后化为一般形式即可，如（y﹣1）（y+2）=0，后化为一般形式为y2+y﹣2=0．11．如图，点A，B，C都在圆O上，若∠C=34°，则∠AOB的度数为68°．【考点】圆周角定理．【分析】由点A，B，C都在圆O上，若∠C=34°，根据在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．即可求得答案．【解答】解：∵点A，B，C都在圆O上，∠C=34°，∴∠AOB=2∠C=68°．故答案为：68°．【点评】此题考查了圆周角定理．此题比较简单，注意掌握数形结合思想的应用．12．如图，C是以AB为直径的⊙O上一点，已知AB=5，BC=3，则圆心O到弦BC的距离是 2 ．【考点】圆周角定理；勾股定理；三角形中位线定理；垂径定理．【专题】计算题．【分析】过O点作OD⊥BC，D点为垂足，则DB=DC，所以OD为△BAC的中位线，即有OD=AC；由AB 为⊙O的直径，得到∠ACB=90°，由勾股定理可求得AC，即可得到OD的长．【解答】解：过O点作OD⊥BC，D点为垂足，如图，∵AB为⊙O的直径，∴∠ACB=90°，∴AB2=BC2+AC2，即AC==4，又∵OD⊥BC，∴DB=DC，而OA=OB，∴OD为△BAC的中位线，即有OD=AC，所以OD=×4=2，即圆心O到弦BC的距离为2．故答案为2．【点评】本题考查了圆周角定理．在同圆或等圆中，同弧和等弧所对的圆周角相等，一条弧所对的圆周角是它所对的圆心角的一半．同时考查了勾股定理和垂径定理以及中位线的性质．13．如图，AB是⊙O的直径，点C在AB的延长线上，CD切⊙O于点D，连接AD．若∠A=25°，则∠C= 40 度．【考点】切线的性质；圆周角定理．【专题】计算题．【分析】连接OD，由CD为圆O的切线，利用切线的性质得到OD垂直于CD，根据OA=OD，利用等边对等角得到∠A=∠ODA，求出∠ODA的度数，再由∠COD为△AOD外角，求出∠COD度数，即可确定出∠C的度数．【解答】解：连接OD，∵CD与圆O相切，∴OD⊥DC，∵OA=OD，∴∠A=∠ODA=25°，∵∠COD为△AOD的外角，∴∠COD=50°，∴∠C=90°﹣50°=40°．故答案为：40【点评】此题考查了切线的性质，等腰三角形的性质，以及外角性质，熟练掌握切线的性质是解本题的关键．14．若直角三角形的两直角边长分别为6，8，则这个三角形的外接圆直径是10 ．【考点】三角形的外接圆与外心；勾股定理．【分析】由直角三角形的两直角边长分别为6，8，可求得其斜边，又由直角三角形的斜边是其外接圆的直径，即可求得答案．【解答】解：∵直角三角形的两直角边长分别为6，8，∴斜边长为：=10，∴这个三角形的外接圆直径是10．故答案为：10．【点评】此题考查了三角形的外接圆的性质．此题难度不大，注意直角三角形的斜边是其外接圆的直径．15．某药品原价每盒25元，经过两次连续降价后，售价每盒16元．则该药品平均每次降价的百分数是20% ．【考点】一元二次方程的应用．【专题】增长率问题．【分析】设该药品平均每次降价的百分率为x，根据降价后的价格=降价前的价格（1﹣降价的百分率），则第一次降价后的价格是25（1﹣x），第二次后的价格是25（1﹣x）2，据此即可列方程求解．【解答】解：设该药品平均每次降价的百分率为x，由题意可知经过连续两次降价，现在售价每盒16元，故25（1﹣x）2=16，解得x=0.2或1.8（不合题意，舍去），故该药品平均每次降价的百分率为20%．故答案为：20%．【点评】此题考查了一元二次方程的应用中数量平均变化率问题．原来的数量（价格）为a，平均每次增长或降低的百分率为x的话，经过第一次调整，就调整到a（1±x），再经过第二次调整就是a（1±x）（1±x）=a（1±x）2．增长用“+”，下降用“﹣”．16．若x=1是关于x的一元二次方程x2+3mx+n=0的解，则6m+2n= ﹣2 ．【考点】一元二次方程的解．【分析】先把x=1代入x2+3mx+n=0，得到3m+n=﹣1，再把要求的式子进行整理，然后代入即可．【解答】解：把x=1代入x2+3mx+n=0得：1+3m+n=0，3m+n=﹣1，则6m+2n=2（3m+n）=2×（﹣1）=﹣2；故答案为：﹣2．【点评】此题考查了一元二次方程的解，解题的关键是把x的值代入，得到一个关于m，n的方程，不要求m．n的值，要以整体的形式出现．17．直角三角形的两直角边是3：4，而斜边的长是15cm，那么这个三角形的面积是54cm2．【考点】勾股定理．【分析】根据直角三角形的两直角边是3：4，设出两直角边的长分别是3x、4x，再根据勾股定理列方程求解即可．【解答】解：设两直角边分别是3x、4x，根据勾股定理得：（3x）2+（4x）2=225，解得：x=±3（负值舍去），则3x=9，4x=12．故这个三角形的面积是×9×12=54cm2．故答案为：54cm2．【点评】此题主要根据勾股定理来确定等量关系，也考查了三角形的面积公式．18．如图，每个正方形由边长为1的正方形组成，正方形中黑色、白色小正方形的排列规律如图所示，在边长为n（n≥1）的正方形中，设黑色小正方形的个数为P1，白色小正方形的个数为P2，当偶数n= 12 时，P2=5P1．【考点】一元二次方程的应用；规律型：图形的变化类．【分析】此题找规律时，显然应分两种情况分析：当n是奇数时，黑色小正方形的个数是对应的奇数；当n是偶数时，黑色小正方形的个数是对应的偶数．分别表示偶数时P1和P2的值，然后列方程求解，进行分析．【解答】解：观察图形可知：1，5，9，13，…，则（奇数）2n﹣1；4，8，12，16，…，则（偶数）2n．由上可知n为偶数时P1=2n，白色与黑色的总数为n2，∴P2=n2﹣2n，根据题意假设存在，则n2﹣2n=5×2n，n2﹣12n=0，解得n=12，n=0（不合题意舍去）．故存在偶数n=12，使得P2=5P1．故答案为：12．【点评】此题考查了一元二次方程的应用，以及规律型：数字得变化类，弄清题意是解本题的关键．此题的难点在于必须分情况找规律．三、解答题（本大题共8小题，共计86分．请在答题卡指定区域内作答，解答时应写出证明过程或演算步骤）19．（1）计算：（1﹣）0+|﹣|﹣（﹣1）2015+（）﹣1（2）解方程：（x+4）2=5（x+4）【考点】实数的运算；零指数幂；负整数指数幂；解一元二次方程-因式分解法．【专题】计算题；实数；一次方程（组）及应用．【分析】（1）原式第一项利用零指数幂法则计算，第二项利用绝对值的代数意义化简，第三项利用乘方的意义计算，最后一项利用负整数指数幂法则计算即可得到结果；（2）方程移项后，利用因式分解法求出解即可．【解答】解：（1）原式=1++1+4=+6；（2）方程移项得：（x+4）2﹣5（x+4）=0，分解因式得：（x+4）（x+4﹣5）=0，解得：x1=﹣4，x2=1．【点评】此题考查了实数的运算，以及解一元二次方程﹣因式分解法，熟练掌握运算法则是解本题的关键．20．如图，在单位长度为1的正方形网格中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格图中进行下列操作：（1）利用网格线确定该圆弧所在圆的圆心D点的位置，并写出D点的坐标为（2，0）；（2）利用网格线过C点画出⊙D的切线．【考点】切线的判定；垂径定理．【分析】（1）利用垂径定理可作AB和BC的垂直平分线，两线的交点即为D点，可得出D点坐标；（2）连接OC，作出与OC垂直的直线CE即可．【解答】解：（1）如图1，分别作AB、BC的垂直平分线，两线交于点D，∴D点的坐标为（2，0），故答案为：（2，0）；（2）连接OC，作出与OC垂直的直线CE，CE即为过C点的⊙D的切线，如图2所示．【点评】本题主要考查了切线的判定方法、垂径定理、确定圆心的方法；由线段垂直平分线确定出点D的坐标是解题的关键．21．已知关于x的方程mx2+x+1=0，试按要求解答下列问题：（1）当该方程有一根为1时，试确定m的值；（2）当该方程有两个不相等的实数根时，试确定m的取值范围．【考点】根的判别式；一元二次方程的解．【专题】计算题．【分析】（1）将x=1代入方程得到关于m的方程，求出方程的解即可得到m的值；（2）由方程有两个不相等的实数根，得到根的判别式的值大于0，列出关于m的不等式，求出不等式的解集即可得到m的范围．【解答】解：（1）将x=1代入方程得：m+1+1=0，解得：m=﹣2；（2）由方程有两个不相等的实数根，得到△=b2﹣4ac=1﹣4m＞0，且m≠0，解得：m＜且m≠0．【点评】此题考查了一元二次方程根的判别式，根的判别式的值大于0，方程有两个不相等的实数根；根的判别式的值等于0，方程有两个相等的实数根；根的判别式的值小于0，方程没有实数根．22．如图，学校准备修建一个面积为48m2的矩形花园．它的一边靠墙，其余三边利用长20m的围栏．已知墙长9m，问围成矩形的长和宽各是多少？【考点】一元二次方程的应用．【专题】几何图形问题．【分析】设宽为xm，则长为m，然后根据48平方米的长方形即可列出方程，解方程即可解决问题．【解答】解：设宽为x m，则长为m．由题意，得 x•=48，解得 x1=4，x2=6．当x=4时，20﹣2×4=12＞9（舍去），当x=6时，20﹣2×6=8．答：围成矩形的长为8m、宽为6m．【点评】此题是利用一元二次方程解决实际问题，解题关键是找到关键描述语，从而找到等量关系准确的列出方程．23．小明在研究由矩形纸片折叠等边三角形之后，经过探究，他用圆形纸片也折叠出了等边三角形，以下是他的折叠过程：第一步：将圆形纸片沿直径AM对折，然后打开；第二步：将纸片沿折痕BC 翻折使点M落在圆心I处，然后打开，连接AB、AC．（1）在图③中BC与IM的位置关系是互相垂直平分；（2）小明折叠出的△ABC是等边三角形吗？请你说明理由．【考点】翻折变换（折叠问题）．【分析】（1）利用折叠的性质易得IM垂直平分BC，BC垂直平分IM，即BC和IM互相垂直平分；（2）连结IB、BM、MC，如图，由BC和IM互相垂直平分可判断四边形BMCI为菱形，易得△IBM和△TMC为等边三角形，则∠BIM=∠CIM=60°，然后根据圆周角定理得到∠BAC=∠BIC=60°，加上AB=AC，于是可判断△ABC为等边三角形．【解答】解：（1）∵圆形纸片沿直径AM对折，∴IM垂直平分BC，∵纸片沿折痕BC翻折使点M落在圆心I处，∴BC垂直平分IM，即BC和IM互相垂直平分；故答案为互相垂直平分；（2）△ABC为等边三角形．理由如下：连结IB、BM、MC，如图，∵BC和IM互相垂直平分，∴四边形BMCI为菱形，∴IB=BM=MC=IC，∴IB=BM=MC=IC=IM，∴△IBM和△TMC为等边三角形，∴∠BIM=∠CIM=60°，∴∠BAC=∠BIC=60°，而AM垂直平分BC，∴AB=AC，∴△ABC为等边三角形．【点评】本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了等边三角形的判定．24．某工厂现有80台机器，每台机器平均每天生产300件产品，现准备增加一批同类机器以提高生产总量，在试生产中发现，由于其它生产条件没变，因此每增加一台机器，每台机器平均每天将少生产4件产品．问应增加多少台机器，才可以使每天的生产总量达到22000件？【考点】一元二次方程的应用．【分析】设增加x台机器，可以使每天的生产总量达到22000件，根据题意列出方程，解方程即可．【解答】解：设增加x台机器，依题意得：（80+x）（300﹣4x）=22000，解得x1=20，x2=﹣25（不合题意，舍去）．答：应增加20台机器，才可以使每天的生产总量达到22000件．【点评】本题考查了一元二次方程的应用、一元二次方程的解法；根据题意列出方程是解决问题的关键．25．阅读新知：移项且合并同类项之后，只含有偶次项的四次方程称作双二次方程．其一般形式为ax4+bx2+c=0（a≠0），一般通过换元法解之，具体解法是设 x2=y，则原四次方程化为一元二次方程：ay2+by+c=0，解出y之后代入x2=y，从而求出x的值．例如解：4x4﹣8y2+3=0解：设x2=y，则原方程可化为：4y2﹣8y+3=0∵a=4，b=﹣8，c=3∴b2﹣4ac=﹣（﹣8）2﹣4×4×3=16＞0∴y==∴y1=，∴y2=∴当y1=时，x2=∴x1=，x2=﹣；当y1=时，x2=∴x3=，x4=﹣小试牛刀：请你解双二次方程：x4﹣2x2﹣8=0归纳提高：思考以上解题方法，试判断双二次方程的根的情况，下列说法正确的是①②③④（选出所有的正确答案）①当b2﹣4ac≥0时，原方程一定有实数根；②当b2﹣4ac＜0时，原方程一定没有实数根；③当b2﹣4ac≥0，并且换元之后的一元二次方程有两个正实数根时，原方程有4个实数根，换元之后的一元二次方程有一个正实数根一个负实数根时，原方程有2个实数根；④原方程无实数根时，一定有b2﹣4ac＜0．【考点】换元法解一元二次方程．【专题】阅读型．【分析】先设y=x2，则原方程变形为y2﹣2y﹣8=0，运用因式分解法解得y1=﹣2，y2=4，再把y=﹣2和4分别代入y=x2得到关于x的一元二次方程，然后解两个一元二次方程，最后确定原方程的解．根据阅读新知和小试牛刀即可判断①②③④．【解答】解：x4﹣2x2﹣8=0设y=x2，则原方程变为：y2﹣2y﹣8=0．分解因式，得（y+2）（y﹣4）=0，解得，y1=﹣2，y2=4，当y=﹣2时，x2=﹣2，x2+2=0，△=0﹣4×2＜0，此方程无实数解；当y=4时，x2=4，解得x1=﹣2，x2=2，所以原方程的解为x1=﹣2，x2=2．根据阅读新知和小试牛刀即可判断①②③④；故答案为①②③④．【点评】本题考查了换元法解一元二次方程：当所给方程是双二次方程时，可考虑用换元法降次求解．26．如图，在平面直角坐标系中，面积为16cm2的正方形AOBC的边OA、OB分别在y轴、x轴上，点P在x轴上自左向右运动，连接PA，将PA绕点P顺时针旋转90°到PD，连接DB，设PO=xcm．（1）OA= 4 cm；（2）在点P运动的过程中，△PDB的面积可以达到正方形面积的吗？若能，请求出x的值；若不能，请说明理由．（3）连接AB，当点P在OB边上（不含点O、B）运动时，以点A为圆心、以AB为半径的圆与△PDB 的边DB相切吗，为什么？【考点】圆的综合题．【分析】（1）由正方形的面积即可得出OA的长；（2）连接AD、AB，作DM⊥OB于M，则∠DMB=90°，由正方形的性质得出∠ABO=45°，OB=OA=4cm，由勾股定理得出AB，由旋转的性质得出∠APD=90°，PD=PA，证出△APD是等腰直角三角形，得出∠ADP=∠ABO，证出A、P、D、B四点共圆，由圆周角定理和圆内接四边形的性质得出。

2018年江苏省徐州市初中毕业、升学考试数学学科满分：140分一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置）1．（2018江苏徐州，1，3分）4的相反数是A．14 B．14- C．4 D．－4【答案】D2．（2018江苏徐州，2，3分）下列计算正确的是A．2221a a-=B．22()ab ab=C．235a a a+=D．236()a a=3．（2018江苏徐州，3，3分）下列图形中，既是轴对称图形，又是中心对称图形的是A．B．C．D．【答案】A4．（2018江苏徐州，4，3分）右图是由5个相同的正方体搭成的几何体，其左视图是A．B．C．D．【答案】D5．（2018江苏徐州，5，3分）抛掷一枚质地均匀的硬币，若前3次都是正面朝上，则第4次正面朝上的概率A．小于12B．等于12C．大于12D．无法确定【答案】A6．（2018江苏徐州，6，3分）某市从不同学校随机抽取100名初中生，对“学校统一使用数学教辅用书的册数”进行调查，统计结果如下：册数0 1 2 3人数13352923关于这组数据，下列说法正确的是A．众数是2册B．中位数是2册C．极差是2册D．平均数是2册【答案】B7．（2018江苏徐州，7，3分）如图，在平面直角坐标系中，函数y kx=与2yx=-的图象交于A、B两点，过A作y轴的垂线，交函数4yx=的图象于点C．连接BC，则△ABC的面积为A．2 B．4 C．6 D．8【答案】C8．（2018江苏徐州，8，3分）若函数y kx b=+的图象如图所示，则关于x的不等式20kx b+<的解集为A．3x<B．3x>C．6x<D．6x>【答案】D二、填空题9．（2018江苏徐州，9，3分）五边形的内角和为 .【答案】540°10．（2018江苏徐州，10，3分）我国自主研发的某型号手机处理器采用10nm工艺，已知1nm＝0.000 000 001m，则10nm用科学计数法可表示为 .【答案】1×10－8nm11．（2018江苏徐州，11，3分）化简：32-＝ .【答案】2－312．（2018江苏徐州，12，3分）若2x-在实数范围内有意义，则x的取值范围是 .【答案】x≥213．（2018江苏徐州，13，3分）若2m＋n＝4，则代数式6－2m－n的值为 .【答案】214．（2018江苏徐州，14，3分）若菱形的两条对角线的长分别为6cm和8cm，则其面积为cm2. 【答案】2415．（2018江苏徐州，15，3分）如图，Rt△ABC中，∠ABC＝90°，D为AC的中点，若∠C＝55°，则∠ABD＝ .【答案】35°16．（2018江苏徐州，16，3分）如图，扇形的半径为6，圆心角θ为120°，用这个扇形围成一个圆锥的侧面，所得圆锥的底面半径为 .【答案】217．（2018江苏徐州，17，3分）如图，每个图案均有边长相等的黑、白两色正方形按规律拼接而成，照此规律，第n个图案中白色正方形比黑色正方形多个（用含n的代数式表示）.【答案】4n＋318．（2018江苏徐州，18，3分）如图，AB为⊙O的直径，AB＝4，C为半圆AB的中点.P为AC上一动点，延长BP至点Q，使BP•BQ＝AB2.若点P由A运动到C，则点Q的运动路径长为 .【答案】419．（2018•徐州，19①，5）计算：（1）2013112018()82--+-+；（2）2222a b a ba b a b-+÷--．【解答过程】原式＝－1＋1－2＋2＝019.（2018•徐州，19②，5）计算：（2）2222a b a ba b a b-+÷--．【解答过程】原式＝()()22a b a b a ba b a b+--⨯-+＝22a b-20．（2018•徐州，20①，5）解方程：2210x x-+=；【解答过程】解：把方程左边因式分解得：（2x＋1）(x－1)＝0，∴x1＝12-，x2＝1．20．（2018•徐州，20①，5）解不等式组：4281136x xx x>-⎧⎪-+⎨≤⎪⎩．【解答过程】解不等式4x>2x－8，可得x>－4，解不等式1136x x-+≤，得3x≤，所以不等式组的解集为：43x-<≤．21．（2018•徐州，21，7分）不透明的袋中装有1上红球与2个白球，这些球除颜色外都相同，将其搅匀．（1）从中摸出1个球，恰为红球的概率等于；（2）从中同时摸出2个球，摸到红球的概率是多少？（用树状图或列表的方法写出分析过程）【解答过程】（1）13；（2）列表如下：红球白球1 白球2红球白球1 ＋红球白球2＋红球白球1 红球＋白球1 白球2＋白球1 白球2 红球＋白球2 白球1 ＋白球2一共有6种等可能事件，摸到红球的情况有4种，所以(42 63P==摸到红球）．22．（2018•徐州，22，7分）在”书香校园“活动中，某校为了解学生家庭藏书情况，随机抽取本校部分学生进行调查，并绘制成部分统计图表如下：家庭藏书情况统计表类别家庭藏书情况统计表学生人数A 0≤m≤25 20B 26≤m≤100 aC 101≤m≤200 50D m≥201 66根据以下信息，解答下列问题：（1）该样本容量为，a＝；（2）在扇形统计图中，“A”对应的扇形的圆心角为；（3）若该校有2000名学生，请估计全校学生中家庭藏书200本以上的人数．【解答过程】（1）200，64；（2）36（3）662000200⨯＝660（名）答：家庭藏书200本以上的人数为660名．23．（2018•徐州，23，8分）如图，在矩形ABCD中，AD＝4，点E在边AD上，连接CE，以CE为边向右上方作正方形CEFG，作FH⊥AD，垂足为H，连接AF．（1）求证：FH＝ED；（2）当AE为何值时，△AEF的面积最大？【解答过程】（1）∵四边形CGFE 是正方形， ∴EF ＝CE ，∠EFC ＝90°， ∴∠FEH ＋∠CED ＝90°， ∵FH ⊥AD∴∠FEH ＋∠EFH ＝90°， ∴∠EFH ＝∠CED ， 在△FEH 和△ECD 中，EFH CED FHE EDC EF EC ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△FEH ≌△ECD ， ∴FH ＝ED ．（2）设AE ＝x ，由（1）可得：FH ＝DE ＝(4－x )， ∴2111(4)2222AEF S AE FH x x x x ∆=⨯=-=-+， ∵ 102-<，∴当x ＝212()2-⨯-＝2时， △AEF 的面积最大．24．（2018•徐州，24，8分）徐州至北京的高铁里程约为700km ，甲、乙两人从徐州出发，分别乘坐“徐州号”高铁与“复兴号”高铁B 前往北京．已知A 车的平均速度比B 车的平均速度慢80km /n ，A 车的行驶时间比B 车的行驶时间多40%，两车的行驶时间分别为多少？【解答过程】设B 车行驶的时间为x 小时间，则A 车行驶的时间为（1＋40%）x 小时， 根据题意：70070080(140%)x x+=+，解得：x ＝2.5，经检验x ＝2.5是分式方程的解． （1＋40%）x ＝3.5小时．答两车行驶时间分别为3.5小时和2.5小时．25．（2018•徐州，25，8分）如图，AB为⊙O的直径，点Ｃ在⊙O外，∠ABC的平分线与⊙O交于点Ｄ，∠Ｃ＝90°．（1）CD与⊙O有怎么的位置关系？请说明理由；（２）若∠CDB＝60°，AB＝6，求AD的长．【解答过程】解：（1）连接OD，则OD＝OB，∴∠2＝∠3，∵BD平分∠ABC，∴∠2＝∠1，∴∠1＝∠3，∴OD∥BC，321CDOA∵∠C＝90°，∴BC⊥CD，∴OD⊥CD，∴CD是⊙O的切线．（2）∵∠CDB＝60°，∠C＝90°，∴∠2＝∠1＝∠3＝30°，∴∠AOD＝∠2＋∠3＝30°＋30°＝60°，∵AB＝6，∴OA＝3，∴603180ADππ=⨯⨯=．26．（2018•徐州，26，8分）如图，1号数在2号楼的南侧，两楼的高度均为90m，楼间距为AB．冬至日正午，太阳光线与水平面所成的角为32.3°，1号数在2号楼墙面上的影高为CA；春分日正午，太阳光线与水平面所成的角为55.7°，1号数在2号楼墙面上的影高为DA．已知CD＝42m．（1）求楼间距AB；（2）若2号楼共有30层，层高均为3m，则点C位于第几层？（参考数据：sin32.3°≈0.53，cos32.3°≈0.85，tan32.3°≈0.63，sin55.7°≈0.83，cos55.7°≈0.56，tan55.7°≈1.47）．【解答过程】解：（1）过点C，D分别作CE⊥PB，DF⊥PB，垂足分别为E，F．则有AB＝CE＝DF，EF＝CD＝42．2号楼1号楼FEDCP由题意可知：∠PCE＝32.3°，∠PDF＝55.7°，在Rt△PCE中，PE＝CE⨯tan32.3°＝0.63CE；在Rt△PDF中，PF＝CE⨯tan55.7°＝1.47CE；∵PF－PE＝EF，∴1.47CE－0.63CE＝42，∴AB＝CE＝50（m）答：楼间距为50m．（2）由（1）得：PE＝0.63CE＝31.5（m），∴AC＝BP－PE＝90－31.5＝58.5（m），58.53÷＝19.5，∴点C位于第20层答：点C位于第20层．27．（2018江苏徐州，27，10分）如图，在平面直角坐标系中，二次函数y＝－x2+6x－5的图像与x轴交于A、B两点，与y轴交于点C，其顶点为P，连接PA、AC、CP，过点C作y轴的垂线l，（1）求点P、C的坐标；（2）直线l上是否存在点Q，使△PBQ的面积等于△PAC的面积的2倍？若存在，求出点Q的坐标，若不存在，请说明理由。

A. unknown)9. _________ :A. WhateverB. HoweverC. Whenever)10. 一Tommy, don't make a mess in your room.—OK, Mum, I'll ________ my toys at once. A. take ont B. put awayC ・ play with)11. Tile International Robot Show at 10:00 a.m. and2018年徐州市中考总复习九下阶段复习综合测试、单项填空。

(15分))1. The Nobel Prize in Literature 2012 was awarded to Mo Yan, ____________ famous Chinesewrite 匚And he is ______ f irst Chinese to win the prize. A. a; aB. a; theC. lhe; theD. the; a)2. —Look at the clouds, so beautiful!—Wow, so many different _________ , such as horses, sheep, flowers, etc. A. sizes B. shapes C ・ colours D. styles )3. We decide to make _______ a rule for us roommates to turn off the lights at 10:30 p.m. A. thatB. thisC. itD. one)4. —Life on Mars will be better than life on Earth ___________ many ways. —But I think there are also many disadvantages ________________ living there. A. on; to B. in; of C. at; of D. for; to )5. You can park on ____ s ide of the road. Look at the sign H No parking"1. A. bothB. noneC ・ eitherD. neither)6. ~ _________ do you know about Columbus?一Oh, he is a great man who discovered America.A. WhatB. WhoC. WhereD. Which)7. Nick's brother ________ the navy in 2011 and _________ the navy since then.A. joined; has joinedB. joined in; has joined in C ・ joined in; has been in D. joined; has been in)8. The side effects(副作用)that the medicine has are still ___________ to us. More research isneeded ・ B. unnecessary C. unusual D.uncommonyoudo, don !t miss the play, for iCs so hard for me to get the tickets. D. WhetherD. look for _ at 4:30 p.m.A. is open; is closedB. opens; closesC. open; closeD. opened; is closed)12. Wang Yaping and Liu Yang are our __________ i n China ・ We?e proud _______ them.A. women astronauts; ofB. woman astronauts; ofC. women astronauts; inD. woman astronauts; in)13. —Hello, may I speak to Tom? —Please hold on and Fll __________ you _________A. put; ontB. put; off C ・ put; through D. put; on)14. The light bulb which was invented by Edison ____________ now ・A. was widely used B ・ is widely used C ・ will be widely usedD. used widely)15・—China's first moon car H Yutu n has arrived on the Moon surface ・一 ____________ ! Ifs a huge step for our space exploratioruA. My pleasureB. Good ideaC. How excitingD. Good luck、完形填空。

江苏省徐州市撷秀中学2024届中考英语模拟精编试卷含答案注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

Ⅰ. 单项选择1、For everyone’s safety，we _______ always remember the law against driving after drinking.A．could B．should C．might D．would2、---What’s your hobby ? ---______collecting balls, I also like different kinds of CDs.A．Besides B．Except C．Beside D．About3、Excuse me. Can you tell me ______?A．where is there a good place to liveB．where a good place to liveC．where is a good place to liveD．where there is a good place to live4、Never ____ till tomorrow what may be done today. In this way, you can get most and learn best.A．put on B．put down C．put off5、--- May I speak to John?--- Sorry, he ____________Japan. But he _________in two days.A．has been to, will come backB．has gone to, will be backC．has been in, would come backD．has gone to, won't cone back6、My grandparents live in an old apartment with floors and they are on the floor.A．fifth; three B．fifth; third C．five; three D．five;: third7、An _________ is a scientific test that is done to study what happens and to get new knowledge.A．experiment B．experience C．advantage8、Our history teacher is very ________. She never plays jokes with us.A．serious B．funny C．nervous D．patient9、—I think this skirt is very nice.—I agree. But it’s 500 yuan. I don’t think I can it.A．afford B．find C．put D．see10、There are fewer and fewer tigers in India. The situation will continue _______ humans stop hunting them for their fur and bones.A．if B．unless C．because D．sinceⅡ. 完形填空11、If actions speak 1 than words, in the following story, perhaps sweet is also louder.Mr. Hathway's students stuck some sweets on a large piece of cardboard. It 2 , "To Mr. Hathway. You are a special teacher. I have loved all your lessons this year. Thank you for turning me into a wonderful world this year. It's the summer holiday now, so take time out to have a 3 . You should have a nice picnic, but be 4 with the lion. Or you just lie on the beach(海滩). I'll 5 you a lot like jelly(果冻).You are one in a million.Rob Hathway, who has been teaching Year 6 pupils(小学生), told the BBC he was sad to see his kids leave but this present will often make him 6 them."I was so thankful for teaching such a 7 class. On the last Thursday of term I got chocolates, cards and wine from my pupils, but when this one was given to me, I was so 8 by it. I was a bit sad to see them off 9 glad that they have done so well and got ready for the next step at middle school."When asked if he would 10 all the chocolate bars, Mr. Hathway said he just ate chocolate sometimes but as there was quite a lot he would share it with his family.Sweet!1．A．louder B．bigger C．longer D．higher2．A．has B．says C．writes D．copies3．A．rest B．time C．test D．sleep4．A．friendly B．careful C．careless D．polite5．A．miss B．forget C．thank D．help6．A．think B．think of C．think through D．think over7．A．big B．scary C．lovely D．natural8．A．sad B．tired C．surprised D．lucky9．A．so B．and C．when D．but10．A．eat B．drink C．sell D．buyⅢ. 语法填空12、Dear editor,Last week I 1．(visit) our zoo, and I was very surprised 2．(find) hardly anyone there. Zoos are important places .They are like living textbooks for young people. They provide homes for many endangered animals and help to educate the public about 3．(care) for them. If we 4．(not support) our zoos, they 5．(not have) enough money to take care of so many fine animals. I urge all of your readers to visit our wonderful zoo soon.Sincerely,Animal FriendⅣ. 阅读理解A13、根据表中信息选择最佳答案。

九年级语文质量抽测试卷时间：120分钟 分值:120分 出卷人:张洪武一、基础积累与运用（27分） 1、古诗词默写（10分）①过尽千帆皆不是，_____________，______________ 。

(温庭筠《望江南》) ②塞下秋来风景异，_______________。

(范仲淹《渔家傲·秋思》) ④李清照《武陵春》中写愁的诗句是源_______________，_______________。

⑤《观刈麦》中最能体现劳动人民辛苦劳动场景的句子是_______________， ____________。

⑥更深月色半人家，_______________。

(刘方平《月夜》) ⑦_______________，人迹板桥霜。

(温庭筠《商山早行》) ⑧_______________，只有香如故。

(陆游《卜算子·咏梅》) 2、下列注音全部正确的一项是( )（3分）A. 相契 qi è 枘凿 r ùi 喑哑 y īn 廓然无累ku ò B 襁褓 qi ǎng 灵柩 ji ù 分外 f èn 强聒不舍gu ō C. 栖息 q ī 油膏g ǎo 留滞 zh ì 欺上媚下m èi D. 不朽 xi ǔ 田圃 p ǔ 曙光 sh ǔ 气吞斗牛do ù 3、下列词语书写全部正确的一项是( )（3分）A. 凌驾 风骚 睿智 脑羞成怒B.扶掖 佝偻 凭吊 言行相故C. 损落 禁锢 亵渎 重倒覆辙D.灰烬 庸碌 旁骛 恪尽职守 4.阅读下面文字，回答（1）—（3）题。

（6分）我扑向七月的清晨，深深地呼吸着雨后甜润的空气。

瞬（）间，我惊住了，像是无意中扑进了一幅巨大的画卷，失去了中心和方向。

我的眼前，一片xi āng （ ）着露珠的绿茵茵的草滩，草滩上生长着黄灿灿的油菜花，在这绿色和黄色的背后，又xi án （ ）接着一派无边无际的蓝色湖水。

2018-2019 第二学期撷秀期末考试试卷二、选择题（每小题1分，共15分）21.________ film The Wandering Earth was shown in February. It is really ________ amazing film.A. A; aB. The; anC. A; theD. The; a22. -- I’ll do some washing Jack, would you please clean the floor?-- Why ________? Susan is sitting there doing nothing.A. herB. sheC. myD. me23. Would you like to share the room ________ your brother?A. andB. onC. ofD. with24. Let’s open the window and enjoy some ________ air?A. gentleB. freshC. luckyD. famous25. -- You should write a ________ passage in the English exam.-- I think it’s not difficult for us to write ________ if you try your best.A. 70 words; 70 wordsB. 70 –word; 70 wordsC. 70 words; 70-wordD. 70 words; 70- words26. I always believe that ________ is difficult if we try our best to do it.A. somethingB. anythingC. everythingD. nothing27. ________ my home, you will go ________ a post office.A. On your way; pastB. On your way; passC. On your way to; pastD. On your way to; passed28. -- Look at the boy running there. Is it David?-- It ________ be him. I saw him in the classroom just now.A. mustn’tB. can’tC. couldn’tD. must29. Wow, your classroom is clean and tidy! Who ________ it just now?A. cleanedB. cleansC. will cleanD. is cleaning30. -- What did you do the day before yesterday?-- My family went camping. We ________ a tent near the lake. It was great fun.A. put onB. put upC. put outD. put away31. -- Do ants rest? I think they’re moving around ________?-- Sure. They rest when they are tired just like us.A. at that timeB. at the same timeC. all the timeD. some time32. -- I ________ my key at school, mum.-- You are always that ________!A. forgot; carefulB. forgot; carelessC. left; carefulD. left; careless33. -- ________ is it from your home to Wanda Plaza?-- It’s only about 1km.A. How longB. How oftenC. How farD. How soon34. -- Listen! Someone is playing the piano.-- Wow! ________ wonderful music!A. HowB. How anC. WhatD. What an35. -- Do you think it is a good idea to eat chicken soup when you have a cold?-- ________. Many people agree with it.A. Sooner or laterB. No problem.C. Never mind.D. Believe it or not.三、完形填空（每小题1分，共10分）There was a young flower in the desert where all was dry and sad-looking. It was growing by itself, ____36____ every day and saying to the sun, " ____37____ shall I grow up?" And the sun would say "Be patient! Each time I____38____ you, you grow a little." She was happy, ____39____ she would have a chance to bring beauty to this corner of sand. And this is ____40____ she wanted to do--bring a little bit of beauty to this world.One day a hunter came by and stepped on her. She was going to die and she felt so ____41____. Not because she was dying, but because she would____42____ have a chance to bring a little bit of beauty to this corner of the desert. A small person with wings saw her. He reached ____43____ and touched her -- and gave her a ____44____ life. From then on, she ____45____ to grow up again. At last, she grew up to be a beautiful flower. And this corner of the desert also became so beautiful because of the little flower.36.A. playing B. sleeping C. enjoying D. standing37.A. When B. How C. What D. Why38.A. hit B. feed C. touch D. love39.A. because B. but C. or D. so40.A. that B. what C. why D. which41.A. afraid B. sad C. tired D. happy42.A. never B. always C. seldom D. often43. A. up B. in C. down D. off44.A. first B. second C. third D. fourth45.A. stopped B. forgot C. wanted D. started四、阅读理解（每小题2分，共20分）A46. Mr. Smith plans to take his 14-year-old daughter and 10-year-old son to the zoo. How much should he pay in all?A. $ 30. 00B. $24. 00C. $18. 00D. $12. 0047. When is the visiting time?A. At 8:30 a.m. on Monday.B. At 9:30 a.m. on Friday.C. At 3:00 p.m. on Sunday.D. At 5:00 p.m. on Tuesday.48. What can we do at the zoo?A. Give some food to the dogs.B. Touch the monkey.C. Go close to the animals.D. Take a few nice photos.BI'm thankfulI am thankful for my dog and my cat,And my teddy bear so soft and fat.I am thankful for potatoes,And for nice ________,And for all the nice food that my mum cooks.I am thankful for my mum and my dad.They both love me whether(是否）I am good or bad.I am thankful for the flowers,And cool summer showers(阵雨）。