第十讲 图形的剪拼

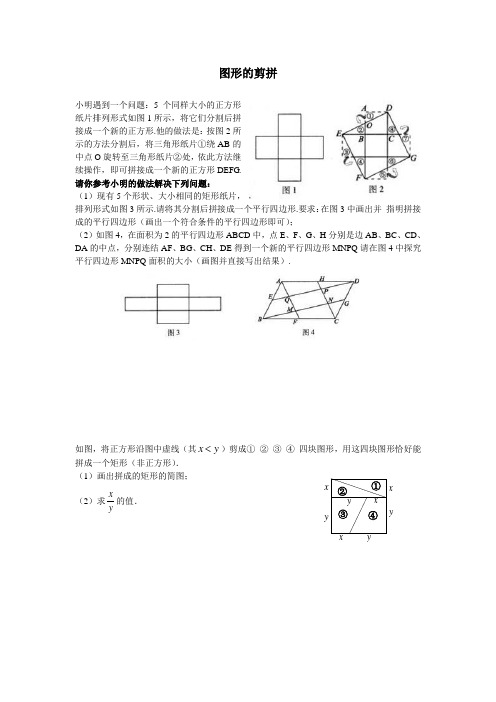
图形的剪拼小明遇到一个问题：5个同样大小的正方形纸片排列形式如图1所示，将它们分割后拼接成一个新的正方形.他的做法是：按图2所示的方法分割后，将三角形纸片①绕AB 的中点O 旋转至三角形纸片②处，依此方法继续操作，即可拼接成一个新的正方形DEFG . 请你参考小明的做法解决下列问题：（1）现有5个形状、大小相同的矩形纸片，排列形式如图3所示.请将其分割后拼接成一个平行四边形.要求：在图3中画出并 指明拼接成的平行四边形（画出一个符合条件的平行四边形即可）；（2）如图4，在面积为2的平行四边形ABCD 中，点E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点，分别连结AF 、BG 、CH 、DE 得到一个新的平行四边形MNPQ 请在图4中探究平行四边形MNPQ 面积的大小（画图并直接写出结果）.如图，将正方形沿图中虚线（其x y ）剪成① ② ③ ④ 四块图形，用这四块图形恰好能拼成一个矩形（非正方形）． （1）画出拼成的矩形的简图；（2）求xy的值．yy xy x y x x④③②①小明想把一个三角形拼接成面积与它相等的矩形．他先进行了如下部分操作，如图1所示：①取△ABC 的边AB 、AC 的中点D 、E ，联结DE ；②过点A 作AF ⊥DE 于点F ；（1）请你帮小明完成图1的操作，把△ABC 拼接成面积与它相等的矩形．（2）若把一个三角形通过类似的操作拼接成一个与原三角形面积相等的正方形，那么原三角形的一边与这边上的高之间的数量关系是________________．（3）在下面所给的网格中画出符合（2）中条件的三角形，并将其拼接成面积与它相等的正方形．已知等边三角形纸片ABC 的边长为8，D 为AB 边上的点，过点D 作DG BC ∥交AC 于点G ．DE BC ⊥于点E ，过点G 作GF BC ⊥于点F ，把三角形纸片ABC 分别沿DG DE GF ，，按图1所示方式折叠，点A B C ，，分别落在点A '，B '，C '处．若点A '，B '，C '在矩形DEFG 内或其边上，且互不重合，此时我们称A B C '''△（即图中阴影部分）为“重叠三角形”．（1）若把三角形纸片ABC 放在等边三角形网格中（图中每个小三角形都是边长为1的等边三角形），点A B C D ，，，恰好落在网格图中的格点上．如图2所示，请直接写出此时重叠三角形A B C '''的面积；（2）实验探究：设AD 的长为m ，若重叠三角形A B C '''存在．试用含m 的代数式表示重叠三角形A B C '''的面积，并写出m 的取值范围（直接写出结果，备用图供实验，探究使用）．ABCDEF（图1）A GC F B ' C ' E BD A '图1 AG C F B ' C ' E B D A ' 图2 A A解：（1）重叠三角形A B C '''的面积为 ；（2）用含m 的代数式表示重叠三角形A B C '''的面积为 ；m 的取值范围为 ．问题：现有5个边长为1的正方形，排列形式如图1，请把它们分割后拼接成一个新的正方形．要求：画出分割线并在正方形网格图（图中每个小正方形的边长均为1）中用实线画出拼接成的新正方形．小东同学的做法是：设新正方形的边长为(0)x x >．依题意，割补前后图形的面积相等，有25x =，解得5x =．由此可知新正方形的边长等于两个正方形组 成的矩形对角线的长．于是，画出如图2所示的分割线，拼出如图3所示的新正方形．请你参考小东同学的做法，解决如下问题：现有10个边长为1的正方形，排列形式如图4，请把它们分割后拼接成一个新的正方形．要求：在图4中画出分割线，并在图5的正方形网格图（图中每个小正方形的边长均为1）中用实线画出拼接成的新正方形． 说明：直接画出图形，不要求写分析过程． 解：图1 图2 图3 图4 图5图4F E DC BA如图1是一个三棱柱包装盒，它的底面是边长为10cm 的正三角形，三个侧面都是矩形．现将宽为15cm 的彩色矩形纸带AMCN 裁剪成一个平行四边形ABCD （如图2），然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴（要求包贴时没有重叠部分），纸带在侧面缠绕三圈，正好将这个三棱柱包装盒的侧面全部包贴满．在图3中，将三棱柱沿过点A 的侧棱剪开，得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究. （1）请在图4中画出拼接后符合条件的平行四边形； （2）请在图2中，计算裁剪的角度（即∠ABM 的度数）.已知菱形纸片ABCD 的边长为8，∠A=60°，E 为AB 边上的点，过点E 作E F ∥BD 交AD 于点F ．将菱形先沿EF 按图1所示方式折叠，点A 落在点A '处，过点A '作GH ∥BD 分别交线段BC 、DC 于点G 、H,再将菱形沿GH 按图1所示方式折叠，点C 落在点C '处， C G '与C 'H 分别交A E '与A F '于点M 、N ．若点C '在△CN DBMA 图2图1C'A 'N M HG FE DCBAAB CDE F GHM N A 'C'DCBAA 'EF 的内部或边上，此时我们称四边形A MC N ''（即图中阴影部分）为“重叠四边形”．图1 图2 备用图（1）若把菱形纸片ABCD 放在菱形网格中（图中每个小三角形都是边长为1的等边三角形），点A 、B 、C 、D 、E 恰好落在网格图中的格点上．如图2所示，请直接写出此时重叠四边形A MC N ''的面积；（2）实验探究：设AE 的长为m ，若重叠四边形A MC N ''存在．试用含m 的代数式表示重叠四边形A MC N ''的面积，并写出m 的取值范围（直接写出结果，备用图供实验，探究使用）． 解：（1）重叠四边形A MC N ''的面积为 ；（2）用含m 的代数式表示重叠四边形A MC N ''的面积为______________；m 的取值范围为_____________．1）观察与发现小明将三角形纸片()ABC AB AC >沿过点A 的直线折叠，使得AC 落在AB 边上，折痕为AD ，展开纸片（如图①）；再次折叠该三角形纸片，使点A 和点D 重合，折痕为EF ，展平纸片后得到AEF △（如图②）．你认为AEF △是什么形状的三角形？A A图⑤图④图③GF FC'GD'FABCDEABC D EABCD E（2）实践与运用将矩形纸片ABCD （AB ＜CD ）沿过点B 的直线折叠，使点A 落在BC 边上的点F 处，折痕为BE （如图③）；再沿过点E 的直线折叠，使点D 落在BE 上的点D '处，折痕为EG （如图④）；再展平纸片（如图⑤）．猜想△EBG 的形状，证明你的猜想，并求图⑤中∠FEG 的大小．（1）如图22（1），△ABC 中，DE ∥BC 分别交AB ，AC 于D ，E 两点，过点E 作EF ∥AB 交BC 于点F ．请按图示数据填空：四边形DBFE 的面积S = ，△EFC 的面积1S = ， △ADE 的面积2S = ． 22（1）探究发现（2）在（1）中，若BF a =，FC b =，DE 与BC 间的距离为h ．请证明2124S S S =． 拓展迁移（3）如图22（2），□DEFG 的四个顶点在△ABC 的三边上，若△ADG 、△DBE 、△GFC 的面积分别为2、5、3，试利用．．（2．）中的结论．．．．求△ABC 的面积． 22（2）问题背景：在△ABC 中，AB 、BC 、AC 三边的长分别为2、13、17，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格(每个小正方形的边长为1)，再在网BCDG FE AB CD FEAS1S 2 S 3 6 2格中画出格点△ABC （即△ABC 三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC 的高，而借用网格就能计算出它的面积．AB C图3图2图1(1)请你将△ABC 的面积直接填写在横线上．________ 思维拓展：(2)我们把上述求△ABC 面积的方法叫做构图法．若△ABC 三边的长分别为2a 、25a 、26a (0)a >，请利用图2的正方形网格(每个小正方形的边长为a )画出相应的△ABC ，并求出它的面积是： ． 探索创新：(3)若△ABC 三边的长分别为224m n +、2216m n +、222m n +(0,,)m n o m n >>≠ ，请运用构图法在图3指定区域内画出示意图，并求出△ABC 的面积为： ．小伟遇到这样一个问题：如图1，在梯形ABCD 中，AD ∥BC ，对角线AC 、BD 相交于点O ．若梯形ABCD 的面积为1，试求以AC 、BD 、AD ＋BC 的长度为三边长的三角形的面积．A B D CE F 图3小伟是这样思考的：要想解决这个问题，首先应想办法移动这些分散的线段，构造一个三角形，再计算其面积即可．他先后尝试了翻折、旋转、平移的方法，发现通过平移可以解决这个问题．他的方法是过点D 作AC 的平行线交BC 的延长线于点E ，得到的△BDE 即是以AC 、BD 、AD ＋BC 的长度为三边长的三角形(如图2)．参考小伟同学的思考问题的方法，解决下列问题：如图3，△ABC 的三条中线分别为AD 、BE 、CF ．(1)在图3中利用图形变换画出并指明以AD 、BE 、CF的长度为三边长的一个三角形(保留画图痕迹)； (2)若△ABC 的面积为1，则以AD 、BE 、CF 的长度为三边长的三角形的面积等于_______． 如图1，在△ABC 中，已知∠BAC ＝45°，AD ⊥BC 于D ，BD ＝2，DC ＝3，求AD 的长. 小萍同学灵活运用轴对称知识，将图形进行翻折变换如图1.她分别以AB 、AC 为对称轴，画出△ABD 、△ACD 的轴对称图形，D 点的对称点为E 、F ，延长EB 、FC 相交于G 点，得到四边形AEGF 是正方形.设AD =x ，利用勾股定理，建立关于x 的方程模型，求出x 的值. （1）请你帮小萍求出x 的值.(2) 参考小萍的思路，探究并解答新问题： 如图2，在△ABC 中，∠BAC ＝30°，AD ⊥BC 于D ，AD ＝4.请你按照小萍的方法画图,得到四边形AEGF ，求△BGC 的周长.（画图所用字母与图1中的字母对应）图1 图222．阅读下列材料：小明遇到一个问题：如图1，正方形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 和DA 边上靠近A 、B 、C 、D 的n 等分点，连结AF 、BG 、CH 、DE ，形成四边形MNPQ ．求四边形MNPQ 与正方形ABCD 的面积比（用含n 的代数式表示）．小明的做法是：先取n=2，如图2，将△ABN 绕点B 顺时针旋转90゜至△CBN ′，再将△ADM 绕点D 逆时针旋转90゜至△CDM ′，得到5个小正方形，所以四边形MNPQ 与正方形ABCD 的面积比是15； BBCAD OADC EO图2图1然后取n=3，如图3，将△ABN 绕点B 顺时针旋转90゜至△CBN ′，再将△ADM 绕点D 逆时针旋转90゜至△CDM ′，得到10个小正方形，所以四边形MNPQ 与正方形ABCD 的面积比是410，即25； ……请你参考小明的做法，解决下列问题：（1）在图4中探究n=4时四边形MNPQ 与正方形ABCD 的面积比（在图4上画图并直接写出结果）；（2）图5是矩形纸片剪去一个小矩形后的示意图，请你将它剪成三块后再拼成正方形（在图5中画出并指明拼接后的正方形）．22. 阅读下列材料：小贝遇到一个有趣的问题：在矩形ABCD 中，AD=8cm ，AB=6cm. 现有一动点P 按下列方式在矩形内运动：它从A 点出发，沿着AB 边夹角为45︒的方向作直线运动，每次碰到矩形的一边，就会改变运动方向，沿着与这条边夹角为45︒的方向作直线运动，并且它一直按照这种方式不停地运动，即当P 点碰到BC 边，沿着BC 边夹角为45︒的方向作直线运动，当P 点碰到CD 边，再沿着与CD 边夹角为45︒的方向作直线运动，…，如图1所示，问P 点第一次与D 点重合前与边相碰几次，P 点第一次与D 点重合时所经过的路线的总长是多少. 小贝的思考是这样开始的：如图2，将矩形ABCD 沿直线CD 折迭，得到矩形A 1B 1CD ，由轴对称的知识，发现P 2P 3=P 2E ，P 1A=P 1E.请你参考小贝的思路解决下列问题：M’N’Q P N G H F E DCB A M Q P NG H F E D C B A M M’N’M A B C D E F H G N P Q C P G D Q H M N F B E A 图图 图1 图3 图4图5 圖1 ABC D P P 1P 2 P 3 A B C D EP A 1 P 1 P 2 P 3 B 1 圖2(1) P 点第一次与D 点重合前与边相碰_____次；P 点从A 点出发到第一次与D 点重合时所经过的路径的总长是_________cm ；(2) 进一步探究：改变矩形ABCD 中AD 、AB 的长，且满足AD>AB ，动点P 从A 点出发，按照阅读材料中动点的运动方式，并满足前后连续两次与边相碰的位置在矩形ABCD 相邻的两边上。

（五年级）备课教员：***第十讲图形的剪拼一、教学目标：知识目标掌握不同类型的图形的剪拼方法。

能力目标经历观察、思考、分析、交流、归纳、抽象等活动，进一步培养学生的应用知识的能力及动手操作能力。

情感目标体验从身边得到数学规律的成就感，在解题中感受动手操作带来的成就感，体验数学充满探索和创造的乐趣。

二、教学重点：根据题目找到合适的方法进行剪拼。

三、教学难点：分割线的确立与拼接中应用图形特殊性质灵活应用。

四、教学准备：PPT、一样的直角非等腰三角形和长方形卡片若干五、教学过程：第一课时（50分钟）一、导入（5分)【设计意图：通过简单的图形拼合，让学生理解拼合的概念，逐步引入本堂课图形的剪拼的学习。

】师：同学们，这个是什么图形？生：直角三角形。

师：是的。

你觉得这两个三角形能拼成什么图形呢？大家动手试一试。

生1：大三角形。

生2：长方形。

生3：平行四边形。

师：大家都非常棒。

按一定的要求可以把几个图形拼成一个图形，叫做图形的拼合。

现在将三角形放下，请你们用手中的长方形剪出你们认为好看的图形。

生1：两个三角形。

生2：两个长方形。

生：……师：非常好。

把一个图形按某种要求分成几个图形，就叫做图形的分割。

如果用你们剪开的图形再拼成新的一个新的图形，叫做图形的剪拼。

那么这节课我们就一起来学习图形的剪拼。

【探究新知，引入新课：学生已经熟悉了各种组合图形的面积计算，这节课我们就将所学的数学知识应用到图形的剪拼当中。

】【板书课题：图形的剪拼】二、探索发现授课（40分）（一）例题1：（10分）下面的十个图形都是由六个面积为1平方厘米的小正方形拼成的，但周长却不完全相同，周长等于12厘米的图形有几个？讲解重点：复习周长的概念，封闭图形一周的长度叫做周长。

然后重点介绍用平移法巧求周长。

师：同学们还记得什么叫周长吗？生：图形封闭一周的长度。

师：是的。

题目让我们找出这十个图形中周长为12厘米的图形。

那么可以怎么找呢？生：找出这些图形外围有几个小正方形的边长。

本讲主要学习三大图形处理方法：1．理解掌握图形的分割； 2．理解掌握图形的拼合； 3．理解图形的剪拼．本讲中很多类型的题目还要求同学们去动手尝试．通过本讲知识的学习，让同学们了解不同图形的分割、拼合、剪拼的方法，锻炼同学们的平面想象能力以及增强学生的动手操作能力． 把一个几何图形按某种要求分成几个图形，就叫做图形的分割．反过来，按一定的要求也可以把几个图形拼成一个完美的图形，就叫做图形的拼合． 将一个或者多个图形先分割开，再拼成一种指定的图形，则叫做图形的剪拼． 我们在图形的分割、拼合和剪拼的过程中，都要结合所提供的图形特点来思考．如果把一个图形分割成若干个大小、形状相等的部分，那么就要想办法找图形的对称点，把图形先分少，再分多．图形中，如果有数量方面的要求，可以先从数量入手，找出平分后每块上所含数量的多少，再结合数量来分割图形．如果是要把几个图形拼合成一个大图形，要特别注意每条边的长度，把相等的边长拼合在一起，先拼少的，再拼多的．如果是剪拼图形，要抓住“剪、拼前后图形的面积相等”这个关键，根据已知条件和图形的特点，通过分析推理和必要的计算，确定剪拼的方法．板块一 图形的分割【例 1】 用一条线段把一个长方形平均分割成两块，一共有多少种不同的分割法？BAO【解析】 怎样把一个图形按照规定的要求分割成若干部分呢？这就是图形的分割问题．按照规定的要求合理分割图形，是很讲究技巧的，多做这种有趣的训练，可以培养学生的创造性思维，发展空间观念，丰富想象，提高观察能力．这道题要求把长方形平均分割成两块，过长方形中心的任意一条直线都可以把长方形平均分割成两块，根据这点给出如下分法(如右图)： ⑴ 做长方形的两条对角线，设交点为O⑵ 过O 点任作一条直线AB ，直线AB 将长方形平均分割成两块．知识点拨例题精讲教学目标第四讲：图形的剪拼可见用线段平分长方形的分法是无穷多的．【巩固】画一条直线，将六边形分成大小相等、形状相同的两部分，这样的直线有 条． 【解析】 无数条．任何过六边形中心的直线均符合要求．【例 2】 把任意一个三角形分成面积相等的4个小三角形，有许多种分法．请你画出4种不同的分法． 【解析】 根据等底等高的三角形面积相等这一结论，只要把原三角形分成4个等底等高的小三角形，它们的面积必定相等．而要得到这4个等底等高的小三角形，只需把原三角形的某条边四等分，再将各分点与这边相对的顶点连接起来就行了．根据上面的分析，可得如左下图所示的三种分法．又因为4 1 4 22=⨯=⨯，所以，如果我们把每一个小三角形的面积看做1，那么14⨯就可以视为把三角形的面积直接分成4等份，即分成4个面积为1的小三角形；而22⨯可以视为先把原三角形分成两等份，再把每一份分别分成两等份．根据前面的分析，在每次等分时，都要想办法找等底等高的三角形． 根据上面的分析，又可以得到如右下图的另两种分法．AB C C B AABC【例 3】 怎样把一个等边三角形分别分成8块和9块形状、大小都一样的三角形．→ 【解析】 ⑴分成8块的方法是：先取各边的中点并把它们连接起来，得到4个大小、形状相同的三角形，然后再把每一个三角形分成两部分，得到如左上图所示的图形．⑵分成9块的方法是：先把每边三等分，然后再把分点彼此连接起来，得到加上右上图所示的符合条件的图形．【例 4】 下图是一个直角梯形，请你画一条线段，把它分成两个形状相同并且面积相等的四边形．321DC BA 1FE 221D C B A【解析】 直角梯形的上底为1，下底为2，要分成两个相同的四边形，需要一条边可以分成1和2，AD 边长正好为3，所以AD 边分成两段，找到AD 的三等分点E ，现在，CD AE =，DE AB =，BF EF =，所以还要找到BC 的中点F ，连接EF ，就把梯形ABCD 分成完全相同的两部分．如右上图．【例 5】 在一块长方形的地里有一正方形的水池(如下图)．试画一条直线把除开水池外的这块地平分成两块．AO【解析】 用连对角线的办法找出这块长方形地的中心O 和正方形水池的中心A ．过O 、A 画一条直线，这条直线正好能把除开水池外的这块地平分为两块(如右上图)．【例 6】 把下图四等分，要求剪成的每个小图形形状、大小都一样．除了剪正方形外，你还有别的方法吗？2060402020【解析】 先把图形分成2040⨯相等的两块，每一块中再分成相等的两份，这样就不难分成四块了，如右上图．【例 7】 下图是一个34⨯的方格纸，请用四种不同的方法将它分割成完全相同的两部分，但要保持每个小方格的完整．【解析】 分成的两块每块有1226÷=(个)小格，并且这两块要关于中心点对称，大小和形状完全一样，我们从对称线入手，介绍一种分割技巧——染色法，先选中一个小格，找它关于中心点或中心线的对称位置，标上相应的符号．当找它关于中心线的对称位置时是一种情况，关于中心点的对称位置是另一种情况，具体如下图所示．【例 8】 下图是一个被挖去了为总面积四分之一小正方形的大正方形，请你将它分成大小形状完全一样的四部分．【解析】 要求把阴影部分分成四个大小、形状都相同的四个图形，先不考虑形状，大小相同也就是面积相等，也就是把整个图形的面积分成四份，分割后的每一部分占一份．考虑先把阴影部分分成12个小正方形再分成四份，这样每份正好有3个小正方形．再看形状，三个小正方形只能排成“－”形或者“∟”形．答案如下图．【例 9】 下图是由五个正方形组成的图形．把它分成形状、大小都相同的四个图形，应怎样分？【解析】 如果不考虑分成的四个图形的形状，只考虑它们的面积，这就要求把原来五个正方形分成四个面积相等的图形，每个图形的面积应是1个多正方形．我们把每个正方形各分成四个面积相等的小正方形，分成的每块图形应有五个这样的小正方形．根据图形的对称性，我们很快就能得到如右上图的分法．也可以将中间的正方形分成四个小正方形，如右上图．【例 10】 已知左下图是由同样大小的5个正方形组成的．试将图形分割成4块形状、大小都一样的图形．【解析】 已知图形是由同样大小的5个正方形组成的，要分成4块同样大小的图形，则每块图形是54个正方形．由此想到，若把每个正方形都分成4等份，则分割成的每一块中应包含5份．再稍经试验，即得右上图的解(图内部的实线为分割线)．【例 11】下图是由18个小正方形组成的图形，请你把它分成6个完全相同的图形．【解析】 通过计算，18÷6=3，说明基本形状是由三个小正方形组成，三个正方形有两种形式：与，通过观察，上面的图形具有对称性，不可能分成6个，再由6结合染色法，如下图．666555444333222111【例 12】 一个正三角形形状的土地上有四棵大树(如下图所示)，现要把这块正三角形的土地分成和它形状相同的四小块，并且要求每块地中都要有一棵大树．应怎样分？【解析】 由于土地的形状为正三角形，由题意可知，把大三角形的面积分成四份，每一块占一份，且形状与原三角形相同，于是我们想到取大正三角形的各边中点，依次连接各边中点，即可将这块大正三角形的土地分成与它相等的四份，如右上图所示．【总结】本题若死守三角形面积等于底⨯高的一半，则无以下手，引导学生转换一下思考角度，取原三角形各边中点，将原三角形分成面积相等的四部分，问题即可解决．【例 13】 将下图分割成大小、形状相同的三块，使每一小块中都含有一个○．【解析】 图中一共有18个小方格，要求分割成大小、形状相同的三块，每一块有：1836÷=(块)，而且分割成大小、形状相同的三块，可以看出图形的中心点是O ，而且上面的部分是对称的，但是只有5块，需要对称的再加上一块，再由图形的特点，可以判断应分为右下图的三部分．O【例 14】 请把下面这个长方形沿方格线剪成形状、大小都相同的4块，使每一块内都含有“奥数读本”这四个字中的一个，该怎么剪？本读数奥【解析】 图中“奥数”与“读本”中的两个字都是挨着的，所以肯定要在它们中间分割，因此，首先在他们中间划出分割线，因为要将这个长方形分成大小、形状完全相同的4块，因为长方形是64⨯的，所以分割后的每一块都有6小块组成，可以考虑先把长方形分成相同的两部分，再把每一部分分成相同的两部分，如下图所示．本读数奥答案不唯一．板块二 图形的拼合【例 15】 用两块大小一样的等腰直角三角形能拼成几种常见的图形？ 【解析】 建议用等腰直角三角板，把不同的边进行重合，不要漏掉旋转重合，或者准备一些等腰直角三角形的纸片，由学生拼接后贴到黑板上，见下图：【例 16】下面哪些图形自身用4次就能拼成一个正方形？【解析】 用4块图(4)和图(5)那样的图形显然能够拼成一个大正方形．其实用图(1)、图(2)、图(3)也能拼成一个大正方形，拼法见下图．【例 17】用下面的3个图形，拼成右边的大正方形．【解析】 首先数一数所有的空格数，一共只有16个，只能组成44⨯的正方形，使用目标倒推法，在右边的大正方形中拼图，仍然使用染色法，相当于把已知图形往右边的大正方形中放，这样就很容易拼合了，如下图：【例 18】有6个完全相同的，你能将它们拼成下面的形状吗？【解析】 利用染色法以及图形的对称性，对称轴两侧都有三个小图形，按照下面的顺序标号即可完成．1111＇1＇1＇→2222＇2＇2＇1111＇1＇1＇→3＇3＇3＇3332222＇2＇2＇1111＇1＇1＇【例 19】(保良局亚洲区城市小学数学邀请赛)三种塑料板的型号如图：(A ) (B ) (C )已有A 型板30块，要购买B 、C 两种型号板若干，拼成55⨯正方形10个，B 型板每块价格5元，C 型板每块价格为4元．请你考虑要各买多少块，使所花的总钱数尽可能少，那么购买B 、C 两种板要花多少元？【解析】 要使花的钱尽可能的少，已有30个A 型板最好能用上，而价格较贵的B 型板尽可能少用，因为A型与B 型的面积都为3，所以在拼成的55⨯的正方形中，除了C 型外，余下的面积应能被3整除．有25449-⨯=或254121-⨯=能被3整除知，只能用4块C 型板或1块C 型板，考虑尽可能多地使用A 型板，有如下图1、图2 的拼法：BC CCC B AAA AAA BC A图1 图2图1的拼法要花445226⨯+⨯=(元)，图2的拼法要花459+=(元)，因为只有30块A 型板，所以在10快55⨯的正方形中，图2的拼法只能有4块，剩下6块用图1拼法，共需：94266192⨯+⨯=(元)【例 20】试用图a 中的8个相等的直角三角形，拼成图b 中的空心正八边形和图c 中的空心正八角星．【解析】 把一个直角三角形的斜边与另一个直角三角形的一条直角边重合，同时，斜边上的一个锐角顶点与直角顶点重合，像这样依次摆放下去，便可得空心正八边形．若把一个直角三角形的斜边与另一个直角三角形的直角边的一部分重合，但顶点均不重合，依次摆放下去，便可由这八个相等的直角三角形组成空心正八角星．练习1. 把任意一个三角形分成面积相等的2个小三角形，有许多种分法．请你画出3种不同的分法．AB CC B ACBA【解析】 根据等底等高的三角形面积相等这一结论，只要把原三角形分成2个等底等高的小三角形，它们的面积必定相等．而要得到这2个等底等高的小三角形，只需找出原三角形的某条边的中点与这边相对的顶点连接起来就行了．根据上面的分析，可得如图所示的三种分法．课后练习练习2. 右图是一个44⨯的方格纸，请用六种不同的方法将它分割成完全相同的两部分，但要保持每个小方格的完整．【解析】 因为要分割成完全相同的两块，即大小、形状完全相同．方格纸一共有4416⨯=(个)小格，所以分成的两块每块有1628÷=(个)小格，并且这两块要关于中心点对称，大小和形状完全一样，应用染色法，从中心点的一侧入手染色，逐步推进．(建议教师同时呈现六幅空的44⨯格图，不同的变化在不同的图上同时呈现)如下图：3＇2＇5＇1＇6＇7＇3265418＇874＇3＇328＇1754686＇5＇1＇4＇2＇7＇8＇312＇2764585＇6＇3＇7＇1＇4＇4＇322＇1564787＇6＇3＇5＇1＇8＇ 3＇277＇1453868＇5＇2＇4＇1＇6＇ 6＇781＇1546323＇4＇7＇5＇8＇2＇练习3. 下图是一个被挖去了为总面积四分之一小正方形的大正方形，请你将它分成大小形状完全一样的两部分．如果分三部分呢？【解析】 从形状，面积两方面综合考虑，很容易就能得到答案．答案如右上图．练习4. 用3个等腰直角三角形拼图，要求边与边完全重合，能拼出几种图形？ 【解析】 这种类型的题需要学生亲自操作，建议教师准备材料与学生互动．一共可以拼成如下图的几种形状：测试1、图中是由三个正三角形组成的梯形．你能把它分割成4个形状相同、面积相等的梯形吗？月测备选【解析】 这道题的要点在于通过计算解决问题，要求把原来三个正三角形分成四个大小、形状都相同的四个梯形，先不考虑形状，大小相同也就是面积相等，即把整个梯形的面积分成四份，分割后的每一个梯形占一份，可以考虑把每一个三角形的面积分成四份，再把三个正三角形中的每一个小三角形合成要求的梯形，这种类型的题目可以从中点入手，找到每个正三角形的中点并连接，如右上图．测试2、用同样大小的四块等腰直角三角板，能否拼出一个三角形、一个正方形、一个长方形、一个梯形、一个平行四边形五种图形？若能，画出示意图． 【解析】 能用四块同样大小的等腰直角三角板拼出一个三角形、一个正方形、一个长方形、一个梯形、一个平行四边形五种图形．建议用等腰直角三角板，把不同的边进行重合，不要漏掉旋转重合，或者准备一些等腰直角三角形的纸片，由学生拼接后贴到黑板上，具体拼法如图所示．测试3、用“四连块”拼成一个正方形，按编号画入右边图中．④③②①【解析】 首先数一数所有的空格数，一共只有16个，只能组成44 的正方形，目标倒推，在右边的大正方形中拼图，仍然使用染色法，相当于把已知图形往右边的大正方形中放，这样就很容易拼成了，注意标号的位置，具体如下图所示：①→①③→①③②→①③④②测试4、把右图剪成形状、大小相等的8个小图形，怎么剪？作出分出的小图形．【解析】 总格数为12，用总格数除以8，得到每个小图形应该是一个半小正方形，根据平均一个小图形的格数作图，如右图．。

五年级［奥数作业］第10讲：图形的剪拼x［必做与选做］1.用24块面积都是1平方分米的正方形木块拼成的长方形［不含正方形］中,最小的周长是［］分米。

A. 24B. 20C. 16D. 12解析：根据正方形拼组长方形的方法,把24写成几个偶数乘积的形式,即可得出答案。

24=2×2×2×3,24可以分别写成2×12,4×6,8×3,24×1四种形式,即能拼出长、宽分别为12、2；6、4；8、3或24、1四种长方形,最小周长为：［4+6］×2=10×2=20［分米］。

选B。

2.如图长方形纸片,假如按图中所示剪成四块,这四块纸片可拼接成一个正方形,那么所拼成的正方形的边长是［］厘米。

A. 12B. 13C. 14D. 15解析：先算长方形的面积,可知长方形的面积为9×［12+4］=144［平方厘米］, 所以拼成的正方形的面积也是144平方厘米,根据正方形的面积公式,可知边长为12厘米。

选A。

3.将6个长为2厘米、宽为1厘米的长方形拼成一个大长方形,长方形的周长最短为［］厘米。

A. 16B. 26C. 14D. 18解析：先算出6个小长方形的面积,6×2×1=12［平立厘米］,12=2×2×3,12可以分别写成1×12,3×4,6×2三种形式。

即能拼出长、宽分别为12、1；4、3或6、2三种长方形,最小周长为：［3+4］×2=14［厘米］。

选C。

4.左下图是两个同样大的小方格组成的图形,我们可以用不同的方法把这两块图形拼成一个轴对称图形。

例如右下图就是这样的轴对称图形,沿虚线折叠,虚线两边的图形就完全重合了。

那么符合条件的拼法有［］种。

A. 4B. 3C. 2D. 1解析：将左图拼成轴对称图形,能拼成以下3种轴对称图形。

选B。

5.在下列图形中,图形A可以用6个如图［1］所示的图形组成,在其余图形中,图［］也可以用6个如图［1］所示的图形组成。

第四讲图形的剪拼有一天，小动物们在草地上做游戏．小狗齐齐看到一个图形，是一个正方形缺了一部分，齐齐想：这个图形如果剪一剪、拼一拼，成为一个正方形的框(中间含有一个正方形的空缺)就可以用来当野餐的餐桌了．可是该怎么剪、怎么拼才能符合要求呢【分析】（法1）先把这个图形分成一样的8个小正方形，然后沿折线剪开，就可以拼成右边的图．（法2）先把这个图形分成一样的4个小长方形，然后沿折线剪开，就可以拼成右边的图形．方法1方法2同学们，我们已经学过一些简单的基本几何图形，如、□、△、○等，通过折、剪、拼，这些图形之间是可以相互变化的，这不仅可以锻炼我们的动手能力，还能拓展我们的思维，使我们的头脑越来越灵活．今天这节课就用我们灵巧的小手来玩一玩拼图游戏吧！例1要把一个正方形剪成形状相同、大小相等的4个图形，该怎样分【分析】把一个正方形分成形状、大小相等的4个图形，我们可以先让学生把这个正方形分成形状、大小相等的2个图形，然后再把这两个图形继续分成形状、大小相等的4份．有些方法中我们也可以利用对称图形的特点来分．本题有很多种解法，这里只列举最常用的几种：．［拓展］一个长6厘米，宽4厘米的长方形，从中间剪开，如图所示，得到2个大小、形状都相同的长方形，这两个新长方形的周长是多少？［分析］切割开之后，新形成的2个小长方形除了原有长方形的边之外，新产生了两条边，如下图虚线所示，每个新长方形的周长是：34214+⨯=（）（厘米）．两个新长方形的周长是14+14=28（厘米）．例2你能把下面的图形分成7个长方形吗？动手画一画．【分析】可以分成7块含有2个小方格的长方形，答案如下（答案不唯一）：【分析】不能，因为如果可分的话，每块图形中一定是一个黑色、一个白色．那么黑白方格应分别有7个，但图中白色方格只有6个．例3你能将下面的图形分割成4个形状相同、大小相等的图形吗图形与图形之间都是有内在联系的，这种相互间内在的联系，对以后学习图形的面积至关重要．在这节课中我们组织学生按照规定（形状和面积）的要求，把一个几何图形分割成几个图形这样的活动，通过学生的动手操作和图形的变化，动手动脑巧剪图形教学点为您准备了挂图.我来做你能把下面的图形分成7个长方形，使每个长方形中包含相连的2个小方格吗【分析】 首先可以把这个图形分成12个小正方形，要把这个图形分成大小相等的4个图形，那么每个小图形必须包含：1243÷=个小方格，然后我们再来考虑分得的形状相同，通过尝试我们就可以得到答案．在分割不规则图形时，我们可以考虑把这个图形分割成若干个规则图形，然后再来进一步思考．答案如图：［拓展］ 你能把下面的两个图形分割成4个形状相同、大小相等的图形吗［分析］ 答案如下：［拓展］ 下图是由18个小正方形组成的图形，请你把它分成6个完全相同的图形。

（四年级）备课教员：×××第十讲图形的拼割一、教学目标： 1. 四年级奥数（教案）第10讲：图形的拼割2. 通过观察、操作,初步感知所学图形之间的关系。

3. 通过大量拼摆图形,发现图形中由简单到复杂的变化及联系,感受图形美。

4. 通过数学活动,培养用数学进行交流、合作探究和创新意识。

二、教学重点：发现并感知图形之间的变化及联系三、教学难点：掌握基本图形的构成方式,抽象思维能力的培养,引导创新的意识。

四、教学准备：PPT；每个小组发一个信封（里面装五种“俄罗斯方块”图形各4张、四个相同正方形,六个相同的长方形,六角星1个,每个小组发一副七巧板）；一把小剪刀。

五、教学过程：第一课时（50分钟）一、导入（5分)师：出示阿尔法的小车（这个车是由三角形、长方形、正方形、圆形等图形组成的。

）师：引导学生观察：看了阿尔法的小车,你有什么发现？生：发现很多不同形状的图形。

师：揭示课题：聪明的阿尔法用一些简单的图形就拼组出了那么漂亮的小车子,今天这节课咱们也来学习——《图形的拼割》。

（板书课题：图形的拼割）二、探索发现授课（40分）（一）例题1：（13分）你玩过“俄罗斯方块”的游戏吗？如果让你用游戏中几个相同的图形去拼成一个正方形,你会怎样拼呢？（俄罗斯方块）师：你们有玩过手机游戏吗？生：有。

师：那都有玩过什么样的游戏呢？生：（自己解答）师：俄罗斯方块,不知道大家玩过没？里面都会出现哪种的图形？生：（自由回答）师：我们常见的是不是有这些？（出示俄罗斯方块）T字型闪电型 L型田字型一字型师：今天我们就来一起玩一下俄罗斯方块。

生：可以。

师：我们都知道玩俄罗斯方块的时候当凑成一排以后,会自动消失掉,现在我们改一下规则,我们用一个正方形来代替这个玩法。

师：如果要你用几个相同的图形组成一个正方形,你最少要用几个？生：因为正方形的四个边都相等,而这些图形都是由四个小正方形组成的,所以我们最少要用到四个这样的图形才能组成一个正方形。

图形的剪拼总结：第一大类：正方形拼正方形的拼图：1、一个正方形拼成一个正方形： 总结：（1）条件是： ； （2）方法是： 。

（2010.5崇文一模）22．正方形A B C D 的边长为a ，等腰直角三角形F A E 的斜边A E b =（a b 2<），且边A D 和A E 在同一直线上 ．小明发现：当b a =时，如图①，在B A 上选取中点G ，连结F G 和C G ,裁掉F A G ∆和C H D ∆的位置构成正方形F G C H ．（1）类比小明的剪拼方法，请你就图②和图③两种情形分别画出剪拼成一个新正方形的示意图．（2）要使（1）中所剪拼的新图形是正方形，须满足=AEBG ．答案：（2010.5崇文一模）22．（1）（2）21．2、两个正方形拼成一个正方形： 总结：（1）条件是： ； （2）方法是： 。

可用上述方法将3、三个正方形拼成一个正方形等；总结：（1）条件是：；（2）方法是：。

4、平行四边形拼成正方形：（2010.5大兴一模）22. 如图8-1、9-1，现将二张形状、大小完全相同的平行四边形透明纸片，分别放在方格纸中，方格纸中的每个小正方形的边长均为1，并且平行四边形纸片的每个顶点与小正方形的顶点重合．分别在图8-1、图9-1中，经过平行四边形纸片的任意一个顶点画一条裁剪线，沿此裁剪线将平行四边形纸片裁成两部分，按所采裁图形的实际大小，在图8-2中拼成正方形，在图9-2中拼成一个角是135的三角形．要求：（1）裁成的两部分在拼成几何图形时要互不重叠且不留空隙；（2）所拼出的几何图形的各顶点必须与小正方形的顶点重合.（2010.5大兴一模）答案：22.第二大类：三角形与正方形的拼图：1、一个三角形拼成一个正方形： 总结：（1）条件是： ； （2）方法是： 。

（2010.5西城一模）22．在△ABC 中， BC ＝a ，BC 边上的高h ＝a 2，沿图中线段DE 、CF将△ABC 剪开，分成的三块图形恰能拼成正方形CFHG ，如图1所示． 请你解决如下问题：已知：如图2，在△A ′B ′C ′中， B ′C ′＝a ，B ′C′边上的高h ＝a 21．请你设计两种不同的分割方法，将△A ′B ′C ′沿分割线剪开后，所得的三块图形恰能拼成一个正方形，请在图2、图3中，画出分割线及拼接后的图形．（2010.5西城一模答案）22．解：AA ′B ′C ′图3 A ′B ′C ′图4B ′A ′B ′C① ②③图5 图6A ′C ′②③ ①2、四个三角形拼成正方形： （2010.5海淀一模）：22．阅读：如图1，在A B C ∆和D E F ∆中，90A B C D E F ∠=∠=︒,,A B D E a ==B C E F b == ()b a <,B 、C 、D 、 E 四点都在直线m 上，点B 与点D 重合.连接AE 、FC ，我们可以借助于A C E S ∆和F C E S ∆的大小关系证明不等式：222a b ab +>（0b a >>）.证明过程如下:∵,,.B C b B E a E C b a ===- ∴11(),22A C E S E C A B b a a ∆=⋅=- 11().22F C E S E C F E b a b ∆=⋅=-∵0b a >>, ∴F C E S A C ES ∆∆>.即a ab b a b )(21)(21->-.∴22b ab ab a ->-. ∴222a b ab +>. 解决下列问题：（1）现将△DEF 沿直线m 向右平移，设()B D k b a =-,且01k ≤≤.如图2,当B D E C =时, k = .利用此图,仿照上述方法,证明不等式：222a b ab +>（0b a >>）.（2）用四个与A B C ∆全等的直角三角形纸板进行拼接，也能够借助图形证明上述不等式.请你画出一个．．示意图，并简要说明理由.（2010.5海淀一模答案）22．（1）12k =；--------------------------1分证明：连接AD 、BF .可得1()2B D b a =-.∴ ()()11112224A B D S B D A B b a a a b a ∆=⋅=⨯⨯-⋅=-，E图1F图2()()11112224F B D S B D F E b a b b b a ∆=⋅=⨯⨯-⋅=-.∵ 0>>a b ， ∴ FBD ABD S S ∆∆<， 即()14a b a -()14b b a <-.∴ ab b a ab -<-22.∴ ab b a 222>+.--------------------------2分 （2）答案不唯一，图1分，理由1分. 举例：如图，理由： 延长BA 、FE 交于点I . ∵ 0>>a b ，∴ IB C E A B C D S S >矩形矩形， 即 )()(a b a a b b ->-. ∴ 22a ab ab b ->-.∴ ab b a 222>+.--------------------------4分 举例：如图，理由：四个直角三角形的面积和11422S a b a b =⨯⋅=，大正方形的面积222S a b =+. ∵ 0>>a b ， ∴ 21S S >.∴ ab b a 222>+.--------------------------4分同类题：（2010房山一模）22．阅读下列材料：小明遇到一个问题：如图1，正方形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 和DA 边上靠近A 、B 、C 、D 的n 等分点，连结AF 、BG 、CH 、DE ，形成四边形MNPQ ．求四边形MNPQ 与正方形ABCD 的面积比（用含n 的代数式表示）．小明的做法是：先取n=2，如图2，将△ABN 绕点B 顺时针旋转90゜至△CBN ′，再将△ADM 绕点D 逆时针旋转90゜至△CDM ′，得到5个小正方形，所以四边形MNPQ 与正方形ABCD 的面积比是15；然后取n=3，如图3，将△ABN 绕点B 顺时针旋转90゜至△CBN ′，再将△ADM 绕点D 逆时针旋转90゜至△CDM ′，得到10个小正方形，所以四边形MNPQ 与正方形ABCD 的面积比是410，即25；……请你参考小明的做法，解决下列问题：（1）在图4中探究n=4时四边形MNPQ 与正方形ABCD 的面积比（在图4上画图并直接写出结果）；（2）图5是矩形纸片剪去一个小矩形后的示意图，请你将它剪成三块后再拼成正方形（在图5中画出并指明拼接后的正方形）．（2010房山一模）答案： 22.BEA DCBA----------------------1分 ------------------3分四边形MNPQ 与正方形ABCD 的 拼接后的正方形是 正方形ABCD ． 面积比是917． --------------------2分 -------------------4分3、四边形拼成平行四边形：（2010.5昌平一模）22．阅读下列材料:将图1的平行四边形用一定方法可分割成面积相等的八个四边形．．．，如图2，再将图2中的八个四边形适当组合拼成两个面积相等且不全等的平行四边形.（要求：无缝隙M’N’E B A Q P N G H F E D C B AM M’N’A B E H C P G D Q H M NFB E A 图 图1 图3 图4 图5AC D 图①ACD图②FE且不重叠）请你参考以上做法解决以下问题：（1）将图4的平行四边形分割成面积相等的八个三角形．．．； （2）将图5的平行四边形用不同于（1）的分割方案，分割成面积相等的八个三角形．．．，再将这八个三角形适当组合拼成两个面积相等且不全等的平行四边形，类比图2，图3，用数字1至8标明.（2010.5昌平一模）答案： 22．（本小题满分5分） 解：如图所示：（1）图4分割正确． ······························································································· 1分 （2）图5分割正确， ······························································································· 3分 图5拼接正确． ······························································································· 5分785612346781234857786图4图521356图34图2图1542133、三角形翻成等腰三角形：（2010.5密云一模）22．（1）观察与发现：在一次数学课堂上，老师把三角形纸片A B C （AB ＞AC ）沿过A 点的直线折叠，使图1图24图365312图5图46877584321得AC 落在AB 边上，折痕为AD ，展开纸片（如图①）；再次折叠该三角形纸片，使点A 和点D 重合，折痕为EF ，展平纸片后得到A E F △（如图②）．有同学说此时的A E F △是等腰三角形，你同意吗？请说明理由． （2）实践与运用将矩形纸片A B C D 沿过点B 的直线折叠，使点A 落在BC 边上的点F 处，折痕为BE （如图③）；再沿过点E 的直线折叠，使点D 落在BE 上的点D '处，折痕为E G （如图④）；再展平纸片（如图⑤）．试问：图⑤中α∠的大小是多少？（直接回答，不用说明理由）．（2010.5密云一模）答案：22．（本小题满分4分）解：（1）同意．如图，设AD 与EF 交于点M ，由折叠知，∠BAD =∠CAD ，∠AME =∠AMF =90O ． ------------------------------1分∴ 根据三角形内角和定理得∠AEF =∠AFE ． ------------------------------------2分∴ △AEF 是等腰三角形．················ 3分（2）图⑤中的大小是22．5o ．·············· 4分第 大类：杂题：（2010.5石景山一模）：22．（1）如图1，把边长是3的等边三角形的各边三等分，分别以居中那条线段为一边向外作等边三角形，并去掉居中的那条线段，得到图2，再把图2中图形各边三等分，分别以居中那条线段为一边向外作等边三角形，并去掉居中的那条线段，得到一个新图形，则这个新图形的周长是 ；（2）如图3，在55⨯的网格中有一个正方形，把正方形的各边三等分，分别以居中那条图1 图2 ED C F BA图③ED C ABF G C ' D 'ADECB α图④图⑤线段为斜边向外作等腰直角三角形，去掉居中的那条线段，得到图4，请把图4中的图形剪拼成正方形，并在图4中画出剪裁线，在图5中画出剪拼后的正方形．（2010.5石景山一模）：答案： 22．（1）16 …………………………………………1分 （2）各2分（2010-5通州一模）24．小华用两块不全等的等腰直角三角形的三角板摆放图形.（1）如图①所示△ABC ，△DBE ，两直角边交于点F ，过点F 作FG ∥BC 交AB 于点G ，连结BF 、AD ，则线段BF 与线段AD 的数量关系是 ；直线BF 与直线AD 的位置关系是 ，并求证：FG ＋DC ＝AC ；（2）如果小华将两块三角板△ABC ，△DBE 如图②所示摆放，使D B C 、、三点在一条直线上，AC 、DE 的延长线相交于点F ，过点F 作FG ∥BC ，交直线AE 于点G ，连结AD ，FB ，则FG 、DC 、AC 之间满足的数量关系式是 ；（3）在（2）的条件下，若AG ＝DC ＝5，将一个45°角的顶点与点B 重合，并绕点B 旋转，这个角的两边分别交线段FG 于P 、Q 两点（如图③），线段DF分别与线段BQ 、BP 相交于M 、N 两点，若PG ＝2，求线段MN 的长．图3 图4 图5（第24题图①） （第24题图②）（第24题图③）（2010-5通州一模）答案：24．（1）结论：则线段BF 于线段AC 的数量关系是：相等；直线BF 于直线AC 的位置关系是：互相垂直； .......................................................................(1分)证明： ABC ∆、BDE ∆是等腰直角三角形 ∴︒=∠=∠=∠45BDE BAC ABC ，BCAD ⊥∴︒=∠45CFD∴CFCD = ............................................................(2分)BCFG // ︒=∠=∠45ABC AGF∴AFFG =FCAF AD +=∴DCFG AD += ............................................................(3分)G F ED C BA（2）FG 、DC 、AD 之间满足的数量关系式是DC AD FG+=；..........(4分) （3）过点B 作FG BH ⊥垂足为H ，过点P 作AG PK⊥垂足为K ......(5分) BC FG //,C 、D 、B 在一条直线上， 可证AFG ∆、DCF ∆是等腰直角三角形， 5,27==CD AG∴根据勾股定理得：25,7===FD FG AF∴2==BC AC∴3=BDFG BH ⊥，∴CF BH //，︒=∠90BHFBC FG //∴四边形CFHB 是矩形∴2,5==FH BH，BC FG //∴︒=∠45G5==∴BH HG ，25=BGAG PK ⊥，2=PG∴2==KG PK24225=-=∴BK︒=∠︒=∠45,45HGB PBQ∴︒=∠45GBH21∠=∠∴AG PK ⊥，FG BH ⊥︒=∠=∠∴90BKP BHQBQH ∆∴∽BPK ∆BH BKQH PK =∴∴=QH 45 ............................................................(6分) 43=∴FQ BC FG //∴FQM DBM MFQ D ∠=∠∠=∠,∴FQM ∆∽DBM ∆ 24=DM ............................................................(7分) FNP DNB MFQ D ∠=∠∠=∠, ∴BDN ∆∽PFN ∆ ∴PF BD FN DN = ∴8215=DN ∴8217821524=-=MN............................................................(8分)。