数字电路代数化简逻辑门

数字电路逻辑代数化简
数字电路是现代电子设备中的重要组成部分，它们由逻辑门和
触发器等基本元件组成，用于处理和传输数字信号。

在数字电路中，逻辑代数化简是一项重要的技术，它可以帮助简化逻辑电路的设计，减少元件的数量，提高电路的性能和可靠性。

逻辑代数化简是利用布尔代数的原理，通过逻辑运算的规则，
将复杂的逻辑表达式简化为最简形式的过程。

这个过程可以通过代
数方法、卡诺图法等多种技术来实现。

逻辑代数化简的目标是找到
一个等价的最简化的逻辑表达式，以实现电路的最小化设计。

在数字电路的设计中，逻辑代数化简具有以下重要作用：
1. 减少元件数量，通过逻辑代数化简，可以将逻辑表达式简化
为最简形式，从而减少电路中的逻辑门数量，降低成本和功耗。

2. 提高电路性能，简化后的逻辑电路通常具有更快的响应速度
和更小的延迟，从而提高电路的性能。

3. 减少设计复杂性，简化后的逻辑表达式更易于理解和维护，
减少了设计的复杂性，提高了电路的可靠性。

逻辑代数化简是数字电路设计中不可或缺的一环，它的应用可以使电路设计更加高效和可靠。

随着数字电路的不断发展和应用，逻辑代数化简技术也将继续发挥重要作用，为电子设备的性能提升和成本降低提供强大支持。

数字电路化简
数字电路化简是一种复杂的技术，用于设计数字逻辑电路和数字系统。

它有助于减少电路的复杂性，提高工作效率，降低系统成本。

数字电路化简的主要步骤包括：识别可以合并和简化的信号路径，替换大型逻辑门为小型数字电路模块，处理多个输入和输出端口，将多层信号生成简单的逻辑图形，并使用SIMD，MIMD补偿延迟，更改信号路径，并使用复杂的电路设计来提高系统的效率。

此外，数字电路化简还可以使用多种低功耗电路设计和高效分析工具，提高系统的功率利用率和性能等。

通过使用数字电路化简技术和电路设计工具，可以减少设计时间和研发成本，并可以更快更准确地完成电路设计，使系统可靠性更高，维护更容易，竞争优势更强。

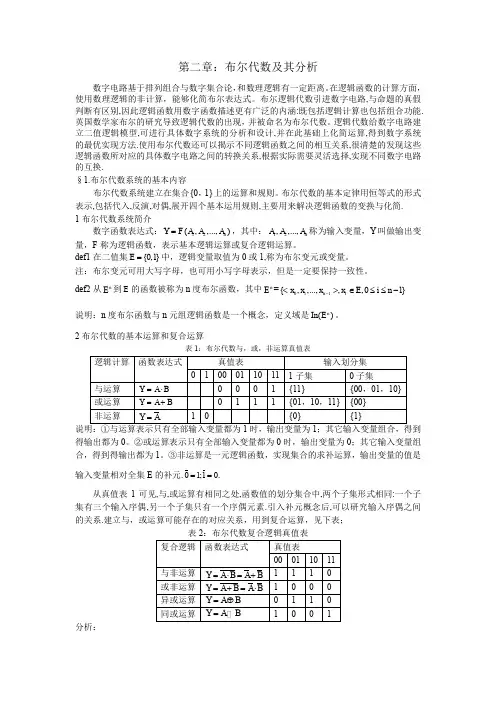
第二章：布尔代数及其分析数字电路基于排列组合与数字集合论，和数理逻辑有一定距离。

在逻辑函数的计算方面，使用数理逻辑的非计算，能够化简布尔表达式。

布尔逻辑代数引进数字电路,与命题的真假判断有区别,因此逻辑函数用数字函数描述更有广泛的内涵:既包括逻辑计算也包括组合功能.英国数学家布尔的研究导致逻辑代数的出现，并被命名为布尔代数。

逻辑代数给数字电路建立二值逻辑模型,可进行具体数字系统的分析和设计,并在此基础上化简运算,得到数字系统的最优实现方法.使用布尔代数还可以揭示不同逻辑函数之间的相互关系,很清楚的发现这些逻辑函数所对应的具体数字电路之间的转换关系,根据实际需要灵活选择,实现不同数字电路的互换.§1.布尔代数系统的基本内容布尔代数系统建立在集合{0，1}上的运算和规则。

布尔代数的基本定律用恒等式的形式表示,包括代入,反演,对偶,展开四个基本运用规则,主要用来解决逻辑函数的变换与化简. 1布尔代数系统简介数字函数表达式：12(,,...,)n Y F A A A =，其中：12,,...,n A A A 称为输入变量，Y 叫做输出变量，F 称为逻辑函数，表示基本逻辑运算或复合逻辑运算。

def1在二值集{0,1}E =中，逻辑变量取值为0或1,称为布尔变元或变量。

注：布尔变元可用大写字母，也可用小写字母表示，但是一定要保持一致性。

def2从n E 到E 的函数被称为n 度布尔函数，其中n E =011{,,...,,,01}n i x x x x E i n -<>∈≤≤- 说明：n 度布尔函数与n 元组逻辑函数是一个概念，定义域是()n In E 。

2布尔代数的基本运算和复合运算表1：布尔代数与，或，非运算真值表说明：①与运算表示只有全部输入变量都为1时，输出变量为1；其它输入变量组合，得到得输出都为0。

②或运算表示只有全部输入变量都为0时，输出变量为0；其它输入变量组合，得到得输出都为1。

数字逻辑与电路设计的基本原理数字逻辑与电路设计是现代电子技术中最基础、最重要的学科之一，它涉及到数字电路的设计、分析和优化，常用于计算机系统、数字通信系统、无线电系统、嵌入式系统等领域。

数字逻辑与电路设计的基本原理是理解和掌握数字电路的关键，下面将详细介绍。

一、数字逻辑的基本概念数字逻辑是研究数字信号的运算规律和推理规则的一门学科，它主要关注信号的离散性质和逻辑运算。

在数字逻辑中，使用二进制的位表示数据和信号，通过逻辑运算来实现数字信号的处理和控制。

数字逻辑的基本概念包括逻辑门、真值表、逻辑代数等。

1. 逻辑门逻辑门是数字电路的基本组成部分，用于实现逻辑运算。

常见的逻辑门包括与门、或门、非门、异或门等。

它们通过控制输入信号的组合，来实现不同的逻辑运算功能，如与、或、非、异或等。

2. 真值表真值表是用来表示逻辑函数的表格，它列举了所有可能的输入组合和相应的输出结果。

通过真值表，可以清晰地了解逻辑函数的逻辑关系和运算规律，从而进行数字电路的设计和分析。

3. 逻辑代数逻辑代数是研究逻辑运算的代数系统，它涉及到逻辑函数、逻辑表达式、逻辑运算规则等内容。

逻辑代数通过逻辑运算符和逻辑变量的组合，构造逻辑表达式来描述逻辑运算。

二、数字电路的设计方法数字电路的设计方法包括组合逻辑电路设计和时序逻辑电路设计两种基本方法。

1. 组合逻辑电路设计组合逻辑电路是由逻辑门组成的电路，其中输出仅依赖于当前的输入。

组合逻辑电路的设计主要包括三个步骤：（1）确定逻辑功能：根据问题要求，确定所需的逻辑函数和逻辑运算关系。

（2）绘制真值表：通过真值表列举所有输入组合及对应的输出结果。

（3）逻辑门电路实现：根据真值表，选用逻辑门并进行适当的连接，设计电路。

2. 时序逻辑电路设计时序逻辑电路是由组合逻辑电路和触发器等时序元件组成的电路，其中输出不仅依赖于当前的输入，还受到过去的输入和存储状态的影响。

时序逻辑电路的设计主要包括以下几个步骤：（1）确定状态图：根据问题要求，确定电路的状态集和状态转移规则。