数电逻辑代数及其化简

一、数电知识要点第一章 数制与编码1、码制：各种码制之间的转换(整数,小数)2、带符号数的原码、反码和反码3、二进制编码：自然二进制码、格雷码4、BCD 码：8421BCD 码、余三码等第二章 逻辑函数及其化简1、逻辑代数的基本运算及复合运算：与、或、非、与非、或非、异或、同或与运算： 全1得1，有0得0；或运算：有1得1，全0得0； 非运算：10 01==异或：相同得0，相异得1同或：相同得1，相异得02、逻辑运算基本公式及常用规则：1) 十个基本公式2) 逻辑运算常用规则：代入规则；反演规则；对偶规则3、逻辑函数表示方法1）真值表2）逻辑函数表达式：与或表达式；或与表达式；与非-与非表达式；或非-或非表达式；最小项表达式；最大项表达式（概念、性质、两者之间的关系）3）逻辑电路图(与电路分析设计结合)：由逻辑表达式到电路图；由电路图写逻辑表达式；4）卡诺图（化简：最多四变量）求逻辑函数的最简与或表达式和或与表达式第三章组合逻辑电路1、集成电路主要电气指标：输入/输出电压；输入/输出电流；噪声容限；扇出系数；输出结构：推拉式输出；开路输出；三态输出2、常用组合逻辑模块3-8译码器、数据选择器、加法器、数值比较器3、组合逻辑电路分析分析步骤：1）由给定的逻辑图逐级写出逻辑函数表达式；2)由逻辑表达式列出真值表；3)分析、归纳电路的逻辑功能。

4、组合电路的设计设计步骤：列真值表—写出适当的逻辑表达式—画电路图。

其中第二步写逻辑表达式时根据设计要求有所不同：1)用门电路设计：与或电路/与非-与非电路：卡诺图化简求最简与或表达式或与电路/或非-或非电路：卡诺图化简求最简或与表达式2)用3-8译码器+与非门设计：写最小项表达式3)用3-8译码器+与门设计：写最大项表达式4)用数据选择器设计：通过卡诺图降维得出数据选择器的各位地址信号Ai和各路数据Di的表达式5、逻辑险象的判别和消除第四章时序电路分析1、各类触发器的特性方程、约束方程、状态表、状态图(RS,JK,D)2、集成计数器74163工作原理、功能及应用（如何构成任意模的计数器、序列信号发生器）3、时序电路的分析1)由触发器构成的米里型/莫尔型同步时序电路的分析步骤：分析电路类型—写激励方程和输出方程—求次态方程—状态表、状态图—功能。

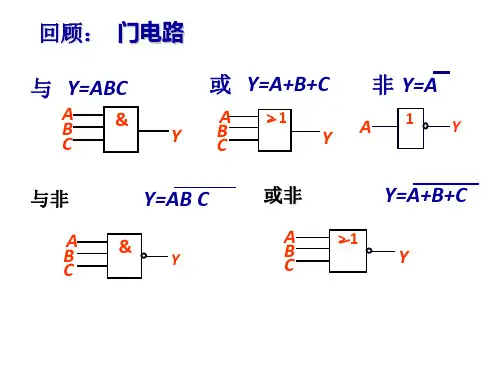
一文看懂，数电中逻辑函数的，代数，化简法常用公式
1.交换律： A+B=B+A;---@1 AB=BA;---@2
2.结合律：(A+B)+C=A+(B+C);---@3 (AB)C=A(BC);---@4
3.分配律： A(B+C)=AB+BC;---@5 A+BC=(A+B)(A+C);---@6
4.吸收率： A+AB=A;---@7 A(A+B)=A;---@8
5.其他常用：A+!AB=A+B;---@9 A(!A+B)=AB@10
以上逻辑运算基本定律中，恒等式大多是成对出现的，且具有对偶性。

用完全归纳法可以证明所列等式的正确性，方法是：列出等式的左边函数与右边函数的真值表，如果等式两边的真值表相同，说明等式成立。

但此方法较为笨拙，下面以代数方法证明其中几个较难证明的公式。

@7式证明：A+AB=A(1+B)=A;
@8式证明：A(A+B)=AA+AB=A+AB=A;由七式易得；
@6式证明：
A+BC=(A+AB)+BC;此处由@7式可得A=A+AB;
=A+AB+BC=A+B(A+C);此处由@5式可得AB+BC=B(A+C);
=A+AC+B(A+C);此处由@7式可得A=A+AC;
=A(A+C)+B(A+C);
=(A+B)(A+C); 得证。

@9式证明： A+!AB=A(1+B)+!AB;
=A+AB+!AB;
=A+B(A+!A);
=A+B;得证。

数电公式法化简
在数字电路中，使用布尔代数的基本法则可以对逻辑表达式进行化简。

下面介绍几个常见的数电公式化简的方法：
1.代数法：利用布尔代数的基本规则（如分配律、结合律、德摩根定律等）对逻辑表达式中的项进行展开和合并，以简化逻辑电路。

2.卡诺图法：卡诺图是一种将逻辑表达式可视化的方法。

通过将逻辑函数的真值表转化为卡诺图，可以直观地找出逻辑表达式中的最简形式。

3.真值表法：列出逻辑函数的真值表，并找出其中的规律，通过观察真值表中的1的分布情况，判断哪些项可以合并，从而得到最简形式。

4.极小项与极大项法：将逻辑函数表示为与或表达式后，利用极小项（逻辑函数为1的最小项）和极大项（逻辑函数为0的最大项）来化简逻辑函数。

将重复出现的项进行合并和消去。

需要注意的是，在化简过程中，应注意遵循布尔代数的基本规则，并要合理利用化简后的逻辑表达式的特点，例如选择合适的公式展开
顺序、尽量合并重复的项等。

除了以上方法外，还可以使用电路分解、电路索引和逻辑运算性
质等技巧来帮助化简逻辑表达式。

需要根据具体题目的要求和逻辑表
达式的复杂程度选择适合的方法进行化简。

第2章 逻辑代数和逻辑函数化简基本概念：逻辑代数是有美国数学家George Boole 在十九世纪提出,因此也称布尔代数,是分析和设计数字逻辑电路的数学工具。

也叫开关代数，是研究只用0和1构成的数字系统的数学。

2.1 基本逻辑运算和复合逻辑运算基本逻辑运算：“与”、“或”、“非”。

复合逻辑运算：“与非”、“或非”、“与或非”、“异或”、“同或”等。

基本逻辑运算1.“与”运算①逻辑含义：当决定事件成立的所有条件全部具备时，事件才会发生。

②运算电路：开关A 、B 都闭合，灯F 才亮。

③表示逻辑功能的方法：表达式：F =A •B 逻辑符号：功能说明：有0出0，全1出1。

在大规模集成电路可编程逻辑器件中的表示符号：A B国家标准 A B以前的符号A B欧美符号开关A 、B 的状态代表输入：“0”表示断开； “1”表示闭合。

灯F 的状态代表输出：“0”表示亮； “1”表示灭。

通过“•”接入到此线上的输入信号都是该与门的一个输入端。

推广：当有n 个变量时：F =A 1A 2A 3∙∙∙A n “与”运算的几个等式： 0•0=0，0•1=0，1•1=1A •0=0（0-1律），A •1=A （自等律），A •A =A （同一律），A •A •A =A （同一律）。

2.“或”运算①逻辑含义：在决定事件成立的所有条件中，只要具备一个，事件就会发生。

②运算电路：开关A 、B 只要闭合一个，灯F 就亮。

③表示逻辑功能的方法： 逻辑功能：有1出1，全0出0。

真值表：（略） 表达式：F =A +B 逻辑符号：推广：当有n 个变量时：F =A 1+A 2+A 3+∙∙∙+A n“或”运算的几个等式： 0+0=0，0+1=1，1+1=1A +0=A （自等律）A +1=1（0-1律），A +A =A （同一律）。

上次课小结：与、或的功能、表达式等，几个等式。

3．“非”运算①逻辑含义：当决定事件的条件具备时，事件不发生；当条件不具备时，事件反而发生了。

数电逻辑表达式化简
数电逻辑表达式的化简是指将复杂的逻辑表达式简化为更简单的形式。

化简的目的是减少逻辑门的数量，简化电路结构，提高电路的可靠性和性能。

常用的逻辑表达式化简方法有两种：代数化简和卡诺图化简。

1. 代数化简：
- 使用布尔代数定律和布尔运算规则进行化简。

常用的代数
化简定律有：吸收定律、分配定律、德摩根定律等。

- 通过代数化简，将逻辑表达式中存在的冗余项、重复项、
冗长项等进行合并、简化，以达到减少逻辑门数量的目的。

2. 卡诺图化简：
- 将逻辑函数的真值表按照输入的组合方式进行分组，并绘
制成卡诺图。

- 通过对卡诺图的分析，找出逻辑函数中的主要项和次要项，去除冗余项，并将其化简为最简的逻辑表达式。

- 卡诺图化简方法适用于逻辑函数较复杂的情况，可以有效
地降低逻辑门的数量。

需要注意的是，在进行逻辑表达式化简时，要关注逻辑函数的功能需求，并根据具体的电路设计要求选择适合的化简方法。

数电逻辑表达式化简摘要：1.数电逻辑表达式的概念与意义2.化简数电逻辑表达式的方法3.化简过程的实例演示4.化简后的表达式应用场景5.总结与展望正文：【1.数电逻辑表达式的概念与意义】在数字电子电路中，逻辑表达式是一种描述电路功能和逻辑关系的重要手段。

它采用布尔代数，通过运算符（如AND、OR、NOT等）连接变量，表示电路中各信号的逻辑关系。

化简数电逻辑表达式，就是将一个复杂的逻辑表达式转化为一个更简单、更容易理解和分析的形式。

【2.化简数电逻辑表达式的方法】化简数电逻辑表达式的常用方法有以下几种：1）代入法：将表达式中的一个变量用另一个变量表示，从而简化表达式。

2）乘法公式：利用乘法公式（如分配律、结合律等）简化表达式。

3）除法公式：利用除法公式（如分配律、结合律等）简化表达式。

4）德摩根定律：将表达式中的乘法项转化为加法项，或将加法项转化为乘法项。

5）卡诺图：将逻辑表达式转化为图形化表示，便于观察和化简。

【3.化简过程的实例演示】以一个简单的逻辑表达式为例：A ·B +C · D化简过程如下：1）利用乘法公式，将表达式转化为：(A · B) + (C · D)2）利用德摩根定律，将表达式转化为：A ·B +C ·D = A + B · C + D3）将表达式中的变量用另一个变量表示，得到简化后的表达式：A +B ·C + D【4.化简后的表达式应用场景】化简后的逻辑表达式更易于分析和设计数字电子电路。

在实际应用中，化简后的表达式可以帮助工程师快速了解电路的逻辑功能，简化电路分析与设计过程，提高工作效率。

【5.总结与展望】数电逻辑表达式的化简是数字电子电路设计与分析的重要环节。

掌握化简方法，善于运用乘法公式、德摩根定律等工具，能够将复杂的逻辑表达式简化，为电路设计提供便利。

数电逻辑表达式化简（原创实用版）目录1.数电逻辑表达式的概念2.数电逻辑表达式的化简方法3.化简过程中的技巧和注意事项4.实际应用案例正文【1.数电逻辑表达式的概念】数电逻辑表达式（Digital Logic Expression，简称 DLE）是用来描述数字电路中逻辑关系的数学表达式。

在数字电路设计中，逻辑表达式是非常重要的，它可以帮助我们理解和分析电路的工作原理，同时也可以指导我们设计出符合要求的电路。

【2.数电逻辑表达式的化简方法】数电逻辑表达式的化简是指将复杂的逻辑表达式简化为简单的逻辑表达式，这样可以使我们更容易理解和分析逻辑关系。

化简的方法主要有以下几种：（1）逻辑代数法：利用逻辑代数的运算法则，如德摩根定律、分配律等，将复杂的逻辑表达式化简为简单的逻辑表达式。

（2）卡诺图法：通过画出逻辑表达式的卡诺图，然后通过卡诺图的化简规则，将复杂的逻辑表达式化简为简单的逻辑表达式。

（3）逻辑门法：利用逻辑门的特性，如与门、或门、非门、与非门、或非门、异或门等，将复杂的逻辑表达式化简为简单的逻辑表达式。

【3.化简过程中的技巧和注意事项】在化简过程中，有一些技巧和注意事项需要我们掌握：（1）在化简逻辑表达式时，应尽量保持逻辑表达式的逻辑意义不变。

（2）在化简过程中，可以适当地使用逻辑代数的运算法则，这样可以使化简过程更加简便。

（3）在绘制卡诺图时，应准确地表示出逻辑表达式的逻辑关系，这样才能保证化简的准确性。

【4.实际应用案例】假设我们有一个逻辑表达式：A·B·（C·D）+（A·B·C）·（A·B·D），我们可以通过逻辑代数法和卡诺图法将其化简为：A·B·C·D。

在这个过程中，我们首先利用逻辑代数法将逻辑表达式化简为：A·B·C·D+A·B·C·D，然后再利用卡诺图法将其进一步化简为：A·B·C·D。