离散数学之命题符号化共33页

教学设计
课程名称《离散数学》教师姓名申莹授课题目命题公式及符号化
授课章节§1.3命题公式与翻译
授课对象数学与应用数学专业
教学目标掌握利用联结词把命题符号化的方法
教学方式启发式
教学内容命题符号化的方法
教学重点命题的分析
教学难点条件联结词的使用
教学方法和策略采用多媒体课件辅助，首先分析命题可以用何种联结词表示，再说明使用联结词时的注意事项；注意师生互动，以学生为教学主体，共同完成教学目标。

学情分析
学生已经掌握了命题公式的真值表的画法，思考具有同样
个数的命题变元共有多少种命题公式
教学评价师生互动，启发式教学引导学生思考并进而解决问题；深入分析，用例题加深学生对知识点的理解.
课程资源参考书目，网上课程视频，网络微课教学 JINING UNIVERSITY。

解 当被问战士回答“对”，则逻辑学家开启所指的门从容离
去。当被问战士回答“否”，则逻辑学家开启另一门从容离去。
分析：如果被问者是诚实战士，他回答“对” 。则另 一 名战士是说谎战士，他回答“是”，那么，这扇门 不是死亡门。
如果被问者是诚实战士，他回答“否”。则另 一名是说谎战士，他回答“不是”，那么，这扇门是 死亡门。
说明:在数理逻辑中，即使p、q没有内在联系， 但仍有意义.
(5)等价式:p，q 为两命题，复合命题“p 当且仅当 q” 称作 p 与 q 的等价式，记作 p q，符号“ ”称作等价 联结词，p q 为真当且仅当 p 与 q 的真值相同。
Байду номын сангаас
p
q p q
0
0
1
0
1
0
1
0
0
1
1
1
例1.6 1）集合A中没有元素当且仅当集合A是空集。 2）当王刚心情愉快时，他唱歌；反之，当 他唱歌时，一定心情愉快。 3）三角形三边相等的充要条件是三个角相等。 4) 2+2=5的充要条件是太阳从西边升起。
罗素将集合分为两类，一类是集合 A 本身是 A 的一个
元素，即 A A；另一类是集合 A 本身不是 A 的一个
元素，即 A A 。构造一个集合 S：S={A|AA},问 S 是
不是它自己的一个元素。即 S S 还是 S S 。
原子命题： 称由简单陈述句构成的命题为简单命题
或原子命题，
命题符号化：用小写英文字母(或带下标)p,q，r，…， pi , qi , ri , ……表示命题，称为命题符号化．用数字 1（或 T）表示真，用 0(或 F)表示假，则任何命题的真值不是 1 就是 0，但决不可能既可以为 1 又可以为 0。

P 0 0 1 1 Q 0 1 0 1 P∧Q 0 0 0 1
例4
设P：我们去看电影。Q：房间里有十张桌子。则
P ∧ Q表示“我们去看电影并且房间里有十张桌子。”
10
3. 析取“∨”（相容或）[讲解教材P3-5关于或]
4. 定义1.3
由命题P和Q利用“∨”组成的复合命题，称 为析取式复合命题，记作“P∨Q”（读作“P或Q”）。 当且仅当P和Q至少有一个取值为真时，P∨Q取值为真。
练习1-1
1. 判断下列语句哪些是命题，若是命题，则指出其真值。
（1） （2） 只有小孩才爱哭。 X+6=Y ( 是 假 ) ( 不是 ) (是 真) ( 不是 )
（3）
银是白的。
（4） 起来吧，我的朋友。 2． 将下列命题符号化
（1） 我看见的既不是小张也不是老李。 解 令P：我看见的是小张；Q：我看见的是老李。 则该命题可表示为¬ P∧¬ Q （2） 如果晚上做完了作业并且没有其它的事，他就会 看电视或听音乐。 解 令 P：他晚上做完了作业；Q：他晚上有其它的事； R：他看电视； S：他听音乐。 则该命题可表示为（P∧¬ Q）→（R∨S）
28
1.3 等值演算
• 定义1.10 设A和B是两个命题公式, 若等价式A↔B 是重言式，则称公式A 和B等值，记为A B,称 AB为等 值式。
• 注意： （1）符号“”与“↔”的区别与联系 “”不是联结词，AB不表示一个公式， 它表示两个公式间的一种关系，即等值关系。 “↔”是联结词，A↔B是一个公式。 AB 当且仅当 A↔B 是永真公式。
1 0 1 0 1 0 1 0
0 0 1 1 1 1 1 1
0 0 0 1 0 0 0 1
1 1 0 1 0 0 0 1

离散数学命题符号一、离散数学命题符号的定义在离散数学中，命题是一个陈述句，可以判断为真或为假。

为了准确地表示命题，在离散数学中引入了命题符号。

命题符号主要用于表示命题的逻辑关系，以及对命题的运算。

1. 命题变量和命题符号离散数学中，命题变量被表示为字母，常用的命题变量包括p、q、r等。

命题符号则用来表示对命题变量的操作和运算关系。

常用的命题符号包括逻辑与（∧）、逻辑或（∨）、非（¬）等。

2. 逻辑连接词离散数学中，逻辑连接词用于将多个命题连接起来，形成复合命题。

常见的逻辑连接词有：- 逻辑与（∧）：表示两个命题都为真时，复合命题为真；否则为假。

- 逻辑或（∨）：表示两个命题至少一个为真时，复合命题为真；否则为假。

- 非（¬）：表示对命题的否定。

3. 命题符号的优先级为了保证命题的运算顺序和结果的准确性，在离散数学中，命题符号有一定的优先级。

常见的命题符号优先级从高到低依次为：- ¬（非）- ∧（逻辑与）- ∨（逻辑或）二、离散数学命题符号的应用1. 命题的合取和析取在离散数学中，逻辑与（∧）和逻辑或（∨）的运算被广泛应用于命题的合取和析取。

- 合取：当多个命题同时为真时，可以使用合取运算符（∧）将这些命题合并成为一个复合命题。

例如，当p表示“今天下雨”、q表示“今天天气阴沉”时，合取命题p∧q表示“今天同时下雨并且天气阴沉”。

- 析取：当多个命题至少一个为真时，可以使用析取运算符（∨）将这些命题合并成为一个复合命题。

例如，当p表示“今天下雨”、q表示“今天天气阴沉”时，析取命题p∨q表示“今天下雨或者天气阴沉”。

2. 命题的否定在离散数学中，非（¬）运算符常用于对命题的否定。

如果p为真，则¬p为假；如果p为假，则¬p为真。

例如，若p表示“今天下雨”，则¬p表示“今天不下雨”。

3. 命题的复合运算通过组合使用逻辑连接词和命题符号，可以对多个命题进行复合运算。

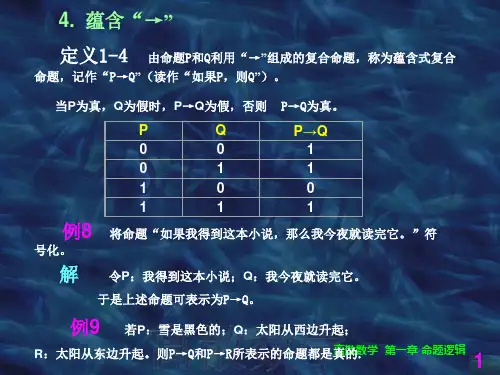
《离散数学》符号表全称量词（任意量词）存在量词├断定符（公式在L 中可证）╞满足符（公式在 E 上有效，公式在 E 上可满足）┐命题的“非”运算∧命题的“合取”（“与”）运算∨命题的“析取”（“或”，“可兼或”）运算→命题的“条件”运算命题的“双条件”运算的A B命题A与B等价关系A B 命题 A 与 B 的蕴涵关系A 公式 A的对偶公式wff 合式公式iff 当且仅当V 命题的“不可兼或”运算（“异或门” ）↑命题的“与非” 运算（“与非门”）↓命题的“或非”运算（“或非门” ）□模态词“必然”◇模态词“可能”φ空集∈属于（不属于）A （·）集合 A 的特征函数P（A）集合 A 的幂集A 集合 A 的点数A A A （A n）集合A的笛卡儿积R 2R R ( R nR n 1) 关系 R 的“复合”R阿列夫零阿列夫包含真包含∪ 集合的并运算 ∩ 集合的交运算 - （～）集合的差运算集合的对称差运算mm同余加mm同余乘〡限制[ x] R集合关于关系 R 的等价类 A/ R集合 A 上关于 R 的商集 R ( A)集合 A 关于关系 R 的划分 R (A)集合 A 关于划分 的关系 [a]元素 a 产生的循环群 [a] R元素 a 形成的 R 等价类 C r由相容关系 r 产生的最大相容类 I环，理想Z /( n)模 n 的同余类集合a b(mod k)a 与b 模 k 相等r ( R)关系 R 的自反闭包 s( R)关系 R 的对称闭包R ，t( R) 关系 R 的传递闭包R ，rt (R) 关系 R 的自反、传递闭包Hi . 矩阵 H 的第 i 个行向量H. j 矩阵 H 的第 j 个列向量CP 命题演绎的定理（ CP 规则）EG 存在推广规则（存在量词引入规则）ES 存在量词特指规则（存在量词消去规则）UG 全称推广规则（全称量词引入规则）US 全称特指规则（全称量词消去规则）I A，R0 恒等关系A 集合 A 的补集X X 所有 X 到自身的映射Y X 所有从集合 X 到集合 Y 的函数K[ A] ( A) 集合 A 的势（基数）R 关系r 相容关系R 否关系R 补关系R 1 （ R c）逆关系R S 关系 R 与关系 S 的复合R R R , R n 关系 R 的n次幂nB2 B2 , B2r 布尔代数 B2的 r 次幂rB2r 含有 2r个元素的布尔代数domf 函数 f 的定义域（前域）ranf 函数 f 的值域f： X Y （ X f Y ） f 是X到Y的函数GCD (x, y) x, y 最大公约数LCM (x, y) x, y 的最小公倍数e 幺元零元a 1 元素 a 的逆元aH (Ha ) H 关于a的左（右）陪集Ker ( f ) 同态映射 f 的核（或称 f 的同态核）A，B，C 合式公式n二项式系数kn多项式系数n1 ,n2 , , n p[1 ，n] 1 到 n 的整数集合[ x]k x( x 1) (x k 1)[ x]k x( x 1) (x k 1)C n k 组合数d (u, v) 点 u 与点 v 间的距离d (v) 点 v 的度数d (v) 点 v 的出度d (v) 点 v 的入度G (V ,E) 点集为 V ，边集为 E 的图G 图G的补图G G图G与图G同构G平面图 G 的对偶图W(G)图 G 的连通分支数(G)图G的点连通度(G)图G的边连通度(G)图G的最小点度(G)图G的最大点度A(G)图 G 的邻接矩阵P(G)图 G 的可达矩阵M(G)图 G 的关联矩阵K n n 阶完全图K n,m完全二分图C复数集N自然数集（包含0 在内）N正自然数集P素数集Q有理数集Q正有理数集Q负有理数集R实数集Z整数集Z m{[ 1] , [ 2] ,,[ m]}Set集范畴Top拓扑空间范畴Ab交换群范畴Grp群范畴Mon单元半群范畴Ring有单位元的（结合）环范畴Rng环范畴CRng交换环范畴R-mod环R的左模范畴mod-R环R的右模范畴Field域范畴Poset偏序集范畴。

说明： x yG(x, y) 和 x yG(x, y)表示的含义不同！
第 10 页
四、符号化
例2 在一阶逻辑中将下面命题符号化。
(1)人都爱美。
(2)有人用左手写字。
个体域分别为：
(a) D为人类集合 (b) D为全总个体域
解: (a)设F(x):x爱美，G(x):x用左手写字，则
(1) xF(x) (2) xG(x)
， L(x,y): x与y跑得同样快。 (5) ﹁ x y(F(x) G(y) H(x, y)) (6) ﹁ x y(F(x) F(y) L(x, y))
第 16 页
总结和作业
➢ 小结 ◆ 理解个体词、谓词、量词的含义 ◆ 掌握一阶逻辑命题的符号化
➢ 作业（做书上）
课本63-64页 4(1) (3), 5(1) (3)，6 (1) (3) (5)
第1 页
第四章 一阶逻辑基本概念
➢ 命题逻辑的局限性
在命题逻辑中，研究的基本单位是简单命题，对简单 命题不再进行分解，并且不考虑命题之间的内在联系和数 量关系。
➢ 一阶逻辑所研究的内容
为了克服命题逻辑的局限性，将简单命题再细分，分 析出个体词、谓词和量词，以期达到表达出个体与总体的 内在联系和数量关系。 ◆ §4.1一阶逻辑命题符号化 ◆ §4.2一阶逻辑公式及解释 ◆ §5.1一阶逻辑等值式与置换规则 ◆ §5.2一阶逻辑前束范式
第四章 一阶逻辑基本概念
➢ 苏格拉底三段论
◆ 所有的人都是要死的。 ◆ 苏格拉底是人。 ◆ 所以，苏格拉底是要死的。 试证明此推理。 解：令p:所有的人都是要死的,q:苏格拉底是人,r:苏格拉底 是要死的，则 前提：p，q 结论：r 推理的形式结构： p Ù q ® r

如果写成 (PQ)∨(P R)，就表明两种作法都是假的时候，我说 的才是假话.这显然不对.
若写成(PQ) (P R)时，当P为F，Q为F时，即天没下雨而我没 上街，此时我说的是假话，但是表达式 (PQ) (P R) 的真值却是
“T” ，因为此时(P R)的真值是“T”.
4
二、复合命题的符号化(翻译) 有了命题演算的合式公式的概念,我们可以把自然语言
中的有些语句(复合命题),翻译成数理逻辑中的符号形式. 基本步骤如下:
1)首先要明确给定命题的含义. 2)对于复合命题，找联结词，用联结词断句，分解出各
个原子命题. 3)设原子命题符号，并用逻辑联结词联结原子命题符号，
构成给定命题的符号表达式.
5
例2 说离散数学无用且枯燥无味是不对的. P：离散数学是有用的. Q：离散数学是枯燥无味的. 该命题可写成： (P∧Q). 例3 如果小张与小王都不去，则小李去. P：小张去. Q：小王去. R：小李去. 该命题可写成： (P∧Q)R. 如果小张与小王不都去，则小李去. 该命题可写成： (P∧Q)R, 也可以写成： (P∨QP∧Q， PR， P∨Q∧R，PQ ∨S , (P W) Q)； 下面的式子才是合式公式：
(P∧Q)，(PR)，((P∨Q)∧R). 按照合式公式定义最外层括号必须写. 约定：为方便，最外层括号可以不写，上面的合式
公式可以写成： P∧Q，PR，(P∨Q)∧R.
命题公式及符号化
一、 命题公式
1.定义1-3.1 命题演算的合式公式
合式公式是由命题变元、命题常量、联结词和圆括号按 一定的逻辑关系联结起来的符号串.我们以如下递归的形 式来定义合式公式：
(1)单个命题变元是一个合式公式. (2)若A是合式公式，则┐A也是合式公式. (3)若A，B是合式公式，则(A∧B)，(A∨B)，(AB)，

离散数学之命题符号化
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、Байду номын сангаас力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ；权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊，可是金 子可以 拉着它 的鼻子 走。— —莎士 比
61、奢侈是舒适的，否则就不是奢侈 。——CocoCha nel 62、少而好学，如日出之阳；壮而好学 ，如日 中之光 ；志而 好学， 如炳烛 之光。 ——刘 向 63、三军可夺帅也，匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里，与其说好 的教师 是幸福 ，不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战，就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
谢谢！

当P和Q的真值相同时,P↔Q取真,否则取假。
例10
P
Q
P Q
0
0
1
0
1
0
1
0
0
1
1
1
非本仓库工作人员，一律不得入内。
解
令P：某人是仓库工作人员；
Q：某人可以进入仓库。
则上述命题可表示为P↔Q。
离散数学 第一章 命题逻辑
8
例11 黄山比喜马拉雅山高，当且仅当3是素数
令P：黄山比喜马拉雅山高；Q：3是素数 本例可符号化为PQ
离散数学 第一章 命题逻辑
6
例. P： 月亮下山 Q： 3+3=6
则P→Q： 若月亮下山,则3+3=6 （并没有实质蕴含关系，仍承认）
Q→P： 叫做P→Q的逆命题 ┐P→┐Q ： 叫做P→Q的反命题 ┐Q→┐P： 叫做P→Q的逆反命题
离散数学 第一章 命题逻辑
7
5．等值“↔”
定义1-5 由命题P和Q，利用“↔”组成的复合命题，称为等值式 复合命题，记作“P↔Q” （读作“P当且仅当Q”）。
21
2
條件否定¬(P→Q)的真值表:
P
Q
0
0
0
1
1
0
1
1
于是得到：¬(P→Q) 与 P∧¬Q 等价。
P∧¬Q 0 0 1 0
換個角度來看，既然下雨地就會溼；那麼如果地是乾的，就一定是沒有下雨。 下面的真偽值表可以反應這個關係：
P
Q
¬Q → ¬P
0
0
1
0
1
1
1
0
0
1
1
1
「非 Q則非P」為「若 P 則 Q」之逆否命題（contrapositive），和「若 P 則 Q 」 為等價之命題。我們稱 Q 為 P之必要條件。

• 注意：命题变元本身不是命题，只有给它一个 解释，才变成命题。
二.合式公式 ( wff ) (well formed formulas)
• 1.定义：
⑴ 单个命题变元是个合式公式。
⑵ 若A是合式公式，则A是合式公式。
⑶ 若A和B是合式公式，则(A∧B)， (A∨B)，(AB)和(AB)都是合式公式.
• 若写成(PQ) (P R)时，当P为F，Q为F时，即天没 下雨而我没上街，此时我说的是假话，但是表达式
(PQ) (P R) 的真值却是“T” ，因为此时(P R)的
真值是“T”。所以这个表达式也不对。
作业： P33 – 1.2, 1.4 , 1.5
1-3 命题公式及命题符号化
一.常值命题与命题变元
• 常值命题：即是我们前面所说的命题。它是有 具体含义 (真值)的。例如：“3是素数。”就 是常值命题。
• 命题变元：用大写的英字母如P、Q等表示任何 命题。称这些字母为命题变元。
• 对命题变元作指派(给命题变元一个解释)：将 一个常值命题赋予命题变元的过程，或者是直 接赋给命题变元真值“T”或“F”的过程。
11
100
十进制数 0 1 2 3 4 5 6 7 8
9
二进制数 0 1 10 11 100 101 110 111 1000 1001
注:有效数字前加0不影响数值，如000=0，001=1，010=10，011=11
• 为了有序地列出A(P1,P2,…,Pn)的真值表， 可以将F看成0，将T看成1，按照二进制 数00…0, 00…01, 00…010, …, 11…10, 11…1(即十进制的0,1,2,…. ,2n -1)的次序 进行指派列真值表。
• 例5.人不犯我，我不犯人；人若犯写成：(PQ)∧(PQ)

离散数学命题符号化证明
将离散数学中的命题符号化证明分为两个部分：命题符号化和证明。

命题符号化是将离散数学中的概念和问题转化为形式化的符号表示。

在这一步骤中，我们需要定义命题符号化的语言和符号系统，并将离散数学中的概念及其关系用符号表示出来。

常用的符号包括逻辑连接词（如“与”、“或”、“非”）、量词（如“存在”、“全称”）以及特定的符号表示概念（如集合运算符号、关系运算符号等）。

在进行命题符号化时，我们还需要考虑符号系统的规范性和一致性，以确保符号表示的准确性和易读性。

证明是在命题符号化的基础上，利用逻辑推理方法进行推导，从已知的命题出发，通过逻辑推理推导出所要证明的命题。

证明可以采用直接证明、间接证明、数学归纳法等不同的证明方法。

在进行证明时，需要使用逻辑推理规则和定理，如分析规则、合取规则、析取规则、双重否定规则、蕴含规则、假言推理规则等。

证明过程中还需要小心地注意到每一步推理的合法性，避免出现逻辑错误。

总的来说，离散数学中的命题符号化证明是将离散数学中的概念和问题转化为符号表示，并通过逻辑推理方法推导出所要证明的命题。

这一过程需要严密的逻辑思维和推理能力，以确保证明的正确性和严谨性。

离散数学符号∀全称量词∃存在量词├ 断定符（公式在L中可证）╞ 满足符（公式在E上有效，公式在E上可满足）﹁命题的“非”运算，如命题的否定为﹁p∧命题的“合取”（“与”）运算∨命题的“析取”（“或”，“可兼或”）运算→ 命题的“条件”运算↔ 命题的“双条件”运算的p<=>q命题p与q的等价关系p=>q命题p与q的蕴涵关系A* 公式A的对偶公式wff 合式公式iff 当且仅当↑ 命题的“与非” 运算（“与非门” ）↓ 命题的“或非”运算（“或非门” ）□ 模态词“必然”◇模态词“可能”∅空集∈属于A∈B,即“A属于B”∉不属于P(A) 集合A的幂集|A| 集合A的点数R²=R○R [R=R○R] 关系R的“复合”א阿列夫⊆包含⊂（或下面加≠）真包含∪集合的并运算∩ 集合的交运算-或\ 集合的差运算〡限制集合关于关系R的等价类A/R集合A上关于R的商集[a] 元素a产生的循环群I环，理想Z/(n) 模n的同余类集合r(R) 关系R的自反闭包s(R) 关系R的对称闭包CP 命题演绎的定理（CP 规则）EG 存在推广规则（存在量词引入规则）ES 存在量词特指规则（存在量词消去规则）UG 全称推广规则（全称量词引入规则）US 全称特指规则（全称量词消去规则）R 关系r 相容关系R○S 关系与关系的复合domf 函数的定义域（前域）ranf 函数的值域f:x→y f是x到y的函数(x,y) x与y的最大公约数[x,y] x与y的最小公倍数aH(Ha) H关于a的左（右）陪集Ker(f) 同态映射f的核（或称f同态核）[1，n] 1到n的整数集合d(A,B),|AB|,或AB点A与点B间的距离d(V) 点V的度数G=(V,E) 点集为V，边集为E的图GW(G) 图G的连通分支数k(G) 图G的点连通度Δ(G) 图G的最大点度A(G) 图G的邻接矩阵P(G) 图G的可达矩阵M(G) 图G的关联矩阵C复数集I 虚数集N 自然数集（包含0在内）N*（N+）正自然数集，正整数集（*表示从集合中去掉元素“0”）P素数集Q 有理数集R 实数集Z 整数集Set 集范畴Top 拓扑空间范畴Ab 交换群范畴Grp 群范畴Mon 单元半群范畴R ing 有单位元的（结合）环范畴R ng 环范畴C R ng 交换环范畴R-mod 环R的左模范畴mod-R环R的右模范畴Field 域范畴Poset 偏序集范畴部分希腊字母数学符号。

例如: 逻辑学中著名的三段论:
凡偶数都能被2整除. 6是偶数. 所以, 6能被2整除.
这个推理是数学中的真命题, 是正确的, 但在命题逻辑中却无 法判断其正确性, 用p,q,r分别表示以上三个命题. 则得到推理的形式结构为:
(p∧q)→r
由于上式不是重言式, 因而不能由它判断推理的正确性. 原因 在于各命题的内在联系没有表示出来. 为了克服命题逻辑的局限性, 应该将原子命题再细分, 分析出 个体词, 谓词和量词, 以便达到表达出命题的内在联系和命题 之间的逻辑关系. 这就是一阶逻辑所研究的内容.
解
(1) 令M(x): x 为实数 ; F(x): x能写成整数之比. 则
x (M(x)→ F(x))
不是 x (M(x) ∧ F(x))
假命题
(2) 令M(x): x 为素数; G(x): x为偶数. 则
x (M(x)∧G(x))
不是 x (M(x) → G(x))
真命题
(3) 令M(x): x 是人; H(x): x登上过木星. 则
2. 谓词: 用来刻划个体词的性质或个体词之间相互关系的词. 例如: (1) 在命题“是无理数”中, “…是无理数”是谓词.
(2) 在命题“x 是有理数”中, “…是有理数”是谓词. (3) 在命题“小王与小李同岁”中, “…与…同岁”是谓词. (4) 在命题“x与y具有关系L”中, “…与…具有关系L”是谓词. 注 ① 常用大写字母F, G, H 等来表示谓词. ② 表示具体性质或关系的谓词称为谓词常项; 表示抽象或泛指的性质或关系的谓词称为谓词变项. ③ F(a): 表示个体常项a具有性质F (F是谓词常项或变项); F(x): 表示个体变项x具有性质F (F同上); F(a,b): 表示个体常项a, b具有关系F (同上); F(x,y): 表示个体变项 x, y具有关系F (同上) . 一般地, 用P(x1,x2,…,xn)表示含n(n≥1)个个体变项x1,x2,…,xn 的n元谓词. 它可看成以个体域为定义域, 以{0,1}为值域的n元函数关系. 当P取常项, 且(x1,x2,…,xn)取定常项(a1,a2,…,an)时, P(a1,a2,…,an)是一个命 题.

(5) 王晓红生于1975年或1976年.
.
14
解 令 p:2是素数, q:3是素数, r:4是素数, s:6是素数, 则 (1), (2), (3) 均为相容或. 分别符号化为: p∨r , p∨q, r∨s, 它们的真值分别为 1, 1, 0.
(4), (5) 为排斥或. 令 t :小元元拿一个苹果，u:小元元拿一个梨， 则 (4) 符号化为 (t∧u) ∨(t∧u). 令v :王晓红生于1975年,w:王晓红生于1976年, 则 (5) 既可符号化为 (v∧w)∨(v∧w), 又可 符号化为 v∨w .
pq pq pq qp qp pq qp qp
注意： pq 与 qp 等值（真值相同）
.
18
联结词与复合命题(续)
5. 等价式与等价联结词“”
定义 设p，q为二命题，复合命题 “p当且仅当q”称 作p与q的等价式，记作pq. 称作等价联结词. 并规定pq为真当且仅当p与q同时为真或同时为 假.
说明: (1) pq 的逻辑关系:p与q互为充分必要条件 (2) pq为真当且仅当p与q同真或同假
.
真命题 假命题 真值不确定 疑问句 感叹句 祈使句 悖论
(3)~(7)都不是命题
8
命题的分类Leabharlann 简单命题(原子命题)： 简单陈述句构成的命题
复合命题： 由简单命题与联结词按一定规则复合 而成的命题
.
9
简单命题符号化
用小写英文字母 p, q, r, … ,pi,qi,ri (i≥1）表示 简单命题 用“1”表示真，用“0”表示假
例如，令 p： 2 是有理数，则 p 的真值为 0 q：2 + 5 = 7，则 q 的真值为 1
.