非线性物理(单摆杜芬方程)讲义
- 格式:ppt
- 大小:958.00 KB
- 文档页数:33


非线性物理基础一、孤立波1. 孤立水波孤立波是一种在水面上传播的具有特殊性质的波动,其形状是一个孤立的波峰,传播过保持形状不变。
孤立波不同于水波,水波在传播过程会弥散开去而不能保持其形状。
2.孤立水波的发现1834年,J S Russell(英国)在爱丁堡格拉斯哥运河旁观看船的行驶,偶然观察到孤立波这一奇特现象。
3.水槽实验重物从水槽的一端掉下,观察水波的激起情况。
Russell 速度公式:v2 = g ( h + a )h表示水深,a 为水波的振幅。
水波越高,传播越快。
4.用不可压缩流体观点导出Russell公式Boussinesg (1871年)和Rayleigh(1876年)假设孤立水波有一个比水深大得多的长度范围,根据非粘滞不可压缩流体的运动方程推导了Russell的公式,同时得到“波包”公式:u(x, t)= a sech2 [β( x -v t ) ]v2 = g ( h + a )β-2 = 4 h2 ( h + a )/3a其中a > 0, 且a << h 才成立。
u(x, t) 是何种微分方程的解?5.水波方程的建立1895年,D J Korteweg 在G de Vrise 的指导下,撰写博士论文,选择了水槽中孤立波的数学描述问题。
u t + αu u x + u xxx = 0u 为波的振幅,α为常数。
这个方程称为KdV方程。
u(x,t) = (12/α)sech2(x – 4 t)在KdV方程中,第二项是非线性的,该项为零时,化为齐次波动方程,其解代表色散解。
只有当非线性项和色散项调配适合时,才会出现孤立波。
二、孤立子1.孤立子的“由来”1834年发现孤立水波(J S Russell)1895年建立水波方程(KdV方程)1955年揭示除水外,其它介质中也可存在非线性孤立波(Fermi, Pasta, and Ulam)(64个质点用非线性弹簧相连,研究能量分布)1965年研究等离子体中非线性孤波的相互碰撞过程,孤波不会改变其形状,Zabusky and Kruskal 首次引入了“孤立子”概念。

第十六章非线性物理简介引子:英国的海岸线有多长--浅谈分形理论1967年,美国科学家曼德尔布罗在《科学》杂志上发表了一篇文章,题目是“英国的海岸线有多长?统计自相似和分形维”。
海岸线曲曲弯弯,包含了数不清的小湾和小半岛。
如果一个巨人一步能跨一公里,他可以沿着海岸走,丈量出海岸线的一个长度。
如果他一步只有五百米,他就会丈量出一个长一些的长度。
如果是一个一步只有一米的人来丈量,他可以分辨出更多的细节,得到更长的长度。
随着尺子变小,长度越来越长。
那英国的海岸线到底有多长?这看起来平庸的问题却开创了一门新的学科—分形几何学。
分形一词是由拉丁文“fractus”转化而来,原意为不规则的、支离破碎的物体。
1975年,曼德尔布罗翻阅儿子拉丁语字典时得到启发,用该词创造出一个新英文单词“fractal”,用以描述他一直研究的各种不规则的几何体。
1982年,他在《大自然的断裂状物体几何》中写道:“为什么几何给人的印象那么枯燥乏味?原因之一是它不能描绘出云彩、山峰或树的自然形状。
因为云朵不是球面,山坡不是锥体,海岸不是圆形,树皮不光滑,闪电也不是直线。
”那么隐藏在这些不规则形状之后的是什么呢?曼德尔布罗发现:“如果你仔细观察一棵树,就会发现它的每一部分都形似它的整体。
”这样的例子在自然界里比比皆是:花菜、雪花、闪电、云彩、山峰、肺、血管…曼德尔布罗认为这种部分与整体的自相似性就是自然结构的基本特性,他在1986给出定义“一分形乃以其某种方式使部分相似于整体的形状”。
分形概念一经提出很快就越出数学的范畴。
在物理学里,分形结构就有很多:一维准晶体,枝晶生长图样,聚合物生长,介电击穿形成的放电图样,逾渗模型里的集团结构,相变过程的临界行为,布朗运动,混沌系统里的奇异吸引子等等。
20世纪90年代,美国宇宙学家林德甚至提出,真空场的起伏波,由于时空膨胀而冻结,成为新的时空膨胀点,从而使整个宇宙生长为一个分形时空树。
现在分形的研究已成为非线性科学研究中的一个重要内容,并扩展到生态、生命、经济、人文等许多领域,在一些电子艺术中甚至出现奇异绚丽的分形视觉艺术作品,在计算机上也可以生成美丽如画的自然风光。

摘要单摆是日常生活中常见的一种物理现象,用一根细绳的一端拴着一个重物,把另一端固定,当重物来回摆动时,就形成了一个单摆模型。
本文讨论理想单摆和非线性单摆的分析方法,着重讨论非线性单摆的角度和角速度的关系及用摄动法求解一类特殊非线性单摆(duffing振子)。
并介绍几种常用的数学求解单摆方程的方法。
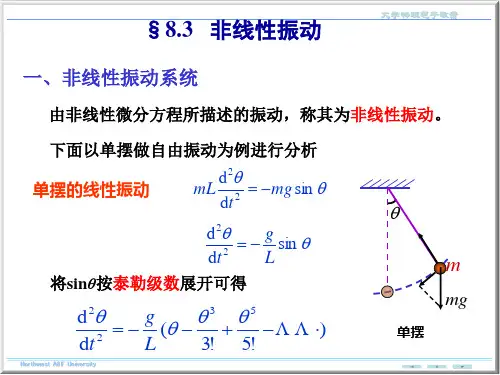
关键字:无阻尼;周期强迫;任意角度;阻尼振子;非线性;摄动法;平均法AbstractSingle pendulum is a common physic phenomenon in our life. Tie an object with a line, fasten the other side. When the object rock around, we can get a single pendulum.The main content of this paper is to discuss the method of analysis the ideal single pendulum and the nonlinear single pendulum. We put our eye on the relationship between the angle speed and the angle acceleration. Then we will use perturbation method to solve one special angle pendulum equation. At last we will introduce some common ways to solve the problem.Keywords:no damp, period forced, any angle, damp flap, nonlinear,perturbation method, average method.II目录一、无阻尼振荡的分析 (1)二、周期强迫振动的分析 (4)三、摆角为任意角度的分析 (5)四、阻尼振子的分析 (8)五、有摩擦强迫振动的分析 (10)六、非线性振子的分析 (12)七、摄动法求解duffing振子方程(perturbation method) (15)1、正规摄动法(regular perturbation method) (16)2、Poicarè法: (17)八、用平均法求解单摆方程 (19)参考文献 (21)附件 (22)III一、无阻尼振荡的分析1一、无阻尼振荡的分析如图所示,忽略细绳重量,也不计小球受到的空气阻力,则上诉单摆可看成理想单摆,对其进行受力分由牛顿第二定律得:θsin mg ma -=(1)因为2222dtd l dt s d a θ== )(θl s= (2)把(2)代入(1)式可得 0sin 22=+θθmg dtd ml (3)将(3)两端同除以ml 可得 0sin 22=+θθlgdtd (4)令lg=0ω,其中0ω为自然频率.则(4)可变为 0sin 2022=+θωθdtd (5) 当θ很小时,θθ=sin 故有,02022=+θωθdt d (6)解此方程得:ti ti eC e C t 0021)(ωωθ-+= (7)若θ为实数,则有θθ=*,即t i t i ti t i e C e C e C e C 000021*2*1ωωωω--+=+ (8)所以, *21C C =, *12C C = (9)令ϕi e A C 21=,ϕi e AC -=22.一、无阻尼振荡的分析2则有())cos(2)(0)()(00ϕωθϕωϕω+=+=+-+t A e e A t t i t i (10) )cos()(0ϕωθ+=t A t (11)从能量守恒方面考虑:0022=+θωθdt d 可变形为 020=+⋅⎪⎭⎫⎝⎛θωθθθdtd d dt d d (12) 令dtd θθ=',则有 0''20=+θωθθθd d (13) 两边同时乘以θd ,得到 0''20=+θθωθθd d (14)在对两边求积分, ⎰⎰⎰=+θθθωθθd d d 0''20 (15)积分结果为 E =+220221'21θωθ (16)令2'21θ=T (动能),22021θω=V (势能).则有E V T =+,机械能守恒.E =+220221'21θωθ为椭圆方程:00.20.40.60.811.2 1.4 1.6 1.82tt h e t a /d t h e t a图1 a一、无阻尼振荡的分析3-1.5-1-0.500.51 1.5xy图 1 b 图1 a 的图像为摆动角度θ及角度θ的导数随时间变化的曲线,其中实线表示角度θ随时间的变化,点线表示θ的导数(即角速度)随时间的变化。

非线性电路理论及应用报告• Duffing方程介绍与仿真应用姓名:马博学号:25班级:硕3022班完成时间:在非线性振动理论研究中,Duffing方程是一种具有代表性的微分方程式。
本文首先对Duffing方程进行了简单介绍,包括其类型以及根据电路的推导等;其次,本文对硬特性的Duffing方程进行了不同参数下的Mat lab仿真;最后,本文介绍了Duffing方程的微弱信号频率检测,以Holmes型Duffing方程为例进行了分析说明。
关镀词:Duffing方程;非线性;Mat la b仿真;混沌;弱信号检测1Duffing方程简介非线性振动问题的研究通常包括定性研究与定量研究。
定性研究的主要内容包括方程解的存在性、唯一性、周期性和稳定性的研究等。
著名的Duffing方程在非线性动力学系统的研究中占有重要地位。
其特点之一是在Duffing方程等号右边加上了外加强迫项,进而形成了非自治非线性系统。
正是由于系统的本征频率与外加周期强迫项的频率的相互作用,才使得该方程中蕴含着极其丰富的内容:倍周期分叉、混沌、清晰大周期等现象⑴。
(Duffing方程的准形式为:d2x ^dx /、、+ / +g(x) = /(x,t)dt~ dt其中5>0为阻尼系数,g(x)是含有三次方项的非线性函数,/(x,t)为一周期函数。
Duffing方程通常作如下分类⑵:1.假设g(x)满足超线性条件lim型十L T—OO x则称Duffing方程是超线性的;2.假设g(x)满足次线性条件lim 型=0L T—oc 牙则称Duffing方程是次线性的;3.假设g(x)满足半线性条件0 < lim inf < lim sup ^―— < -+<olxlT8 牙Ldoc x则称Duffing方程是半线性的。
若将Duffing方程规范化,有以下四种基本类型⑶:d2x f dx八彳八”-—T + ^ —+ X(t) + X (t) = j cos(t) (1-1)d2x . dx八彳八彳八,+x(t)x(t)=/cos(t)+(1-2)dxd2x+ k — + x3(t) = f cos(t) (1-3)crx f dx、勺八 c眉 + 匚- x(t) + F (t) = f cos(t) (1一4)其中k大于零,是阻尼系数,/cos(t)是系统外力。





单摆的非线性动力学分析亚兵(交通大学车辆工程专业,,730070)摘要:研究单摆的运动,从是否有无阻尼和驱动力方面来分析它们对单摆运动的影响。
对于小角度单摆的运动,从单摆的动力学方程入手,借助雅普诺夫一次近似理论,推导出单摆的运动稳定性情况。
再借助绘图工具matlab,对小角度和大角度单摆的运动进行仿真,通过改变参数,如阻尼大小、驱动力大小等绘出单摆运动的不同相图,对相图进行分析比较,从验证单摆运动的稳定性情况。
关键词:单摆;振动;阻尼;驱动力Abstract:The vibration of simple pendulum is studied by analyzing whether or not damp and drive force itsinfluence of the simple pendulum. For small angle pendulum motion, pendulum dynamic equation from the start, with an approximate Lyapunov theory of stability of motion is derived pendulum situation.Drawing tools with help from matlab, small angle and wide-angle pendulum motion simulation, by changing the parameters, such as damping size, drive size draw simple pendulum of different phase diagram, analysis and comparison of the phase diagram, from the verification the stability of the situation pendulum movement.Key words: simple pendulum; vibration; damp; drive force1 引言单摆是一种理想的物理模型[1],单摆作简谐振动(摆角小于5°)时其运动微分方程为线性方程,可以求出其解析解,而当单摆做大幅度摆角运动时,其运动微分方程为非线性方程,我们很难用解析的方法讨论其运动,这个时候可以用MATLAB软件对单摆的运动进行数值求解,并可以模拟不同情况下单摆的运动。
非线性物理
非线性物理是指研究物体对外力的非线性反应,以及它们引发的种种现象,有时这些现象可能是不可预见的。
它是研究物理现象的一种方法或技术,它的历史可以追溯到19世纪的19世纪中期。
近年来,非线性物理学在许多科学领域得到了广泛的应用,包括力学、声学、电磁学、凝聚态物理学、自动控制、生物物理学以及计算机科学等等。
非线性物理学的研究既可以涉及到原子分子层面的物理学问题,也可以涉及到宏观尺度的物理学问题。
非线性物理有多种不同的研究方法,其中最常用的方法是基于数学模型的分析,例如拉普拉斯方程、谱估计和李雅普诺夫方程等等。
这些数学模型可以用来描述物理现象,是研究非线性物理的基础。
除了基于数学模型的分析外,非线性物理学还包括实验室实验,在实验室实验中,研究者可以采用各种各样的研究方法,例如激光劈裂、非线性光学、固体态物理学和量子力学等。
这些实验将帮助研究者对现有的非线性物理理论进行验证和检验,也可能帮助提出新的非线性物理理论。
此外,非线性物理学还包括计算物理学的研究,通过计算物理学,研究者可以借助计算机来模拟物理实验,以及对非线性物理理论进行分析和模拟。
总之,非线性物理学是一门非常广泛的学科,研究不同层次的物理现象,从原子分子到力学等。
它是定量分析和模拟物理系统非常重要的一门学科,也是一门非常有趣的学科,为研究物理学提供了重要
的理论指导。
第一章非线性振动初步一、教学目标1、理解无阻尼单摆的相图;2、能分析出阻尼单摆的相图;3、了解杜芬方程、范德玻耳方程;4、掌握线性单摆的受迫振动;5、了解杜芬方程的受迫振动。
6、了解庞加莱映射。
二、教学重点1、阻尼单摆的相图2、杜芬方程三、教学难点杜芬方程、范德玻耳方程四、教学方法讲授并适当运用课件辅助教学五、教学建议在学习本章之前应复习《力学》中有关谐振子、单摆、共振的内容。
六、教学过程一、无阻尼单摆的自由振荡1、小角度无阻尼单摆 椭圆点单摆,一个由摆线l 联着的重量为mg 的摆锤所组成的力学系统,是力学教科书中通常都要进行讨论的一个简单的动力学模型。
其实我们将会看到,它具有非常复杂的动力学行为,是一个复杂系统。
我们研究一个理想的单摆,即忽略摆线l 质量,认为整个系统的质量都集中在摆锤上,是一个具有集中参数的数学摆,如图1-1所示。
因为如果把摆线与摆锤的质量一起计算,单摆就是一个具有分布参数的摆,与此相应的数学模型是偏微分方程,处理起来很复杂。
理想单摆的数学表达是常微分方程,研究起来就要容易得多了。
图1-1 数学摆首先忽略一切阻尼,例如忽略摆锤在运动中受到的空气阻力、摆线与悬挂点之间的摩擦力等等。
由牛顿第二运动定律,摆锤质量为m 的单摆的运动方程为:ml d dt mg 22θθ=-sin (1-1-1)式中θ为摆角,g 为重力加速度。
将等式右边项移到到左边,并以ml 相除后有:0sin 22=+θθl g dt d设 l g /0=ω,它是以单位时间的弧度为单位的角频率0ω,则式(1-1-1)可写为:0sin 2022=+θωθdt d (1-1-2)由于正弦函数是非线性的,因此这是一个二阶非线性微分方程。
用级数展开正弦函数:+-+-=!7!5!3sin 753x x x x x (1-1-3)如果x 很小,则可以忽略三次以上的高次项,即x x ≈sin 。
这就是说当单摆的摆角很小时,式(1-1-2)变为线性微分方程:02022=+θωθdt d (1-1-4)方程(1-1-4)的解可以通过如下的代换解获得:t e λθ=式中为常数。