复合函数及其性质

复合函数求原函数公式复合函数是高等数学中的一个重要概念，它在微积分、微分方程等领域中都有着广泛的应用。

求原函数是微积分的基本问题之一，而复合函数求原函数则是其中的一个重要分支。

本文将介绍复合函数求原函数的公式及其应用，希望能够对读者有所帮助。

一、复合函数的定义和性质复合函数是由两个或多个函数组合而成的新函数。

假设有两个函数f(x)和g(x)，则它们的复合函数h(x)可以表示为：h(x) = f(g(x))其中，g(x)称为内函数，f(x)称为外函数。

复合函数的定义域是内函数的定义域，值域是外函数的值域。

例如，若有f(x) = x^2和g(x) = 2x + 1，则它们的复合函数为h(x) = f(g(x)) = (2x+1)^2。

复合函数有以下性质：1. 复合函数的可结合性：设有三个函数f(x)、g(x)和h(x)，则(f g) h = f (g h)。

2. 复合函数的可逆性：若f(x)和g(x)都是可逆函数，则它们的复合函数h(x) = f(g(x))也是可逆函数，其逆函数为(g^-1 f^-1)(x)。

3. 复合函数的导数公式：设有两个函数f(x)和g(x)，则它们的复合函数h(x) = f(g(x))的导数为：h'(x) = f'(g(x)) * g'(x)其中，f'(x)和g'(x)分别为f(x)和g(x)的导数。

此公式也被称为链式法则。

二、复合函数求原函数的公式求原函数是微积分中的一个基本问题，而复合函数求原函数则是其中的一个重要分支。

对于给定的复合函数h(x) = f(g(x))，我们需要求出它的原函数F(x)。

根据微积分的基本公式，我们有：F(x) = ∫ h(x) dx要求出F(x)，我们需要将h(x)表示为基本函数的复合形式，并借助基本积分公式求解。

1. 外函数为幂函数若外函数f(x)为幂函数，则可以将复合函数h(x)表示为：h(x) = f(g(x)) = (g(x))^n其中，n为正整数。

复合函数的几个性质及其应用2复合函数的性质及其应用有关函数的知识是高中数学的重要内容，也是高考及竞赛的重点、热点，同时也是难点。

由几种初等函数复合而成的函数更因其概念抽象，综合程度较高，解题方法灵活，给教与学带来了一些困难，现行教科书上并未对其作系统介绍，本文拟讨论形如y=f[g(x)]的复合函数的几个性质及其应用。

复合函数的定义：一般地，若函数y=f(u)的定义域为P ，而函数u=g(x) 的定义域为M ，值域为C ，并且C 包含在P 内，那么对于M 内的每一个值x 经过中间变量u ，相应地得到唯一确定的一个值y ，于是y 经过中间变量u 而成为x 的函数，记为：y=f[g(x)]。

这种函数称为复合函数。

（函数u=g(x)的值不超过函数y=f(u)的定义域是极重要的）。

y=f(u)叫做复合函数的外函数，u=g(x)叫做复合函数的内函数。

一、 定义域 ：复合函数y=f[g(x)]的定义域是函数u=g(x)的定义域中使值属于y=f(u)的定义域的部分。

例1， 设函数f(x)的定义域是[0，4]，求函数f(2x )的定义域解：∵f(x)的定义域为[0，4] ∴0≤2x ≤4， 即-2≤x ≤2∴f(2x )的定义域为 [-2，2]二、值域：求复合函数的值域时即要考虑内函数的值域又要兼顾外函数的定义域。

例2 求函数)32(log 25.0+-=x x y 的值域解：∵ 44)1(3222≥+--=+-x x x 又0322>+-x x∴43202≤+-<x x345得： ⎪⎪⎩⎪⎪⎨⎧≥+-=≥+-=≤-≤>-045)1(01)0(1230023k g k g k k k 解得：0≤k ≤54若y=f(x)具有单调性由复合函数单调性很容易得出以下结论：1、y=f(x)与y=-f(x)的单调性相异;2、若f(x)≠0则y=f(x)与)(1x f y =的单调性相异; 3、若f(x)＞0则y=f(x)与)(x f y =的单调性一致. 例5 讨论 21x xy += 的单调性 解：∵21x xy += 是奇函数∴在(-∞, 0)与(0, +∞)上具有相同的单调性， 当x ＞0时2111x y +=2x y = 递增 ⇒ 21x y =递减 ⇒211x y +=递减⇒2111x y +=递增。

数学中的复合函数函数的复合与分解数学中的复合函数：函数的复合与分解数学中的复合函数是指由两个或多个函数组合而成的函数。

在数学领域中，复合函数是一个重要的概念，它可以帮助我们更好地理解和分析各种数学问题。

本文将介绍复合函数的概念，以及如何进行函数的复合与分解。

一、复合函数的定义与性质复合函数是由两个或多个函数构成的新函数。

设有函数f(x)和g(x)，如果g的定义域是f的值域，那么可以定义g与f的复合函数，记作g(f(x))，它的定义为：g(f(x))=g∘f(x)。

复合函数的计算方式是先计算内层函数（即f(x)），再将结果作为外层函数（即g(x)）的自变量进行计算。

复合函数的性质包括：1. 结合律：对于函数f(x)，g(x)和h(x)，有(g∘f)∘h=g∘(f∘h)，即复合函数的结果与计算顺序无关。

2. 幺元：对于任意函数f(x)，都有f∘I(x)=f(x)，其中I(x)是恒等函数。

3. 逆元：对于可逆函数f(x)，复合函数f∘f^(-1)(x)和f^(-1)∘f(x)都等于自变量x。

二、函数的复合与分解函数的复合与分解是指利用已知的函数（包括基本函数和已知的复合函数）构造新的函数或将一个函数分解成多个函数的组合。

1. 函数的复合函数的复合即为将一个函数的输出作为另一个函数的输入。

设有函数f(x)和g(x)，函数g的定义域是f的值域，那么可以定义g与f的复合函数，记作g(f(x))，表示先通过函数f(x)计算出一个中间结果，再将该结果作为g(x)的输入进行计算。

例如，设f(x)=2x，g(x)=x+1，那么可以计算g(f(x))，首先计算f(x)=2x，然后将其代入g(x)中得到g(f(x))=f(x)+1=2x+1。

2. 函数的分解函数的分解是将一个函数拆解成多个函数的组合。

这在求解复杂函数问题时非常有用。

分解可以按照多种方式进行，取决于具体的问题和需要。

例如，设有复合函数g(f(x))=h(x)，我们可以将g(x)拆解为f(x)和h(x)的组合，即g(x)=f(h(x))。

浅谈复合函数复合函数是一种非常有用的数学工具，它可以用来描述多个函数之间的关系。

在本文中，我们将讨论复合函数的定义、性质以及如何求解复合函数。

首先，让我们来了解一下复合函数的定义。

定义：若函数 f 和 g 都是定义在一个集合 D 上的函数，则将函数 g 当作函数 f 的输入，并得到函数 h，则称函数 h 为函数 f 和 g 的复合函数，记作 h = f(g(x))。

例如，若函数f(x)=x^2+1，函数g(x)=x+1，则函数h = f(g(x))=f(x+1)=(x+1)^2+1。

注意，复合函数的定义并不是将函数 f 和 g 相乘或相加，而是将函数 g 作为函数 f的输入。

现在，让我们来看一看复合函数的一些性质。

性质 1：复合函数的定义域是函数 g 的定义域。

性质 2：复合函数的值域是函数 f 的值域。

性质 3：若函数 f 和 g 都是单射函数，则复合函数 h 也是单射函数。

性质 4：若函数 f 和 g 都是可导函数，则复合函数 h 也是可导函数。

性质 5：若函数 f 和 g 都是连续函数，则复合函数 h 也是连续函数。

接下来，我们来讨论如何求解复合函数。

假设我们已经知道函数 f 和 g，并想要求出复合函数 h。

那么，我们需要做的就是将函数 g 代入函数 f 中，并得到函数 h。

例如，若函数f(x)=x^2+1，函数g(x)=x+1，则函数h = f(g(x))=f(x+1)=(x+1)^2+1。

注意，在求解复合函数时，我们需要先将函数 g 代入函数 f 中，再得到函数 h。

因此，我们可以将复合函数表示为 h(x)=f(g(x))。

此外，我们还可以使用复合函数的运算法则来求解复合函数。

这一运算法则规定，若函数 f 和 g 分别为函数 h 和 k 的复合函数，则函数 f 和 g 的复合函数为(f∘g)(x)=f(g(x))。

例如，若函数 f(x)=x^2+1，函数 g(x)=x+1，函数 h(x)=x^3+1，函数 k(x)=x+2，则函数 f 和 g 的复合函数为(f∘g)(x)=f(g(x))=(x+1)^2+1，函数 h 和 k 的复合函数为(h∘k)(x)=h(k(x))=(x+2)^3+1。

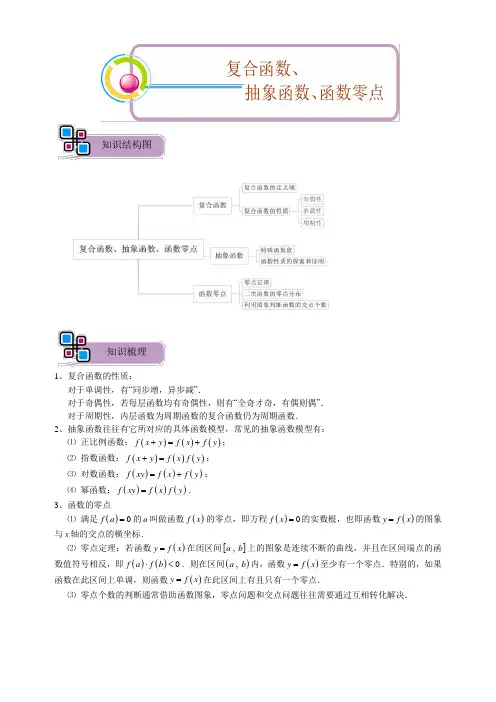
1、复合函数的性质：对于单调性，有“同步增，异步减”．对于奇偶性，若每层函数均有奇偶性，则有“全奇才奇，有偶则偶”． 对于周期性，内层函数为周期函数的复合函数仍为周期函数．2、抽象函数往往有它所对应的具体函数模型，常见的抽象函数模型有： ⑴ 正比例函数：()()()f x y f x f y +=+； ⑵ 指数函数：()()()f x y f x f y +=； ⑶ 对数函数：()()()f xy f x f y =+； ⑷ 幂函数：()()()f xy f x f y =．3、函数的零点⑴ 满足()0f a =的a 叫做函数()f x 的零点，即方程()0f x =的实数根，也即函数()y f x =的图象与x 轴的交点的横坐标．⑵ 零点定理：若函数()y f x =在闭区间[],a b 上的图象是连续不断的曲线，并且在区间端点的函数值符号相反，即()()0f a f b ⋅<．则在区间(),a b 内，函数()y f x =至少有一个零点．特别的，如果函数在此区间上单调，则函数()y f x =在此区间上有且只有一个零点．⑶ 零点个数的判断通常借助函数图象，零点问题和交点问题往往需要通过互相转化解决．知识梳理知识结构图复合函数、 抽象函数、函数零点1、（2007北京理）对于函数①()()lg 21f x x =-+，②()()22f x x =-，③()()cos 2f x x =+，判断如下三个命题的真假： 命题甲：()2f x +是偶函数；命题乙：()f x 在(),2-∞上是减函数，在()2,+∞上是增函数； 命题丙：()()2f x f x +-在(),-∞+∞上是增函数．能使命题甲、乙、丙均为真的所有函数的序号是 ．A ．①③B ．①②C ．③D ．②【解析】 D2、 （2011北京理13）已知函数()()32212x x f x x x ⎧⎪=⎨⎪-<⎩，≥，，若关于x 的方程()f x k =有两个不同的实根，则实数k 的取值范围是 ．【解析】 ()0,1；1、()213log 54y x x =-+的单调递增区间为（ ）A ．(),1-∞B ．5,2⎛⎫-∞ ⎪⎝⎭C ．5,42⎛⎫⎪⎝⎭D ．()4,+∞ 2、设函数()xf x a -=（0a >且1a ≠），()24f =，则（ ）A ．()()21f f ->-B ．()()12f f ->-C ．()()12f f >D ．()()22f f ->3、已知()()log 2a f x ax =-是[]0,1上的减函数，则a 的值可能为（ ） A ．12 B ．32C ．2D ．3 4、已知函数()2x f x x =+，()2log g x x x =+，()2log 2h x x =-的零点分别为a 、b 、c ，则（ ）A ．a b c <<B ．a c b <<C ．b a c <<D ．c a b <<5、已知函数()()()2f x x a x b =---（a b <），并且α、β是方程()0f x =的两个根（αβ<），则实数a 、b 、α、β的大小关系是（ ）A ．a b αβ<<<B ．a b αβ<<<C ．a b αβ<<<D ．a b αβ<<<6、已知函数()22f x x x c =-+，()()1f x f x =，()()()1n n f x f f x -=（2n ≥，n *∈N ），若函数()n f x x -不存在零点，则c 的取值范围是（ ） A ．14c <B ．34c ≥C ．94c >D ．94c ≤ 小题热身真题再现7、下列关于函数()()log 1x a f x a =-（0a >且1a ≠）的命题： ① 无论a 取何值，()f x 均为R 上的增函数； ② 无论a 取何值，()f x 的值域均为R ； ③ 无论a 取何值，()f x 一定有零点； ④ 存在某个a ，使得()f x 恰好有两个零点．其中正确的命题个数为（ ）A ．0B ．1C ．2D ．38、若单调函数()f x （x ∈R ）满足()()()f x y f x f y +=⋅，则()f x 的值域为（ ） A ．R B ．()(),00,-∞+∞ C ．()0,+∞ D ．不能确定9、已知函数()2243f x x x -=-+-，设()()()()F x p f f x f x =⋅+，其中p 为负实数．若()F x 在区间(),3-∞-上是减函数，在区间()3,0-上是增函数，则p 的值为（ ）A ．1-B ．18-C ．116-D ．12-10、已知函数()2f x ax bx c =++（0a ≠），则关于x 的方程()()20m f x nf x p ++=⎡⎤⎣⎦（实数,,,,,0a b c m n p ≠）的解集不可能是（ ）A ．{}1,2B ．{}1,4C ．{}1,2,3,4D ．{}1,4,16,641 2 3 4 5 6 7 8 9 10 AABAACCCCD考点：复合函数的定义域与值域 【例1】 ⑴函数()12xf x ⎛⎫= ⎪⎝⎭的定义域为 ，值域为 ．⑵函数211()2x f x -⎛⎫= ⎪⎝⎭的定义域为 ，值域为 ．⑶函数21122log log 2y x x ⎛⎫=+- ⎪⎝⎭的定义域为_________，值域为____________． 【解析】 ⑴ [)0,+∞，(]0,1；⑵ [11]-，，1,12⎡⎤⎢⎥⎣⎦；⑶ [)1042⎛⎤+∞ ⎥⎝⎦，，，[0)+∞，；4.1复合函数经典精讲【例2】 ⑴已知函数()()2lg 21f x ax x =++的定义域为R ，求实数a 的取值范围．⑵已知函数()()2lg 21f x axx =++的值域为R ，求实数a 的取值范围．【解析】 ⑴ ()1,+∞；⑵[]0,1；【拓1】 ⑴ 已知()32log f x x =+，[]1,9x ∈，求函数()()22y f x f x =+⎡⎤⎣⎦的值域．⑵ 设2,1(),1x x f x x x ⎧⎪=⎨<⎪⎩≥，()g x 是二次函数，若()f g x ⎡⎤⎣⎦的值域是[)0,+∞，求函数()g x 的值域．⑶ 设[]2,8x ∈，函数()()21()log log 2a a f x ax a x =⋅的最大值是1，最小值是18-，求a 的值．【解析】 ⑴ []6,13⑵ [)0,+∞． ⑶ 12a =．考点：复合函数的性质初步【例3】 ⑴函数()212log 56y x x =-+的单调增区间为（ ）A ．52⎛⎫+∞ ⎪⎝⎭，B ．(3)+∞，C ．52⎛⎫-∞ ⎪⎝⎭， D ．(2)-∞，⑵函数2212x x y -++⎛⎫= ⎪⎝⎭的单调递增区间是（ ）A ．11,2⎡⎤-⎢⎥⎣⎦B ．(],1-∞-C ．[)2,+∞D ．1,22⎡⎤⎢⎥⎣⎦⑶函数421x x y =-+的值域为_______，单调递减区间为________．【解析】 ⑴ D ；⑵ D ；⑶ 3,4⎡⎫+∞⎪⎢⎣⎭；(),1-∞-．考点：复合函数的性质综合【例4】 ⑴函数()()212log 23f x x ax =-+，若()f x 在(],1-∞内是增函数，则a 的取值范围为________；若()f x 的单调递增区间是(],1-∞，则a 的取值范围为________． ⑵已知函数()()31axf x a -=≠，若()f x 在区间(]0,1上是减函数，则实数a 的取值范围是 ． ⑶若函数()()2log 2a f x x x =+（0a >且1a ≠）在区间10,2⎛⎫⎪⎝⎭内恒有()0f x >，则()f x 的单调增区间是 ．【解析】 ⑴ [12)，；{1}．⑵()(],01,3-∞；⑶1,2⎛⎫-∞- ⎪⎝⎭考点：抽象函数的函数值问题 【例5】 ⑴若奇函数()f x （x ∈R ）满足()21f =，()()()22f x f x f +=+，则()1f = ； ⑵定义在实数R 上的函数()y f x =具有如下性质： ①对任意x ∈R ，都有()()33f x f x =⎡⎤⎣⎦；②对任意12x x ∈R ，，且12x x ≠，都有()()12f x f x ≠． 则()()()101f f f -++=________． ⑶已知函数()f x （x ∈R ）满足()12f =，()()()2f x y f x f y xy +=++，则 ()2f = ，()3f = ，()3f -= ．⑷()f x 是定义在(0)+∞，上的增函数，对正实数x 、y 都有()()()f xy f x f y =+成立．则不等式()2log 0f x <的解集为_ ______．【解析】 ⑴12； ⑵ 0；⑶ 6，12，6； ⑷ ()1,2；【拓2】 定义在[]0,1上函数()f x 满足：① ()00f =；② ()()11f x f x +-=； ③ ()132x f f x ⎛⎫= ⎪⎝⎭；④ 对任意12,x x []0,1∈，若12x x <，则()()12f x f x ≤． 则()1f = ，12f ⎛⎫= ⎪⎝⎭ ，13f ⎛⎫= ⎪⎝⎭ ，18f ⎛⎫= ⎪⎝⎭． 【追问】12013f ⎛⎫= ⎪⎝⎭．【解析】 ()11f =；1122f ⎛⎫= ⎪⎝⎭；1132f ⎛⎫= ⎪⎝⎭；1184f ⎛⎫= ⎪⎝⎭． 【追问】112013128f ⎛⎫=⎪⎝⎭． 4.2抽象函数考点：抽象函数的性质【例6】 ⑴若函数()f x （x ∈R ，且0x ≠）对任意的非零实数,x y 满足()()()f xy f x f y =+．求证：()f x 为偶函数．⑵定义在R 上的函数()f x 同时满足下列条件：① 对任意x ，y ∈R ，恒有()()()f x y f x f y +=+； ② 当0x >时，()0f x <，且()12f =-．判断函数()f x 的奇偶性，并求函数()f x 在区间[]2,4-上的最大值和最小值．【解析】 ⑴ 令1,1x y ==-得(1)(1)(1)f f f -=+-，于是(1)0f =；再令1x y ==-得(1)2(1)0f f =-=，于是(1)0f -=．令1y =-得()()(1)()f x f x f f x -=+-=，又()f x 的定义域关于原点对称．故()f x 为偶函数． ⑵ ()f x 在区间[]2,4-上的最大值是(2)4f -=，最小值为(4)8f =-．【备注】本题可以通过函数原型快速得到答案或得到启发．对于⑴()ln f x x =（x ∈R ）是符合函数的函数原型； 对于⑵()2f x x =-（x ∈R ）是符合函数的函数原型．【拓3】 函数()f x 的定义域为R ，且()f x 的值不恒为0，又对于任意的实数m ，n ，总有()()22n m f m f n mf nf⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭成立． ⑴ 求(0)f 的值；⑵ 求证：()0t f t ⋅≥对任意的t ∈R 成立； ⑶ 求所有满足条件的函数()f x ．【解析】 ⑴ (0)0f =；⑵ 对任意t ∈R ，令2m n t ==，得2(2)4()f t t f t =⋅，于是21()(2)04t f t f t ⋅=≥； ⑶ ()f x x =．考点：零点定理【例7】 ⑴函数()237x f x x =+-在区间[02]，上的零点必在下面的区间（ ）内．Ａ．102⎡⎤⎢⎥⎣⎦， Ｂ．112⎡⎤⎢⎥⎣⎦，Ｃ．312⎡⎤⎢⎥⎣⎦， Ｄ．322⎡⎤⎢⎥⎣⎦， ⑵设函数()32log x f x a x+=-在区间()1,2内有零点，则实数a 的取值范围是（ ） A ．()31,log 2-- B ．()30,log 2 C ．()3log 2,1 D ．()31,log 4 【解析】 ⑴ C ；⑵ C ；4.3函数零点考点：函数图象与零点、交点问题【例8】 ⑴方程2log (3)2x x +=的解的情况是（ ）A ．仅有一根B ．有两个正根C ．有一个正根和一个负根D ．有两个负根⑵已知()2881651x x f x x x x -⎧=⎨-+>⎩，≤，，()ln g x x =，则()f x 与()g x 的图象的交点个数为（ ）A ．1B ．2C ．3D ．4⑶若函数()x f x a x a =--（0a >且1a ≠）有两个零点，则实数a 的取值范围是 ． ⑷若不等式2log 0a x x -<对102x ⎛⎫∈ ⎪⎝⎭，恒成立，则实数a 的取值范围是_______．【解析】 ⑴ C ；⑵ C ；⑶ (1,)+∞；⑷ 1116⎡⎫⎪⎢⎣⎭，；考点：复合函数的零点问题【例9】 ⑴已知函数()y f x =和()y g x =在[]2,2-的图象如下所示：-22-22y -11-11Ox-22-22y -11-11Oxf xg x 给出下列四个命题：①方程()0f g x =⎡⎤⎣⎦有且仅有6个根 ②方程()0g f x =⎡⎤⎣⎦有且仅有3个根 ③方程()0f f x =⎡⎤⎣⎦有且仅有5个根 ④方程()0g g x =⎡⎤⎣⎦有且仅有4个根 其中正确的命题是 ．（将所有正确的命题序号填在横线上）． ⑵设1,11()1,1x x f x x ⎧≠⎪-=⎨⎪=⎩，若关于x 的方程()()20f x bf x c ++=⎡⎤⎣⎦有三个不同的实数解123,,x x x ，则222123x x x ++等于 ． 【解析】 ⑴ ①③④；⑵ 5；【拓4】 已知()2f x x px q =++，关于x 的方程()()0f f x =有且只有一个实数根，求证：p 与q 同时大于0或者p 与q 同时等于0．【解析】 关于x 的方程()()0f f x =有且只有一个实数根，()f x 的图象只有如图两种情形（分别对应0∆>和0∆=的情形）．进而容易证明命题成立．y=x 2y=x 1x 2x 1 yOx O xy一、选择题 1、设()()23132x x f x k =-+⋅+，当0x >时()f x 恒取正值，则k 的取值范围为（ ） A ．(),1-∞- B ．(),221-∞- C ．()1,221-- D ．()221,221---【解析】 B ；2、设函数3y x =与212x y -⎛⎫= ⎪⎝⎭的图象的交点为00()x y ，，则0x 所在的区间是（ ）A ．(01)，B ．(12)，C ．(23)，D ．(34)，【解析】 B ；3、 关于x 的方程1log (0x aa x a =>且1)a ≠（ ）A ．仅当1a >时，有唯一解B ．仅当01a <<时，有唯一解C ．有唯一解D ．无解【解析】 C ．4、 设函数()f x x x bx c =++，给出下列四个命题：①当0c =时，()y f x =是奇函数；②当00b c =>，时，方程()0f x =只有一个实根； ③函数()y f x =的图象关于点(0)c ，对称； ④方程()0f x =至多有两个实根；其中正确命题的个数为（ ）A ．1个B ．2个C ．3个D ．4个【解析】 C ；二、填空题 5、 设函数22()log log (1)f x x x =+-，则()f x 的定义域是_______；()f x 的最大值是_____．【解析】 (0,1)；2-．6、 函数22()log (3)log (1)f x x x =++-的值域是___________，单调递增区间为_______．【解析】 (,2]-∞，(3,1)--．课后习题7、 若log (2)a y ax =-在[]01，上是x 的减函数，则a 的取值范围是______． 【解析】 (12)a ∈，；三、解答题 8、已知定义域为R 的函数()f x 满足：()()()f x y f x f y +=，且()31f >． ⑴求()0f ；⑵求证：()41f -<．【解析】 ⑴ (0)1f =；⑵ 3(3)(2)(1)(1)1f f f f ==>，故(1)1f >，从而24(4)(2)(1)1f f f ==>．令4,4x y ==-得，(4)(4)(0)1f f f -==，故1(4)1(4)f f -=<．命题得证． 【备注】()()()f x y f x f y +=的函数原型是指数函数()x f x a =，由(3)1f >知，1a >． 9、函数()2x f x =和()3g x x =的图象的示意图如图所示．设两函数的图象交于点()11,A x y 、()22,B x y ，且12x x <．x 1x 2BA C 2C 1yO x⑴ 请指出示意图中曲线1C 、2C 分别对应哪一个函数？⑵ 若[]1,1x a a ∈+，[]2,1x b b ∈+，且{},1,2,3,4,5,6,7,8,9,10,11,12a b ∈，指出a 、b 的值，并说明理由；⑶ 结合函数图象示意图，请把()πf 、()πg 、()2013f 、()2013g 四个数从小到大顺序排列．【解析】 ⑴ 1C 对应函数()3g x x =，2C 对应函数()2x f x =；⑵ 如下表，可得1a =，9b =．1 2 3 4 5 6 7 8 9 10 11 12()f x 2 4 8 16 32 64 128 256 512 1024 2048 4096 ()g x1 8 27 641252163435127291000 1331 1728()()()() 10、已知关于x 的二次方程22210x mx m +++=．⑴ 若方程有两根，其中一根在区间()1,0-内，另一根在区间()1,2内，求m 的范围． ⑵ 若方程两根均在区间()0,1内，求m 的范围．【解析】 ⑴5162m -<<-．⑵1122m -<-≤。

复合函数总结复习复合函数是高中数学中的重要概念，也是数学建模、微积分等领域的基础知识之一、复合函数的概念在数学中具有广泛的应用，能够帮助我们更好地理解、推导和解决各种数学问题。

1.复合函数的定义复合函数是由两个或多个函数通过其中一种运算相结合形成的函数。

如果有两个函数f(x)和g(x)，则它们的复合函数可以表示为(f∘g)(x)，读作“f环g”。

2.复合函数的基本性质（1）结合律：对于三个函数f(x)，g(x)和h(x)，有[(f∘g)∘h](x)=[f∘(g∘h)](x)，即复合函数的结合顺序不影响最终的结果。

（2）非交换性：一般情况下，复合函数是不可交换的，即[f∘g](x)≠[g∘f](x)。

这是因为函数运算是有顺序的，不同的函数组合可能会产生不同的结果。

（3）单位元：对于任何函数f(x)，有[f∘g](x)=[g∘f](x)=f(x)，其中g(x)是一个恒等函数，即g(x)=x。

这意味着恒等函数在复合运算中充当单位元的作用。

（4）反函数：如果f(x)和g(x)互为反函数，则[f∘g](x)=[g∘f](x)=x。

这是因为反函数的复合运算等于恒等函数。

3.复合函数的求导法则对于复合函数的导数求解，有以下几个常用的法则：（1）链式法则：设 y = f(u) 和 u = g(x) 为两个函数，若 f(x)和 g(x) 都可导，则复合函数 y = f(g(x)) 的导数为 dy/dx = (dy/du)* (du/dx)，其中 dy/du 表示 f(u) 对 u 的导数，du/dx 表示 g(x) 对x 的导数。

（2）反函数法则：设 y = f(x) 和 x = f^(-1)(y) 为两个互为反函数的函数，若 f(x) 可导，则反函数 f^(-1)(y) 在点 y 处的导数为dy/dx = 1 / (dx/dy)。

（3）指数函数和对数函数的导数：设 y = a^x 和 y = log_a x 分别为指数函数和对数函数，其中 a>0，且a ≠ 1，则有 dy/dx = ln⁡a* a^x 和 dy/dx = 1 / (ln⁡a * x)。

函数的复合与反函数的概念与性质函数是数学中非常重要的概念之一，而函数的复合与反函数也是函数学习的关键内容。

本文将从函数的复合与反函数的概念和性质两个方面进行介绍，帮助读者更好地理解和掌握这两个概念。

一、函数的复合函数的复合是指通过两个或多个函数的运算得到一个新的函数。

简单来说，如果有函数f(x)和g(x)，那么将g(x)作为f(x)的自变量，就得到了f(g(x))。

这里，f(g(x))即为函数f和函数g的复合函数。

1. 复合函数的定义假设函数f(x)和g(x)都是定义在数域D上的函数，那么f(x)和g(x)的复合函数f(g(x))定义为：对于D中任意一个x，都有f(g(x))=f(g(x))。

2. 复合函数的性质（1）结合律：如果有三个函数f(x)、g(x)、h(x)，那么f(g(h(x)))和(f∘g)∘h(x)是相等的。

（2）不遵循交换律：一般情况下，f(g(x))和g(f(x))是不相等的。

这是因为函数的复合是从右向左进行运算的。

二、反函数反函数是指对于一个函数f(x)，如果存在一个函数g(x)，使得g(f(x))=x，那么g(x)就是f(x)的反函数。

1. 反函数的定义假设函数f(x)是定义在数域D上的函数，如果存在一个函数g(x)，使得对于D中任意一个x，都有g(f(x))=x，那么g(x)就是f(x)的反函数。

2. 反函数的性质（1）反函数存在的条件：函数f(x)的反函数存在的条件是，f(x)必须是一个双射函数。

即f(x)既是一对一函数，又是满射函数。

（2）反函数的性质：f(x)的反函数g(x)具有以下性质：- 如果f(x)的定义域和值域分别为D和R，那么g(x)的定义域和值域分别为R和D。

- g(f(x))=x，对于f(x)的定义域D中的任意一个x，都有g(f(x))=x成立。

- f(g(x))=x，对于g(x)的定义域R中的任意一个x，都有f(g(x))=x成立。

三、复合函数与反函数的关系复合函数和反函数有一定的关系，主要表现在以下两个方面：1. 复合函数的反函数如果函数f(x)和g(x)互为反函数，那么有以下两个结论：- f(g(x))=x，对于g(x)的定义域R中的任意一个x，都有f(g(x))=x成立。

复合函数的性质及应用
复合函数是一种函数组合，一个函数可以计算并得出另外一个函数的值。

它
可以将函数A与函数B组合起来，即C(x)=A(B(x))，这里A被称为外函数，B被
称为内函数，外函数的参数是来自内部函数的结果，外函数的结果是内部函数的参数。

复合函数具有以下特性：
1、复合函数是使用多个函数或表达式组合起来的函数，它有助于简化复杂的函数。

2、复合函数是链式调用的一种实现，即结果的每一个步骤都是另一个函数的输入，形成一种函数链。

3、复合函数具有联合分析效果，可以精确理解复杂的业务逻辑，包括对参数的把握以及变量之间的关系。

复合函数的应用：
1、仿真与机器学习：在机器学习和仿真中，复合函数可以用于表示模拟模型，用于优化计算结果。

2、数据处理：复合函数可以用于表示数据处理流程，能够更好地把握复杂的数据处理过程，实现数据转换。

3、图形处理：复合函数在图形处理中可以用于表示图像变换、投影、层次和
3D等，以实现精确度和鲁棒性，实现图像质量的提升。