浅谈复合函数的连续性

复合函数的连续性总结复合函数是高等数学中一个重要的概念，它在微积分、实分析等领域有着广泛的应用。

在学习复合函数的连续性时，我们需要深入理解其定义、性质和相关定理，以便能够正确应用于实际问题的求解中。

下面，我将对复合函数的连续性进行总结，希望能够帮助大家更好地理解和掌握这一知识点。

首先，我们来回顾一下复合函数的定义。

设有两个函数f(x)和g(x)，则它们的复合函数定义为(f∘g)(x)=f(g(x))。

也就是说，先对自变量进行g(x)的映射，再对映射的结果进行f(x)的映射，从而得到复合函数(f∘g)(x)。

在复合函数的连续性讨论中，我们通常关注的是当g(x)和f(x)都在某一点连续时，复合函数是否也在该点连续。

其次，我们来探讨复合函数的连续性定理。

首先是复合函数的基本性质，若f(x)在点x0连续，g(x)在点y0=g(x0)连续，则复合函数(f∘g)(x)在点x0连续。

这一性质直观地说明了连续函数的复合仍然是连续函数。

其次是复合函数的复合连续性定理，若f(x)在点y0连续，g(x)在点x0连续，并且g(x)在点x0的邻域内有定义，则复合函数(f∘g)(x)在点x0连续。

这一定理进一步拓展了复合函数的连续性条件，使得我们能够更灵活地应用于实际问题中。

在实际问题中，我们经常会遇到复合函数的连续性求解。

这时，我们可以利用已知函数的连续性和复合函数的连续性定理来判断复合函数的连续性。

具体来说，我们首先要分析已知函数f(x)和g(x)的连续性，然后根据复合函数的连续性定理来判断复合函数(f∘g)(x)在给定点的连续性。

如果f(x)和g(x)都在给定点连续，那么复合函数也在该点连续；如果其中一个函数在给定点不连续，那么复合函数在该点也不连续。

总的来说，复合函数的连续性是一个重要的数学概念，它在实际问题中有着广泛的应用。

通过深入理解复合函数的定义、性质和连续性定理，我们能够更好地掌握这一知识点，为解决实际问题提供有力的数学工具。

复合函数的连续性1. 复合函数的定义复合函数是由两个函数组合而成的函数。

设有函数 f 和 g，复合函数可以表示为 g(f(x))。

在这里，f(x) 的输出成为 g 的输入。

2. 复合函数的连续性定义我们知道，一个函数 f 在某个点 a 处连续，意味着当 x 趋近于a 时，f(x) 趋近于 f(a)。

类似地，对于复合函数 g(f(x))，当 x 趋近于某个点 a 时，g(f(x)) 应该趋近于 g(f(a))。

3. 复合函数的连续性定理假设函数 f 在点 a 处连续，并且函数 g 在点 b 处连续，同时 f(a) = b。

那么复合函数 g(f(x)) 在点 a 处连续。

这个定理说明了当两个函数的连续性相互配合时，复合函数的连续性也能保持。

这是因为在 a 处连续的 f(x) 会使得 g(f(x)) 在 a 处连续。

4. 复合函数的连续性示例例如，考虑函数 f(x) = sin(x) 和 g(x) = x^2。

函数 f(x) 在任何点处都是连续的，而函数 g(x) 在任何点处也是连续的。

现在考虑复合函数 g(f(x)) = (sin(x))^2。

由于 sin(x) 在任何点处连续，根据上述定理，复合函数 g(f(x)) 也在任何点处连续。

5. 复合函数的连续性的应用复合函数的连续性在数学领域和科学研究中有广泛的应用。

例如，在微积分中，复合函数的连续性是求导和积分的基础。

另一个应用是在实际问题的建模中。

通过将现实世界中的问题转化为复合函数，我们可以更好地理解问题的性质，并为解决问题提供便利。

结论复合函数的连续性是一个重要的数学概念。

它描述了将一个函数作为另一个函数的输入时，函数的连续性是否被保持。

复合函数的连续性定理为我们提供了一个有用的工具来判断复合函数的连续性。

同时，复合函数的连续性在数学和科学研究中有广泛的应用。

以上是对复合函数的连续性的简要介绍。

了解复合函数的连续性不仅有助于我们更好地理解数学理论，还有助于我们应用数学解决实际问题。

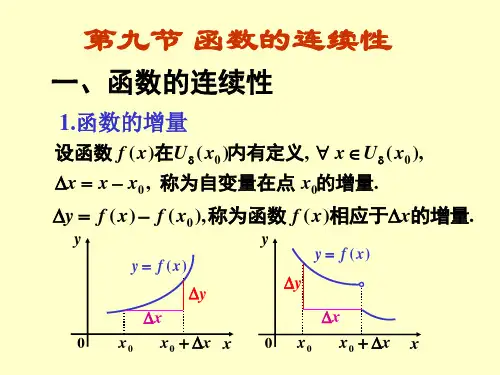
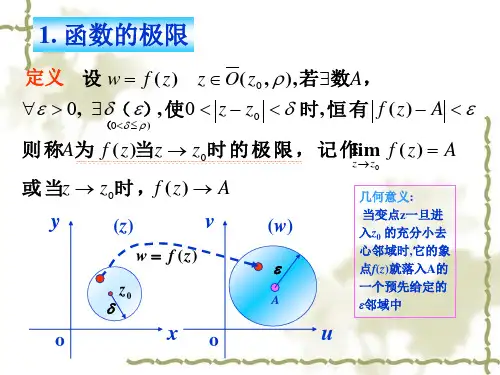
§4 函数的连续性1．函数连续的概念一个连续量y 随着另一个连续量x 连续地变化——连续函数定义3.7 设()f x 在包含0x 的一个开区间有定义．如果 0lim x x →()f x ＝0()f x ，则称函数()f x 在0x 是连续的．0x 称为()f x 的连续点． 否则，称0x 是()f x 的间断点．从定义可见，()f x 在0x 连续，当且仅当()f x 满足下列三个条件： (i) ()f x 在0x 附近有定义，特别是()f x 在0x 有定义； (ii) 极限0lim x x →()f x 存在；(iii) 上述极限值恰好为函数值0()f x ．对照 函数在0x 有极限 和 函数在0x 连续：lim ()x x f x A →= 0>∀⇔ε，0>∃δ，当δ<-<||00x x 时，有 ε<-|)(|A x f)()(lim 00x f x f x x =→ 0>∀⇔ε，0>∃δ，当δ<-||0x x 时，有ε<-|)()(|0x f x f两者的差别就只有“一点”等价定义：令0x x x -=∆，称为自变量（在0x 点）的增量，)()()()()(0000x f x x f x f x f x f y -∆+=-=∆=∆，称为函数（在0x 点）的增量当0x x →时，有 00→-=∆x x x ，于是 )(x f 在0x 是连续 )()(l i m 00x f x f x x =⇔→0>∀⇔ε，0>∃δ，当δ<-||0x x 时，有ε<-|)()(|0x f x f 0>∀⇔ε，0>∃δ，当δ<∆||x 时，有ε<-∆+|)()(|00x f x x f )()(l i m 000x f x x f x =∆+⇔→∆0)]()([lim lim 000=-∆+=∆⇔→∆→∆x f x x f y x x)()0()(lim )0()(lim 0000x f x f x f x f x f x x x x =+==-=⇔+-→→ )(x f ⇔在0x 左连续且右连续函数在0x 连续定义为 0l i m x x →()f x ＝0()f x也可以写作 0lim x x →()f x ＝(f 0lim x x →x )．这表示，在函数连续的情况下，求极限可以直接把自变量的极限代入，或者说，极限运算0lim x x →与函数对应法则f 可以交换次序．定义3. 8 设()f x 定义在),(b a 内，若它在),(b a 内的每一点都是连续的，则称()f x 在区间),(b a 是连续的． 设()f x 定义在],[b a ，若它在),(b a 的每一点都连续，且在a 点右连续，在b 点左连续，则称()f x 在区间],[b a 是连续的。

函数的连续性图第九节 函数的连续性和间断点有了极限的概念，我们就可以来讨论函数的一种重要特性——连续性。

首先，我们应注意到连续性也是客观现实的反映，是从许多自然现象的观察中抽象出来的一种共同特性。

如气温T 随时间t 的变化而连续变化，铁棒长度l 随着温度u 的变化而连续变化等。

它们的共同特性是：一方面在变化，另一方面是在逐渐变化的。

可在很短一段时间内，T 的变化很小；同样当温度u 变化很小时，l 的变化也很小。

这些现象反映在数学上就是自变量有一个微小的变化时，函数的变化也是微小的。

下面我们就专门来讨论这种概念。

一、函数的连续性1. 预备知识改变量：设变量u 从它的一个初值1u 变到终值2u ，终值与初值的差21u u -，就叫u 的改变量，记作21u u u ∆=-。

改变量也叫增量。

注意：①1u ，2u 并不是u 可取值的起点和终点，而是u 变化过程中从1u 变到2u 。

②u ∆可正可负。

③u ∆是一个整体记号，不是某个量∆与变量u 的乘积。

2. 函数()y f x =在0x x =处连续的定义 定义1 当自变量x 在点0x 的改变 量x ∆为无穷小时，相应函数的改变量 ()()()()000y f x x f x f x f x ∆=+∆-=- 也是同一过程中的无穷小量，即0lim 0x y ∆→∆=，则称()f x 在0x 处连续，见图1-37.定理1 ()f x 在0x 处连续的充要条 件是()()00lim x x f x f x →=。

证明 由定义1，()()()()()()00000lim 0lim 0lim lim 0lim .x x x x x x x x x y f x f x f x f x f x f x ∆→→→→→∆=⇔-=⎡⎤⎣⎦⇔-=⇔= 由定理1，我们可将定义1改写为以下定义2. 定义2 如果0ε∀>，0δ∃>，当0x x δ-<时，有()()0f x f x ε-<，则()f x 在0x 处连续。

目录引言 (1)1．一元函数的连续性和可微性 (1)1.1一元函数的连续性 (1)1.1.1 定义 (1)1.1.2 定理 (2)1.1.3 间断点及其分类 (4)1.2 一元函数的可微性 (8)1.2.1 可微的定义 (8)1.2.2微分的运算法则 (9)1.2.3 可导、可微以及连续之间的关系 (9)2.二元函数的连续性和可微性 (11)2.1二元函数的连续性 (11)2.1.1 定义 (11)2.1.2 定理 (11)2.2二元函数的可微性 (13)2.2.1 二元函数可微性的定义 (13)2.2.2 偏导数的定义 (13)2.2.3 定理 (14)2.2.4 微分的几何应用 (15)2.2.5 偏导数的连续性、函数可微性、可偏导性与函数连续性的关系. (17)结束语 (24)参考文献 (25)致谢 (26)引言连续性和可微性是函数的重要特性，从几何形象上粗略地说，连续函数在坐标系上的图像是一条连续不断的曲线，下面就简单的介绍一元函数的连续性和可微性和二元函数的连续性和可微性.对一元函数，连续性和可微性是等价的，它是函数增量与自变量增量之间关系的另一种表达式，函数的微分是函数增量的线性主要部分，可微和可导是等价的，因而求一元函数的导数和微分的方法是相同的.一元函数的可导性是比连续性更强的性质，可导必连续，而连续未必可导.微积不但是数学的许多分支以及物理、化学、计算机、机械、建筑等领域的基本数学工具，在社会、经济等领域中也得到越来越广泛的应用.另一方面，微分所反映的数学思想也是日常生活与工作中认识问题、研究问题所难以或缺的.函数的连续性、可导性与可微性是高等数学中最基本、最重要的概念，这三个概念是微积分的重要组成部分，本文在对比函数连续性、可导性与可微三个概念的基础上，深入讨论了三者之间的联系与区别，为学生深入理解和学习微积分学理清了思路.一元函数连续性、可导性与可微性的概念连续函数是高等数学中重点讨论的一类函数.连续性是函数的一个重要特性，它反映了许多自然现象的一种共同特征.而多元函数是一元函数的推广，它具有比一元函数更复杂的性质.就一般的二元函数来说，连续性和可微性是不等价的，学习数学分析之后，我们知道当二元函数的两个偏导数都连续时，函数可微.首先证明了当二元函数的一个偏导数存在，另一个偏导数连续时，函数可微.然后考虑了一般的多元函数的情形，得到了当多元函数的某个偏导数连续，而其余偏导数存在时，函数可微.由此可见可微性与偏导存在性间的关系是复杂的.本文通过具体实例对多元微分学中的几个重要概念间的进行分析讨论，主要研究二元函数的连续性，偏导存在性，可微性等概念以及它们之间因果关系，在掌握了二元函数的有关理论与研究方法之后,再将它推广到一般的多元函数中去.1．一元函数的连续性和可微性1.1一元函数的连续性1.1.1 定义定义1 设函数f 在某0()U x 内有定义，若0lim ()()x x f x f x →=，则称f 在点0x 连续．由于函数在一点的连续性是通过极限来定义的，因而也可以直接用εδ-方式来叙述，即：若对任给的0ε>，使得当0x x δ-<时有0()()f x f x ε-<，则称f 在点0x 连续．若f 在区间上的每一点都连续，则称f 为上的连续函数． 定义2 设函数f 在某()()()00U x U x +-内有定义.若()()()()0000lim lim x x x x f x f x f x f x +-→→⎛⎫== ⎪⎝⎭， 则称f 在点0x 右（左）连续.1.1.2 定理定理1 函数f 在0x 连续的充要条件是：f 在点0x 既是左连续，又是右连续. 定理2（局部有界性）若函数f 在点0x 连续，则f 在某0()U x 内有界.定理3（局部保号性）若函数f 在点0x 连续，且0()0f x >（或0<)，则对任何正数0()r f x <（或0()r f x <-），存在某0()U x ，使得对一切0()x U x ∈，有()(())f x r f x r ><-或．例1.1 “()f x 在x a =连续”是()f x 在点x a =处连续的（ ）条件 （Ａ）必要非充分（Ｂ）充分非必要 （Ｃ）充要（Ｄ）既非充分又非必要解：()f x 在x a =连续，()f x ⇒在x a =连续，()f x 在x a =连续⇒()f x 在x a =连续，如，1,()1,x af x x a ≥⎧=⎨-<⎩，()1f x =，()f x 在x a =连续，但()f x 在x a =间断.故选（B ）定理4（四则运算）若函数f 和g 在点0x 连续，则g f ±，f g ⋅，/f g （这里0)(0≠x g ） 也都在点0x 连续.定理5 若函数f 在点0x 连续，g 在点0u 连续，)(00x f u =，则复合函数f g 在点0u 连续.证 由于g 在点0u 连续，对于任给的，存在10δ>，使得当01u u δ-<时有()()0g u g u ε-< （1.1）又由()00u f x =及()u f x =在点0x 连续，故对上述10δ>，存在0δ>，使得当0x x δ-<时有()()001u u f x f x δ-=-<.联系（1）得：对任给的0ε>，存在0δ>，当01u u δ-<时有()()()()0g f x g f x ε-<.这就证明了f g 在点0u 连续.例1.2 设()f x 在x a =处连续，()g x 在x a =处间断，又()0f a ≠，则（ ）． （Ａ）[]()g f x x a =在处间断， （Ｂ）[]()f g x x a =在处间断， （Ｃ）[]2()g x x a =在处间断， （Ｄ）()()g x x a f x =在处间断． 解： 分析一 连续与不连续的复合可能连续，也可能间断，故（A ），（B ）不对.不连续函数的相乘可能连续，故（C ）也不对，因此，选（D ）.分析二 ()f x 在x a =处连续，()g x 在x a =处间断，又()0f a ≠，⇒()()g x x a f x =在处间断，若不然，⇒()(),()()g x g x f x f x =在x a =连续，与已知矛盾，选（D ）. 定理6（最大、最小值定理）若函数f 在闭区间[]b a ,上连续，则f 在[]b a ,上有最大值和最小值.推论 （有界性定理）若函数f 在闭区间[]b a ,上连续，则f 在[]b a ,上有界. 定理7（介值性定理）若函数f 在闭区间[]b a ,上连续，且)()(b f a f ≠，若μ为介于)(a f 与)(b f 之间的任何实数，则至少存在一点()b a x ,0∈，使得μ=)(0x f ．推论（根的存在定理）若函数f 在闭区间[]b a ,上连续，且)(a f 与)(b f 异号（即()()0f a f b <，则只是存在一点()b a x ,0∈，使得0()0f x =，即方程()0f x =在(,)a b 内至少有一个根.例1.3 证明：若0r >，n 为正整数，则存在唯一正数0x ，使得0nx r =（0x 称为 r 的n 次正根（即算术根），记作0x =）． 证 先证存在性.由于当x →+∞时有n x →+∞，故必存在正数a ，使得n a r >，因()n f x x =在[]0,a 上连续，并有(0)()f r f a <<，故由介值性定理，至少存在着一点()00,x a ∈，使得00()nf x x r ==．再证唯一性.设正数1x 使得1n x r =，则有()()12101010011...0n n n n n x x x x x x x x ----=-+++=．由于第二个括号内的数为正数，所以只能010x x -=，即01x x =．定理8（反函数的连续性）若函数f 在[]b a ,上严格单调并连续，则反函数1-f 在其定义域[][])(),()(),(a f b f b f a f 或上连续.例 1.4 由于sin y x =在区间,22ππ⎡⎤-⎢⎥⎣⎦上严格单调且连续，故其反函数1sin y x -=在区间[]1,1-上连续.定理9 （一致连续性定理）若函数f 在闭区间[],a b 上连续，则f 在[],a b 上一致连续.定理10 一切基本初等函数都是其定义域上的连续函数. 定理11 任何初等函数都是在其定义区间上的连续函数.1.1.3 间断点及其分类定义 2 设函数f 在某00()U x 内有定义，若f 在点0x 无定义，或f 在点0x 有定义而不连续，则称点0x 为函数f 间断点或不连续点.若0x 为函数f 间断点，则必出现下列情形之一： （ⅰ）f 在点0x 无定义，或极限0lim ()x x f x →不存在.（ⅱ）f 在点0x 有定义，极限0lim ()x x f x →存在，但00lim ()()x x f x f x →≠.据此，我们可对函数的间断点作如下分类：（１）可去间断点 若lim ()x x f x A →=．而f 在点0x 无定义，或有定义但0()f x A ≠，则称0x 为f 的可去间断点.（２）跳跃间断点 若函数f 在点0x 的左、右极限都存在，但lim ()lim ()x x x x f x f x +-→→≠． 则称0x 为f 的跳跃间断点.（３）函数的所有其他形式的间断点，即使得函数至少有一侧极限不存在的那些点，称为第二类间断点.图1.1 可去间断点 图1.2图1.3 跳跃间断点判断函数连续性的方法：（１）若是初等函数，则在它的定义域区间上处处连续. （２）用连续性运算法则.（３）分别判断左右连续性或按定义判断.例1.5 设有定义在(),-∞∞上的函数()f x ：（A ）1,0(),0sin x f x x x x=⎧⎪=≠⎨⎪⎩（B ）sin ,0()cos 1,0x x f x x x ≤⎧=⎨->⎩（C ）1(1),0()1,0x x x f x x ⎧⎪+≠=⎨⎪=⎩ （D ）11(1),0()1,0x x f x xx ⎧+≠⎪=⎨⎪=⎩（1)在定义域上连续的是（ ），(2)函数()f x 以0x =为第二类间断点的是（ ）．解 （1） 00x x <>与时上述()f x 均分别与某初等函数相同，故连续． 只需在考察哪个函数()f x 在0x =处连续.注意到(),0()(),0g x x f x h x x ≤⎧=⎨>⎩,其中()g x 在(],0-∞连续，()h x 在[)0,+∞连续，因(]()()(,0)()f x g x x f x =∈-∞⇒在0x =左连续，若又有(0)(0)g h =[)()()(0,)()f x h x x f x ⇒=∈+∞⇒在0x =右连续，因此()f x 在0x =连续.(B)的()f x 满足0sin (cos 1),x x xx ===-又sin ,cos 1x x -均连续()0f x x ⇒=在连续，因此，（B ）中的()(),f x -∞+∞在连续，应选（B ）．（２）关于（A ）：由00sin sin lim ()lim 1,lim ()lim 1,x x x x x xf x f x x x++--→→→→====-- ⇒ 0x =是()f x 的第一类间断点（跳跃间断点）.关于（C ）：由1lim ()lim(1)(0)xx x f x x e f →→=+=≠，⇒ 0x =是()f x 的第一类间断点（可去间断点）． 已证（B ）中()f x 在0x =连续，因此选（D ），我们也可以直接考察（D ），由111ln(10001lim ()lim(1)lim =+x x x x x x f x e x++++→→→=+=∞）， ⇒ 0x =是()f x 的第二类间断点．例1.6 设(),()f x g x 在0x x =均不连续，则在0x x =处（ ）. （Ａ）()()f x g x +吗，()()f x g x ⋅均不连续.（Ｂ）()()f x g x +不连续，()()f x g x ⋅的连续性不确定. （Ｃ）()()f x g x +的连续性不确定，()()f x g x ⋅不连续．（Ｄ）()()f x g x +，()()f x g x ⋅的连续性均不确定．解：如：1,0()0,0x f x x ≥⎧=⎨<⎩，0,0()1,0x g x x ≥⎧=⎨<⎩，在0x =均不连续，但()()1f x g x +=．()()0f x g x ⋅=在0x =均连续.又如：1,0()0,0x f x x ≥⎧=⎨<⎩，2,0()0,0x g x x ≥⎧=⎨<⎩，在0x =均不连续，而3,0()()0,0x f x g x x ≥⎧+=⎨<⎩，2,0()()0,0x f x g x x ≥⎧⋅=⎨<⎩在0x =均不连续，因此选（D ）．例1.7 讨论下列函数的连续性并判断其间断点的类型.（１）21()(1)arctan 1f x x x =++，（２）ln(1),0()10x x x f x x x +⎧>⎪⎪=⎪-≤<⎪⎩，(３) sin 201sin cos ,0()0,0xt dt x x f x x x ⎧⎪⎪≠=⎨⎪=⎪⎩⎰解：（１）这是初等函数，它在定义域（20x ≠）上连续，因此1x ≠±时均连续，1x =±时，2101lim (1)arctan()2()12x x x ππ→++=⨯-=--， 2101lim (1)arctan()2()12x x x ππ→-+=⨯+=-， 故1x =是第一类间断点（跳跃间断点），又10lim 0x y →-+=，10lim 0x y →--=，故1x =-也是第一类间断点（可去间断点）.（２）在区间()0,+∞，[)1,0-上，函数y 分别与某初等函数相等，因而连续，在0x =处无定义，而ln(1)lim lim 1x x x y x++→→+==，0lim lim lim 1x x x y x---→→→===， 0x ⇒=是第一类间断点（可去间断点）．（３) 记sin 20()cos x g x t dt =⎰，又变限几分的性质及复合函数的连续性，知()g x 是连续函数，再由连续函数的运算法则，知0x ≠时()1()sin g x f x x x=连续，由于 200()limlimcos(sin )cos 10x x g x x x x→→==≠，而01lim sin x x →±不存在，所以0()1limsin x g x x x→±不存在，即0x =是()f x 的第二类间断点． 1.2 一元函数的可微性1.2.1 可微的定义设函数()y f x =，当自变量0x x =有增量x ∆时，若存在于x ∆无关的常数0()A x ，使得函数的增量00()()y f x x f x ∆=+∆-可表为0()()y A x x o x ∆=∆+∆ (0)x ∆→，则称()f x 在0x x =处可微，0()A x x ∆称为()f x 在0x x =处的微分，记为00()()x x x x dyA x x dfA x x ===∆=∆或．微分的几何意义： 00()()y f x x f x ∆=+∆-是曲线()y f x =在点0x x =处相应于自变量增量x ∆的纵坐标0()f x 的增量，微分0x x dy=是曲线()y f x =在点()000,()M x f x 处的切线相应于自变量增量x ∆的纵坐标的增量.如下图所示图1.4定理1 函数f 在点0x 可微的充要条件是函数f 在点0x 可导，而且上式中0()A x 等于)(0x f '，即'()dy f x dx =．1.2.2微分的运算法则[()()]()()d u x v x du x dv x ±=± [()()]()()()()d u x v x v x du x u x dv x =+ 2()()()()()()()()u x v x du x u x dv x d v x v x -= dx x g u f x g f d )()())((''= ，其中()u g x =例1.8 求22ln cos y x x x =+的微分解：2222(ln cos )(ln )(cos )dy d x x x d x x d x =+=+ ()222ln ()ln (cos )xd x x d x d x =++ 2(2ln 12sin )x x x dx =+-．1.2.3 可导、可微以及连续之间的关系一元函数的可导性与可微性是等价的，函数的可导性是比可微性更强的性质，可导必连续，连续未必可导，例如，13y x y x ==与在0x =连续，但不可导.例1.9 设0()0f x ≠，()f x 在0x x =连续，则()f x 在0x x =可导是()f x 在0x x =可导的（ ）．（Ａ）充分非必要 （Ｂ）充分必要 （Ｃ）必要非充分 （Ｄ）非充分非必要解：由0()0f x ≠00()0()0f x f x ⇒><或，因()f x 在0x x =连续，则()f x 在0x 某邻域是保号的，即0δ∃>，当0x x δ-<时，00000()()00()0()()0()0(),()0f x f x f x f x x x f x f x f x f x δ⎧>>>⎧⎪⇒-<=⎨⎨<<-<⎩⎪⎩，，时，，，因此选（B ）．例1.10 设()00x f x x ≥=<，则（ ）．（Ａ）()f x 在0x =处不连续 （Ｂ）(0)f '存在（Ｃ）(0)f '不存在，曲线()y f x =在点()0,0处不存在切线 （Ｄ）(0)f '不存在，曲线()y f x =在点()0,0处存在切线 解： 由()()0lim 00x f x f →==，故()f x 连续()()000limlim x x f x f x++→→-==+∞， ()()000limlim x x f x f x --→→-==-∞． ()y f x =的图形如图1.5所示，()f x 在0x =的左右极限都不存在，因此）（0f '不存在． ()y f x =存在切线0x =，选（D ）． 例1.11 讨论函数2202(1cos ),0()1,01cos ,0xx x x f x x t dt x x -⎧<⎪⎪==⎨⎪⎪>⎩⎰在0x =的连续性和可导性.解：我们可先讨论函数在0x =的可导性，因为当()f x 在0x =可导或)0(+'f ,)0(-'f 均存在但不相等时，均可得()f x 在0x =连续，由()f x 分段定义的具体形式，可按定义求出)0(+'f ,)0(-'f 来讨论）（0f '是否存在. 222'020000cos 1()(0)cos 2sin (0)lim limlim lim 022xx x x x t dt f x f x x x x f xx x +++→→→→----=====⎰， 2'320000()(0)2(1cos )2(sin )2cos 1(0)lim lim lim lim 0332x x x x f x f x x x x x f x x x x---→→→→-----=====， 因此，0)0()0(='='-+f f ，即()f x 在0x =可导，因而也必连续.2.二元函数的连续性和可微性2.1二元函数的连续性2.1.1 定义设f 为定义在点集2D R ∈上的二元函数，0P D ∈（它或者是D 的聚点，或者是D 的孤立点），对于任给的正数ε，总存在相应的正数δ，只要()0;P U P D δ∈，就有0()()f P f P ε-<，则称f 关于集合D 在点0P 连续.若f 在D 上任何点都关于集合D 连续，则称f 为D 上的连续函数.2.1.2 定理定理1（复合函数的连续性）设函数(),u x y ϕ=和(),v x y φ=在xy 平面上点()000,P x y 的某邻域内有定义，并在点0P 连续；函数(),f u v 在uv 平面上点()000,Q u v 的某邻域内有定义，并在点0Q 连续，其中()000,u x y ϕ=，()000,v x y φ=.则复合函数()()(),,,,g x y f x y x y ϕφ=⎡⎤⎣⎦在点0P 也连续.证 由f 在点0Q 连续可知：任给正数ε，存在相应正数η，使得当0u u η-<，0v v η-<时有()()00,,f u v f u v ε-<，又由,ϕφ在点0Q 连续可知：对上述正数η，总存在正数δ，使得当0x x δ-<，0y y δ-<时，都有()()000,,u u x y x y ϕφη-=-<， ()()000,v v x y x y φφη-=--<，综合起来，当0x x δ-<，0y y δ-<时，便有()()()()0000,,,,g x y g x y f x y f x y ε-=-<，所以说复合函数()()(),,,,g x y f x y x y ϕφ=⎡⎤⎣⎦在点0P 连续.定理2（有界性与最大、最小值定理）若函数f 在有界闭区域2D R ∈上连续，则f 在D 上有界，且能取得最大值与最小值.定理3（一致连续性定理）若函数f 在有界闭区域2D R ∈上连续，则f 在D 上一致连续.即对任何0ε>，总存在只依赖于ε的正数δ，使得对于一切点P 、Q ，只要(),P Q ρδ<，就有()()f P f Q ε-<．定理4（介值性定理）设函数f 在有界闭区域区域2D R ∈上连续，若1P ，2P 为D 中任意两点，且()()12f P f P <，则对任何满足不等式()()12f P f P μ<<，的实数μ，必存在点0P D ∈，使得()0f Pμ=． 定理5（有界性与最大值最小值定理）若函数f 在有界闭区域区域2D R ∈上连续，则f 在D 上有界，且能取得最大值与最小值．证 先证则f 在D 上有界.倘若不然，则对每个正整数n ，必存在点n P D ∈，使得 (),1,2,n f P n n >=⋅⋅⋅ （2.1） 于是得到一个有界点列{}n P D ⊂，且总能使{}n P 中有无穷多个不同的点.由聚点定理的推论，有界无限点列{}2n P R ⊂必存在收敛子列{}k n P，设0lim k n k P P →∞=，且因D 是闭区域，从而0P D ∈.由于f 在D 上连续，当然在点0P 也连续，因此有()()0lim k n k f P f P →∞=，这与不等式（2）相矛盾，所以f 是D 上的有界函数.下面证明f 在D 上能取得最大值、最小值.为此设()()inf ,sup m f D M f D ==，可证必有一点Q D ∈，使()f Q M =（同理可证存在D Q ∈'，使m Q f =')(）.如若不然，对任意P D ∈，都有()0M f P ->.考察D 上的连续函数()()1F P M f P =-，由前面的证明知道，在D 上有界.又因F 不能在D 上达到上确界M ，所以存在收敛点列{}n P D ⊂，使()lim n n f P M →∞=，于是有lim n →∞=+∞，这导致与F 在D 上有界的结论想矛盾.从而证得f在D 上能取得最大值.2.2二元函数的可微性2.2.1 二元函数可微性的定义设函数(),z f x y =在点()000,P x y 的某邻域()0U P 内有定义，对于()0U P 中的点()()00,,P x y x x y y =+∆+∆，若函数f 在点0P 处的全增量z ∆可表示为：()()000,,o z f x x y y f x y ∆=+∆+∆-()A x B y o ρ=∆+∆+ （2.2）其中,A B 是仅与点0P 有关的常数，ρ=()ορ是较ρ高阶的无穷小量，则称函数f 在点0P 可微，并称（1）式中关于,x y ∆∆的线性函数A x B y =∆+∆为函数f 在点0P 的全微分，记作()000,P dzdf x y A x B y ==∆+∆ （2.3）由（2.1）、（2.3）可见dz 是z ∆的线性主部，特别当,x y ∆∆充分小时，全微分dz 可作为全增量z ∆的近似值，即()()()()0000,,f x y f x y A x x B y y ≈+-+-.全微分的几何意义： 函数(),z f x y =在点()000,P x y 的全微分在几何上表示曲面(),z f x y =在点()()0000,,,x y f x y 处切平面上点的竖坐标的增量.2.2.2 偏导数的定义设函数(),z f x y =，(),x y D ∈，若()00,x y D ∈，且()0,f x y 在0x 的某邻域内有定义，则当极限()()()00000000,,,limlim x x x f x y f x x y f x y x x ∆→∆→∆+∆-=∆∆，存在时，称这个极限为函数f 在点()00,x y 关于x 的偏导数，记作()00,x f x y 或()00,x y fx∂∂．若(),z f x y =在点()000,P x y 存在()00,f x y x ∂∂与()00,f x y y∂∂，称(),z f x y =在点()000,P x y 可偏导.偏导数的几何意义：()00,f x y x∂∂即曲面(),z f x y =与平面0y y =的交线在点()()00000,,,M x y f x y 处的切线对x 轴的斜率；()00,f x y y∂∂即曲面(),z f x y =与平面0x x =的交线在点()()00000,,,M x y f x y 处的切线对y 轴的斜率.2.2.3 定理定理1（可微的必要条件）若二元函数在其定义域内一点()00,x y 处可微，则f 在该点关于每个自变量的偏导数都存在，且（1）式中的()00,x A f x y =，()00,y B f x y =．依此函数f 在点()00x y 的全微分可唯一地表示为()()()000000,,,x y x y dff x y x f x y y =⋅∆+⋅∆．与一元函数类似，由于自变量的增量等于自变量的微分，即x dx ∆=， y dy ∆=．所以全微分又可以写为()()0000,,x y dz f x y dx f x y dy =+．定理2（可微的充分条件）若函数(),z f x y =的偏导数在点()00,x y 的某邻域内存在，且x f ，y f 在点()00,x y 处连续，则函数f 在点()00,x y 处可微.证 我们把全增量z ∆写作()()0000,,z f x x y y f x y ∆=+∆+∆-()()()()00000000,,,,f x x y y f x y y f x y y f x y =+∆+∆-+∆++∆-⎡⎤⎡⎤⎣⎦⎣⎦ 在第一个括号里，它是函数()0,f x y y +∆关于x 的偏增量；在第二个括号里，则是函数()0,f x y 关于y 的偏增量.对它们分别用一元函数的拉格朗日中值定理，得()()01000212,,,0,1x y z f x x y y x f x y y y θθθθ∆=+∆+∆∆++∆∆<< (2.4)由于x f 与y f 在点()00,x y 连续，因此有()()01000,,x x f x x y y x f x y θα+∆+∆∆=+ （2.5）()()00200,,y y f x y y f x y θβ++∆=+ （2.6）其中当()(),0,0x y ∆∆→时，0,0αβ→→，将（4），（5）带入（3）式，则得()()0000,,x y z f x y x f x y y x y αβ∆=∆+∆+∆+∆，故函数f 在点()00,x y 可微.定理 3 设函数在点()00,x y 的某邻域内存在偏导数，若(),x y 属于该邻域，则存在()010x x x ξθ=+-和()020y y y ηθ=+-，120,1θθ<<，使得()()()()()()00000,,,,x y f x y f x y f y x x f x y y ξη==-+-．定理4 曲面(),z f x y =在点()()00000,,,P x y f x y 存在不平行于z 轴的切平面∏的充要条件是函数f 在点()000,P x y 可微.求分段函数在分段点的全微分１ 用定义求),(00y x f x '，),(00y x f y '，即求xy x f y x x f y x f x x ∆-∆+='→∆),(),(lim),(0000000和yy x f y y x f y x f y y ∆-∆+='→∆),(),(lim),(0000000，若偏导不存在，则不可微，若存在，则２．２计算22),),(limyx yf x f y x f y y x x f pyf x f f y x y x ∆+∆∆'-∆'--∆+∆+=∆'-∆'-∆→（ρ，若极限为0，则可微，否则不可微，可微时，dy y x f dx y x f dz y x ）0000,(),('+'=．2.2.4 微分的几何应用1空间曲面的且平面与法线若空间曲面S 的方程为(),,0F x y z =，()0000,,M x y z 是S 上的一点，则S 在0M 点的且平面方程为()()()()()()0000000F M F M F M x x y y z z x y z∂∂∂-+-+-=∂∂∂． 法线方程为()()()()()()000000x x y y z z F M F M F M xyz ---==∂∂∂∂∂∂．其中(),,F x y z 在点M 处有连续偏导数且()()()2220000F M F M F M x y x ∂∂∂⎛⎫⎛⎫⎛⎫++≠ ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭．例2.1 试求抛物面22z ax by =+在点()0000,,M x y z 处的切平面方程与法线方程. 解 因为()000,2x f x y ax =，()000,2y f x y by =，过M 的切平面方程为()()0000022z z ax x x by y y -=-+-，由于22000z ax by =+，化简为000220ax x by y z z +--=．过M 的法线方程为00000221x x y y z z ax by ---==-． 2 空间曲线的切线去法平面若空间曲线Γ的参数方程为()x x t =，()y y t =，()z z t =()t αβ≤≤，又()()()()()0000000,,,,M x y z x t y t z t =是Γ上的一点，则Γ在点0M 的切线方程为)(()(000t z z z t y y y t x x x '-='-='-）．法平面方程为0))(())(())((000000=-'+-'+-'z z t z y y t y x x t x ．其中，()x t ，()y t ，()z t 在0t t =可导且0)()()020202≠'+'+'t z t y t x （.3 近似计算例2.2 求 3.961.08的近似值．解 设(),y f x y x =，令01x =，04y =，0.08x ∆=，0.04y ∆=-，则有()3.96001.08,f x x y y =+∆+∆ ()()()1,41,41,4x y f f x f y ≈+∆+∆ ()4140.081ln10.04=+⨯+⨯⨯-10.32 1.32=+=．2.2.5 偏导数的连续性、函数可微性、可偏导性与函数连续性的关系.可以从可微性的定义看出，函数在可微点处必连续，但在函数的连续点处不一定存在偏导数，更不能保证函数在该点连续.如下图所示图1.6定理5 如果函数).(y x f z =的偏导数yzx z ∂∂∂∂、在点),(y x 连续，则函数在该点可微分． 证明：因为我们只限于讨论在某一区域内有定义的函数（对于偏导数也如此），所以假定偏导数在点),(y x P 连续，就含有偏导数在该点的某一领域内必然存在的意思．设点),(y y x x ∆+∆+为这领域内任意一点，考察函数的全增量)],(),([)],(),([),(,(y x f y y x f y y x f y y x x f y x f y y x x f z -∆++∆+-∆+∆+=-∆+∆+=∆）在第一个方括号内的表达式，由于y y ∆+不变，因而可以看做是x 的一元函数),(y y x f ∆+的增量．于是，应用拉格朗日中值定理，得到xy y x x f y y x f y y x x f x ∆∆+∆+=∆+-∆+∆+),(),(),(1θ )10(<<θ又依假设，),(y x f x 在点),(y x 连续，所以上式可写为xx y x f y y x f y y x x f x ∆+∆=∆+-∆+∆+1),(),(),(ε （2.7）其中1ε为y x ∆∆、的函数，且当0,0→∆→∆y x 时，01→ε． 同理可证第二个方括号内的表达式可写为y y y x f y x f y y x f y ∆+∆=-∆+2),(),(),(ε （2.8） 其中2ε为y ∆的函数，且当002→→∆ε时，y ．由（2.7）、（2.8）两式可见，在偏导数连续的假定下，全增量z ∆可以表示为y x y y x f x y x f z y x ∆+∆+∆+∆=∆21),(),(εε容易看出2121εερεε+≤∆+∆yx ，它是随着0)0,0()→→∆∆ρ即，（y x 而趋于零的.这就证明了).(y x f z =在点),(y x P 是可微分的.定理6如果函数).(y x f z =在点),(y x 可微分，那么函数在该点必定连续 证明：由全微分定义可知：函数).(y x f z =在点),(y x 的全增量）ρο(),(),(+∆+∆=∆-∆+∆+=∆y B x A z y x f y y x x f z可得0lim 0=∆→z ρ.从而),(]),([lim ),(lim 0)0,0(),(y x f z y x f y y x x f y x =∆+=∆+∆+→→∆∆ρ因此函数).(y x f z =在点),(y x 处．定理7如果函数).(y x f z =在点),(y x 可微分，则函数在点),(y x 的偏导数yzx z ∂∂∂∂、必定存在，且函数).(y x f z =在点),(y x 的全微分为y yzx x z dz ∆∂∂+∆∂∂=. 证明：设函数).(y x f z =在点),(y x P 可微分．于是，对于点P 的某个领域内的任意一点),(y y x x P ∆+∆+'，式子(2.9)总成立)(ρο+∆+∆=∆y B x A z (2.9)特别当0=∆y 时，（2.9）式也应成立，这时x ∆=ρ，所以（2.9）式成为)(),(),(x x A y x f y x x f ∆+∆⋅=-∆+ο．上式两边各除以,x ∆在令0→∆x 而取得极限，就得A xy x f y x x f x =∆-∆+→∆),(),(lim，从而偏导数xz∂∂存在，且等于A.同样可证B y z =∂∂.所以该定理得证．例2.3 下列函数在()0,0处不连续的是（ ）(A)()()()()(),0,0,0,,0,0x y f x y x y ≠==⎩(B)()()()()()3322,,0,0,0,,0,0x y x y x yf x y x y ⎧-≠⎪+=⎨⎪=⎩(C)()()()()(),0,0,0,,0,0x y f x y x y ≠==⎩(D)()()()()()221,,0,0,0,,0,0x y x y f x y x y =+=⎪=⎩解（A ）中， (),f x y x =≤=， 故有， （A ）连续.(B)中，()3333222222,x y x y f x y x y x y x y x y-=≤+≤++++，则有()()()(),0,0lim,0,00x y f x y f →==,(),f x y 在点()0,0连续(C ），当(),x y 沿直线y x =趋于()0,0时，()()2,0,00f x y f ==≠=，因此，(),f x y 在点()0,0不连续.(D)，221sinx y +有界，⇒ ()()()()(()22,0,0,0,01lim ,lim 00,0x y x y f x y f x y →→===+ ⇒(),f x y 在点()0,0连续.例2.4 设函数(),f x y 在点()00,P x y 的两个偏导数'x f 和'y f 都存在，则（ ） (A)()0lim ,y y x x f x y →→存在(B)()00lim ,x x f x y →及()00lim ,y y f x y →都存在(C)(),f x y 在P 点必连续 (D)(),f x y 在P 点必可微解 函数()0,f x y 和()0,f x y 已成为一元函数，二元函数(),f x y 在点()00,P x y 对x 的偏导数等于一元函数()0,f x y 在0x 点倒数，因为偏导数'x f 在点P 存在，所以()0,f x y 在0x x =处必连续，从而()00lim ,x x f x y →存在，同理()00lim ,y y f x y →存在.选(B).如上例中，()()()()()22,,0,0,0,,0,0xyx y x y f x y x y ⎧≠⎪+=⎨⎪=⎩，(),f x y 在P 点不连续.例2.5 讨论函数()()()()()22,,0,0,0,,0,0xy x y x y f x y x y ⎧≠⎪+=⎨⎪=⎩，(),f x y 在点()0,0处的连续性，并判断偏导是否存在.解 先判断(),f x y 在点()0,0处是否可偏导，由于()()()()000000,,0,00,0limlim 0x x f x x y f x y f x f x x∆→∆→+∆-+∆-==∆∆ 即()0,00fx∂=∂，同理()0,00f y∂=∂，因此偏导数都存在，考察(),f x y 在点()0,0的连续性，令y kx =，则 ()022220lim ,lim (1)(1)x y kx x kx kf x y k x k →=→==++，即当(),x y 沿不同直线y kx =趋于()0,0时(),f x y 有不同的极限，因此(),f x y 在点()0,0不连续.例2.6 设()()()()()2222,,0,0,0,,0,0x y x y x y f x y x y ⎧≠⎪+=⎨⎪=⎩，讨论(),f x y 在()0,0处的连续性和可微性，并求()0,0df.解 当()(),0,0x y ≠时，2322222222()f xy x y x x y x y ∂=-∂++，当()(),0,0x y =时，因()(),00f x x =∀，于是()0,0f x∂=∂()()0,00,0lim0x f x f x∆→+∆-=∆.同理可得，当()(),0,0x y ≠时，2232222222()f x y x y y x y x y ∂=-∂++，()0,00f y ∂=∂.考察f x ∂∂，fy∂∂在()0,0的连续性，注意到 2221x x y ≤+，2221y x y ≤+，2322222222()f xy x y x x y x y ∂=-∂++， 故4fx x ∂≤∂， 4f y y ∂≤∂,()()()0,0,0,0lim0x y f fx x →∂∂==∂∂，()()()0,0,0,0lim0x y f fy y →∂∂==∂∂即f x ∂∂，fy∂∂在点()0,0处均连续，因此(),f x y 在点()0,0可微.于是()()()0,00,00,00f f dfdx dy xy∂∂=+=∂∂例2.7证明函数z =()0,0连续但偏导数不存在. 证明 因为()((),0,0lim00,0x y z →==，所以z =()0,0连续，又()()0,00,0xz x z x x∆+∆-=∆∆，当0x ∆→时，极限不存在，因此()0,0x z 不存在.同理可得，()0,0y z 也不存在.例2.8 证明函数()222222()sin 0,0,0x y x y f x y x y ⎧++≠⎪=⎨⎪+≠⎩在点()0,0连续且偏导存在，但偏导在()0,0不连续，而f 在原点()0,0可微.证明 要证明(),f x y 在()0,0连续，即证()()()(),0,0lim,0,0x y f x y f →=，由()()()()22,0,0lim00,0x y x y f →+==，所以(),f x y 在()0,0连续.当220x y +=时 ()()()000,00,01lim lim sin 00,0x x x f x f x f x x∆→∆→+∆-=∆==∆∆ 当220x y +≠时(),2sin x f x y x = 而()(),0,0lim 20x y x →=，()(,0,0limx y →不存在，因此()()(),0,0lim,x x y f x y →不存在，从而(),x f x y 在点()0,0不连续.同理可证(),y f x y 在点()0,0不连续. 然而()(,0,00,00,0limx y f f x f y∆∆→∆-∆-∆()(22,0,0lim0x y ∆∆→==所以f 在原点()0,0可微.例2.9证明函数22220(,)0,0x y f x y x y +≠=⎪⎪+=⎩在原点两个偏导存在，但不可微.证明 由偏导数定义:000lim )0,0()0,0(lim )0,0(00=∆-=∆-∆+=→∆→∆x xf x f f x x x .同理可求得0)0,0(=x f .下面利用可微的定义来证明其不可微性. 用反证法.若函数f 在原点可微，则应是较22y x ∆+∆=ρ的高阶无穷小量，为此考察极限220limy x yx ∆+∆∆∆→ρ.当动点(,)x y 沿直线y mx =趋于(0,0)时，则(,)(0,0)2222(,)(0,0)limlim 11x y y mxx y xy m mx y m m →=→==+++. 这一结果说明动点沿不同斜率m 的直线趋于原点时，对应的极限值也不同.因此所讨论的极限不存在.故函数f 在原点不可微.结束语以上就是本文所讨论的函数的连续性和可微性，深刻的掌握其定义和用法很重要，掌握其解法能够简化或解决很多问题，这不仅可以体现在理论研究中，而且在处理许多实际问题时也别具特色.函数连续性和可微性的应用贯穿于初高等数学各部分的内容中，对其整理归纳可以提高我们分析问题和解决问题的能力.由于可微性在社会科学和自然科学的许多方面都有应用，它的解法灵活多样，因此本文的重点是能够运用初高等数学的相关知识灵活地解决实际问题；但有些题目只能用一些固定的方法来解决，这些方法有一定的局限性,因此本文的难点是掌握求积分的一些特殊的解法.本文主要是对函数连续性和可微性问题的类型和相应的解题方法进行较深入地探讨，以形成较完整的理论体系.通过本文的论述，我们可以更全面地了解连续性和可微性以及他们之间的联系，具有一定的应用价值.另外，熟练掌握此部分内容对数学的学习也大有帮助.在这一过程中，我们更系统地分析了连续性可微性问题的类型和解决方法，使我们更能体会到前人探索的艰辛，以及获得成功时的喜悦之情，从而激发了我们对数学的兴趣，当然由于多元函数连续性和可微性关系复杂，证明的方法也很多，加之我们的专业知识有限以及研究方法不成熟，文中难免出现不足之处.例如：对问题类型的讨论不够深刻和全面，由于求解解法的灵活性，本文只是归纳了部分连续性和可微性问题类型和解法，因此不能囊括所有的问题.总之，这篇论文还有很多地方值得商榷，望老师和同学们提出宝贵的意见.参考文献[1] 张禾端，高等代数（第三版），北京：高等教育出版社，1992年4月第九版[2] 马小土，硕士研究生入学考试1000题，第三版，北京：中国人民大学出版社，2000，4[3] 华东六省工科数学系列教材编委会.高等数学学习指导书[M].沈阳：辽宁科学技术出版社，1991[4] 李永乐，数学复习全书（理工类）.高等数学[M].北京：国家行政学院出版社，2011[5] 徐森林，薛春华.数学分析（第二册）[M].北京：清华大学出版社，2006[6] 裴礼文.数学分析中的典型问题和解题方法[M].北京：高等教育出版社，1993[7] 清华大学数学科学系《微积分》编写组.微积分[M].北京：清华大学出版社，2004[8] 电子科技大学应用数学系编.微积分[M].成都：电子科技大学出版社，2000[9] 童武.全国硕士研究生入学考试历年试题精解（数学三）[M].北京：北京大学出版社，2004[10] 同济大学应用数学系编.高等数学[M].北京：高等教育出版社，2004，12[11] 同济大学应用数学系编.高等数学习题集[M].上海：上海财经大学出版社.2006，9[12] 童雪耐，对称区域上的积分，数学通报，1991[13] 刘玉链，数学分析讲义（下册，第三版），北京：高等教育出版社，1996[14] 张志军，熊德之.微积分及其应用[M].北京：科学出版社.2007[15] 华东师范大学数学系编.数学分析（第二版）[M]. 北京：高等教育出版社.1991致谢逝者如斯，不舍昼夜，四次春去春又来，岁月稍纵即逝.此时，回头想想这段短暂的求学路，时而喜悦，时而惆怅.在这个美丽的校园里，原本天真幼稚的我如今已蜕变成一个睿智、沉稳的青年，感谢命运的安排，让我有幸结识了许多良师益友，是他们教我如何品味人生，让我懂得如何更好的生活！人生处处是驿站，已是挥手作别之时，在此，向所有帮助过我的人献上我最诚挚的谢意！本学位论文是在我的指导老师宋强的亲切关怀与细心指导下完成的.从课题的选择到论文的最终完成，宋老师始终都给予了细心的指导和不懈的支持，并且在耐心指导论文之余，宋老师仍不忘拓展我们的文化视野，让我们感受到了‘可微性’的美妙与乐趣.值得一提的是，宋老师宅心仁厚，不慕荣利，对学生认真负责，在他的身上，我们可以感受到一个学者的严谨和务实，这些都让我们获益菲浅，并且将终生受用无穷.毕竟“经师易得，人师难求”，希望借此机会向宋老师表示最衷心的感谢！此外，本文最终得以顺利完成，也是其他同学的帮助分不开的，虽然他们没有直接参与我的论文指导，但在开题时也给我提供了不少的意见，提出了一系列可行性的建议，在此向他们表示深深的感谢！。

数学分析第四章函数的连续性第四章函数的连续性§1 连续性概念连续函数是数学分析中着重讨论的一类函数.从几何形象上粗略地说, 连续函数在坐标平面上的图象是一条连绵不断的曲线.当然我们不能满足于这种直观的认识, 而应给出函数连续性的精确定义, 并由此出发研究连续函数的性质.本节中先定义函数在一点的连续性和在区间上的连续性.一函数在一点的连续性定义1 设函数f 在某U( x0 ) 内有定义.若lim x → x f ( x ) = f ( x0 ) , ( 1)则称f 在点x0 连续.例如, 函数 f ( x ) = 2 x + 1 在点x = 2 连续, 因为又如,函数limx →2f ( x) = limx →2( 2 x + 1 ) = 5 = f (2 ) .f ( x) =x sin1x, x ≠ 0 ,0 , x = 0在点x = 0 连续, 因为lim x →0 f ( x) = limx →0x sin1x= 0 = f ( 0) .为引入函数y = f ( x ) 在点x0 连续的另一种表述, 记Δx = x - x0 , 称为自变量x( 在点x0 ) 的增量或改变量.设y0 = f ( x0 ) , 相应的函数y ( 在点x0 ) 的增量记为Δy = f ( x ) - f ( x0 ) = f ( x0 + Δx) - f ( x0 ) = y - y0 .注自变量的增量Δx 或函数的增量Δy 可以是正数, 也可以是0 或负数.引进了增量的概念之后, 易见“函数y = f ( x ) 在点x0 连续”等价于lim Δy = 0 .Δx →070第四章函数的连续性由于函数在一点的连续性是通过极限来定义的 , 因而也可直接用ε- δ方式来叙述 , 即 : 若对任给的ε> 0 , 存在δ> 0 , 使得当 | x - x 0 | < δ时有| f ( x) - f ( x 0 ) | < ε,( 2)则称函数 f 在点 x 0 连续 .由上述定义 , 我们可得出函数 f 在点 x 0 有极限与 f 在 x 0 连续这两个概念之间的联系 .首先 , f 在点 x 0 有极限是 f 在 x 0 连续的必要条件 ; 进一步说“, f 在点 x 0 连续”不仅要求 f 在点 x 0 有极限 , 而且其极限值应等于 f 在 x 0 的函数值 f ( x 0 ) .其次 , 在讨论极限时 , 我们假定 f 在点 x 0 的某空心邻域U °( x 0 ) 内有定义 ( f 在点 x 0 可以没有定义 ) , 而“ f 在点 x 0 连续”则要求 f 在某 U( x 0 ) 内 ( 包括点 x 0 ) 有定义 , 此时由于 (2 ) 式当 x = x 0 时总是成立的 , 所以在极限定义中的“0 < | x - x 0 | < δ”换成了在连续定义中的“ | x - x 0 | < δ”.最后 , (1 ) 式又可表示为lim x → xf ( x) = f lim x ,x → x可见“ f 在点 x 0 连续”意味着极限运算lim x → x与对应法则 f 的可交换性 .例 1 证明函数 f ( x ) = x D( x ) 在点 x = 0 连续 , 其中 D ( x ) 为狄利克雷函数 .证由 f (0 ) = 0 及| D( x ) | ≤ 1 , 对任给的ε> 0 , 为使| f ( x ) - f ( 0) | = | xD( x ) | ≤ | x | < ε, 只要取δ= ε, 即可按ε- δ定义推得 f 在 x = 0 连续. □相应于 f 在点 x 0 的左、右极限的概念 , 我们给出左、右连续的定义如下 : 定义 2 设函数 f 在某 U + ( x 0 ) ( U - ( x 0 ) ) 内有定义 .若lim x → x +f ( x) = f ( x 0 ) lim -x → xf ( x) = f ( x 0 ) , 则称 f 在点 x 0 右 ( 左 ) 连续 .根据上述定义 1 与定义 2 , 不难推出如下定理 .定理 4.1 函数 f 在点 x 0 连续的充要条件是 : f 在点 x 0 既是右连续 , 又是左连续 .例 2 讨论函数在点 x = 0 的连续性 .解因为f ( x ) =x + 2 , x ≥ 0 , x - 2 , x < 0lim x → 0 +lim x → 0 -f ( x ) = lim x → 0 + f ( x) = lim x → 0 -( x + 2 ) = 2 ,( x - 2) = - 2 , 而 f (0 ) = 2 , 所以 f 在点 x = 0 右连续 , 但不左连续 , 从而它在 x = 0 不连续 ( 见●§1 连续性概念 71图 4 - 1 ) .□二间断点及其分类定义 3 设函数 f 在某U °( x 0 ) 内有定义 .若 f 在点 x 0 无定义 , 或 f 在点 x 0 有定义而不连续 , 则称点 x 0 为函数 f 的间断点或不连续点 .按此定义以及上一段中关于极限与连续性之间联系的讨论 , 若 x 0 为函数 f 的间断点 , 则必出现下列情形之一:图 4 - 1( i ) f 在点 x 0 无定义或极限l im x → xf ( x ) 不存在 ; 0 ( ii ) f 在点 x 0 有定义且极限lim x → xf ( x ) 存在① , 但lim x → xf ( x) ≠ f ( x 0 ) .据此 , 我们对函数的间断点作如下分类 : 1. 可去间断点若lim x → xf ( x ) = A ,而 f 在点 x 0 无定义 , 或有定义但f ( x 0 ) ≠ A , 则称 x 0 为 f 的可去间断点 .例如 , 对于函数 f ( x ) = | sgn x | , 因 f ( 0) = 0 , 而lim x → 0f ( x) = 1 ≠ f (0 ) ,故 x = 0 为 f ( x ) = | sgn x | 的可去间断点 . 又如函数 g ( x ) =sin x, 由于 xlim x → 0g ( x ) = 1 , 而 g 在 x = 0 无定义 , 所以 x = 0 是函数 g 的可去间断点 .设 x 0 为函数 f 的可去间断点 , 且lim x → xf ( x ) = A .我们按如下方法定义一个 0函数 f ^: 当x ≠ x 0 时 , f ^( x ) = f ( x) ; 当 x = x 0 时 , f ^( x 0 ) = A .易见 , 对于函数f ^, x 0 是它的连续点 .例如 , 对上述的 g( x) = sin x , 我们定义x则 g^在 x = 0 连续 .g ^( x ) = sin x x, x ≠ 0 , 1 , x = 0 ,2. 跳跃间断点若函数 f 在点 x 0 的左、右极限都存在 , 但lim x → x +f ( x) ≠ lim x → x -f ( x) , 则称点 x 0 为函数 f 的跳跃间断点 .例如 , 对函数 f ( x ) = [ x ] ( 图 1 - 8) , 当 x = n ( n 为整数 ) 时有①这里所说的极限存在是指存在有限极限 , 即不包括非正常极限 .72第四章函数的连续性lim x → n -[ x] = n - 1 , lim x → n +[ x] = n , 所以在整数点上函数 f 的左、右极限不相等 , 从而整数点都是函数 f ( x ) = [ x ] 的跳跃间断点 .又如符号函数 s gn x 在点 x = 0 处的左、右极限分别为 - 1 和 1 , 故 x = 0 是 sgn x 的跳跃间断点 ( 图 1 - 3) .可去间断点和跳跃间断点统称为第一类间断点 .第一类间断点的特点是函数在该点处的左、右极限都存在 .3. 函数的所有其他形式的间断点 , 即使得函数至少有一侧极限不存在的那些点 , 称为第二类间断点 .例如 , 函数 y = 1 当x → 0 时不存在有限的极限 , 故 x = 0 是 y =1的第二类x x 间断点 .函数 s in 1 在点 x = 0 处左、右极限都不存在 , 故 x = 0 是 s in 1的第二类x x间断点 .又如 , 对于狄利克雷函数 D( x ) , 其定义域 R 上每一点 x 都是第二类间断点 .三区间上的连续函数若函数 f 在区间 I 上的每一点都连续 , 则称 f 为 I 上的连续函数 .对于闭区间或半开半闭区间的端点, 函数在这些点上连续是指左连续或右连续 .例如 , 函数 y = c, y = x , y = sin x 和 y = cos x 都是 R 上的连续函数 .又如函数 y =1 - x 2在 ( - 1 , 1 ) 每一点处都连续 , 在 x = 1 为左连续 , 在 x = - 1 为右连续 , 因而它在 [ - 1 , 1] 上连续 .若函数 f 在区间 [ a , b] 上仅有有限个第一类间断点 , 则称 f 在[ a, b] 上分段连续 .例如 , 函数 y = [ x ] 和 y = x - [ x] 在区间 [ - 3 , 3 ] 上是分段连续的 .在§3 中我们将证明任何初等函数在其定义区间上为连续函数 .同时 , 也存在着在其定义区间上每一点处都不连续的函数 , 如前面已提到的狄利克雷函数 .例 3 证明 : 黎曼函数R ( x) =1 , 当 x = p q qp 、q 为正整数 , p 6q / 为既约真分数 , 0 , 当 x = 0 , 1 及 (0 , 1 ) 内无理数在 (0 , 1 ) 内任何无理点处都连续 , 任何有理点处都不连续 .证设ξ∈ ( 0 , 1) 为无理数 .任给ε> 0 不妨设ε< 12, 满足1 ≥ε的正整q数 q 显然只有有限个 ( 但至少有一个 , 如 q = 2) , 从而使R( x ) ≥ε的有理数x ∈(0 , 1 ) 只有有限个至少有一个 , 如 12, 设为 x 1 , , x n .取δ = min | x 1 - ξ| , , | x n - ξ| ,ξ, 1 - ξ ,3 §1 连续性概念73则对任何x ∈ U(ξ;δ) ( ì ( 0 , 1) ) , 当 x 为有理数时有R( x ) < ε, 当 x 为无理数时 R ( x ) = 0 .于是 , 对任何x ∈ U(ξ;δ) , 总有R ( x) - R(ξ) = R ( x ) < ε .这就证明了 R ( x ) 在无理点ξ处连续 .现设 p 为 (0 , 1 ) 内任一有理数 .取ε0 =1 , 对任何正数δ( 无论多么小 ) , 在 q2 q Up q;δ 内总可取到无理数x ( ∈ ( 0 , 1) ) , 使得 R( x ) - R pq = 1 q > ε0 . 所以 R ( x ) 在任何有理点处都不连续 .□习题1. 按定义证明下列函数在其定义域内连续 :( 1) f ( x ) = 1; ( 2) f ( x ) = | x | .x2. 指出下列函数的间断点并说明其类型 :( 1) f ( x ) = x + 1 ; ( 2) f ( x) = sin x;x | x |( 3) f ( x ) = [ | cos x | ] ; (4) f ( x) = sgn | x | ;( 5) f ( x ) = sgn ( cos x ) ;x , x 为有理数 ,( 6) f ( x ) =( 7) f ( x ) = - x , x 为无理数 ; 1x + 7, - ∞ < x < - 7 , x , - 7≤ x ≤1( x - 1 )sin 1, 1 < x < + ∞ .x - 13. 延拓下列函数 , 使其在 R 上连续 :( 1) f ( x ) = x - 8 ; ( 2) f ( x) = 1 - cos x;x - 2 x 2( 3) f ( x ) = x cos 1.x2 24. 证明: 若 f 在点 x 0 连续 , 则 | f | 与 f 也在点 x 0 连续 .又问 : 若 | f | 或 f 那么 f 在 I 上是否必连续 ?在 I 上连续 , 5. 设当x ≠0 时f ( x) ≡ g( x ) , 而f ( 0) ≠ g (0 ) .证明 : f 与 g 两者中至多有一个在 x = 0 连续 .6. 设 f 为区间 I 上的单调函数 .证明: 若x 0 ∈ I 为 f 的间断点 , 则x 0 必是 f 的第一类间断点 .n n - 174第四章函数的连续性7. 设函数 f 只有可去间断点 , 定义g( x ) = lim y → xf ( y) .证明 g 为连续函数 .8. 设 f 为 R 上的单调函数 , 定义g( x) = f ( x + 0 ) .证明 g 在 R 上每一点都右连续 .9. 举出定义在 [0 , 1 ]上分别符合下述要求的函数 :( 1) 只在 1 , 1 和 1三点不连续的函数 ;2 3 4 ( 2) 只在 1 , 1 和 1三点连续的函数 ;2 3 4 ( 3) 只在 1( n = 1 , 2 , 3 , )上间断的函数 ;n( 4) 只在 x = 0 右连续 , 而在其他点都不连续的函数 .§2 连续函数的性质一连续函数的局部性质若函数 f 在点 x 0 连续 , 则 f 在点 x 0 有极限 , 且极限值等于函数值 f ( x 0 ) . 从而 , 根据函数极限的性质能推断出函数 f 在 U ( x 0 ) 的性态 .定理 4.2 ( 局部有界性 ) 若函数 f 在点 x 0 连续 , 则 f 在某 U( x 0 ) 内有界 . 定理 4 .3 ( 局部保号性 ) 若函数 f 在点 x 0 连续 , 且 f ( x 0 ) > 0 ( 或 < 0 ) , 则对任何正数 r < f ( x 0 ) ( 或 r < - f ( x 0 ) ) , 存在某U ( x 0 ) , 使得对一切x ∈ U( x 0 ) 有f ( x) > r ( 或 f ( x ) < - r) .注在具体应用局部保号性时 , 常取 r = 12f ( x 0 ) , 则 ( 当 f ( x 0 ) > 0 时 ) 存在某 U( x 0 ) , 使在其内有 f ( x) > 12f ( x 0 ) .定理 4 .4 ( 四则运算 ) 若函数 f 和 g 在点 x 0 连续 , 则f ± g , f ·g,6f g( x 0 ) ≠ 0) 也都在点 x 0 连续 .以上三个定理的证明 , 都可从函数极限的有关定理直接推得 .g /( 这里对常量函数 y = c 和函数 y = x 反复应用定理 4.4 , 能推出多项式函数P( x) = a 0 x + a 1 x + + a n - 1 x + a n和有理函数 R ( x ) = P( x)Q( x)( P , Q 为多项式 ) 在其定义域的每一点都是连续的 .同样 , 由 sin x 和 cos x 在 R 上的连续性 , 可推出 tan x 与 cot x 在其定义域的每0 §2 连续函数的性质75一点都连续 .关于复合函数的连续性 , 有如下定理 : 定理 4.5 若函数 f 在点 x 0 连续 , g 在点 u 0 连续 , u 0 = f ( x 0 ) , 则复合函数 g f 在点 x 0 连续 .证由于 g 在 u 0 连续 , 对任给的ε> 0, 存在δ1 > 0 , 使得当| u - u 0 | < δ1 时有| g( u) - g( u 0 ) | < ε . ( 1) 又由 u 0 = f ( x 0 ) 及 u = f ( x ) 在点x 0 连续 , 故对上述δ1 > 0 , 存在δ> 0 , 使得当 | x - x 0 | < δ时有 | u - u 0 | = | f ( x ) - f ( x 0 ) | < δ1 .联系 ( 1 ) 得 : 对任给的ε> 0 , 存在δ> 0 , 当 | x - x 0 | < δ时有| g ( f ( x ) ) - g( f ( x 0 ) ) | < ε . 这就证明了 g f 在点 x 0 连续 .□ 注根据连续性的定义 , 上述定理的结论可表为lim x → xg( f ( x) ) = g lim x → xf ( x ) = g( f ( x 0 ) ) .( 2)例 1 求lim sin (1 - x 2) .解 sin ( 1 - x 2 ) 可看作函数 g( u) = sin u 与 f ( x ) = 1 - x 2的复合 .由 ( 2) 式得lim sin ( 1 - x 2 ) = sin lim(1 - x 2) = sin 0 = 0 .□x → 1x → 1注若复合函数 g f 的内函数 f 当x → x 0 时极限为 a , 而a ≠ f ( x 0 ) 或 f 在 x 0 无定义 ( 即 x 0 为 f 的可去间断点 ) , 又外函数 g 在u = a 连续 , 则我们仍可用上述定理来求复合函数的极限 , 即有lim x → xg( f ( x ) ) = g lim x → xf ( x) .( 3)读者还可证明 : ( 3 ) 式不仅对于x → x 0 这种类型的极限成立 , 而且对于x → + ∞ , x → - ∞或x → x ±等类型的极限也是成立的 .例 2 求极限 :(1 ) lim2 - sin x; (2 ) lim2 - sin x .x → 0解 (1 ) limx → 0 x 2 - sin x x x → ∞= 2 - lim x → 0 xsin x = 2 - 1 = 1; x(2 ) lim 2 -= 2 - lim sin x = 2 - 0 = 2 . □x → ∞ x x → ∞ x二闭区间上连续函数的基本性质设 f 为闭区间 [ a , b] 上的连续函数 , 本段中我们讨论 f 在 [ a , b] 上的整体性质 .。

复合函数的连续性总结引言：相信在学习数学的过程中，大家对于函数的连续性都不会感到陌生。

连续性是数学中极为重要的概念之一，它在解析几何、微积分以及其他数学领域都有广泛的应用。

而复合函数的连续性则是连续性的一种特殊情况，本文将就这一主题进行总结和探讨。

一、函数的连续性回顾：在研究复合函数的连续性之前，我们首先需要对函数的连续性有一个全面的了解。

函数在某一点处连续，意味着该点的函数值与自变量在该点的极限值相等。

而函数在整个定义域上连续，意味着函数在定义域内的每一个点都具有连续性。

二、复合函数的定义：复合函数是多个函数按照一定的顺序组合而成的新函数。

具体而言，若有两个函数f(x)和g(x)，那么它们的复合函数可以表示为f(g(x))。

三、复合函数连续性的判定：1. 复合函数的连续性定理：如果在某点a处，g(x)在a点连续，而f(x)在g(a)点连续，则复合函数f(g(x))在点a连续。

这个定理表明，当复合函数的各个组成部分在适当的点上都是连续的时候，复合函数本身也将是连续的。

2. 复合函数的间断性定理：如果在某点a处，g(x)在a点连续，而f(x)在g(a)点处不连续，则复合函数f(g(x))在点a不连续。

这个定理说明，只要组成复合函数的任何一个函数在某一点的值不具备连续性，复合函数在该点也不会是连续的。

四、复合函数连续性的实际应用：复合函数的连续性在数学以及其他学科中都有广泛的应用。

下面我们就以一些实例来具体说明：1. 物理学中的速度与加速度关系：在物理学中，我们可以将物体的速度看作是位移对时间的导数，加速度则是速度对时间的导数。

假设一个物体的速度函数为v(t)，加速度函数为a(t)，我们可以用复合函数f(g(t))来表示速度与加速度的关系，其中f(x)表示速度，g(x)表示时间。

通过研究f(g(t))的连续性，我们可以得出该物体的运动情况。

2. 经济学中的需求曲线：在经济学中，需求曲线常常用来描述价格与需求之间的关系。

高等数学课件：函数的连续性高等数学课件：函数的连续性1.7函数的连续性教学目的:理解函数连续性的概念，会判断函数的连续性。

掌握连续函数的四则运算，知道反函数及复合函数的连续性，掌握初等函数的连续性, 知道间断点的概念及分类，会判断其类型。

教学重点:函数连续性的概念, 连续函数的四则运算，知道反函数及复合函数的连续性. 教学内容:1.6.1函数的连续性1 函数在一点的连续性xUx()xx定义1 设函数在点的某个邻域内有定义，自变量在点处有增量yfx,()000，相应地函数值的增量 ,x,,，,,yfxxfx()() 00xx如果，就称函数fx()在点处连续，称为函数fx()的连续点。

lim0,,y00,,x0x函数fx()在点处连续还可以描述如下。

0xUx()设函数yfx,()在点的某个邻域内有定义，如果，就称函数lim()()fxfx,000xx,0xfx()在点处连续。

0左连续及右连续的概念。

xlim()()fxfx,lim()()fxfx,如果，称函数fx()在点处左连续;如果，称函000,，xx,xx,00x数fx()lim()lim()fxfx,在点处右连续。

由于lim()fx存在的充要条件是，因此，根0,，xx,xxxx,,000xx据函数连续的定义有下述结论:若函数yfx,()在点的某个邻域内有定义，则它在点处00x连续的充分必要条件是在点处左连续且右连续。

02 区间上的连续函数如果函数在开区间上每一点都连续，我们称函数在开区间内连续，如果函数开区间内连续，在区间的左端点右连续，右端点左连续，就称函数在闭区间上连续。

yx,sin(,),,，,例1 证明在内连续。

x,,,,，,x(,)证明，当有增量时，对应的函数值的增量,x,,xx,,,,，,,,，yxxxxsin()sin2sincos ,,22,,,,xx,x,,sin,由于， cos1x，,,,222,,,,,xxx,,所以 02sincos2,,,，,,,yxx,,222,,45xx当时，由夹逼准则得，因此在点处连续，由于的任 ,,y0yx,sin,,x0意性，在内连续。

目录1引言 (1)2多元函数的连续、偏导数及可微........................... ... (1)2.1多元函数的连续性 (1)2.2 多元函数的偏导数 (3)2.3多元函数的可微性 (4)2.4多元函数连续性、偏导数存在性、及可微间的关系 (7)2.4.1二元函数连续性与偏导存在性间的关系 (7)2.4.2二元函数的可微性与偏导存在性间的关系 (8)2.4.3二元函数的连续性与可微性间的关系 (10)3小结.................................... .. (11)参考文献 (12)致谢辞 (13)1 引言对于一元函数而言，函数()y f x =在0x 极限存在、连续、可微，这三个概念的关系是很清楚的，即可微一定连续，但连续不一定可微，连续一定有极限，但有极限不一定连续.简单表示为：可微⇒连续⇒极限存在(且不可逆)对于二元函数而言，它既不同于一元函数有可导与可微的等价关系，也没有一元函数的“可导必连续”的关系.但对于二元函数的可微性，可以证明，若二元函数(,)z f x y =在点0p (0x ,0y )可微，则函数(,)f x y 在点0p （0x ，0y ） 连续，偏导存在；若二元函数(,)z f x y =的两个偏导数'x f （x,y ）与'y f (x,y)在点0p （0x ，0y ）连续，则函数(,)f x y 在0p （0x ，0y ）可微.因此对于函数的连续、偏导存在、可微、偏导连续，有下列蕴涵关系：偏导连续⇒可微⇒(连续，偏导存在);它们反方向结论不成立.多元函数是一元函数的推广，因此它保留着一元函数的许多性质，但也有某些差异，而且情况也更复杂一些.下面我们分别从多元函数的可微性、偏导存在性、连续性，进而到它们之间的关系进行具体的探讨.2多元函数的连续、偏导数及可微性2.1 多元函数的连续性一个一元函数若在某点存在左导数和右导数，则这个一元函数必在这点连续.但对于二元函数(,)f x y 来说，即使它在某点000(,)p x y 既存在关于x 的偏导数00(,)x f x y ，又存在关于y 的偏导数00(,)y f x y ，(,)f x y 也未必在000(,)p x y 连续.甚至，即使在000(,)p x y 的某邻域0()U p 存在偏导数(,)x f x y （或(,)y f x y ），而且(,)x f x y （或(,)y f x y ）在点000(,)p x y 连续，也不能保证(,)f x y 在000(,)p x y 连续.如函数(,)f x y =21sin ,00,0x y y y ⎧⎛⎫+≠⎪ ⎪⎪⎝⎭⎨⎪⎪=⎩关于具体验算步骤不难得出.不过，我们却有如下的定理.定理1 设函数(,)f x y 在点000(,)p x y 的某邻域0()U p 内有定义，若0(,)f x y 作为y 的一元函数在点y=0y 连续，(,)x f x y 在0()U p 内有界，则(,)f x y 在点000(,)p x y 连续.证明 任取00(,)x x y y ++ 0()U p ∈，则0000(,)(,)f x x y y f x y ++-00000000(,)(,)(,)(,)f x x y y f x y y f x y y f x y =++-+++- （1） 由于(,)x f x y 在0()U p 存在，故对于取定的0y y + ，0(,)f x y y + 作为x 的一元函数在以0x 和0x x + 为端点的闭区间上可导，从而据一元函数微分学中的Lagrange 中值定理，存在(0,1)θ∈，使0000(,)(,)f x x y y f x y y ++-+ = 00(,)x f x x y y xθ++将它代入（1）式得0000(,)(,)f x x y y f x y ++-000000(,)(,)(,)x f x x y y x f x y y f x y θ=++++- （2） 由于00(,)x x y y θ++ 0()U p ∈，故00(,)x f x x y y θ++ 有界，因而当(,)(0,0)x y → 时，有00(,)0x f x x y y x θ++→又，据定理的条件知，0(,)f x y 在0y y =连续，故当(,)(0,0)x y → 时，又有0000(,)(,)0f x y y f x y +-→所以，由（2）知，有00000lim (,)(,)y x f x x y y f x y →→++- =0这说明(,)f x y 在00(,)x y 连续. 同理可证如下的定理定理2 设函数(,)f x y 在点000(,)p x y 的某邻域0()U p 有定义，(,)y f x y 在0()U p 内 有界，0(,)f x y 作为x 的一元函数在点0x x =连续，则(,)f x y 在点000(,)p x y 连续. 定理1和定理2可推广到更多元的情形中去.定理 3[5] 设函数12(,,,)n f x x x ⋅⋅⋅在点000012(,,,)n p x x x ⋅⋅⋅的某邻域0()U p 内有定义，12(,,)i x n f x x x ⋅⋅⋅在0()U p 有界{}0111(1,2,),(,,,,)i i i n i n f x x x x x -+∈⋅⋅⋅⋅⋅⋅⋅⋅⋅作为111,,,i i n x x x x -+⋅⋅⋅⋅⋅⋅的n-1元函数在点0000111(,,,)i i n x x x x -+⋅⋅⋅⋅⋅⋅连续，则 12(,,,)n f x x x ⋅⋅⋅在点000012(,,,)n p x x x ⋅⋅⋅连续.证明 任取00001122(,,,,,)i i n n x x x x x x x x ++⋅⋅⋅+⋅⋅⋅+ 0()U p ∈，则111(,,,,)(,,)i i n n i n f x x x x x x f x x x +⋅⋅⋅+⋅⋅⋅+-⋅⋅⋅⋅⋅⋅=00011(,,,,)i i n n f x x x x x x +⋅⋅⋅+⋅⋅⋅+111111(,,,,,)i i i i i n n f x x x x x x x x x --++-+⋅⋅⋅++⋅⋅⋅+1111111(,,,,,)(,,,)i i i i i n n i n f x x x x x x x x x f x x x --++++⋅⋅⋅++⋅⋅⋅+-⋅⋅⋅⋅⋅⋅由于1(,,,ix i n f x x x ⋅⋅⋅⋅⋅⋅）在0(U p ）内存在，故对于固定的{}0(1,2,,j j x x j n +∈⋅⋅⋅ \{}),i0000111111(,,,,,,)i i i i i n n f x x x x x x x x x --+++⋅⋅⋅++⋅⋅⋅+ 作为i x 的一元函数在以01x 和0i i x x +为端点的闭区间上可导，从而据一元微分学中的Lagrange 中值定理，存在(0,1)θ∈，使111111(,,,,,)i i i i i i n n f x x x x x x x x x x --+++⋅⋅⋅+++⋅⋅⋅+-00000111111(,,,,,)i i i i i n n f x x x x x x x x x --+++⋅⋅⋅++⋅⋅⋅+=00000111111(,,,,,)ix i i i i i i n n i f x x x x x x x x x x x θ--+++⋅⋅⋅+++⋅⋅⋅+由于111111(,,,,,)i i i i i i n n x x x x x x x x x x θ--+++⋅⋅⋅+++⋅⋅⋅+ 0()U p ∈故111111(,,,,,)i x i i i i i i n n f x x x x x x x x x x θ--+++⋅⋅⋅+++⋅⋅⋅+ 有界因而，当111(,,,,,,)(0,,0)i i i n x x x x x -+⋅⋅⋅⋅⋅⋅→⋅⋅⋅ 时，111111(,,,,,)0i x i i i i i i n n i f x x x x x x x x x x x θ--+++⋅⋅⋅+++⋅⋅⋅+→ .又，据定理的条件知，0111(,,,,,)i i i n f x x x x x -+⋅⋅⋅⋅⋅⋅作为111,,,,i i n x x x x -+⋅⋅⋅⋅⋅⋅的1n -元函数在点0111(,,,,)o i i n x x x x -+⋅⋅⋅⋅⋅⋅连续，故当111(,,,,,,)(0,0,0)i i i n x x x x x -+⋅⋅⋅⋅⋅⋅→⋅⋅⋅ 时，有111111(,,,,,)i i i i i n n f x x x x x x x x x --+++⋅⋅⋅++⋅⋅⋅+ 0111(,,,,,)0i i i n f x x x x x -+-⋅⋅⋅⋅⋅⋅→所以，由（3）知，当111(,,,,,,)(0,0,0)i i i n x x x x x -+⋅⋅⋅⋅⋅⋅→⋅⋅⋅ 时，有111111(,,,,,)i i i i i i n n f x x x x x x x x x x --+++⋅⋅⋅+++⋅⋅⋅+ 0111(,,,,,)0i i i n f x x x x x -+-⋅⋅⋅⋅⋅⋅→这说明111(,,,,,,)i i i n f x x x x x -+⋅⋅⋅⋅⋅⋅在点000000111(,,,,,)i i i n p x x x x x -+⋅⋅⋅⋅⋅⋅连续. 证毕.2.2多元函数的偏导数我们知道高等数学及数学分析教材中有：////0000(,)(,)xyyx f x y f x y =此式成立的条件为：偏导数//xy f 和//yx f 在00(,)x y 都连续.下面给出一个更若条件下二元混合偏导数求导次序无关的条件.定理4 若函数(,)f x y 在0p 00(,)x y 的某邻域内偏导数/x f ，/y f 及//yx f 存在，且//yx f 在0p 对y 连续，则偏导数//xy f 在0p 存在，且 ////0000(,)(,)xyyx f x y f x y = 证明 不妨设000(,)p x y 的邻域为 ：{}000()(,)(,),(,)U p x y x U x y y δδ=∈∈ 又设x在0x 有增量x 00(0,(,))x x x U x δ≠+∈ ，y在0y 有增量y 00(0,(,))y y y U y δ≠+∈ ，则要证极限////0000000(,)(,)(,)limx x xyy f x y y f x y f x y y→+-= （1）存在且值为//00(,)xy f x y .因为/x f 在0()U p 存在，所以/0000000(,)(,)(,)limx x f x x y y f x y y f x y y x→++-++=及 /0000000(,)(,)(,)limx x f x x y f x y f x y x→+-=都存在，将其代入（1）式右端得//00(,)xy f x y 00lim limy x →→= [][]00000000(,)(,)(,)(,)f x x y y f x y y f x x y f x y y x++-+-+- （2）作辅助函数 (,)(,)(,)x y f x x y f x y ϕ=+-因为/y f 在0()U p 存在，所以///(,)(,)(,)y y y x y f x x y f x y ϕ=+- 在0()U p 存在，故对函数0(,)x y ϕ，在以0y 和0y y + 为端点的区间上应用Lagrange 中值定理，得/000000(,)(,)(,)y x y y x y x y y y ϕϕϕθ+-=+ (01)θ<<而由(,)x y ϕ的构造可知，上式即[]0000(,)(,)f x x y y f x y y ++-+ []0000(,)(,)f x x y f x y -+-//0000(,)(,)y y f x x y y f x y y θθ⎡⎤=++-+⎣⎦ y(01)θ<<将其代入（2）式右端得//0000//0000(,)(,)(,)lim limy y xy y x f x x y y f x y y yf x y y xθθ→→⎡⎤++-+⎣⎦= //000000(,)(,)lim limy y y x f x x y y f x y y xθθ→→++-+= (0)y ≠又因为//yx f 在0()U p 存在，所以//00000(,)(,)limy y x f x x y y f x y y xθθ→++-+ //00(,)yx f x y y θ=+//////0000000(,)lim (,)(,)xy yx yx y f x y f x y y f x y θ→=+= （//yxf 在0p 对y 连续）定理得证.2.3 多元函数的可微性考察函数的可微性时，如果知道偏导数连续，则函数一定可微.但是偏导数连续性条件常常不满足，或不易判断.熟知函数在点0p 可微的必要条件是各个偏导数在0p 处存在.如果函数(,)z f x y =在0p 处的全增量可表示为：z=A x+B y+()ορ则常数A 与B 一定为A=x f (0p ) B=y f (0P ) 且函数在0P 处可微.于是验证函数可微性的一个方法是检验极限：0limρ→00()()x y Z f p f p yρ-- 是否等于零,然而这先要求偏导数A=0()x f p 和B=0()y f p .有无可能不求偏导数，而设法判断可微性？例1 考虑函数Z=()()221()sin ,0,00,,0,0x y x y x y⎧+≠⎪⎪⎨⎪⎪=⎩在（0，0）处的可微性.由 Z=22()()sinx y ⎡⎤+⎣⎦ 知limlim0Zρρρ→→== 能否判定此函数在（0，0）可微？事实上，上式极限等价于()Z o ρ= 或写成00()Z x y o ρ=++ 由全微分定义即知此函数在（0,0）可微，(0,0)(0,0)0x y f f ==且(0,0)dz =0这个例子启示我们有可能通过考察极限0limZρρ→ 判断某些函数的可微性.我们可以证明如下的定理定理5[2] 设n 元函数()z f p =在0p 的某个邻域内有定义，且极限0lim Zρρ→ 存在，记为α(1) 若0α≠，则函数()z f p =在0p 处不可微；(2) 若α=0，则函数在0p 处可微且00dz p =，其中ρ=. 我们以二元函数为例证明.证明（1）反证.设函数(,)z f x y =在000(,)p x y =处可微，则()Z A x B y o ρ=++由0lim0zραρ→=≠ 及上式可得220A B +≠ 考察等式()A xB yZo ρρρρ+=-两边的极限.令cos ,sin ,02x y ρθρθθπ==≤< ，则 左=0lim lim (cos sin )A x B yA B ρρθθρ→→+=+ 极限不存在 （220A B +≠）右=0lim0Zραρ→=≠ 矛盾.故函数(,)z f x y =在0p 处不可微.（2）若0lim0Zρρ→= 即()Z o ρ= 则有 00()Z x y o ρ=++故z=f(x,y)在0p 处可微.且00dz p = 这时有0000(,)(,)0x y f x y f x y == 需要说明的是，0limZρρ→ 不存在时，函数()z f p =在0p 点的可微性不确定.我们熟知如果一个多元函数的所有偏导数在某一点都存在并连续，则它一定在该点可微.那么是不是非得满足这一条件才可微呢？以下我们介绍一个较弱条件小关于多元函数可微的定理.定理6[3] 若n+1元函数1(,,)n f x x y ⋅⋅⋅关于y 的偏导数对n+1个变量连续，关于1,n x x ⋅⋅⋅可微（即把1,(,)n f x x y ⋅⋅⋅中的y 看成常数后可微），则n+1元函数1,(,)n f x x y ⋅⋅⋅可微.证明 因为1,(,)n f x x y ⋅⋅⋅关于1,n x x ⋅⋅⋅可微，所以1//111(,,)(,,)n x n x n n f a a b x f a a b x ⋅⋅⋅+⋅⋅⋅⋅⋅⋅= 1111(,...,)(,...,)()n n n f a x a x b f a a b ορ++-+ （1）其中1ρ=1(,,)n f x x y ⋅⋅⋅关于y 有连续的偏导数，有Lagrange 中值定理，在b 与b+y 之间存在ζ满足/11(,,)y n n f a x a x y ζ+⋅⋅⋅+=1111(,,)(,,)n n n n f a x a x b y f a x a x b +⋅⋅⋅++-+⋅⋅⋅+由连续性有//1110lim (,)(,,)y n n y n f a x a x f a a b ρζ→+⋅⋅⋅+=⋅⋅⋅其中ρ=，所以//111(,,)(,,)()y n y n n f a a b y f a x a x y o ζρ⋅⋅⋅=+⋅⋅⋅++=1111(,,)(,,)()n n n n f a x a x b y f a x a x b o ρ+⋅⋅⋅++-+⋅⋅⋅++ （2）（1）+（2）得1///1111(,,)(,,)(,,)nx n x n n y n f a a b x f a a b x f a a b y ⋅⋅⋅+⋅⋅⋅⋅⋅⋅+⋅⋅⋅=1111(,,)(,,)()()n n n f a x a x b y f a a b o o ρρ+⋅⋅⋅++-⋅⋅⋅++因为10ρρ≤≤，所以1()()o o ρρ=，即1(,,)n f x x y ⋅⋅⋅可微.推论 若n(n ≥2)元函数1(,,)n f x x ⋅⋅⋅的偏导数存在，且至多有一个偏导不连续，则1(,,)n f x x ⋅⋅⋅可微.证明 对n 作数学归纳.当n=2时，不妨设2/x f 连续，而由一元函数可导与可微的关系知12(,)f x x 关于1x 可微，由定理12(,)f x x 可微.设n=k 时结论成立，则当n=k+1时，不妨设11(,,)k k f x x x +⋅⋅⋅关于1k x +有连续偏导数，此时1//,kx x f f ⋅⋅⋅仍最多有一个不连续，由假设11(,,)k k f x x x +⋅⋅⋅关于1,k x x ⋅⋅⋅可微.所以11(,,)k k f x x x +⋅⋅⋅可微.2.4 多元函数连续性、偏导数存在性、及可微间的关系多元函数是一元函数的推广，因此它保留着一元函数的许多性质，但也有些差异，这些差异主要是由多元函数的“多元”而产生的.对于多元函数，我们着重讨论二元函数，在掌握了二元函数的有关理论和研究方法之后，在将它推广到一般的多元函数中去.本文将通过具体实例来讨论二元函数连续性、偏导数存在性、及可微间的关系. 2.4.1 二元函数连续性与偏导存在性间的关系(1) 函数(,)f x y 在点000(,)p x y 连续，但偏导不一定存在. 例 2证明函数(,)f xy =(0,0)连续偏导数不存在.证明：因为(,)(0,0)(,)(0,0lim(,)lim0(0,0)x y x y f x y f →→===， 故函数(,)f x y =(0,0)连续.由偏导数定义：01,0(0,0)(0,0)(0,0)limlim1,x x x x f x f f x xx→→>⎧+-===⎨-<⎩故(0,0)x f 不存在.同理可证(0,0)y f 也不存在.(2)函数(,)f x y 在点000(,)p x y 偏导存在，但不一定连续.例 3 函数22,0(,)1,x y xy f x y xy ⎧+=⎪=⎨⎪≠⎩在点(0,0)处(0,0)x f ，(0,0)y f 存在，但不连续证明 由偏导数定义：0(0,0)(0,0)(0,0)lim lim 0x x x f x f f x x→→+-===同理可求得(0,0)0y f =因为22(,)(0,0)(,)(0,0)lim(,)lim()1(0,0)0x y x y f x y x y f →→=+=≠=故函数22,0(,)1,x y xy f x y xy ⎧+=⎪=⎨⎪≠⎩在点(0,0)处不连续.综上可见，二元函数的连续性与偏导存在性间不存在必然的联系. 2.4.2 二元函数的可微性与偏导存在性间的关系(1) 可微与偏导存在定理7 （可微的必要条件）若二元函数(,)f x y 在其定义域内一点000(,)p x y 处可微，则f 在该点关于每个自变量的偏导都存在，且000000(,)(,)(,)x y df x y f x y dx f x y dy =+注1 定理1的逆命题不成立，及二元函数(,)f x y 在点000(,)p x y 处的偏导即使存在，也不一定可微.例4证明函数2222(,)0,x y f x y x y +≠=⎪⎪+=⎩在原点两个偏导存在，但不可微.证明 由偏导数定义：00(0,0)(0,0)00(0,0)lim limx x x f x f f xx→→+--===同理可求得(0,0)0y f =下面利用可微的定义来证明其不可微性. 用反证法.若函数f 在原点可微，则[](0,0)(0,0)(0,0)(0,0)x y x y f df f x y f f dx f dy ⎡⎤-=++--+=⎣⎦应是较ρ=22limlimf dfx y x yρρρ→→-=+当动点(,)x y 沿直线y m x =趋于(0,0)时，则(,)(0,0)2222(,)(0,0)limlim 11x y y mxx y xy m m x ymm→=→==+++这一结果说明动点沿不同斜率m 的直线趋于原点时，对应的极限值也不同.因此所讨论的极限不存在.故函数f 在原点不可微.(2) 偏导连续与可微定理8 （可微的充分条件）若二元函数(,)z f x y =的偏导在点000(,)p x y 的某邻域内存在，且x f 与y f 在点000(,)p x y 处连续，则函数(,)f x y 在点000(,)p x y 可微.注2 偏导连续是函数可微的充分而非必要条件.例5 证明函数()222222221sin ,0(,)0,0x y x y x y f x y x y ⎧++≠⎪+⎪=⎨⎪⎪+=⎩在点（0，0）处可微，但(,)x f x y ，(,)y f x y 在（0，0）点却间断.证明 22(,),0x y x y ∀+≠，有222222121(,)2sincosx x f x y x x y x y x y =-+++222222121(,)2sincosy y f x y y x yx yx y=-+++（1）当y=x 时，极限22111lim (,)lim (2sincos)22x x x f x x x xxx→→=-不存在，则(,)x f x y 在（0，0）点间断.同理可证(,)y f x y 在（0，0）点间断.（2）因2(,0)(0,0)1(0,0)limlim sinx x x f x f f x xx→→-===2(0,)(0,0)1(0,0)limlim sin0y y y f y f f y yy→→-===则(0,0)(0,0)0,x y df f dx f dy =+=2222222211(,)(0,0)()sinsin((,):0)f f x y f x y x y x y x yρρ=-=+=∀+≠+从而2221sin 1limlimlim sin0f df ρρρρρρρρρ→→→-===即函数(,)f x y 在点（0，0）可微. 2.4.3二元函数的连续性与可微性间的关系类似于一元函数的连续性与可微性间的关系，即二元函数(,)f x y 在000(,)p x y 可微 则必然连续，反之不然.例6证明函数(,)f x y =在点（0，0）连续，但它在点（0，0）不可微.证明 （1）因为000lim (,)lim0(0,0)x x y y f x y f →→→→===故函数(,)f x y =在点(0,0)连续.（2）因为(0,0)(0,0)f f x y f =++-=(0,0)(0,0)0x y df f dx f dy =+=所以limlim lim x x y y f dfρρ→→→→→-== 当动点(,)x y 沿着线y x = 趋于(0,0)时，有1lim 0x y →→=≠即0lim0f dfρρ→-≠ ，故(,)f x y 在原点(0,0)不可微.综上所述二元函数连续性、偏导存在性及可微性间的关系如图所示：3 小结对于多元函数的连续性，偏导存在性，可微性等概念以及它们之间因果关系的研究，是多元微分学中的一个难点.本文在分别给出了一系列关于多元函数可微、可偏导，可连续的定理之后，主要以二元函数为例，通过具体实例对多元微分学中的几个重要概念间的关系进行了一些探讨.和一元微分学相比，尽管多元微分学有许多和一元微分学情形相似，但一元函数到多元函数确有不少质的飞跃，而从二元到三元以上的函数，则只有技巧上的差别，而无本质上的不同.学习多元微分学就要紧紧抓住这两个特点，既看到它们的相同之处，又要注意不同之点.参考文献：[1] 同济大学应用数学系，高等数学.（第五版，下册）[M] 北京：高等教育出版社，2002，6.[2] 刘波,李晓楠.关于多元函数可微性的一个注记[J]高等数学研究，2008.3：36—38.[3] 汪明瑾. 一个关于多元函数可微的定理[J] 高等数学研究，2001.3：8.[4] 李晓芬. 关于混合偏导求导次序无关的条件[J] 山西师大学报（自然科学版）1996.6：1—2.[5] 李超. 有关多元函数连续性的几个新结论[J] 韶关学院学报（自然科学版）2002.6:1－4.[6] 华东师范大学数学系.数学分析（三版）[M]北京：高等教育出版社，2004，5.[7] 张鸿,门艳红. 讨论二元函数连续性、偏导存在性、及可微性间关系[J] 哈尔滨师范大学自然科学学报，2006.1：32—34.[8] 周良金,王爱国.偏导数存在、函数连续及可微间的关系[J]高等函授学报（自然科学版），2005，10：34—40.[9] 刘玉琏，傅沛仁．数学分析讲义（三版）[M]北京：高等教育出版社，2001，2.[10] 刘玉琏，等．数学分析讲义学习辅导书（二版）[M]北京：高等教育出版社，2004，7.谢辞经过半年的忙碌和工作，本次毕业论文设计已经接近尾声，作为一个本科生的毕业论文，由于经验的匮乏，难免有许多考虑不周全的地方，如果没有导师的督促指导，以及一起工作的同学们的支持，想要完成这个设计是难以想象的.在这里首先要感谢我的论文指导老师张璐老师.张老师平日里工作繁多，但在我做毕业设计的每个阶段，从选题到查阅资料，论文提纲的确定，中期论文的修改，后期论文格式调整等各个环节中都给予了我悉心的指导.除了敬佩张老师的专业水平外，他的治学严谨和科学研究的精神也是我永远学习的榜样，并将积极影响我今后的学习和工作，在此谨向张老师致以诚挚的谢意和崇高的敬意！在论文即将完成之际，我的心情无法平静，从开始进入课题到论文的顺利完成，有多少可敬的师长、同学、朋友给了我无言的帮助，在这里请接受我诚挚的谢意!最后我还要感谢培养我长大含辛茹苦的父母，谢谢你们!最后，我要向在百忙之中抽时间对本文进行审阅、评议和参加本人论文答辩的各位师长表示感谢！。