大一电路第9章正弦稳态电路的分析例题
- 格式:ppt
- 大小:1.34 MB
- 文档页数:39


Chapter 9 正弦稳态电路分析一、填空题1. 负载的功率因数λ与负载阻抗ϕ∠=Z Z 的关系是___ ___ 。
2. 负载上电压与电流的相位差与其阻抗角的关系是____ ___ 。
3. 正弦稳态电路负载L Z 从给定电源),(i i i S jX R Z U += 获得最大功率的条件是____ _ _,此最大功率等于_____ __ 。
4. 用电压相量U 与电流相量I计算复功率的公式是=S ____ _, S的实部等于____ __功率,虚部等于____ __ 功率,模等于_ ____功率。
5. 瞬时功率在一个周期内的平均值叫做___ ___ 功率。
6. 设电感L 上的电压为 V t U u u L ) sin( 2ϕω+=,则电感上的平均功率为P =__ ____ ,无功功率Q =___ ___ ,Q 的单位是__ ____ 。
7. 设电容C 上的电压为 V t U u u L) sin( 2ϕω+=,则电容上的平均功率P =__ __ ,无功功率 Q =____ __,Q 的单位是___ ____ 。
8. 某复阻抗Z 上的电压与电流的相量分别为U与I,则其复功率=s~ 。
9. 含RLC 电路的串联谐振角频率为____ ___ ;并联谐振角频率____ _ 。
10. RLC 串联电路的品质因数Q 与电路参数间的关系____ ___ 。
11. RLC 并联电路的品质因数Q 与电路参数间的关系_____ __ 。
12. RLC 串联谐振电路的品质因数Q 越___ __,选择性越好。
13. RLC 并联电路的谐振角频率为0ω,当0ωω=时呈阻性,当0ωω<时呈__ __,当0ωω>时呈___ ___ 。
14. 对某RLC 串联电路端口外加电压源供电,改变 ω 使该端口处于谐振状态时, __ 最大,_____ 最小,功率因数=λ。
15. 对某 RLC 并联电路端口外加电流源供电,改变 ω 使该端口处于谐振状态时,____ _ 最大,___ __ 最小,功率因数_____=λ。


第9章 正弦稳态电路的分析 答案例 如图所示正弦稳态电路,已知I1=I2=10A,电阻R 上电压的初相位为零,求相量•I 和•S U 。
解: 电路中电阻R 和电容C 并联,且两端电压的初相为0。
由电阻和电容傻姑娘的电压与电流的相位关系可知:电阻电流•1I 与电压•R U 同相,电容电流•2I 超前电压•R U 相角90○,故ο0101∠=•I A ο90102∠=•I A由KCL 方程,有 ()101021j I I I +=+=•••A由KVL 方程,有 ︒•••∠==++-=+=9010010010010010010101j j I I j U S V例 如图所示正弦稳态电路,R 1=R 2=1Ω。
(1)当电源频率为f 0时,X C2=1Ω,理想电压表读数V 1=3V ,V 2=6V ,V 3=2V,求I S 。
(2)电路中电阻、电容和电感的值不变,现将电源的频率提高一倍,即为2 f 0,若想维持V 1的读数不变,I S 问应变为多少如果把电源的频率提高一倍,而维持V1的读数不变,即R1上的电压有效值U R1=3V,那么R1上的电流的有效值I也不变,此时仍把•I设置为参考相量,故︒•∠=03I A。
由于L和C1上的电流•I不变,根据电感和电容上电压有效值与频率的关系,电源的频率提高一倍,电感上电压表的读数增大一倍,而电容上电压表的读数降为原来的一半,故电源得频率提高一倍,X C2也降为原来得一半,即所以例如图所示正弦稳态电路,已知I1=10A,I2=20A,R2=5Ω,U=220V,并且总电压•U与总电流•I同相。
求电流I和R,X2,X C的值。
例 如图所示正弦稳态电路,已知有效值U 1=1002V, U=5002V ,I 2=30A ,电阻R=10Ω,求电抗X 1,X 2和X 3的值。
由电路可得两边取模得已知2550=U V ,所以6002=U V ,故有。

第9章 正弦稳态电路的分析典型例题例9-1 有一电感线圈,已测得其电阻为Ω16,如果在其两端施加Hz 50,V 110的电压,并测得线圈中的电流为A 5。
试计算线圈的电感。
解 实际电感线圈的电路模型可看作是电阻与电感的串联。
由已知得其等效阻抗为Ω===22A5V 110I U Z 则 Ω=-=-= 1516222222R Z X L 于是,电感线圈的电感为mH 48H 048.0502152==⨯===f X X L L L同理,对于n 个导纳并联而成的电路,其等效导纳为n eq Y Y Y Y +++= 21当电路中的电压、电流均采用关联参考方向时,各个导纳的电流分配为∙∙⋅=I Y Y I eqK K (n ,3,2,1K =)式中∙I 为并联电路的端口总电流,K ∙I 为第K 个导纳K Y 上的分流。
例9-2 电路如例9-2题图所示,已知:Ω+= 916.61j Z ,Ω-= 45.22j Z ,端口电压为 V 30 220∠=∙U ,试求各电磁系仪表的读数,并作出相量图。
解 串联电路的等效阻抗为=-++=+=.8)45.2()916.6(21j j Z Z Z eq根据欧姆定律有A 0 22 3010V 30220∠=Ω∠∠==∙∙eq Z U I 各元件的端电压为V55.68.239022)916.6(11 ∠=∠⨯+==∙∙j I Z U V 586.1030 22)45.2(22 -∠=∠⨯-==∙∙j I Z U 由于电磁系仪表所测的是各电压、电流的有效值,所以各表读数分别为:A 22=AV 8.2391=V ,V 6.1032=V 。
例9-2题的相量图u∙Iuu例9-2题图选∙I 作为参考相量, 电压、电流相量图如图所示。
例9-3 电路如例9-3题图 所示,已知V 040∠=∙S U ,s rad 3000=ω。
试求电流i ,C i ,L i ,并作出相量图。
解 已知V 040∠=∙S U (且设为参考相量),各支路电流如图所示。
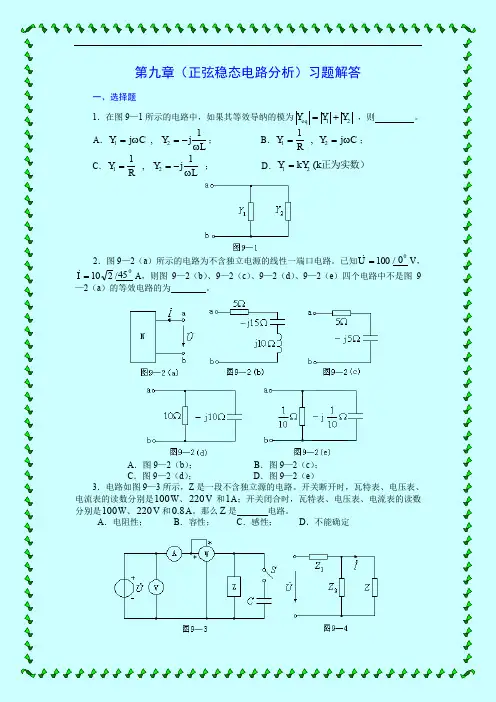
第九章(正弦稳态电路分析)习题解答一、选择题1.在图9—1所示的电路中,如果其等效导纳的模为21Y Y Y eq += ,则 。
A .L Y C Y ω-=ω=1j, j 21; B .C Y RY ω==j , 121;C .L Y R Y ω-==1j , 121 ;D .正为实数)k kY Y ( 21=2.图9—2(a )所示的电路为不含独立电源的线性一端口电路。
已知00 /100=UV ,045 /210=I A ,则图9—2(b )、9—2(c )、9—2(d )、9—2(e )四个电路中不是图9—2(a )的等效电路的为 。
A .图9—2(b );B .图9—2(c );C .图9—2(d );D .图9—2(e )3.电路如图9—3所示,Z 是一段不含独立源的电路。
开关断开时,瓦特表、电压表、电流表的读数分别是100W 、220V 和1A ;开关闭合时,瓦特表、电压表、电流表的读数分别是100W 、220V 和8.0A 。
那么Z 是 电路。
A .电阻性;B .容性;C .感性;D .不能确定4.电路如图9—4所示,U固定不变。
如果 ,则改变Z (Z 不等于无限大)时,I不变。
A .21Z Z =; B .21Z Z -=; C .21Z Z =; D .)Arg()Arg(21Z Z =5.Ω=10R 的电阻,F 1μ=C 的电容与电感L 串联,接到频率1000Hz 的正弦电压源上。
为使电阻两端的电压达到最高,电感应取 。
A .1H ;B .π21H; C .21H ; D .241πH二、填空题1.若Ω=3R ,Ω=ω6L ,Ω=ω2011C ,Ω=ω2012C ,则图9—5所示电路的输入阻抗为 j4)3(-Ω。
.2.线性一端口电路如图9—6所示,A /02 V ,30/5000=-=I U。
则此一端口电路吸收的复功率,有功功率、无功功率分别为V A 30/1000、W 350、50Var 。

第九章正弦稳态电路的分析正弦稳态电路的分析应用相量法。
通过引入相量法,建立了阻抗和导纳的概念,给出了KCL,KVL和欧姆定律的相量形式,由于它们与直流电路的分析中所用的同一公式在形式上完全相同,因此能够把分析直流电路的方法,原理,定律,例如,网孔法(回路法),结点法,叠加定理,戴维宁定理,等效电源原理等等直接应用于分析正弦电路的相量模型,其区别仅在于:(1)不直接引用电压电流的瞬时表达式来表征各种关系,而是用对应的向量形式来表征各种关系;(2)相应的运算不是代数运算,而是复数的运算,因而运算比直流复杂。
但根据复数运算的特点,可画出向量图,利用向量图的几何关系来帮助分析和简化计算,从而扩大了求解问题的思路和方法。
(3)引入了一些新的概念,如平均功率,无功功率,视在功率,复功率,最大功率传输,谐振等。
认识以上区别,对正弦稳态电路的分析是有益的。
9-1试求图示各电路的输入阻抗Z和导纳Y。
解:(a)Z=1+=1+=Y====S(b) Z==Y=(c) Y=SZ=题9-1图设端口电压相量为,根据KVL,得所以输入阻抗为导纳设端口电压,电流相量为,,根据KCL,得且有所以输入阻抗导纳注:本题的求解过程说明,引入阻抗和导纳的概念以后,正弦电路的输入阻抗(或导纳)的定义与计算和直流电路输入电阻(或电导)的定义与计算是相似的。
即输入阻抗若有n个阻抗串联,等效阻抗若有n个导纳并联,等效导纳为只不过Z和Y是复数。
9-2已知图示电路中,。
试求电路中合适的元件值(等效)。
解:把u用余弦函数表示有u和I的相量形式为,根据入端导纳的定义,有既图示的两并联元件为电导和电容,其参数为注:以上计算表明,导纳的模等于电流与电压的模值之比,导纳角等于电流与电压的相位差,若导纳角,表示电流超前电压,导纳为电容性,反之为电感性。
9-3 附图中N为不含独立源的一端口,端口电压u,电流I分别如下列各式所示。
试求没一种情况下的输入阻抗Z和导纳Y,并给出等效电路图(包括元件的参数值)。


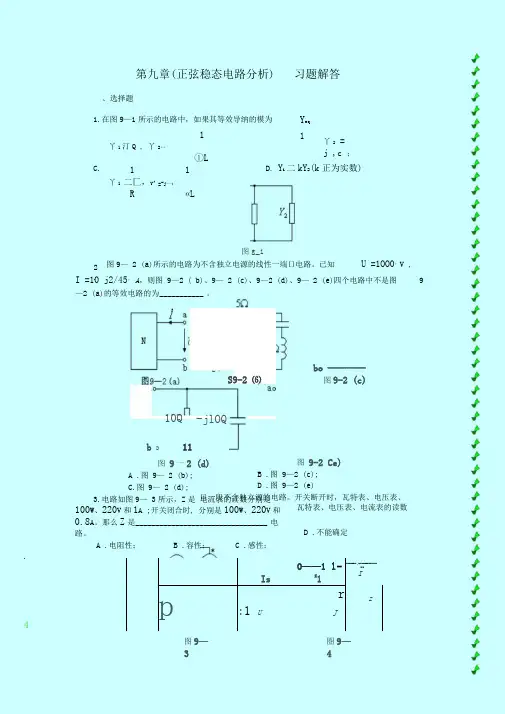
、选择题第九章(正弦稳态电路分析)习题解答1.在图9—1所示的电路中,如果其等效导纳的模为C .1丫1汀Q , 丫2…①L11 丫1 二匚,Y^ =-j —;R«LY eq1丫2 =j ,c ;D . Y i 二kY 2(k 正为实数)图g_i图9— 2 (a )所示的电路为不含独立电源的线性一端口电路。
已知U =1OO0°V ,I =10 j2/45° A ,则图 9—2 ( b )、9— 2 (c )、9—2 (d )、9— 2 (e )四个电路中不是图 9—2 (a )的等效电路的为 ___________ 。
2. S9-2 ⑹10Q -jlOQbo --------图9-2 (c)b D11图 9一2 (d)A .图 9— 2 (b );C .图 9— 2 (d );3.电路如图9— 3所示,Z 是 电流表的读数分别是100W 、220V 和1A ;开关闭合时, 分别是100W 、220V 和0.8A 。
那么Z 是 _________________________________ 电路。
A .电阻性;B .容性;C .感性;图 9-2 Ce)B .图 9—2 (c ); D .图 9—2 (e ) 旦一段不含独立源的电路。
开关断开时,瓦特表、电压表、 瓦特表、电压表、电流表的读数 D .不能确定%O ——1 l -IsZ1---------- ► -----------------■■I 4pr:1 UJTz图9—圏9—入阻抗为(3 - j4)门。
09-52 .线性一端口电路如图 9—6所示, 吸收的复功率,有功功率、无功功率分别为U - -50 /300V, I =2/0^A 。
则此一端口电路100/30°VA 、50 .. 3W 、50Var 。
4.在图9 — 8所示电路中,已知电流表 表V 2的读数为20 V ,则电压表V 的读数为A 的读数为2A ,电压表V 的读数10V ,电压V 。

第九章 正弦稳态电路的分析例题◆例9-1 RLC 串联电路如图9-3所示,其中R=15Ω,L=12mH ,C=5μF ,端电压u=1002cos(5000t)V 。
试求电路中的电流i (瞬时表达式)和各元件的电压相量。
解: 用相量法求解时,可先写出已知相量和设定待求相量,本例已知U=100∠0°V ,I 、U R 、U L 和U C 为待求相量,如图所示。
然后计算各部分阻抗:Z R ==15Ω Z L =jwL=j60Z C =Cjω1− =-j40Ω Z eq = Z R + Z L + Z C =(15+j20)Ω =25∠53.13°Ω(感性阻抗)I=A Z U eq Soo &13.53250100∠∠= =4∠-53.13°A 各元件电压相量为:U R =RI=60∠-53.13°VU L =jwLI=240∠36.87°V U C =I Cj &ω1−=160∠-143.13°V 正弦电流i 为i=42cos(5000t ∠-53.13°)A注意,本例中有U L >U S ,U C >U S 。
(如果本例的电源频率可变,则等效阻抗 Z eq (jw)会不会变为容性阻抗或电阻性阻抗?)◆例9-2 图示电路中R 1=10Ω,L=0.5H ,R 2=1000Ω,C=10μF ,U S =100V ,ω=314rad/s 。
求各支路电流和电压U 10。
解: 令U S =100∠0°V(参考相量),设各支路电流相量为I 、I 1和I 2,如图所示。
各阻抗计算如下:Z R1=10Ω,Z R2=1000ΩZ L =j ωL=j157Ω,Z C =Cjω1−=-318.47Ω Z R2与Z C 的并联等效阻抗为Z 12,有Z 12=CR C R Z Z Z Z +22 =Ω−−47.3181000)47.318(1000j j =303.45∠-72.33°Ω=(92.11-j289.13)Ω总的输入阻抗Zeq 为Zeq=Z 12+Z R1+Z L =(102.11-j132.13)Ω=166.99∠-52.30°Ω 各支路电流和电压U 10计算如下:I=eqS Z U& =0.60∠52.30°A U 10=Z 12I=182.07∠-20.03°AI 1=C Z U10& =0.57∠69.97°AI 2=210R Z U& =0.18∠-20.03°A◆例9-3 画出第一题电路9图(9-3所示)的相量图。
第九章正弦交流稳态电路习题9—1 图9—25所示电路,当开关S 合上和断开时,电流表的读数不变,求:L X 和C X 的关系。
9—2 图9—26所示电路正弦交流电路,电压60=U V ,Ω=Ω=40,40C X R ,开 关S 于位置1时,电压表的读数○V =48V 。
求:开关S 于位置2时电压表的读数。
图9—25 图9—269—3图9—27所示电路,222L R U U U +=是否正确?试用相量图说明。
9—4 图9—28所示电路正弦交流电路中,已知Ω=10R ,Ω=101C ,bc ab U U =,U与I同相。
求:电路的阻抗Z 。
图9—27 图9—289—5 图9—29所示电路正弦交流电路中,已知Ω=71R ,Ω=12R ,2=L H ,1=C F ,4=ωrad/s 。
求:(1)输入阻抗;(2)用两个串联元件等效时,元件的参数值;(3)用两个并联元件等效时,元件的参数值。
9—6 为确定电感线圈的参数R 和L ,用一只Ω1000电阻1R 与线圈并联,如图9—30所示,另以一电流表依次测得各支路的电流为:04.0=I A ,035.01=I A ,01.02=I A 。
已知Hz f 50=,试计算R 和L 。
图9—29 图9—309—7 如图9—31所示的电感线圈接到120=U V 的直流电源上时,电流为20A ,接到50=f Hz ,220=U V 的交流电源上时,电流为25A 。
求:线圈的R 和L 。
9—8 图9—32所示电路中,已知Ω=100R ,Hz f 50=,要使1U 和2U 间相位差为︒60,则C 应为多大?图9—31 图9—329—9 阻抗为Ω+=1.01.0j Z l 的输电线末端,接上10=P kW ,9.0cos =φ的感性负载,如图9—33所示,负载两端电压2202=U V 。
求:线路输入端的电压1U 及功率因数φcos 。
9—10 图—34所示正弦交流电路中,1,121=Ω==L R R H ,C 可变,10=ωrad/s 。
第九章正弦稳态电路的分析例9-1电路如图(a)所示,已知:R=15Ω,L=0.3mH, C=0.2mF,求i ,u R ,u L ,u C。
(a)(b)(c)解:电路的相量模型如图(b)所示,其中:因此总阻抗为总电流为电感电压为电阻电压为电容电压为相量图如图(c)所示,各量的瞬时式为:注意 :U L=8.42>U=5,说明正弦电路中分电压的有效值有可能大于总电压的有效值。
例9-2RL 串联电路如图(a)所示,求在ω=106rad/s 时的等效并联电路图(b)。
( a )( b )解:RL 串联电路的阻抗为:导纳为:得等效并联电路的参数例9-3求图示电路的等效阻抗,已知ω= 105 rad/s 。
例 9 — 3 图解:感抗和容抗为:所以电路的等效阻抗为例9-4图示电路对外呈现感性还是容性?解:设输出电压输出电压和输入电压的比值例 9 — 5 图因为当,上式比值为实数,则u1和u0同相位,此时有例9-6求图 (a) 电路中各支路的电流。
已知电路参数为:例 9 — 6 图( a )( b )解:电路的相量模型如图(b)所示。
设则各支路电流为例9-7列写图(a)电路的回路电流方程和节点电压方程例 9 — 7 图(a)解:选取回路电流方向如图(b)所示,回路电流方程为:回路 1回路 2回路 3回路 4( b )( c )结点选取如图(c)所示,则结点电位方程为:结点 1结点 2结点 3例9-8求图(a)电路中的电流已知:例 9 — 8 图(a)(b)解:方法一:应用电源等效变换方法得等效电路如图(b)所示,其中方法二:应用戴维南等效变换图( c )( d )求开路电压:由图(c)得求等效电阻:把图(c)中的电流源断开得等效电路如图(d)所示,因此电流例9-9求图(a)所示电路的戴维南等效电路。
例 9 — 9 图( a )( b )解:把图(a)变换为图(b),应用 KVL 得解得开路电压求短路电流:把图(b)电路端口短路得所以等效阻抗:例9-10用叠加定理计算图(a)电路的电流,已知例 9 — 10 ( a )( b )( c )解:画出独立电源单独作用的分电路如图(b)和(c)所示,由图(a)得:由图(b)得则所求电流例9-11已知图示电路:Z =10+j50Ω,Z1=400+j1000Ω,问:β等于多少时,相位差90°?例 9 — 11 图解:根据 KVL 得所以令上式的实部为零,即得: ,即电压落后电流90°相位。
第九章正弦稳态电路的分析习题集第九章正弦稳态电路的分析习题集9-1 试求题9-1图所⽰各电路的输⼊阻抗Z 和导纳Y 。
解:()a 2(1)1(12)21j j Z j j j ?-=+=-Ω-1112(0.20.4)125j Y j s Z j +====+- ()b 1(11)1(21)111j j Z j j j -?+=+=-Ω+-1121(0.40.2)215j Y j s Z j +====+- ()c (4040)(4040)4040404040j j Z j j -?+==Ω++- 110.02540Y s Z ====()d ()U j LI rI j L r I ωω=-=- ()U Z j L r Iω==-Ω2211()j L rY s Z j L r L r ωωω--====-+ 9-2 将题9-2图所⽰三⾓形【图()a 】和星型【图()b 】联结的电路等效为星型和三⾓形联结的电路。
9-3 题9-3图中N 为不含独⽴电源的⼀端⼝,端⼝电压、电流分别为下列各式所⽰,试求每⼀种情况下的输⼊阻抗Z 和导纳Y ,并给出等效电路图(包含元件参数值)。
(1)200cos(314)10cos(314)u t V i t A =??=? (2)0010cos(1045)2cos(1090)u t V i t A=- (3)00100cos(260)5cos(230)u t V i t A ?=+??=-?? (4)0040cos(10017)8sin(10090)u t V i t A ?=+??=+??解:(1)000,0U V I A == , 120,0.05U Z Y S I Z ==Ω==等效电路的等效电阻为20Ω。
(2) 0045,90UV I A ==- , 05135( 3.536 3.536),UZ j I==∠=-+Ω011135(0.1410.141)5Y j S Z ==∠-=-- (3)0060,30UV I A ==- 00100603020,5U Z j I ==∠+=Ω 110.0520Y j S Z j ===-(4)0017,0UV I A == 04017(4.78 1.46),8U Z j I ==∠=+Ω 1(0.1910.0585)Y j S Z==-9-4 已知题9-4图所⽰电路中030)s u t V ω=+,电流表A 的读数为5A ,4L ω=Ω,求电流表1A 、2A 的读数。