第七章 平面图形的认识(二)1

第7章《平面图形的认识（二)》考点+易错知识梳理重难点分类解析考点1 和平移有关的图形周长、面积计算【考点解读】本考点解题时,一般运用平移的性质(如:连接平移前后对应点的线段的长等于平移的距离）来解决有关图形的周长、面积计算问题.例 1 如图所示是重叠的两个直角三角形,将直角三角形ABC 沿BC 方向平移到DEF ∆.如果8AB =c ｍ，4BE =cm,3DH =cm ，那么图中阴影部分的面积为 ｃm 2．分析:阴影部分是一个梯形,用我们目前所学的知识无法求出该梯形的上、下底和高，因而不能运用梯形的面积公式求其面积.注意到DEF ∆是由ABC ∆经过平移得到的,因此ABC DEF S S ∆∆=,即HEC DEF ABEH S S S S ∆∆+=+阴影梯形，于是ABEH S S =阴影梯形1(883)4262=+-⨯=（cm ２). 答案：26【规律·技法】本题考查平移的性质:经过平移,对应点所连的线段平行(或在同一条直线上)且相等，对应线段平行（或在同一条直线上）且相等,对应角相等。

解题的关键是找到平移的对应点。

【反馈练习】1。

(2018·苏州期中)如图,将ABC ∆沿BC 方向平移2 cm 得到DEF ∆.若ABC ∆的周长为16 ｃm ，则四边形ABFD 的周长为( ）A 。

16 c ｍ Ｂ． 18 c ｍ C. ２0 c ｍ Ｄ。

２2 ｃｍ点拨:由平移的性质可知2BE FC AD ===ｃm,AC DF =。

2。

（201８·扬州期末）如图是某公园里一处长方形风景欣赏区ABCD ，长50AB =m ，宽30BC =m,为方便游人观赏,公园特意修建了如图所示的小路（图中非阴影部分）,小路的宽均为1 m ，那么小明沿着小路的中间从出口A 到出口B 所走的路线（图中虚线)长为 m.点拨:分别求出小明横向和纵向移动的距离即可。

考点2 利用平行线的性质和三角形内角和定理求角度大小【考点解读】本考点解题时要熟练掌握平行线的性质与三角形内角和定理，这是解题的基础,要善于分解图形，即将较复杂的图形分解出“两条平行线被第三条直线所截"与“三角形”的图形,然后分析各角之间的联系．例2 (2０17·重庆)如图，//AB CD ,E 是CD 上一点,42AEC ∠=︒,EF 平分AED ∠交AB于点F ，求AFE ∠的度数．分析:由互补的性质求出AED ∠的度数,由角平分线的定义得出DEF ∠的度数，再由平行线的性质即可求出AFE ∠的度数.解答：因为42AEC ∠=︒,所以18042138AED ∠=︒-︒=︒。

第七章 平面图形的认识（二）一、知识梳理1、在同一平面上，两条直线的位置关系有 或者 .练习：平面内三条直线的交点个数可能有 ( )A. 1个或3个B.2个或3个C.1个或2个或3个D.0个或1个或2个或3个2、判定与性质：什么叫做平行线？在同一平面内， 的两直线叫平行线。

的两直线平行。

判 定性 质（1） ，两直线平行。

（2） ，两直线平行。

（3） ，两直线平行。

（1）两直线平行， 。

（2）两直线平行， 。

（3）两直线平行，互补。

如果两条直线互相平行，那么其中一条直线上任意两点到另一条直线的距离相等,这个距离称为平行线之间的距离。

（等积变形）（2）如图，长方形ABCD 的面积为16，四边形BCFE 为梯形，BC 与DE 交于点G,则阴）如图，对面积为，使得记其面积为S 1；第二次操作，分别延长A 1B 1，B 1C 1，C 1A 1至点A 2，B 2，C 2，使得A 2B 1=2A 1B 1，B 2C 1=2B 1C 1，C 2A 1=2C 1A 1，顺次连接A 2，B 2，C 2，得到△A 2B 2C 2，记其面积为S 2；…；按此规律继续下去，可得到△A 5B 5C 5，则其面积S 5= ．（4）已知方格纸中的每个小方格是边长为1的正方形，A ，B 两点在小方格的顶点上，位置如图所示，在小方格的顶点上确定一点C ，连接AB ，AC ，BC ，使△ABC 的面积为3个平方单位．则这样的点C 共有 个．（1）如图，边长为3cm ，与5cm 的两个正方形并排放在一起，在大正方形中画一段以它的一个顶点为圆心，边长为半径的圆弧，则阴影部分的面积是______cm 2（π取3）．F3、图形的平移 在平面内，将一个图形沿着________________移动____________，这样的____________叫做图形的平移。

4、平移的性质(1)平移不改变图形的_______、________，只改变图形的_________。

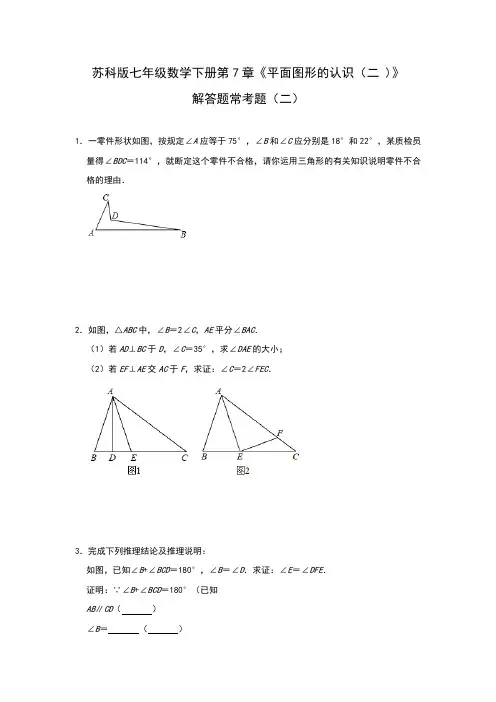
苏科版七年级数学下册第7章《平面图形的认识（二 )》解答题常考题（二）1．一零件形状如图，按规定∠A应等于75°，∠B和∠C应分别是18°和22°，某质检员量得∠BDC＝114°，就断定这个零件不合格，请你运用三角形的有关知识说明零件不合格的理由．2．如图，△ABC中，∠B＝2∠C，AE平分∠BAC．（1）若AD⊥BC于D，∠C＝35°，求∠DAE的大小；（2）若EF⊥AE交AC于F，求证：∠C＝2∠FEC．3．完成下列推理结论及推理说明：如图，已知∠B+∠BCD＝180°，∠B＝∠D．求证：∠E＝∠DFE．证明：∵∠B+∠BCD＝180°（已知AB∥CD（）∠B＝（）又∵∠B＝∠D（已知）＝（等量代换）∴AD∥BE（）∠E＝∠DFE（）4．如图，AB∥CD，∠FGB＝154°，FG平分∠EFD，求∠AEF的度数．5．如图，已知在△ABC中，∠C＝90°，BE平分∠ABC，且BE∥AD，∠BAD＝20°，求∠AEB 的度数．6．如图，已知∠AGF＝∠ABC，∠1+∠2＝180°．（1）试判断BF与DE的位置关系，并说明理由；（2）若BF⊥AC，∠2＝140°，求∠AFG的度数．7．感知：如图①，∠ACD为△ABC的外角，易得∠ACD＝∠A+∠B（不需证明）；探究：如图②，在四边形ABDC中，试探究∠BDC与∠A、∠B．、∠C之间的关系，并说明理由；应用：如图③，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，若∠A＝50°，则∠ABX+∠ACX＝度；拓展：如图④，BE平分∠ABD，CE平分∠ACD，若∠BAC＝100°，∠BDC＝150°，则∠BEC ＝度．8．如图，已知∠A＝90°+x°，∠B＝90°﹣x°，∠CED＝90°，4∠C﹣∠D＝30°，射线EF∥AC．（1）判断射线EF与BD的位置关系，并说明理由；（2）求∠C，∠D的度数．9．如图，AD为△ABC的高，BE为△ABC的角平分线，若∠EBA＝34°，∠AEB＝80°，求∠CAD的度数．10．将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起（其中，∠A＝60°，∠D＝30°；∠E＝∠B＝45°）．（1）如图1，①若∠DCE＝40°，求∠ACB的度数；②若∠ACB＝150°，直接写出∠DCE的度数是度．（2）由（1）猜想∠ACB与∠DCE满足的数量关系是．（3）若固定△ACD，将△BCE绕点C旋转，①当旋转至BE∥AC（如图2）时，直接写出∠ACE的度数是度．②继续旋转至BC∥DA（如图3）时，求∠ACE的度数．11．如图，已知AB∥CD，直线分别交AB、CD于点E，F，∠EFB＝∠B，FH⊥FB．（1）已知∠B＝20°，求∠DFH；（2）求证：FH平分∠GFD；（3）若∠CFE：∠B＝4：1，则∠GFH的度数．12．如图，AB∥CD，点E在线段AB上，连接EC、ED、AD，且AD⊥CE于F，ED平分∠CEB，若∠ADC＝40°，∠A﹣∠B＝10°，求∠BDE的度数．13．如图，∠ABC＝180°﹣∠A，EF∥BD，∠1+∠2＝96°，DO⊥AD交EF于点O．求∠BDO 的度数．14．如图，已知：AB∥CD，DB⊥BC，∠1＝40°，求∠2的度数．完成下面的证明过程：证明：∵AB∥CD（），∴∠1＝∠BCD＝40°（）．∵BD⊥BC，∴∠CBD＝．∵∠2+∠CBD+∠BCD＝（），∴∠2＝．15．已知：如图所示，AB∥CD，AE交CD于点C，DE⊥AE，垂足为E，∠A+∠1＝60°，求：∠D的度数．参考答案1．解：如图，延长BD与AC相交于点E，∵∠1是△ABE的外角，∠A＝75°，∠B＝18°，∴∠1＝∠B+∠A＝75°+18°＝93°，同理，∠BDC＝∠1+∠C＝93°+22°＝115°，∵李师傅量得∠BCD＝114°，不是115°，∴这个零件不合格．2．（1）解：∵∠C＝35°，∠B＝2∠C，∴∠B＝70°，∴∠BAC＝75°，∵AE平分∠BAC，∴∠EAC＝37.5°，∵AD⊥BC，∴∠ADC＝90°，∴∠DAC＝55°，∴∠DAE＝55°﹣37.5°＝17.5°；（2）证明：∵EF⊥AE，∴∠AEF＝90°，∴∠AED+∠FEC＝90°，∵∠DAE+∠AED＝90°，∴∠DAE＝∠FEC，∵AE平分∠BAC，∴∠EAC＝∠BAC＝（180°﹣∠B﹣∠C）＝（180°﹣3∠C）＝90°﹣∠C，∵∠DAE＝∠DAC﹣∠EAC，∴∠DAE＝∠DAC﹣（90°﹣∠C）＝90°﹣∠C﹣90°+∠C＝∠C，∴∠FEC＝C，∴∠C＝2∠FEC．3．证明：∵∠B+∠BCD＝180°（已知），∴AB∥CD（同旁内角互补，两直线平行），∴∠B＝∠DCE（两直线平行，同位角相等），∵∠B＝∠D（已知），∴∠DCE＝∠D（等量代换），∴AD∥BE（内错角相等，两直线平行），∴∠E＝∠DFE（两直线平行，内错角相等），故答案为：同旁内角互补，两直线平行，∠DCE，两直线平行，同位角相等；∴∠DCE；∠D；内错角相等，两直线平行；两直线平行，内错角相等．4．解：∵AB∥CD，∠FGB＝154°，∴∠GFD＝180°﹣∠FGB＝180°﹣154°＝26°，∵FG平分∠EFD，∴∠EFD＝2∠GFD＝2×26°＝52°，∵AB∥CD，∴∠AEF＝∠EFD＝52°．5．解：∵BE∥AD，∴∠ABE＝∠BAD＝20°，∵BE平分∠ABC，∴∠EBC＝∠ABE＝20°，∵∠C＝90°，∴∠AEB＝∠C+∠CBE＝90°+20°＝110°．6．解：（1）BF∥DE，理由如下：∵∠AGF＝∠ABC，∴GF∥BC，∴∠1＝∠3，∵∠1+∠2＝180°，∴∠3+∠2＝180°，∴BF∥DE；（2）∵BF∥DE，BF⊥AC，∴DE⊥AC，∵∠1+∠2＝180°，∠2＝140°，∴∠1＝40°，∴∠AFG＝90°﹣40°＝50°．7．解：探究：连接AD并延长至点F，由外角定理可得∠BDF＝∠BAD+∠B，∠CDF＝∠C+∠CAD；且∠BDC＝∠BDF+∠CDF及∠BAC＝∠BAD+∠CAD；相加可得∠BDC＝∠A+∠B+∠C；应用：由探究的结论易得：∠ABX+∠ACX+∠A＝∠BXC，又因为∠A＝50°，∠BXC＝90°，所以∠ABX+∠ACX＝90°﹣50°＝40°；故答案为：40；拓展：由探究的结论易得∠BDC＝∠BAC+∠ABC+∠ACB，易得∠ABC+∠ACB＝50°；而∠BEC＝（∠ABC+∠ACB）+∠A，代入∠BAC＝100°，∠BDC＝150°，易得∠BEC＝125°故答案为：1258．解：（1）EF∥BD，∵∠A+∠B＝（90+x）°+（90﹣x）°＝180°，∴AC∥BD，∵EF∥AC，∴EF∥BD；（2）∵AC∥EF∥BD，∴∠CEF＝∠C，∠DEF＝∠D，∵∠CED＝90°，∴∠C+∠D＝90°，联立，解得．9．解：∵BE为△ABC的角平分线，∴∠CBE＝∠EBA＝34°，∵∠AEB＝∠CBE+∠C，∴∠C＝80°﹣34°＝46°，∵AD为△ABC的高，∴∠ADC＝90°，∴∠CAD＝90°﹣∠C＝44°．10．解：（1）①∵∠DCE＝40°，∴∠ACE＝∠ACD﹣∠DCE＝50°，∴∠ACB＝∠ACE+∠ECB＝50°+90°＝140°；②∵∠ACB＝150°，∠ACD＝90°，∴∠ACE＝150°﹣90°＝60°，∴∠DCE＝∠ACD﹣∠ACE＝90°﹣60°＝30°，故答案为：30；（2）∵∠ACB＝∠ACD+∠BCE﹣∠DCE＝90°+90°﹣∠DCE，故答案为：∠ACB+∠DCE＝180°；（3）①∵BE∥AC，∴∠ACE＝∠E＝45°，故答案为：45°；②∵BC∥DA，∴∠A+∠ACB＝180°，又∵∠A＝60°，∴∠ACB＝180°﹣60°＝120°，∵∠BCE＝90°，∴∠BCD＝∠ACB﹣∠ECB＝120°﹣90°＝30°．11．解：（1）∵AB∥CD，∠B＝20°，∴∠DFB＝20°，∵FH⊥FB，∴∠BFH＝90°，∴∠DFH＝90°﹣∠DFB＝70°；（2）证明：∵AB∥CD，∴∠DFB＝∠B，∵∠EFB＝∠DFB，∵∠DFB+∠DFH＝90°，∴∠EFB+∠GFH＝90°，∴∠GFH＝∠DFH，∴FH平分∠GFD；（3）∵AB∥CD，∴∠CFB+∠B＝180°，∵∠EFB＝∠B，∠CFE：∠B＝4：1，∴∠EFB＝30°，∴∠GFH＝90°﹣30°＝60°．故答案为：60°．12．解：∵AB∥CD，∵∠A﹣∠B＝10°，∴∠B＝30°，∵AD⊥EF，∴∠AFE＝90°，∴∠AEF＝50°，∴∠BEC＝130°，∵DE平分∠BEC，∴∠BED＝∠BEC＝65°，∴∠BDE＝180°﹣30°﹣65°＝85°．13．解：∵∠ABC＝180°﹣∠A，即∠ABC+∠A＝180°，∴AD∥BC，∴∠1＝∠3，又∵EF∥BD，∴∠2＝∠3，∴∠1＝∠2，又∵∠1+∠2＝96°，∴2∠1＝96°，∠1＝48°，又∵DO⊥AD，∴∠ADO＝90°，∴∠BDO＝90°﹣∠1＝42°．答：∠BDO的度数为42°．14．证明：∵AB∥CD（已知），∴∠1＝∠BCD＝40°（两直线平行，同位角相等）．∵BD⊥BC，∴∠CBD＝90°．∵∠2+∠CBD+∠BCD＝180°（三角形内角和定理），∴∠2＝50°．故答案为：已知，两直线平行，同位角相等，90°，180°，三角形内角和定理，50°．15．解：∵AB∥CD，∴∠A＝∠1，∵∠A+∠1＝60°，∴∠1＝∠A＝30°，∴∠ECD＝∠1＝30°，∵DE⊥AE，∴∠DEC＝90°，∴∠D＝180°﹣∠DEC﹣∠ECD＝60°．。

七年级数学下册期末知识点总结（苏教版）知识点总结目录第七章平面图形的认识(二) 1第八章幂的运算 2第九章整式的乘法与因式分解 3第十章二元一次方程组 4第十一章一元一次不等式 4第十二章证明 9第七章平面图形的认识(二)一、知识点：1、三线八角① 如何由线找角：一看线，二看型。

同位角是F型;内错角是Z型;同旁内角是U型。

② 如何由角找线：组成角的三条线中的公共直线就是截线。

2、平行公理：如果两条直线都和第三条直线平行，那么这两条直线也平行。

简述：平行于同一条直线的两条直线平行。

补充定理：如果两条直线都和第三条直线垂直，那么这两条直线也平行。

简述：垂直于同一条直线的两条直线平行。

3、平行线的判定和性质：判定定理性质定理条件结论条件结论同位角相等两直线平行两直线平行同位角相等内错角相等两直线平行两直线平行内错角相等同旁内角互补两直线平行两直线平行同旁内角互补4、图形平移的性质：图形经过平移，连接各组对应点所得的线段互相平行(或在同一直线上)并且相等。

5、三角形三边之间的关系：三角形的任意两边之和大于第三边;三角形的任意两边之差小于第三边。

若三角形的三边分别为a、b、c，则6、三角形中的主要线段：三角形的高、角平分线、中线。

注意：①三角形的高、角平分线、中线都是线段。

②高、角平分线、中线的应用。

7、三角形的内角和：三角形的3个内角的和等于180_deg;;直角三角形的两个锐角互余;三角形的一个外角等于与它不相邻的两个内角的和;三角形的一个外角大于与它不相邻的任意一个内角。

8、多边形的内角和：n边形的内角和等于(n-2)_bull;180_deg;;任意多边形的外角和等于360_deg;。

第八章幂的运算幂(power)指乘方运算的结果。

an指将a自乘n次(n个a相乘)。

把an看作乘方的结果，叫做a的n次幂。

对于任意底数a,b，当m，n为正整数时，有am_bull;an=am+n (同底数幂相乘,底数不变,指数相加)am_divide;an=am-n (同底数幂相除,底数不变,指数相减)(am)n=amn (幂的乘方,底数不变,指数相乘)(ab)n=anan (积的乘方,把积的每一个因式乘方,再把所得的幂相乘)a0=1(a_ne;0) (任何不等于0的数的0次幂等于1)a-n=1/an (a_ne;0) (任何不等于0 的数的-n次幂等于这个数的n次幂的倒数) 科学记数法:把一个绝对值大于10(或者小于1)的整数记为a_times;10n的形式(其中1_le;|a|_lt;10),这种记数法叫做科学记数法.复习知识点：1.乘方的概念求n 个相同因数的积的运算，叫做乘方，乘方的结果叫做幂。

平面图形的认识（二）知识点总复习及强化练习【知识梳理】1.平行线的认识（1）认识三线八角：如图，两条直线被第三条直线所截，分成了八个角。

（2）平行的判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行。

（3）平行的性质：两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补。

2.三角形的认识（1）三角形的三边关系：两边之和大于第三边，两边之差小于第三边。

（2）三角形的内角和：三角形的内角和是180°（3）三角形内外角关系：一个外角大于和它不相邻的任意一个内角，等于和它不相邻的两个内角和。

（4）三角形的分类：直角三角形；锐角三角形；钝角三角形。

（5）三角形的三线：角平分线；中线；高线。

3.多边形的外角和与内角和公式。

【例题精讲】题型一：平行的判定与性质例1.如图所示，AB∥CD，AF平分∠CAB，CF平分∠ACD．计算(1)∠B+∠E+∠D=________；(2)∠AFC=________.例2.如图，AB∥CD，∠A=120°，∠1=72°，则∠D的度数为__________．题型二：折叠问题例1.如图，将一张长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，ED′的延长线与BC交于点G．若∠EFG=55°，则∠1=__________．与AD交于点G，例2.如图，把矩形ABCD沿EF折叠，点A、B分别落在A′、B′处．A′B′若∠1 =50°，则∠AEF=（）A．110°B．115°C．120°D．130°题型三：多边形的内角和与外角和例1.一多边形内角和为2340°，若每一个内角都相等，求每个外角的度数．．．．．．．。

例2.一个零件的形状如图，按规定∠A=90°，∠ABD和∠ACD，应分别是32°和21°，检验工人量得∠BDC=148°，就断定这个零件不合格，运用三角形的有关知识说明零件不合格的理由．例3.如图，已知∠DAB+∠D=180°，AC平分∠A，且∠CAD=25°，∠B=95°（1）求∠DCA的度数；（2）求∠ACE的度数．题型四：拓展延伸例1.如图①是长方形纸带，将纸带沿EF折叠成图②，再沿BF折叠成图③.（1）若∠DEF=200，则图③中∠CFE度数是多少？（2）若∠DEF=α，把图③中∠CFE用α表示.例2.如图，△ABC中，BE，CD为角平分线且交点为点O，当∠A=600时，（1）求∠BOC的度数；（2）当∠A=1000时，求∠BOC的度数；（3）若∠A=α时，求∠BOC的度数。

平面图形的认识二知识点及试作者:日期: 2第七章平面图形的认识(二)、平行线1、同位角、内错角、同旁内角的定义两条线(a,b )被第三条(c)直线所截，在截线的同旁，被截两直线的同一方，把这种位置关系的角称为同位角(corresponding angles) 如图：Z1与/8, Z2与/7,/3与/6,/4与/5均为同位角。

两条线(a,b )被第三条(c)直线所截，两个角分别在截线的两侧，且在两条被截直线之间，具有这样位置关系的一对角叫做内错角。

如图：/1与/6,72与/5均为同位角。

两条线(a,b )被第三条(c)直线所截，两个角都在截线的同一侧，且在两条被截线之间，具有这样位置关系的一对角互为同旁内角(interior angles of thesame side ) 。

女口图：71与7 5,72与7 6均为同位角。

2、平行线的性质(1)两直线平行，同位角相等。

(2)两直线平行，内错角相等。

(3)两直线平行，同旁内角互补。

3、平行线的判定(1)同位角相等，两直线平行。

(2)内错角相等，两直线平行。

(3)同旁内角互补，两直线平行。

(4)平行于同一直线的两直线平行4、平移平移是指在平面内，将一个图形沿着某个方向移动一定的距离，这样的图形运动叫做图形的平移(translation )，简称平移。

5、平移的性质经过平移，对应线段平行(或共线)且相等，对应角相等，对应点所连接的线段平行且相等；平移变换不改变图形的形状、大小和方向(平移前后的两个图形是全等形)。

(1)图形平移前后的形状和大小没有变化，只是位置发生变化；(2)图形平移后，对应点连成的线段平行且相等(或在同一直线上)(3)多次平移相当于一次平移。

(4)多次对称后的图形等于平移后的图形。

(5)平移是由方向，距离决定的。

(6)经过平移，对应线段平行(或共线)且相等，对应角相等，对应点所连接的线段平行且相等。

二、三角形1、由三条不在同一直线上的三条线段首尾依次相接组成的图形叫做三角形。

苏科版七年级下册数学第7章平面图形的认识（二）含答案一、单选题(共15题，共计45分)1、如图，纸片△ABC中，∠A=55°，∠B=75°，将纸片的一角折叠，使C落在△ABC内，则∠1+∠2等于（）A.130°B.50°C.100°D.260°2、如图，直线a，b被直线c所截，下列条件能判断a∥b的是（）A.∠1=∠2B.∠1=∠4C.∠3+∠4=180°D.∠2=30°，∠4=35°3、如图所示，△ABC中，∠C＝90°，AB的垂直平分线交BC于点D，连接AD，若∠CAD＝20°，则∠B＝（）A.20°B.30C.35°D.40°4、如图，工人师傅做了一个长方形窗框ABCD，E、F、G、H分别是四条边上的中点，为了使它稳固，需要在窗框上钉一根木条，这根木条不应钉在（）A.A，C两点之间B.E，G两点之间C.B，F两点之间D.G，H 两点之间5、如图，在中，，，，将沿射线的方向平移，得到，再将绕点逆时针旋转一定角度后，点恰好与点重合，则平移的距离为（）A.2B.3C.4D.56、如图，AB//CD, ∠CED=90°, ∠BED=40°, 则∠C 的度数是（）A.30°B.40°C.50°D.60°7、如图，在菱形ABCD中，菱形的边长为5，对角线AC的长为8，延长AB至E，BF平分∠CBE，点G是BF上的任意一点，则△ACG的面积为（）A.20B.12C.D.248、如图是某广场用地板铺设的部分图案，中央是一块正六边形的地板砖，周围是正三角形和正方形的地板砖．从里向外的第1层包括6个正方形和6个正三角形，第2层包括6个正方形和18个正三角形，依此递推，第10层中含有正三角形个数是（）A.102个B.114个C.126个D.138个9、如图所示，△ABC中AB边上的高是（）A.线段CDB.线段CBC.线段DAD.线段CA10、如图，CD∥AB，∠1＝120°，∠2＝80°，则∠E的度数是( )A.40°B.60°C.80°D.120°11、如图，N，C，A 三点在同一直线上，在△ ABC 中，∠A：∠ABC：∠ACB=3：5：10，又△MNC≌△ABC，则∠BCM：∠BCN 等于( )A.1：2B.1：3C.2：3D.1：412、如图，，，，则的度数为（）A. B. C. D.13、如图，分别为的，边的中点，将此三角形沿折叠，使点落在边上的点处．若，则等于（）A. B. C. D.14、如图，直线l1∥l2，若∠1=140°，∠2=70°，则∠3的度数是（）A.70°B.80°C.65°D.60°15、如图，BE、CF是△ABC的角平分线，∠ABC=80°，∠ACB=60°，BE、CF相交于D，则∠CDE的度数是（）A.60°B.70°C.80°D.50°二、填空题(共10题，共计30分)16、如图，△ACB和△ECD都是等腰直角三角形，CA＝CB，CE＝CD，△ACB的顶点A在△ECD的斜边DE上，CD交AB于点F，若AE＝，AD＝2，则△ACF的面积为________.17、如图，在△ABC中，AB＝AC，点D，点E分别是BC，AC上一点，且DE⊥AD，若∠BAD＝55°，∠B＝50°，则∠DEC的度数为________.18、如图，直线，点在直线上，且，＝，则的度数是________.19、已知三角形的三边长分别为2，a－1，4，则化简|a－3|－|a－7|的结果为________．20、如果将点B先向右移动4个单位长度，再向左移动6个单位长度后，这时点B表示的数是－6，则点B最初在数轴上表示的数为________．21、已知等腰三角形的底角为15°，腰长为30cm，则此等腰三角形的面积为________．22、如图，已知矩形纸片的一条边经过一个含30°角的直角三角尺的直角顶点，矩形纸片的一组对边分别与直角三角尺的两边相交，∠2=115°，则∠1的度数是________．23、如图，平面上直线a，b分别经过线段OK两端点（数据如图），则a，b相交所成的锐角是________．24、如图，△ABC中，AB=5，AC=7，BO平分∠ABC，CO平分∠ACB，MN经过点O，与AB、AC相交于点M、N，且MN∥BC，则△AMN的周长等于________．25、如图，点B，D在⊙O上，且在直径AC的两侧，连结OD，AD，BC，AB。

1. 的一对角称为同位角 同位角相等,2. 的一对角称为内错角 内错角相等,3. 的一对角称为同旁内角1.１，若A=3，则 ∥ ； 若2=E ，则 ∥ ； 若 + = 180°，则2．直线a,b,c 在同一平面内，若a ⊥c，b⊥c，则a b ．由此可得结论：3. 如图２，写出一个能判定直线a ∥b 的条件：4. 推理填空：（1）∵∠A =∠ （已知）， ∴AC∥ED（ ）；（2）∵∠2 =∠ （已知）， ∴AC∥ED（ ）； （3）∵∠A +∠ = 180°（已知）， ∴AB∥FD（ ）；（4）∵∠2 +∠ = 180°（已知），∴AC∥ED（ ）；5.说理题∠D =∠A，∠B =∠FCB，求证：ED∥CF．由此可得结论：图１ 1 2 3A F C DB EEB AF D CG321FE D C B A1．如图1，已知∠1 = 100°，AB∥CD，则∠2 = ，∠3 = ，∠4 = ． 2．如图2，直线AB 、CD 被EF 所截，若∠1 =∠2，则∠AEF +∠CFE = ．3．如图3所示（1）若EF∥AC，则∠A +∠ = 180°，∠F + ∠ = 180°（ ）． （2）若∠2 =∠ ，则AE∥BF．（ ） （3）若∠A +∠ = 180°，则AE∥BF．（ ） 4．如图4，AB∥CD，∠2 = 2∠1，则∠2 = ．5. 推理填空：如图，EF ∥AD,∠1=∠2,∠BAC=70°.将求∠AGD 的过程填写完整. 解: 因为EF ∥AD,所以∠2=____(____________________________) 又因为∠1=∠2所以∠1=∠3(______________)所以AB ∥_____(_____________________________) 所以∠BAC+______=180°(___________________________)6. 说理题如图，已知∠ABE +∠DEB = 180°，∠1 =∠2，求证：∠F =∠G．图124 3 1ABCD E1 2 A B DCEF图2 1 2 3 45AB C D FE 图312 AB CDE F图412 AC B F GED图22CD图21BF 知识检测：1、如图1，已知AB ∥CD ，直线L 分别交AB 、CD•于点E 、F ，EG 平分∠BEF ，若∠EFG=40°，则∠EGF的度数是（ ）A ．60°B ．70°C ．80°D ．90°(1) (2)2、如图2，AB ∥DE ，∠E=65°，则∠B+∠C•的度数是（ ） A ．135° B ．115° C ．65° D ．35°3、如图，∠1=∠B ，∠2=∠3，∠4=80º，试求∠ADC 的度数。

平面图形的认识 ( 二 )一、直线平行的条件1、同位角、内错角、同旁内角的定义两条线（ a,b ）被第三条（ c ）直线所截，在截线的同旁，被截两直线的同一方，把这类地点关系的角称为同位角(corresponding angles) 如图：∠ 1 与∠ 8，∠ 2 与∠ 7 ，∠ 3 与 ∠ 6，∠ 4 与∠ 5 均为同位角。

两条线（ a,b ）被第三条（ c ）直线所截，两个角分别在截线的双侧，且在两条被截直线之间，拥有这样地点关系的一对角叫做内错角 。

如图：∠ 1 与∠ 6，∠ 2 与∠ 5 均为同位角。

两条线（ a,b ）被第三条（ c ）直线所截，两个角都在截线的同一侧，且在两条被截线之间，拥有这样地点关系的一对角互为 同旁内角（interior angles of thesame side ） 。

如图：∠ 1 与∠ 5，∠ 2 与∠6 均为同位角。

例 1、如图，∠ 1 与∠ C 是两条直线 ______被第三条直线 ______所截构成的 ______角 . ∠ 2 与∠ B 是两条直线 ______被第三条直线 ______所截构成的 ______角；∠ B 与∠ C 是两条直线 _ _____被第三条直线 ______ 所截构成的 ______角 .例 2、如图，∠ 1、∠ 2、∠ 3、∠ 4、∠ 5、∠ 6 中，是同位角的有 __________________ ；是内错角的有 ___________ _______；是同旁内角的有 __________________.DE1 A3 42352BC1 6例 1 图例 2 图 例 3 图例 1.AE 、BC 、 CD 、同位角， AE 、 BC 、AB 、内错角；例 2. ∠1 与∠3、∠4 与∠6，∠2 与∠ 4、∠3 与∠ 5，∠2 与∠5、∠ 1与∠ 6、∠ 3与∠ 4、∠1 与∠2、∠5与∠ 6；2、平行线的判断（1）同位角相等 , 两直线平行。