附合导线内业计算培训资料

子学习情境2—7 附合导线内业计算附合导线计算与闭合导线计算步骤基本相同，但是由于二者布设形式不同，表现在角度闭合差和坐标增量闭合差的计算公式上略有差别。

下面着重介绍其不同之处。

(一)角度闭合差计算与调整设附合导线如图2-7—1所示。

起始边BA和终边CD的坐标方位角αBA及αCD都是已知的，B、A、C、D为已知的高级控制点，βi为观测角值（i=1，2，…，n）,附合导线编号从起始点A开始，并将A点编成1号点，终点C编成n点。

图2—7—1从已知边BA的坐标方位角αBA开始,依次用导线各左角推算出终边CD的坐标方位角αCD′，即α1,2=αBA+β1±180°α2,3=α1，2+β2±180°……αCD′=α（n-1），n+βn±180°将上列等式两端分别相加，得αCD′= αBA + ∑β± n×180°由于导线左角观测值总和Σβ中含有误差，上面推算出的αCD′与CD边已知值αCD不相等，两者的差数即为附合导线的角度闭合差Wβ,即Wβ=αCD′—αCD =Σβ+αBA - αCD ± n×180°写成一般形式，即Wβ=Σβ+α始–α终± n×180° (2—7-1）附合导线闭合差允许值的计算公式及角度闭合差的调整方法，与闭合导线相同.值得指出的是，计算式（2—7—1）中的Σβ时,包含了连接角，故在调整角度闭合差时，也应包括连接角在内。

Wβ绝对值的大小，说明角度观测的精度。

一般图根导线的Wβ的允许值，即其极限中误差,应为Wβ允=±40″n（2—7—2）式中n 为导线折角个数（包括两个导线的定向角)。

若|W β｜〉 | W β允|，则应重新观测各折角；若|W β｜ ≤ | W β允|，通常将W β反号，平均分配到各折角的观测值中。

调整分配值称角度改正数,以V β表示，即V β= —W β/n （2-7—3）角度及其改正数取至秒，如果上式不能整除，可将余数凑给短边夹角的改正数中，最后使∑V β= —W β.将角度观测值加上改正数后,即得改正后的角值，也称平差角值.改正后的导线水平角之间必须满足正确的几何关系。

测绘中级附合导线测量的内业计算的方法步骤1.数据整理：将所有野外测量得到的数据整理并记录在测量数据表中，包括所有测角、测距的观测值和对应的仪器误差。

2.角度计算：按照附合导线中的角度连接关系，计算方位角、前方差以及前后角差等。

首先，计算第一站的初始方位角，即参考方位角。

其次，计算后续各站的方位角，可以使用闭合导线平差法或者条件方程平差法。

最后，计算前后角差，验证闭合条件是否满足。

3.距离计算：根据实地测距所得的观测值，考虑仪器误差等因素，计算出各测线的长度。

常用的计算方法包括直接计算法、估计法和逐差法。

4.坐标计算：根据已知的控制点坐标和测量所得的距离和角度，计算出各测站点的坐标。

常用的计算方法包括方位角距离平差法和三角测量法等。

5.平差计算：根据所得的测角、测距和坐标数据，进行平差计算，得到更为准确的测量结果。

常用的平差方法有角度平差、距离平差和坐标平差等。

6.误差分析：对测量结果进行误差分析，包括观测误差和计算误差。

观测误差一般通过残差分析来评估，计算误差可以通过方差分析和误差传递公式来分析。

7.结果检查：对计算结果进行检查，验证闭合导线是否满足精度要求，是否存在明显的错误。

若检查发现有误，需要重新检查数据，重新计算。

8.输出成果：将最终的计算结果进行整理和输出，包括测线图、测量报告和计算表格等。

以上是测绘中级附合导线测量的内业计算方法步骤。

在实际工程中，根据具体的测量任务和要求，可能还需要进行其他的计算和处理，如高程计算、误差传递分析等。

因此，在进行内业计算时，还需根据具体情况进行灵活运用和适当调整。

附合导线平差内业计算附合导线平差内业计算一、主要公式（左角）：如图：有： αB1=αA B +βB ±180°α12=αB1+β1±180° α23=α12+β2±180° α3C =α23+β3±180°αCD =α3C +βC ±180°计算终边坐标方位角的一般公式为：α终边′=α始边+Σβ测±n ×180°角度闭合差：ƒβ测=α终边′-α终边 ，ƒβ允=±10n （一级导线技术要求），式中n 为导线观测角个数。

如果ƒβ测>ƒβ允 ，则说明测角误差超限，应停止计算，重新检测角度。

如果ƒβ测>ƒβ允，说明测角精度符合要求，此时需要进行角度闭合差的调整。

调整是应注意:当用左角计算α终边′时，改正数的符号与ƒβ测符号相反；当用右角计算α终边′时，改正数的符号与ƒβ测符号相同。

可将闭合差按相反符号平均分配给各观测角，而得出改正角：V 改=-ƒβ测/n式中n 内角的个数，计算的改正数，取位至秒。

根据公式β＝β测+V改 得出改正后的观测角，继而算出新的方位角。

为了检核，最后应重新推算结束边的坐标方位角，它应与已知数值相等。

否则，应重新推算。

坐标增量闭合差：ΔX AB =D AB ×COS(αAB ),ΔY AB =D AB ×SIN(αAB ) ΔX B1=D B1×COS(αB1),ΔY B1=D B1×SIN(αB1) ΔX 12=D 12×COS(α12),ΔY 12=D 12×SIN(α12) ΔX 23=D 23×COS(α23),ΔY 23=D 23×SIN(α23) ΔX 3C =D 3C ×COS(α3C ),ΔY 3C =D 3C ×SIN(α3C )按附合导线的要求，各边坐标增量代数和的理论值ΣΔX i 、ΣΔY i ，应等于终、起两点的已知坐标值之差。

附合导线计算
摘要：
一、附合导线计算的定义和作用
二、附合导线计算的基本原理
1.角度的计算
2.距离的计算
三、附合导线计算的具体步骤
1.确定起点和终点
2.测量角度和距离
3.计算附合导线
四、附合导线计算的注意事项
1.测量数据的准确性
2.计算过程的准确性
五、附合导线计算在实际工程中的应用
1.地形测绘
2.建筑物测量
3.地理信息系统
正文：
附合导线计算，是指在测量学中，根据一定的测量原理和计算方法，通过测量地面上两点之间的角度和距离，计算出这两点之间的导线方程，从而确定两点之间空间位置关系的过程。

它在工程测量、地形测绘、建筑物测量等领域
有着广泛的应用。

附合导线计算的基本原理主要包括角度的计算和距离的计算。

角度的计算是根据三角形的正切公式，通过已知的角度和边长，计算出未知的角度。

距离的计算是根据勾股定理，通过已知的边长和角度，计算出未知的边长。

附合导线计算的具体步骤包括：确定起点和终点，这是计算的起点和终点；测量角度和距离，这是获取计算所需的数据；计算附合导线，这是根据测量数据，通过计算得出导线方程。

在附合导线计算的过程中，需要注意的事项主要有测量数据的准确性和计算过程的准确性。

测量数据的准确性是指测量出的角度和距离数据要尽可能的准确，以便保证计算结果的准确性。

计算过程的准确性是指在计算过程中，要严格按照计算公式进行计算，避免计算错误。

附合导线计算在实际工程中的应用主要包括地形测绘、建筑物测量和地理信息系统等。

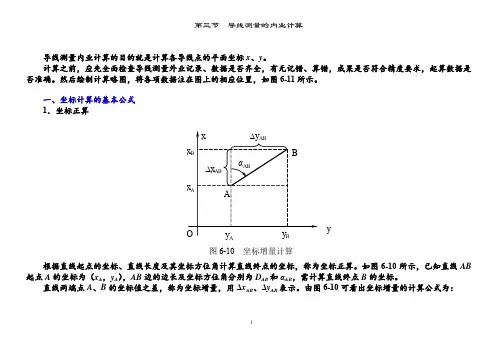
第三节 导线测量的内业计算导线测量内业计算的目的就是计算各导线点的平面坐标x 、y 。

计算之前，应先全面检查导线测量外业记录、数据是否齐全，有无记错、算错，成果是否符合精度要求，起算数据是否准确。

然后绘制计算略图，将各项数据注在图上的相应位置，如图6-11所示。

一、坐标计算的基本公式 1．坐标正算根据直线起点的坐标、直线长度及其坐标方位角计算直线终点的坐标，称为坐标正算。

如图6-10所示，已知直线AB 起点A 的坐标为（x A ，y A ），AB 边的边长及坐标方位角分别为D AB 和αAB ，需计算直线终点B 的坐标。

直线两端点A 、B 的坐标值之差，称为坐标增量，用Δx AB 、Δy AB 表示。

由图6-10可看出坐标增量的计算公式为：y图6-10坐标增量计算⎭⎬⎫=-=∆=-=∆AB AB A B AB AB AB A B AB D y y y D x x x ααsin cos （6-1）根据式（6-1）计算坐标增量时，sin 和cos 函数值随着α角所在象限而有正负之分，因此算得的坐标增量同样具有正、负号。

坐标增量正、负号的规律如表6-5所示。

⎭⎬⎫+=∆+=+=∆+=AB AB A AB A B AB AB A AB A B D y y y y D x x x x ααsin cos （6-2）例6-1 已知AB 边的边长及坐标方位角为456380m 62.135'''︒==AB AB D α，，若A 点的坐标为m 82.658m 56.435==A A y x ，，试计算终点B 的坐标。

解 根据式（6-2）得m 62.792456380sin m 62.135m 82.658sin m 68.457456380cos m 62.135m 56.435cos ='''︒⨯+=+=='''︒⨯+=+=AB AB A B AB AB A B D y y D x x αα2．坐标反算根据直线起点和终点的坐标，计算直线的边长和坐标方位角，称为坐标反算。

闭合及附合导线测量内业计算方法(好东西)1. 导线方位角计算公式当β为左角时α前=α后+β左-180°当β为右角时α前=α后-β右+180°2. 角度闭合差计算fβ=(α始-α终)+∑β左-n*180°fβ=(α始-α终)-∑β右+n*180°3. 观测角改正数计算公式Vβ=±fβ/ n若观察角为左角，应以与闭合差相反的符合分配角度闭合差，若观察角为右角，应以与闭合差相同的符合分配角度闭合差。

4. 坐标增量闭合差计算∑△X=X终-X始∑△Y= Y终-Y始Fx=∑△X测-∑△XFY=∑△Y测-∑△Y5. 坐标增量改正数计算公式VX=- Fx/∑D³DiVY=-FY/∑D³Di² ²所以：∑VX= - Fx ∑VY= - FY6. 导线全长绝对闭合差F=SQR（FX^2+FY^2）7. 导线全长相对闭合差K=F/∑D=1/∑D/F8. 坐标增量计算导线测量的内业方法本人不才悉心整理出来的望能给同行业人士提供点资料（一）闭合导线内业计算已知A点的坐标XA＝450.000米，YA＝450.000米，导线各边长，各内角和起始边AB的方位角αAB如图所示，试计算B、C、D、E各点的坐标。

1角度闭合差：图6—8 闭合导线算例草图角度的改正数△β为：2、导线边方位角的推算BC边的方位角CD边的方位角AB边的方位角右角推算方位角的公式：（校核）3、坐标增量计算设D12、α12为已知，则12边的坐标增量为：4、坐标增量闭合差的计算与调整因为闭合导线是一闭合多边形，其坐标增量的代数和在理论上应等于零，即：但由于测定导线边长和观测内角过程中存在误差，所以实际上坐标增量之和往往不等于零而产生一个差值，这个差值称为坐标增量闭合差。

分别用表示：缺口AA′的长度称为导线全长闭合差，以f表示。

由图可知：图6—9 闭合导线全长闭合差导线相对闭合差。