下载文档原格式
极射赤平投影CAD图解一、序言岩质边坡稳定性分析方法有许多，但无论是平面滑动的单一楔形断面滑体、单滑块和多滑块分析法，还是楔体滑动的仿平面分析法、楔体分割法、立体分析法、霍克分析法以及《岩土工程勘察规范》（GB50021－94）推荐法等，在计算边坡稳定性系数时，需要知道滑体控制平面（包括结构面和坡面、坡顶面）或直线（包括平面的法线）的地质产状，以及平面与平面、直线与直线、直线与平面间夹角等。
其中平面和直线的产状可以通过现场测量获取，除此之外的几何参数，在没有发明极射赤平投影之前，都是用计算法求得，不仅它们的计算公式复杂，而且计算过程繁琐，也很容易出错。
如果采用极射赤平投影求解边坡稳定性分析所需的几何参数，那就可以简化这些几何参数的计算过程，而且一般情况下只需要在现场测量出各个控制平面的地质产状即可。
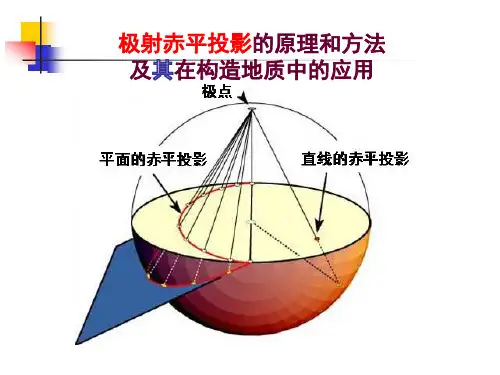
二、极射赤平投影的基本原理（一）投影要素极射赤平投影（以下简称赤平投影）以圆球作为投影工具，其进行投影的各个组成部分称为投影要素，包括：1.投影球（也称投射球）：以任意长为半径的球。
2.球面：投影球的表面称为球面。
3.赤平面（也称赤平投影面）：过投影球球心的水平面。
4.大圆：通过球心的平面与球面相交而成的圆，统称为大圆（如图一（a）中ASBN、PSFN、NESW），所有大圆的直径相等，且都等于投影球的直径。
当平面直立时，与球面相交成的大圆称为直立大圆（如图一（a）中PSFN）；当平面水平时，与球面相交成的大圆称为赤平大圆或基圆（如图一（a）中NESW）；当平面倾斜时，与球面相交成的大圆称为倾斜大圆（如图一（a）中ASBN）。
5.小圆：不过球心的平面与球面相而成的圆，统称为小圆（如图一（b）、（c）中AB、CD、FG、PACB）。
当平面直立时，与球面相交成的小圆称为直立小圆（如图一（b）中DC）；当平面水平时，与球面相交成的小圆称为水平小圆（如图一（b）中AB）；当平面倾斜时，与球面相交成的小圆称为倾斜小圆（如图一（b）中FG或图一（c）中PACB）。
极射赤平投影基本作图方法极射赤平投影基本作图方法§1 极射赤平投影的基本原理一、投影要素1、投影球—以任意长为半径的球，球面即球表面2、赤平面—过投影球球心的水平面3、基圆—赤平面与球面相交的大圆，或称赤平大圆凡过球心的平面与球面相交的大圆，统称为大圆，不过球心的一球面与球面相交所成的圆统称小圆。
4、极射点—球上两极发射点，分上半球投影和下球投影。
二、平面和直线的投影的解析（一）平面投影1、过球心的平面投影任何一个过球心的无限伸展的平面（岩层面、断层面、节理面或轴面等），必然于球面相交成球面大圆，球面大圆与极射点的连线必然穿过赤平面，在赤平面上这些穿透点的连线即为该平面的相应大圆的赤平投影，简称大圆弧。
1）直立大圆（平面）——为基圆直径2）水平大圆（平面）——为基圆本身3）倾斜大圆（平面）——以基圆直径为弧的大圆弧性质：球面大圆投影后在赤平面上仍为一个圆。
2、不过球心的平面投影不过球心的平面与球面相交成直径小于球直径的小圆、球面小圆投影仍为一个小圆。
1）直立小圆（平面）——部分为基圆内一条弧，部位为基圆外一条弧2）水平小圆（平面）——为基圆的同心圆3）倾斜小圆（平面）①全部位于圆基内的小圆②部位于基圆内，部分在基圆外③全部在基圆外性质：1）球面大圆或球面小圆投影在赤平面仍为一个圆2）半径角距相等的球面小圆（即面积相等的小圆），其投影小圆面积不等，近基圆圆心处，远离圆在大。
3）任何过极射点（P）的球面大圆或小圆其赤平投影均为一条直线。
4）球面大圆或小圆在赤平面上的投影圆的圆心（R’）与作图圆心（C）是不重合的；只有水平球面大圆和水平球面小圆投影后，投影圆心（R’）作图圆心（C）与基圆的圆心O点重合，并且投影圆的圆心（R’）与基圆圆心（O）愈远，R’与C分离愈大。
（二）直线投影过球心的直线无限延伸心交于球面两点，称极点。
1、铅直线投影点为基圆圆心2、水平线投影点为基圆直径的两个端点3、倾斜线股影点，一个在基圆内，另一个在基圆外，称对距点，其角距为180°三、投影网：吴尔福网和施密特网（一）吴氏网的结构及成因原理吴氏网的结构：基圆、径几大圆弧、纬向小圆弧、东西、南北经纬线，间距2°，误差±0.5°1、基圆，赤平大圆，代表水平面，0°-360°方位角刻度2、经向大圆弧，由一系列走向SN的，向东或西倾斜，倾角不同（0°-90°），间隔2°的投影大圆弧（代表倾斜平面）组成。
极射赤平投影CAD图解一、序言岩质边坡稳定性分析方法有许多，但无论是平面滑动的单一楔形断面滑体、单滑块和多滑块分析法，还是楔体滑动的仿平面分析法、楔体分割法、立体分析法、霍克分析法以及《岩土工程勘察规范》（GB50021－94）推荐法等，在计算边坡稳定性系数时，需要知道滑体控制平面（包括结构面和坡面、坡顶面）或直线（包括平面的法线）的地质产状，以及平面与平面、直线与直线、直线与平面间夹角等。
其中平面和直线的产状可以通过现场测量获取，除此之外的几何参数，在没有发明极射赤平投影之前，都是用计算法求得，不仅它们的计算公式复杂，而且计算过程繁琐，也很容易出错。
如果采用极射赤平投影求解边坡稳定性分析所需的几何参数，那就可以简化这些几何参数的计算过程，而且一般情况下只需要在现场测量出各个控制平面的地质产状即可。
二、极射赤平投影的基本原理（一）投影要素极射赤平投影（以下简称赤平投影）以圆球作为投影工具，其进行投影的各个组成部分称为投影要素，包括：1.投影球（也称投射球）：以任意长为半径的球。
2.球面：投影球的表面称为球面。
3.赤平面（也称赤平投影面）：过投影球球心的水平面。
4.大圆：通过球心的平面与球面相交而成的圆，统称为大圆（如图一（a）中ASBN、PSFN、NESW），所有大圆的直径相等，且都等于投影球的直径。
当平面直立时，与球面相交成的大圆称为直立大圆（如图一（a）中PSFN）；当平面水平时，与球面相交成的大圆称为赤平大圆或基圆（如图一（a）中NESW）；当平面倾斜时，与球面相交成的大圆称为倾斜大圆（如图一（a）中ASBN）。
5.小圆：不过球心的平面与球面相而成的圆，统称为小圆（如图一（b）、（c）中AB、CD、FG、PACB）。
当平面直立时，与球面相交成的小圆称为直立小圆（如图一（b）中DC）；当平面水平时，与球面相交成的小圆称为水平小圆（如图一（b）中AB）；当平面倾斜时，与球面相交成的小圆称为倾斜小圆（如图一（b）中FG或图一（c）中PACB）。
极射赤平投影基本作图方法
§1 极射赤平投影的基本原理
一、投影要素
1、投影球—以任意长为半径的球，球面即球表面
2、赤平面—过投影球球心的水平面
3、基圆—赤平面与球面相交的大圆，或称赤平大圆
凡过球心的平面与球面相交的大圆，统称为大圆，不过球心的一球面与球面相交所成的圆统称小圆。
4、极射点—球上两极发射点，分上半球投影和下球投影。
二、平面和直线的投影的解析
（一）平面投影
1、过球心的平面投影
任何一个过球心的无限伸展的平面（岩层面、断层面、节理面或轴面等），必然于球面相交成球面大圆，球面大圆与极射点的连线必然穿过赤平面，在赤平面上这些穿透点的连线即为该平面的相应大圆的赤平投影，简称大圆弧。
1）直立大圆（平面）——为基圆直径
2）水平大圆（平面）——为基圆本身
3）倾斜大圆（平面）——以基圆直径为弧的大圆弧
性质：球面大圆投影后在赤平面上仍为一个圆。
2、不过球心的平面投影
不过球心的平面与球面相交成直径小于球直径的小圆、球面小圆投影仍为一个小圆。
1）直立小圆（平面）——部分为基圆内一条弧，部位为基圆外一条弧
2）水平小圆（平面）——为基圆的同心圆
3）倾斜小圆（平面）
①全部位于圆基内的小圆
②部位于基圆内，部分在基圆外
③全部在基圆外
性质：1）球面大圆或球面小圆投影在赤平面仍为一个圆
2）半径角距相等的球面小圆（即面积相等的小圆），其投影小圆面积不等，近基圆圆心处，远离圆在大。
3）任何过极射点（P）的球面大圆或小圆其赤平投影均为一条直线。
4）球面大圆或小圆在赤平面上的投影圆的圆心（R’）与作图圆心（C）是不重合的；只有水平球面大圆和水平球面小圆投影后，投影圆心（R’）作图圆心（C）与基圆的圆心O点重合，并且投影圆的圆心（R’）与基圆圆心（O）愈远，R’与C分离愈大。
（二）直线投影
过球心的直线无限延伸心交于球面两点，称极点。
1、铅直线投影点为基圆圆心
2、水平线投影点为基圆直径的两个端点
3、倾斜线股影点，一个在基圆内，另一个在基圆外，称对距点，其角距为180°
三、投影网：吴尔福网和施密特网
（一）吴氏网的结构及成因原理
吴氏网的结构：基圆、径几大圆弧、纬向小圆弧、东西、南北经纬线，间距2°，误差±0.5°
1、基圆，赤平大圆，代表水平面，0°-360°方位角刻度
2、经向大圆弧，由一系列走向SN的，向东或西倾斜，倾角不同（0°-90°），间隔2°的投影大圆弧（代表倾斜平面）组成。
3、纬向小圆，为一系列走向东西、直立小圆的投影小圆弧组成。
（二）吴氏网和施氏网的主要区别
吴氏网上，面积大小相等小圆，投影后成面积不等的小圆。
施氏网上，面积相等的球面小圆，投影后成加级曲线，面积等于球面小球面积二分之一。
一般求面、线的角距用吴氏网；而研究面、线群统计（极点图和等表图）用施氏网。
为了便于大量的极点投影，采用同心圆（水平小圆）和放射线（直立大圆）相成极等角度网和极等面积网（赖特网）投点。
投射线表示化石向方位同心圆表示倾角。
§2 赤平投影网的基本作图方法
一般步骤：①画“+”中心，②标出E、S、W、N方位（顺钟向）
一、平面的赤平投影
步骤：1、基圆顺钟找倾向；2、东西直径定倾角（由圆周向圆心数）；3、径向圆弧以平面。
二、直线的投影（步骤同1、2即可）
三、法线的投影，关键理解和面垂直，倾向相反，倾角互余。
作业：P15，练习题1、2
补充3、已经线理产状（倾伏向和倾伏角）①150°<26°，②250°<50°，③330°<78°，④42°<10°。
试用吴氏网求出投影点。
§2基本作图法
四、求两相交直线构成的平面产状
五、求相交两面直线的夹角及其角平分线
六、求平面上一直线的倾伏和侧伏
七、求两平面的交线的产状
八、求两平面的夹角及其等分面
九、求一直线与一平面的平角
注意：①复习线状构造产状要素，倾伏向和倾伏角及侧伏角
②两平面间平角与平面之两法线间夹角之关系为互补关系
作业：1、四——九共6个例题作为学习题
2、P16 练习题3，4，5
十、求一平面（或直线）绕一水平轴旋转后的产状
1、预备知识
①水平轴与基圆的直径一致：其旋转轨迹就相对于把要旋转的点（直线或面的法线的投影）沿某一纬度旋转，角度在纬度上定，旋转方向，根据已知条件定，一平面绕轴旋转，产状变化，走向与轴平行时则倾向或一致或相反。
②纬向小圆弧的构造是旋转板平的双圆锥，其锥度为直立小圆；下半部圆锥面的产状与上半部圆锥的拉互关系。
2、例：一平面AB产状130°<50°，（RCD）走向60逆时针水平沿走向旋转30°
作法：①作出AB平面投影，RCD st.60°
②转动RCD与N.S重合
③将AB弧上任意点反钟向（向SE方向）旋30°，得新点，连接新点即在。
注意有的点不够30°，要到外对焦去数。
3、用面的法线旋转
十一、求一平面（或直线）绕一倾斜轴旋后的产状
有间接法和直接法这分。
均很繁琐。
仅介绍前者，分二步：①高倾斜轴为水平轴。
②按十法旋转再要原。
例：平面160°<40°，绕倾斜轴R（30°<30°），顺时针旋转120°，求该平面旋转后的产状。
方法：①作平面P和R的投影
②将R沿纬向弧转成水平轴至基圆上R’，P同步沿所在纬向弧运移到P1
③将R’转到SN径上，P1绕R’转120°（顺钟向），P2-P3
④R’复原到R，P3同步运移到P4，P4点即是
十二、求作小圆，已知小圆投影圆心及其角距
例：一小圆投影圆心（相当旋转轴）产状10°<70°，小圆半径角距55°（相当于旋转轴与一直线夹角），求投影小圆（相当于求该直线绕旋转一圈的圆锥体的度面。
方法：
①作投影圆心R（10°<70°），并转到EW或SN径上，也可以在R的某大圆弧上取55°的角距半径。
②使R落在直径线上，以小圆角距的线长度为直径作小圆，即成。
③若已知R和小圆圆周上一点A，同法可作小圆。
方法是大圆弧上量RA角距，使R转至直径上，以R为准，分别量RA角距，得直径角距，即可得小圆。
十三、求作小圆，已知小圆投影圆心（R）方位及其圆周上两点
例：已知小圆圆心R的方位290°，小圆周上两点A、B，求作小圆及其投影圆心R的产状。
1）作A、B及290°方向线
2）作AB两点的垂直平分线与290°方向线交于C点，C点即为小圆O的作圆中心
3）以C为圆心，CA=CB 为半径作圆，而且小圆与290°方向线相交得小圆直径角距
4）在位于EW直径上的290°方向线上，找小圆投影圆心R，即取角距的一半的点。
十四、求小圆圆周上两点之间的弧度
例：见作法十三及图1-21，已求得小圆及小圆圆周上AB弧。
其弧度量法：
1）直接法：即作与R⊥的大圆弧GMH，再过RA及RB分别作大圆弧，交GMH为A′、B′，同前沿线度移至A′、B′，延长R′A、OA′、OB′、R′B′至基圆周A〞B〞，OA〞,OB〞直线圆心角即得
3）注意A、B间的弧度有三个，θ或360-θ
十五、求两小圆在同一大圆上同步旋转后的产状
便：两小圆投影圆心R1，R2，半径角距为θ1，θ2，求两小圆同前转至水平时的小圆转特。
方法：
1）据方法二、十二作R1，R2及小圆
1
2）使R1、R2位于同一大弧上，并以R1、R2大圆弧的走向线为轴，并将轴转到，SN径上，把R1、R2沿所在纬向弧同前转到水平状态，则R1、R2变为R1，R2
3）分别将R1和R2转到SN径上，以R1和R2为圆心，θ1和θ2为半径角度，描出两小圆。
4）指北标志转回到N。
十六、过通过三点A、B、C作一小圆及投影圆心（R）
作法：1）连接AB、BC分别作中垂线交于C’点，以C’为圆心，C’A、C’B、C’C为半径画圆即为小圆。
2）把C’移到EW径上，取FC’D的角距中点R，为投影圆心
练习，P28，23、25、29。
