柱、锥、球及其简单组合体
- 格式:doc
- 大小:301.56 KB
- 文档页数:8


考点22 空间几何题的面积与体积一、考纲要求1. 直观了解柱、锥、台、球及其简单组合体的结构特征,对柱、锥、台、球的概念的理解不作过高要求,复习时不要过分挖深.2. 多面体与旋转体表面上两点间的最短距离问题,要适当强化,体现了空间问题向平面问题转化.3. 柱、锥、台、球的表面积与体积的计算可能会在高考填空题中出现,注意体现不同几何体之间的联系,同时注意与平面几何中的面积等进行类比.二、近五年江苏高考立体几何中的计算作为江苏考纲必考知识点,每年都会考查,但是江苏高考对立体几何中的运算要求比较简单,近要求计算简单几何体的体积与表面积等简单的运算。
从近五年江苏高考试题可以发现主要考查柱、锥、球的表面积与体积,因此,在复习中要注意把握深度。
三、考点总结:把握空间几何体的结构特征是认识几何体的一个重要方面,也是进一步学习立体几何的基础. 在学习过程中,要通过互相对比的方式来把握它们的实质与不同,既要看到它们之间的不同,也要理解它们之间的联系,这样才能理解它们之间的共性和个性,做到心中有数,心中有图. 近些年来在高考中不仅有直接求多面体、旋转体的面积和体积问题,也有已知面积或体积求某些元素的量或元素间的位置关系问题. 即使考查空间线面的位置关系问题,也常以几何体为依托,因而要熟练掌握多面体与旋转体的概念、性质以及它们的求积公式. 同时也要学会运用等价转化思想,会把组合体求积问题转化为基本几何体的求积问题,会等体积转化求解问题,会把立体问题转化为平面问题求解,会运用“割补法”等求解.四、近五年江苏高考题1、(2019江苏卷)如图,长方体1111ABCD A B C D 的体积是120,E 为1CC 的中点,则三棱锥E -BCD 的体积是_____.2、(2018江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.3、(2017江苏卷)如图,圆柱O 1O 2内有一个球O ,该球与圆柱的上、下底面及母线均相切.记圆柱O 1O 2的体积为V 1,球O 的体积为V 2,则V 1V 2的值是________.4、(2016江苏卷)现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P A 1B 1C 1D 1,下部的形状是正四棱柱ABCDA 1B 1C 1D 1(如图所示),并要求正四棱柱的高O 1O 是正四棱锥的高PO 1的4倍.(1) 若AB =6 m ,PO 1=2 m ,则仓库的容积是多少?(2) 若正四棱锥的侧棱长为6 m ,则当PO 1为多少时,仓库的容积最大?5、(2015江苏卷)现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥与圆柱各一个,则新的底面半径为________.五、三年模拟题型一柱的表面积与体积1、(2019南通、泰州、扬州一调)已知正四棱柱的底面长是3 cm,侧面的对角线长是3 5 cm,则这个正四棱柱的体积为________cm3.2、(2019常州期末)已知圆锥SO,过SO的中点P作平行于圆锥底面的截面,以截面为上底面作圆柱PO,圆柱的下底面落在圆锥的底面上(如图),则圆柱PO的体积与圆锥SO的体积的比值为________.3、(2019苏锡常镇调研(一))已知圆柱的轴截面的对角线长为2,则这个圆柱的侧面积的最大值为________.4、(2019南京三模)有一个体积为2的长方体,它的长、宽、高依次为a,b,1.现将它的长增加1,宽增加2,且体积不变,则所得新长方体高的最大值为.5、(2018南京学情调研)将一个正方形绕着它的一边所在的直线旋转一周,所得圆柱的体积为27πcm3,则该圆柱的侧面积为________cm2.6、(2018南通、泰州一调)如图,铜质六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知正六棱柱的底面边长、高都为4 cm,圆柱的底面积为9 3 cm2.若将该螺帽熔化后铸成一个高为6 cm的正三棱柱零件,则该正三棱柱的底面边长为________cm(不计损耗).7、(2018苏北四市期末)已知正四棱柱的底面边长为3 cm,侧面的对角线长是35cm,则这个正四棱柱的体积是________cm3.8、(2018苏中三市、苏北四市三调)现有一正四棱柱形铁块,底面边长为高的8倍,将其熔化锻造成一个底面积不变的正四棱锥形铁件(不计材料损耗).设正四棱柱与正四棱锥的侧面积分别为1S ,2S ,则12S S 的值为 .9、(2017南通一调)如图,在正四棱柱ABCDA 1B 1C 1D 1中,AB =3 cm ,AA 1=1 cm ,则三棱锥D 1A 1BD 的体积为________cm 3.10.(2017常州期末)以一个圆柱的下底面为底面,并以圆柱的上底面圆心为顶点作圆锥,若所得的圆锥底面半径等于圆锥的高,则圆锥的侧面积与圆柱的侧面积之比为________.题型二 锥的表面积与体积1、(2019扬州期末)底面半径为1,母线长为3的圆锥的体积是________.2、(2019镇江期末) 已知一个圆锥的底面积为π,侧面积为2π,则该圆锥的体积为________.3、(2019泰州期末) 如图,在直三棱柱ABCA 1B 1C 1中,点M 为棱AA 1的中点,记三棱锥A 1MBC 的体积V 1,四棱锥A 1BB 1C 1C 的体积为V 2,则V 1V 2的值是________.4、(2019苏北三市期末)已知正四棱锥的底面边长为23,高为1,则该正四棱锥的侧面积为________.5、(2018苏州暑假测试)如图,正四棱锥PABCD 的底面一边AB 的长为2 3 cm ,侧面积为8 3 cm 2,则它的体积为________cm 3.6、(2018常州期末) 已知圆锥的高为6,体积为8.用平行于圆锥底面的平面截圆锥,得到的圆台体积是7,则该圆台的高为________.7、(2018镇江期末) 已知正四棱锥的底面边长为2,侧棱长为6,则该正四棱锥的体积为________. 8、(2018扬州期末) 若圆锥的侧面展开图是面积为3π且圆心角为2π3的扇形,则此圆锥的体积为________.9、(2018南京、盐城、连云港二模)在边长为4的正方形ABCD 内剪去四个全等的等腰三角形(如图1中阴影部分),折叠成底面边长为2的正四棱锥SEFGH(如图2),则正四棱锥SEFGH 的体积为________.(图1) (图2)10、(2018苏锡常镇调研(一))若正四棱锥的底面边长为 2 cm ,侧面积为8 cm 2,则它的体积为________cm 3.11、(2017苏锡常镇调研(一)) 已知正四棱锥的底面边长是2,侧棱长是3,则该正四棱锥的体积为________.题型三 球的表面积与体积1、(2019苏州期末)如图,某种螺帽是由一个半径为2的半球体挖去一个正三棱锥构成的几何体,该正三棱锥的底面三角形内接于半球底面大圆,顶点在半球面上,则被挖去的正三棱锥体积为________.2、(2019苏州三市、苏北四市二调)设P,A,B,C为球O表面上的四个点,PA,PB,PC两两垂直,且PA=2 m,PB=3 m,PC=4 m,则球O的表面积为________m2.3、(2018无锡期末)直三棱柱ABCA1B1C1中,已知AB⊥BC,AB=3,BC=4,AA1=5,若三棱柱的所有顶点都在同一球面上,则该球的表面积为________.4、(2018苏州期末)鲁班锁是中国传统的智力玩具,起源于中国古代建筑中首创的榫卯结构,它的外观是如图所示的十字立方体,其上下、左右、前后完全对称,六根等长的正四棱柱体分成三组,经90°榫卯起来.若正四棱柱的高为5,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积至少为________(容器壁的厚度忽略不计,结果保留π).。








9.5 柱、锥、球及其简单组合体一、选择题(本大题共10小题,共30.0分)1.下列几何体是旋转体的是()A. 五棱柱B. 六棱锥C. 八棱台D. 球2.长方体的一个顶点出发的三条边的长分别是3,4,5,且它的八个顶点都在同一个球面上,则这个球的表面积是()A. √22πB. 25√2πC. 50πD. 200π3.已知圆锥的母线长为6,母线与轴的夹角为30°,则此圆锥的表面积为()A. 9πB. 18πC. 27πD. 54π4.若一个圆锥的轴截面是面积为1的等腰直角三角形,则该圆锥的侧面积为()A. √2πB. πC. 2πD. 4π5.两个球的半径之比为1∶3,那么两个球的表面积之比为()A. 1∶9B. 1∶27C. 1∶3D. 1∶16.已知圆锥的底面直径与高都是4,则该圆锥的侧面积为()A. 4πB. 4√3πC. 4√5πD. 87.正三棱柱ABC−A1B1C1的边长为2,侧棱长为√3,D为BC中点,则三棱锥A−DB1C1体积为()A. 3B. 32C. 1 D. √328.已知圆锥的侧面展开图为半圆,半圆的面积为50π,则圆锥的全面面积是()A. 25πB. 50πC. 75πD. 100π9.若一个圆柱的轴截面是面积为16的正方形,则这个圆柱的侧面积为()A. 9πB. 16πC. 272π D. 128π10.圆锥的母线长是4,侧面积是4π,则该圆锥的高为()A. √15B. 4C. 3D. 2二、填空题(本大题共8小题,共24.0分)11.已知正四棱锥的底面边长为4cm,高为√5cm,则该四棱锥的侧面积____________12.若一圆锥的底面半径为3,体积是12π,则该圆锥的侧面积等于_________13.球的表面积为16πcm2,则球的半径为___________cm.14.已知底面是边长为1正方形,侧棱长为√2的直棱柱的各顶点均在同一个球面上,则该球的体积为______15.在棱长为2的正方体ABCD−A1B1C1D1中,点E是棱B1B的中点,则三棱锥D1−DEC1的体积为________.16.已知圆柱底面半径为1,母线长与底面的直径相等,则该圆柱的表面积为.17.若圆锥的侧面面积为2π,底面面积为π,则该圆锥的体积为.18.若将一个圆锥的侧面沿一条母线剪开,是半径为3,圆心角为23π的扇形,则该圆锥的体积为__________.三、解答题(本大题共6小题,共46.0分)19.如图,已知AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,,AB//CD,AD=AF=CD=2,AB=4.(1)求证:AC⊥平面BCE;(2)求三棱锥E−BCF的体积.20.如图,菱形ABCD和直角梯形CDEF所在平面互相垂直,AB=DE=4,CF=2,∠BAD=60º,DE//CF,CD⊥DE.(1)求证:BD⊥AF;(2)求四棱锥A−CDEF的体积.21.如图,四棱锥P−ABCD的底面ABCD是边长为2的正方形,PA⊥面ABCD,PA=√3,点M是棱PC的中点.(Ⅰ)证明:PA//面BMD;(Ⅱ)求三棱锥M−PAD的体积.π,求它的表面积.22.已知球的体积为500323.如图,在三棱柱ABC−A1B1C1中侧棱垂直于底面,且AC⊥BC,点D是AB的中点.(Ⅰ)求证:AC⊥BC1;(Ⅱ)若AC=BC=√2,AA1=2,求三棱锥A−B1CD的体积.24.如图所示,已知ABCD是直角梯形,∠ABC=90∘,AD//BC,AD=2,AB=BC=1,PA⊥平面ABCD.(1)证明:PC⊥CD;(2)若E是PA的中点,证明:BE//平面PCD;(3)若PA=3,求三棱锥B−PCD的体积.。
【课题】9.5 柱、锥、球及其简单组合体(一)
【教学目标】
知识目标:
了解棱柱、棱锥的结构特征及表面积、体积的计算.
能力目标:
(1)能看懂棱柱、棱锥的直观图;
(2)会计算棱柱、棱锥的表面积、体积;
(3)培养学生的空间想象能力计算技能和计算工具使用技能.
情感目标:
(1)参与数学实验,认知棱柱、棱锥的模型与直观图,培养数学直觉,感受科学思维.(2)关注生活中的数学模型,体会数学知识的应用.
(3)经历合作学习的过程,尝试探究与讨论,树立团队合作意识.
【教学重点】
正棱柱、正棱锥的结构特征及相关的计算.
【教学难点】
正棱柱、正棱锥的相关计算.
【教学设计】
教材首先介绍了多面体、旋转体的概念.然后通过观察模型,说明棱柱、棱锥、圆柱、圆锥、球的结构特征及其面积、体积的计算公式.正棱柱的侧面积、全面积、体积的计算公式经常使用,不要把侧面积、全面积计算公式记混了.
侧面都是全等的矩形的直四棱柱不一定是正四棱柱.底面是正方形的四棱柱不一定是正四棱柱.四棱锥P-ABCD中,如果棱锥的侧棱长相等,那么它一定是正四棱锥.如果棱锥的底面是正方形,那么它不一定是正四棱锥.
例1是求正三棱柱的侧面积和体积的题目,例2是求正三棱锥的侧面积和体积的题目,
要记住边长为a的正三角形的面积为2
S .
【教学备品】
教学课件.
【课时安排】
2课时.(90分钟)
【教学过程】
过程行为行为意图间*揭示课题
9.5 柱、锥、球及其简单组合体
【知识回顾】
在九年制义务教育阶段,我们学习过直棱柱、圆柱、圆锥、球等几何体.
(1)(2)(3)(4)
图9−55
象直棱柱(图9−55(1))那样,由若干个平面多边形围成的封闭的几何体叫做多面体,围成多面体的各个多边形叫做多面体的面,两个面的公共边叫做多面体的棱,棱与棱的交点叫做多面体的顶点,不在同一个面上的两个顶点的连线叫做多面体的对角线.
像圆柱(图9−55(2))、圆锥(图9−55(3))、球(图9−55(4))那样的封闭几何体叫做旋转体.
*创设情境兴趣导入
【观察】
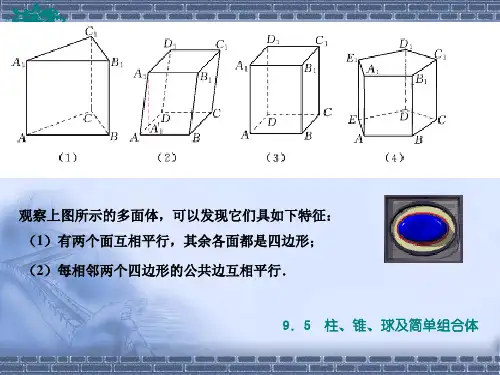
图9−56
观察图9−56所示的多面体,可以发现它们具如下特征:(1)有两个面互相平行,其余各面都是四边形;
(2)每相邻两个四边形的公共边互相平行.介绍
质疑
讲解
说明
引导
分析
了解
思考
思考
启发
学生
思考
引导
学生
分析
10
*动脑思考探索新知
【新知识】
有两个面互相平行,其余每相邻两个面的交线都互相平行
的多面体叫做棱柱,互相平行的两个面,叫做棱柱的底面,其
余各面叫做棱柱的侧面.相邻两个侧面的公共边叫做棱柱的侧
棱.两个底面间的距离,叫做棱柱的高.
图9−56所示的四个多面体都是棱柱.讲解思考
图9−57
观察正棱柱的表面展开图(图9−57),可以得到正棱柱的侧面积、全面积计算公式分别为
(
=
S ch
正棱柱侧
=+(
2
S ch S
过 程
行为 行为 意图 间
其中, 底S 表示正棱锥的底面的面积,h 是正棱锥的高. 25
*巩固知识 典型例题
【知识巩固】
例 1 已知一个正三棱柱的底面边长为4 cm ,高为5 cm ,
求这个正三棱柱的侧面积和体积.
解 正三棱锥的侧面积为
S 侧=ch =3×4×5 = 60(2
cm ). 由于边长为4 cm 的正三角形面积为
234434
⨯=(2cm ),
所以正三棱柱的体积为
435V S h ==⨯底=203(3
cm ). 【小提示】
边长为a 的正三角形的面积为2
34
S a =
.
说明
强调
引领 讲解 说明
讲解 说明 观察 思考 主动 求解 思考 理解 通过例题进一步领会 带领学生 思考
35 *创设情境 兴趣导入
观察图9−58所示的多面体,可以发现它们具如下特征:有一个面是多边形,其余各面都是三角形,并且这些三角形有一个公共顶点.
质疑 引导 分析
思考
启发 学生思考 40 *动脑思考 探索新知
【新知识】 具备上述特征的多面体叫做棱锥.多边形叫做棱锥的底面(简称底),有公共顶点的三角形面叫做棱锥的侧面,各侧面
(3)
图9−58
图9−59
观察正棱锥的表面展开图(图9−59),可以得到正棱锥的侧面积、全面积(表面积)计算公式分别为
h c '=2
1
正棱锥侧 (9.4) S h c +'=1
. (9.5)
过 程
行为 行为 意图 间
锥容器中装满沙子,然后倒入正三棱柱形状的容器中,发现:连续倒三次正好将正三棱柱容器装满.
分析
57 *动脑思考 探索新知
【新知识】
实验表明,对于同底等高的棱锥与棱柱,棱锥的体积是棱柱体积的三分之一.即
h S V 底正棱锥
3
1
=. (9.6) 其中, 底S 表示正棱锥的底面的面积,h 是正棱锥的高. 讲解 说明
理解 记忆
带领 学生 分析
62 *巩固知识 典型例题
【知识巩固】
例 2 如图9−62,正三棱锥P-ABC 中,点O 是底面中心,PO =12 cm ,斜高PD =13 cm .求它的侧面积、体积(面积精确到0.12cm ,体积精确到13cm ).
图9−60
解 在正三棱锥P-ABC (图9−60)中,高PO =12 cm ,斜高PD =13 cm .
在直角三角形POD 中, OD =22PD PO -=221312- =5(cm ). 在底面正三角形ABC 中,
CD =3OD =15(cm ).
所以底面边长为
AC =10
3 cm .
所以侧面积与体积分别约为
11
310313 22
S ch '==⨯⨯⨯侧≈337.7(2cm ).
2111
(103)sin6012332V S h ==⨯⨯⨯⨯o 正棱锥底≈520(3cm ).
说明 强调
引领 讲解 说明
观察 思考 主动 求解
通过例题进一步领会
72 *运用知识 强化练习
及时
【教师教学后记】。