(完整版)八年级勾股定理典型练习题含答案

13.11勾股定理的应用练习（1）

第1题. 如图，△ABC中，∠ACB=90º，CD为AB边上的高，若∠A=30º，AB=16，则BC=______，BD=______，CD=______．

答案：8，4，43．

第2题. 如图是一种“牛头形”图案，其作法是：从正方形1开始，以它的一边为斜边，向外作等腰直角三角形，然后再以其直角边为边，分别向外作正方形2，以此类推，若正方形1的边长为64cm，则正方形7的边长为_________cm．

答案：8．

第3题. 甲、乙两人从同一地点出发，甲往东走了4km，乙往南走了3km，这时，甲、乙两人相距______．

答案：5km

第4题. 如果梯子底端离建筑物9m，那么15m长的梯子可达到建筑物的高度是______．

答案：12m

第5题. 如图，一扇宽为4米，高为3米的栅栏门，需要一根长______米的木条像图中那样固定．

答案：5

第6题. 一块土地的形状如图所示，90,20,15,7,BDABBCCD米米米求这块土地的面积?

答案：234平方米

第7题. 某菜农修建一个塑料大棚（如图），若棚宽a=4m，高b=3m，长d=35m，求覆盖在顶上的塑料薄膜的面积． A B C

D

4 4 3 3 2 2

1

3米

4米

A

B C D

a b c d 答案：175m2

第8题. 一游泳池长48cm，小方和小朱进行游泳比赛，从同一处出发，小方平均速度为3m/秒，小朱为3.1m/秒．但小朱一心想快，不看方向沿斜线游，而小方直游，俩人到达终点的位置相距14m．按各人的平均速度计算，谁先到达终点，为什么？

答案：小朱用16.13秒,小方用16秒,小方先到达终点

第9题. 如图，正方形ACDE的面积为25cm，测量出AB=12cm，BC=13cm，问E、A、B三点在一条直线上吗？为什么？

答案：在一条直线上，理由略

第10题. 从A到B有两种路线，一种走直线由A到B，另一种走折线，先从A直线到C，再由C直线到B，其中ACB成直角，已知A到C为600m，C到B为800m，问从A到B走直线比走折线少走多少米？

一、选择题

1．已知：△ABC中，BD、CE分别是AC、AB边上的高，BQ＝AC，点F在CE的延长线上，CF＝AB，下列结论错误的是（ ）．

A．AF⊥AQ B．AF=AQ C．AF=AD D．FBAQ

2．△ABC的三边分别为,,abc，下列条件能推出△ABC是直角三角形的有（ ）

①222acb;②2()()0ababc;③ ∠A＝∠B∠C; ④∠A∶∠B∶∠C＝1∶2∶3 ;⑤111,,345abc;⑥10,a 24,b 26c

A．2个 B．3个 C．4个 D．5个

3．如图，ABC中，有一点P在AC上移动．若56ABACBC，，则APBPCP的最小值为( )

A．8 B．8.8 C．9.8 D．10

4．如图，在ABC中，90A，6AB，8AC，ABC与ACB的平分线交于点O，过点O作ODAB于点D，若则AD的长为( )

A．2 B．2 C．3 D．4

5．棱长分别为86cmcm，的两个正方体如图放置，点A，B，E在同一直线上，顶点G在棱BC上，点P是棱11E F的中点.一只蚂蚁要沿着正方体的表面从点A爬到点P，它爬行的最短距离是( )

A．(3510)cm

B．513cm C．277cm D．(2583)cm

6．以线段a、b、c 的长为边长能构成直角三角形的是（ ）

A．a=3，b=4，c=6 B．a=1，b=2，c=3

C．a=5，b=6，c=8 D．a=3，b=2，c=5

7．如图，已知数轴上点P表示的数为1，点A表示的数为1，过点A作直线l垂直于PA，在l上取点B，使1AB，以点P为圆心，以PB为半径作弧，弧与数轴的交点C所表示的数为（ ）

A．5 B．51 C．51 D．51

8．如图，“赵爽弦图”是由四个全等的直角三角形和一个小正方形构成的大正方形，若直角三角形的两直角边长分别为5和3，则小正方形的面积为（ ）

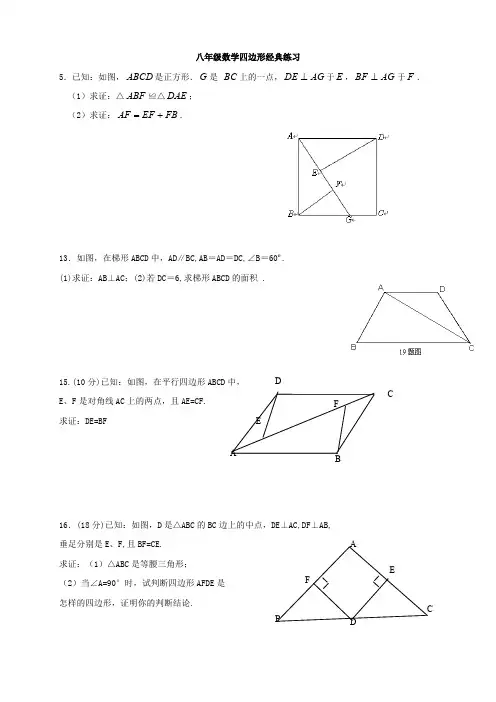
ng are good f 八年级数学四边形经典练习

5．已知：如图，是正方形．是 上的一点，于，于． ABCDGBCAGDEEAGBFF

（1）求证：△≌△； ABFDAE

（2）求证：．FBEFAF

13．如图，在梯形ABCD中，AD∥BC,AB＝AD＝DC,∠B＝60º.

(1)求证：AB⊥AC；(2)若DC＝6,求梯形ABCD的面积 .

15.(10分)已知：如图，在平行四边形ABCD中，

E、F是对角线AC上的两点，且AE=CF.

求证：DE=BF E

16．(18分)已知：如图，D是△ABC的BC边上的中点，DE⊥AC,DF⊥AB,

垂足分别是E、F,且BF=CE.

求证：（1）△ABC是等腰三角形；

（2）当∠A=90°时，试判断四边形AFDE是

怎样的四边形，证明你的判断结论.D

BAFC

DE

CA

BF ime and All things in their being are go

od for so18.（10分）如图，在菱形ABCD中，E为AD中点，

EF⊥AC交CB的延长线于F.

求证：AB与EF互相平分

18、（本题10分）如图，BD平分∠ABC，DE∥BC，EF∥AC，试判断BE与CF是否相等？并说

明理由。

D

CFE

BA

H

G hings in their being are goo 19．（本题14分）如图，正方形ABCD中对角线AC、BD相交于O，E为AC上一点，

AG⊥EB交EB于G，AG交BD于F。 （1）说明OE=OF的道理；

（2）在（1）中，若E为AC延长线上，AG⊥EB交EB的延长线于G，AG、BD的延长线交

于F，其他条件不

变，如图2，则结论：“OE=OF”还成立吗？请说明理由。

2. Rt△ABC中，∠C=90°。CD是AB边上的中线，过A作CD的平行线，过C作AB的平行线，两线交于E。

求证：四边形ADCE是菱形 ime and All things in their being are good for som

依提木孔乡中学 买买提依力·吾司曼

《勾股定理》练习题

一、选择题（12×3′=36′）

1．已知一个Rt△的两边长分别为3和4，则第三边长的平方是（ ）

A、25 B、14 C、7 D、7或25

2．下列各组数中，以a，b，c为边的三角形不是Rt△的是（ ）

A、a=1.5，b=2,c=3 B、a=7,b=24,c=25

C、a=6,b=8,c=10 D、a=3,b=4,c=5

3．若线段a，b，c组成Rt△，则它们的比为（ ）

A、2∶3∶4 B、3∶4∶6 C、5∶12∶13 D、4∶6∶7

4．Rt△一直角边的长为11，另两边为自然数，则Rt△的周长为（ ）

A、121 B、120 C、132 D、不能确定

5．如果Rt△两直角边的比为5∶12，则斜边上的高与斜边的比为（ ）

A、60∶13 B、5∶12 C、12∶13 D、60∶169

6．如果Rt△的两直角边长分别为n2－1，2n（n>1），那么它的斜边长是（ ）

A、2n B、n+1 C、n2－1 D、n2+1

7．已知Rt△ABC中，∠C=90°，若a+b=14cm，c=10cm，则Rt△ABC的面积是（ ）

A、24cm2 B、36cm2 C、48cm2 D、60cm2

8．等腰三角形底边上的高为8，周长为32，则三角形的面积为（ ）

A、56 B、48 C、40 D、32

9．三角形的三边长为（a+b）2=c2+2ab,则这个三角形是( )

A. 等边三角形; B. 钝角三角形; C. 直角三角形; D. 锐角三角形.

10．某市在旧城改造中，计划在市内一块如图所示的三角形空地上种植草皮以美化环境，已知这种草皮每平方米售价a元，则购买这种草皮至少需要（ ）

八年级下《勾股定理》单元检测题含答案

《勾股定理》单元检测题

一、选择题（每小题只有一个正确答案）

1．设直角三角形的两条直角边分别为a和b，斜边长为c，已知1213bc，，则a=( )

A. 1 B. 5 C. 10 D. 25

2．在下列四组数中，不是勾股数的一组数是（ ）

A. 15817abc，， B. 91215abc，，

C. 72425abc，， D. 357abc，，

3．一个三角形的三边长为15，20，25，则此三角形最大边上的高为（ ）

A. 10 B. 12 C. 24 D. 48

4．如图，有一个由传感器控制的灯A装在门上方离地高4.5 m的墙上，任何东西只要移至距该灯5 m及5 m以内时，灯就会自动发光，请问一个身高1.5 m的学生要走到离墙多远的地方灯刚好发光？（ ）

A. 4 m B. 3 m C. 5 m D. 7 m

5．下列选项中，不能用来证明勾股定理的是( )

A. B. C. D.

6．若直角三角形的三边长分别为ab、a、ab，且a、b都是正整数，则三角形其中一边的长可能为（ ）

A. 22 B. 32 C. 62 D. 82

7．如图，△ABC中，AC=3，BC= 5，AD⊥BC交BC于点D，AD=125，延长BC至E使得CE=BC，将△ABC沿AC翻折得到△AFC，连接EF，则线段EF的长为（ ）

A. 6

B. 8

C. 325 D. 323

8．如图,点P是平面坐标系中一点,则点P到原点的距离是（ ）

A. 3 B. 2 C. 7 D. 5

9．如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm2 ， 则该半圆的半径为（ ）

A. (4+5)cm

2019-2020 年八年级下册勾股定理同步练习题附答案

1．已知直角三角形中 30°角所对的直角边长是 2 3 cm，则另一条直角边的长是（ ）

A. 4cm B. 4 3 cm C. 6cm D. 6 3 cm

2．△ ABC中， AB＝ 15，AC＝ 13，高 AD＝ 12，则△ ABC的周长为（ ）

A． 42 B． 32 C．42 或 32 D． 37 或 33

3．一架 25 分米长的梯子，斜立在一竖直的墙上，这时梯足距离墙底端 7 分米 . 如果梯子的

顶端沿墙下滑 4 分米，那么梯足将滑动 ( )

A. 9 分米 B. 15 分米 C. 5 分米 D. 8 分米

4． 如图，学校有一块长方形花铺， 有极少数人为了避开拐角走 “捷

径”，在花铺内走出了一条 “路 ”．他们仅仅少走了 步路

（假设 2 步为 1 米），却踩伤了花草．

3m “路”

5. 在△ ABC 中，∠ C＝ 90 °，（ 1 ）已知 a＝ 2.4， b＝ 3.2，则 c

＝ ；（ 2）已知 c＝ 17，b＝ 15，则△ ABC面积等于 ； 4m

（ 3）已知∠ A＝ 45°， c＝18，则 a＝ . 第 4 题图

6. 一个矩形的抽斗长为 24cm，宽为 7cm, 在里面放一根铁条， 那么铁条最长可以是 ． 7. 在 Rt △ABC中，∠ C＝ 90°， BC＝ 12cm， S 2

ABC＝ 30cm ，则 AB＝.

△

8. 等腰△ ABC 的腰长 AB＝ 10cm，底 BC为 16cm，则底边上的高为 ，面积为.

9. 一个直角三角形的三边为三个连续偶数，则它的三边长分别为 ．

10．一天， 小明买了一张底面是边长为 260cm 的正方形， 厚 30cm 的床垫回家． 到了家门口，

典型例题

知识点一、直接应用勾股定理或勾股定理逆定理

例1：如图，在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段，其中能构成一个直角三角形三边的线段是（ ）

A. CD、EF、GH B. AB、EF、GH

C. AB、CD、GH D. AB、CD、EF

勾股定理说到底是一个等式，而含有未知数的等式就是方程。所以，在利用勾股定理求线段的长时常通过解方程来解决。勾股定理表达式中有三个量，如果条件中只有一个已知量，必须设法求出另一个量或求出另外两个量之间的关系，这一点是利用勾股定理求线段长时需要明确的思路。

方程的思想：通过列方程（组）解决问题，如：运用勾股定理及其逆定理求线段的长度或解决实际问题时，经常利用勾股定理中的等量关系列出方程来解决问题等。

例3：一场罕见的大风过后，学校那棵老杨树折断在地，此刻，张老师正和占明、清华、绣亚、冠华在楼上凭栏远眺。

清华开口说道：“老师，那棵树看起来挺高的。”

“是啊，有10米高呢，现在被风拦腰刮断，可惜呀！”

“但站立的一段似乎也不矮，有四五米高吧。”冠华兴致勃勃地说。

张老师心有所动，他说：“刚才我跑过时用脚步量了一下，发现树尖距离树根恰好3米，你们能求出杨树站立的那一段的高度吗？”

占明想了想说：“树根、树尖、折断处三点依次相连后构成一个直角三角形。” “勾股定理一定是要用的，而且不动笔墨恐怕是不行的。”绣亚补充说。

几位男孩子走进教室，画图、计算，不一会就得出了答案。同学们，你算出来了吗？

思路分析：

1）题意分析： 本题考查勾股定理的应用

2）解题思路：本题关键是认真审题抓住问题的本质进行分析才能得出正确的解答

常通过作辅助线构造直角三角形将它们转化为直角三角形问题等。

解题后的思考：

分类讨论思想是解题时常用的一种思想方法，同学们如果掌握了这种方法，可以使思维的条理性、缜密性、灵活性得到培养，才能在解题中真正做到不重不漏。

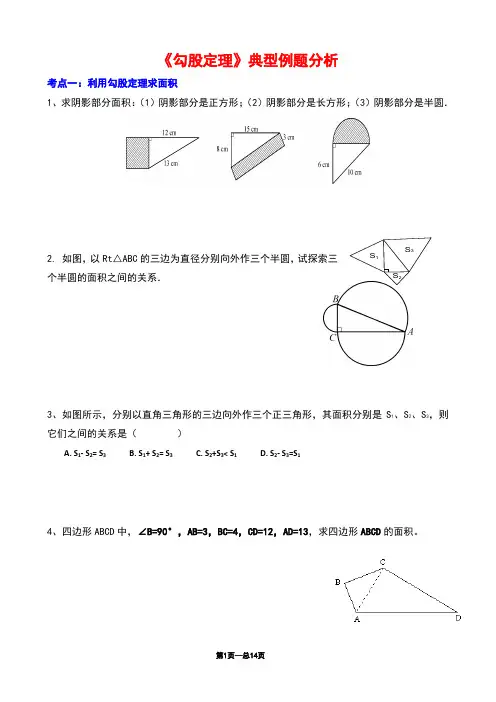
第1页—总14页 《勾股定理》典型例题分析

考点一：利用勾股定理求面积

1、求阴影部分面积：（1）阴影部分是正方形；（2）阴影部分是长方形；（3）阴影部分是半圆．

2. 如图，以Rt△ABC的三边为直径分别向外作三个半圆，试探索三个半圆的面积之间的关系．

3、如图所示，分别以直角三角形的三边向外作三个正三角形，其面积分别是S1、S2、S3，则它们之间的关系是（ ）

A. S1- S2= S3 B. S1+ S2= S3 C. S2+S3< S1 D. S2- S3=S1

4、四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD的面积。

S3S2S1

第2页—总14页 考点二：在直角三角形中，已知两边求第三边

1．在直角三角形中,若两直角边的长分别为1cm，2cm ，则斜边长为 ．

2．已知直角三角形的两边长为3、2，则另一条边长的平方是

3、已知直角三角形两直角边长分别为5和12， 求斜边上的高．

4、把直角三角形的两条直角边同时扩大到原来的2倍，则斜边扩大到原来的（ ）

A． 2倍 B． 4倍 C． 6倍 D． 8倍

5、在Rt△ABC中，∠C=90°

①若a=5，b=12，则c=___________；

②若a=15，c=25，则b=___________；

③若c=61，b=60，则a=__________；

④若a∶b=3∶4，c=10则Rt△ABC的面积是=________。

6、如果直角三角形的两直角边长分别为1n2，2n（n>1），那么它的斜边长是（ ）

A、2n B、n+1 C、n2－1 D、1n2

7、在Rt△ABC中，a,b,c为三边长，则下列关系中正确的是（ ）

2018-2019学年八年级数学上册第一章检测卷

时间：120分钟 满分：120分

一、选择题(本大题共6小题，每小题3分，共18分，每小题只有一个正确的选项)

1．下列各组数，能构成直角三角形的是( )

A．4，5，6 B．12，16，20

C．5，10，13 D．8，39，40

2．如图，在Rt△ABC中，∠A＝90°，BC＝2.5cm，AC＝1.5cm，则AB的长为( )

A．3.5cm B．2cm C．3cm D．4cm

3．如图，有一块边长为24米的正方形绿地，在绿地旁边B处有健身器材，由于居住在A处的居民践踏了绿地，小明想在A处树立一个标牌“少走▇米，踏之何忍”，请你计算后帮小明在标牌的“▇”填上适当的数字是( )

A．3米 B．4米 C．5米 D．6米

4．在△ABC中，AB＝12，BC＝16，AC＝20，则△ABC的面积为( )

A．96 B．120 C．160 D．200

5．如图，等腰三角形底边BC的长为10cm，腰长AB为13cm，则腰上的高为( )

A．12cm B.6013cm C.12013cm D.135cm

6．如图所示为一种“羊头”形图案，其作法是：从正方形①开始，以它的一边为斜边，向外作等腰直角三角形，然后再以其直角边为边，分别向外作正方形②和②，„„，依此类推，若正方形①的面积为64，则正方形⑤的面积为( )

A．2 B．4 C．8 D．16

二、填空题(本大题共6小题，每小题3分，共18分)

7．在Rt△ABC中，∠C＝90°，BC＝9，AC＝12，则AB＝________． 8．如图，一架长为4m的梯子，一端放在离墙脚2.4m处，另一端靠墙，则梯子顶端离墙脚________m.

9．如图，在△ABC中，AB＝5cm，BC＝6cm，BC边上的中线AD＝4cm，则∠ADB的度数是________．

10．如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，以点A为圆心，AC长为半径画弧，交AB于点D，则BD＝__________．

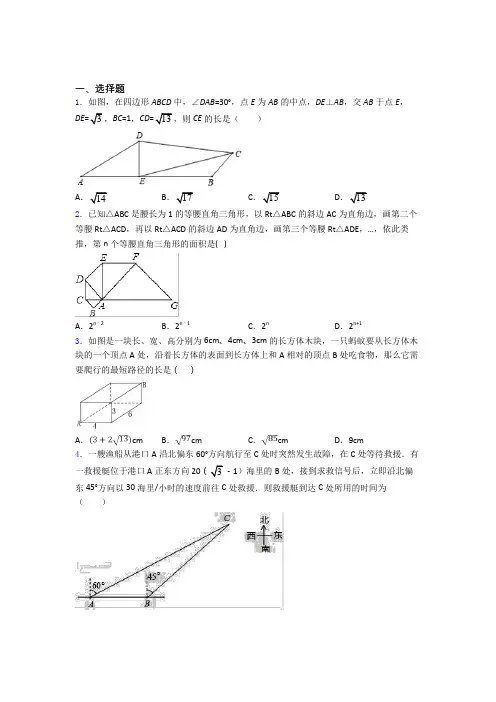
一、选择题

1．如图，在四边形ABCD中，∠DAB=30°，点E为AB的中点，DE⊥AB，交AB于点E，DE=3，BC=1，CD=13，则CE的长是（ ）

A．14 B．17 C．15 D．13

2．已知△ABC是腰长为1的等腰直角三角形，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推，第n个等腰直角三角形的面积是( )

A．2n﹣2 B．2n﹣1 C．2n D．2n+1

3．如图是一块长、宽、高分别为6cm、4cm、3cm的长方体木块，一只蚂蚁要从长方体木块的一个顶点A处，沿着长方体的表面到长方体上和A相对的顶点B处吃食物，那么它需要爬行的最短路径的长是（ ）

A．cm B．cm C．cm D．9cm

4．一艘渔船从港口A沿北偏东60°方向航行至C处时突然发生故障，在C处等待救援．有一救援艇位于港口A正东方向20（3﹣1）海里的B处，接到求救信号后，立即沿北偏东45°方向以30海里/小时的速度前往C处救援．则救援艇到达C处所用的时间为（ ）

A．33小时 B．23小时

C．223 小时 D．2323小时

5．在Rt△ABC中，∠C=90°，∠A=30°，BD是∠ABC的平分线，交AC于点D，若CD=1，则AB的长是（

）

A．2 B． 23 C． 43 D．4

6．A、B、C分别表示三个村庄，AB1700米，800BC米，AC1500米，某社区拟建一个文化活动中心，要求这三个村庄到活动中心的距离相等，则活动中心P的位置应在（ ）

A．AB的中点 B．BC的中点

C．AC的中点 D．C的平分线与AB的交点

7．如图，是我国古代著名的“赵爽弦图”的示意图，此图是由四个全等的直角三角形拼接而成，其中AE=10，BE=24，则EF的长是（ ）

A．14 B．13 C．143 D．142

八年级数学勾股定理典型题专项练习

一、选择题

1、下列各数组中，不能作为直角三角形三边长的是 ( )

A. 9,12,15 B.5,12,13 C. 6,8,10 D. 3,5,7

2、将直角三角形的各边都缩小或扩大同样的倍数后，得到的三角形 ( )

A.可能是锐角三角形 B.不可能是直角三角形

C.仍然是直角三角形 D.可能是钝角三角形

3、在测量旗杆的方案中，若旗杆高为21m，目测点到杆的距离为15m，则目测点到杆顶的距离为（设目高为1m） ( )

A.20m B.25m C.30m D.35m

4、一等腰三角形底边长为10cm，腰长为13cm，则腰上的高为 ( )

A. 12cm B. C. D.

5、已知直角三角形一个锐角60°，斜边长为1，那么此直角三角形的周长是（ ）

A.52 B.3 C.3+2 D.332

二、填空题

6、如图,64、400分别为所在正方形的面积，则图中字母A所代表的正方形面积是 _______ .

7、如图，一根树在离地面9米处断裂，树的顶部落在离底部12米处.树折断之前有______米.

8、已知甲往东走了4km，乙往南走了3km，这时甲、乙两人相距 .

9、一个长方形的长为12cm，对角线长为13cm，则该长方形的周长为 . 10、以直角三角形的三边为边向形外作正方形P、Q、K，若SP＝4，SQ＝9，则Sk＝ .

一、选择题

1．如图：在△ABC中，∠B=45°，D是AB边上一点，连接CD，过A作AF⊥CD交CD于G，交BC于点F．已知AC=CD，CG=3，DG=1，则下列结论正确的是（ ）

①∠ACD=2∠FAB ②27ACDS ③272CF ④ AC=AF

A．①②③ B．①②③④ C．②③④ D．①③④

2．△ABC的三边分别为,,abc，下列条件能推出△ABC是直角三角形的有（ ）

①222acb;②2()()0ababc;③ ∠A＝∠B∠C; ④∠A∶∠B∶∠C＝1∶2∶3 ;⑤111,,345abc;⑥10,a 24,b 26c

A．2个 B．3个 C．4个 D．5个

3．如图，已知1号、4号两个正方形的面积之和为7，2号、3号两个正方形的面积之和为4，则a、b、c三个正方形的面积之和为（ ）

A．11 B．15 C．10 D．22

4．如图，在△ABC中，∠ABC＝45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，H是BC边的中点，连结DH、BE与相交于点G，以下结论中正确的结论有（ ）

（1）△ABC是等腰三角形；（2）BF＝AC；（3）BH：BD：BC＝1：2：3；（4）GE2+CE2＝BG2．

A．1个 B．2个 C．3个 D．4个

5．如图是一块长、宽、高分别为6cm、4cm、3cm的长方体木块，一只蚂蚁要从长方体木块的一个顶点A处，沿着长方体的表面到长方体上和A相对的顶点B处吃食物，那么它需要爬行的最短路径的长是（ ）

A．cm B．cm C．cm D．9cm

6．若△ABC中，AB=AC=25，BC=4，则△ABC的面积为（ ）

A．4 B．8 C．16 D．52

7．已知,,abc是ABC的三边，且满足222()()0ababc，则ABC是（ ）

A．直角三角形 B．等边三角形

1 第十七章勾股定理

时间：120分钟 满分：120分

一、选择题(每小题3分，共30分)

1．如图，Rt△ABC中，∠ACB＝90°，若AB＝15cm，则正方形ADEC和正方形BCFG的面积之和为( C )

A．150cm2 B．200cm2

C．225cm2 D．无法计算

第1题图 第2题图 第3题图

2．如图，有一块直角三角形纸片，两直角边AB＝6，BC＝8，将△ABC折叠，使AB落在斜边AC上，折痕为AD，则BD的长为( A )

A．3 B．4 C．5 D．6

3．如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案．已知大正方形面积为49，小正方形面积为4，若用x，y表示直角三角形的两直角边(x>y)，下列四个说法：①x2＋y2＝49；②x－y＝2；③2xy＋4＝49；④x＋y＝9.其中说法正确的是( B )

A．①② B．①②③

C．①②④ D．①②③④

4．在平面直角坐标系中，点P(3，4)到原点的距离是( C )

A．3 B．4

C．5 D．±5

5．在△ABC中，AB＝1，AC＝2，BC＝5，则该三角形为( B )

A．锐角三角形 B．直角三角形

C．钝角三角形 D．等腰直角三角形

6．把一个边长为1的正方形如图所示放在数轴上，以正方形的对角线为半径画弧交数轴于点A，则点A对应的数是( B )

A．1 B.2 C.3 D．2

2

第6题图 第7题图

7．如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为30海里的A处，轮船沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则此时轮船所在位置B处与灯塔P之间的距离为( D )

A．60海里 B．45海里

依提木孔乡中学 买买提依力·吾司曼

《勾股定理》练习题

一、选择题（12×3′=36′）

1．已知一个Rt△的两边长分别为3和4，则第三边长的平方是（ ）

A、25 B、14 C、7 D、7或25

2．下列各组数中，以a，b，c为边的三角形不是Rt△的是（ ）

A、a=1.5，b=2,c=3 B、a=7,b=24,c=25

C、a=6,b=8,c=10 D、a=3,b=4,c=5

3．若线段a，b，c组成Rt△，则它们的比为（ ）

A、2∶3∶4 B、3∶4∶6 C、5∶12∶13 D、4∶6∶7

4．Rt△一直角边的长为11，另两边为自然数，则Rt△的周长为（ ）

A、121 B、120 C、132 D、不能确定

5．如果Rt△两直角边的比为5∶12，则斜边上的高与斜边的比为（ ）

A、60∶13 B、5∶12 C、12∶13 D、60∶169

6．如果Rt△的两直角边长分别为n2－1，2n（n>1），那么它的斜边长是（ ）

A、2n B、n+1 C、n2－1 D、n2+1

7．已知Rt△ABC中，∠C=90°，若a+b=14cm，c=10cm，则Rt△ABC的面积是（ ）

A、24cm2 B、36cm2 C、48cm2 D、60cm2

8．等腰三角形底边上的高为8，周长为32，则三角形的面积为（ ）

A、56 B、48 C、40 D、32

9．三角形的三边长为（a+b）2=c2+2ab,则这个三角形是( )

A. 等边三角形; B. 钝角三角形; C. 直角三角形; D. 锐角三角形.

10．某市在旧城改造中，计划在市内一块如图所示的三角形空地上种植草皮以美化环境，已知这种草皮每平方米售价a元，则购买这种草皮至少需要（ ）

新北师大版八年级上学期第一章勾股定理典型练习题

一．选择题（共15小题）

1．如图，在6个边长为1的小正方形及其部分对角线构成的图形中，如图从A点到B点只能沿图中的线段走，那么从A点到B点的最短距离的走法共有（ ）

A．1种 B．2种 C．3种 D．4种

2．如图，有两颗树，一颗高10米，另一颗高4米，两树相距8米．一只鸟从一颗树的树梢飞到另一颗树的树梢，问小鸟至少飞行（ ）A．8米 B．10米 C．12米 D．14米

3．如图，已知直线a∥b，且a与b之间的距离为4，点A到直线a的距离为2，点B到直线b的距离为3，AB=230．试在直线a上找一点M，在直线b上找一点N，满足MN⊥a且AM+MN+NB的长度和最短，则此时AM+NB=（ ）

A．6 B．8 C．10 D．12

4．已知：如图，无盖无底的正方体纸盒ABCD-EFGH，P，Q分别为棱FB，GC上的点，且FP=2PB，GQ=21QC，若将这个正方体纸盒沿折线AP-PQ-QH裁剪并展开，得到的平面图形是（ ）

A．一个六边形 B．一个平行四边形 C．两个直角三角形 D．一个直角三角形和一个直角梯形

5．园丁住宅小区有一块草坪如图所示．已知AB=3米，BC=4米，CD=12米，DA=13米，且AB⊥BC，这块草坪的面积是（ ）

A．24米2 B．36米2 C．48米2 D ．72米2

6．如图，沿AC方向开山修路，为加快施工进度，要在小山的另一边同时施工，从AC上的一点B取∠ABD=120°，BD=210m，∠D=30°，要正好能使A、C、E成一直线，那么E、D两点的距离等于（ ）

A．1053m B．2103 m C．703 m D．105m

1 勾股定理典型例题归类总结

题型一：直接考查勾股定理

例１.在ABC中，90C．

⑴已知6AC，8BC．求AB的长 ⑵已知17AB，15AC，求BC的长

跟踪练习：

1.在ABC中，90C.

（1）若a=5,b=12,则c= ;

（2）若a:b=3:4,c=15,则a= ,b= .

（3）若∠A=30°，BC=2,则AB= ，AC= .

2. 在Rt△ABC中，∠C=90°，∠A，∠B，∠C分别对的边为a，b，c，则下列结论正确的是( )

A、 B、 C、 D、

3.一个直角三角形的三边为三个连续偶数，则它的三边长分别为( )

A、2、4、6 B、4、6、8 C、6、8、10 D、3、4、5

4.等腰直角三角形的直角边为2，则斜边的长为（ ）

A、 B、 C、1 D、2

5.已知等边三角形的边长为2cm，则等边三角形的面积为（ ）

A、 B、 C、1 D、

6.已知直角三角形的两边为2和3，则第三边的长为___________.

7.如图，∠ACB=∠ABD=90°，AC=2，BC=1，，则BD=___________.

8.已知△ABC中，AB=AC=10，BD是AC边上的高线，CD=2，那么BD等于（ ）

A、4 B、6 C、8 D、

9.已知Rt△ABC的周长为，其中斜边，求这个三角形的面积。

10. 如果把勾股定理的边的平方理解为正方形的面积，那么从面积的角度来说，勾股定理可以推广.

(1)如图，以Rt△ABC的三边长为边作三个等边三角形，则这三个等边三角形的面积1S、2S、3S之间有何关系？并说明理由。

（2）如图，以Rt△ABC的三边长为直径作三个半圆，则这三个半圆的面积1S、2S、3S之间有何关系？

（3）如果将上图中的斜边上的半圆沿斜边翻折180°，请探讨两个阴影部分的面积之和与直角三角形的面积之间的关系，并说明理由。（此阴影部分在数学史上称为“希波克拉底月牙”） 2