苏科版-数学-九年级上册-加权平均数的实际应用举例
- 格式:doc
- 大小:34.50 KB
- 文档页数:2





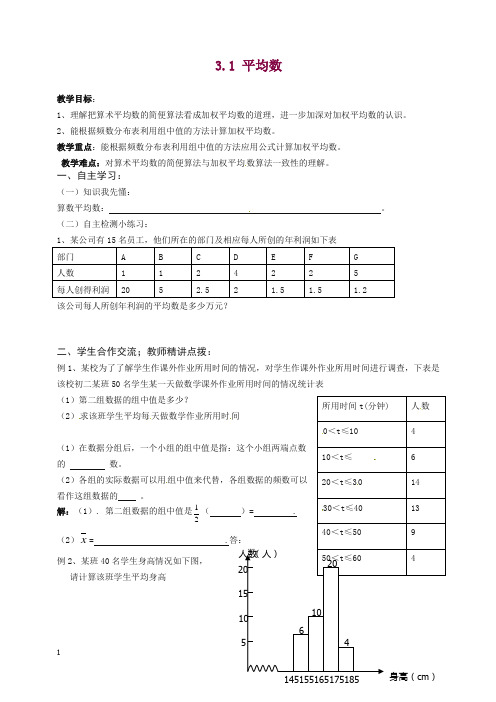
3.1 平均数教学目标:1、理解把算术平均数的简便算法看成加权平均数的道理,进一步加深对加权平均数的认识。
2、能根据频数分布表利用组中值的方法计算加权平均数。
教学重点:能根据频数分布表利用组中值的方法应用公式计算加权平均数。
教学难点:对算术平均数的简便算法与加权平均数算法一致性的理解。
一、自主学习:(一)知识我先懂:算数平均数:。
(二)自主检测小练习:该公司每人所创年利润的平均数是多少万元?二、学生合作交流;教师精讲点拨:例1、某校为了了解学生作课外作业所用时间的情况,对学生作课外作业所用时间进行调查,下表是该校初二某班50名学生某一天做数学课外作业所用时间的情况统计表(1)第二组数据的组中值是多少?(2)求该班学生平均每天做数学作业所用时间(1的数。
(2)各组的实际数据可以用组中值来代替,各组数据的频数可以看作这组数据的。
解:(1). 第二组数据的组中值是21()(2)x= .答:例2、某班40名学生身高情况如下图,请计算该班学生平均身高数0<t≤1030<t≤4012三、练习巩固1. 教材练习第1,2题。
2.八年级一班有学生50人,八年级二班有学生45人。
期末数学测试中,一班学生的平均分为81.5分,二班学生的平均分是83.4分,这两个班的平均分是多少?四、课堂小结:算术平均数:一般的:在求n 个数的算术平均数时,如果1x 出现1f 次,2x 出现2f 次,…k x 出现k f 次(这里1f +2f +…k x =n )那么着n 个数的算术平均数是x = 。
x 也叫这k 个数的加权平均数。
其中1f , 2f …k f 。
分别叫 的权。
五、课堂检测:1、下表是截至到2002年费尔兹奖得主获奖时的年龄,根据表格中的信息计算获费尔兹奖 得主获奖时的平均年龄?六、教学反思:教学目标6 38≤X <40。
加权平均数的实际应用举例在实际问题中,人们往往根据问题的重要程度的不同,选用不同权重计算平均数,请看两例.例 1 一次演讲比赛,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再演讲内容:演讲能力:演讲效果=5:4:1的比例计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:请决出两人的名次.分析:这个问题可以看成是求两名选手三项成绩的加权平均数,演讲内容:演讲能力:演讲效果=5:4:1,说明演讲内容、演讲能力、演讲效果三项成绩在总成绩中的重要程度,5、4、1分别是三项成绩的权.解:选手A 的最后得分是:90145195495585=++⨯+⨯+⨯. 选手B 最后得分是:91145195485595=++⨯+⨯+⨯ 由上可知选手B 获得第一名,选手A 获得第二名.评注:本题是一道与加权平均数的计算有关的实际问题,解决问题的关键在于正确理解加权平均数的计算方法.例 2 一家外贸公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩如下:(1)如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,应该录用谁?(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按2:2:3:3的比确定,应该录用谁?分析:(1)这家公司按照3:3:2:2的比确定听、说、读、写的成绩,说明各项成绩的“重要程度”有所不同,听、说的成绩比读、写的成绩更加“重要”,计算两明候选人的平均成绩,实际上是请听、说、读、写四项成绩的加权平均数,3,3,2,2,分别是它们的权.(2)由于录取时侧重考虑笔译能力,所以在四项成绩的权的分配上与(1)有所不同,读、写的权大一些.解:(1)听、说、读、写的成绩按照3:3:2:2的比确定,则甲的平均成绩为3.792233282285380373=+++⨯+⨯+⨯+⨯, 乙的平均成绩为812233275278383385=+++⨯+⨯+⨯+⨯. 显然,乙的成绩比甲的成绩高,所以从成绩看,应该录取乙.(2)听、说、读、写的成绩按照2:2:3:3的比确定,则甲的平均成绩为 7.803322382385280273=+++⨯+⨯+⨯+⨯; 乙的平均成绩为3.793322375378280285=+++⨯+⨯+⨯+⨯. 显然甲的成绩比乙的成绩高,所以从成绩看,应该录用甲.评注:从以上计算可以看出,侧重不同的权重,计算的加权平均数的值不同,数据的权能够反映出数据的相对“重要程度”.。
初中-数学-打印版
如何计算一组数据的加权平均数?
如何计算一组数据的加权平均数?
难易度:★★★★
关键词:加权平均数
答案:
加权平均数是不同比重数据的平均数,加权平均数就是把原始数据按照合理的比例来计算.
【举一反三】
典例:某商场用加权平均数来确定什锦糖的单价,由单价为15元/千克的甲种糖果10千克,单价为12元/千克的乙种糖果20千克,单价为10元/千克的丙种糖果30千克混合成的什锦糖果的单价应定为( )
A.11元/千克
B.11.5元/千克
C.12元/千克
D.12.5元/千克
思路引导:一般来讲,解决此类要清楚加权平均数的计算方法,本题首先计算出甲种糖果、乙种糖果、丙种糖果的总钱数,然后再除以总的千克数.
标准答案:B.
初中-数学-打印版。
《加权平均数》教学素材
加权平均数教学素材
简介
加权平均数是一种常用的统计方法,用于计算具有不同权重的
数值在整体中的平均值。
它在各种领域中有广泛的应用,例如金融、经济、工程等。
本文档将介绍加权平均数的概念、计算方法以及实
际应用案例,供教学参考和素材使用。
概念
加权平均数是一种对数值进行加权处理后求平均的方法。
在计
算加权平均数时,每个数值与其对应的权重相乘,并将所有乘积相加,再除以总权重,得到平均数。
计算方法
计算加权平均数的步骤如下:
1. 将每个数值与其对应的权重相乘。
2. 将所有乘积相加。
3. 将总乘积除以总权重,得到加权平均数。
实际应用案例
以下是一些实际应用案例,展示加权平均数在不同领域中的用途:
- 金融领域:计算股票组合的加权平均收益率,以评估投资绩效。
- 经济领域:计算城市人口的加权平均年龄,以了解人口结构。
- 工程领域:计算不同材料的加权平均密度,以设计结构强度。
总结
加权平均数是一种常用的统计方法,用于计算具有不同权重的
数值在整体中的平均值。
它的计算方法简单明了,广泛应用于各个
领域。
通过了解加权平均数的概念和实际应用案例,可以帮助学生
更好地理解和运用这一概念。
加权平均数的实际应用举例
在实际问题中,人们往往根据问题的重要程度的不同,选用不同权重计算平均数,请看两例.
例1 一次演讲比赛,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再演讲内容:演讲能力:演讲效果=5:4:1的比例计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
请决出两人的名次.
分析:这个问题可以看成是求两名选手三项成绩的加权平均数,演讲内容:演讲能力:演讲效果=5:4:1,说明演讲内容、演讲能力、演讲效果三项成绩在总成绩中的重要程度,5、4、1分别是三项成绩的权. 解:选手A 的最后得分是:
901
45195495585=++⨯+⨯+⨯. 选手B 最后得分是:91145195485595=++⨯+⨯+⨯ 由上可知选手B 获得第一名,选手A 获得第二名.
评注:本题是一道与加权平均数的计算有关的实际问题,解决问题的关键在于正确理解加权平均数的计算方法.
例2 一家外贸公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩如下:
(1)如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,应该录用谁?
(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按2:2:3:3的比确定,应该录用谁?
分析:(1)这家公司按照3:3:2:2的比确定听、说、读、写的成绩,说明各项成绩
的“重要程度”有所不同,听、说的成绩比读、写的成绩更加“重要”,计算两明候选人的平均成绩,实际上是请听、说、读、写四项成绩的加权平均数,3,3,2,2,分别是它们的权.
(2)由于录取时侧重考虑笔译能力,所以在四项成绩的权的分配上与(1)有所不同,读、写的权大一些.
解:(1)听、说、读、写的成绩按照3:3:2:2的比确定,则甲的平均成绩为3.792
233282285380373=+++⨯+⨯+⨯+⨯, 乙的平均成绩为812
233275278383385=+++⨯+⨯+⨯+⨯. 显然,乙的成绩比甲的成绩高,所以从成绩看,应该录取乙.
(2)听、说、读、写的成绩按照2:2:3:3的比确定,则甲的平均成绩为
7.803
322382385280273=+++⨯+⨯+⨯+⨯; 乙的平均成绩为3.793
322375378280285=+++⨯+⨯+⨯+⨯. 显然甲的成绩比乙的成绩高,所以从成绩看,应该录用甲.
评注:从以上计算可以看出,侧重不同的权重,计算的加权平均数的值不同,数据的权能够反映出数据的相对“重要程度”.。