2001级高数(下)期终试卷答案
- 格式:ppt
- 大小:401.50 KB
- 文档页数:20

2001年广东普通高等学校招生统一考试数学试题一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.不等式31--x x >0的解集为A .{x|x<1}B .{x|x>3}C .{x|x<1或x>3}D .{x|1<x<3}2.若一个圆锥的轴截面是等边三角形,其面积为3,则这个圆锥的全面积是A.3π B.33π C.6π D.9π3.极坐标方程ρ2cos2θ=1所表示的曲线是A .两条相交直线B .圆C .椭圆D .双曲线4.若定义在区间(-1,0)内的函数f(x)=log2a(x+1)满足f(x)>0,则a的取值范围是 A .(0,21) B.(0,21] C.(21,+∞) D.(0,+∞)5.已知复数z=i 62+,则argZ1是A .3πB.35π C.6π D.611π6.函数y=2-x+1(x>0)的反函数是A .y=log211-x ,x∈(1,2); B.y=-log211-x ,x∈(1,2) C.y=log211-x ,x∈(1,2); D.y=-log211-x ,x∈(1,2]7.若0<α<β<4π,sinα+cosα=a,sinβ+cosβ=b,则A .a>b B.a<b C.ab<1 D.ab>28.在正三棱柱ABC —A 1B1C1中,若AB=2BB1,则AB 1与C1B所成的角的大小为 A .60° B.90° C.45° D.120°9.设f(x)、g(x)都是单调函数,有如下四个命题中,正确的命题是①若f(x)单调递增,g(x)单调递增,则f(x)-g(x)单调递增; ②若f(x)单调递增,g(x)单调递减,则f(x)-g(x)单调递增; ③若f(x)单调递减,g(x)单调递增,则f(x)-g(x)单调递减; ④若f(x)单调递减,g(x)单调递减,则f(x)-g(x)单调递减 A . ①③ B.①④ C.②③ D.②④10.对于抛物线y2=4x上任意一点Q ,点P (a ,0)都满足|PQ|≥|a|,则a 的取值范围是 A .(-∞,0) B .(-∞,2) C .[0,2] D .(0,2)11.一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜 记三种盖法屋顶面积分别为P1、P2、P3.若屋顶斜面与水平面所成的角都是α,则A .P 3>P 2>P 1 B.P 3>P 2=P 1 C.P 3=P2>P1 D.P 3=P 2=P 112.如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A 向结点B 传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为A .26 B.24 C.20 D.19二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)13.已知甲、乙两组各有8人,现从每组抽取4人进行计算机知识竞赛,比赛人员的组成共有 种可能(用数字作答14.双曲线116922=-yx的两个焦点为F1、F2,点P 在双曲线上,若PF1⊥PF2,则点P 到x轴的距离为 15.设{an}是公比为q的等比数列,Sn是它的前n项和.若{Sn}是等差数列,则q= 16.圆周上有2n个等分点(n>1),以其中三个点为顶点的直角三角形的个数为 三、解答题(本大题共6小题,共74分.17.(本小题满分10分)求函数y=(sinx+cosx)2+2cos2x的最小正周期.18.(本小题满分12分)已知等差数列前三项为a,4,3a,前n项的和为Sn,Sk =2550.(Ⅰ)求a及k的值;(Ⅱ)求)111(lim 21nn S S S +++∞→19.(本小题满分12分)如图,在底面是直角梯形的四棱锥S—ABCD 中,∠ABC=90°,SA⊥面ABCD ,SA =AB =BC=1,AD=21.(Ⅰ)求四棱锥S —ABCD 的体积;(Ⅱ)求面SCD 与面SBA 所成的二面角的正切值.20.(本小题满分12分)设计一幅宣传画,要求画面面积为4840 cm 2,画面的宽与高的比为λ(λ<1),画面的上、下各留8cm空白,左、右各留5cm空白.怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小?如果要求λ∈]43,32[,那么λ为何值时,能使宣传画所用纸张面积最小?21.(本小题满分14分)已知椭圆1222=+yx的右准线l 与x 轴相交于点E ,过椭圆右焦点F 的直线与椭圆相交于A 、B 两点,点C 在右准线l 上,且BC∥x 轴 求证直线AC 经过线段EF 的中点. 22.(本小题满分14分)设f(x)是定义在R 上的偶函数,其图象关于直线x=1对称 对任意x1,x2∈[0,21],都有f(x1+x2)=f(x1)·f(x2),且f (1)=a>0. (Ⅰ)求f)41(),21(f ;(Ⅱ)证明f(x)是周期函数;(Ⅲ)记an=f(2n+n21),求)(ln lim n n a ∞→.2001年广东普通高等学校招生统一考试数学试题参考答案一、选择题1.C 2.A 3.D 4.A 5.B 6.A 7.B 8.B 9.C 10.B 11.D 12.D 二、填空题13.4900 14.516 15.1 16.2n (n -1)三、解答题17.解:y=(sinx+cosx)2+2cos2x=1+sin2x+2cos2x=sin2x+cos2x+2=2)42sin(2++πx 8分所以最小正周期T=π. 10分 18.解:(Ⅰ)设该等差数列为{an},则a 1=a,a2=4,a3=3a,Sk=2550. 由已知有a +3a =2×4,解得首项a 1=a=2,公差d =a 2-a1=2. 2分 代入公式S k=k·a1+d k k ⋅-2)1(得255022)1(2=⋅-+⋅k k k∴k2+k-2550=0解得k =50,k =-51(舍去)∴a =2,k =50. 6分 (Ⅱ)由d n n a n S n ⋅-+⋅=2)1(1得S n=n(n+1),12111111111111(-)(-)(-)1223(1)12231nS S S n n n n +++=+++=+++⨯⨯++ 111+-=n 1)111(lim )111(lim 21=+-=+++∴∞→∞→n S S S n nn 12分19.解:(Ⅰ)直角梯形ABCD 的面积是M 底面=AB AD BC ⋅+)(21=43125.01=⨯+ 2分∴四棱锥S —ABCD 的体积是414313131=⨯⨯=⨯⨯=底面MSA V 4分(Ⅱ)延长BA 、CD 相交于点E ,连结SE ,则SE 是所求二面角的棱 6分∵AD∥BC,BC=2AD∴EA=AB=SA,∴SE⊥SB ∵SA⊥面ABCD ,得面SEB ⊥面EBC ,EB 是交线.又BC⊥EB,∴BC⊥面SEB ,故SB 是SC 在面SEB 上的射影,∴CS ⊥SE, 所以∠BSC是所求二面角的平面角 10分 ∵SB=SB BC BC AB SA ⊥==+,1,222 ∴tg∠BSC=22=SBBC即所求二面角的正切值为22 12分20.解:设画面高为xcm,宽为λxcm,则λx2=4840 1分 设纸张面积为S ,则有 S=(x+16)(λx+10)=λx2+(16λ+10)x+160, 3分 将x=λ1022代入上式得S=5000+44)58(10λλ+5分55(1)88λ==<即时,S 取得最小值,此时,高:x=884840=λc m,宽:λx=558885=⨯cm 8分如果λ∈[43,32],可设122334λλ≤<≤,则由S 的表达式得 S(λ1)-S(λ2)=44)5858(102211λλλλ--+ =)58)((104421121λλλλ--25,8038≥>->故因此S(λ1)-S(λ2)<0,所以S (λ)在区间[43,32]内单调递增. 从而,对于λ∈[43,32],当λ=32时,S (λ)取得最小值 答:画面高为88cm、宽为55cm 时,所用纸张面积最小;如果要求λ∈[43,32],当λ=32时,所用纸张面积最小. 12分21.证明:依设,得椭圆的半焦距c=1,右焦点为F (1,0),右准线方程为x=2,点E 的坐标为(2,0),EF 的中点为N (23,0) 3分若AB 垂直于x 轴,则A (1,y1),B(1,-y1),C(2,-y1), ∴AC 中点为N (23,0),即AC 过EF 中点N.若AB 不垂直于x 轴,由直线AB 过点F ,且由BC ∥x 轴知点B 不在x 轴上,故直线AB 的方程为y=k(x-1),k≠0.记A (x1,y1)和B(x2,y2),则C (2,y2)且x1,x2满足二次方程1)1(2222=-+x k x即(1+2k2)x2-4k2x+2(k2-1)=0,∴x1+x2=22212221)1(2,214kkx x kk+-=+ 10分又x21=2-2y21<2,得x1-23≠0,故直线AN ,CN 的斜率分别为k1=32)1(2231111--=-x x k x y )1(2232222-=-=x k y k ∴k1-k2=2k·32)32)(1()1(1121-----x x x x∵(x1-1)-(x2-1)(2x1-3)=3(x1+x2)-2x1x2-4 =0)]21(4)1(412[2112222=+---+k kkk∴k1-k2=0,即k1=k2,故A 、C 、N 三点共线.所以,直线AC 经过线段EF 的中点N. 14分 22.(Ⅰ)解:因为对x1,x2∈[0,21],都有f(x1+x2)=f(x1)·f(x 2),所以22)]41([)41()41()4141()21()]21([)21()21()2121()1(]1,0[,0)2()2()22()(f f f f f f f f f f x xf x f xx f x f =⋅=+==⋅=+=∈≥⋅=+= f(1)=a>0, 3 分∴4121)41(,)21(a f a f == 6分(Ⅱ)证明:依题设y=f(x)关于直线x=1对称, 故f(x)=f(1+1-x),即f(x)=f(2-x),x∈R 又由f(x)是偶函数知f(-x)=f(x),x∈R , ∴f(-x)=f(2-x),x∈R ,将上式中-x以x代换,得f(x)=f(x+2),x∈R这表明f(x)是R 上的周期函数,且2是它的一个周期. 10分 (Ⅲ)解:由(Ⅰ)知f(x)≥0,x∈[0,1] ∵]21)1(21[)21()21(nn n f nn f f ⋅-+=⋅=11()[(1)]22f f n nn=⋅-⋅=1111()()()[()]2222nf f f f n n n n=⋅⋅⋅=21)21(a f = ∴n a nf 21)21(= 12分 ∵f(x)的一个周期是2 ∴f(2n+n21)=f(n21),因此a n =n a 210)ln 21(lim )(ln lim ==∴∞→∞→a na n n n 14分。

2001年普通高等学校招生全国统一考试数 学(理工农医类)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.第I 卷1至2页.第II 卷3至9页.共150分.考试时间120分钟.第I 卷(选择题 60分)注意事项:1. 答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写 在答题卡上.2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需 改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.3.考试结束,监考人将本试卷和答题卡一并收回.一、选择题:本大题共12小题;第每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若0cos sin >θθ,则θ在A .第一、二象限B .第一、三象限C .第一、四象限D .第二、四象限 【答案】B【解析】0cos sin >θθ,则sin θ与cos θ同号,B 正确.2.过点(1,1)(1,1)A B --,且圆心在直线02=-+y x 上的圆的方程是 A .()()41322=++-y x B .()()41322=-++y xC .()()41122=-+-y x D .()()41122=+++y x【答案】C【解析】显然过A B ,两点的直线与已知直线平行,过A B ,两点分别作,x y 轴的垂线,与已知直线相交于点(1,1)M ,则(1,1)M 为圆心,半径为2,C 正确.3.设{}n a 是递增等差数列,前三项的和为12,前三项的积为48,则它的首项是 A .1 B .2 C .4 D .6 【答案】B【解析】由已知得12312313212,48,2a a a a a a a a a ++==+=,解得12a =.4.若定义在区间(10)-,内的函数()2log (1)a f x x =+满足0)(>x f ,则a 的取值范围是 A .1(0,)2 B .1(0,]2C .1(,)2+∞ D .(0,)+∞【答案】A【解析】当(10)x ∈-,,则1(0,1)x +∈,由0)(>x f ,则021a <<,则1(0,)2a ∈.5.极坐标方程)4sin(2πθρ+=的图形是【答案】C【解析】化为直角坐标方程为2222((122x y -+-=,只有C 正确.6.函数)0(1cos ≤≤-+=x x y π的反函数是A .)20)(1arccos(≤≤--=x x yB .)20)(1arccos(≤≤--=x x y πC .)20)(1arccos(≤≤-=x x yD .)20)(1arccos(≤≤-+=x x y π 【答案】A【解析】∵0x π-≤≤,∴02y ≤≤,又0x π≤-≤,∴1cos cos()y x x -==-, ∴cos(1)x arc y -=-,即cos(1)x arc y =--,反函数为)20)(1arccos(≤≤--=x x y .7.若椭圆经过原点,且焦点为)0,3(),0,1(21F F ,则其离心率为 A .43 B .32 C .21 D .41 【答案】C【解析】易知椭圆的中心为(2,0),且2,1a c ==,则12c e a ==.8.若0,sin cos ,sin cos 4a b παβααββ<<<+=+=,则A .b a <B .b a >C .1<abD .2>ab 【答案】A【解析】由题设sin(),sin()44a b ππαβ=+=+,又4442ππππαβ<+<+<,所以b a <.9.在正三棱柱111C B A ABC -中,若12BB AB =,则1AB 与B C 1所成的角的大小为A .60︒B .90︒C .105︒D .75︒【答案】B则【解析】如图,取11A B 的中点D ,连接1,BD C D ,若12AB BB =,1111,,AB BD AB C D BD C D D ⊥⊥=,∴1AB ⊥平面1C DB ,而1C B ⊂面1C DB ,∴11AB C B ⊥,故答案为90︒.10.设()()f x g x ,都是单调函数,有如下四个命题:①若)(x f 单调递增,)(x g 单调递增,则)()(x g x f -单调递增; ②若)(x f 单调递增,)(x g 单调递减,则)()(x g x f -单调递增; ③若)(x f 单调递减,)(x g 单调递增,则)()(x g x f -单调递减; ④若)(x f 单调递减,)(x g 单调递减,则)()(x g x f -单调递减; 其中,正确的命题是A .①③B .①④C .②③D .②④ 【答案】C【解析】若)(x g 单调递减,则()g x -单调递增,所以)()(x g x f -单调递增,②正确;同理③正确.11.一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜.记三种盖法屋顶面积分别为123P P P ,,.若屋顶斜面与水平面所成的角都是α,则A .123P P P >>B .123P P P =>C .123P P P >=D .123P P P ==【答案】D【解析】本题考查平面图形在另一平面内的射影理解与有关计算,其斜面与房屋的底面所成的角都是α,又有cos S S α=底斜,故有123P P P ==.【编者注】此公式《新课标》不作要求.12.如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相连.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A 向结点B 传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为A .26B .24C .20D . 19 【答案】D【解析】从A 到B 有四条线路,从上到下记为1234,,,l l l l ,且123412,12l l l l +≤+≤,在单位时间内可以通过的最大信息量分别为3,4,6,6,D 正确.第II 卷(非选择题 90分)注意事项:1. 第II 卷共7页,用钢笔或圆珠笔直接答在试题卷中. 2. 答卷前将密封线内的项目填写清楚.二.填空题:本大题共4小题;每小题4分,共16分,把答案填在题中横线上.13.若一个圆锥的轴截面是等边三角形,其面积为3,则这个圆锥的侧面积是 . 【答案】2π【解析】由已知可得圆锥的的底面半径和母线长分别为1和2,侧面积为2rl ππ=.14.双曲线116922=-y x 的两个焦点为12F F ,,点P 在双曲线上.若12PF PF ⊥,则点P 到x 轴的距离为 .【答案】516 【解析】方法一:设(,)P x y ,12(5,0)(5,0)F F -,,由12PF PF ⊥得00155y y x x --⋅=-+-,即 2225x y +=,与双曲线方程联立得225625y =,则165y =. 方法二:设12,PF m PF n ==,由抛物线定义和题设222126,100m n m n FF -=+==,可得32mn =,利用面积相等关系12121122P PF PF F F y ⋅=⋅得165y =.15.设{}n a 是公比为q 的等比数列,n S 是它的前n 项和.若{}n S 是等差数列,则=q . 【答案】1【解析】若{}n S 是等差数列,则1322S S S +=,11231223()2()a a a a a a a a +++=+⇒=,所以1q =.16.圆周上有2n 个等分点(1>n ),以其中三个点为顶点的直角三角形的个数为 . 【答案】2(1)n n -【解析】由题意知,只有三角形的一条边过圆心,才能组成直角三角形,∵圆周上有2n 个等分点,∴共有n 条直径,每条直径可以和除去本身的两个定点外的点组成直角三角形, ∴可做22n -个直角三角形,根据分步计数原理知共有(22)2(1)n n n n -=-.三、解答题:本大题共6小题;共74分,解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)如图,在底面是直角梯形的四棱锥ABCD S -中,∠90=ABC °,SA ⊥面ABCD ,11,2SA AB BC AD ====. (Ⅰ)求四棱锥ABCD S -的体积;(Ⅱ)求面SCD 与面SBA 所成的二面角的正切值.【解】本小题考查线面关系和棱锥体积计算,以及空间想象能力和逻辑推理能力.满分12分.(I )直角梯形ABCD 的面积是()110.531224M BC AD AB +=+⋅=⨯=底面, ……2分 ∴四棱推ABCD S -的体积是113113344V SA M =⨯⨯=⨯⨯=底面.……4分(II )延长,BA CD 相交于点E ,连结SE ,则SE 是所求二面角的棱. ……6分∵//,2AD BC BC AD =,∴EA AB SA ==,∴SE SB ⊥. ∵SA ⊥面ABCD ,得面AEB ⊥面EBC ,EB 是交线, 又BC EB ⊥,∴BC ⊥面SEB ,故SB 是CS 在面SEB 上的射影,∴CS SE ⊥,所以BSC ∠是所求二面角的平面角. ……10分222,1,SB SA AB BC BC SB ∴=+==⊥.2tan 2BC BSC SB ∴∠==. 即所求二面角的正切值为22. ……12分18.(本小题满分12分)已知复数31)1(i i z -=. (Ⅰ)求1arg z 及1z ;(Ⅱ)当复数z 满足1=z ,求1z z -的最大值.【解】本小题考查复数的基本性质和基本运算,以及分析问题和解决问题的能力.满分12分.(Ⅰ)31(1)22z i i i =-=-, ……3分将1z 化为三角形式,得⎪⎭⎫⎝⎛+=47sin 47cos 221ππi z ,∴47arg 1π=z ,221=z . ……6分 (Ⅱ)设cos sin z i αα=+,则1(cos 2)(sin 2)z z i αα-=-++,()()22212sin 2cos ++-=-ααz z942sin()4πα=+-, ……9分当sin()14πα+=时,21z z -取得最大值249+.从而得到1z z -的最大值为122+. ……12分19.(本小题满分12分)设抛物线)0(22>=p px y 的焦点为F ,经过点F 的直线交抛物线于A B ,两点. 点C 在抛物线的准线上,且//BC x 轴. 证明直线AC 经过原点O .【解】本小题考查抛物线的概念和性质,直线的方程和性质,运算能力和逻辑推理能力.满分12分. 证明一:因为抛物线)0(22>=p px y 的焦点为(,0)2pF ,所以经过 点F 的直线AB 的方程可设为2p my x +=, 代人抛物线方程得2220y pmy p --=,若记1122(,),(,)A x y B x y ,则12,y y 是该方程的两个根,所以212y y p =-.因为BC ∥x 轴,且点C 在准线2p x =-上,所以点C 的坐标为2(,)2py -, 故直线CO 的斜率为111222x y y p p y k ==-=即k 也是直线OA 的斜率,所以直线AC 经过原点O . 证明二:如图,记x 轴与抛物线准线l 的交点为E ,过A 作AD l ⊥,D 是垂足.则////AD FE BC .……2分 连结AC ,与EF 相交手点N ,则||||||||||,||||||||||EN CN BF NF AF AD AC AB BC AB === ……6分根据抛物线的几何性质,||||,||||AF AD BF BC == ……8分||||||||||||||||AD BF AF BC EN NF AB AB ⋅⋅∴===,即点N 是EF 的中点,与抛物线的顶点O 重合,所以直线AC 经过原点O .…12分20.(本小题满分12分)已知n m i ,,是正整数,且n m i <≤<1.(Ⅰ)证明:in i i m i P m P n <; (Ⅱ)证明:mn n m )1()1(+>+.【解】本小题考查排列、组合、二项式定理、不等式的基本知识和逻辑推理能力.满分12分.(Ⅰ)证明:对于1i m <≤有(1)im p m m i =⋅⋅-+,⋅-⋅=m m m m m p i i m 1…mi m 1+-⋅, 同理 11...i n i p n n n i n n n n--+=⋅⋅⋅…, ……4分由于m n <,对整数1,2,,1k i =-,有mkm n k n ->-, 所以 i im i i n mp n p >,即im i i n i p n p m >. ……6分(Ⅱ)证明:由二项式定理有()inni inCm m ∑==+01,()i mmi i mCn n ∑==+01, ……8分由(Ⅰ)知i n i p m >(1)i im n p i m n <≤<,而 !i p C i m im=,!i p C i n in =, ……10分所以,(1)i i i in m m C n C i m n ><≤<.因此,∑∑==>mi im i mi i niC n Cm 22. 又 10000==m n C n C m ,mn nC mC m n ==11,()n i m C m in i ≤<>0.∴∑∑==>mi im i ni i niC n Cm 0. 即(1)(1)nmm n +>+. ……12分21.(本小题满分12分)从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业.根据规划,本年度投入800万元,以后每年投入将比上年减少51.本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加41.(Ⅰ)设n 年内(本年度为第一年)总投入为n a 万元,旅游业总收入为n b 万元.写出n n b a ,的表达式;(Ⅱ)至少经过几年旅游业的总收入才能超过总投入?【解】本小题主要考查建立函数关系式、数列求和、不等式等基础知识;考查综合运用数学知识解决实际问题的能力.满分12分.(I )第1年投入为800万元.第2年投入为1800(1)5⨯-万元,……,第n 年投入为11800(1)5n -⨯-万元.所以,n 年的总收入为111111800800(1)800(1)800(1)555n n k n k a --==+⨯-+⋅⋅⋅+⨯-=⨯-∑44000[1()]5n =⨯-. ……3分第1年旅游业收入为 400万元,第 2年旅游业收入为 1400(1)4⨯+万元,……,第n 年旅游业收人为11400(1)4n -⨯+万元.所以,n 年内的旅游业总收入为111111400400(1)400(1)400(1)444n n k n k b --==+⨯++⋅⋅⋅+⨯+=⨯+∑51600[()1]4n =⨯-. ……6分(Ⅱ))设至少经过年旅游业的总收入才能超过总投入,由此0n n b a ->,即541600[()1]4000[1()]045n n ⨯--⨯-> 化简得455()2()7054n n ⨯+⨯->, ……9分设4()5n x =,代入上式得25720x x -+>,解此不等式,得2,15x x <>(舍去).即 42()55n <,由此得 5n ≥.答:至少经过5年旅游业的总收入才能超过总投入. ……12分22.(本小题满分14分)设)(x f 是定义在R 上的偶函数,其图象关于直线1=x 对称,对任意]21,0[,21∈x x ,都有1212()()()f x x f x f x +=⋅,且0)1(>=a f .(Ⅰ)求)21(f 及)41(f ; (Ⅱ)证明)(x f 是周期函数; (Ⅲ)记)212(nn f a n +=,求)(ln lim n n a ∞→.【解】本小题主要考查函数的概念、图象,函数的奇偶性和周期性以及数列极限等基础知识;考查运算能力和逻辑思维能力,满分14分.(Ⅰ)因为对121,[0,]2x x ∈,都有1212()()()f x x f x f x +=+,所以()()()0,[0,1]22x xf x f f x =⋅≥∈.∵211111(1)()()()[()]22222f f f f f =+=⋅=,2111111()()()()[()]244444f f f f f =+=⋅=. ……3分0)1(>=a f ,∴112411(),()24f a f a ==. ……6分(Ⅱ)证明:依题设()y f x =关于直线1x =对称,故()(11)f x f x =+-,即()(2),f x f x x R =-∈, ……8分 又由()f x 是偶函数知()(),f x f x x R -=∈,∴()(2),f x f x x R -=-∈, 将上式中x -以x 代换,得()(2),f x f x x R =+∈.这表明()f x 是R 上的周期函数,且2是它的一个周期. ……10分 (Ⅲ)由(Ⅰ)知()0,[0,1]f x x ≥∈.∵111111()()((1))()((1))222222f f n f n f f n n n n n n =⋅=+-⋅=⋅-⋅ 111()()()222f f f n n n ==⋅⋅⋅1[()]2n f n=,121()2f a =,资料内容仅供您学习参考,如有不当之处,请联系改正或者删除 ----完整版学习资料分享---- ∴121()2n f a n=. ∵()f x 的一个周期是2, ∴11(2)()22f n f n n+=,因此12n n a a =, ……12分 ∴1lim(ln )lim(ln )02n n n a a n→∞→∞==. ……14分。

2001年广东普通高等学校招生统一考试数 学 试 题2001.7说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.三角函数的积化和差公式)]sin()[sin(21cos sin βαβαβα-++=)]sin()[sin(21sin cos βαβαβα--+=)]cos()[sin(21cos cos βαβαβα-++=)]cos()[cos(21sin sin βαβαβα--+-=正棱台、圆台的侧面积公式S台侧=21(c ′+c )l其中c ′、c 分别表示上、下底面周长,lV=h S S S S )(31+'+'其中S ′、S 分别表示上、下底面积,h 表示高.第Ⅰ卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.不等式31--x xA .{x|x<1}B .{x|xC .{x|x<1或x>3}D .{x|1<x<3}2.若一个圆锥的轴截面是等边三角形,其面积为3π B.33π6πD.9π3.极坐标方程ρ2cos2θA B C .椭圆 D4.若定义在区间(-1,0)内的函数f(x)=log2a(x+1)满足f(x)>0,则aA .(0,21) 21] 21,+∞) D.(0,+∞) 5.已知复数z=i 62+,则argZ1是A .3πB.35π C.6π611π6.函数y=2-x+1(x>0)A .y=log211-x ,x y=-log211-x ,xC.y=log211-x ,x∈(1,2)D.y=-log211-x ,x∈(1,2]7.若0<α<β<4π,sinα+cosα=a,sinβ+cosβ=b,则A .a>b B.a<bab<1 ab>28.在正三棱柱ABC —A 1B1C1中,若AB=2BB1,则AB 1与C1B所成的角的大小A .60° 45° 120°9.设f(x)、g(x①若f(x)单调递增,g(x)单调递增,则f(x)-g(x ②若f(x)单调递增,g(x)单调递减,则f(x)-g(x ③若f(x)单调递减,g(x)单调递增,则f(x)-g(x ④若f(x)单调递减,g(x)单调递减,则f(x)-g(xA . ①③10.对于抛物线y2=4x上任意一点Q ,点P (a ,0)都满足|PQ|≥|a|,则a 的A .(-∞,0)B .(-∞,2)C .[0,2]D .(0,11记三种盖法屋顶面积分别为P1、P2、P3.若屋顶斜面与水平面所成的角都是α,则A .P 3>P 2>P 1 P 3>P 2=P 1P 3=P2>P1 D.P 3=P 2=P 112.如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A 向结点B 传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为A B.24(非选择题 共90分)二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)13.已知甲、乙两组各有8人,现从每组抽取4人进行计算机知识竞赛,比赛人员的组 成共有 种可能(用数字作答)14.双曲线116922=-y x 的两个焦点为F1、F2,点P 在双曲线上,若PF1⊥PF2,则点P 到x轴的距离为15.设{an}是公比为q的等比数列,Sn是它的前n项和.若{Sn}是等差数列,则q=16.圆周上有2n个等分点(n>1),以其中三个点为顶点的直角三角形的个数为 三、解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)求函数y=(sinx+cosx)2+2cos2x的最小正周期. 18.(本小题满分12分)已知等差数列前三项为a,4,3a,前n项的和为Sn,Sk =2550. (Ⅰ)求a及k的值;(Ⅱ)求)111(lim 21nn S S S +++∞→ 19.(本小题满分12分)如图,在底面是直角梯形的四棱锥S—ABCD 中,∠ABC=90°,SA⊥面ABCD ,SA =AB =BC=1,AD=21. (Ⅰ)求四棱锥S —ABCD 的体积;(Ⅱ)求面SCD 与面SBA 所成的二面角的正切值. 20.(本小题满分12分)设计一幅宣传画,要求画面面积为4840 cm 2,画面的宽与高的比为λ(λ<1),画面的上、下各留8cm空白,左、右各留5cm空白.怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小?如果要求λ∈]43,32[,那么λ为何值时,能使宣传画所用纸张面积最小?21.(本小题满分14分)已知椭圆1222=+y x 的右准线l 与x 轴相交于点E ,过椭圆右焦点F 的直线与椭圆相 交于A 、B 两点,点C 在右准线l 上,且BC∥xAC 经过线段EF 的中点.22.(本小题满分14分) 设f(x)是定义在R 上的偶函数,其图象关于直线xx1,x2∈[0,21],都有f(x1+x2)=f(x1)·f(x2),且f (1)=a>0. (Ⅰ)求f)41(),21(f ;(Ⅱ)证明f(x)是周期函数; (Ⅲ)记an=f(2n+n21),求)(ln lim n n a ∞→.参考答案一、选择题1.C 2.A 3.D 4.A 5.B 6.A 7.B 8.B 9.C 10.B 11.D 12.D 二、填空题13.4900 14.51615.1 16.2n (n -1) 三、解答题17.解:y=(sinx+cosx)2+2cos2x=1+sin2x+2cos2x=sin2x+cos2x+2 5分=2)42sin(2++πx 8分所以最小正周期T=π. 10分 18.解:(Ⅰ)设该等差数列为{an},则a 1=a,a2=4,a3=3a,Sk=2550. 由已知有a +3a =2×4,解得首项a 1=a=2,公差d =a 2-a1=2. 2分 代入公式S k=k·a1+d k k ⋅-2)1(得255022)1(2=⋅-+⋅k k k ∴k2+k-2550=0解得k =50,k =-51(舍去)∴a =2,k =50. 6分 (Ⅱ)由d n n a n S n ⋅-+⋅=2)1(1得S n=n(n+1), )11-1()31-21()21-11( )1(132121111121++++=+++⨯+⨯=+++n n n n S S S n111+-=n 9分 1)111(lim )111(lim 21=+-=+++∴∞→∞→n S S S n n n 12分19.解:(Ⅰ)直角梯形ABCD 的面积是M 底面=AB AD BC ⋅+)(21=43125.01=⨯+ 2分∴四棱锥S —ABCD 的体积是414313131=⨯⨯=⨯⨯=底面M SA V 4分(Ⅱ)延长BA 、CD 相交于点E ,连结SE ,则SE 是所求二面角的棱 6分 ∵AD∥BC,BC=2AD∴EA=AB=SA,∴SE⊥SB∵SA⊥面ABCD ,得面SEB ⊥面EBC ,EB 是交线.又BC⊥EB,∴BC⊥面SEB ,故SB 是SC 在面SEB 上的射影, ∴CS ⊥SE,所以∠BSC是所求二面角的平面角 10分 ∵SB=SB BC BC AB SA ⊥==+,1,222∴tg∠BSC=22=SB BC 即所求二面角的正切值为2212分 20.解:设画面高为xcm,宽为λxcm,则λx2=4840 1分 设纸张面积为S ,则有S=(x+16)(λx+10)=λx2+(16λ+10)x+160, 3分 将x=λ1022代入上式得S=5000+44)58(10λλ+5分当8)185(85,5==λλλ即时,S 取得最小值, 此时,高:x=884840=λc m,宽:λx=558885=⨯cm 8分 如果λ∈[43,32],可设433221≤≤λλ ,则由S 的表达式得S(λ1)-S(λ2)=44)5858(102211λλλλ--+=)58)((104421121λλλλ-- 10分由于058,85322121 λλλλ-≥故 因此S(λ1)-S(λ2)<0,所以S (λ)在区间[43,32]内单调递增. 从而,对于λ∈[43,32],当λ=32时,S (λ)取得最小值答:画面高为88λ∈[43,32],当λ=32时,所用纸张面积最小. 12分 21.证明:依设,得椭圆的半焦距c=1,右焦点为F (1,0),右准线方程为x=2,点E 的坐标为(2,0),EF 的中点为N (23,0) 3分 若AB 垂直于x 轴,则A (1,y1),B(1,-y1),C(2,-y1), ∴AC 中点为N (23,0),即AC 过EF 中点N. 若AB 不垂直于x 轴,由直线AB 过点F ,且由BC ∥x 轴知点B 不在x 轴上,故直线AB 的方程为y=k(x-1),k≠0.记A (x1,y1)和B(x2,y2),则C (2,y2)且x1,x2满足二次方程1)1(2222=-+x k x 即(1+2k2)x2-4k2x+2(k2-1)=0,∴x1+x2=22212221)1(2,214k k x x k k +-=+ 10分又x21=2-2y21<2,得x1-23≠0, 故直线AN ,CN 的斜率分别为k1=32)1(2231111--=-x x k x y )1(2232222-=-=x k y k ∴k1-k2=2k·32)32)(1()1(1121-----x x x x∵(x1-1)-(x2-1)(2x1-3) =3(x1+x2)-2x1x2-4=0)]21(4)1(412[2112222=+---+k k k k∴k1-k2=0,即k1=k2,故A 、C 、N 三点共线.所以,直线AC 经过线段EF 的中点N. 14分 22.(Ⅰ)解:因为对x1,x2∈[0,21],都有f(x1+x2)=f(x1)·f(x 2), 所以22)]41([)41()41()4141()21()]21([)21()21()2121()1(]1,0[,0)2()2()22()(f f f f f f f f f f x xf x f x x f x f =⋅=+==⋅=+=∈≥⋅=+=f(1)=a>0, 3 分∴4121)41(,)21(a f a f == 6分(Ⅱ)证明:依题设y=f(x)关于直线x=1对称, 故f(x)=f(1+1-x), 即f(x)=f(2-x),x∈R又由f(x)是偶函数知f(-x)=f(x),x∈R , ∴f(-x)=f(2-x),x∈R ,将上式中-x以x代换,得f(x)=f(x+2),x∈R这表明f(x)是R 上的周期函数,且2是它的一个周期. 10分 (Ⅲ)解:由(Ⅰ)知f(x)≥0,x∈[0,1] ∵]21)1(21[)21()21(nn n f n n f f ⋅-+=⋅= nnf n f n f n f nn f n f )]21([)21()21()21( ]21)1[()21( =⋅⋅⋅==⋅-⋅=21)21(a f = ∴n a nf 21)21(= 12分∵f(x)的一个周期是2∴f(2n+n 21)=f(n21),因此a n =n a 210)ln 21(lim )(ln lim ==∴∞→∞→a na n n n 14分。

2010年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟,第Ⅰ卷1至3页,第Ⅱ卷4至11页。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1. 答第Ⅰ卷前,考生务必将自己的姓名和准考证号填写在答题卡上,并在规定位置粘贴考试用条形码。
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,答在试卷上的无效。
3. 本卷共10小题,每小题5分,共50分。
参考公式:·如果事件A 、B 互斥,那么 ·如果事件A 、B 相互独立,那么 P(A ∪B)=P(A)+P(B) P(AB)=P(A)P(B)·棱柱的体积公式V=Sh, 棱锥的体积公式V=13sh , 其中S 标示棱柱的底面积。
其中S 标示棱锥的底面积。
h 表示棱柱的高。
h 示棱锥的高。
一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)i 是虚数单位,复数1312i i-+=+ (A)1+i (B)5+5i (C)-5-5i (D)-1-i【答案】A【解析】本题主要考查复数代数形式的基本运算,属于容易题。
进行复数的除法的运算需要份子、分母同时乘以分母的共轭复数,同时将i 2改为-1. 1312i i-+=+-+551(12)(12)5i i i i +==++-(13i )(1-2i) 【温馨提示】近几年天津卷每年都有一道关于复数基本运算的小题,运算时要细心,不要失分哦。
(2)函数f(x)=23x x +的零点所在的一个区间是(A)(-2,-1)(B)(-1,0)(C)(0,1)(D)(1,2)【答案】B【解析】本题主要考查函数零点的概念与零点定理的应用,属于容易题。
由1(1)30,(0)102f f -=-<=>及零点定理知f(x)的零点在区间(-1,0)上。

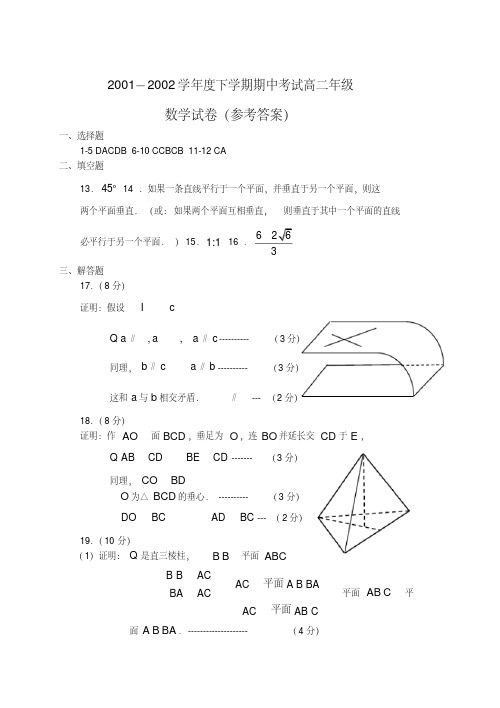
2001年全国普通高等学校招生全国统一考试数学(理工农医类)一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)若0cos sin >θθ,则θ在(A)第一、二象限 (B)第一、三象限 (C)第一、四象限 (D)第二、四象限 (2)过点A(1,-1),B(-1,1)且园心在直线x+y-2=0上的圆珠笔的方程是 (A)(x-3)2+(y+1)2=4 (B)(x+3)2+(y-1)2=4 (C)(x-1)2+(y-1)2=4 (B)(x+1)2+(y+1)2=4(3)设{a n }是递增等差数列,前三项的和为12,前三项的积为48,则它的首项是 (A)1 (B)2 (C)4 (D)6(4)若定义在区间(-1,0)内的函数f (x )= log 2a (x + 1)满足f (x )> 0,则 a 的取值范围是 (A)(0,21) (B) (0,21] (C) (21,+∞) (D) (0,+∞) (5)极坐标方程)4sin 2πθρ+=的图形是(6)函数)0(1cos ≤≤-+=x x y π的反函数是 (A) )20)(1arccos(≤≤--=x x y (B) )20)(1arccos(≤≤--=x x y π (C) )20)(1arccos(≤≤-=x x y(D) )20)(1arccos(≤≤-+=x x y π(7)若椭圆经过原点,且焦点为F 1(1,0),F 2(3,0),则其离心率为 (A)43 (B)32 (C)21 (D)41 (8)若b a =+=+<<<ββααπβαcos sin ,cos sin ,40,则(A)a <b(A)a >b(A)ab <1(D)ab >2(9)在正三棱柱ABC -A 1 B 1C 1中,若AB =2BB 1,则AB 与C 1B 所成的角的大小为 (A)60° (B)90° (C)105° (D)75°(10)设f (x )、g (x )都是单调函数,有如下四个命题:①若f (x )单调速增,g (x )单调速增,则f (x )-g (x ))单调递增; ②若f (x )单调速增,g (x )单调速减,则f (x )-g (x ))单调递增; ③若f (x )单调速减,g (x )单调速增,则f (x )-g (x ))单调递减; ④若f (x )单调速减,g (x )单调速减,则f (x )-g (x ))单调递减; 其中,正确的命题是(A)①③ (B)①④ (C)②③ (D)②④(11)一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜.记三种盖法屋顶面积分别为P 1、P 2、P 3.若屋顶斜面与水平面所成的角都是α,则 (A)P 3>P 2>P 1 (B) P 3>P 2=P 1 (C) P 3=P 2>P 1 (D) P 3=P 2=P 1(12)如图,小圆圈表示网络的结点,结点之间的连线表承它们有网线相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A 向结点B 传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为(A)26 (B)24 (C)20 (D)19二.填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.(13)若一个圆锥的轴截面是等边三角形,其面积为3,则这个圆锥的侧面积是_________.(14)双曲线116922=+y x 的两个焦点为F 1、F 2,点P 在双曲线上.若PF ⊥PF 2,则点P 到x 轴的距离为_________。
2001年广东普通高等学校招生统一考试数学试题一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.不等式31--x x >0的解集为A .{x|x<1}B .{x|x>3}C .{x|x<1或x>3}D .{x|1<x<3}2.若一个圆锥的轴截面是等边三角形,其面积为3,则这个圆锥的全面积是A.3π B.33π C.6π D.9π3.极坐标方程ρ2cos2θ=1所表示的曲线是A .两条相交直线B .圆C .椭圆D .双曲线4.若定义在区间(-1,0)内的函数f(x)=log2a(x+1)满足f(x)>0,则a的取值范围是 A .(0,21) B.(0,21] C.(21,+∞) D.(0,+∞)5.已知复数z=i 62+,则argZ1是A .3πB.35π C.6πD.611π6.函数y=2-x+1(x>0)的反函数是A .y=log211-x ,x∈(1,2); B.y=-log211-x ,x∈(1,2) C.y=log211-x ,x∈(1,2); D.y=-log211-x ,x∈(1,2]7.若0<α<β<4π,sinα+cosα=a,sinβ+cosβ=b,则A .a>b B.a<b C.ab<1 D.ab>28.在正三棱柱ABC —A 1B1C1中,若AB=2BB1,则AB 1与C1B所成的角的大小为 A .60° B.90° C.45° D.120°9.设f(x)、g(x)都是单调函数,有如下四个命题中,正确的命题是①若f(x)单调递增,g(x)单调递增,则f(x)-g(x)单调递增; ②若f(x)单调递增,g(x)单调递减,则f(x)-g(x)单调递增; ③若f(x)单调递减,g(x)单调递增,则f(x)-g(x)单调递减; ④若f(x)单调递减,g(x)单调递减,则f(x)-g(x)单调递减 A . ①③ B.①④ C.②③ D.②④10.对于抛物线y2=4x上任意一点Q ,点P (a ,0)都满足|PQ|≥|a|,则a 的取值范围是 A .(-∞,0) B .(-∞,2) C .[0,2] D .(0,2)11.一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜 记三种盖法屋顶面积分别为P1、P2、P3.若屋顶斜面与水平面所成的角都是α,则A .P 3>P 2>P 1 B.P 3>P 2=P 1 C.P 3=P2>P1 D.P 3=P 2=P 112.如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A 向结点B 传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为A .26 B.24 C.20 D.19二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)13.已知甲、乙两组各有8人,现从每组抽取4人进行计算机知识竞赛,比赛人员的组成共有 种可能(用数字作答)14.双曲线116922=-yx的两个焦点为F1、F2,点P 在双曲线上,若PF1⊥PF2,则点P 到x轴的距离为15.设{an}是公比为q的等比数列,Sn是它的前n项和.若{Sn}是等差数列,则q= 16.圆周上有2n个等分点(n>1),以其中三个点为顶点的直角三角形的个数为 三、解答题(本大题共6小题,共74分.17.(本小题满分10分)求函数y=(sinx+cosx)2+2cos2x的最小正周期.18.(本小题满分12分)已知等差数列前三项为a,4,3a,前n项的和为Sn,Sk =2550.(Ⅰ)求a及k的值;(Ⅱ)求)111(lim 21nn S S S +++∞→19.(本小题满分12分)如图,在底面是直角梯形的四棱锥S—ABCD 中,∠ABC=90°,SA⊥面ABCD ,SA =AB =BC=1,AD=21.(Ⅰ)求四棱锥S —ABCD 的体积;(Ⅱ)求面SCD 与面SBA 所成的二面角的正切值.20.(本小题满分12分)设计一幅宣传画,要求画面面积为4840 cm 2,画面的宽与高的比为λ(λ<1),画面的上、下各留8cm空白,左、右各留5cm空白.怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小?如果要求λ∈]43,32[,那么λ为何值时,能使宣传画所用纸张面积最小?21.(本小题满分14分)已知椭圆1222=+yx的右准线l 与x 轴相交于点E ,过椭圆右焦点F 的直线与椭圆相交于A 、B 两点,点C 在右准线l 上,且BC∥x 轴 求证直线AC 经过线段EF 的中点. 22.(本小题满分14分)设f(x)是定义在R 上的偶函数,其图象关于直线x=1对称 对任意x1,x2∈[0,21],都有f(x1+x2)=f(x1)·f(x2),且f (1)=a>0.(Ⅰ)求f)41(),21(f ;(Ⅱ)证明f(x)是周期函数;(Ⅲ)记an=f(2n+n21),求)(ln lim n n a ∞→.2001年广东普通高等学校招生统一考试数学试题参考答案一、选择题1.C 2.A 3.D 4.A 5.B 6.A 7.B 8.B 9.C 10.B 11.D 12.D 二、填空题13.4900 14.516 15.1 16.2n (n -1)三、解答题17.解:y=(sinx+cosx)2+2cos2x=1+sin2x+2cos2x=sin2x+cos2x+2=2)42sin(2++πx 8分所以最小正周期T=π. 10分 18.解:(Ⅰ)设该等差数列为{an},则a 1=a,a2=4,a3=3a,Sk=2550. 由已知有a +3a =2×4,解得首项a 1=a=2,公差d =a 2-a1=2. 2分 代入公式S k=k·a1+d k k ⋅-2)1(得255022)1(2=⋅-+⋅k k k∴k2+k-2550=0解得k =50,k =-51(舍去)∴a =2,k =50. 6分 (Ⅱ)由d n n a n S n ⋅-+⋅=2)1(1得S n=n(n+1),12111111111111(-)(-)(-)1223(1)12231nS S S n n n n +++=+++=+++⨯⨯++ 111+-=n1)111(lim )111(lim 21=+-=+++∴∞→∞→n S S S n nn 12分19.解:(Ⅰ)直角梯形ABCD 的面积是M 底面=AB AD BC ⋅+)(21=43125.01=⨯+ 2分∴四棱锥S —ABCD 的体积是414313131=⨯⨯=⨯⨯=底面MSA V 4分(Ⅱ)延长BA 、CD 相交于点E ,连结SE ,则SE 是所求二面角的棱 6分∵AD∥BC,BC=2AD∴EA=AB=SA,∴SE⊥SB ∵SA⊥面ABCD ,得面SEB ⊥面EBC ,EB 是交线.又BC⊥EB,∴BC⊥面SEB ,故SB 是SC 在面SEB 上的射影,∴CS ⊥SE, 所以∠BSC是所求二面角的平面角 10分 ∵SB=SB BC BC ABSA ⊥==+,1,222∴tg∠BSC=22=SBBC即所求二面角的正切值为22 12分20.解:设画面高为xcm,宽为λxcm,则λx2=4840 1分 设纸张面积为S ,则有S=(x+16)(λx+10)=λx2+(16λ+10)x+160, 3分 将x=λ1022代入上式得S=5000+44)58(10λλ+5分55(1)88λ==<即时,S 取得最小值,此时,高:x=884840=λc m,宽:λx=558885=⨯cm 8分如果λ∈[43,32],可设122334λλ≤<≤,则由S 的表达式得 S(λ1)-S(λ2)=44)5858(102211λλλλ--+ =)58)((104421121λλλλ--25,8038≥>->故因此S(λ1)-S(λ2)<0,所以S (λ)在区间[43,32]内单调递增. 从而,对于λ∈[43,32],当λ=32时,S (λ)取得最小值答:画面高为88cm、宽为55cm 时,所用纸张面积最小;如果要求λ∈[43,32],当λ=32时,所用纸张面积最小. 12分21.证明:依设,得椭圆的半焦距c=1,右焦点为F (1,0),右准线方程为x=2,点E 的坐标为(2,0),EF 的中点为N (23,0) 3分若AB 垂直于x 轴,则A (1,y1),B(1,-y1),C(2,-y1), ∴AC 中点为N (23,0),即AC 过EF 中点N.若AB 不垂直于x 轴,由直线AB 过点F ,且由BC ∥x 轴知点B 不在x 轴上,故直线AB 的方程为y=k(x-1),k≠0.记A (x1,y1)和B(x2,y2),则C (2,y2)且x1,x2满足二次方程1)1(2222=-+x k x即(1+2k2)x2-4k2x+2(k2-1)=0,∴x1+x2=22212221)1(2,214kkx x kk+-=+ 10分又x21=2-2y21<2,得x1-23≠0,故直线AN ,CN 的斜率分别为k1=32)1(2231111--=-x x k x y )1(2232222-=-=x k y k∴k1-k2=2k·32)32)(1()1(1121-----x x x x∵(x1-1)-(x2-1)(2x1-3)=3(x1+x2)-2x1x2-4 =0)]21(4)1(412[2112222=+---+k k kk∴k1-k2=0,即k1=k2,故A 、C 、N 三点共线.所以,直线AC 经过线段EF 的中点N. 14分 22.(Ⅰ)解:因为对x1,x2∈[0,21],都有f(x1+x2)=f(x1)·f(x 2),所以22)]41([)41()41()4141()21()]21([)21()21()2121()1(]1,0[,0)2()2()22()(f f f f f f f f f f x xf x f xx f x f =⋅=+==⋅=+=∈≥⋅=+= f(1)=a>0, 3 分∴4121)41(,)21(a f a f == 6分(Ⅱ)证明:依题设y=f(x)关于直线x=1对称, 故f(x)=f(1+1-x),即f(x)=f(2-x),x∈R 又由f(x)是偶函数知f(-x)=f(x),x∈R , ∴f(-x)=f(2-x),x∈R ,将上式中-x以x代换,得f(x)=f(x+2),x∈R这表明f(x)是R 上的周期函数,且2是它的一个周期. 10分 (Ⅲ)解:由(Ⅰ)知f(x)≥0,x∈[0,1] ∵]21)1(21[)21()21(nn n f nn f f ⋅-+=⋅=11()[(1)]22f f n nn=⋅-⋅=1111()()()[()]2222nf f f f n n n n=⋅⋅⋅=21)21(a f = ∴n a nf 21)21(= 12分 ∵f(x)的一个周期是2 ∴f(2n+n21)=f(n21),因此a n =n a 210)ln 21(lim )(ln lim ==∴∞→∞→a na n n n 14分。
2001年广东省普通高等学校本科插班生招生考试《高等数学》试题一、填空题(每小题2分,共26分)1、设k x x g x x f +=+=4)(,23)(且()[]()[]x f g x g f =,则k= 。
2、如果32sin 3lim0=→x kx x ,则k= 。
3、设⎪⎩⎪⎨⎧=≠+=0,)1(0,)(x kx x a x mx f ,(k ,m 为常数),)(x f 在0=x 处连续,=a 。
4、曲线xf 2=在点(1,2)的法线方程式 。
5、设参数方程⎩⎨⎧==ta x ta y cos sin 2,则=-4πt dxdy 。
6、计算⎰='⋅dx x f x f x )()(332 。
7、若2)23(0=-⎰dx x a,则=a 。
8、⎰+=x xe dt t f x sin )(220,则=)(x f 。
9、⎰=-∞210dt ae (a 为常数),则a = 。
10、设)ln(22y x z+=,则全微分=dz 。
11、改变二次积分的次序⎰⎰=dy y x f dx s e ),(ln 01。
12、幂级数∑=+kn n n x n 133的收敛半径R= 。
13、微积分方程022=+dx xe dy x 的通解是=y 。
二、计算题(一)(每小题5分,共30分)1、xe e x x x 20sin 2lim -+-→。
2、设(),42arcsin 22-+-+=f e x x x y 其中f 为可微函数,求dy 。
3、求函数53)(23+-=x x x f 的单调区间及极值。
4、计算⎰-dxx x sin cos 22ππ。
5、设yxx yz +=sin ,求yzx z ∂∂∂∂,。
6、求级数∑=⋅-mn nnn x 14)4(的收敛范围。
三、计算题(二)(每小题6分,共36分)1、若3)1sin(lim 221=-++→x bax x x ,求b a ,的值。
2、已知函数0201sin 2)(≤≤<⎪⎩⎪⎨⎧=x x x x x x f(1)写出函数)(x f 的定义域;(2)讨论函数)(x f 在0=x 的连续性与可导性。
昆明理工大学2001级高等数学[下]期末试卷一、填空(每小题4分,共24分)1.函数22ln(1)z x y =--的定义域是 ,函数在 是间断的. 2.设函数22sin()z x y =+,则z x ∂=∂ ,z y∂=∂ . 3.函数23z x xy =+在 点(1,2)处沿x 轴负方向的方向导数等于 . 4.设2222:x y z a ∑++=,则曲面积分222()xy z dS ∑++⎰⎰= .5.设:11,02D x y -≤≤≤≤,则二重积分2Dx yd σ⎰⎰= .6.如果微分方程的通解的所有任意常数的值确定后,所得到的微分方程的解称之为 解. 二、解答下列各题(每小题6分,共18分) 1.求函数22ax by z e+=(,a b 为常数)的全微分.2.求曲面2220x y z +-=在点(1,1,3)处的切平面方程和法线方程. 3.求微分方程(1)x x e yy e '-=的通解. 三、解答下列各题(每小题6分,共18分) 1.设(),z xy xF u =+而,()y u F u x =为可导函数,试计算z z x y x y∂∂+∂∂. 2.计算三重积分,.zdxdydz Ω⎰⎰⎰其中Ω是由曲面222z x y =--及22z x y =+所围成的闭区域. 3.计算曲面积分xyzdydz ∑⎰⎰,其中∑是柱面222(0)x y a x +=≥介于平面0y =及(0)y h h =>之间部分的前侧。
四、(12分)求微分方程''3'2cos y y y x -+=的通解.五、(12分)求曲线积分22(1),(1)Lydx x dyx y ---+⎰其中:(1)(8分)L 为圆周2220x y y +-=的正向.(2)(4分)L 为椭圆22480x y x +-=的正向 六、(10分)求表面积为36,而体积为最大的长方体的体积.七、(7分)讨论函数22223222220(,)()00x y x y f x y x y x y ⎧+≠⎪=⎨+⎪+=⎩ 在(0,0)处的连续性.昆明理工大学2002级高等数学(下)期末试卷一.填空题(每小题4分,共40分)1.设函数33z x y y x =-,则全微分dz =2.设函数(,),u f x y xy f =+具有一阶连续偏导数,则ux∂=∂3.二重积分120(,)yI dy f x y dx =⎰⎰,改变积分次序后I = .4.直角坐标系下的三次积分3222111222110)x x y xI dx dy fx y z dz ------=++⎰⎰⎰化为球坐标系下的三次积分I =5.若区域2222:x y z R Ω++=,则三重积分xyzdxdydz Ω⎰⎰⎰=6.当λ= 时,(2)()x y d x x y d y λ+++为某二元函数(,)u x y 的全微分.7.曲线积分22()LI x y dx =-⎰,其中L 是抛物线2y x =上从点(0,0)A 到(2,4)B 的一段弧,则I = .8.当∑为xoy 面内的一个闭区域D 时,曲面积分与二重积分的关系为(,,)f x y z dS ∑⎰⎰= .9.二阶常系数齐次线性微分方程''2'0y y y ++=的通解为y =10. 二阶常系数非齐次线性微分方程''2'2x y y y e --+=的特解形式为y *= 二.(10分)(,)u v Φ具有连续偏导数,证明由方程(,)0cx az cy bz Φ--= 所确定的函数(,)z f x y =满足z zab c x y∂∂+=∂∂ 三.(10分)由锥面22z x y =+及抛物面22z x y =+所围立体体积四.(10分)求螺旋线cos ,sin ,x a y a z b θθθ===在(,0,0)a 处的切线方程及法平面方程.五、(10分)利用高斯公式计算曲面积分11()()x xI f dydz f dzdx zdxdy y y x y∑=++⎰⎰, 其中()f u 具有二阶连续导数,∑为上半球面222z a x y =--与0z =所围成空间闭区域Ω的整个边界曲面的外侧. 六.(10分)设曲线积分2()[2()]Lyf x dx xf x x dy +-⎰在右半平面(0)x ≥内与路径无关,其中()f x 可导且(1)1f =,求()f x .七.(10分)二阶常系数非齐次线性微分方程''2'33y y y x --=,求其通解.昆明理工大学2003级高等数学[下]期末试卷一.填空题(每小题4分,共32分)1.设函数2()y z tg x =,则z x ∂∂ ,zy∂∂ .2.曲线2233,,x t y t z t ===在(1,1,1)M 处的切线方程为.3.交换二次积分次序,2220(,)y y dy f x y dx =⎰⎰.4.设L 为右半圆周:221(0)x y x +=≥,则曲线积分LI yds =⎰.5.设∑为平面1234x y z++=在第一卦限中的部分,则曲面积分()234x y z dS ∑++=⎰⎰ .6.级数13!n n n n n∞=∑的敛散性为 .7.幂级数2121nn n x n ∞=+∑的收敛半径R= ,收敛区间为 .8.求微分方程229200d y dyy dx dx-+=的通解为 . 二.解答下列各题(每小题7分,共35分) 1.设0,z e xyz dz -=求.2.讨论函数22(1)2z x y =--是否有极值. 3.求幂级数11n n nx∞-=∑在收敛区间(1,1)-内的和函数.4.求微分方程sin ()1dyxy x dx y π⎧+=⎪⎨⎪=⎩的特解.5.求微分方程1y y '''+=的通解.三.(11分)利用格林公式计算曲线积分(1cos )(sin 2)x x LI e y dx e y x dy =-+-⎰,其中L 为从原点(0,0)0O A π到(,)的正弦曲线sin y x =. 四.(11分)利用高斯公式计算曲面积分23I ydydz x dzdx z dxdy ∑=++⎰⎰,其中∑是球面2222x y z a ++=的内侧.五.(11分)求由锥面22z x y =+及旋转抛物面22z x y =+所围成的立体的体积.昆明理工大学2004级高等数学[下]期末试卷一.填空题(每小题4分,共32分) 1.设函数(),y z f f x =可微,则z z xy x y∂∂+=∂∂ . 2.曲线2233,,x t y t z t ===在t =1处的法平面方程为: . 3.设区域D 由,2y x x ==及1y x =所围,则化二重积分(,)DI f x y d σ=⎰⎰为先x y 后的二次积分后的结果为 .4.设L 为圆弧:222,0x y y +=≥,则曲线积分22()LI x y ds =+=⎰.5.设22:(01)z x y z ∑=+≤≤,则曲面积分2I ds ∑=⎰= .6.级数11(1)[]23nn nn ∞=-+∑收敛于 . 7.幂级数11n n nx∞-=∑的收敛半径R= ,收敛区间为 .8.二阶常系数非齐次线性微分方程324''12'9x y y y e-++=的特解形式为y *= .(不要求计算)二.解答下列各题(每小题7分,共28分)1.求函数z =(,)0y xF z z=,其中F 具有一阶连续偏导数,求dz . 2.讨论224()z x y x y =--的极值. 3.将函数23()2f x x x =--展开成x 的幂级数,并求展开式成立的区间.4.求微分方程1cos sin 2dy dx x y y=+的通解.三.(10分)设L 为222(0)x y a a +=>沿顺时针方向的上半圆,计算曲线积分22LI xy dy x ydx =-⎰.四.(10分)求由球面2222()x y z a a ++-=及222z x y =+所围成的立体的体积. 五.(10分)利用高斯公式计算曲面积分242I xzdydz y dzdx yzdxdy ∑=-+⎰⎰,其中∑是球面2221x y z ++=外侧的上半部分. 六、(10分)求()f x ,使曲线积分2[(2)()][()]LI y xy f x y dx xy f x dy '=+-++/⎰与路径无关,其中()f x 具有二阶连续导数,且(0)0,(0)1f f '==/.。