2.3长方体和正方体·2012数学苏教版六上-步步为营

长方体和正方体一、长方体和正方体的认识要素立体图诂、、棱面顶点数量特征数量特征数量特征[ 长方体12互相平行的棱长度相等6相对的面完全相同8[同一个顶点引出的三条棱分别叫做长、宽、高特殊长方体12垂直于正方形面的棱长度相等6两个面是正方形，其余四个面是完全相同的长方形8正方体12所有的棱长度都相等6所有面都是正方形且完全相同8一个长方体至少可以有两个面是正方形，最多可以有6各面是正方形，但不会存在3个、4个、5个面是正方形！练习：（1）判断并改正：1、长方体的六个面一定是长方形；（）2、正方体的六个面面积一定相等；（）3、一个长方体（非正方体）最多有四个面面积相等；（）4、相交于一个顶点的三条棱相等的长方体一定是正方体。

（）7、长方体的三条棱分别叫做长、宽、高。

（）8、有两个面是正方形的长方体一定是正方体。

（）9、有三个面是正方形的长方体一定是正方体。

（）11、有两个相对的面是正方形的长方体，另外四个面的面积是相等的。

（）12、长方体和正方体最多可以看到3个面。

（）13、正方体不仅相对的面的面积相等，而且所有相邻的面的面积也都相等。

（）14、长方体（不包括正方体）除了相对的面相等，也可能有两个相邻的面相等。

（）15、一个长方体中最少有4条棱长度相等，最多有8条棱长度相等。

（）（2）填空：\1、一个长方体最多有（）个面是正方形，最多有（）条棱长度相等。

2、一个长方体的底面是一个正方形，则它的4个侧面是（）形。

3、正方体不仅相对的面相等，而且所有相邻的面（）,它的六个面都是相等的（）形。

4、把长方体放在桌面上，最多可以看到（）个面。

最少可以看到（）个面。

【知识点2】棱长和公式：长方体棱长和=（长+宽+高）×4 J正方体棱长和=棱长xl2棱长和的变形：长+宽+高=棱长和÷ 4棱长=棱长和÷ 1220Cr例如：有一个礼盒需要用彩带捆扎，捆扎效果如图，打结部分需要10厘米彩带，一共需要多长的彩 带 分析：本题虽然并未直接提出求棱长和，但山于彩带的捆扎是和棱相互平行的，因此，在解决问题 时首先确定每部分彩带与那条棱平行，从而间接去求棱长和。

苏教版六年级上长方体和正方体在苏教版六年级上册的数学学习中，长方体和正方体是非常重要的几何图形。

它们在我们的日常生活中随处可见，从房屋的建筑结构到日常使用的各种盒子，都离不开长方体和正方体的身影。

长方体是一个由六个矩形面围成的立体图形。

这六个面两两相对，相对的面完全相同。

它有 8 个顶点和 12 条棱。

其中，4 条长棱的长度相等，4 条宽棱的长度相等，4 条高棱的长度相等。

举个例子，我们常见的书本，通常就是一个长方体。

书本的封面和封底就是长方体的上下面，这两个面的大小通常是相同的。

书本的侧面就是长方体的前后面和左右面，它们也分别两两相对且相等。

而正方体则是一种特殊的长方体，它的六个面都是完全相同的正方形，12 条棱的长度也都相等，8 个顶点。

像我们玩的魔方，就是一个典型的正方体。

学习长方体和正方体，首先要掌握它们的特征。

比如，长方体相对的面面积相等，而正方体每个面的面积都相等。

在计算长方体和正方体的表面积时，方法也有所不同。

长方体的表面积等于（长×宽＋长×高＋宽×高）×2。

这是因为长方体有六个面，相对的两个面面积相等，所以分别求出三个不同面的面积之和，再乘以 2 就得到了表面积。

例如，一个长方体的长是 5 厘米，宽是 3 厘米，高是 4 厘米。

那么它的表面积就是：＼＼begin{align}＆（5×3 ＋ 5×4 ＋ 3×4)× 2\＼＝＆（15 ＋ 20 ＋ 12)× 2\＼＝＆47× 2\＼＝＆94（平方厘米）＼end{align}＼正方体的表面积则等于棱长×棱长×6。

因为正方体的六个面都相同，每个面都是一个正方形，正方形的面积等于边长的平方，所以正方体的表面积就是一个面的面积乘以 6。

假如一个正方体的棱长是 6 厘米，那么它的表面积就是：＼＼begin{align}＆6×6× 6\＼＝＆36× 6\＼＝＆216（平方厘米）＼end{align}＼再来说说它们的体积计算。

一长方体和正方体（教案）20232024学年数学六年级上册苏教版一、教学内容今天我要向大家介绍的是苏教版六年级上册数学的第五章——长方体和正方体。

这一章主要内容包括长方体和正方体的特征、表面积和体积的计算方法。

通过本章的学习，大家将能够理解长方体和正方体的基本概念，掌握它们的性质和计算方法。

二、教学目标本节课的教学目标有三点：一是让学生理解长方体和正方体的特征，知道它们之间的关系；二是让学生掌握长方体和正方体的表面积和体积的计算方法；三是培养学生的空间想象力，提高他们的数学思维能力。

三、教学难点与重点本节课的重点是长方体和正方体的特征以及表面积和体积的计算方法。

难点在于让学生理解长方体和正方体之间的关系，以及如何运用这些关系来计算表面积和体积。

四、教具与学具准备为了让大家更好地理解长方体和正方体，我准备了一些立体模型和图纸。

这些模型和图纸可以帮助大家直观地看到长方体和正方体的内部结构，以及它们之间的关系。

五、教学过程1. 导入：我会从生活中的一些实例引入，比如家具、建筑等，让大家观察并思考它们是什么几何体。

2. 讲解：接着，我会向大家讲解长方体和正方体的特征，以及它们之间的关系。

我会结合模型和图纸，让大家更直观地理解这些概念。

3. 练习：在讲解之后，我会给大家一些练习题，让大家运用所学的知识来解决问题。

我会逐一解答大家的问题，确保大家能够掌握这些知识。

六、板书设计板书设计如下：长方体和正方体的特征：1. 长方体：有六个面，相对的面面积相等，有12条棱，相对的棱长度相等，有8个顶点。

2. 正方体：有六个面，相对的面面积相等，有12条棱，相对的棱长度相等，有8个顶点。

长方体和正方体的表面积和体积的计算方法：1. 表面积：长方体表面积 = (长×宽 + 长×高 + 宽×高)×2；正方体表面积 = 棱长×棱长×6。

2. 体积：长方体体积 = 长×宽×高；正方体体积 = 棱长×棱长×棱长。

六年级上册数学教案长方体和正方体的认识苏教版我今天要为大家带来的是六年级上册数学教案——长方体和正方体的认识，这是苏教版教材中的一章。

一、教学内容我们今天的学习内容主要包括苏教版六年级上册数学教材中第七单元“长方体和正方体”的章节。

这部分内容主要介绍了长方体和正方体的定义、特征、表面积和体积的计算方法等。

二、教学目标通过今天的学习，我希望孩子们能够理解长方体和正方体的基本概念，掌握它们的特征，学会计算它们的表面积和体积，并能运用这些知识解决实际问题。

三、教学难点与重点本节课的重点是让孩子们掌握长方体和正方体的特征，以及表面积和体积的计算方法。

难点则是如何让孩子们理解并掌握长方体和正方体的空间结构。

四、教具与学具准备为了帮助孩子们更好地理解长方体和正方体的结构，我准备了一些立体模型，以及一些用于计算表面积和体积的实际物品，如尺子、胶带等。

五、教学过程1. 引入：我通过展示一些生活中的长方体和正方体物品，如牙膏盒、魔方等，让孩子们初步感受长方体和正方体的特征。

2. 讲解：我利用立体模型，向孩子们讲解长方体和正方体的定义、特征，以及表面积和体积的计算方法。

3. 练习：孩子们在课堂上进行一些实际操作，如用尺子测量物品的长、宽、高，计算它们的表面积和体积。

4. 应用：孩子们运用所学知识解决一些实际问题，如计算魔方的表面积和体积。

六、板书设计我在黑板上写下长方体和正方体的特征、表面积和体积的计算公式，以及一些关键的步骤和要点。

七、作业设计1. 题目：计算一个长方体和一个正方体的表面积和体积。

答案：长方体的长为4cm，宽为3cm，高为2cm，表面积为52cm²，体积为24cm³；正方体的边长为3cm，表面积为54cm²，体积为27cm³。

2. 题目：一个长方体的长、宽、高分别为6cm、4cm、3cm，求它的表面积和体积。

答案：表面积为96cm²，体积为72cm³。

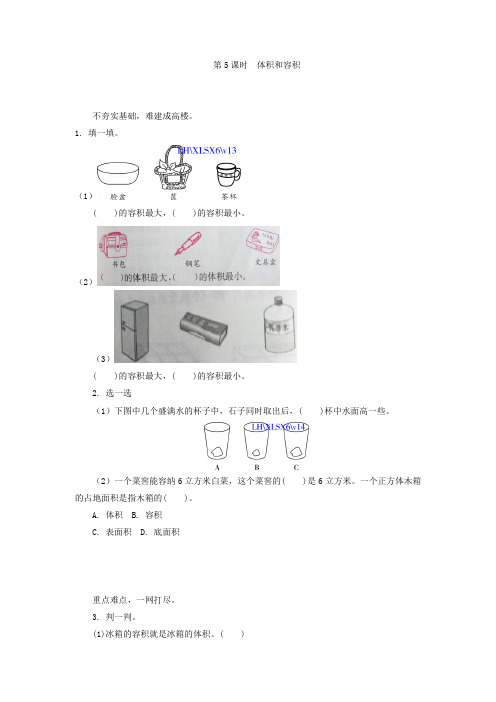
第5课时体积和容积不夯实基础，难建成高楼。

1. 填一填。

（1）( )的容积最大，( )的容积最小。

（2）（3）( )的容积最大，( )的容积最小。

2. 选一选（1）下图中几个盛满水的杯子中，石子同时取出后，( )杯中水面高一些。

（2）一个菜窖能容纳6立方米白菜，这个菜窖的( )是6立方米。

一个正方体木箱的占地面积是指木箱的( )。

A. 体积B. 容积C. 表面积D. 底面积重点难点，一网打尽。

3. 判一判。

(1)冰箱的容积就是冰箱的体积。

( )(2)游泳池里注满水，水的体积就是游泳池的容积。

( )4. 蛋糕房里有两种无盖纸盒，里面都放了若干个同样大的小蛋糕，且正好放满（如下图）。

哪一个纸盒的容积要大一些？在下面的括号里画“√”。

( ) ( )5. 选择合适的词填在括号里。

（1）盛满水的水桶，( )的体积就是( )的容积。

（水桶水）（2）盛满瓜子的盒子，( )的体积就是( )的容积。

（瓜子盒子）6. 下面是三堆砖块，每块砖的大小相等，形状相同。

①②③第( )堆砖的体积最大，第( )堆和第( )堆砖的体积相等。

举一反三，应用创新，方能一显身手！7. 下面三个物体的体积是否一样大？如果每个小正方体的体积是1立方厘米，你能说出每个物体的体积是多少立方厘米吗？第5课时1.（1）筐茶杯（2）书包钢笔（3）冰箱文具盒2.（1）B （2）B D3. (1)(2)4. 第一个5.（1）水水桶（2）瓜子盒子6. ②①③7. 第一个是6立方厘米，第二个是6立方厘米，第三个也是6立方厘米，三个物体的体积一样大。

第二单元长方体和正方体教学内容：教科书第10～37页教学要求：1、使学生通过观察、操作等活动认识长方体、正方体的面、棱、顶点以及长宽高（棱长）的含义，掌握长方体和正方体的特征。

2、使学生在活动中进一步积累空间与图形的学习经验，增强空间观念，发展数学思考。

3、使学生理解并掌握长方体和正方体的表面积的含义和计算方法，能运用长方体和正方体的表面积的计算方法解决一些简单的实际问题。

4、使学生进一步感受立体图形的学习价值，增强学习数学的兴趣。

5、进一步巩固长方体和正方体的表面积的含义和计算方法，能根据所求问题的具体特点选择计算方法解决一些简单的实际问题。

6、引导学生通过操作活动，初步认识体积和容积的意义。

7、使学生通过观察、操作等活动认识体积单位，初步具有1立方米、1立方分米、1立方厘米的实际大小的观念。

8、使学生经历操作、观察、猜想、验证、交流和归纳等数学活动的过程，探索并掌握长方体和正方体的体积公式，能应用公式正确计算长方体和正方体的体积，并能解决相关的简单实际问题。

9、使学生经历1立方分米＝1000立方厘米、1立方米＝1000立方分米的推导过程，明白相邻的两个体积单位之间的进率是1000的道理。

10、会应用对比的方法，记忆并区分长度单位、面积单位和体积单位，掌握它们相邻两个单位间的进率。

教学重点、难点：通过观察、操作等活动认识长方体、正方体的面、棱、顶点以及长宽高（棱长）的含义，掌握长方体和正方体的特征。

在活动中进一步积累空间与图形的学习经验，增强空间观念，发展数学思考。

使学生通过观察、操作等活动认识体积单位，初步具有1立方米、1立方分米、1立方厘米的实际大小的观念。

教学时间：约14课时第一课时长方体和正方体的认识（1）教学内容：教学第10-11页的例1、例2，完成随后的练一练及练习三1-5题。

教学要求：1.知识与技能：使学生通过观察、操作等活动认识长方体、正方体的面、棱、顶点以及长宽高（棱长）的含义，掌握长方体和正方体的特征。

苏教版六年级上册《长方体和正方体》数学教案一、教学目标1.了解长方体和正方体的概念及属性。

2.能够分类长方体和正方体。

3.掌握计算长方体和正方体的表面积和体积的公式。

4.应用所学知识解决实际问题。

二、教学重难点1.长方体和正方体的概念及属性。

2.长方体和正方体的分类方法。

3.计算长方体和正方体的表面积和体积。

三、教学过程1.导入环节通过一些实物或图片向学生展示长方体和正方体的形状，让学生能够初步认识这两种几何体，引导学生思考长方体和正方体具有什么相同和不同的属性。

2.讲授长方体和正方体的概念及属性首先通过黑板、幻灯片等教具向学生讲解长方体和正方体的概念及属性。

同时，让学生能够了解这两种几何体的公共点和差异点。

3.分类长方体和正方体讲解长方体和正方体的分类方法。

帮助学生学习如何根据长方体和正方体的不同属性，将其分类，为后续的计算打下基础。

4.计算长方体和正方体的表面积和体积（1）计算长方体的表面积和体积公式讲解长方体如何利用公式计算表面积和体积，并围绕例题进行讲解。

（2）计算正方体的表面积和体积公式讲解正方体如何利用公式计算表面积和体积，并围绕例题进行讲解。

5.练习长方体和正方体的计算对学生进行个人或小组练习，巩固所学知识。

老师可以出一些练习题，在课堂上标准的讲解答案。

6.实际应用结合实际生活中的情境，让学生能够应用所学的知识，解决一些与长方体和正方体相关的问题。

例如，我们可以利用一些常见的包装箱、图书馆书架、橱柜、电视、笔记本电脑等实物作为教学案例，让学生考虑如何计算它们的表面积和体积，从而更好地理解长方体和正方体的实际应用。

7.课堂总结回顾本节课所学内容，强调重要的知识点和难点，让学生对所学知识形成全面而深刻的理解。

四、课后作业1.参加课堂练习题目的解答。

2.完成教师布置的相关作业。

3.自主练习，巩固所学知识。

五、教学反思本次课着重介绍了长方体和正方体的概念和计算方法，涵盖了丰富的实例和教材，为学生打下了良好的基础。

六年级数学上册长方体和正方体教案苏教版第一章：长方体和正方体的定义及特征1.1 教学目标让学生理解长方体和正方体的定义。

让学生掌握长方体和正方体的特征。

1.2 教学内容长方体和正方体的定义。

长方体和正方体的特征。

1.3 教学步骤1. 引入长方体和正方体的概念。

2. 讲解长方体和正方体的定义。

3. 通过实物或图片展示长方体和正方体的特征。

5. 进行课堂练习，巩固学生对长方体和正方体的理解和掌握。

第二章：长方体和正方体的表面积和体积2.1 教学目标让学生理解长方体和正方体的表面积和体积的计算方法。

让学生能够运用表面积和体积的计算方法解决实际问题。

2.2 教学内容长方体和正方体的表面积和体积的计算方法。

实际问题中的表面积和体积的计算。

2.3 教学步骤1. 引入长方体和正方体的表面积和体积的概念。

2. 讲解长方体和正方体的表面积和体积的计算方法。

3. 通过例题展示如何运用表面积和体积的计算方法解决实际问题。

4. 让学生进行练习题，巩固学生对长方体和正方体的表面积和体积的计算方法的掌握。

5. 进行课堂讨论，让学生分享自己的解题思路和方法。

第三章：长方体和正方体的展开图3.1 教学目标让学生理解长方体和正方体的展开图的概念。

让学生能够通过展开图理解长方体和正方体的结构和特征。

3.2 教学内容长方体和正方体的展开图的概念。

通过展开图理解长方体和正方体的结构和特征。

3.3 教学步骤1. 引入长方体和正方体的展开图的概念。

2. 展示长方体和正方体的展开图。

3. 讲解如何通过展开图理解长方体和正方体的结构和特征。

5. 进行课堂练习，巩固学生对长方体和正方体的展开图的理解和掌握。

第四章：长方体和正方体的应用题4.1 教学目标让学生能够运用长方体和正方体的知识解决实际问题。

培养学生的应用能力和解决问题的能力。

4.2 教学内容长方体和正方体的应用题。

解决实际问题中的长方体和正方体的应用题。

4.3 教学步骤1. 引入长方体和正方体的应用题的概念。