下载文档原格式
第25章概率25.1.1事件1
“天有不测风云”
原意是指刮风、下雨、阴天、晴天这些天气状况很难预料.
它被引申为：世界上很多事情具有偶然性，人们不能事先判定这些事情是否会发生。
降水概率90%
要的数字概念，正是在研究这些规律中产生的。
人们用
发生的可能性的大小。
例如，天气预报说明天的降水概
就意味着明天有很大可能下雨（雪）。
现在概率的应用日益广泛。
本章中，我们将学习一些概率初步
知识，从而提高对偶然事件发生规律的认识。
学习目标：
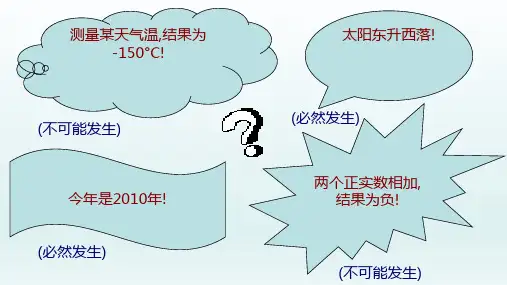
1.了解必然事件、不可能事件、随机事件的特点。
2.会判断一个事件是什么事件。
思考:
下列哪些现象是必然发生的,哪些现象是不可能发生的?。
如果从结果能否预知的角度来看，可以分为两大类：另一类现象的结果是无法预知的，即在一定的条件下，出现那种
结果是无法预先确定的，这类现象称为随机现象．一类现象的结果总是确定的，即在一定的条件下，它所出现的结
果是可以预知的，这类现象称为确定性现象；
在自然界和实际生活中，我们会遇到各种各样的现象．
在一定条件下:
必然会发生的事件叫做必然事件;
必然不会发生的事件或者不可能发生的事件叫做不可能事件;可能会发生，也可能不发生的事件叫做不确定事件或随机事件.特征：事先不能预料即具有不确定性。
5名同学参加演讲比赛，以抽签方式决定每个人的出场顺序。
签筒中有5根形状大小相同的纸签，上面分别标有出场的序号1，2，3，4，5。
小军首先抽签，他在看不到的纸签上的数字的情况从签筒中随机（任意）地取一根纸签。
（1）抽到的序号有几种可能的结果？（2）抽到的序号小于6吗？
（3）抽到的序号会是0吗？
（4）抽到的序号会是1吗？
（5）请你用自己的语言叙述随机事件的定义。
在同样条件下，随机事件可能发生，也可能不发生，那么它发生的可能性有多大呢？能否用数值进行刻画呢？这是我们下面要讨论的问题。
请看下面两个试验。
试验1：从分别标有1，2，3，4，5号的5根纸签中随机地抽取一根，抽出的签上号码有5种可能，即1，2，3，4，5。
由于纸签形状、大小相同，又是随机抽取，所以每个号被抽到的可能性大小相等，都是全部可能结果总数的1/5。
试验2：掷一枚骰子，向上的一面的点数有6种可能，即1，2，3，4，5，6。
由于骰子形状规则、质地均匀，又是随机掷出，所以出现每种结果的可能性大小相等，都是全部可能结果总数的1/6。
上述数值1/5和1/6反映了试验中相应随机事件发生的可能性大小。
概率的定义：
一般地，对于一个随机事件A，我们把刻画其发生可能性大小的数值，称为随机事件A发生的概率，记作P（A）。
归纳：
一般地，如果在一次试验中，有n种可能的结果，并且它们发
生的可能性都相等，事件A包含其中的m种结果，那么事件A发
生的概率
m
P（A）=
n
回忆刚才两个试验，它们有什么共同特点吗？
可以发现，以上试验有两个共同特点：
（1）每一次试验中，可能出现的结果只有有限个；（2）每一次试验中，各种结果出现的可能性相等。
