下载文档原格式
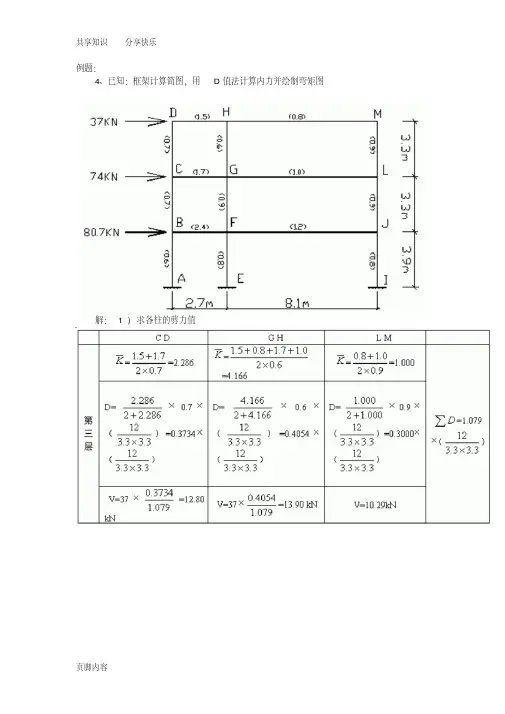
例题：4、已知：框架计算简图，用D值法计算内力并绘制弯矩图解： 1 ）求各柱的剪力值2 ）求出各柱的反弯点高度yh3）求各柱的柱端弯矩第三层M CD=12.800.41 3.3kN·m=17.32 kN·mM DC=12.800.59 3.3 kN·m =24.92 kN·mM GH=13.900.45 3.3 kN·m =20.64 kN·mM HG=13.900.55 3.3 kN·m =25.23 kN·mM LM=10.290.35 3.3 kN·m =11.88 kN·mM ML=10.290.65 3.3 kN·m =22.07 kN·m第二层M BC=34.720.50 3.3 kN·m =57.29 kN·mM FG=47.800.50 3.3 kN·m =78.87 kN·mM CB=57.29 kN·mM GH=78.87 kN·mM JL=28.480.45 3.3 kN·m =42.29 kN·mM ML=28.480.55 3.3 kN·m =51.69 kN·m 第一层M AB=56.680.55 3.9 kN·m =121.6 kN·mM EF=77.510.55 3.9 kN·m =166.3 kN·mM BA=56.680.45 3.9 kN·m =99.47 kN·mM FE=77.510.45 3.9 kN·m =136.0 kN·mM IJ=57.560.575 3.9 kN·m =129.1 kN·mM JI=57.560.425 3.9 kN·m =95.41 kN·m4）求各横梁梁端的弯矩第三层M DH= M DC=24.92 kN·mM DH=25.23 kN·m =16.45 kN·mM HM=25.23 kN·m =8.776 kN·mM MH= M ML=22.07 kN·m第二层M CG= M CD+ M CB =17.32 kN·m +57.29 kN·m =24.92 kN·m M GC=（20.64+78.87）kN·m =62.65 kN·mM GC=（20.64+78.87）kN·m =36.86 kN·mM LG= M LM+ M LJ =11.88 kN·m +51.69 kN·m =63.57 kN·m 第一层M BF= M BC+ M BA =57.29 kN·m +99.47 kN·m =156.8 kN·m M FB=（136.0+78.87）kN·m =143.2 kN·mM FJ=（136.0+78.87）kN·m =71.62 kN·mM JF= M JL+ M JI =42.29 kN·m +95.41 kN·m =137.7 kN·m 5）绘各横梁与柱的弯矩图（单位：kN·m）如下图所示。
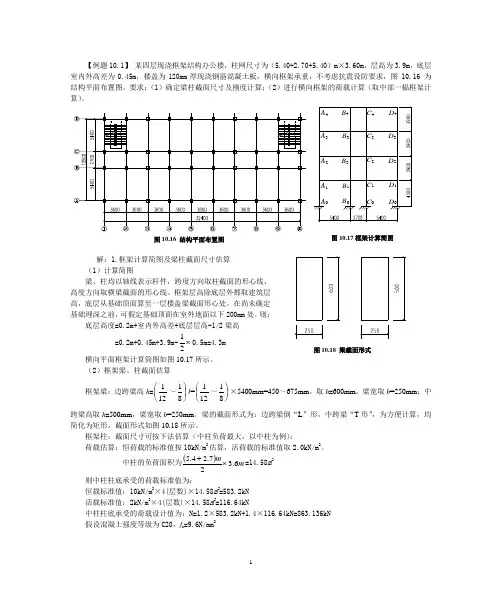
1【例题10.1】 某四层现浇框架结构办公楼，柱网尺寸为（5.40+2.70+5.40）m ×3.60m ，层高为3.9m ，底层室内外高差为0.45m ，楼盖为120mm 厚现浇钢筋混凝土板，横向框架承重，不考虑抗震设防要求，图 10.16 为结构平面布置图。
要求：（1）确定梁柱截面尺寸及刚度计算；（2）进行横向框架的荷载计算（取中部一榀框架计算）。
解：1.框架计算简图及梁柱截面尺寸估算（1）计算简图梁、柱均以轴线表示杆件，跨度方向取柱截面的形心线，高度方向取横梁截面的形心线。
框架层高除底层外都取建筑层高，底层从基础顶面算至一层楼盖梁截面形心处。
在尚未确定基础埋深之前，可假定基础顶面在室外地面以下200mm 处。
则：底层高度=0.2m+室内外高差+底层层高-1/2梁高=0.2m+0.45m+3.9m-⨯210.5m=4.3m 横向平面框架计算简图如图10.17所示。
（2）框架梁、柱截面估算 框架梁：边跨梁高h =⎝⎛121～⎪⎭⎫81l = ⎝⎛121～⎪⎭⎫81×5400mm=450～675mm ，取h =600mm ，梁宽取b =250mm ；中跨梁高取h =500mm ，梁宽取b =250mm 。
梁的截面形式为：边跨梁倒“L ”形，中跨梁“T 形”，为方便计算，均简化为矩形，截面形式如图10.18所示。
框架柱：截面尺寸可按下法估算（中柱负荷最大，以中柱为例）：荷载估算：恒荷载的标准值按10kN/m 2估算，活荷载的标准值取2.0kN/m 2。
中柱的负荷面积为()m m 6.327.24.5⨯+=14.58m 2则中柱柱底承受的荷载标准值为：恒载标准值：10kN/m 2×4(层数)×14.58m 2=583.2kN活载标准值：2kN/m 2×4(层数)×14.58m 2=116.64kN中柱柱底承受的荷载设计值为：N=1.2×583.2kN+1.4×116.64kN=863.136kN假设混凝土强度等级为C20，f c =9.6N/mm 2图10.17框架计算简图图10.18 梁截面形式2柱的截面面积 26.99.08631369.0mm N N f N A c ⨯=≥=99900mm 2选用柱的截面面积为400mm ×500mm ，实际面积为200000mm 2。
D值法例题详解内部编号：（YUUT-TBBY-MMUT-URRUY-UOOY-DBUYI-0128）例题：4、已知：框架计算简图，用D值法计算内力并绘制弯矩图解： 1 ）2 ）3）求各柱的柱端弯矩第三层MCD=kN·mMDC=kN·m = kN·mMGH=kN·m = kN·mMHG=kN·m = kN·mMLM=kN·m = kN·mMML=kN·m = kN·m 第二层MBC=kN·m = kN·mMFG=kN·m = kN·mMCB= kN·mMGH= kN·mMJL=kN·m = kN·mMML=kN·m = kN·m 第一层MAB=kN·m = kN·mMEF=kN·m = kN·mMBA=kN·m = kN·mMFE=kN·m = kN·mMIJ=kN·m = kN·mMJI=kN·m = kN·m 4）求各横梁梁端的弯矩第三层MDH = MDC= kN·mMDH=kN·m = kN·mMHM=kN·m = kN·mMMH = MML= kN·m第二层MCG = MCD+ MCB= kN·m + kN·m = kN·mMGC=（+）kN·m = kN·mMGC=（+）kN·m = kN·mMLG = MLM+ MLJ= kN·m + kN·m = kN·m第一层MBF = MBC+ MBA= kN·m + kN·m = kN·mMFB=（+）kN·m = kN·mMFJ=（+）kN·m = kN·mMJF = MJL+ MJI= kN·m + kN·m = kN·m5）绘各横梁与柱的弯矩图（单位：kN·m）。
结构计算-D值法主要内容：D 值法内容分解：1）两种计算⽅法的⽐较，引出较精确的 D 值法；2）具体计算步骤作⽤在框架上的⽔平荷载主要有风荷载和地震作⽤，它们均可简化成作⽤在框架节点上的⽔平集中⼒。
由于⽔平荷载均可简化为⽔平集中⼒的形式，所以⾼层多跨框架在⽔平荷载作⽤下的弯矩图通常如图1所⽰。
各杆的弯矩图均为直线，且均有⼀弯矩为零的点，称为反弯点。
该点弯矩为零，但有剪⼒，如图1中所⽰的，。
如果能求出各柱的剪⼒及其反弯点位置，则各柱端弯矩就可算出，进⽽根据节点⼒矩平衡可算出梁端弯矩。
因此必须确定各柱间剪⼒的分配⽐和确定各柱的反弯点的位置⼀、反弯点法回顾反弯点法的适⽤条件为梁的线刚度⼚与柱的线刚度■之⽐⼤于3,其计算过程如下：（1）反弯点位置的确定由于反弯点法假定梁的线刚度⽆限⼤，则柱两端产⽣相对⽔平位移时，柱两端⽆任何转⾓，且弯矩相等，反弯点在柱中点处。
因此反弯点法假定：对于上部各层柱，反弯点在柱中点；对于底层柱，由于柱脚为固定端，转⾓为零，但柱上端转⾓不为零，且上端弯矩较⼩，反弯点上移，故取反弯点在距固定端2/3⾼度处。
（2）柱的侧移刚度反弯点法中⽤侧移刚度 d 表⽰框架柱两端有相对单位侧移时柱中产⽣的剪⼒，它与柱两端的约束情况有关。
由于反弯点法中梁的刚度⾮常⼤，可近似认为节点转⾓为零，则根据两端⽆转⾓但有单位⽔平位移时杆件的杆端剪⼒⽅程，最后得 ,V 12i fd 三—⼕歸占卅（1）式中，V 为柱中剪⼒，J 为柱层间位移，h 为层⾼（3）同⼀楼层各柱剪⼒的分配根据⼒的平衡条件、变形协调条件和柱侧移刚度的定义，可以得出第j 层第i 根柱的剪⼒为：式中，?为第j 层各柱的剪⼒分配系数，所有⽔平荷载的总和，即第j 层由外荷载引起的总剪⼒。
这⾥，需要特别强调的是，⼆⼇‘ 与第j 层所承担的⽔平荷载是有所区别的。
由式（2）可以看出，在同⼀楼层内，各柱按侧移刚度的⽐例分配楼层剪⼒。
⑵m 为第j 层柱⼦总数，⼀'为第j 层以上（4）柱端弯矩的计算由于前⾯已经求出了每⼀层中各柱的反弯点⾼度和柱中剪⼒，那么柱端弯矩可按下式计算：柱下端弯矩柱上端弯矩叫⼚农h-训（3）式中，；'为第j 层第i 根柱的反弯点⾼度，‘ ■'为第j 层的柱⾼（5）梁端弯矩的计算梁端弯矩可由节点平衡求出，如图图3节点弯矩对于边柱对于中柱 (5a )式中，⼆、-分别为左边梁和右边梁的线刚度。
