当前位置：文档之家 › 材料力学习题册答案-第3章 扭转

材料力学习题册答案-第3章 扭转

  • 格式：doc
  • 大小：574.50 KB
  • 文档页数：9

下载文档原格式

  / 9

合集下载

3章材料力学课后习题题解

3章材料力学课后习题题解

Me
Me

l
r0=30mm ，t=2mm，l=300mm ，φ=0.76o
T 2 r02t 1.2 106 = 2 3.14 302 2 =106MPa ；
Me
Me

l
l = r0 r0 30 0.76 = 1.326 103 rad
l 300 180
3.18 某阶梯形圆轴受扭如图所示，材料的切变模量为G= 80GPa ，许用切应力，[τ]=100MPa，单位长度许用扭转角 [θ]=1.5o/m，试校核轴的强度和刚度。 解： 扭矩图如图所示； 1.2kN·m
MT 16M T max = 3 = 3 d min d min 16 16 1.2 103 = =48.9MPa<[ ] 3 9 3.14 50 10 MT 1.2 106 180 max 4 d GI p 9 80 10 32 32 1.2 106 180 o 1.4 /m 9 4 12 80 10 50 10
3.1 试画下列各杆的扭矩图。
2M e
(a)
3kN·m
4kN·m
2kN·m
1kN·m
(c)
3kN·m
3M e
Me
+ 1kN·m
1kN·m
+
2kN·m 2kN·m
2M e
+
Me
(b)
Me 3M e
6kN·m 10kN·m
(d)
4kN·m
+
2kN·m
2M e
3M e
6kN·m
3.4 薄壁圆筒受力如图所示，其平均半径r0=30mm ，壁厚 t=2mm，长度l=300mm ，当外力偶矩Me=1.2kN时，测得 圆筒两端面之间的扭转角φ=0.76o，试计算横截面上的扭 转切应力和圆筒材料的切变模量G。

材料力学习题册_参考答案(1-9章)

材料力学习题册_参考答案(1-9章)

第一章 绪 论一、选择题1．根据均匀性假设，可认为构件的（ C ）在各处相同。

A．应力B． 应变C．材料的弹性系数D． 位移2．构件的强度是指（ C ），刚度是指（ A ），稳定性是指（ B ）。

A．在外力作用下构件抵抗变形的能力B．在外力作用下构件保持原有平衡 状态的能力C．在外力作用下构件抵抗强度破坏的能力3．单元体变形后的形状如下图虚线所示，则 A 点剪应变依次为图(a) （ A ），图(b)（ C ），图(c) （ B ）。

A． 0B． 2rC． rD．1.5 r4.下列结论中( C )是正确的。

A．内力是应力的代数和； B．应力是内力的平均值； C．应力是内力的集度； D．内力必大于应力； 5. 两根截面面积相等但截面形状和材料不同的拉杆受同样大小的轴向拉力，它们的应 力是否相等（ B ）。

A．不相等； B．相等； C．不能确定； 6．为把变形固体抽象为力学模型，材料力学课程对变形固体作出一些假设，其中均匀性假设是指（ C ）。

A. 认为组成固体的物质不留空隙地充满了固体的体积； B. 认为沿任何方向固体的力学性能都是相同的； C. 认为在固体内到处都有相同的力学性能； D. 认为固体内到处的应力都是相同的。

二、填空题1.材料力学对变形固体的基本假设是 连续性假设 ， 均匀性假设 ， 各向同性假设 。

2．材料力学的任务是满足 强度 ， 刚度 ， 稳定性 的要求下，为设计经济安全的构-1-件提供必要的理论基础和计算方法。

3．外力按其作用的方式可以分为 表面力 和 体积力 ，按载荷随时间的变化情况可以分为 静载荷 和 动载荷 。

4．度量一点处变形程度的两个基本量是 （正）应变ε 和 切应变γ。

三、判断题1．因为构件是变形固体，在研究构件平衡时，应按变形后的尺寸进行计算。

（ × ）2．外力就是构件所承受的载荷。

（×）3．用截面法求内力时，可以保留截开后构件的任一部分进行平衡计算。

材料力学习题解答[第三章]

材料力学习题解答[第三章]
题3-24图
解：A-A截面上内力为：
截面的几何性：
欲使柱截面内不出现拉应力,则有：
＝0（a）
分别代入（a）式得：
解之得：
此时： MPa
3-25传动轴上装有甲、乙两个皮带轮，它们的直径均为 ，重量均为 ，其受力情况如图示。若轴的直径为 。试分析该轴的危险截面和危险点，计算危险点的应力大小，并用图形标明该点所受应力的方向。
解:(1)约束反力:
(2)各杆轴力
题3-3图
(3)各杆的正应力
3-4钢杆 直径为20mm，用来拉住刚性梁 。已知F=10kN，求钢杆横截面上的正应力。
解:
题3-4图
3-5图示结构中，1、2两杆的横截面直径分别为10mm和20mm，试求两杆内的应力。设结构的横梁为刚体。
解:取BC段分析， 题3-5图
取AB段分析:
根据力矩平衡：
内力图如图所示。截面的几何特性计算：
危险点面在A面的D1和D2点，则合成弯矩为：
3-28圆截面短柱，承受一与轴线平行但不与轴线重合的压载荷F作用，圆截面半径为r，现要求整个截面只承受压应力，试确定F作用的范围。
解：压力引起的压应力：
而
解之得Zc=题3-21图所以：来自最大压应力在槽底上各点：
（3）如果在左侧也开槽，则为轴心受压：
3-22图示短柱受载荷 和 作用，试求固定端角点A、B、C及D的正应力，并确定其中性轴的位置。
题3-22图
解：在ABCD平面上的内力：
横截面的几何特性：
应力计算：
中性轴方程为：
3-23图3-64所示为一简易悬臂式吊车架。横梁AB由两根10号槽钢组成。电葫芦可在梁上来回移动。设电动葫芦连同起吊重物的重量共重 。材料的 。试求在下列两种情况下，横梁的最大正应力值：（1）、只考虑由重量W所引起的弯矩影响；（2）、考虑弯矩和轴力的共同影响。

材料力学答案第三章

材料力学答案第三章

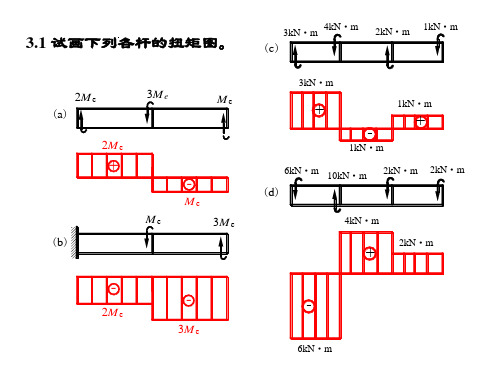
第三章 扭转第三章答案3.1 作图示各杆的扭矩图。

解：4kN·m6kN·m10kN·m 6kN·m4kN·m4kN·m3.2 T 为圆杆截面上的扭矩，试画出截面上与T 对应的剪应力分布图。

解：3.3 图示钢制圆轴，d 1 = 40mm, d 2 = 70mm, M eA = 1.4kN m ⋅, M eB = 0.6kN m ⋅, M eC = 0.8kN m ⋅,[]θ = 1o /m. []τ = 60MPa, G = 80GPa. 试校核轴的强度与刚度。

解：1）校核强度[]113311161660047.7MPa 4B t T m W d ττππ⨯====<⨯[]223322161680011.9MPa 7C t m T W d ττππ⨯====<⨯满足强度条件。

0.8kN·m2）校核刚度119412118032600180 1.71/m 80104010P T GI θπππ-⨯=⋅=⋅=︒⨯⨯⨯⨯222180328001800.24/m 80107010P T GI θπππ⨯=⋅=⋅=︒⨯⨯⨯⨯[]max 1 1.71/m θθθ==︒>此轴不满足刚度条件。

3.4 图示一传动轴，主动轮I 传递力偶矩m k N 1⋅, 从动轮II 传递力偶矩0.4m k N ⋅, 从动轮III 传递力偶矩0.6m k N ⋅。

已知轴的直径d = 40mm ，各轮间距各轮间距l = 500mm ，材料的剪切弹性模量G = 80GPa 。

（1）合理布置各轮的位置；（2）求出轴在合理位置时的最大剪应力和轮间的最大扭转角 。

0.6kN·m解：max 336161660047.7MPa 410t T m W d τππ-⨯====⨯⨯Ⅰ主动轮Ⅰ放在Ⅱ、Ⅲ轮之间，此时轴的最大扭矩最小。

max 494832326000.50.015rad8010410P Tl mlGI G d φππ-==⨯⨯==⨯⨯⨯⨯3.5 一空心圆轴和实心圆轴用法兰联结。

材料力学全部习题解答

材料力学全部习题解答

弹性模量
b
E 2 2 0 M P a 2 2 0 1 0 9P a 2 2 0 G P a 0 .1 0 0 0
s
屈服极限 s 240MPa
强度极限 b 445MPa
伸长率 ll010000m ax2800
由于 280;故0该50 材0料属于塑性材料;
13
解：1由图得
弹性模量 E0 3.550110063700GPa
A x l10.938m m
节点A铅直位移
A ytan 4 l150co sl4 2503.589m m
23
解：1 建立平衡方程 由平衡方程
MB 0 FN1aFN22aF2a
FN 2 FN1
得： FN12F1N22F
l1
l2
2.建立补充方程
3 强度计算 联立方程1和方
程（2）;得
从变形图中可以看出;变形几何关
l
l0
断面收缩率
AAA110000d22d22d2121000065.1900
由于 2故.4 属6 % 于 塑5 性% 材料;
15
解：杆件上的正应力为
F A
4F D2 -d2
材料的许用应力为
要求
s
ns
由此得
D 4Fns d2 19.87mm
s
取杆的外径为
D19.87m m
16
FN1 FN 2
Iz= I（ za） I（ zR ） =1 a2 4
2R4 a4 R 4 =
64 12 4
27
Z
解 a沿截面顶端建立坐标轴z;，y轴不变; 图示截面对z，轴的形心及惯性矩为
0 .1
0 .5
y d A 0 .3 5 y d y2 0 .0 5 y d y

工程力学--材料力学第4版第三章习题答案

工程力学--材料力学第4版第三章习题答案

题3-2图试绘下列各轴的扭矩图，并求出 。

已知ma=2o oN ・ m,mb=4OoN.m,mc=6ooN,m.<10<b)弟二早习题3-1试求图视各轴在指定横截面17、2・2和3・3上的扭矩，并在各截面上表示出钮 矩的方向。

3・2试绘岀下列各轴的钮矩图，并求c=©==®zz ©=3m 2m3znm4 税(a)3-4 一传动轴如图所示，已知 ma=i3oN..cm, mb=3OoN.cm , mc=iooN.cm,md=7oN.cm;^$段轴的直径分别为：Dab=5cm, Dbc=7・5cm, Dcd=5cm （1）画出扭矩图；<2）求1-4、2-2、3-3截面的最大切应力。

3・5图示的空心圆轴，外径D=8cm,内径d二6・巧5,承受扭矩m=ioooN.m・（1）求弘、％（2）绘出横截而上的切应力分布图；（3）求单位长度扭转角，已知G=8ooooMpa・3-6已知变截而钢轴上的外力偶矩^^SooN.m, =i2ooN.m,试求最大切应力和最大相对扭矩。

已知G=8o*l沪Pa.题3-6图3-7 一钢轴的转矩n=24o/min.传递功率丹=44」kN.m.已知L可=4ol\4pa,2」」3,G=8o*l，MPa,试按强度和刚度条件计算轴的直径解：轴的直径由强度条件确泄，3-8图示实心轴通过牙嵌离合器把功率传给空心轴。

传递的功率=7-5kw,轴的转速n=ioor/min,试选择实心轴直径和空心轴外径叫2。

己知％/空2 =0.5，[rlL J=4oMpa・3-9图示AB轴的转速 n=i2or/min,AK B 轮上输入功率丹=4okw,此功率的一半通过锥齿轮传给垂直轴V,另一半功率由水平轴H传走。

已知锥齿轮的节圆直径 a=6oomm：各轴宜径为^=ioomm, ^2=8omm, ^3=6omm, t^=2oMPa.试对各轴进行强度校核。

3-1。

船用推进器的轴，一段是实心的，直径为28omm,列一段是空心的，其内径为外径的一半。

材料力学第三章答案

材料力学第三章答案【篇一：材料力学习题册答案-第3章扭转】是非判断题二、选择题0 b 2t?d316?1?? ? b wp??d316?1?? ?2c wp??d316?1?? ? d w3p??d316?1?? ?46.对于受扭的圆轴，关于如下结论：①最大剪应力只出现在横截面上；②在横截面上和包含杆件的纵向截面上均无正应力；③圆轴内最大拉应力的值和最大剪应力的值相等。

现有四种答案，正确的是（ a ）a ②③对 b①③对 c①②对d 全对 7.扭转切应力公式?mnp?i?适用于（ d）杆件。

pa 任意杆件；b 任意实心杆件；c 任意材料的圆截面；d 线弹性材料的圆截面。

9.若将受扭实心圆轴的直径增加一倍，则其刚度是原来的（ d a 2倍； b 4倍； c 8倍； d 16倍。

三、计算题1.试用截面法求出图示圆轴各段内的扭矩t，并作扭矩图2.图示圆轴上作用有四个外力偶矩 me1 =1kn/m, me2 =0.6kn/m,）me3= me4 =0.2kn/m, ⑴试画出该轴的扭矩图；⑵若 me1与me2的作用位置互换，扭矩图有何变化？(1)(2)解： me1与me2的作用位置互换后，最大扭矩变小。

3.如图所示的空心圆轴，外径d=100㎜，内径d=80㎜，m=6kn/m,m=4kn/m.请绘出轴的扭矩图，并求出最大剪应力解：扭矩图如上，则轴面极惯性矩id4?d4)(1004?804)(10?3)4p=?(32??32?5.8?10?6m4㎜，l=500tr4?103?50?103ip5.8?104．图示圆形截面轴的抗扭刚度为g ip，每段长1m,试画出其扭矩图并计算出圆轴两端的相对扭转角。

ab+ad=cdab=t1l?90?gipgipad=bc=t2l100gipgipcd=t3l40gipgip?90?100?4050?gipgip【篇二：《材料力学》第3章扭转习题解】[习题3-1] 一传动轴作匀速转动，转速n?200r/min，轴上装有五个轮子，主动轮ii输入的功率为60kw，从动轮，i，iii，iv，v依次输出18kw，12kw，22kw和8kw。

材料力学第三章答案 景荣春


案
网
ww
w.
kh
da
w.
co
长度的变化） 皆为应力与应变成正比关系。 3 个弹性常量 E , G , μ 之间关系为 G =
课
3-5 圆轴扭转时如何确定危险截面、危险点及强度条件？ 答 等截面圆轴扭转时的危险截面为扭矩最大的横截面，变截面圆轴扭转时的危险截面 在其扭矩与扭转截面系数比值最大的横截面；其危险点在该横截面的外边缘。强度条件为
τ max =
后
50 ⎛ ⎞ 8 × 1.5 × 10 3 × 50 × 10 −3 ⎜ 4 × + 2 ⎟ 8 FD(4c + 2) 8 ⎝ ⎠ = 458 MPa = 解 （1） τ max = 3 50 ( ) πd 4c − 3 ⎛ ⎞ π × 8 3 × 10 −9 × ⎜ 4 × − 3 ⎟ 8 ⎝ ⎠ τ max − [τ ] 8 = × 100% = 1.78% < 5% [τ ] 450
课
后
答
案
（1）求轴内的最大扭矩； （2）若将轮 A 与轮 C 的位置对调，试分析对轴的受力是否有利。
网
轮 B ，轮 C 与轮 D 为从动轮，输出功率分别为 PB = 10 kW， P C = P D = 30 kW。
解 （1） M B = 9549 ×
PB 10 = 9549 × = 191 N ⋅ m 500 n P 70 M A = 9549 × A = 9549 × = 1337 N ⋅ m 500 n
27
m
E 。 2(1 + μ )
思考题 3-6 解图
3-7 从强度方面考虑，空心圆轴为何比实心圆轴合理？ 答 对于相同的横截面面积 （即用相同量材料） ， 空心圆轴比实心圆轴的抗扭截面系数大， 从而强度高。 3-8 如何计算扭转变形？怎样建立刚度条件？什么样的构件需要进行刚度校核？ 答 （1）写出扭矩方程或扭矩图；相距 l 的两截面间的扭转角

材料力学习题册答案-第3章 扭转(完整资料).doc

此文档下载后即可编辑第三章扭转一、是非判断题1.圆杆受扭时，杆内各点处于纯剪切状态。

（×）2.杆件受扭时，横截面上的最大切应力发生在距截面形心最远处。

（×）3.薄壁圆管和空心圆管的扭转切应力公式完全一样。

（×）4.圆杆扭转变形实质上是剪切变形。

（×）5.非圆截面杆不能应用圆截面杆扭转切应力公式，是因为非圆截面杆扭转时“平截面假设”不能成立。

（√）6.材料相同的圆杆，他们的剪切强度条件和扭转强度条件中，许用应力的意义相同，数值相等。

（×）7.切应力互等定理仅适用于纯剪切情况。

（×）8.受扭杆件的扭矩，仅与杆件受到的转矩（外力偶矩）有关，而与杆件的材料及其横截面的大小、形状无关。

（√）9.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。

（√）10.受扭圆轴的最大切应力只出现在横截面上。

（×）11.受扭圆轴内最大拉应力的值和最大切应力的值相等。

（√ ）12.因木材沿纤维方向的抗剪能力差，故若受扭木质圆杆的轴线与木材纤维方向平行，当扭距达到某一极限值时，圆杆将沿轴线方向出现裂纹。

（ × ）二、选择题1.内、外径之比为α的空心圆轴，扭转时轴内的最大切应力为τ，这时横截面上内边缘的切应力为 （ B ）A τ；B ατ；C 零；D （1- 4α）τ 2.实心圆轴扭转时，不发生屈服的极限扭矩为T ，若将其横截面面积增加一倍，则极限扭矩为（ C ）A0 B 20T 0 D 40T 3.两根受扭圆轴的直径和长度均相同，但材料C 不同，在扭矩相同的情况下，它们的最大切应力τ、τ和扭转角ψ、ψ之间的关系为（ B ）A 1τ=τ2, φ1=φ2B 1τ=τ2, φ1≠φ2C 1τ≠τ2, φ1=φ2D 1τ≠τ2, φ1≠φ2 4.阶梯圆轴的最大切应力发生在（ D ）A 扭矩最大的截面；B 直径最小的截面；C 单位长度扭转角最大的截面；D 不能确定。

工程力学--材料力学第4版第三章习题答案

第三章习题3-1试求图视各轴在指定横截面1-1、2-2和3-3上的扭矩，并在各截面上表示出钮矩的方向。

3-2试绘出下列各轴的钮矩图，并求。

3-3试绘下列各轴的扭矩图，并求出。

已知ma=,mb=,mc=600N,m.3-4 一传动轴如图所示，已知ma=130N..cm, mb= , mc=, md=;各段轴的直径分别为：Dab=5cm, Dbc=, Dcd=5cm(1)画出扭矩图；（2）求1-1、2-2、3-3截面的最大切应力。

3-5 图示的空心圆轴，外径D=8cm,内径d=,承受扭矩m=.(1)求、（2）绘出横截面上的切应力分布图；（3）求单位长度扭转角，已知G=80000Mpa.3-6 已知变截面钢轴上的外力偶矩=, =, 试求最大切应力和最大相对扭矩。

已知G=80*Pa.3-7一钢轴的转矩n=240/min. 传递功率=已知=40Mpa,=,G=80*MPa, 试按强度和刚度条件计算轴的直径解：轴的直径由强度条件确定，。

3-8图示实心轴通过牙嵌离合器把功率传给空心轴。

传递的功率=,轴的转速n=100r/min,试选择实心轴直径和空心轴外径。

已知/=，=40Mpa.3-9 图示AB轴的转速n=120r/min,从B轮上输入功率=40kw,此功率的一半通过锥齿轮传给垂直轴V，另一半功率由水平轴H传走。

已知锥齿轮的节圆直径=600mm；各轴直径为=100mm, =80mm, =60mm, =20MPa，试对各轴进行强度校核。

3-10 船用推进器的轴，一段是实心的，直径为280mm，另一段是空心的，其内径为外径的一半。

在两段产生相同的最大切应力的条件下，求空心部分轴的外径D.3-11 有一减速器如图所示。

已知电动机的转速n=960r/min, 功率=5kw；轴的材料为45钢，=40MPa 试按扭转强度计算减速器第一轴的直径。

3-12 一传动轴传动功率=3kw，转速n=27r/min，材料为45钢，许用切应力=40MPa。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第三章扭转
一、是非判断题
1.圆杆受扭时，杆内各点处于纯剪切状态。

（×）
2.杆件受扭时，横截面上的最大切应力发生在距截面形心最远处。

（×）
3.薄壁圆管和空心圆管的扭转切应力公式完全一样。

（×）
4.圆杆扭转变形实质上是剪切变形。

（×）
5.非圆截面杆不能应用圆截面杆扭转切应力公式，是因为非圆截面杆扭转时“平截面假设”不能成立。

（√）
6.材料相同的圆杆，他们的剪切强度条件和扭转强度条件中，许用应力的意义相同，数值相等。

（×）
7.切应力互等定理仅适用于纯剪切情况。

（×）
8.受扭杆件的扭矩，仅与杆件受到的转矩（外力偶矩）有关，而与杆件的材料及其横截面的大小、形状无关。

（√）
9.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。

（√）
10.受扭圆轴的最大切应力只出现在横截面上。

（×）
11.受扭圆轴内最大拉应力的值和最大切应力的值相等。

（√）
12.因木材沿纤维方向的抗剪能力差，故若受扭木质圆杆的轴线与木材纤维方向平行，当扭距达到某一极限值时，圆杆将沿轴线方向出现裂纹。

（×）
二、选择题
1.内、外径之比为α的空心圆轴，扭转时轴内的最大切应力为τ，这时横截面上内边缘的切应力为 （ B ）
A τ；
B ατ；
C 零；
D （1- 4α）τ 2.实心圆轴扭转时，不发生屈服的极限扭矩为T ，若将其横截面面积增加一倍，则极限扭矩为（ C ）
0 B 20T 0 D 40T 3.两根受扭圆轴的直径和长度均相同，但材料C 不同，在扭矩相同的情况下，它们的最大切应力τ、τ和扭转角ψ、ψ之间的关系为（ B ）
A 1τ=τ2, φ1=φ2
B 1τ=τ2, φ1≠φ2
C 1τ≠τ2, φ1=φ2
D 1τ≠τ2, φ1≠φ2 4.阶梯圆轴的最大切应力发生在（ D ） A 扭矩最大的截面； B 直径最小的截面； C 单位长度扭转角最大的截面； D 不能确定。

5.空心圆轴的外径为D ，内径为d, α=d ／D,其抗扭截面系数为 （ D ） A ()3
1 16
p D W πα=
- B ()3
2
1 16
p D W πα=
-
C ()3
3
1 16
p D W πα=
- D ()3
4
1 16
p
D W
πα=
-
6.对于受扭的圆轴，关于如下结论： ①最大剪应力只出现在横截面上；
②在横截面上和包含杆件的纵向截面上均无正应力；
③圆轴内最大拉应力的值和最大剪应力的值相等。

现有四种答案，正确的是（ A ）
A ②③对
B ①③对
C ①②对
D 全对 7.扭转切应力公式n
P p
M I τρ=
适用于（ D ）杆件。

A 任意杆件； B 任意实心杆件； C 任意材料的圆截面； D 线弹性材料的圆截面。

8.单位长度扭转角θ与（ A ）无关。

A 杆的长度； B 扭矩； C 材料性质； D 截面几何性质。

9.若将受扭实心圆轴的直径增加一倍，则其刚度是原来的（ D ） A 2倍； B 4倍； C 8倍； D 16倍。

三、计算题
1.试用截面法求出图示圆轴各段内的扭矩T ，并作扭矩图
2.图示圆轴上作用有四个外力偶矩1 e M =1KN/m, 2e M =0.6KN/m, 3e M
= 4e M =0.2KN/m, ⑴试画出该轴的扭矩图；⑵若1 e M 与2e M 的作用位置互换，扭矩图有何变化？
(1)(2)
解：1 e M 与2e M 的作用位置互换后，最大扭矩变小。

3.如图所示的空心圆轴，外径D=100㎜，内径d=80㎜，l=500㎜，M=6kN/m,M=4kN/m.
请绘出轴的扭矩图，并求出最大剪应力
解：扭矩图如上，则轴面极惯性矩
I P =
4
44443)
64()
(10080)(10 5.81032
32
D d m ππ----=
=⨯
则最大剪应力τmax =33
6
R 4105010P 34.45.810
P T a MPa I ⨯⨯⨯==⨯
4．图示圆形截面轴的抗扭刚度为G I P ，每段长1m,试画出其扭矩图并计算出圆轴两端的相对扭转角。

解：φAD= φAB+ φBC +φCD φAB=190
P P
T L GI GI -= φBC=2100P P T L GI GI = φCD=340P P T L GI GI = 所以φAD=901004050
P P
GI GI -++=
5.如图所示的阶梯形传动轴中，A 轮输入的转矩M=800N •m,B ﹑C 和D 轮输出的转矩分别为B M =C M =300N •m ，D M =200N •m 。

传动轴的许用切应力[τ]=400Mpa,许用扭转角[θ]=1°/m,材料的剪切弹性模量G=80Gpa.
⑴试根据轴的强度条件和刚度条件，确定传动轴各段的直径。

⑵若将传动轴改为等截面空心圆轴，并要求内外直径之比α=d/D=0.6,试确定轴的外径；并比较两种情况下轴的重量。

解： （1）max τ=
max 3
16max
T T T W d
π=≤［ τ］ []max max
max 4
32P T T GI G d θθπ=
=≤ 对于AB 段 11d d ≥≥138.5d mm ≥ 同理得AC 段的d 2 43.7mm ≥ CD 段d 3 34.8mm ≥
所以d 1应取值38.5mm ，d 2应取值43.7mm,d 3应取值34.8mm (2) []max max max max 3416(1)
t t T T T W W D ττπα===≤- []max max max 4432(1)
P T T GI G D θθπα=
=≤- 所以D=4.17m
6.图示的传动轴长l=510㎜，直径D=50㎜。

现将此轴的一段钻成内径d=25㎜的内腔，而余下一段钻成d=38㎜的内腔。

若材料的许用切应力[τ]=70Mpa,试求： ⑴此轴能承受的最大转矩max e M M
⑵若要求两段轴内的扭转角相等，则两段的长度应分别为多少？
M M e
e
M
解：⑴设半径为ρ P I M ρτ=
P I
M τρ
= P I 取441D -)32d π（，ρ=2
D
[]()[]()44441132
1609.86162D d D d M N M D
D
π
ττπ--=
=
=•
⑵P T GI θ=
1112()P P Tl T l l GI GI -∴= 即 1
14444
12()()3232
l l l D d D d ππ-=
-- 解得1l =298.1mm l 2=211.9mm
7.如图所示钢轴AD 的材料许用切应力[τ]=50Mpa ，切变模量G=80Gpa,许用扭转角[θ]=0.25°／m 。

作用在轴上的转矩M=800N •m ，1200N •m ，M=400N •m 。

试设计此轴的直径。

M/
解：由题意轴中最大扭矩为800N •Mg 根据轴的强度条件τmax=
max 3
16max T T T W d π=≤［ τ］ 所以d
24.3410m -≥=⨯ 根据轴的刚度条件[].
max max
4
32max T T GIp G d ϕθπ==≤所以
2
2.5210d m -≥=⨯ 即轴的直径应取值4
3.4mm.
8. 钻探机钻杆外经D=60㎜,内径d=㎜,功率P=7.355KW ，轴的转速n=180r/min,杆钻入土层的深度l=40m,材料的切变模量G=80Gpa ，许用切应力[τ]=40Mpa ，假设土壤对钻杆的阻力沿长度均匀分布，试求： ⑴土壤对钻杆单位长度的阻力矩m ； ⑵作钻杆的扭矩图，并进行强度校核； ⑶计算A 、B 截面的相对扭转角。

390.18N·m
解：（1）T=M=9549 7.355
390.18180
N m N m ⨯
•=• 由平衡方程0;X M =∑ 由ML-T=0 则M= T
L
=9.75N m m •
(2)扭矩图如图所示
[][]34max max max max 34
16= ,W = (1) 16(1).8MPa<40,P p T T D W D MPa πταττπατ-∴=≤-=即17钻刚满足强度条件
（3）两端截面的相对扭转角为
Φ= 2
00.1482l
P p
mx ml rad GI GI ==⎰
感谢土木0902班石李、臧明远同学！。