2015年高中数学综合训练5

周三检测题2015/1/211．设z ＝10i 3＋i，则z 的共轭复数为 ( ) A ．－1＋3i B ．－1－3i C ．1＋3i D ．1－3i2． “－3<m <5”是“方程x 25－m ＋y 2m ＋3＝1表示椭圆”的 ( ) A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．直线y ＝kx ＋2与抛物线y 2＝8x 有且只有一个公共点，则k 的值为( ) A ．1B ．1或3C ．0D ．1或0 4.由曲线y =2y x y =-及轴所围成的图形的面积为 （ ） A. 103 B.4 C. 163 D.65．若双曲线x 2a －y 2b ＝1(a >0，b >0)和椭圆x 2m ＋y 2n＝1(m >n >0)有共同的焦点F 1，F 2，P 是两条曲线的一个交点，则|PF 1|·|PF 2|＝( )A ．m 2－a 2 B.m － a C.12(m －a ) D ．m －a 6．已知函数()f x 是定义在R 上的偶函数, 且在区间[0,)+∞单调递增．若实数a 满足212(log )(log )2(1)f a f f a ≤+, 则a 的取值范围是（ ）A ．[1,2]B ．10,2⎛⎤ ⎥⎝⎦C ．1,22⎡⎤⎢⎥⎣⎦D ．(0,2] 7．执行如图所示的程序框图，若输入的x 的值为1，则输出的n 的值为____．8．已知实数,x y 满足⎪⎩⎪⎨⎧≥≤≥-010y x y x 且目标函数by ax z +=2 )0,0(>>b a 的最大值是1，则ab的最大值为9.已知F 为双曲线C ：x 2－my 2＝3m (m >0)的一个焦点，则点F 到C 的一条渐近线的距离为10．在平面直角坐标系xOy 中，设椭圆x 2a 2＋y 2b 2＝1(a >b >0)的焦距为2c ，以点O 为圆心，a 为半径作圆M .若过点P ⎝⎛⎭⎫a 2c ，0作圆M 的两条切线互相垂直，则该椭圆的离心率为________．11 . ABC ∆中，角,,A B C 所对的边分别为,,a b c 且22sin cos 212A B C ++=． （1）求角C 的大小；（2）若向量(3,)m a b =，向量(,)3b n a =-，且m n ⊥，()()16m n m n +⋅-=，求,,a bc 的值．12.如图，在底面为直角梯形的四棱锥P —ABCD 中，AD ∥BC ，∠ABC ＝90°，P A ⊥平面ABCD ，P A ＝3，AD ＝2，AB ＝23，BC ＝6.(1)求证：BD ⊥平面P AC ；(2)求二面角P —BD —A 的大小.13．在等差数列{a n }中，a 1＋a 3＝－8，a 2＋a 4＝－14.(1)求数列{a n }的通项公式；(2)设数列{a n ＋b n }是首项为1，公比为c 的等比数列，求数列{b n }的前n 项和S n .14．已知椭圆C ：x 2a 2＋y 2b 2＝1 (a >b >0)的离心率为63，右焦点为(22，0)，斜率为1的直线l 与椭圆C 交于A 、B 两点，以AB 为底边作等腰三角形，顶点为P (－3,2)．(1)求椭圆C 的方程； (2)求△PAB 的面积．周三检测题2015/1/211-6 DBD CDC7. 3 8.81 9. 3 10. 22 11．解：（1）∵22sin cos 212A B C ++= ∴2cos 212sin cos()cos 2A B C A B C +=-=+=-， ∴22cos cos 10C C +-=，∴1cos 2C =或cos 1C =- (0,),C π∈∴3C π= （2）∵⊥ ∴22303b a -=，即229b a = 又16)()(=-⋅+，∴1698822=+b a ，即2229b a +=② 由①②可得221,9a b ==，∴1,3a b ==又2222cos 7,c a b ab C =+-=∴c =1,3,a b c ===12.(1)证明 如图，建立坐标系，则A (0,0,0)，B (23，0,0)，C (23，6,0)，D (0,2,0)，P (0,0,3)，∴AP →＝(0,0,3)，AC →＝(23，6,0)，BD →＝(－23，2,0).∴BD →·AP →＝0，BD →·AC →＝0.∴BD ⊥AP ，BD ⊥AC .又∵P A ∩AC ＝A ，∴BD ⊥面P AC .(2)解 设平面ABD 的法向量为m ＝(0,0,1)，设平面PBD 的法向量为n ＝(x ，y ，z )，则n ·BD →＝0，n ·BP →＝0.∵BP →＝(－23，0,3)，∴⎩⎨⎧ －23x ＋2y ＝0，－23x ＋3z ＝0解得⎩⎪⎨⎪⎧y ＝3x ，z ＝233x . 令x ＝3，则n ＝(3，3,2)，∴cos 〈m ，n 〉＝m·n |m||n |＝12. ∴二面角P —BD —A 的大小为60°.13.解：(1)设数列{a n }的公差为d ，∵a 1＋a 3＝－8，a 2＋a 4＝－14，∴⎩⎪⎨⎪⎧2a 1＋2d ＝－8，2a 1＋4d ＝－14，解得a 1＝－1，d ＝－3.∴数列{a n }的通项公式为a n ＝a 1＋(n －1)d ＝－1－3(n －1)＝－3n ＋2.(2)由数列{a n ＋b n }是首项为1，公比为c 的等比数列，得a n ＋b n ＝c n －1，即－3n ＋2＋b n ＝c n －1，∴b n ＝3n －2＋c n －1，∴S n ＝[1＋4＋7＋…＋(3n －2)]＋(1＋c ＋c 2＋…＋c n －1)＝n (3n －1)2＋(1＋c ＋c 2＋…＋c n －1)． ∴当c ＝1时，S n ＝n (3n －1)2＋n ＝3n 2＋n 2；当c ≠1时，S n ＝n (3n －1)2＋1－c n 1－c ＝n (3n －1)2＋c n －1c －1.综上，数列{b n }的前n 项和S n ＝⎩⎪⎨⎪⎧ 3n 2＋n 2， c ＝1，n (3n －1)2＋c n－1c －1，c ≠1.14．解 (1)由已知得c ＝22，c a ＝63.解得a ＝23，又b 2＝a 2－c 2＝4.所以椭圆C 的方程为x 212＋y 24＝1.(2)设直线l 的方程为y ＝x ＋m .由⎩⎪⎨⎪⎧y ＝x ＋m x 212＋y24＝1，得4x 2＋6mx ＋3m 2－12＝0. ①设A 、B 的坐标分别为(x 1，y 1)，(x 2，y 2) (x 1<x 2)，AB 中点为E (x 0，y 0)， 则x 0＝x 1＋x 22＝－3m4，y 0＝x 0＋m ＝m4；因为AB 是等腰△PAB 的底边，所以PE ⊥AB .所以PE 的斜率k ＝2－m4－3＋3m 4＝－1.解得m ＝2.此时方程①为4x 2＋12x ＝0.解得x 1＝－3，x 2＝0.所以y 1＝－1，y 2＝2.所以|AB |＝3 2.此时，点P (－3,2)到直线AB ：x －y ＋2＝0的距离d ＝|－3－2＋2|2＝322，所以△PAB 的面积S ＝12|AB |·d ＝92.。

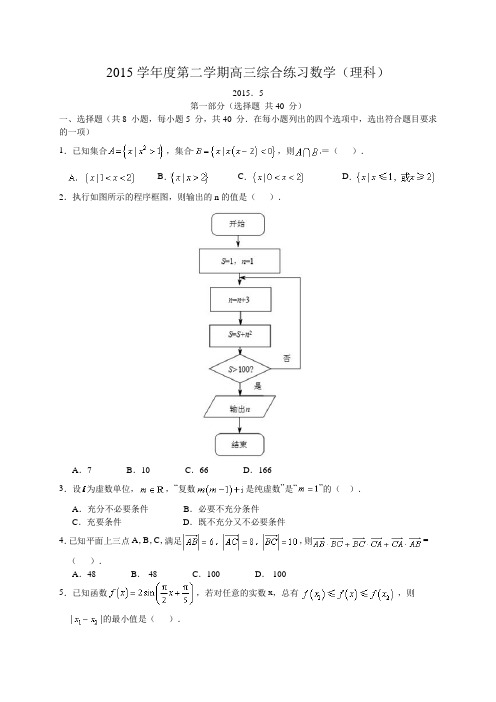
2015学年度第二学期高三综合练习数学（理科）2015．5第一部分（选择题共40 分）一、选择题（共8 小题，每小题5 分，共40 分．在每小题列出的四个选项中，选出符合题目要求的一项）1．已知集合，集合，则＝（）．B．C．D．2．执行如图所示的程序框图，则输出的n的值是（）．A．7 B．10 C．66 D．1663．设为虚数单位，，“复数是纯虚数”是“”的（）．A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分又不必要条件4．已知平面上三点A，B，C，满足，则=（）．A．48 B．-48 C．100 D．-1005．已知函数，若对任意的实数x，总有，则的最小值是（）．A．2 B．4 C．D．26．已知双曲线与抛物线有一个公共的焦点F，且两曲线的一个交点为P．若，则双曲线的渐近线方程为（）．7．已知函数，若对任意，都有成立，则实数m的取值范围是（）．8．如图，将一张边长为1的正方形纸ABCD折叠，使得点B始终落在边AD上，则折起部分面积的最小值为（）．第Ⅱ卷（非选择题共110 分）二、填空题：本小题共6 小题，每小题5 分，共30 分．9．展开式中含项的系数是__________．10．已知圆C的圆心在直线x－y=0上，且圆C与两条直线x＋y=0和x＋y－12=0都相切，则圆C的标准方程是__________．11．如图，已知圆B的半径为5，直线AMN与直线ADC为圆B的两条割线，且割线AMN过圆心B．若AM=2，，则AD=__________．12．某四棱锥的三视图如图所示，则该四棱锥的侧面积为__________．13．已知点在函数的图像上，则数列的通项公式为__________；设O为坐标原点，点，则，中，面积的最大值是__________．14．设集合，集合A中所有元素的个数为__________；集合A 中满足条件“”的元素个数为__________．三、解答题：本大题共6 小题，共80 分．解答应写出必要的文字说明、证明过程或演算步骤．15．（本小题共13分）在梯形ABCD中，（Ⅰ）求AC的长；（Ⅱ）求梯形ABCD的高．某学科测试中要求考生从A，B，C三道题中任选一题作答，考试结束后，统计数据显示共有600名学生参加测试，选择A，B，C三题答卷数如下表：（Ⅰ）某教师为了解参加测试的学生答卷情况，现用分层抽样的方法从600份答案中抽出若干份答卷，其中从选择A题作答的答卷中抽出了3份，则应分别从选择B，C题作答的答卷中各抽出多少份？（Ⅱ）若在（Ⅰ）问中被抽出的答卷中，A，B，C三题答卷得优的份数都是2，从被抽出的A，B，C三题答卷中再各抽出1份，求这3份答卷中恰有1份得优的概率；（Ⅲ）测试后的统计数据显示，B题的答卷得优的有100份，若以频率作为概率，在（Ⅰ）问中被抽出的选择B题作答的答卷中，记其中得优的份数为X，求X的分布列及其数学期望EX．如图，在直角梯形ABCD中，．直角梯形ABEF可以通过直角梯形ABCD以直线AB为轴旋转得到，且平面平面ABCD．（Ⅰ）求证：；（Ⅱ）求直线BD和平面BCE所成角的正弦值；（Ⅲ）设H为BD的中点，M，N分别为线段FD，AD上的点（都不与点D重合）．若直线平面MNH，求MH的长．18．（本小题共13分）已知点M为椭圆的右顶点，点A，B是椭圆C上不同的两点（均异于点M），且满足直线MA与直线MB斜率之积为14．（Ⅰ）求椭圆C的离心率及焦点坐标；（Ⅱ）试判断直线AB是否过定点：若是，求出定点坐标；若否，说明理由．19．（本小题共14分）已知函数．（Ⅰ）当时，求函数的单调区间；（Ⅱ）若在区间(1,2)上存在不相等的实数成立，求的取值范围；（Ⅲ）若函数有两个不同的极值点，，求证：．20．（本小题共13分）已知数列，是正整数1，2，3，，n的一个全排列．若对每个都有或3，则称为H数列．（Ⅰ）写出满足的所有H数列；（Ⅱ）写出一个满足的数列的通项公式；（Ⅲ）在H数列中，记．若数列是公差为d的等差数列，求证：或．参考答案及评分标准高三数学（理科）一、选择题：题号（1）（2）（3）（4）（5）（6）（7）（8）答案 A B B C A C D B二、填空题：题号（9）（10）（11）（12）（13）（14）答案三、解答题：15．（本小题共13 分）解：（Ⅰ）在中，因为，所以．由正弦定理得：，即．（Ⅱ）在中，由余弦定理得：，整理得，解得（舍负）．过点作于，则为梯形的高．因为，，所以．在直角中，．即梯形的高为．16．（本小题共13 分）解：（Ⅰ）由题意可得：题 A B C答卷数180 300 230抽出的答卷数 3 5 2应分别从题的答卷中抽出份，份．（Ⅱ）记事件：被抽出的三种答卷中分别再任取出份，这份答卷中恰有份得优，可知只能题答案为优，依题意．（Ⅲ）由题意可知，题答案得优的概率为，显然被抽出的题的答案中得优的份数的可能取值为，且．；；；；；．随机变量的分布列为：所以．17．（本小题共14分）证明：（Ⅰ）由已知得，．因为平面平面，且平面平面，所以平面，由于平面，所以．（Ⅱ）由（1）知平面所以，．由已知，所以两两垂直．以为原点建立空间直角坐标系（如图）．因为，则，，，，所以，，设平面的一个法向量．所以，即．令，则．设直线与平面所成角为，因为，所以．所以直线和平面所成角的正弦值为．（Ⅲ）在为原点的空间直角坐标系中，，，，，．设，即．，则，，．若平面，则．即．．解得．则，．18．（本小题共13分）解：（Ⅰ）椭圆的方程可化为，则，，．故离心率为，焦点坐标为，．（Ⅱ）由题意，直线的斜率存在，可设直线的方程为，，，则，．由得．判别式．所以，，因为直线与直线的斜率之积为，所以，所以．化简得，所以，化简得，即或．当时，直线方程为，过定点．代入判别式大于零中，解得．当时，直线的方程为，过定点，不符合题意．故直线过定点．19．（本小题共14分）解：（Ⅰ）当时，，．由，解得，．当时，，单调递增；当时，，单调递减；当时，，单调递增．所以的单调增区间为，单调减区间为．（Ⅱ）依题意即求使函数在上不为单调函数的的取值范围．，设，则，．因为在上为增函数．当，即当时，函数在上有且只有一个零点，设为，当时，，即，为减函数；当时，，即，为增函数，满足在上不为单调函数．当时，，，所以在上成立（因在上为增函数），所以在上成立，即在上为增函数，不合题意．同理时，可判断在为减函数，不合题意．综上．（Ⅲ）．因为函数有两个不同的零点，即有两个不同的零点，即方程的判别式，解得．由，解得，．此时，．随着变化，和的变化情况如下：+ +极大值极小值所以是的极大值点，是的极小值点，所以是极大值，是极小值所以因为，所以，所以．20．（本小题共13分）解：（Ⅰ）满足条件的数列有两个：．（Ⅱ）由（1）知数列满足，把各项分别加后，所得各数依次排在后，因为，所得数列显然满足或，，即得数列．其中，．如此下去即可得到一个满足的数列为：（其中）（写出此通项也可以（其中））（Ⅲ）由题意知，，且．有解：①，，，则，这与是矛盾的．②时，与①类似可得不成立．③时，，则不可能成立．④时，若或，则或．若或，则，类似于③可知不成立．④时，若同号，则，由上面的讨论可知不可能；若或，则或；⑤时，若异号，则，不行；若同号，则，同样由前面的讨论可知与矛盾．综上，只能为或，且（2）中的数列是的情形，将（2）中的数列倒过来就是，所以为或．。

第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.23sin()6π-=( )（A ）2- （B ）12-（C ）12（D ）2【答案】C 【解析】试题分析：根据题意23231sin sin 4sin 6662ππππ⎛⎫⎛⎫-=-== ⎪⎪⎝⎭⎝⎭，所以答案为C. 考点：1.诱导公式;2.常见角的三角函数值.2.设4log a =π，14log b =π，4c =π，则a ，b ，c 的大小关系是（ ）（A ） b c a >> （B ）a c b >> （C ） a b c >> （D ）b a c >> 【答案】D 【解析】试题分析：根据对数函数的性质知：4414log 1,log 0,1a b c πππ=<=<=>，所以c a b >>，答案为D.考点：1.对数函数的单调性;2.对数比较大小.3.已知{}n a 为各项都是正数的等比数列，若484a a ⋅=，则567a a a ⋅⋅=（ ）（A ）4 （B ）8 （C ）16 （D ）64 【答案】B 【解析】试题分析：由于数列{}n a 是正各项都是正数的等比数列，所以根据等比数列的性质可知：248664,2a a a a ==∴=，356768a a a a ==，所以答案为B.考点：1.等比数列的性质;2.等比数列的求值.4.甲、乙两名同学8次数学测验成绩如茎叶图所示，12,x x 分别表示甲、乙两名同学8次数学测验成绩的平均数，12,s s 分别表示甲、乙两名同学8次数学测验成绩的标准差，则有（ ） （A ）12x x >，12s s < （B ）12x x =，12s s < （C ）12x x =，12s s = （D ）12x x <，12s s >【答案】B 【解析】试题分析：根据题意甲，乙的平均数分别为：185x =和285x =，方差分别为：()()()()()()()()22222222211[79857885868585858585848591859285]8s =-+-+-+-+-+-+-+-=1758=；()()22221[778578858s =-+-()()()()()2222283858585858587859285+-+-+-+-+-+()22349385]8+-=；所以12x x =，12s s <，答案为B. 考点：1.茎叶图;2.平均值和方差.5.已知p ，q 是简单命题，那么“p q ∧是真命题”是“p ⌝是真命题”的（ ）（A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件 （D ）既不充分也不必要条件 【答案】D 【解析】试题分析：若p q ∧是真命题，则p 为真命题，且q 为真，而p ⌝为假命题，所以“p q ∧是真命题”是p ⌝为真命题的既不充分也不必要条件，所以答案为D. 考点：1.充要条件;2.含有逻辑联结词的命题的真假性.6.若实数y x ,满足不等式组330101x y x y y +-≤⎧⎪-+≥⎨⎪≥-⎩，，，则2||z x y =+的取值范围是（ ）7 83 5 5 7 2 38 9 4 5 5 6 1 2 9 7 8乙甲（A ）[1,3]- （B ）[1,11] （C ）]3,1[ （D ）]11,1[- 【答案】D 【解析】试题分析：画出可行域，当6,1x y ==-时，z 取得最大值max 11z =；当时，z 取得最小值min 1z =-.答案为：D.考点：1.线性规划;2.最优解问题.7.定义在R 上的函数()f x 满足)()6(x f x f =+.当)1,3[--∈x 时，2)2()(+-=x x f ,当)3,1[-∈x 时，x x f =)(，则(1)(2)(3)(2015)f f f f ++++=（ ）（A ）336 （B ）355 （C ）1676 （D ）2015 【答案】A 【解析】试题分析：根据)()6(x f x f =+可知：()f x 是周期为6的周期函数，且()()()()()()()()1234561210101f f f f f f +++++=++-++-+=， ()()20156335513351336f f =⨯+=⨯+=，所以答案为A.考点：1.函数的周期性;2.利用函数的周期性求函数值.8.为提高信息在传输中的抗干扰能力，通常在原信息中按一定规则加入相关数据组成传输信息．设定原信息为012a a a ，其中{0,1}i a ∈（0,1,2i =），传输信息为00121h a a a h ，001h a a =⊕，102h h a =⊕，⊕运算规则为：000⊕=，011⊕=，101⊕=，110⊕=．例如原信息为111，则传输信息为01111．传播信息在传输过程中受到干扰可能导致接收信息出错，则下列信息一定有误的是（ ）（A ）11010 （B ）01100 （C ）10111 （D ）00011 【答案】C 【解析】试题分析：根据信息时的规则，中间三位是需要传输的信息，前后为生产信息. A.11010传输信息001102101,101,110h a a h h a =⊕=⊕==⊕=⊕=，正确； B.01100传输信息001102110,110,000h a a h h a =⊕=⊕==⊕=⊕=，正确； C.10111传输信息001102011,011,h 110h a a h a =⊕=⊕==⊕=⊕=，错误；D.00011传输信息，001102000,011h a a h h a =⊕=⊕==⊕=⊕=正确； 考点：1.创新题;2.推理.第Ⅱ卷（共90分）二、填空题（每题4分，满分16分，将答案填在答题纸上）9.若1)nx的二项展开式中各项的二项式系数的和是64，则n = ，展开式中的常数项为 ．（用数字作答） 【答案】6,15考点：1.二项式系数和;2.二项式的同通项公式.10.已知正数,x y 满足x y xy +=，那么x y +的最小值为 ． 【答案】4 【解析】试题分析：因为：0,0x y >>，由均值不等式得：22x y x y xy +⎛⎫+=≤ ⎪⎝⎭，令x y t +=，则240,4t t t -≥≥.考点：1.均值不等式求最值;2.还原法解不等式.11.若直线12(32x t t y t =-+⎧⎨=-⎩，为参数)与曲线4cos (sin x a y a θθθ=+⎧⎨=⎩，为参数，0a >)有且只有一个公共点，则a = ．【解析】试题分析：将参数方程1232x ty t =-+⎧⎨=-⎩化为一般方程得：20x y +-=参数方程4cos sin x a y a θθ=+⎧⎨=⎩化为一般方程得：()2224x y a -+=(p ,q)若直线与圆有一个公共点，则圆心到直线的距离为a：d a ===考点：1.直线的参数方程化普通方程;2.圆的参数方程化普通方程;3.直线和圆的位置关系.12.若双曲线22221(0,0)x y a b a b-=>>截抛物线24y x =的准线所得线段长为b ，则a = ．【解析】试题分析：抛物线的准线方程为1x =-，又直线1x =-截双曲线的弦长为b ，则有222141b a b -=，解得：5a =. 考点：1.抛物线的定义;2.双曲线的标准方程.13.已知非零向量,a b 满足||1=b ，a 与-b a 的夹角为120，则||a的取值范围是 ． 【答案】⎛⎝⎦【解析】试题分析： 如图在ABC ∆中，若b a -与a 的夹角为120︒，则60B ∠=︒，又1b =，由正弦定理1sin 60sin a A =︒，则23sin ,0120,0sin 1a A A A =<<︒<<，所以：230,a ⎛∈ ⎝⎦.考点：1.向量的线性运算;2.三角形的正弦定理;3.三角函数值域.14.如图，平面中两条直线1l 和2l 相交于点O ，对于平面上任意一点M ，若,p q 分别是M 到直线1l 和2l 的距离，则称有序非负实数对(,)p q 是点M 的“距离坐标”． 给出下列四个命题：① 若0p q ==，则“距离坐标”为(0,0)的点有且仅有1个．② 若0pq =，且0p q +≠，则“距离坐标”为(,)p q 的点有且仅有2个． ③ 若0pq ≠，则“距离坐标”为(,)p q 的点有且仅有4个． ④ 若p q =，则点M 的轨迹是一条过O 点的直线． 其中所有正确命题的序号为 ． 【答案】①②③考点：1.平面点和直线的位置关系;2.分类讨论思想.三、解答题 （本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.）15.已知函数2sin 22sin ()sin x xf x x-=．（Ⅰ）求()f x 的定义域及其最大值； （Ⅱ）求()f x 在(0,π)上的单调递增区间．【答案】（Ⅰ）()f x 的定义域为{|}x x k k ∈≠π,∈R Z ；最大值为（Ⅱ）()f x 在(0,π)上的单调递增区间为3[,4ππ).【解析】试题分析：（Ⅰ）若原函数有意义，需满足分母不为零即sin 0x ≠，进而求得原函数的定义域，同时将原函数利用倍角公式化为一角一函数，进而求得其最值；（Ⅱ）利用换元法求得()f x 的单调增区间，同时注意其定义域{|}x x k k ∈≠π,∈R Z ，进而求得其单调递增区间. 试题解析：（Ⅰ）由sin 0x ≠，得x k k ≠π(∈)Z ．所以()f x 的定义域为{|}x x k k ∈≠π,∈R Z ． …………………2分因为2sin 22sin ()sin x xf x x -=，2cos 2sin x x =-)4x π=+， …………………6分所以()f x的最大值为 …………………7分 （Ⅱ）函数cos y x =的单调递增区间为[22k k π+π,π+2π]（k ∈Z ）由224k x k ππ+π≤+≤π+2π，x k k ≠π(∈)Z ，且(0,x ∈π)，所以()f x 在(0,π)上的单调递增区间为3[,4ππ)． ……13分考点：1.三角函数的定义域及最值;2.三角函数的单调递增区间.16.某校高一年级开设A ，B ，C ，D ，E 五门选修课，每位同学须彼此独立地选三门课程，其中甲同学必选A 课程，不选B 课程，另从其余课程中随机任选两门课程．乙、丙两名同学从五门课程中随机任选三门课程．（Ⅰ）求甲同学选中C 课程且乙同学未选中C 课程的概率；（Ⅱ）用X 表示甲、乙、丙选中C 课程的人数之和，求X 的分布列和数学期望．【答案】（Ⅰ）415；（Ⅱ）X 为分布列为：420331814028()0123757575757515E X =⨯+⨯+⨯+⨯==.【解析】试题分析：（Ⅰ）首先求得甲同学选中C 课程的概率和乙同学选中C 课程的概率，进而求得甲选中而乙未选中的概率为415；（Ⅱ）丙同学选中C 课程的概率为35，进而得到X 的可能取值为：0,1,2,3，进而求得各自的概率，得到其分布列和期望.试题解析：（Ⅰ）设事件A 为“甲同学选中C 课程”，事件B 为“乙同学选中C 课程”．则1223C 2()C 3P A ==，2435C 3()C 5P B ==．因为事件A 与B 相互独立，所以甲同学选中C 课程且乙同学未选中C 课程的概率为224()()()()[1()]3515P AB P A P B P A P B ==-=⨯=． …………………4分（Ⅱ）设事件C 为“丙同学选中C 课程”．则2435C 3()C 5P C ==．X 的可能取值为：0,1,2,3．1224(0)()35575P X P ABC ===⨯⨯=． (1)()()()P X P ABC P ABC P ABC ==++2221321232035535535575=⨯⨯+⨯⨯+⨯⨯=．(2)()()()P X P ABC P ABC P ABC ==++2322231333335535535575=⨯⨯+⨯⨯+⨯⨯=．23318(3)()35575P X P ABC ===⨯⨯=． X 为分布列为：EFA()0123757575757515E X =⨯+⨯+⨯+⨯==．………13分考点：1.相互独立事件的概率;2.事件的分布列和期望.17.如图，三棱柱ABC DEF -的侧面BEFC 是边长为1的正方形，侧面BEFC ⊥侧面ADEB ，4AB =，60DEB ∠=，G 是DE 的中点．（Ⅰ）求证：CE ∥平面AGF ； （Ⅱ）求证：GB ⊥平面BEFC ；（Ⅲ）在线段BC 上是否存在一点P ，使二面角P GE B --为45，若存在，求BP 的长；若不存在，说明理由．【答案】（Ⅰ）证明见解析；（Ⅱ）证明见解析；（Ⅲ）存在，BP =.【解析】试题分析：（Ⅰ）要证明CE ∥平面AGF ，需证明HG ∥CE （其中H 为CD 的中点，G 为DE 的中点）；（Ⅱ）根据勾股定理求得222BG BE GE +=，所以GB BE ⊥，利用面面垂直的判定定理得到GB ⊥平面BEFC ，所以；（Ⅲ）根据题意建立空间直角坐标系，进而求得平面BGE 的法向量(0,0,1)=m ，平面PGE 的法向量，进而利用公式及二面角P GE B --为45.求得2BP =.试题解析：（Ⅰ）证明：连接CD 与AF 相交于H ，则H 为CD 的中点，连接HG ．因为G 为DE 的中点，所以HG ∥CE ．因为CE ⊄平面AGF ，HG ⊂平面AGF ，所以CE ∥平面AGF ． ………4分（Ⅱ）证明：1BE =，2GE =，在△GEB 中，60GEB ∠=，BG ．因为222BG BE GE +=， 所以GB BE ⊥．因为侧面BEFC ⊥侧面ADEB ，侧面BEFC侧面ADEB BE =，GB ⊂平面ADEB ，所以GB ⊥平面BEFC ． ………8分（Ⅲ）解：,,BG BE BC 两两互相垂直，建立空间直角坐标系B xyz -．假设在线段BC 上存在一点P ，使二面角P GE B --为45． 平面BGE 的法向量(0,0,1)=m ，设(0,0,),[0,1]P λλ∈．G (0,1,0)E ．所以()GP λ=，(,0)GE =．设平面PGE 的法向量为(,,)x y z =n ，则0,0.GP GE ⎧⋅=⎪⎨⋅=⎪⎩n n所以0,0.z y λ⎧+=⎪⎨+=⎪⎩A令1z =，得y λ=，x =所以PGE的法向量为,1)λ=n ．因为1⋅=m n ，所以112=，解得[]0,1λ=，故BP =． 因此在线段BC 上存在一点P ，使二面角P GE B --为45，且2BP =. ………14分考点：1.线面平行的判定定理;2.面面垂直的性质定理;3.空间向量. 18.已知函数()exf x x a -=+⋅．（Ⅰ）当2e a =时，求()f x 在区间[1,3]上的最小值； （Ⅱ）求证：存在实数0[3,3]x ∈-，有0()f x a >.【答案】（Ⅰ）当2=x 时，)(x f 有最小值为3；（Ⅱ）证明见解析. 【解析】试题分析：（Ⅰ）利用求导求得2'()1e xf x -=-，进而得到()f x 的单调性求得其最小值；（Ⅱ）“存在实数0[3,3]x ∈-，有a x f >)(”等价于()f x 的最大值大于a .对原函数()f x 求导，进而对a 分情况，33330,,,0a a e e a e a e --≤≥<<<≤，得到对任意实数a 都存在]3,3[-∈x 使a x f >)(成立.试题解析：（Ⅰ）当2e a =时，2()exf x x -=+，]3,1[∈x ；因为2'()1e xf x -=-，由0)(='x f ，2=x .则x ，)(x f '，)(x f 关系如下：所以当2=x 时，)(x f 有最小值为3. ………5分 （Ⅱ）“存在实数0[3,3]x ∈-，有a x f >)(”等价于()f x 的最大值大于a .因为'()1e xf x a -=-，所以当0≤a 时，]3,3[-∈x ，0)('>x f ，)(x f 在)3,3(-上单调递增， 所以()f x 的最大值为(3)(0)f f a >=. 所以当0≤a 时命题成立.当0>a 时，由0)(='x f 得a x ln =. 则x ∈R 时，x ，)(x f '，)(x f 关系如下：考点：1.利用求导判断单调性;2.分类讨论思想.19.已知椭圆C 的中心在原点O ，焦点在x，且椭圆C 上的点到两个焦点的距离之和为4． （Ⅰ）求椭圆C 的方程；（Ⅱ）设A 为椭圆C 的左顶点，过点A 的直线l 与椭圆交于点M ，与y 轴交于点N ，过原点与l 平行的直线与椭圆交于点P ．证明：2||||2||AM AN OP ⋅=．【答案】（Ⅰ）2214x y +=；（Ⅱ）证明见解析.【解析】试题分析：（Ⅰ）根据题意，4e a ==，得到,,a b c 的方程，进而求得椭圆C 的方程；（Ⅱ）设直线AM 的方程为：y kx =，同时联立椭圆方程，由韦达定理进而求得222284(,)1414k k M k k -++，得到228(1)||||14k AM AN k +=+，同理得到222882||14k OP k +=+，进而结论得到证明.试题解析：（Ⅰ）设椭圆C 的标准方程为22221(0)x y a b a b +=>>，由题意知222,24,a b c c aa ⎧=+⎪⎪=⎨⎪=⎪⎩解得2a =，1b =．所以椭圆C 的标准方程为2214x y +=．……………………………5分（Ⅱ）设直线AM 的方程为：(2)y k x =+，则(0,2)N k ．由 22(2)44,y k x x y =+⎧⎨+=⎩，得2222(1+4)161640k x k x k ++-=（*）．设(2,0)A -，11(,)M x y ，则2-，1x 是方程（*）的两个根，所以2122814k x k -=+． 所以222284(,)1414k k M k k -++．||AM =214k ==+．||AN ==228(1)||||14k AM AN k +==+．设直线OP 的方程为：y kx =．由 2244,y kx x y =⎧⎨+=⎩，得22(14)40k x +-=． 设00(,)P x y ，则202414x k =+，2202414k y k =+． 所以22244||14k OP k +=+，222882||14k OP k +=+． 所以2||||2||AM AN OP ⋅=． ……………13分考点：1.椭圆的标准方程;2.韦达定理.20.已知数列{}n a 的前n 项和为n S ，且满足1(3)a a a =≠，n n n S a 31+=+，设n n n S b 3-=，n *∈N ．(Ⅰ)求证：数列{}n b 是等比数列；(Ⅱ)若1n n a a +≥，n *∈N ，求实数a 的最小值； （Ⅲ）当4=a 时，给出一个新数列{}n e ，其中3,1,, 2.n n n e b n =⎧=⎨≥⎩设这个新数列的前n 项和为n C ，若n C 可以写成p t (,t p *∈N 且1,1>>p t )的形式，则称n C 为“指数型和”．问{}n C 中的项是否存在“指数型和”，若存在，求出所有“指数型和”；若不存在，请说明理由．【答案】(Ⅰ) 12)3(-⨯-=n n a b ；(Ⅱ) a 的最小值为9-；（Ⅲ）没有“指数型和”.【解析】试题分析：(Ⅰ)根据题意将原条件化简，得到12n n b b +=，进而利用等比数列的定义，证明数列{}n b 是等比数列；(Ⅱ)根据(Ⅰ)的结论，利用1,2,n n n a S S n n *-=-≥∈N ，得到数列{}n a 的通项公式，进而得到关于a 的不等式，求得a 的最小值；（Ⅲ）根据(Ⅱ)得到12-=n n b ，再对p 按奇偶性进行分类讨论，进而得到结论.试题解析：(Ⅰ) 因为111132332n n n n n n n b S S b ++++=-=+-=，n *∈N ，且3≠a ， 所以{}n b 是首项为3a -，公比为2等比数列．所以12)3(-⨯-=n n a b ． ………4分 (Ⅱ) 由(Ⅰ)可得12)3(3-⨯-=-n n n a S ，1,2,n n n a S S n n *-=-≥∈N ．12,123(3)2,2n n n a n a a n --=⎧=⎨⨯+-⨯≥⎩因为n n a a ≥+1，所以9-≥a ，且3≠a ．所以a 的最小值为9-． ………9分（Ⅲ）由(Ⅰ)当4=a 时，12-=n n b当2≥n 时，13242n nC -=++++12+=n ，31=C ，所以对正整数n 都有12+=n nC ．由12+=n p t ，n p t 21=-，(,t p *∈N 且1,1>>p t )，t 只能是不小于3的奇数．① 当p 为偶数时，np p pt t t 2)1)(1(122=-+=-，因为12+pt 和12-p t 都是大于1的正整数，所以存在正整数h g ,，使得gp t212=+，h p t 212=-，222=-h g ,2)12(2=--hg h ，所以22=h 且112=--h g 2,1==⇒g h ，相应的3=n ，即有233=C ，3C 为“指数型和”；② 当p 为奇数时，)1)(1(112-++++-=-p p t t t t t ，由于121-++++p t t t 是p 个奇数之和，仍为奇数，又1-t 为正偶数，所以np t t t t 2)1)(1(12=++++-- 不成立，此时没有“指数型和”． ………14分考点：1.等比数列的定义;2.通项公式;3.分类讨论思想.。

2015届高三数学综合检测试题5姓名 得分一、选择题：（本大题共10道小题，每小题5分，共50分。

每小题只有一个正确答案）1．设集合{}1,1,2,3A =-，{B x y ==，则A B 为（ ）A ．{}1,1,2,3-B ．{}1,2,3C ．{}2,3D ．[1,)+∞2． 某赛季，甲、乙两名篮球运动员都参加了7场比赛，他们所有比赛得分的情况用如下图所示的茎叶图表示，则甲、乙两名运动员得分的平均数分别为（ ）A ．14, 13B ．13, 12C ．14, 12D ．12, 14 3．在△ABC 中，已知a =5 2 , c = 10, A = 30°, 则∠B 为（ ）A ． 105°B ． 60°C ．15°D ． 105°或15° 4. 函数()(xxf x e e e -=-为自然对数的底数)在定义域内是（ ）Ａ．奇函数 Ｂ．偶函数 Ｃ．既是奇函数又是偶函数 Ｄ．既不是奇函数也不是偶函数 5. 有一个几何体的三视图及其尺寸如图所示（单位：cm ），则该几何体的表面积．．．为（ ） A ．212cm π B. 215cm π C. 224c m π D. 236cm π 6．已知点（a ，2b ）在直线x+y=3上移动，则2a +4b 的最小值是（ ） A ．8 B ．6 C ． 23 D ．24 7. 函数2()1log f x x =+与1()2x g x -+=在同一直角坐标系下的图象大致是（ ）8. 已知O 是坐标原点，点)2,1(A ，若点),(y x M 为平面区域210100x y x y x -+≥⎧⎪++≥⎨⎪≤⎩上的一个动点 ，则⋅的最小值是（ ）A ．０B ． 12- C ．－２ D ． －39．已知函数22,0(),()()11,02x x f x g x f x x x x x ->⎧⎪==-⎨-++≤⎪⎩则函数的零点的个数是（ ） A ．0个 B ．1 个 C ．2 个 D ．3个10. 已知直线l 的倾斜角为π43，直线l 1经过点l l a B A 与且1),1,(),2,3(-垂直，直线l 2：b a l by x +=++平行，则与直线1012等于（ ）甲乙0129655418355728 1二、填空题(本大题共5道小题，每小题5分，共25分.)11．若2lg （x －2y ）＝lg x ＋lg y ，则xy的值为________； 12．若关于x 的不等式210ax ax +-<解集为R, 则a 的取值范围是______ __；13．已知数列﹛n a ﹜为等比数列，且2113725a a a +=， 则212a a 的值为________；14．阅读右边程序框图，输出的结果S 的值为________；（本大题共6小题，共75分. 解答应写出文字说明、证明过程或演算步骤.）16．（12分）已知函数()sin()f x A x ωϕ=+，x ∈R （其中ππ0,0,22A ωϕ>>-<<），其部分图像如图所示．（1）求函数()f x 的解析式； （2）已知横坐标分别为1-、1、5的三点M 、N 、P 都在函数()f x 的图像上，求sin MNP ∠的值．17．（12分）某校在高三年级开设了A ，B ，C 三个兴趣小组，为了对兴趣小组活动的开展情况进行调查，用分层抽样方法从A ，B ，C 三个兴趣小组的人员中，抽取若干人组成调查小组，有关数据见下表（单位：人）（1）求x ，y 的值； （2）若从A ，B 两个兴趣小组抽取的人中选2人作专题发言，求这2人都来自兴趣小组B 的概率．18. （12分）如图，在四棱锥P ABCD -中，底面ABCD 为正方形，PA ⊥面ABCD ，PA AB =，点E 是PD 的中点．（1）求证：PB //平面ACE ； （2）若四面体E ACD -的体积为23，求AB 的长．19．（13分）已知数列{}n a 的前n 项和223,()n S n n n N *=++∈ （1）求通项n a ； （2）求和=n T 14332211111+++++n n a a a a a a a a .20. （13分）研究表明：学生的接受能力依赖于老师持续讲课所用的时间。

1.[2014·洛阳统考]等比数列{a n }的前n 项和为S n ，已知S 1,2S 2,3S 3成等差数列，则{a n }的公比为( )A ．2B ．3 C.12D.13解析：因为a n ＝a 1q n －1，又4S 2＝S 1＋3S 3，所以4(a 1＋a 1q )＝a 1＋3(a 1＋a 1q ＋a 1q 2)，解得{a n }的公比q ＝13.故选D.答案：D2. [2014·湖北模拟]已知等比数列{a n }中，各项都是正数，且a 1，12a 3,2a 2成等差数列，则a 9＋a 10a 7＋a 8＝( ) A. 1＋ 2 B. 1－ 2 C. 3＋2 2D. 3－2 2解析：设等比数列{a n }的公比为q (q >0)，则由题意得a 3＝a 1＋2a 2，即a 1q 2＝a 1＋2a 1q ，q2－2q －1＝0，解得q ＝1± 2.又q >0，所以q ＝1＋2，所以a 9＋a 10a 7＋a 8＝q 2a 7＋a 8a 7＋a 8＝q 2＝(1＋2)2＝3＋22，选C.答案：C3. [2014·河北教学质量监测]已知数列{a n }满足：a 1＝1，a n ＋1＝a na n ＋2(n ∈N *)．若b n ＋1＝(n －λ)(1a n＋1)(n ∈N *)，b 1＝－λ，且数列{b n }是单调递增数列，则实数λ的取值范围为( )A. λ>2B. λ>3C. λ<2D. λ<3解析：由已知可得1a n ＋1＝2a n＋1，1a n ＋1＋1＝2(1a n ＋1)，1a 1＋1＝2≠0，则1a n＋1＝2n ，b n ＋1＝2n(n－λ)，b n ＝2n －1(n －1－λ)(n ≥2，n ∈N *)，b 1＝－λ也适合上式，故b n ＝2n －1(n －1－λ)(n ∈N *)．由b n ＋1>b n ，得2n(n －λ)>2n －1(n －1－λ)，即λ<n ＋1恒成立，而n ＋1的最小值为2，故实数λ的取值范围为λ<2.答案：C4. [2013·江西高考]某住宅小区计划植树不少于100棵，若第一天植2棵，以后每天植树的棵数是前一天的2倍，则需要的最少天数n (n ∈N *)等于________．解析：S n ＝－2n1－2＝2n ＋1－2≥100，得n ≥6.答案：65. [2013·重庆高考]已知{a n}是等差数列，a1＝1，公差d≠0，S n为其前n项和，若a1，a2，a5成等比数列，则S8＝________.解析：因为{a n}为等差数列，且a1，a2，a5成等比数列，所以a1(a1＋4d)＝(a1＋d)2，解得d＝2a1＝2，所以S8＝64.答案：64。

2014-2015年高一数学必修五试题一、选择题（本大题共10小题，每小题5分，共50分）.1．已知集合2{(1)37,},A x x x x R =-<+∈0,1x B x x ⎧⎫=≤⎨⎬+⎩⎭则A B ⋂= ( )A ．[]1,0-B ．()1,0-C ．(]1,0-D ．[)1,0-2．在ABC ∆中，若2,60a b B ︒===，则此三角形（ )A ．无解B ．有一解C ．有两解D ．解的个数无法确定 3．在数列{}n a 中，1121,,2nn n a a a a +==+则该数列的第5项为（ ） A ．12 B ．25 C ．13 D ．23 4．如图所示，表示阴影部分的二元一次不等式组是（ ）A ．202400x y x y x --<⎧⎪+->⎨⎪≥⎩B ．20240x y x y x --<⎧⎪+-<⎨⎪≥⎩C ．202400x y x y x -->⎧⎪+-<⎨⎪≥⎩D ．202400x y x y x -->⎧⎪+->⎨⎪≥⎩5．等比数列{}n a 的前项和为n S ，已知123,2,3S S S A ．3-B ．13-C ．3D ．136．设01b a <<<，则下列不等式不成立的是（ ）A ．222ba<< B ．11220log log a b << C ．21ab b << D ．21ab a <<7．在ABC ∆中，角A 、B 、C 所对的边分别为a b c 、、，若角3C π>，sin 2sin a C b A =，则下列结论正确的有 （ ）个①一定是锐角三角形；②一定是等腰三角形；③可能是等腰直角三角形；④可能是等边三角形 A ．1 B ．2 C ．3 D ．48．已知等差数列{}n a ，{}n b 的前n 项和分别为,n n S T ，且9593n n S n T n +=+，则使得n na b 为整数的正整数的个数是（ ）A ．5B ．4C ．3D ．29．若数列{}n a 满足：132a =，112(2,3,4,)221n n a n a -=-=+，且有一个形如sin()n a A n ωϕ=+的通项公式，其中,,A ωϕ均为实数，且0ω>，则此通项公式n a 可以为（ ）A ．32sin 236n a n ππ⎛⎫=- ⎪⎝⎭B ．2233n a n ππ⎛⎫=+ ⎪⎝⎭C ．325sin 236n a n ππ⎛⎫=-+ ⎪⎝⎭D ．233n a n ππ⎛⎫=- ⎪⎝⎭10．定义在R 上的函数()y f x =是减函数，且对任意的a R ∈，都有()()0f a f a -+=，若x y 、满足不等式22(2)(2)0f x x f y y -+-≤，则当14x ≤≤时，2x y -的最小值为（ ）A ．4-B ．1-C ．0D ．8二、填空题（本大题共5小题，每小题5分，共25分） 11．《莱因徳纸草书》是世界上最古老的数学著作之一。

2014—2015学年高一数学必修五综合试卷一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．不等式0121≤+-x x 的解集为( ) A ．⎝⎛⎭⎫－∞，－12∪[1，＋∞) B ．⎣⎡⎦⎤－12，1 C ．⎝⎛⎦⎤－∞，－12∪[1，＋∞) D ．⎝⎛⎦⎤－12，1 2．若0<<b a ，则下列不等式不能成立的是 ( )A ．ba 11> B ．ba 22> C ．b a >D ．ba )21()21(>3．不等式16)21(1281≤<x 的整数解的个数为 （ ）A ．10B ．11C ．12D ．134．等差数列{}n a 中，如果39741=++a a a ，27963=++a a a ，则数列{}n a 前9项的和为( ) A ．297B ．144C ．99D ．665．若数列{}n a 满足关系：111n na a +=+，51=a ，则5a ＝( )． A ．32B ．85C ．53D ．1386．ABC ∆中，已知︒=135B ，︒=15C ，5=a ，则最大边长为 （ ） A ．25 B ．34 C ．35 D ．247．在锐角三角形△ABC 中，4||=，1||=，△ABC 的面积为3，则∙的值为（ ） A ．2 B ．-2 C ．4 D ．-48．若c b a ,,满足c b a >>，且0<⋅c a ，则下列选项中不一定成立的是( )A ．ac ab >B ．ac bc >C ．0)(<-c a acD ．22ab c b <9．当]21,0(∈x 时，若不等式012≥++ax x 恒成立，则a 的最小值为（ ）A ．25- B ．2- C ．1- D ．3-10．数列{}n a 满足21=a ，1111+-=++n n n a a a ，其前n 项积为n T ，则=2014T ( )A ．61 B ．61- C ．6 D ．6- 11．已知0,0>>y x ，且112=+yx ，若m m y x 222+>+恒成立，则实数m 的取值范围是( ) A ．(－∞，－2]∪[4，＋∞) B ．(－2，4) C ．(－∞，－4]∪[2，＋∞) D ．(－4，2) 12．设数列{}n a 的前n 项和为n S ，令nS S S T nn +++=21，称n T 为数列n a a a ,,,21 的“理想数”，已知数列50021,,,a a a 的“理想数”为2004，那么数列12,50021,,,a a a 的“理想数”为( )A ．2012B ．2013C ．2014D ．2015第Ⅱ卷（非选择题 共90分）二、填空题(本大题共有4 题,每题5分,共20分)13．在ABC ∆中，已知B A tan ,tan 是x 的方程01)1(2=+++x p x 的两个根，则=∠C ________．14．在ABC ∆中， 60,3,8===A c b ，则此三角形的外接圆的面积为 .15．设变量x ，y 满足约束条件⎪⎩⎪⎨⎧≤+≤+--≤8201223y x y x x y ,则x y 的最大值是 _．16．已知n S 是等差数列{}n a 的前n 项和，且576S S S >>，给出下列五个命题： ①0<d ；②012>S ；③012<S ；④数列{}n S 中的最大项为11S ；⑤||||76a a >. 其中正确的命题有 。

2015年全国大联考高考数学五模试卷（理科）一、选择题：本大题共12小题，每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）已知复数z满足z=（i为虚数单位）,则在复平面内对应的点位于（）A．第一象限 B．第二象限 C．第三象限 D．第四象限2．(5分)集合M=｛x｜1＜x+1≤3｝,N={x｜x2﹣2x﹣3＞0｝，则(∁R M）∩(∁R N）等于（) A．(﹣1,3）B．（﹣1，0）∪(2，3）C．（﹣1,0］∪[2，3) D．[﹣1，0］∪（2，3］3．(5分）某市场调查员在同一天对本市的5家商场的某商品的一天销售量及其价格进行调查，5家商场的售价x(元)和销售量y(件)之间的一组数据如下表所示：价格x（元）9 9.5 10 10.5 11销售量y（件) 11 a 8 6 5由散点图可知，销售量y与价格x之间有较好的线性相关关系，且回归直线方程是=﹣3。

2x+4a，则实数a等于(）A．7 B．8.5 C．9 D．104．(5分）已知随机变量X服从正态分布N（2，σ2），P（X≤3)=0。

72，则P(1＜X＜3）等于(）A．0.28 B．0。

44 C．0。

56 D．0。

845．(5分）在（1﹣x）3（1+x）8的展开式中，含x2项的系数是（）A．6 B．﹣6 C．7 D．﹣76．(5分)给出下列三个类比结论．①“（ab)n=a n b n”类比推理出“（a+b）n=a n+b n；②已知直线a，b，c，若a∥b,b∥c，则a∥c．类比推理出：已知向量a，b，c，若a∥b，b∥c,则a∥c；③同一平面内，直线a，b，c，若a⊥b，b⊥c，则a∥c．类比推理出：空间中,已知平面α，β，γ，若α⊥β，β⊥γ,则α∥γ．其中结论正确的个数是()A．0 B．1 C．2 D．37．（5分）要从8名教师中选派4人去参加一个研讨会，其中教师甲是领队必须去，而乙、丙两位教师不能同去，则不同的选派方法有（）A．18种B．24种C．30种D．48种8．（5分）某程序框图如图所示，该程序运行后输出的值是（）A．6 B．7 C．8 D．99．（5分)（2014•福建模拟)将一个质点随机投放在关于x，y的不等式组所构成的三角形区域内，则该质点到此三角形的三个顶点的距离均不小于1的概率是（）A．B．C．D．10．（5分）已知2a=3b=6c，k∈Z，不等式＞k恒成立，则整数k的最大值为（）A．6 B．5 C．3 D．411．（5分）（2014•海淀区一模）已知A(1，0），点B在曲线G:y=ln（x+1）上,若线段AB与曲线M：y=相交且交点恰为线段AB的中点，则称B为曲线G关于曲线M的一个关联点．记曲线G关于曲线M的关联点的个数为a，则（）A．a=0 B．a=1 C．a=2 D．a＞212．（5分)（2014•长春四模）设，则对任意正整数m，n（m＞n），都成立的是（）A．B．C．D．二、填空题:本大题共4小题，每小题5分，共20分.把答案填在答题卷中的横线上. 13．(5分)已知i是虚数单位，则|+|=．14．（5分）（2015•江苏模拟)某高校在某年的自主招生考试成绩中随机抽取50名学生的笔试成绩，绘制成频率分布直方图如图所示，若要从成绩在［85,90),［90，95），［95，100］三组内的学生中,用分层抽样的方法抽取12人参加面试，则成绩在［90，100]内的学生应抽取的人数为．15．（5分)某市有A、B两所示范高中响应政府号召，对该市甲、乙两个教育落后地区开展支教活动．经上级研究决定：向甲地派出3名A校教师和2名B校教师,向乙地派出3名A 校教师和3名B校教师．由于客观原因，需从拟派往甲、乙两地的教师中各自任选一名互换支教地区，则互换后A校教师派往甲地区人数不少于3名的概率为．16．（5分）已知双曲线（a＞0，b＞0）的左右焦点分别为F1，F2,过F1作圆：x2+y2=的切线，切点为E,延长F1E交双曲线右支于点P，若｜OP｜=|F1F2|（O为坐标原点),则双曲线的离心率为．三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤. 17．（10分）（2014春•玉田县期中）已知点P n(a n，b n)满足a n+1=a n•b n+1，b n+1=（n∈N*）且点P1的坐标为（1,﹣1)．（1）求过点P1,P2的直线l的方程;（2）试用数学归纳法证明：对于n∈N＊，点P n都在（1）中的直线l上．18．（12分)（2015•濮阳一模)某城市随机抽取一年（365天)内100天的空气质量指数API的监测数据，结果统计如下：API ［0,50](50,100］（100，150］（150，200]（200,250］（250，300］＞300空气质量优良轻微污染轻度污染中度污染中度重污染重度污染天数 4 13 18 30 9 11 15（1）若某企业每天由空气污染造成的经济损失S(单位:元）与空气质量指数API（记为ω)的关系式为：S=，试估计在本年内随机抽取一天，该天经济损失S大于200元且不超过600元的概率；（2）若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染，完成下面2×2列联表，并判断能否有95%的把握认为该市本年空气重度污染与供暖有关？附：P(K2≥k0）0。

2015年华南师大附中高三综合测试数学（理科）2015.5本试卷共4页，21小题， 满分150分． 考试用时120分钟．注意事项：1．答卷前，考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上．用2B 铅笔将试卷类型（A ）填涂在答题卡相应位置上． 2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上． 3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．4．作答选做题时，请先用2B 铅笔填涂选做题的题号对应的信息点，再作答．漏涂、错涂、多涂的，答案无效．5．考生必须保持答题卡的整洁．考试结束后，将试卷和答题卡一并交回．第一部分 选择题（40分）一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．设i 为虚数单位,若复数()()2282i z m m m =+-+-是纯虚数,则实数m =：A ．2B ．4-或2C ．2或4-D ． 4- 2．已知命题p ：∃α∈R ，cos (π－α) = cos α；命题q : ∀x ∈R ，x 2 + 1 > 0. 则下面结论正确的是：A. p ∨q 是真命题B. p ∧q 是假命题C. ¬ q 是真命题D. p 是假命题3．若 x 、y 满足约束条件 ⎩⎪⎨⎪⎧ 2x + 2y ≥1x ≥y 2x －y ≤1且向量 a = (3,2)，b = (x ,y )，则 a ·b 的取值范围是： A. [54,4]B. [72,5]C. [54,5]D. [72,4]4. 同时具有性质“①最小正周期是π，②图象关于直线3π=x 对称；③在]3,6[ππ-上是增函数”的一个函数是：A ．)62sin(π+=x yB ．)32cos(π+=x y C ． )62cos(π-=x yD ． )62sin(π-=x y5. 函数f (x )＝|log 2(x ＋1)| 的图象大致是：6. 已知点 F 是抛物线 y 2 = 4x 的焦点，M 、N 是该抛物线上两点，| MF | + | NF | =6，则 MN 中点的横坐标为： A. 32 B. 2C. 52D. 37. 设函数)(x f y =在R 上有定义，对于任一给定的正数p ，定义函数⎩⎨⎧>≤=p x f p px f x f x f p )(,)(),()(，则称函数)(x f p 为)(x f 的“p 界函数”若给定函数2,12)(2=--=p x x x f ，则下列结论不．成立的是： A. [](0)[(0)]p p f f f f = B. [](1)[(1)]p p f f f f = C. [][(2)](2)p p f f f f = D. [][(3)](3)p p f f f f =8. 若直角坐标平面内两相异点A 、B 两点满足：① 点A 、B 都在函数 f (x ) 的图象上；② 点A 、B 关于原点对称，则点对 (A ，B ) 是函数 f (x ) 的一个“姊妹点对”. 点对 (A ，B ) 与 (B ，A ) 可看作是同一个“姊妹点对”. 已知函数 f (x ) = ⎩⎪⎨⎪⎧ x 2 + 2x ，x < 0 x + 1e x ，x ≥0 ，则 f (x ) 的“姊妹点对”有： A. 0 个 B. 1 个 C. 2 个 D. 3 个第二部分 非选择题（110分）二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分． （一）必做题（9～13题）9. 不等式12x x -<的解集为 *** . 10.2612)x x-（的展开式的常数项是 *** （用数字作答）.11. 图一是一个算法的流程图，则最后输出的S 是 *** ．12．某三棱锥的三视图如图二所示，正视图、侧视图均为直角三角形，则该三棱锥的四个面中，面积最大的面的面积是 *** .13. 数字“2015”中，各位数字相加和为8，称该数为“如意四位数”，则用数字0,1,2,3,4,5组成的无重复数字且大于2015的“如意四位数”有 *** 个.（二）选做题（14～15题，考生只能从中选做一题）14 . （坐标系与参数方程选做题）设曲线C 的参数方程为4cos 14sin x a y θθ=+⎧⎨=+⎩(θ是参数，0>a )，直线l 的极坐标方程为3cos 4sin 5ρθρθ+=，若曲线C与直线l 只有一个公共点，则实数a 的值是 *** ．15. （几何证明选做题）如图，⊙O 上一点C 在直径AB 上的射影为D ，且4CD =，8BD =，则⊙O 的半径等于*** .三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本题满分12分）已知,,a b c 分别是ABC ∆的角,,A B C 所对的边，且2c =，3C π=。

2015年高一数学强化训练（5）20150821一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1. （2013年高考山东卷（文））已知集合B A 、均为全集}4,3,2,1{=U 的子集,且(){4}U A B = ð,{1,2}B =,则U A B = ð（ ）A ．{3}B ．{4}C ．{3,4}D ．∅【答案】A2. （2013年高考辽宁卷（文））已知点()()1,3,4,1,A B AB -则与向量同方向的单位向量为（） A ．3455⎛⎫ ⎪⎝⎭，- B ．4355⎛⎫ ⎪⎝⎭，-C ．3455⎛⎫- ⎪⎝⎭，D ．4355⎛⎫- ⎪⎝⎭，【答案】A3. （2013年高考山东卷（文））将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91,现场做的9个分数的茎叶图后来有一个数据模糊,无法辨认,在图中以x 表示:则7个剩余分数的方差为（ ） A ．1169B ．367C ．36 D【答案】B4. （2013年高考天津卷（文））已知过点P (2,2) 的直线与圆225(1)x y +=-相切, 且与直线10ax y -+=垂直, 则a =（ ） A ．12-B ．1C ．2D ．12【答案】C5. （2013年高考重庆卷（文））已知函数3()sin 4(,)f x ax b x a b R =++∈,2(lg(log 10))5f =,则(lg(lg 2))f =（8 7 79 4 0 1 0 9 1x） A ．5-B ．1-C ．3D ．4【答案】C6. （2013年高考课标Ⅰ卷（文））执行右面的程序框图,如果输入的[1,3]t ∈-,则输出的S 属于（） A ．[3,4]-B ．[5,2]-C ．[4,3]-D ．[2,5]-【答案】A7. （2013年高考湖南（文））已知事件“在矩形ABCD 的边CD 上随机取一点P,使△APB 的最大边是AB”发生的概率为.21,则ADAB=____（ ）A ．12B ．14 C D 【答案】D8. （2013年高考课标Ⅰ卷（文））函数()(1cos )sin f x x x =-在[,]ππ-的图像大致为【答案】C;9. （2013年高考浙江卷（文））已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是（）A．108cm3B．100 cm3C．92cm3D．84cm3【答案】B10.（2013年高考陕西卷（文））已知点M(a,b)在圆221:O x y+=外, 则直线ax + by = 1与圆O 的位置关系是（）A．相切B．相交C．相离D．不确定【答案】B11.（2013年高考湖北卷（文））将函数sin()y x x x+∈R的图象向左平移(0)m m>个单位长度后,所得到的图象关于y轴对称,则m的最小值是（）A．π12B．π6C．π3D．5π6【答案】B12. （2013年高考湖北卷（文））x 为实数,[]x 表示不超过x 的最大整数,则函数()[]f x x x =-在R 上为（ ）A ．奇函数B ．偶函数C ．增函数D ．周期函数【答案】D二、填空题：本大题共4小题，每小题5分，满分20分．13. （2013年高考课标Ⅱ卷（文））已知正方形ABCD 的边长为2,E 为CD 的 中点,则AE BD ⋅=________.【答案】 214. （2013年高考湖北卷（文））已知圆O :225x y +=,直线l :cos sin 1x y θθ+=(π02θ<<).设圆O 上到直线l 的距离等于1的点的个数为k ,则k =________. 【答案】415. （2013年高考课标Ⅰ卷（文））已知H 是球O 的直径AB 上一点,:1:2AH HB =,AB ⊥平面α,H 为垂足,α截球O 所得截面的面积为π,则球O 的表面积为_______.【答案】92π; 16. （2013年高考安徽（文））定义在R 上的函数()f x 满足(1)2()f x f x +=.若当01x ≤≤时.()(1)f x x x =-,则当10x -≤≤时,()f x =________________.【答案】(1)()2x x f x +=-三、解答题：本大题共6小题，满分70分．解答须写出文字说明、证明过程和演算步骤．17．（本小题满分12分）（2013年高考山东卷（文））设函数2()sin cos (0)f x x x x ωωωω=->,且()y f x =的图象的一个对称中心到最近的对称轴的距离为4π,(Ⅰ)求ω的值(Ⅱ)求()f x 在区间3[,]2ππ上的最大值和最小值 【答案】18. (本小题满分共12分) （2013年高考课标Ⅱ卷（文））经销商经销某种农产品,在一个销售季度内,每售出1t 该产品获利润500元,未售出的产品,每1t 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如右图所示.经销商为下一个销售季度购进了130t 该农产品.以X(单位:t≤100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润. (Ⅰ)将T 表示为X 的函数;(Ⅱ)根据直方图估计利润T 不少于57000元的概率.【答案】19. （本小题满分12分）（2013年高考广东卷（文））从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:(1) 根据频数分布表计算苹果的重量在[90,95)的频率;(2) 用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?(3) 在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率.【答案】(1)重量在[)90,95的频率200.450==;(2)若采用分层抽样的方法从重量在[)80,85和[)95,100的苹果中共抽取4个,则重量在[)80,85的个数541515=⨯=+; (3)设在[)80,85中抽取的一个苹果为x ,在[)95,100中抽取的三个苹果分别为,,a b c ,从抽出的4个苹果中,任取2个共有(,),(,),(,),(,),(,),(,)x a x b x c a b a c b c 6种情况,其中符合“重量在[)80,85和[)95,100中各有一个”的情况共有(,),(,),(,)x a x b x c 种;设“抽出的4个苹果中,任取2个,求重量在[)80,85和[)95,100中各有一个”为事件A ,则事件A 的概率31()62P A ==;20. （本小题满分12分）（2013年高考浙江卷（文））如图,在在四棱锥P-ABCD 中,PA⊥面ABCD,AB=BC=2,AD=CD=7,PA=3,∠ABC=120°,G 为线段PC 上的点.(Ⅰ)证明:BD⊥面PAC ;(Ⅱ)若G 是PC 的中点,求DG 与APC 所成的角的正切值; (Ⅲ)若G 满足PC⊥面BGD,求PGGC的值.【答案】解:证明:(Ⅰ)由已知得三角形ABC是等腰三角形,且底角等于30°,且6030AB CB AD CD ABD CBD ABD CBD BAC BD DB =⎫⎪=⇒∆≅∆⇒∠=∠=∠=⎬⎪=⎭ 且,所以;、BD AC ⊥,又因为PA ABCD BD PA BD PAC BD AC ⊥⇒⊥⎫⇒⊥⎬⊥⎭;(Ⅱ)设AC BD O = ,由(1)知DO PAC ⊥,连接GO ,所以DG 与面APC 所成的角是DGO ∠,由已知及(1)知:1,2BO AO CO DO =====, [来源:学&科&网Z&X&X&K]12tan 2OD GO PA DGO GO ==⇒∠===,所以DG 与面APC 所(Ⅲ)由已知得到:PC ===,因为P C B G D P ⊥∴⊥,在PDC ∆中,PD CD PC ====,设223107)2PG PG x CG x x x PG x GC GC =∴=-∴-=-∴====21. （本小题满分12分）已知以点C (t ，2t )(t ∈R ，t ≠0)为圆心的圆与x 轴交于点O ，A ，与y 轴交于点O ，B ，其中O 为原点. (1)求证：△OAB 的面积为定值；(2)设直线y ＝－2x ＋4与圆C 交于点M ，N ，若OM ＝ON ，求圆C 的方程. (1)证明 ∵圆C 过原点O ，∴OC 2＝t 2＋4t 2.设圆C 的方程是(x －t )2＋(y －2t )2＝t 2＋4t 2，令x ＝0，得y 1＝0，y 2＝4t ；令y ＝0，得x 1＝0，x 2＝2t ， ∴S △OAB ＝12OA ·OB ＝12×|4t |×|2t |＝4，即△OAB 的面积为定值.(2)解 ∵OM ＝ON ，CM ＝CN ，∴OC 垂直平分线段MN . ∵k MN ＝－2，∴k OC ＝12.∴2t ＝12t ，解得t ＝2或t ＝－2.当t ＝2时，圆心C 的坐标为(2,1)，OC ＝5， 此时C 到直线y ＝－2x ＋4的距离d ＝15<5， 圆C 与直线y ＝－2x ＋4相交于两点.当t ＝－2时，圆心C 的坐标为(－2，－1)，OC ＝5， 此时C 到直线y ＝－2x ＋4的距离d ＝95> 5. 圆C 与直线y ＝－2x ＋4不相交， ∴t ＝－2不符合题意，舍去.∴圆C 的方程为(x －2)2＋(y －1)2＝5.22. （本小题满分12分）（2013年高考安徽（文））设函数22()(1)f x ax a x =-+,其中0a >,区间{}|()0I x f x =>.(Ⅰ)求I 的长度(注:区间(,)αβ的长度定义为βα-;(Ⅱ)给定常数()0,1k ∈,当11k a k -≤≤+时,求I 长度的最小值.【答案】解:(1)令2()-10f x x a a x ⎡⎤=+=⎣⎦（）解得 10x = 221ax a =+ 2|01a I x x a ⎧⎫∴=<<⎨⎬+⎩⎭ I ∴的长度212-1a x x a=+ (2) ()0,1k ∈ 则0112k a k <-≤≤+< 由 (1)21aI a=+2221'0(1)a I a -=>+,则01a << 故I 关于a 在(1,1)k -上单调递增,在(1,1)k +上单调递减.()1221-1-2211-k kI k kk ==+++ 22111kI k +=++（）min21-22kI k k =++。