(完整版)高中数学必修五综合测试题 含答案,推荐文档

高一数学必修 5 试题一． 选择题 本大题共 10 小题，每小题 5 分，共 60 分. 在每小题给出的四个选项中，只有一项是符合题目要求的。

）1.由a 1 1 ， d3确定的等差数列a n，当 a n 298 ，序号 n 等于 （）Ａ． 99Ｂ． 100Ｃ． 96Ｄ． 1012.ABC 中，若 a 1, c2, B60 ， ABC 的面（ ）A ．1B ．3 D.3223. 在数列 { a n } 中， a 1 =1， a n 1a n 2 ， a 51 的（）A ． 99 B． 49C． 102 D． 1014. 已知数列 3 ,3,15 , ⋯, 3(2n 1) , 那么 9 是数列的( )（）第12（）第13（）第14（）第15ABCD5. a 1 11 a n1在等比数列中，， q2 ，， 数 n（）232A. 3B. 4C. 5D. 66.△ ABC 中， cosA a， △ ABC 一定是( )cos BbA ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等 三角形7. 定函数 yf ( x) 的 象在下列 中，并且 任意a 1 (0,1) ，由关系式 a n 1f (a n ) 得到的数列 { a n } 足 a n 1a n (n N * ) ， 函数的 象是（ ）ｙｙｙ ｙ1111ｏ1ｏ1ｏ1ｘｏ1ｘｘｘABCD8. 在ABC 中 , a 80,b 100, A 45 , 此三角形解的情况是（）A. 一解B.两解 C. 一解或两解D. 无解9. 在△ ABC 中，如果 sin A :sin B :sin C 2:3: 4 ，那么 cos C 等于（）2211A.B. -C. -D. -333410. 一个等比数列 { a n } 的前 n 和 48，前 2n 和 60， 前 3n和（）A 、 63B 、108C 、75D 、 8311. 在△ ABC 中，∠ A = 60° ,a = 6 ,b = 4 , 足条件的△ ABC( )(A) 无解 (B) 有解(C)有两解(D)不能确定12. 数列 { a n } 中， a 11, a n2a n(nN) ， 2是 个数列的第几（）12101a n二、填空题 ( 本大题共 4 小题，每小题 5 分，共 20 分。

最新人教版高中数学必修五综合测试题及答案2套模块综合检测(A)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．在△ABC 中，已知(a ＋c )(a －c )＝b 2＋bc ，则A 等于( ) A ．30° B ．60° C ．120°D ．150°解析： 由已知得b 2＋c 2－a 2＝－bc ， ∴cos A ＝－12，∴A ＝120°.答案： C2．已知集合A ＝{x ∈R |3x ＋2>0}，B ＝{x ∈R |(x ＋1)(x －3)>0}，则A ∩B ＝( ) A ．(－∞，－1) B ．⎝⎛⎭⎫－1，－23 C ．⎝⎛⎭⎫－23，3 D ．(3，＋∞)解析： A ＝⎩⎨⎧⎭⎬⎫x ∈R |x >－23，B ＝{x ∈R |x >3或x <－1}， ∴A ∩B ＝{x ∈R |x >3}． 答案： D3．等差数列{a n }的公差为1，若a 1，a 2，a 4成等比数列，则a 3＝( ) A ．1 B ．2 C ．－3D ．3解析： ∵a 1，a 2，a 4成等比数列， ∴a 22＝a 1·a 4即(a 1＋1)2＝a 1·(a 1＋3) 解得：a 1＝1，∴a 3＝a 1＋2d ＝3. 答案： D4．已知t ＝a ＋2b ，s ＝a ＋b 2＋1，则t 和s 的大小关系正确的是( ) A ．t ≤s B ．t ≥s C ．t ＜sD ．t >s 解析： ∵t －s ＝a ＋2b －a －b 2－1＝－(b －1)2≤0，∴t ≤s . 答案： A5．各项不为零的等差数列{a n }中，有a 27＝2(a 3＋a 11)，数列{b n }是等比数列，且b 7＝a 7，则b 6b 8＝( )A ．2B ．4C ．8D ．16解析： b 6b 8＝b 27＝a 27，又a 27＝2(a 3＋a 11)＝4a 7，∴a 7＝4，∴b 6b 8＝16，故选D. 答案： D6．△ABC 的三边分别为a ，b ，c ，且a ＝1，B ＝45°，S △ABC ＝2，则△ABC 的外接圆的直径为( )A ．4 3B ．5C ．5 2D ．6 2解析： ∵S △ABC ＝12ac sin B ，∴c ＝42，由余弦定理b 2＝a 2＋c 2－2ac cos B ＝25， ∴b ＝5.由正弦定理2R ＝bsin B ＝5 2.(R 为△ABC 外接圆的半径)答案： C7．在等差数列{a n }中，a 1＝120，公差d ＝－4，若前n 项和S n 满足S n ＜a n (n ∈N *)，则n 的最小值是( )A ．60B ．63C ．70D ．72 解析： S n ＜a n ⇔120n ＋n (n －1)2×(－4)＜120＋(n －1)×(－4)，即n 2－63n ＋62＞0，解得n ＜1(舍去)或n ＞62，∴n 的最小值为63. 答案： B8．在R 上定义运算☆，a ☆b ＝ab ＋2a ＋b ，则满足x ☆(x －2)<0的实数x 的取值范围为( )A ．(0,2)B ．(－2,1)C ．(－∞，－2)∪(1，＋∞)D ．(－1,2)解析： 根据定义得：x ☆(x －2)＝x (x －2)＋2x ＋(x －2)＝x 2＋x －2<0，解得 －2<x <1，所以实数x 的取值范围为(－2，1)，故选B.答案： B9．一艘客船上午9∶30在A 处，测得灯塔S 在它的北偏东30°，之后它以每小时32海里的速度继续沿正北方向匀速航行，上午10∶00到达B 处，此时测得船与灯塔S 相距82海里，则灯塔S 在B 处的( )A ．北偏东75°B ．东偏南75°C ．北偏东75°或东偏南75°D ．以上方位都不对解析：根据题意画出示意图，如图，由题意可知AB ＝32×12＝16，BS ＝82，∠A ＝30°.在△ABS 中，由正弦定理得 AB sin S ＝BSsin A， sin S ＝AB sin A BS ＝16sin 30°82＝22，∴S ＝45°或135°， ∴B ＝105°或15°，即灯塔S 在B 处的北偏东75°或东偏南75°. 答案： C10．数列{a n }的前n 项和为S n ，若a 1＝1，a n ＋1＝3S n (n ≥1)，则a 6＝( ) A ．3×44 B ．3×44＋1 C ．45D ．45＋1解析： 当n ≥1时，a n ＋1＝3S n ，则a n ＋2＝3S n ＋1， ∴a n ＋2－a n ＋1＝3S n ＋1－3S n ＝3a n ＋1， 即a n ＋2＝4a n ＋1.∴该数列从第二项开始是以4为公比的等比数列．又a 2＝3S 1＝3a 1＝3，∴a n ＝⎩⎪⎨⎪⎧1(n ＝1)，3×4n －2(n ≥2). ∴当n ＝6时，a 6＝3×46－2＝3×44.答案： A11．已知平面直角坐标系xOy 上的区域D 由不等式组⎩⎨⎧0≤x ≤2，y ≤2，x ≤2y给定，若M (x ，y )为D 上的动点，点A 的坐标为(2，1)，则z ＝OM →·OA →的最大值为( )A ．4 2B ．3 2C ．4D ．3解析： 由线性约束条件⎩⎨⎧0≤x ≤2，y ≤2，x ≤2y ，画出可行域如图所示，目标函数z ＝OM →·OA →＝2x ＋y ，将其化为y ＝－2x ＋z ，结合图形可知，目标函数的图象过点(2，2)时，z 最大，将点(2，2)的坐标代入z ＝2x ＋y 得z 的最大值为4.答案： C12．在R 上定义运算⊕：x ⊕y ＝x2－y ，若关于x 的不等式x ⊕(x ＋1－a )>0的解集是集合{x |－2≤x ≤2}的子集，则实数a 的取值范围是( )A ．[－1,3]B ．[－3,1]C ．[－3，－1)∪(－1,1]D ．[－1,1)∪(1,3]解析： x ⊕(x ＋1－a )＝x 2－x －1＋a ＝－xx －(a ＋1)>0⇒xx －(a ＋1)<0，(1)⎩⎪⎨⎪⎧a >－10<x <a ＋1≤2⇒－1<a ≤1； (2)⎩⎪⎨⎪⎧a <－1－2≤a ＋1<x <0⇒－3≤a <－1； (3)a ＝－1时，不等式为x x －0<0，x ∈∅显然成立，故选B.答案： B二、填空题(本大题共4小题，每小题4分，共16分．请把正确答案填在题中横线上) 13．在等差数列{a n }中，a 3＋a 7＝37，则a 2＋a 4＋a 6＋a 8＝____________. 解析： 由等差数列的性质知a 2＋a 4＋a 6＋a 8＝2(a 3＋a 7)＝2×37＝74. 答案： 7414．已知关于x 的不等式ax 2＋bx ＋c <0的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x <－2或x >－12，则不等式ax 2－bx ＋c >0的解集为________．解析： 由ax 2＋bx ＋c <0的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x <－2或x >－12得－2，－12为方程ax 2＋bx ＋c ＝0的两根且a <0，∴⎩⎨⎧－2－12＝－b a，－2×⎝⎛⎭⎫－12＝c a，即⎩⎪⎨⎪⎧b ＝52a <0，c ＝a <0，∴不等式ax 2－bx ＋c >0等价于2x 2－5x ＋2<0，解得12<x <2.∴不等式ax 2－bx ＋c >0的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪12<x <2. 答案： ⎩⎨⎧⎭⎬⎫x ⎪⎪12<x <215．在△ABC 中，已知BC ＝12，A ＝60°，B ＝45°，则AC ＝________. 解析： 由正弦定理，得AC sin B ＝BCsin A. 所以AC ＝BC sin A ·sin B ＝12sin 60°sin 45°＝4 6.答案： 4 616．若x ，y 满足约束条件⎩⎪⎨⎪⎧x ≥0，x ＋2y ≥3，2x ＋y ≤3，则x －y 的取值范围是________．解析： 记z ＝x －y ，则y ＝x －z ，所以z 为直线y ＝x －z 在y 轴上的截距的相反数，画出不等式组表示的可行域如图中△ABC 区域所示．结合图形可知，当直线经过点B (1,1)时，x －y 取得最大值0，当直线经过点C (0,3)时，x －y 取得最小值－3.答案： [－3,0]三、解答题(本大题共6小题，共74分．解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分12分)在△ABC 中，已知a ＝23，b ＝6，A ＝30°，求B 及S △ABC . 解析： 在△ABC 中，由正弦定理得a sin A ＝bsin B ，∴sin B ＝b a sin A ＝623·12＝32.又A ＝30°，且a <b ，∴B >A . ∴B ＝60°或120°.①当B ＝60°时，C ＝90°，△ABC 为直角三角形， S △ABC ＝12ab ＝6 3.②当B ＝120°时，C ＝30°，△ABC 为等腰三角形， S △ABC ＝12ab sin C ＝3 3.18．(本小题满分12分)已知等差数列{a n }中，a 1＝1，a 3＝－3. (1)求数列{a n }的通项公式；(2)若数列{a n }的前k 项和S k ＝－35，求k 的值． 解析： (1)设等差数列{a n }的公差为d ， 则a n ＝a 1＋(n －1)d .由a 1＝1，a 3＝－3可得1＋2d ＝－3，解得d ＝－2. 从而a n ＝1＋(n －1)×(－2)＝3－2n . (2)由(1)可知a n ＝3－2n ， 所以S n ＝n [1＋(3－2n )]2＝2n －n 2.由S k ＝－35可得2k －k 2＝－35， 即k 2－2k －35＝0，解得k ＝7或k ＝－5. 又k ∈N *，故k ＝7.19．(本小题满分12分)解关于x 的不等式ax 2－(a ＋1)x ＋1＜0. 解析： 若a ＝0，原不等式可化为－x ＋1＜0， 解得x ＞1；若a ＜0，原不等式可化为⎝⎛⎭⎫x －1a (x －1)＞0 解得x ＜1a或x ＞1；若a ＞0，原不等式可化为⎝⎛⎭⎫x －1a (x －1)＜0， 其解的情况应由1a 与1的大小关系确定，当a ＝1时，解得x ∈∅； 当a ＞1时，解得1a ＜x ＜1；当0＜a ＜1时，解得1＜x ＜1a.综上所述，当a ＜0时，解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x ＜1a或x ＞1； 当a ＝0时，解集为{x |x ＞1}；当0＜a ＜1时，解集为⎩⎨⎧⎭⎬⎫x ⎪⎪1＜x ＜1a ； 当a ＝1时，解集为∅；当a ＞1时，解集为⎩⎨⎧⎭⎬⎫x ⎪⎪1a ＜x ＜1. 20．(本小题满分12分)已知x ，y 满足条件⎩⎪⎨⎪⎧7x －5y －23≤0，x ＋7y －11≤0，4x ＋y ＋10≥0.求：(1)4x －3y 的最大值和最小值； (2)x 2＋y 2的最大值和最小值．解析： (1)不等式组⎩⎪⎨⎪⎧7x －5y －23≤0，x ＋7y －11≤0，4x ＋y ＋10≥0，表示的平面区域如下图所示，其中A (4,1)，B (－1，－6)，C (－3，2)．设z ＝4x －3y ，直线4x －3y ＝0经过原点(0,0)，作一组与4x －3y ＝0平行的直线l ：4x －3y ＝t ，当l 过C 点时，z 值最小；当l 过B 点时，z 值最大．∴z max ＝4×(－1)－3×(－6)＝14， z min ＝4×(－3)－3×2＝－18.(2)设u ＝x 2＋y 2，则u 为点(x ，y )到原点(0,0)的距离．结合不等式组所表示的平面区域可知，点B 到原点的距离最大，而当(x ，y )在原点时，距离为0.∴(x 2＋y 2)max ＝(－1)2＋(－6)2＝37；(x 2＋y 2)min ＝0.21．(本小题满分13分)已知数列{a n }的首项a 1＝23，a n ＋1＝2a na n ＋1，n ＝1,2,3，…(1)证明：数列⎩⎨⎧⎭⎬⎫1a n－1是等比数列；(2)求数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和S n .解析： (1)证明：∵a n ＋1＝2a na n ＋1，∴1a n ＋1＝a n ＋12a n ＝12＋12·1a n ，∴1a n ＋1－1＝12⎝⎛⎭⎫1a n －1， 又a 1＝23，∴1a 1－1＝12， ∴数列⎩⎨⎧⎭⎬⎫1a n －1是以12为首项，12为公比的等比数列．(2)由(1)知数列⎩⎨⎧⎭⎬⎫1a n－1是等比数列，设数列⎩⎨⎧⎭⎬⎫1a n－1的前n 项和为T n ，则T n ＝12⎣⎡⎦⎤1－⎝⎛⎭⎫12n 1－12＝1－⎝⎛⎭⎫12n， ∴S n ＝T n ＋n ＝1－⎝⎛⎭⎫12n ＋n ＝n ＋1－⎝⎛⎭⎫12n . 22．(本小题满分13分)某单位用2 160万元购得一块空地，计划在该地块上建造一栋至少10层，每层2 000平方米的楼房．经测算，如果将楼房建为x (x ≥10)层，则每平方米的平均建筑费用为560＋48x (单位：元)．为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？(注：平均综合费用＝平均建筑费用＋平均购地费用，平均购地费用＝购地总费用建筑总面积)解析： 设楼房每平方米的平均综合费用为f (x )元，则 f (x )＝(560＋48x )＋2 160×10 0002 000x＝560＋48x ＋10 800x.∵x ≥10，∴48x ＋10 800x ≥1 440，当且仅当x ＝15时，等号成立． ∴f (x )≥2 000.因此，当x ＝15时，f (x )取得最小值f (15)＝2 000.答：为了使楼房每平方米的平均综合费用最少，该楼房应建为15层．模块综合检测(B)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．△ABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，a sin A sin B ＋b cos 2A ＝2a ，则ba＝( ) A ．23 B ．2 2 C ． 3D ． 2解析： 由正弦定理，得sin 2A sin B ＋sin B cos 2A ＝2sin A ， 即sin B (sin 2A ＋cos 2A )＝2sin A . 故sin B ＝2sin A ，所以ba ＝ 2.答案： D2．等比数列公比为2，且前4项之和为1，则前8项之和为( ) A ．15 B ．17 C ．19D ．21解析： 由S 8－S 4S 4＝q 4得S 8＝17.答案： B3．如果a ，b ，c 满足c ＜b ＜a 且ac ＜0，那么下列选项中不一定成立的是( ) A ．cb 2＜ab 2 B ．c (b －a )＞0 C ．ab ＜acD ．ac (a －c )＜0 解析： 若b ＝0，则cb 2＝ab 2，∴A 不一定成立． 答案： A4．数列{a n }的通项公式为a n ＝1n ＋1＋n，已知它的前n 项和S n ＝6，则项数n 等于( )A ．6B ．7C ．48D ．49解析： 将通项公式变形得： a n ＝1n ＋1＋n＝n ＋1－n(n ＋1＋n )(n ＋1－n )＝n ＋1－n ，则S n ＝(2－1)＋(3－2)＋(4－3)＋…＋(n ＋1－n ) ＝n ＋1－1，由S n ＝6，则有n ＋1－1＝6，∴n ＝48. 答案： C5．在△ABC 中，b ＝a sin C ，c ＝a cos B ，则△ABC 一定是( ) A ．等腰三角形但不是直角三角形B ．直角三角形但不是等腰三角形C ．等边三角形D ．等腰直角三角形解析： 由c ＝a cos B 得，c ＝a ×a 2＋c 2－b 22ac ，∴a 2＝b 2＋c 2，∴△ABC 为直角三角形， ∴b ＝a sin C ＝a ×ca ＝c ，∴△ABC 是等腰直角三角形． 答案： D6．不等式2x 2－x －1>0的解集是( ) A ．⎝⎛⎭⎫－12，1 B ．(1，＋∞)C ．(－∞，1)∪(2，＋∞)D ．⎝⎛⎭⎫－∞，－12∪(1，＋∞) 解析： ∵Δ＝1＋8＝9>0，∴方程2x 2－x －1＝0有两个不相等的实数根， 解得x 1＝－12，x 2＝1.∴2x 2－x －1>0的解集为⎝⎛⎭⎫－∞，－12∪(1，＋∞)． 答案： D7．设变量x ，y 满足约束条件⎩⎪⎨⎪⎧y ≥0，x －y ＋1≥0，x ＋y －3≤0，则z ＝2x ＋y 的最大值为( )A ．－2B ．4C ．6D ．8解析： 作出可行域，如图阴影部分所示，易求得A (－1，0)，B (3,0)，C (1,2)，由可行域可知，z ＝2x ＋y 过点B (3,0)时，z 有最大值，且z max ＝6.答案： C8．在△ABC 中，角A ，B ，C 所对边的长分别为a ，b ，c ，若a 2＋b 2＝2c 2，则cos C 的最小值为( )A.32B ．22C ．12D ．－12解析： 利用余弦定理求解． ∵cos C ＝a 2＋b 2－c 22ab ＝c 22ab ，又∵a 2＋b 2≥2ab ，∴2ab ≤2c 2， ∴cos C ≥12.答案： C9．当点(x ，y )在直线x ＋3y ＝2上移动时，z ＝3x ＋27y ＋1的最小值是( ) A ．339 B ．7 C ．1＋2 2D ．6解析： z ＝3x ＋27y ＋1≥23x ·27y ＋1＝7.当且仅当3x ＝27y ，即x ＝1，y ＝13时，等号成立．故选B.答案： B10．在△ABC 中，b 2－bc －2c 2＝0，a ＝6，cos A ＝78，则△ABC 的面积S 为( )A.152B ．15C ．2D ．3解析： ∵b 2－bc －2c 2＝0， ∴(b －2c )(b ＋c )＝0.∵b ＋c ≠0，∴b －2c ＝0.∴b ＝2c ， ∴6＝c 2＋4c 2－2c ·2c ×78，∴c ＝2，b ＝4.∴S ＝12bc sin A ＝12×2×4×1－4964＝152. 答案： A11．某学生用一不准确的天平(两臂不等长)称10 g 药品，他先将5 g 的砝码放在左盘，将药品放在右盘使之平衡；然后又将5 g 的砝码放在右盘，将药品放在左盘使之平衡，则此学生实际所得药品( )A ．小于10 gB ．大于10 gC ．大于等于10 gD ．小于等于10 g解析： 设左、右臂长分别为t 1，t 2，第一次称的药品为x 1 g ，第二次称的药品为x 2 g ，则有5t 1＝x 1t 2，x 2t 1＝5t 2，所以x 1＋x 2＝5⎝⎛⎭⎫t 1t 2＋t 2t 1>5×2＝10(g)，即大于10 g.答案： B12．在R 上定义运算⊗：x ⊗y ＝x (1－y )．若不等式(x －a )⊗(x ＋a )＜1对任意实数x 恒成立，则( )A ．－1＜a ＜1B ．0＜a ＜2C ．－12＜a ＜32D ．－32＜a ＜12解析： 因为(x －a )⊗(x ＋a )＝(x －a )(1－x －a )，又不等式(x －a )⊗(x ＋a )＜1对任意实数x 恒成立，所以(x －a )(1－x －a )＜1对任意实数x 恒成立，即x 2－x －a 2＋a ＋1＞0对任意实数x 恒成立，所以相应方程的Δ＝(－1)2－4(－a 2＋a ＋1)＜0，解得－12＜a ＜32.故选C.答案： C二、填空题(本大题共4小题，每小题4分，共16分．请把正确答案填在题中横线上) 13．已知△ABC 的三边长成公比为2的等比数列，则其最大角的余弦值为________． 解析： 利用三边长是公比为2的等比数列，可把三边长表示为a ，2a,2a ，再利用余弦定理求解．设三角形的三边长从小到大依次为a ，b ，c ， 由题意得b ＝2a ，c ＝2a .在△ABC 中，由余弦定理得cos C ＝a 2＋b 2－c 22ab ＝a 2＋2a 2－4a 22×a ×2a ＝－24.答案： －2414．设z ＝x ＋y ，其中x ，y 满足⎩⎪⎨⎪⎧x ＋2y ≥0，x －y ≤0，0≤y ≤k ，若z 的最大值为6，则z 的最小值为________．解析： 如图，x ＋y ＝6过点A (k ，k )，k ＝3，z ＝x ＋y 在点B 处取得最小值，B 点在直线x ＋2y ＝0上，∴B (－6,3)， ∴z min ＝－6＋3＝－3.答案： －315．已知△ABC 中三边a ，b ，c 成等差数列，a ，b ，c 也成等差数列，则△ABC 的形状为________．解析： 由a ，b ，c 成等差数列得a ＋c ＝2b ， ① 由a ，b ，c 成等差数列得a ＋c ＝2b ， ②②2－①得2ac ＝2b ，即b 2＝ac ，①平方得a 2＋2ac ＋c 2＝4b 2， 将b 2＝ac 代入得a 2＋2ac ＋c 2＝4ac ， 即(a －c )2＝0，∴a ＝c . 又∵a ＋c ＝2b ，∴2a ＝2b ， ∴a ＝b ，∴a ＝b ＝c . 答案： 等边三角形16．已知log 2(x ＋y )＝log 2x ＋log 2y ，则xy 的取值范围是____________． 解析： 由已知得x ＋y ＝xy ，又x ＞0，y ＞0， ∴xy ＝x ＋y ≥2xy ，∴xy ≥4. 答案： [4，＋∞)三、解答题(本大题共6小题，共74分．解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分12分)已知{a n }是首项为19，公差为－2的等差数列，S n 为{a n }的前n 项和．(1)求通项a n 及S n ；(2)设{b n －a n }是首项为1，公比为3的等比数列，求数列{b n }的通项公式及前n 项和T n . 解析： (1)∵{a n }是首项为a 1＝19，公差为d ＝－2的等差数列，∴a n ＝19－2(n －1)＝21－2n ，S n ＝19n ＋12n (n －1)×(－2)＝20n －n 2.(2)由题意得b n －a n ＝3n －1，即b n ＝a n ＋3n －1，∴b n ＝3n －1－2n ＋21，∴T n ＝S n ＋(1＋3＋…＋3n －1)＝－n 2＋20n ＋3n －12.18．(本小题满分12分)(2012·江西高考)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c .已知3cos(B －C )－1＝6cos B cos C .(1)求cos A ；(2)若a ＝3，△ABC 的面积为22，求b ，c . 解析： (1)由3cos(B －C )－1＝6cos B cos C ，得3(cos B cos C －sin B sin C )＝－1，即cos(B ＋C )＝－13，从而cos A ＝－cos(B ＋C )＝13.(2)由于0＜A ＜π，cos A ＝13，所以sin A ＝223.又S △ABC ＝22，即12bc sin A ＝22，解得bc ＝6.由余弦定理a 2＝b 2＋c 2－2bc cos A ，得b 2＋c 2＝13，解方程组⎩⎪⎨⎪⎧ bc ＝6，b 2＋c 2＝13，得⎩⎪⎨⎪⎧ b ＝2，c ＝3或⎩⎪⎨⎪⎧b ＝3，c ＝2. 19．(本小题满分12分)已知不等式ax 2－3x ＋6>4的解集为{x |x <1或x >b }， (1)求a ，b ；(2)解不等式ax 2－(ac ＋b )x ＋bc <0.解析： (1)因为不等式ax 2－3x ＋6>4的解集为{x |x <1或x >b }，所以x 1＝1与x 2＝b 是方程ax 2－3x ＋2＝0的两个实数根，且b >1.由根与系数的关系，得⎩⎨⎧1＋b ＝3a ，1×b ＝2a.解得⎩⎪⎨⎪⎧a ＝1，b ＝2.所以a ＝1，b ＝2.(2)不等式ax 2－(ac ＋b )x ＋bc <0，即x 2－(2＋c )x ＋2c <0， 即(x －2)(x －c )<0.当c >2时，不等式(x －2)(x －c )<0的解集为{x |2<x <c }； 当c <2时，不等式(x －2)(x －c )<0的解集为{x |c <x <2}； 当c ＝2时，不等式(x －2)(x －c )<0的解集为∅.综上，当c >2时，不等式ax 2－(ac ＋b )x ＋bc <0的解集为{x |2<x <c }； 当c <2时，不等式ax 2－(ac ＋b )x ＋bc <0的解集为{x |c <x <2}； 当c ＝2时，不等式ax 2－(ac ＋b )x ＋bc <0的解集为∅.20．(本小题满分12分)设S n 是公差不为0的等差数列{a n }的前n 项和，且S 1，S 2，S 4成等比数列．(1)求a 2a 1的值；(2)若a 5＝9，求a n 及S n 的表达式． 解析： (1)设等差数列{a n }的公差是d . ∵S 1，S 2，S 4成等比数列，∴S 22＝S 1S 4，即(2a 1＋d )2＝a 1(4a 1＋6d )， 化简得d 2＝2a 1d ，注意到d ≠0， ∴d ＝2a 1.∴a 2a 1＝a 1＋d a 1＝3a 1a 1＝3.(2)a 5＝a 1＋4d ＝9a 1＝9，∴a 1＝1，d ＝2. ∴a n ＝a 1＋(n －1)d ＝2n －1，S n ＝n (a 1＋a n )2＝n 2.21．(本小题满分13分)如图，渔船甲位于岛屿A 的南偏西60°方向的B 处，且与岛屿A 相距12海里，渔船乙以10海里/时的速度从岛屿A 出发沿正北方向航行，若渔船甲同时从B 处出发沿北偏东α的方向追赶渔船乙，刚好用2小时追上．(1)求渔船甲的速度； (2)求sin α的值．解析： (1)依题意，∠BAC ＝120°，AB ＝12，AC ＝10×2＝20，∠BCA ＝α.在△ABC 中，由余弦定理，得 BC 2＝AB 2＋AC 2－2AB ×AC ×cos ∠BAC ＝122＋202－2×12×20×cos 120°＝784. 解得BC ＝28.所以渔船甲的速度为BC2＝14海里/时．答：渔船甲的速度为14海里/时．(2)方法一：在△ABC 中，因为AB ＝12，∠BAC ＝120°，BC ＝28，∠BCA ＝α， 由正弦定理，得AB sin α＝BC sin 120°.即sin α＝AB sin 120°BC ＝12×3228＝3314.答：sin α的值为3314.方法二：在△ABC 中，因为AB ＝12，AC ＝20，BC ＝28，∠BCA ＝α，由余弦定理，得cos α＝AC 2＋BC 2－AB 22AC ×BC ，即cos α＝202＋282－1222×20×28＝1314.因为α为锐角， 所以sin α＝1－cos 2α＝1－⎝⎛⎭⎫13142＝3314.答：sin α的值为3314.22．(本小题满分13分)热心支持教育事业的李先生虽然并不富裕，但每年都要为山区小学捐款．今年打算用2 000元购买单价为50元的桌子和20元的椅子，希望桌椅的数量之和尽可能多，但椅子数不能少于桌子数，且不多于桌子数的1.5倍，问桌子、椅子各买多少才合适？解析： 设桌子、椅子各买x 张和y 张， 则所买桌椅的总数为z ＝x ＋y . 依题意得不等式组⎩⎪⎨⎪⎧x ≤y ，y ≤1.5x ，50x ＋20y ≤2 000，其中x ，y ∈N *.由⎩⎪⎨⎪⎧ y ＝x ，50x ＋20y ＝2 000，解得⎩⎨⎧x ＝2007，y ＝2007.由⎩⎪⎨⎪⎧y ＝1.5x ，50x ＋20y ＝2 000，解得⎩⎪⎨⎪⎧x ＝25，y ＝752.设点A 的坐标为⎝⎛⎭⎫2007，2007. 点B 的坐标为⎝⎛⎭⎫25，752， 则前面的不等式组所表示的平面区域是以A ⎝⎛⎭⎫2007，2007，B ⎝⎛⎭⎫25，752，O (0,0)为顶点的△AOB 的边界及其内部(如图中阴影所示)．令z ＝0，得x ＋y ＝0，即y ＝－x .作直线l 0：y ＝－x .由图形可知，把直线l 0平移至过点B ⎝⎛⎭⎫25，752时，亦即x ＝25，y ＝752时，z 取最大值．因为x，y∈N*，所以x＝25，y＝37时，z取最大值．故买桌子25张，椅子37张较为合适．。

必修五 综合测试题 (第三套)一．选择题:1. 已知等差数列}{n a 中，12497,1,16a a a a 则==+的值是( )A . 15B . 30 C. 31 D. 642. 若全集U=R,集合M ＝{}24x x >，S ＝301x xx ⎧-⎫>⎨⎬+⎩⎭，则()U M S I ð=( ) A.{2}x x <- B. {23}x x x <-≥或 C. {3}x x ≥ D. {23}x x -≤<3. 若1＋2＋22＋ (2)>128，n ÎN*，则n 的最小值为( ) A. 6 B. 7 C. 8 D. 9 4. 在ABC V 中，60B =o ，2b ac =，则ABC V 一定是( )A 、等腰三角形B 、等边三角形C 、锐角三角形D 、钝角三角形 5. 若不等式022>++bx ax的解集为⎭⎬⎫⎩⎨⎧<<-3121|x x ，则a －b 值是( )A.－10B.－14C. 10D. 14 6. 在等比数列{a n }中，4S =1，8S =3，则20191817a a a a +++的值是( )A ．14B ．16C ．18D ．207．已知12=+y x ，则y x 42+的最小值为( ) A ．8 B ．6 C ．22 D ．238. 黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案，则第n 个图案中有白色地面砖的块数是( ) A.42n +B.42n -C.24n +D.33n +9. 已知变量y x ,满足⎪⎩⎪⎨⎧≥<+≤+-12553034x y x y x ，目标函数是y x z +=2，则有( )A ．3,12min max ==z zB ．,12max=z z 无最小值C ．z z ,3min=无最大值 D ．z 既无最大值，也无最小值10．在R 上定义运算:(1)x y x y ⊗⊗=-，若不等式()()1x a x a -⊗+<对任意实数x 成立，则实数a 的取值范围是( ) A ．11a -<< B ．02a << C ．1322a -<< D ．3122a -<< 二填空题： 11. 在数列{}n a 中，11a =，且对于任意正整数n ，都有1n n a a n +=+，则100a ＝______第1个 第2个 第3个12．在⊿ABC 中，5:4:21sin :sin :sin=C B A ，则角A =13．某校要建造一个容积为83m ，深为2m 的长方体无盖水池，池底和池壁的造价每平方米分别为240元和160元，那么水池的最低总造价为 元。

2019-2020学年高中数学必修五综合测试卷(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1设△ABC的内角A,B,C所对的边分别为a,b,c,若a,b,c成等比数列,且c=2a,则cos B等于()A.14B.34C.√24D.√23答案:B2下列结论正确的是()A.若ac>bc,则a>bB.若a8>b8,则a>bC.若a>b,c<0,则ac<bcD.若√a<√b,则a>b答案:C3等差数列{a n}的前n项和为S n,若a2+a7+a12=30,则S13的值是() A.130 B.65C.70D.75解析:因为a2+a7+a12=(a2+a12)+a7=2a7+a7=3a7=30,所以a7=10.所以S13=13(a1+a13)2=13(a7+a7)2=13a7=130.答案:A4已知锐角△ABC的内角A,B,C的对边分别为a,b,c,若23cos2A+cos 2A=0,a=7,c=6,则b等于()A.10B.9C.8D.5解析:由23cos2A+cos 2A=0,得cos2A=125.∵A∈(0,π2),∴cos A=15.∵cos A=36+b2-492×6b ,∴b=5或b=−135(舍).故选D.答案:D5若在等比数列{a n}中,a4=7,a6=21,则a8等于()A.35B.63C.21√3D.±21√3 答案:B6若在△ABC 中,a=4,b=4√3,A=30°,则角B 的度数等于( ) A.30° B.30°或150° C.60° D.60°或120°答案:D7在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若b 2=ac ,则角B 的取值范围是( ) A .(0,π3]B.[π3,π] C .(0,π6]D.[π6,π) 答案:A8某旅行社租用A,B 两种型号的客车安排900名客人旅行,A,B 两种车辆的载客量分别为36人和60人,租金分别为1 600元/辆和2 400元/辆,若旅行社要求租车总数不超过21辆,且B 型车不多于A 型车7辆,则租金最少为( ) A.31 200元 B.36 000元C.36 800元D.38 400元解析:设需A,B 型车分别为x ,y 辆(x ,y ∈N ),则x ,y 需满足{36x +60y ≥900,x +y ≤21,y -x ≤7,x ∈N ,y ∈N ,设租金为z ,则z=1 600x+2400y ,画出可行域如图中阴影所示,根据线性规划中截距问题,可求得最优解为x=5,y=12,此时z 最小等于36 800.故选C .答案:C9若x>0,y>0,且xy-(x+y )=1,则( )A.x+y ≥2(√2+1)B.xy ≤√2+1C.x+y ≤(√2+1)2D.xy ≥2(√2+1) 解析:∵xy=1+(x+y )≤(x+y 2)2,∴(x+y )2-4(x+y )-4≥0, ∴x+y ≥2(√2+1),当且仅当x=y =√2+1时等号成立. 答案:A10若数列{a n }满足a 1=0,a n+1=a n -√3√3a n +1(n ∈N *),则a 20等于( )A.0B .−√3C.√3D.1解析:由a 1=0,a n+1=n √3√3a +1n ∈N *),得a 2=−√3,a 3=√3,a 4=0,…由此可知数列{a n }是周期数列,周期为3,所以a 20=a 2=−√3. 答案:B11若在R 上定义运算☉:a ☉b=ab+2a+b ,则满足x ☉(x-2)<0的实数x 的取值范围为( ) A.(0,2)B.(-2,1)C.(-∞,-2)∪(1,+∞)D.(-1,2)解析:由题意,得x (x-2)+2x+(x-2)<0,即x 2+x-2<0,解得-2<x<1. 答案:B12已知集合A={t|t 2-4≤0},对于满足集合A 的所有实数t ,关于x 的不等式x 2+tx-t>2x-1恒成立,则x 的取值范围是( ) A.(-∞,-1)∪(3,+∞) B.(-∞,1)∪(3,+∞) C.(-∞,-1) D.(3,+∞)解析:由题意知A={t|-2≤t ≤2},设f (t )=(x-1)t+x 2-2x+1,由条件知f (t )在区间[-2,2]上恒为正值. 于是有{f (-2)>0,f (2)>0,即{x 2-4x +3>0,x 2-1>0.解得x>3或x<-1. 答案:A二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中的横线上)13某住宅小区计划植树不少于100棵,若第一天植2棵,以后每天植树的棵数是前一天的2倍,则需要的最少天数n (n ∈N *)等于 .解析:由题意知每天植树的棵数组成一个以2为首项,2为公比的等比数列, 所以S n =2(1-2n )1-2=2(-1+2n )≥100.所以2n ≥51,n ≥6.答案:614已知点P (x ,y )的坐标满足条件{x +y ≤4,y ≥x ,x ≥1,点O 为坐标原点,则|PO|的最小值等于 ,最大值等于 . 答案:√2 √1015在△ABC 中,角A ,B ,C 所对的边长分别为a ,b ,c.若C=120°,c =√2a ,则a 与b 的大小关系是 .解析:由余弦定理得c 2=a 2+b 2-2ab cos 120°.∵c =√2a,∴2a 2=a 2+b 2+ab ,即a 2=b 2+ab ,a 2-b 2=ab>0.∴a 2>b 2,即a>b.答案:a>b16已知数列{a n }满足a 1=t ,a n+1-a n +2=0(t ∈N *,n ∈N *).记数列{a n }的前n 项和的最大值为f (t ),则f (t )= .答案:{t 2+2t4,t 为偶数,(1+t 2)2,t 为奇数三、解答题(本大题共6小题,共74分.解答时应写出文字说明、证明过程或演算步骤)17(12分)设等差数列{a n }满足a 3=5,a 10=-9. (1)求{a n }的通项公式;(2)求{a n }的前n 项和S n 及使得S n 最大的序号n 的值. 解(1)由a n =a 1+(n-1)d 及a 3=5,a 10=-9,得{a 1+2d =5,a 1+9d =-9,解得{a 1=9,d =-2,所以数列{a n }的通项公式为a n =11-2n. (2)由(1)知,S n =na 1+n (n -1)2a =10n-n 2.因为S n =-(n-5)2+25,所以当n=5时,S n 取得最大值.18(12分)海面上相距10海里的A,B两船,B船在A船的北偏东45°方向上.两船同时接到指令同时驶向C岛,C岛在B船的南偏东75°方向上,行驶了80分钟后两船同时到达C岛,经测算,A船行驶了10√7海里,求B船的速度.解如图所示,在△ABC中,AB=10,AC=10√7,∠ABC=120°.由余弦定理,得AC2=BA2+BC2-2BA·BC·cos 120°,即700=100+BC2+10BC,得BC=20.设B船速度为v,行驶时间为8060=43(小时),路程为BC=20海里,则有v=2043=15(海里/时),即B船的速度为15海里/时.19(12分)在△ABC中,角A,B,C的对边分别为a,b,c,且满足2c-ba =cosBcosA.(1)求角A的大小;(2)若a=2√5,求△ABC面积的最大值.解(1)因为2c-ba =cosBcosA,所以(2c-b)cos A=a cos B.由正弦定理,得(2sin C-sin B)cos A=sin A cos B, 整理得2sin C cos A-sin B cos A=sin A cos B.所以2sin C cos A=sin (A+B)=sin C.在△ABC中,0<C<π,所以sin C≠0.所以cos A=12.又0<A<π,故A=π3.(2)由(1)得A=π3,又a=2√5,则cos A=b 2+c2-a22bc=12,整理得b2+c2=bc+20.由基本不等式,得b2+c2≥2bc,则bc+20≥2bc,所以bc≤20,当且仅当b=c时,等号成立,故三角形的面积S=12bcsin A=12bcsinπ3=√34bc≤√34×20=5√3.所以△ABC面积的最大值为5√3.20(12分)已知等差数列{a n}满足a2=0,a6+a8=-10.(1)求数列{a n}的通项公式;(2)求数列{a n2n-1}的前n项和.解(1)设等差数列{a n}的公差为d,由已知条件可得{a 1+d =0,2a 1+12d =-10,解得{a 1=1,d =-1.故数列{a n }的通项公式为a n =2-n. (2)设数列{an2n -1}的前n 项和为S n , 即S n =a 1+a 22+⋯+a n 2n -1,则S 1=a 1=1,S n 2=a 12+a 24+⋯+a n2n . ∵当n>1时,S n 2=a 1+a 2-a 12+⋯+a n -a n -12n -1−a n 2n=1−(12+14+…+12n -1)−2-n 2n=1−(1-12n -1)−2-n 2n=n2n ,∴S n =n2n -1.当n=1时,S 1=1也符合该公式.综上可知,数列{an2n -1}的前n 项和S n =n2n -1.21(12分)电视台为某个广告公司特约播放两套片集,其中片集甲播映时间为20分钟,广告时间为1分钟,收视观众为60万;片集乙播映时间为10分钟,广告时间为1分钟,收视观众为20万.广告公司规定每周至少有6分钟广告,而电视台每周只能为该公司提供不多于86分钟的节目时间.电视台每周应播映两套片集各多少次,才能获得最高的收视率? 解设片集甲播放x 集,片集乙播放y 集,则有{x +y ≥6,21x +11y ≤86,x ≥0,x ∈N ,y ≥0,y ∈N .要使收视率最高,则只要z=60x+20y 最大即可. 由{21x +11y =86,x +y =6,得M (2,4).由图可知,当x=2,y=4时,z=60x+20y 取得最大值200万. 故电视台每周片集甲和片集乙各播映2集和4集,其收视率最高.22(14分)已知各项均不相等的等差数列{a n }的前4项和S 4=14,且a 1,a 3,a 7成等比数列. (1)求数列{a n }的通项公式; (2)设T n 为数列{1an a n+1}的前n 项和,若Tn ≤λa n+1对任意n ∈N *恒成立,求实数λ的最小值.解(1)设等差数列{a n }的公差为d ,由已知得{4a 1+6d =14,(a 1+2d )2=a 1(a 1+6d ),解得d=1或d=0(舍去),因此a 1=2.故a n =n+1. (2)∵由(1)可知1an a n+1=1(n+1)(n+2)=1n+1−1n+2,∴T n =12−13+13−14+⋯+1n -1−1n+2=n2(n+2). ∵T n ≤λa n+1对任意n ∈N *恒成立,∴n 2(n+2)≤λ(n+2),即λ≥n2(n+2)2对任意n ∈N *恒成立.又n 2(n +2)2=n 2(n 2+4n +4)=12(n +4n+4)≤116,当且仅当n=2时,取“=”.∴λ的最小值为116.。

模块综合测评(一)(时间120分钟，满分150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．若a<1，b>1，那么下列命题中正确的是()A.1a>1b B.ba>1C．a2<b2D．ab<a＋b 【解析】利用特值法，令a＝－2，b＝2.则1a<1b，A错；ba<0，B错；a2＝b2，C错．【答案】 D2．一个等差数列的第5项a5＝10，且a1＋a2＋a3＝3，则有()A．a1＝－2，d＝3 B．a1＝2，d＝－3C．a1＝－3，d＝2 D．a1＝3，d＝－2【解析】∵a1＋a2＋a3＝3且2a2＝a1＋a3，∴a2＝1.又∵a5＝a2＋3d＝1＋3d＝10，d＝3.∴a1＝a2－d＝1－3＝－2.【答案】 A3．已知△ABC的三个内角之比为A∶B∶C＝3∶2∶1，那么对应的三边之比a∶b∶c等于()A．3∶2∶1 B.3∶2∶1C.3∶2∶1 D．2∶3∶1【解析】∵A∶B∶C＝3∶2∶1，A＋B＋C＝180°，∴A＝90°，B＝60°，C＝30°.∴a∶b∶c＝sin 90°∶sin 60°∶sin 30°＝1∶32∶12＝2∶3∶1.【答案】 D4．在坐标平面上，不等式组⎩⎨⎧y ≥x －1，y ≤－3|x |＋1所表示的平面区域的面积为( )A. 2B.32C.322 D ．2【解析】 由题意得，图中阴影部分面积即为所求．B ，C 两点横坐标分别为－1，12.∴S △ABC ＝12×2×⎪⎪⎪⎪⎪⎪12－(－1)＝32. 【答案】 B5．在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，若A ＝π3，b ＝1，△ABC 的面积为32，则a 的值为( )A ．1B ．2 C.32 D. 3【解析】 根据S ＝12bc sin A ＝32，可得c ＝2，由余弦定理得a 2＝b 2＋c 2－2bc cos A ＝3，故a ＝ 3.【答案】 D6．(2016·龙岩高二检测)等差数列的第二，三，六项顺次成等比数列，且该等差数列不是常数数列，则这个等比数列的公比为( )A ．3B ．4C ．5D ．6【解析】 设等差数列的首项为a 1，公差为d ， 则a 2＝a 1＋d ，a 3＝a 1＋2d ，a 6＝a 1＋5d ，又∵a 2·a 6＝a 23，∴(a 1＋2d )2＝(a 1＋d )(a 1＋5d )，∴d ＝－2a 1，∴q ＝a 3a 2＝3.【答案】 A7．若不等式x 2＋ax ＋1≥0对一切x ∈⎝ ⎛⎦⎥⎤0，12恒成立，则a 的最小值为( )A ．0B ．－2C ．－52 D ．－3【解析】 x 2＋ax ＋1≥0在x ∈⎝ ⎛⎦⎥⎤0，12上恒成立⇔ax ≥－x 2－1⇔a ≥⎣⎢⎡⎦⎥⎤－⎝ ⎛⎭⎪⎫x ＋1x max ，∵x ＋1x ≥52， ∴－⎝ ⎛⎭⎪⎫x ＋1x ≤－52，∴a ≥－52.【答案】 C8．(2015·浙江高考)已知{a n }是等差数列，公差d 不为零，前n 项和是S n ，若a 3，a 4，a 8成等比数列，则( )A ．a 1d >0，dS 4>0B ．a 1d <0，dS 4<0C ．a 1d >0，dS 4<0D ．a 1d <0，dS 4>0【解析】 ∵a 3，a 4，a 8成等比数列，∴a 24＝a 3a 8，∴(a 1＋3d )2＝(a 1＋2d )(a 1＋7d )，展开整理，得－3a 1d ＝5d 2，即a 1d ＝－53d 2.∵d ≠0，∴a 1d <0.∵S n ＝na 1＋n (n －1)2d ，∴S 4＝4a 1＋6d ，dS 4＝4a 1d ＋6d 2＝－23d 2<0. 【答案】 B9．在数列{a n }中，a 1＝2，a n ＋1－2a n ＝0(n ∈N *)，b n 是a n 和a n ＋1的等差中项，设S n 为数列{b n }的前n 项和，则S 6＝( )A ．189B ．186C ．180D ．192【解析】 由a n ＋1＝2a n ，知{a n }为等比数列， ∴a n ＝2n . ∴2b n ＝2n ＋2n ＋1， 即b n ＝3·2n －1，∴S 6＝3·1＋3·2＋…＋3·25＝189. 【答案】 A10．已知a ，b ，c ∈R ，a ＋b ＋c ＝0，abc >0，T ＝1a ＋1b ＋1c ，则( ) A ．T >0 B ．T <0 C ．T ＝0 D ．T ≥0【解析】 法一 取特殊值，a ＝2，b ＝c ＝－1， 则T ＝－32<0，排除A ，C ，D ，可知选B.法二 由a ＋b ＋c ＝0，abc >0，知三数中一正两负， 不妨设a >0，b <0，c <0，则T ＝1a ＋1b ＋1c ＝ab ＋bc ＋ca abc ＝ab ＋c (b ＋a )abc＝ab －c 2abc .∵ab <0，－c 2<0，abc >0，故T <0，应选B. 【答案】 B11．△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若B ＝2A ，a ＝1，b ＝3，则c ＝( )A ．2 3B ．2 C. 2 D ．1【解析】 由正弦定理得：a sin A ＝bsin B ， ∵B ＝2A ，a ＝1，b ＝3， ∴1sin A ＝32sin A cos A .∵A 为三角形的内角，∴sin A ≠0. ∴cos A ＝32.又0＜A ＜π，∴A ＝π6，∴B ＝2A ＝π3.∴C ＝π－A －B ＝π2，∴△ABC 为直角三角形． 由勾股定理得c ＝12＋(3)2＝2. 【答案】 B12．一个等比数列前三项的积为2，最后三项的积为4，且所有项的积为64，则该数列有( )A ．13项B ．12项C ．11项D ．10项【解析】 设该数列的前三项分别为a 1，a 1q ，a 1q 2，后三项分别为a 1q n －3，a 1q n－2，a 1q n －1.所以前三项之积a 31q 3＝2，后三项之积a 31q3n －6＝4，两式相乘，得a 61q 3(n －1)＝8，即a 21qn －1＝2.又a 1·a 1q ·a 1q 2·…·a 1qn －1＝64，所以a n 1·q n (n －1)2＝64，即(a 21q n －1)n＝642，即2n ＝642，所以n ＝12.【答案】 B二、填空题(本大题共4小题，每小题5分，共20分，将答案填在题中的横线上)13．在△ABC 中，BC ＝2，B ＝π3，当△ABC 的面积等于32时，sin C ＝________. 【导学号：05920086】【解析】 由三角形的面积公式，得S ＝12AB ·BC sin π3＝32，易求得AB ＝1，由余弦定理，得AC 2＝AB 2＋BC 2－2AB ·BC ·cos π3，得AC ＝3，再由三角形的面积公式，得S ＝12AC ·BC sin C ＝32，即可得出sin C ＝12.【答案】 1214．(2015·湖北高考)若变量x ，y 满足约束条件⎩⎨⎧x ＋y ≤4，x －y ≤2，3x －y ≥0，则3x ＋y 的最大值是________．【解析】 画出可行域，如图阴影部分所示，设z ＝3x ＋y ，则y ＝－3x ＋z ，平移直线y ＝－3x 知当直线y ＝－3x ＋z 过点A 时，z 取得最大值．由⎩⎨⎧x ＋y ＝4，x －y ＝2，可得A (3,1)．故z max ＝3×3＋1＝10.【答案】 1015．国家为了加强对烟酒生产的宏观管理，实行征收附加税政策．现知某种酒每瓶70元，不加附加税时，每年大约产销100万瓶，若政府征收附加税，每销售100元要征税k 元(叫做税率k %)，则每年的产销量将减少10k 万瓶．要使每年在此项经营中所收取附加税金不少于112万元，则k 的取值范围为________．【解析】 设产销量为每年x 万瓶，则销售收入每年70x 万元，从中征收的税金为70x ·k %万元，其中x ＝100－10k .由题意，得70(100－10k )k %≥112，整理得k 2－10k ＋16≤0，解得2≤k ≤8.【答案】 [2,8] 16．观察下列等式： 12＝1， 12－22＝－3， 12－22＋32＝6， 12－22＋32－42＝－10， …照此规律，第n 个等式可为12－22＋32－…＋(－1)n －1n 2＝________. 【解析】 分n 为奇数、偶数两种情况． 第n 个等式为12－22＋32－…＋(－1)n －1n 2.当n 为偶数时，分组求和：(12－22)＋(32－42)＋…＋[(n －1)2－n 2]＝－(3＋7＋11＋15＋…＋2n －1)＝－n2×(3＋2n －1)2＝－n (n ＋1)2.当n 为奇数时，第n 个等式为(12－22)＋(32－42)＋…＋[(n －2)2－(n －1)2]＋n 2＝－n (n －1)2＋n 2＝n (n ＋1)2.综上，第n 个等式为 12－22＋32－…＋(－1)n －1n 2 ＝(－1)n＋1n (n ＋1)2.【答案】 (－1)n ＋1n (n ＋1)2三、解答题(本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤)17．(本小题满分10分)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若m ＝(a 2＋c 2－b 2，－3a )，n ＝(tan B ，c )，且m ⊥n ，求∠B 的值．【解】 由m ⊥n 得(a 2＋c 2－b 2)·tan B －3a ·c ＝0，即(a 2＋c 2－b 2)tan B ＝3ac ，得a 2＋c 2－b 2＝3ac tan B ， 所以cos B ＝a 2＋c 2－b 22ac ＝32tan B ， 即tan B cos B ＝32，即sin B ＝32， 所以∠B ＝π3或∠B ＝2π3.18．(本小题满分12分)在等差数列{a n }中，S 9＝－36，S 13＝－104，在等比数列{b n }中，b 5＝a 5，b 7＝a 7, 求b 6. 【导学号：05920087】【解】 ∵S 9＝－36＝9a 5，∴a 5＝－4， ∵S 13＝－104＝13a 7，∴a 7＝－8. ∴b 26＝b 5·b 7＝a 5 ·a 7＝32. ∴b 6＝±4 2.19．(本小题满分12分)解关于x 的不等式ax 2－2≥2x －ax (a ∈R ). 【导学号：05920088】【解】 原不等式可化为ax 2＋(a －2)x －2≥0⇒(ax －2)(x ＋1)≥0.(1)当a ＝0时，原不等式化为x ＋1≤0⇒x ≤－1；(2)当a >0时，原不等式化为⎝ ⎛⎭⎪⎫x －2a (x ＋1)≥0⇒x ≥2a 或x ≤－1； (3)当a <0时，原不等式化为⎝ ⎛⎭⎪⎫x －2a (x ＋1)≤0.①当2a >－1，即a <－2时，原不等式等价于－1≤x ≤2a ；②当2a ＝－1，即a ＝－2时，原不等式等价于x ＝－1； ③当2a <－1，即－2<a <0时，原不等式等价于2a ≤x ≤－1. 综上所述：当a <－2时，原不等式的解集为⎣⎢⎡⎦⎥⎤－1，2a ；当a ＝－2时，原不等式的解集为{－1}；当－2<a <0时，原不等式的解集为⎣⎢⎡⎦⎥⎤2a ，－1；当a ＝0时，原不等式的解集为(－∞，－1]；当a >0时，原不等式的解集为(－∞，－1]∪⎣⎢⎡⎭⎪⎫2a ，＋∞.20．(本小题满分12分)设△ABC 的内角A ，B ，C 所对应的边分别为a ，b ，c ，已知a ＝1，b ＝2，cos C ＝14.(1)求△ABC 的周长； (2)求cos A 的值．【解】 (1)∵c 2＝a 2＋b 2－2ab cos C ＝1＋4－4×14＝4.∴c ＝2.∴△ABC 的周长为a ＋b ＋c ＝1＋2＋2＝5. (2)∵cos C ＝14，∴sin C ＝1－cos 2C ＝1－⎝ ⎛⎭⎪⎫142＝154. ∴sin A ＝a sin C c ＝1542＝158. ∵a <c ，∴A <C ，故A 为锐角， ∴cos A ＝1－sin 2A ＝1－⎝⎛⎭⎪⎫1582＝78. 21．(本小题满分12分)(2016·宝鸡模拟)已知数列{a n }满足a 1＝5，a 2＝5，a n ＋1＝a n ＋6a n －1(n ≥2)．(1)求证：{a n ＋1＋2a n }是等比数列； (2)求数列{a n }的通项公式．【解】 (1)证明：∵a n ＋1＝a n ＋6a n －1(n ≥2)， ∴a n ＋1＋2a n ＝3a n ＋6a n －1＝3(a n ＋2a n －1)(n ≥2)． 又a 1＝5，a 2＝5，∴a 2＋2a 1＝15， ∴a n ＋2a n －1≠0(n ≥2)， ∴a n ＋1＋2a na n ＋2a n －1＝3(n ≥2)，∴数列{a n ＋1＋2a n }是以15为首项，3为公比的等比数列． (2)由(1)得a n ＋1＋2a n ＝15×3n －1＝5×3n ，则a n ＋1＝－2a n ＋5×3n ， ∴a n ＋1－3n ＋1＝－2(a n －3n )． 又∵a 1－3＝2，∴a n －3n ≠0，∴{a n －3n }是以2为首项，－2为公比的等比数列． ∴a n －3n ＝2×(－2)n －1， 即a n ＝2×(－2)n －1＋3n (n ∈N *)．22．(本小题满分12分)某厂用甲、乙两种原料生产A ，B 两种产品，制造1 t A,1 t B 产品需要的各种原料数、可得到利润以及工厂现有各种原料数如下表：(2)每吨B 产品的利润在什么范围变化时，原最优解不变？当超出这个范围时，最优解有何变化？【解】 (1)生产A ，B 两种产品分别为x t ，y t ，则利润z ＝5x ＋3y ，x ，y 满足⎩⎨⎧2x ＋y ≤14，x ＋3y ≤18，x ≥0，y ≥0，作出可行域如图：当直线5x ＋3y ＝z 过点B ⎝ ⎛⎭⎪⎫245，225时，z 取最大值3715，即生产A 产品245 t ，B产品225 t 时，可得最大利润．(2)设每吨B 产品利润为m 万元，则目标函数是z ＝5x ＋my ，直线斜率k ＝－5m ，又k AB ＝－2，k CB ＝－13，要使最优解仍为B 点， 则－2≤－5m ≤－13，解得52≤m ≤15，则B 产品的利润在52万元/t 与15万元/t 之间时，原最优解仍为生产A 产品245 t ，B 产品225 t ，若B 产品的利润超过15万元/t ，则最优解为C (0,6)，即只生产B 产品6 t ，若B 产品利润低于52万元/t ，则最优解为A (7,0)，即只生产A 产品7 t.。

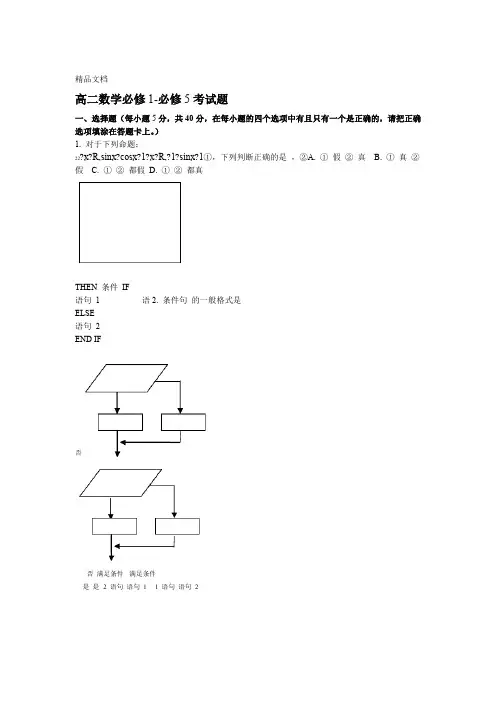
精品文档高二数学必修1-必修5考试题一、选择题（每小题5分，共40分，在每小题的四个选项中有且只有一个是正确的，请把正确选项填涂在答题卡上。

）1. 对于下列命题：22?x?R,sinx?cosx?1?x?R,?1?sinx?1①，下列判断正确的是，②A. ①假②真 B. ①真②假 C. ①②都假 D. ①②都真THEN 条件IF语句 1 语2. 条件句的一般格式是ELSE语句 2END IF否否满足条件满足条件是是 2 语句语句1 1 语句语句2A. B.否否满足条件满足条件满足条件是是 12 语句语句 21 语句语句D.C.名学生，得到他们在某一天各自课外某校为了了解学生的课外阅读情况，随即调查了503.阅读所用时间的数据，结果用右侧的条形图表示。

)(人人数名学生这一天平均每人的课根据条形图可得这50外阅读时间为20小时小时 B. 0.9 A. 0.6 15 D. 1.5 小时小时C. 1.010里面装有底面半径为10cm，4. 有一圆柱形容器，5，有一块金属五棱锥掉足够的水，水面高为12cm2.0 1.5 1.0 0 0.5 ，若五棱锥进水里全被淹没，结果水面高为15cm)小时时间(?，则五棱锥的底面积是的高为3cm??2 2 2 2 D. 300 cmcmC. 30cmA. 100 B. 100 cm 精品文档．精品文档nn}paa?{3??2a的值为5．已知数列,,且则p为等比数列nn?1n的倍数D.2或3 C.2或3 A.2 B.3的一个充分条件是a∥αbβ表示平面,a、表示直线,则6．若α、 b∥b且 B. aαβ＝ A. α⊥β且a⊥β?且aβD. α∥βC. a∥b且b∥αx?x2?a?a f(x)+g(x)=和偶函数g(x)满足7．已知奇函数f(x),若g(a)=a, 则f(a)的值为171544 D. C. A.1 B.21,3][?(x)?xxf(x)?[0,1]f内，2是以8. 已知为周期的偶函数，当时，，那么在区间1k?x)?kx?f(x kk 的（其中的实数）有四个不同的实根，则走为不等于关于l的方程取值范围是111,0)?,0)?((?,0)(1,0)(?423 B．．D．．A C分。

高中数学学习材料马鸣风萧萧*整理制作高中数学必修5测试卷C （含答案）一、选择题：1．在等差数列3，7，11…中，第5项为( )． A ．15B ．18C ．19D ．232．数列{}n a 中，如果n a ＝3n (n ＝1，2，3，…) ，那么这个数列是( )． A ．公差为2的等差数列 B ．公差为3的等差数列 C ．首项为3的等比数列D ．首项为1的等比数列3．等差数列{a n }中，a 2＋a 6＝8，a 3＋a 4＝3，那么它的公差是( )． A ．4B ．5C ．6D ．74．△ABC 中，∠A ，∠B ，∠C 所对的边分别为a ，b ，c ．若a ＝3，b ＝4，∠C ＝60°， 则c 的值等于( )． A ．5B ．13C ．13D ．375．数列{a n }满足a 1＝1，a n ＋1＝2a n ＋1(n ∈N +)，那么a 4的值为( )． A ．4B ．8C ．15D ．316．△ABC 中，如果A a tan ＝B b tan ＝C ctan ，那么△ABC 是( )． A ．直角三角形B ．等边三角形C ．等腰直角三角形D ．钝角三角形7．如果a ＞b ＞0，t ＞0，设M ＝b a ，N ＝tb ta ++，那么( )． A ．M ＞NB ．M ＜NC ．M ＝ND ．M 与N 的大小关系随t 的变化而变化8．如果{a n }为递增数列，则{a n }的通项公式可以为( )． A ．a n ＝－2n ＋3 B ．a n ＝－n 2－3n ＋1 C ．a n ＝n21D ．a n ＝1＋log 2n9．如果a ＜b ＜0，那么( )． A ．a －b ＞0B ．ac ＜bcC ．a 1＞b1D ．a 2＜b 210．我们用以下程序框图来描述求解一元二次不等式ax 2＋bx ＋c ＞0(a ＞0)的过程．令a ＝2，b ＝4，若c ∈(0，1)，则输出区间的形式为( )．A ．MB ．NC ．PD ．∅开始输入a ,b ,c计算△＝b 2－4ac判断△≥0?计算ab x ab x 2221∆+-=∆--=结束判断x 1≠x 2?输出区间N ＝(-∞，x 1)∪(x 2，+∞)输出区间M ＝(-∞，-a b 2)∪(－ab2，+∞) 输出区间 P (-∞，+∞)是否是否11．等差数列{a n }中，已知a 1＝31，a 2＋a 5＝4，a n ＝33，则n 的值为( )．A ．50B ．49C ．48D ．4712．设集合A ＝{(x ,y )｜x ，y ，1―x ―y 是三角形的三边长}，则A 所表示的平面区域(不含边界的阴影部分)是( )．Ox0.50.5yx0.50.5yx0.50.5y x0.50.5y OO OABCD13．若{a n }是等差数列，首项a 1＞0，a 4＋a 5＞0，a 4·a 5＜0，则使前n 项和S n ＞0成立的最大自然数n 的值为( )．A ．4B ．5C ．7D ．814．已知数列{a n }的前n 项和S n ＝n 2－9n ，第k 项满足5＜a k ＜8，则k ＝( )． A ．9B ．8C ．7D ．6二、填空题：本大题共4小题，每小题4分，共16分．将答案填在题中横线上． 15．已知x 是4和16的等差中项，则x ＝ ． 16．一元二次不等式x 2＜x ＋6的解集为 ．17．函数f (x )＝x (1－x )，x ∈(0，1)的最大值为 ．18．在数列{a n }中，其前n 项和S n ＝3·2n ＋k ，若数列{a n }是等比数列，则常数k 的值为 ．三、解答题：本大题共3小题，共28分. 解答应写出文字说明、证明过程或演算步骤. 19．△ABC 中，BC ＝7，AB ＝3，且B Csin sin ＝53． (1)求AC ； (2)求∠A ．20．某工厂修建一个长方体无盖蓄水池，其容积为4 800立方米，深度为3米．池底每平方米的造价为150元，池壁每平方米的造价为120元．设池底长方形长为x米．(1)求底面积，并用含x的表达式表示池壁面积；(2)怎样设计水池能使总造价最低?最低造价是多少?21．已知等差数列{a n}的前n项的和记为S n．如果a4＝－12，a8＝－4．(1)求数列{a n}的通项公式；(2)求S n的最小值及其相应的n的值；a，…，构成一个新的数列{b n}，(3)从数列{a n}中依次取出a1，a2，a4，a8，…，12n－求{b n}的前n项和．参考答案一、选择题 1．C 2．B 3．B 4．C 5．C 6．B 7．A 8．D9．C10．B11．A12．A13．D14．B二、填空题 15．10． 16．(－2，3)． 17．41． 18．－3． 三、解答题19．解：（1）由正弦定理得B AC sin ＝C AB sin ⇒AC AB ＝BC sin sin ＝53⇒AC ＝335⨯＝5．（2）由余弦定理得cos A ＝AC AB BC AC AB ⋅-+2222＝53249259⨯⨯-+＝21-，所以∠A ＝120°．20．解：（1）设水池的底面积为S 1，池壁面积为S 2，则有S 1＝38004 ＝1 600(平方米)．池底长方形宽为x 6001米，则S 2＝6x ＋6×x 6001＝6(x ＋x6001)．（2）设总造价为y ，则y ＝150×1 600＋120×6(x ＋x6001)≥240 000＋57 600＝297 600． 当且仅当x ＝x6001,即x ＝40时取等号． 所以x ＝40时,总造价最低为297 600元．答：当池底设计为边长40米的正方形时，总造价最低，其值为297 600元．21．解：（1）设公差为d ，由题意，⎩⎨⎧ ⇔ ⎩⎨⎧解得⎩⎨⎧所以a n ＝2n －20．（2）由数列{a n }的通项公式可知，当n ≤9时，a n ＜0， 当n ＝10时，a n ＝0， 当n ≥11时，a n ＞0．所以当n ＝9或n ＝10时，S n 取得最小值为S 9＝S 10＝－90． （3）记数列{b n }的前n 项和为T n ，由题意可知b n ＝12-n a ＝2×2n －1－20＝2n －20．所以T n ＝b 1＋b 2＋b 3＋…＋b n＝(21－20)＋(22－20)＋(23－20)＋…＋(2n －20) ＝(21＋22＋23＋…＋2n )－20n＝21221--+n －20n＝2n +1－20n －2．a 4＝－12 a 8＝－4 a 1＋3d ＝－12 a 1＋7d ＝－4d ＝2a 1＝－18。

高中数学必修五综合测试题含答案
编辑整理：
尊敬的读者朋友们：
这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学必修五综合测试题含答案）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学必修五综合测试题含答案的全部内容。

鎌。

模块综合测评(二)(时间120分钟，满分150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．数列1,3,7,15，…的通项a n 可能是( ) A ．2n B ．2n ＋1 C ．2n －1D ．2n －1【解析】 取n ＝1时，a 1＝1，排除A 、B ，取n ＝2时，a 2＝3，排除D. 【答案】 C2．不等式x 2－2x －5>2x 的解集是( ) A ．{x |x ≤－1或x ≥5} B ．{x |x <－1或x >5} C ．{x |1<x <5} D ．{x |－1≤x ≤5}【解析】 不等式化为x 2－4x －5>0，所以(x －5)(x ＋1)>0，所以x <－1或x >5. 【答案】 B3．在正项等比数列{a n }中，a 1和a 19为方程x 2－10x ＋16＝0的两根，则a 8·a 10·a 12等于( )A ．16B ．32C ．64D ．256【解析】 ∵{a n }是等比数列且由题意得a 1·a 19＝16＝a 210(a n >0)，∴a 8·a 10·a 12＝a 310＝64.【答案】 C4．下列不等式一定成立的是( ) A ．lg ⎝ ⎛⎭⎪⎫x 2＋14>lg x (x >0)B ．sin x ＋1sin x ≥2(x ≠k π，k ∈Z ) C ．x 2＋1≥2|x |(x ∈R )D.1x2＋1>1(x∈R)【解析】5．在△ABC中，角A，B，C的对边分别为a，b，c，ac＝3，且a＝3b sin A，则△ABC的面积等于()A.12 B.32C．1 D.3 4【解析】∵a＝3b sin A，∴由正弦定理得sin A＝3sin B sin A，∴sin B＝1 3.∵ac＝3，∴△ABC的面积S＝12ac sin B＝12×3×13＝12，故选 A.【答案】 A6．等比数列{a n}前n项的积为T n，若a3a6a18是一个确定的常数，那么数列T10，T13，T17，T25中也是常数的项是()A．T10B．T13C．T17D．T25【解析】由等比数列的性质得a3a6a18＝a6a10a11＝a8a9a10＝a39，而T17＝a179，故T17为常数．【答案】 C7．已知不等式x2－2x－3<0的解集为A，不等式x2＋x－6<0的解集为B，不等式x 2＋ax ＋b <0的解集是A ∩B ，那么a ＋b 等于( )A ．－3B ．1C ．－1D ．3【解析】 由题意：A ＝{x |－1<x <3}，B ＝{x |－3<x <2}，A ∩B ＝{x |－1<x <2}，由根与系数的关系可知：a ＝－1，b ＝－2，∴a ＋b ＝－3. 【答案】 A8．古诗云：远望巍巍塔七层，红光点点倍加增．共灯三百八十一，请问尖头几盏灯？( )A ．2B ．3C ．4D ．5【解析】 远望巍巍塔七层，说明该数列共有7项，即n ＝7.红光点点倍加增，说明该数列是公比为2的等比数列．共灯三百八十一，说明7项之和S 7＝381.请问尖头几盏灯，就是求塔顶几盏灯，即求首项a 1. 代入公式S n ＝a 1(1－q n )1－q ，即381＝a 1(1－27)1－2，∴a 1＝381127＝3. ∴此塔顶有3盏灯． 【答案】 B9．若实数x ，y 满足⎩⎨⎧x －y ＋1≤0，x >0，则yx 的取值范围是( )A ．(0,1)B ．(0,1]C ．(1，＋∞)D ．[1，＋∞)【解析】 实数x ，y 满足⎩⎨⎧x －y ＋1≤0，x >0的相关区域如图中的阴影部分所示． y x 表示阴影部分内的任意一点与坐标原点(0,0)连线的斜率，由图可知，yx 的取值范围为(1，＋∞)．【答案】 C10．在△ABC 中，若c ＝2b cos A ，则此三角形必是( ) A ．等腰三角形 B ．正三角形 C ．直角三角形D ．有一角为30°的直角三角形【解析】 由正弦定理得sin C ＝2cos A sin B ， ∴sin (A ＋B )＝2cos A sin B ，即sin A cos B ＋cos A sin B ＝2cos A sin B ， 即sin A cos B －cos A sin B ＝0， 所以sin (A －B )＝0. 又因为－π<A －B <π， 所以A －B ＝0， 即A ＝B . 【答案】 A11．函数y ＝x 2＋2x －1(x >1)的最小值是( )A ．23＋2B ．23－2C ．2 3D ．2 【解析】 ∵x >1， ∴x －1>0.∴y ＝x 2＋2x －1＝x 2－2x ＋2x ＋2x －1＝x 2－2x ＋1＋2(x －1)＋3x －1＝(x －1)2＋2(x －1)＋3x －1＝x －1＋3x －1＋2 ≥23＋2. 【答案】 A12．在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，且tan B ＝2－3a 2－b 2＋c 2，BC →·BA→＝12，则tan B 等于( ) A.32 B.3－1 C ．2D ．2－ 3【解析】 由BC →·BA→＝12，得ac cos B ＝12，∴2ac cos B ＝1.又由余弦定理，得b 2＝a 2＋c 2－2ac cos B ＝a 2＋c 2－1， ∴a 2－b 2＋c 2＝1， ∴tan B ＝2－31＝2－ 3.【答案】 D二、填空题(本大题共4小题，每小题5分，共20分，将答案填在题中的横线上)13．已知点P (1，－2)及其关于原点的对称点均在不等式2x ＋by ＋1>0表示的平面区域内，则b 的取值范围是______. 【导学号：05920089】【解析】 点P (1，－2)关于原点的对称点为点P ′(－1，2)． 由题意知⎩⎨⎧2×1－2b ＋1>0，－2＋2b ＋1>0，解得12<b <32. 【答案】 ⎝ ⎛⎭⎪⎫12，3214．(2015·江苏高考)设数列{}a n 满足a 1＝1，且a n ＋1－a n ＝n ＋1(n ∈N *)，则数列⎩⎨⎧⎭⎬⎫1a n 前10项的和为________．【解析】 由题意有a 2－a 1＝2，a 3－a 2＝3，…，a n －a n －1＝n (n ≥2)．以上各式相加，得a n －a 1＝2＋3＋…＋n ＝(n －1)(2＋n )2＝n 2＋n －22.又∵a 1＝1， ∴a n ＝n 2＋n2(n ≥2)． ∵当n ＝1时也满足此式， ∴a n ＝n 2＋n2(n ∈N *)． ∴1a n ＝2n 2＋n ＝2⎝ ⎛⎭⎪⎫1n －1n ＋1. ∴S 10＝2×⎝ ⎛⎭⎪⎫11－12＋12－13＋…＋110－111＝2×⎝ ⎛⎭⎪⎫1－111＝2011.【答案】 201115．已知a ，b ，c 分别为△ABC 三个内角A ，B ，C 的对边，a ＝2，且(2＋b )(sin A －sin B )＝(c －b )sin C ，则△ABC 面积的最大值为________．【解析】 ∵a sin A ＝b sin B ＝csin C ＝2R ，a ＝2， 又(2＋b )(sin A －sin B )＝(c －b )sin C 可化为(a ＋b )(a －b )＝(c －b )·c ， ∴a 2－b 2＝c 2－bc ， ∴b 2＋c 2－a 2＝bc .∴b 2＋c 2－a 22bc ＝bc 2bc ＝12＝cos A ， ∴A ＝60°.∵在△ABC 中，4＝a 2＝b 2＋c 2－2bc ·cos 60°＝b 2＋c 2－bc ≥2bc －bc ＝bc (“＝”当且仅当b ＝c 时取得)， ∴S △ABC ＝12·bc ·sin A ≤12×4×32＝ 3.【答案】 316．若1a <1b <0，已知下列不等式： ①a ＋b <ab ；②|a |>|b |；③a <b ；④b a ＋ab >2； ⑤a 2>b 2；⑥2a >2b .其中正确的不等式的序号为______． 【解析】 ∵1a <1b <0， ∴b <a <0，故③错；又b <a <0，可得|a |<|b |，a 2<b 2， 故②⑤错，可证①④⑥正确． 【答案】 ①④⑥三、解答题(本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤)17．(本小题满分10分)设等差数列{a n }的前n 项和为S n ，已知a 3＝12，且S 12>0，S 13<0.(1)求公差d 的取值范围；(2)问前几项的和最大，并说明理由． 【解】 (1)∵a 3＝12，∴a 1＝12－2d ， ∵S 12>0，S 13<0， ∴⎩⎨⎧12a 1＋66d >0，13a 1＋78d <0， 即⎩⎨⎧24＋7d >0，3＋d <0， ∴－247<d <－3. (2)∵S 12>0，S 13<0， ∴⎩⎨⎧ a 1＋a 12>0，a 1＋a 13<0， ∴⎩⎨⎧a 6＋a 7>0，a 7<0，∴a 6>0， 又由(1)知d <0.∴数列前6项为正，从第7项起为负． ∴数列前6项和最大．18．(本小题满分12分)已知α，β是方程x 2＋ax ＋2b ＝0的两根，且α∈[0,1]，β∈[1,2]，a ，b ∈R ，求b －3a －1的最大值和最小值． 【解】 ∵⎩⎨⎧α＋β＝－a ，αβ＝2b ，∴⎩⎪⎨⎪⎧a ＝－(α＋β)，b ＝αβ2，∵0≤α≤1,1≤β≤2， ∴1≤α＋β≤3,0≤αβ≤2. ∴⎩⎨⎧－3≤a ≤－1，0≤b ≤1，建立平面直角坐标系aOb ，则上述不等式组表示的平面区域如下图所示．令k ＝b －3a －1，可以看成动点P (a ，b )与定点A (1,3)的连线的斜率．取B (－1,0)，C (－3,1)， 则k AB ＝32，k AC ＝12，∴12≤b －3a －1≤32.故b －3a －1的最大值是32，最小值是12. 19．(本小题满分12分)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，满足(2b －c )cos A －a cos C ＝0.(1)求角A 的大小；(2)若a ＝3，试求当△ABC 的面积取最大值时，△ABC 的形状. 【导学号：05920090】【解】 (1)∵(2b －c )cos A －a cos C ＝0，由余弦定理得(2b －c )·b 2＋c 2－a 22bc －a ·a 2＋b 2－c 22ab ＝0， 整理得b 2＋c 2－a 2＝bc ， ∴cos A ＝b 2＋c 2－a 22bc ＝12， ∵0<A <π， ∴A ＝π3.(2)由(1)得b 2＋c 2－bc ＝3及b 2＋c 2≥2bc 得bc ≤3. 当且仅当b ＝c ＝3时取等号． ∴S △ABC ＝12bc sin A ≤12×3×32＝334. 从而当△ABC 的面积最大时，a ＝b ＝c ＝ 3.∴当△ABC 的面积取最大值时△ABC 为等边三角形．20．(本小题满分12分)已知函数y ＝ax 2＋2ax ＋1的定义域为R . (1)求a 的取值范围；(2)解关于x 的不等式x 2－x －a 2＋a <0.【解】 (1)∵函数y ＝ax 2＋2ax ＋1的定义域为R ，∴ax 2＋2ax ＋1≥0恒成立． ①当a ＝0时，1≥0，不等式恒成立； ②当a ≠0时，则⎩⎨⎧a >0，Δ＝4a 2－4a ≤0，解得0<a ≤1.综上可知，a 的取值范围是[0,1]．(2)由x 2－x －a 2＋a <0，得(x －a )[x －(1－a )]<0. ∵0≤a ≤1， ∴①当1－a >a ，即0≤a <12时， a <x <1－a ；②当1－a ＝a ，即a ＝12时，⎝ ⎛⎭⎪⎫x －122<0，不等式无解；③当1－a <a ，即12<a ≤1时， 1－a <x <a .综上，当0≤a <12时，原不等式的解集为(a,1－a )； 当a ＝12时，原不等式的解集为∅；当12<a ≤1时，原不等式的解集为(1－a ，a )．21．(本小题满分12分)若数列{a n }满足a 2n ＋1－a 2n ＝d ，其中d 为常数，则称数列{a n }为等方差数列．已知等方差数列{a n }满足a n >0，a 1＝1，a 5＝3.(1)求数列{a n }的通项公式；(2)求数列⎩⎨⎧⎭⎬⎫a 2n ⎝ ⎛⎭⎪⎫12n的前n 项和．【解】 (1)由a 21＝1，a 25＝9， 得a 25－a 21＝4d ，∴d ＝2.a 2n ＝1＋(n －1)×2＝2n －1， ∵a n >0， ∴a n ＝2n －1.数列{a n }的通项公式为a n ＝2n －1. (2)a 2n ⎝ ⎛⎭⎪⎫12n ＝(2n －1)12n ， 设S n ＝1·12＋3·122＋5·123＋…＋(2n －1)·12n ，① 12S n ＝1·122＋3·123＋5·124＋…＋(2n －1)· 12n ＋1，② ①－②，得12S n ＝12＋2⎝ ⎛⎭⎪⎫122＋123＋…＋12n －(2n －1)·12n ＋1 ＝12＋2·14⎝ ⎛⎭⎪⎫1－12n －11－12－(2n －1)·12n ＋1， 即S n ＝3－2n ＋32n ，即数列⎩⎨⎧⎭⎬⎫a 2n ⎝ ⎛⎭⎪⎫12n 的前n 项和为3－2n ＋32n .22．(本小题满分12分)如图1所示，某海岛上一观察哨A 上午11时测得一轮船在海岛北偏东60°的C 处，12时20分时测得该轮船在海岛北偏西60°的B 处，12时40分该轮船到达位于海岛正西方且距海岛5千米的E 港口，如果轮船始终匀速直线航行，则船速是多少？(结果保留根号)图1【解】 轮船从点C 到点B 用时80分钟，从点B 到点E 用时20分钟，而船始终匀速航行，由此可见，BC ＝4EB .设EB ＝x ，则BC ＝4x ，由已知得∠BAE ＝30°，在△AEC 中，由正弦定理得EC sin ∠EAC＝AE sin C ， 即sin C ＝AE sin ∠EAC EC＝5sin 150°5x ＝12x ， 在△ABC 中，由正弦定理得BC sin ∠BAC＝AB sin C ，即AB＝BC sin Csin 120°＝4x×12xsin 120°＝43＝433.在△ABE中，由余弦定理得BE2＝AE2＋AB2－2AE·AB cos 30°＝25＋163－2×5×433×32＝313，所以BE＝313(千米)．故轮船的速度为v＝313÷2060＝93(千米/时)．。

第一章 解三角形测试一 正弦定理和余弦定理Ⅰ 学习目标1．掌握正弦定理和余弦定理及其有关变形.2．会正确运用正弦定理、余弦定理及有关三角形知识解三角形.Ⅱ 基础训练题一、选择题1．在△ABC 中，若BC ＝2，AC ＝2，B ＝45°，则角A 等于( ) (A)60°(B)30°(C)60°或120°(D)30°或150°2．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，若a ＝2，b ＝3，cos C ＝－41，则c 等于( ) (A)2(B)3 (C)4 (D)53．在△ABC 中，已知32sin ,53cos ==C B ，AC ＝2，那么边AB 等于( ) (A )45 (B)35 (C)920 (D)512 4．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，已知B ＝30°，c ＝150，b ＝503，那么这个三角形是( ) (A)等边三角形 (B)等腰三角形 (C)直角三角形 (D)等腰三角形或直角三角形5．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，如果A ∶B ∶C ＝1∶2∶3，那么a ∶b ∶c 等于( ) (A)1∶2∶3(B)1∶3∶2(C)1∶4∶9(D)1∶2∶3二、填空题6．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，若a ＝2，B ＝45°，C ＝75°，则b ＝________. 7．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，若a ＝2，b ＝23，c ＝4，则A ＝________.8．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，若2cos B cos C ＝1－cos A ，则△ABC 形状是________三角形.9．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，若a ＝3，b ＝4，B ＝60°，则c ＝________. 10．在△ABC 中，若tan A ＝2，B ＝45°，BC ＝5，则 AC ＝________.三、解答题11．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，若a ＝2，b ＝4，C ＝60°，试解△ABC . 12．在△ABC 中，已知AB ＝3，BC ＝4，AC ＝13.(1)求角B 的大小；(2)若D 是BC 的中点，求中线AD 的长.13．如图，△OAB 的顶点为O (0，0)，A (5，2)和B (－9，8)，求角A 的大小.14．在△ABC 中，已知BC ＝a ，AC ＝b ，且a ，b 是方程x 2－23x ＋2＝0的两根，2cos(A＋B )＝1.(1)求角C 的度数； (2)求AB 的长； (3)求△ABC 的面积.测试二 解三角形全章综合练习Ⅰ 基础训练题一、选择题1．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，若b 2＋c 2－a 2＝bc ，则角A 等于( ) (A)6π (B)3π (C)32π (D)65π2．在△ABC 中，给出下列关系式： ①sin(A ＋B )＝sin C②cos(A ＋B )＝cos C ③2cos 2sinCB A =+ 其中正确的个数是( ) (A)0 (B)1(C)2 (D)33．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c .若a ＝3，sin A ＝32，sin(A ＋C )＝43，则b 等于( ) (A)4(B)38(C)6(D)827 4．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，若a ＝3，b ＝4，sin C ＝32，则此三角形的面积是( ) (A)8 (B)6 (C)4 (D)35．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，若(a ＋b ＋c )(b ＋c －a )＝3bc ，且sin A ＝2sin B cos C ，则此三角形的形状是( ) (A)直角三角形 (B)正三角形 (C)腰和底边不等的等腰三角形 (D)等腰直角三角形 二、填空题6．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，若a ＝2，b ＝2，B ＝45°，则角A ＝________.7．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，若a ＝2，b ＝3，c ＝19，则角C ＝________.8．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，若b ＝3，c ＝4，cos A ＝53，则此三角形的面积为________.9．已知△ABC 的顶点A (1，0)，B (0，2)，C (4，4)，则cos A ＝________.10．已知△ABC 的三个内角A ，B ，C 满足2B ＝A ＋C ，且AB ＝1，BC ＝4，那么边BC 上的中线AD 的长为________. 三、解答题11．在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，且a ＝3，b ＝4，C ＝60°.(1)求c ； (2)求sin B .12．设向量a ，b 满足a ·b ＝3，|a |＝3，|b |＝2.(1)求〈a ，b 〉； (2)求|a －b |.13．设△OAB 的顶点为O (0，0)，A (5，2)和B (－9，8)，若BD ⊥OA 于D .(1)求高线BD 的长； (2)求△OAB 的面积.14．在△ABC 中，若sin 2A ＋sin 2B ＞sin 2C ，求证：C 为锐角.(提示：利用正弦定理R CcB b A a 2sin sin sin ===，其中R 为△ABC 外接圆半径) Ⅱ 拓展训练题15．如图，两条直路OX 与OY 相交于O 点，且两条路所在直线夹角为60°，甲、乙两人分别在OX 、OY 上的A 、B 两点，| OA |＝3km ，| OB |＝1km ，两人同时都以4km/h 的速度行走，甲沿方向，乙沿OY 方向.问：(1)经过t 小时后，两人距离是多少(表示为t 的函数)？(2)何时两人距离最近？16．在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，且ca bC B +-=2cos cos . (1)求角B 的值；(2)若b ＝13，a ＋c ＝4，求△ABC 的面积.第二章 数列测试三 数列Ⅰ 学习目标1．了解数列的概念和几种简单的表示方法(列表、图象、通项公式)，了解数列是一种特殊的函数.2．理解数列的通项公式的含义，由通项公式写出数列各项.3．了解递推公式是给出数列的一种方法，能根据递推公式写出数列的前几项.Ⅱ 基础训练题一、选择题1．数列{a n }的前四项依次是：4，44，444，4444，…则数列{a n }的通项公式可以是( ) (A)a n ＝4n (B)a n ＝4n (C)a n ＝94(10n－1)(D)a n ＝4×11n2．在有一定规律的数列0，3，8，15，24，x ，48，63，……中，x 的值是( ) (A)30 (B)35 (C)36 (D)42 3．数列{a n }满足：a 1＝1，a n ＝a n －1＋3n ，则a 4等于( ) (A)4 (B)13 (C)28 (D)43 4．156是下列哪个数列中的一项( ) (A){n 2＋1} (B){n 2－1} (C){n 2＋n } (D){n 2＋n －1} 5．若数列{a n }的通项公式为a n ＝5－3n ，则数列{a n }是( ) (A)递增数列 (B)递减数列 (C)先减后增数列 (D)以上都不对 二、填空题6．数列的前5项如下，请写出各数列的一个通项公式：(1)n a ,,31,52,21,32,1 ＝________；(2)0，1，0，1，0，…，a n ＝________.7．一个数列的通项公式是a n ＝122+n n .(1)它的前五项依次是________； (2)0.98是其中的第________项.8．在数列{a n }中，a 1＝2，a n ＋1＝3a n ＋1，则a 4＝________. 9．数列{a n }的通项公式为)12(3211-++++=n a n (n ∈N *)，则a 3＝________.10．数列{a n }的通项公式为a n ＝2n 2－15n ＋3，则它的最小项是第________项. 三、解答题11．已知数列{a n }的通项公式为a n ＝14－3n .(1)写出数列{a n }的前6项； (2)当n ≥5时，证明a n ＜0.12．在数列{a n }中，已知a n ＝312-+n n (n ∈N *).(1)写出a 10，a n ＋1，2n a ；(2)7932是否是此数列中的项？若是，是第几项？ 13．已知函数xx x f 1)(-=，设a n ＝f (n )(n ∈N ＋). (1)写出数列{a n }的前4项；(2)数列{a n }是递增数列还是递减数列？为什么？测试四 等差数列Ⅰ 学习目标1．理解等差数列的概念，掌握等差数列的通项公式，并能解决一些简单问题. 2．掌握等差数列的前n 项和公式，并能应用公式解决一些简单问题.3．能在具体的问题情境中，发现数列的等差关系，并能体会等差数列与一次函数的关系.Ⅱ 基础训练题一、选择题1．数列{a n }满足：a 1＝3，a n ＋1＝a n －2，则a 100等于( ) (A)98 (B)－195 (C)－201 (D)－1982．数列{a n }是首项a 1＝1，公差d ＝3的等差数列，如果a n ＝2008，那么n 等于( ) (A)667 (B)668 (C)669 (D)670 3．在等差数列{a n }中，若a 7＋a 9＝16，a 4＝1，则a 12的值是( ) (A)15 (B)30 (C)31 (D)644．在a 和b (a ≠b )之间插入n 个数，使它们与a ，b 组成等差数列，则该数列的公差为( )(A)n a b - (B)1+-n a b (C)1++n a b (D)2+-n ab 5．设数列{a n }是等差数列，且a 2＝－6，a 8＝6，S n 是数列{a n }的前n 项和，则( ) (A)S 4＜S 5 (B)S 4＝S 5 (C)S 6＜S 5 (D)S 6＝S 5 二、填空题6．在等差数列{a n }中，a 2与a 6的等差中项是________.7．在等差数列{a n }中，已知a 1＋a 2＝5，a 3＋a 4＝9，那么a 5＋a 6＝________. 8．设等差数列{a n }的前n 项和是S n ，若S 17＝102，则a 9＝________.9．如果一个数列的前n 项和S n ＝3n 2＋2n ，那么它的第n 项a n ＝________.10．在数列{a n }中，若a 1＝1，a 2＝2，a n ＋2－a n ＝1＋(－1)n (n ∈N *)，设{a n }的前n 项和是S n ，则S 10＝________. 三、解答题11．已知数列{a n }是等差数列，其前n 项和为S n ，a 3＝7，S 4＝24．求数列{a n }的通项公式.12．等差数列{a n }的前n 项和为S n ，已知a 10＝30，a 20＝50.(1)求通项a n ；(2)若S n ＝242，求n .13．数列{a n }是等差数列，且a 1＝50，d ＝－0.6．(1)从第几项开始a n ＜0；(2)写出数列的前n 项和公式S n ，并求S n 的最大值.Ⅲ 拓展训练题14．记数列{a n }的前n 项和为S n ，若3a n ＋1＝3a n ＋2(n ∈N *)，a 1＋a 3＋a 5＋…＋a 99＝90，求S 100．测试五 等比数列Ⅰ 学习目标1．理解等比数列的概念，掌握等比数列的通项公式，并能解决一些简单问题. 2．掌握等比数列的前n 项和公式，并能应用公式解决一些简单问题.3．能在具体的问题情境中，发现数列的等比关系，并能体会等比数列与指数函数的关系.Ⅱ 基础训练题一、选择题1．数列{a n }满足：a 1＝3，a n ＋1＝2a n ，则a 4等于( )(A)83 (B)24 (C)48 (D)542．在各项都为正数的等比数列{a n }中，首项a 1＝3，前三项和为21，则a 3＋a 4＋a 5等于( ) (A)33 (B)72 (C)84 (D)189 3．在等比数列{a n }中，如果a 6＝6，a 9＝9，那么a 3等于( )(A)4(B)23 (C)916 (D)3 4．在等比数列{a n }中，若a 2＝9，a 5＝243，则{a n }的前四项和为( ) (A)81 (B)120 (C)168 (D)1925．若数列{a n }满足a n ＝a 1q n －1(q ＞1)，给出以下四个结论： ①{a n }是等比数列； ②{a n }可能是等差数列也可能是等比数列； ③{a n }是递增数列； ④{a n }可能是递减数列. 其中正确的结论是( ) (A)①③ (B)①④ (C)②③ (D)②④ 二、填空题6．在等比数列{a n }中,a 1，a 10是方程3x 2＋7x －9＝0的两根，则a 4a 7＝________. 7．在等比数列{a n }中，已知a 1＋a 2＝3，a 3＋a 4＝6，那么a 5＋a 6＝________. 8．在等比数列{a n }中，若a 5＝9，q ＝21，则{a n }的前5项和为________. 9．在38和227之间插入三个数，使这五个数成等比数列，则插入的三个数的乘积为________.10．设等比数列{a n }的公比为q ，前n 项和为S n ，若S n ＋1，S n ，S n ＋2成等差数列，则q ＝________. 三、解答题11．已知数列{a n }是等比数列，a 2＝6，a 5＝162.设数列{a n }的前n 项和为S n .(1)求数列{a n }的通项公式； (2)若S n ＝242，求n .12．在等比数列{a n }中，若a 2a 6＝36，a 3＋a 5＝15，求公比q .13．已知实数a ，b ，c 成等差数列，a ＋1，b ＋1，c ＋4成等比数列，且a ＋b ＋c ＝15，求a ，b ，c .Ⅲ 拓展训练题14．在下列由正数排成的数表中，每行上的数从左到右都成等比数列，并且所有公比都等于q ，每列上的数从上到下都成等差数列.a ij 表示位于第i 行第j 列的数，其中a 24＝81，a 42＝1，a 54＝5.(2)求a ij 的计算公式.测试六 数列求和Ⅰ 学习目标1．会求等差、等比数列的和，以及求等差、等比数列中的部分项的和. 2．会使用裂项相消法、错位相减法求数列的和.Ⅱ 基础训练题一、选择题1．已知等比数列的公比为2，且前4项的和为1，那么前8项的和等于( ) (A)15 (B)17 (C)19 (D)21 2．若数列{a n }是公差为21的等差数列，它的前100项和为145，则a 1＋a 3＋a 5＋…＋a 99的值为( ) (A)60 (B)72.5 (C)85 (D)1203．数列{a n }的通项公式a n ＝(－1)n －1·2n (n ∈N *)，设其前n 项和为S n ，则S 100等于( ) (A)100 (B)－100 (C)200 (D)－200 4．数列⎭⎬⎫⎩⎨⎧+-)12)(12(1n n 的前n 项和为( )(A)12+n n (B)122+n n (C)24+n n (D)12+n n5．设数列{a n }的前n 项和为S n ，a 1＝1，a 2＝2，且a n ＋2＝a n ＋3(n ＝1，2，3，…)，则S 100等于( ) (A)7000 (B)7250 (C)7500 (D)14950 二、填空题 6．nn +++++++++11341231121 ＝________.7．数列{n ＋n21}的前n 项和为________. 8．数列{a n }满足：a 1＝1，a n ＋1＝2a n ，则a 21＋a 22＋…＋a 2n ＝________. 9．设n ∈N *，a ∈R ，则1＋a ＋a 2＋…＋a n ＝________. 10．n n 21813412211⨯++⨯+⨯+⨯＝________. 三、解答题11．在数列{a n }中，a 1＝－11，a n ＋1＝a n ＋2(n ∈N *)，求数列{|a n |}的前n 项和S n .12．已知函数f (x )＝a 1x ＋a 2x 2＋a 3x 3＋…＋a n x n (n ∈N *，x ∈R )，且对一切正整数n 都有f (1)＝n 2成立.(1)求数列{a n }的通项a n ；(2)求13221111++++n n a a a a a a .13．在数列{a n }中，a 1＝1，当n ≥2时，a n ＝12141211-++++n ，求数列的前n 项和S n .Ⅲ 拓展训练题14．已知数列{a n }是等差数列，且a 1＝2，a 1＋a 2＋a 3＝12.(1)求数列{a n }的通项公式；(2)令b n ＝a n x n (x ∈R )，求数列{b n }的前n 项和公式.测试七 数列综合问题Ⅰ 基础训练题一、选择题1．等差数列{a n }中，a 1＝1，公差d ≠0，如果a 1，a 2，a 5成等比数列，那么d 等于( ) (A)3 (B)2 (C)－2 (D)2或－2 2．等比数列{a n }中，a n ＞0，且a 2a 4＋2a 3a 5＋a 4a 6＝25，则a 3＋a 5等于( ) (A)5 (B)10 (C)15 (D)20 3．如果a 1，a 2，a 3，…，a 8为各项都是正数的等差数列，公差d ≠0，则( ) (A)a 1a 8＞a 4a 5 (B)a 1a 8＜a 4a 5 (C)a 1＋a 8＞a 4＋a 5 (D)a 1a 8＝a 4a 54．一给定函数y ＝f (x )的图象在下列图中，并且对任意a 1∈(0，1)，由关系式a n ＋1＝f (a n )得到的数列{a n }满足a n ＋1＞a n (n ∈N *)，则该函数的图象是()5．已知数列{a n }满足a 1＝0，1331+-=+n n n a a a (n ∈N *)，则a 20等于( )(A)0 (B)－3 (C)3(D)23 二、填空题6．设数列{a n }的首项a 1＝41，且⎪⎪⎩⎪⎪⎨⎧+=+.,,41,211为奇数为偶数n a n a a n nn 则a 2＝________，a 3＝________.7．已知等差数列{a n }的公差为2，前20项和等于150，那么a 2＋a 4＋a 6＋…＋a 20＝________. 8．某种细菌的培养过程中，每20分钟分裂一次(一个分裂为两个)，经过3个小时，这种细菌可以由1个繁殖成________个.9．在数列{a n }中，a 1＝2，a n ＋1＝a n ＋3n (n ∈N *)，则a n ＝________.10．在数列{a n }和{b n }中，a 1＝2，且对任意正整数n 等式3a n ＋1－a n ＝0成立，若b n 是a n 与a n ＋1的等差中项，则{b n }的前n 项和为________. 三、解答题11．数列{a n }的前n 项和记为S n ，已知a n ＝5S n －3(n ∈N *).(1)求a 1，a 2，a 3；(2)求数列{a n }的通项公式； (3)求a 1＋a 3＋…＋a 2n －1的和.12．已知函数f (x )＝422+x (x ＞0)，设a 1＝1，a 21+n ·f (a n )＝2(n ∈N *)，求数列{a n }的通项公式.13．设等差数列{a n }的前n 项和为S n ，已知a 3＝12，S 12＞0，S 13＜0.(1)求公差d 的范围；(2)指出S 1，S 2，…，S 12中哪个值最大，并说明理由.Ⅲ 拓展训练题14．甲、乙两物体分别从相距70m 的两地同时相向运动.甲第1分钟走2m ，以后每分钟比前1分钟多走1m ，乙每分钟走5m . (1)甲、乙开始运动后几分钟相遇？(2)如果甲、乙到达对方起点后立即折返，甲继续每分钟比前1分钟多走1m ，乙继续每分钟走5m ，那么开始运动几分钟后第二次相遇？15．在数列{a n }中，若a 1，a 2是正整数，且a n ＝|a n －1－a n －2|，n ＝3，4，5，…则称{a n }为“绝对差数列”.(1)举出一个前五项不为零的“绝对差数列”(只要求写出前十项)； (2)若“绝对差数列”{a n }中，a 1＝3，a 2＝0，试求出通项a n ； (3)*证明：任何“绝对差数列”中总含有无穷多个为零的项.测试八 数列全章综合练习Ⅰ 基础训练题一、选择题1．在等差数列{a n }中，已知a 1＋a 2＝4，a 3＋a 4＝12，那么a 5＋a 6等于( ) (A)16 (B)20 (C)24 (D)36 2．在50和350间所有末位数是1的整数和( ) (A)5880 (B)5539 (C)5208 (D)48773．若a ，b ，c 成等比数列，则函数y ＝ax 2＋bx ＋c 的图象与x 轴的交点个数为( ) (A)0 (B)1 (C)2 (D)不能确定 4．在等差数列{a n }中，如果前5项的和为S 5＝20，那么a 3等于( ) (A)－2 (B)2 (C)－4 (D)45．若{a n }是等差数列，首项a 1＞0，a 2007＋a 2008＞0，a 2007·a 2008＜0，则使前n 项和S n ＞0成立的最大自然数n 是( ) (A)4012 (B)4013 (C)4014 (D)4015 二、填空题6．已知等比数列{a n }中，a 3＝3，a 10＝384，则该数列的通项a n ＝________. 7．等差数列{a n }中，a 1＋a 2＋a 3＝－24，a 18＋a 19＋a 20＝78，则此数列前20项和S 20＝________. 8．数列{a n }的前n 项和记为S n ，若S n ＝n 2－3n ＋1，则a n ＝________.9．等差数列{a n }中，公差d ≠0，且a 1，a 3，a 9成等比数列，则1074963a a a a a a ++++＝________.10．设数列{a n }是首项为1的正数数列，且(n ＋1)a 21+n －na 2n ＋a n ＋1a n ＝0(n ∈N *)，则它的通项公式a n ＝________. 三、解答题11．设等差数列{a n }的前n 项和为S n ，且a 3＋a 7－a 10＝8，a 11－a 4＝4，求S 13.12．已知数列{a n }中，a 1＝1，点(a n ，a n ＋1＋1)(n ∈N *)在函数f (x )＝2x ＋1的图象上.(1)求数列{a n }的通项公式； (2)求数列{a n }的前n 项和S n ；(3)设c n ＝S n ，求数列{c n }的前n 项和T n .13．已知数列{a n }的前n 项和S n 满足条件S n ＝3a n ＋2.(1)求证：数列{a n }成等比数列； (2)求通项公式a n .14．某渔业公司今年初用98万元购进一艘渔船，用于捕捞，第一年需各种费用12万元，从第二年开始包括维修费在内，每年所需费用均比上一年增加4万元，该船每年捕捞的总收入为50万元.(1)写出该渔船前四年每年所需的费用(不包括购买费用)；(2)该渔船捕捞几年开始盈利(即总收入减去成本及所有费用为正值)？(3)若当盈利总额达到最大值时，渔船以8万元卖出，那么该船为渔业公司带来的收益是多少万元？Ⅱ 拓展训练题15．已知函数f (x )＝412-x (x ＜－2)，数列{a n }满足a 1＝1，a n ＝f (－11+n a )(n ∈N *).(1)求a n ；(2)设b n ＝a 21+n ＋a 22+n ＋…＋a 212+n ，是否存在最小正整数m ，使对任意n ∈N *有b n ＜25m成立？若存在，求出m 的值，若不存在，请说明理由.16．已知f 是直角坐标系平面xOy 到自身的一个映射，点P 在映射f 下的象为点Q ，记作Q＝f (P ).设P 1(x 1，y 1)，P 2＝f (P 1)，P 3＝f (P 2)，…，P n ＝f (P n －1)，….如果存在一个圆，使所有的点P n (x n ，y n )(n ∈N *)都在这个圆内或圆上，那么称这个圆为点P n (x n ，y n )的一个收敛圆.特别地，当P 1＝f (P 1)时，则称点P 1为映射f 下的不动点.若点P (x ，y )在映射f 下的象为点Q (－x ＋1，21y ). (1)求映射f 下不动点的坐标；(2)若P 1的坐标为(2，2)，求证：点P n (x n ，y n )(n ∈N *)存在一个半径为2的收敛圆.第三章 不等式测试九 不等式的概念与性质Ⅰ 学习目标1．了解日常生活中的不等关系和不等式(组)的实际背景，掌握用作差的方法比较两个代数式的大小.2．理解不等式的基本性质及其证明.Ⅱ 基础训练题一、选择题1．设a ，b ，c ∈R ，则下列命题为真命题的是( ) (A)a ＞b ⇒a －c ＞b －c (B)a ＞b ⇒ac ＞bc (C)a ＞b ⇒a 2＞b 2 (D)a ＞b ⇒ac 2＞bc 2 2．若－1＜α＜β＜1，则α－β 的取值范围是( ) (A)(－2，2) (B)(－2，－1) (C)(－1，0) (D)(－2，0) 3．设a ＞2，b ＞2，则ab 与a ＋b 的大小关系是( ) (A)ab ＞a ＋b (B)ab ＜a ＋b (C)ab ＝a ＋b (D)不能确定4．使不等式a ＞b 和ba 11>同时成立的条件是( ) (A)a ＞b ＞0 (B)a ＞0＞b (C)b ＞a ＞0 (D)b ＞0＞a 5．设1＜x ＜10，则下列不等关系正确的是( ) (A)lg 2x ＞lg x 2＞lg(lg x ) (B)lg 2x ＞lg(lg x )＞lg x 2 (C)lg x 2＞lg 2x ＞1g (lg x ) (D)lg x 2＞lg(lg x )＞lg 2x 二、填空题6．已知a ＜b ＜0，c ＜0，在下列空白处填上适当不等号或等号： (1)(a －2)c ________(b －2)c ； (2)a c ________bc； (3)b －a ________|a |－|b |. 7．已知a ＜0，－1＜b ＜0，那么a 、ab 、ab 2按从小到大排列为________.8．已知60＜a ＜84，28＜b ＜33，则a －b 的取值范围是________；ba的取值范围是________. 9．已知a ，b ，c ∈R ，给出四个论断：①a ＞b ；②ac 2＞bc 2；③cbc a >；④a －c ＞b －c .以其中一个论断作条件，另一个论断作结论，写出你认为正确的两个命题是________⇒________；________⇒________.(在“⇒”的两侧填上论断序号).10．设a ＞0，0＜b ＜1，则P ＝23+a b 与)2)(1(++=a a bQ 的大小关系是________.三、解答题11．若a ＞b ＞0，m ＞0，判断a b 与ma mb ++的大小关系并加以证明.12．设a ＞0，b ＞0，且a ≠b ，b a q a b ba p +=+=,22.证明：p ＞q .注：解题时可参考公式x 3＋y 3＝(x ＋y )(x 2－xy ＋y 2).Ⅲ 拓展训练题13．已知a ＞0，且a ≠1，设M ＝log a (a 3－a ＋1)，N ＝log a (a 2－a ＋1).求证：M ＞N .14．在等比数列{a n }和等差数列{b n }中,a 1＝b 1＞0，a 3＝b 3＞0，a 1≠a 3，试比较a 5和b 5的大小.测试十 均值不等式Ⅰ 学习目标1．了解基本不等式的证明过程.2．会用基本不等式解决简单的最大(小)值问题.Ⅱ 基础训练题一、选择题1．已知正数a ，b 满足a ＋b ＝1，则ab ( )(A)有最小值41 (B)有最小值21 (C)有最大值41 (D)有最大值21 2．若a ＞0，b ＞0，且a ≠b ，则( ) (A)2222b a ab ba +<<+ (B)2222b a ba ab +<+< (C)2222ba b a ab +<+<(D)2222ba ab b a +<<+ 3．若矩形的面积为a 2(a ＞0)，则其周长的最小值为( )(A)a (B)2a (C)3a(D)4a4．设a ，b ∈R ，且2a ＋b －2＝0，则4a ＋2b 的最小值是( ) (A)22(B)4(C)24(D)85．如果正数a ，b ，c ，d 满足a ＋b ＝cd ＝4，那么( ) (A)ab ≤c ＋d ，且等号成立时a ，b ，c ，d 的取值唯一 (B)ab ≥c ＋d ，且等号成立时a ，b ，c ，d 的取值唯一 (C)ab ≤c ＋d ，且等号成立时a ，b ，c ，d 的取值不唯一 (D)ab ≥c ＋d ，且等号成立时a ，b ，c ，d 的取值不唯一 二、填空题6．若x ＞0，则变量xx 9+的最小值是________；取到最小值时，x ＝________. 7．函数y ＝142+x x(x ＞0)的最大值是________；取到最大值时，x ＝________. 8．已知a ＜0，则316-+a a 的最大值是________. 9．函数f (x )＝2log 2(x ＋2)－log 2x 的最小值是________.10．已知a ，b ，c ∈R ，a ＋b ＋c ＝3，且a ，b ，c 成等比数列，则b 的取值范围是________. 三、解答题 11．四个互不相等的正数a ，b ，c ，d 成等比数列，判断2da +和bc 的大小关系并加以证明.12．已知a ＞0，a ≠1，t ＞0，试比较21log a t 与21log +t a 的大小.Ⅲ 拓展训练题13．若正数x ，y 满足x ＋y ＝1，且不等式a y x ≤+恒成立，求a 的取值范围. 14．(1)用函数单调性的定义讨论函数f (x )＝x ＋xa(a ＞0)在(0，＋∞)上的单调性； (2)设函数f (x )＝x ＋xa(a ＞0)在(0，2]上的最小值为g (a )，求g (a )的解析式. 测试十一 一元二次不等式及其解法Ⅰ 学习目标1．通过函数图象理解一元二次不等式与相应的二次函数、一元二次方程的联系. 2．会解简单的一元二次不等式.Ⅱ 基础训练题一、选择题1．不等式5x ＋4＞－x 2的解集是( ) (A){x |x ＞－1，或x ＜－4} (B){x |－4＜x ＜－1} (C){x |x ＞4，或x ＜1}(D){x |1＜x ＜4}2．不等式－x 2＋x －2＞0的解集是( ) (A){x |x ＞1，或x ＜－2}(B){x |－2＜x ＜1} (C)R(D)∅3．不等式x 2＞a 2(a ＜0)的解集为( ) (A){x |x ＞±a }(B){x |－a ＜x ＜a } (C){x |x ＞－a ，或x ＜a }(D){x |x ＞a ，或x ＜－a } 4．已知不等式ax 2＋bx ＋c ＞0的解集为}231|{<<-x x ，则不等式cx 2＋bx ＋a ＜0的解集是( )(A){x |－3＜x ＜21} (B){x |x ＜－3，或x ＞21} (C){x －2＜x ＜31}(D){x |x ＜－2，或x ＞31}5．若函数y ＝px 2－px －1(p ∈R )的图象永远在x 轴的下方，则p 的取值范围是( ) (A)(－∞，0) (B)(－4，0] (C)(－∞，－4) (D)[－4，0) 二、填空题6．不等式x 2＋x －12＜0的解集是________. 7．不等式05213≤+-x x 的解集是________.8．不等式|x 2－1|＜1的解集是________. 9．不等式0＜x 2－3x ＜4的解集是________. 10．已知关于x 的不等式x 2－(a ＋a 1)x ＋1＜0的解集为非空集合｛x |a ＜x ＜a1}，则实数a 的取值范围是________.三、解答题11．求不等式x 2－2ax －3a 2＜0(a ∈R )的解集.12．k 在什么范围内取值时，方程组⎩⎨⎧=+-=-+0430222k y x x y x 有两组不同的实数解？Ⅲ 拓展训练题13．已知全集U ＝R ，集合A ＝{x |x 2－x －6＜0}，B ＝{x |x 2＋2x －8＞0}，C ＝{x |x 2－4ax ＋3a 2＜0}.(1)求实数a 的取值范围，使C ⊇(A ∩B )；(2)求实数a 的取值范围，使C ⊇(U A )∩(U B ).14．设a ∈R ，解关于x 的不等式ax 2－2x ＋1＜0.测试十二 不等式的实际应用Ⅰ 学习目标会使用不等式的相关知识解决简单的实际应用问题.Ⅱ 基础训练题一、选择题 1．函数241xy -=的定义域是( )(A){x |－2＜x ＜2}(B){x |－2≤x ≤2} (C){x |x ＞2，或x ＜－2}(D){x |x ≥2，或x ≤－2}2．某村办服装厂生产某种风衣，月销售量x (件)与售价p (元/件)的关系为p ＝300－2x ，生产x 件的成本r ＝500＋30x (元)，为使月获利不少于8600元，则月产量x 满足( ) (A)55≤x ≤60 (B)60≤x ≤65 (C)65≤x ≤70 (D)70≤x ≤753．国家为了加强对烟酒生产管理，实行征收附加税政策.现知某种酒每瓶70元，不征收附加税时，每年大约产销100万瓶；若政府征收附加税，每销售100元征税r 元，则每年产销量减少10r 万瓶，要使每年在此项经营中所收附加税不少于112万元，那么r 的取值范围为( ) (A)2≤r ≤10 (B)8≤r ≤10 (C)2≤r ≤8 (D)0≤r ≤84．若关于x 的不等式(1＋k 2)x ≤k 4＋4的解集是M ，则对任意实常数k ，总有( ) (A)2∈M ，0∈M (B)2∉M ，0∉M (C)2∈M ，0∉M (D)2∉M ，0∈M 二、填空题5．已知矩形的周长为36cm ，则其面积的最大值为________.6．不等式2x 2＋ax ＋2＞0的解集是R ，则实数a 的取值范围是________. 7．已知函数f (x )＝x |x －2|，则不等式f (x )＜3的解集为________.8．若不等式|x ＋1|≥kx 对任意x ∈R 均成立，则k 的取值范围是________. 三、解答题9．若直角三角形的周长为2，求它的面积的最大值，并判断此时三角形形状.10．汽车在行驶过程中，由于惯性作用，刹车后还要继续滑行一段距离才能停住，我们称这段距离为“刹车距离”.刹车距离是分析事故的一个主要因素，在一个限速为40km/h 的弯道上，甲乙两车相向而行，发现情况不对同时刹车，但还是相撞了，事后现场测得甲车刹车的距离略超过12m ，乙车的刹车距离略超过10m .已知甲乙两种车型的刹车距离s (km)与车速x (km/h)之间分别有如下关系：s 甲＝0.1x ＋0.01x 2，s 乙＝0.05x ＋0.005x 2．问交通事故的主要责任方是谁？Ⅲ 拓展训练题11．当x ∈[－1，3]时，不等式－x 2＋2x ＋a ＞0恒成立，求实数a 的取值范围.12．某大学印一份招生广告，所用纸张(矩形)的左右两边留有宽为4cm 的空白，上下留有都为6cm 的空白，中间排版面积为2400cm 2.如何选择纸张的尺寸，才能使纸的用量最小？测试十三 二元一次不等式(组)与简单的线性规划问题Ⅰ 学习目标1．了解二元一次不等式的几何意义，能用平面区域表示二元一次不等式组. 2．会从实际情境中抽象出一些简单的二元线性规划问题，并能加以解决.Ⅱ 基础训练题一、选择题1．已知点A (2，0)，B (－1，3)及直线l ：x －2y ＝0，那么( ) (A)A ，B 都在l 上方 (B)A ，B 都在l 下方 (C)A 在l 上方，B 在l 下方 (D)A 在l 下方，B 在l 上方 2．在平面直角坐标系中，不等式组⎪⎩⎪⎨⎧≤+≥≥2,0,0y x y x 所表示的平面区域的面积为( )(A)1 (B)2 (C)3 (D)43．三条直线y ＝x ，y ＝－x ，y ＝2围成一个三角形区域，表示该区域的不等式组是( )(A)⎪⎩⎪⎨⎧≤-≥≥.2,,y x y x y(B)⎪⎩⎪⎨⎧≤-≤≤.2,,y x y x y(C)⎪⎩⎪⎨⎧≤-≥≤.2,,y x y x y(D)⎪⎩⎪⎨⎧≤-≤≥.2,,y x y x y4．若x ，y 满足约束条件⎪⎩⎪⎨⎧≤≥+≥+-,3,0,05x y x y x 则z ＝2x ＋4y 的最小值是( )(A)－6 (B)－10 (C)5 (D)105．某电脑用户计划使用不超过500元的资金购买单价分别为60元，70元的单片软件和盒装磁盘.根据需要，软件至少买3片，磁盘至少买2盒，则不同的选购方式共有( ) (A)5种 (B)6种 (C)7种 (D)8种 二、填空题6．在平面直角坐标系中，不等式组⎩⎨⎧<>00y x 所表示的平面区域内的点位于第________象限.7．若不等式|2x ＋y ＋m |＜3表示的平面区域包含原点和点(－1，1)，则m 的取值范围是________. 8．已知点P (x ，y )的坐标满足条件⎪⎩⎪⎨⎧≥-+≤≤,033,3,1y x y x 那么z ＝x －y 的取值范围是________.9．已知点P (x ，y )的坐标满足条件⎪⎩⎪⎨⎧≥-+≤≤,022,2,1y x y x 那么x y 的取值范围是________.10．方程|x |＋|y |≤1所确定的曲线围成封闭图形的面积是________. 三、解答题11．画出下列不等式(组)表示的平面区域：(1)3x ＋2y ＋6＞0 (2)⎪⎩⎪⎨⎧≥+--≥≤.01,2,1y x y x12．某实验室需购某种化工原料106kg ，现在市场上该原料有两种包装，一种是每袋35kg ，价格为140元；另一种是每袋24kg ，价格为120元.在满足需要的前提下，最少需要花费多少元？Ⅲ 拓展训练题13．商店现有75公斤奶糖和120公斤硬糖，准备混合在一起装成每袋1公斤出售，有两种混合办法：第一种每袋装250克奶糖和750克硬糖，每袋可盈利0.5元；第二种每袋装500克奶糖和500克硬糖，每袋可盈利0.9元.问每一种应装多少袋，使所获利润最大？最大利润是多少？14．甲、乙两个粮库要向A ，B 两镇运送大米，已知甲库可调出100吨，乙库可调出80吨，而A 镇需大米70吨，B 镇需大米110吨，两个粮库到两镇的路程和运费如下表：问：(1)这两个粮库各运往A 、B 两镇多少吨大米，才能使总运费最省？此时总运费是多少？(2)最不合理的调运方案是什么？它给国家造成不该有的损失是多少？测试十四 不等式全章综合练习Ⅰ基础训练题一、选择题1．设a ，b ，c ∈R ，a ＞b ，则下列不等式中一定正确的是( ) (A)ac 2＞bc 2(B)ba 11< (C)a －c ＞b －c (D)|a |＞|b |2．在平面直角坐标系中，不等式组⎪⎩⎪⎨⎧≥≥+-≤-+2,042,04y y x y x 表示的平面区域的面积是( )(A)23 (B)3 (C)4 (D)6 3．某房地产公司要在一块圆形的土地上，设计一个矩形的停车场.若圆的半径为10m ，则这个矩形的面积最大值是( ) (A)50m 2 (B)100m 2 (C)200m 2 (D)250m 2 4．设函数f (x )＝222x x x +-，若对x ＞0恒有xf (x )＋a ＞0成立，则实数a 的取值范围是( )(A)a ＜1－22(B)a ＜22－1(C)a ＞22－1(D)a ＞1－22 5．设a ，b ∈R ，且b (a ＋b ＋1)＜0，b (a ＋b －1)＜0，则( ) (A)a ＞1 (B)a ＜－1 (C)－1＜a ＜1 (D)|a |＞1二、填空题6．已知1＜a ＜3，2＜b ＜4，那么2a －b 的取值范围是________，ba 的取值范围是________. 7．若不等式x 2－ax －b ＜0的解集为{x |2＜x ＜3}，则a ＋b ＝________.8．已知x ，y ∈R ＋，且x ＋4y ＝1，则xy 的最大值为________. 9．若函数f (x )＝1222--⋅+aax x的定义域为R ，则a 的取值范围为________.10．三个同学对问题“关于x 的不等式x 2＋25＋|x 3－5x 2|≥ax 在[1，12]上恒成立，求实数a的取值范围”提出各自的解题思路. 甲说：“只须不等式左边的最小值不小于右边的最大值.”乙说：“把不等式变形为左边含变量x 的函数，右边仅含常数，求函数的最值.” 丙说：“把不等式两边看成关于x 的函数，作出函数图象.” 参考上述解题思路，你认为他们所讨论的问题的正确结论，即a 的取值范围是________. 三、解答题11．已知全集U ＝R ，集合A ＝{x | |x －1|＜6}，B ＝{x |128--x x ＞0}. (1)求A ∩B ； (2)求(U A )∪B .12．某工厂用两种不同原料生产同一产品，若采用甲种原料，每吨成本1000元，运费500元，可得产品90千克；若采用乙种原料，每吨成本1500元，运费400元，可得产品100千克.今预算每日原料总成本不得超过6000元，运费不得超过2000元，问此工厂每日采用甲、乙两种原料各多少千克，才能使产品的日产量最大？Ⅱ 拓展训练题13．已知数集A ＝{a 1，a 2，…，a n }(1≤a 1＜a 2＜…＜a n ，n ≥2)具有性质P ：对任意的i ，j (1≤i ≤j ≤n )，a i a j 与ij a a 两数中至少有一个属于A .(1)分别判断数集{1，3，4}与{1，2，3，6}是否具有性质P ，并说明理由； (2)证明：a 1＝1，且n nna a a a a a a =++++++---1121121 .测试十五 必修5模块自我检测题一、选择题1．函数42-=x y 的定义域是( )(A)(－2，2) (B)(－∞，－2)∪(2，＋∞) (C)[－2，2] (D)(－∞，－2]∪[2，＋∞) 2．设a ＞b ＞0，则下列不等式中一定成立的是( ) (A)a －b ＜0 (B)0＜ba＜1 (C)ab ＜2ba +(D)ab ＞a ＋b3．设不等式组⎪⎩⎪⎨⎧≥-≥≤0,0,1y x y x 所表示的平面区域是W ，则下列各点中，在区域W 内的点是( )(A))31,21((B))31,21(-(C))31,21(-- (D))31,21(-4．设等比数列{a n }的前n 项和为S n ，则下列不等式中一定成立的是( ) (A)a 1＋a 3＞0 (B)a 1a 3＞0 (C)S 1＋S 3＜0 (D)S 1S 3＜05．在△ABC 中，三个内角A ，B ，C 的对边分别为a ，b ，c ，若A ∶B ∶C ＝1∶2∶3，则a ∶b ∶c 等于( ) (A)1∶3∶2(B)1∶2∶3(C)2∶3∶1(D)3∶2∶16．已知等差数列{a n }的前20项和S 20＝340，则a 6＋a 9＋a 11＋a 16等于( ) (A)31 (B)34 (C)68 (D)70 7．已知正数x 、y 满足x ＋y ＝4，则log 2x ＋log 2y 的最大值是( ) (A)－4 (B)4 (C)－2 (D)28．如图，在限速为90km/h 的公路AB 旁有一测速站P ，已知点P 距测速区起点A 的距离为0.08 km ，距测速区终点B 的距离为0.05 km ，且∠APB ＝60°.现测得某辆汽车从A 点行驶到B 点所用的时间为3s ，则此车的速度介于()(A)60～70km/h (B)70～80km/h (C)80～90km/h (D)90～100km/h 二、填空题9．不等式x (x －1)＜2的解集为________.10．在△ABC 中，三个内角A ，B ，C 成等差数列，则cos(A ＋C )的值为________. 11．已知{a n }是公差为－2的等差数列，其前5项的和S 5＝0，那么a 1等于________.12．在△ABC 中，BC ＝1，角C ＝120°，cos A ＝32，则AB ＝________. 13．在平面直角坐标系中，不等式组⎪⎩⎪⎨⎧≤-+≤-+≥≥030420,0y x y x y x ，所表示的平面区域的面积是________；变量z ＝x ＋3y 的最大值是________.14．如图，n 2(n ≥4)个正数排成n 行n 列方阵，符号a ij (1≤i ≤n ，1≤j ≤n ，i ，j ∈N )表示位于第i 行第j 列的正数.已知每一行的数成等差数列，每一列的数成等比数列，且各列数的公比都等于q .若a 11＝21，a 24＝1，a 32＝41，则q ＝________；a ij ＝________.三、解答题15．已知函数f (x )＝x 2＋ax ＋6.(1)当a ＝5时，解不等式f (x )＜0；(2)若不等式f (x )＞0的解集为R ，求实数a 的取值范围.16．已知{a n }是等差数列，a 2＝5，a 5＝14.(1)求{a n }的通项公式；(2)设{a n }的前n 项和S n ＝155，求n 的值.17．在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，A ，B 是锐角，c ＝10，且34c o s c o s ==a b B A . (1)证明角C ＝90°；(2)求△ABC 的面积.18．某厂生产甲、乙两种产品，生产这两种产品每吨所需要的煤、电以及每吨产品的产值如下表所示.若每天配给该厂的煤至多56吨，供电至多45千瓦，问该厂如何安排生产，19．在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，且cos A ＝31.(1)求A CB 2cos 2sin 2++的值； (2)若a ＝3，求bc 的最大值.20．数列{a n }的前n 项和是S n ，a 1＝5，且a n ＝S n －1(n ＝2，3，4，…).(1)求数列{a n }的通项公式；(2)求证：⋅<++++531111321n a a a a参考答案第一章 解三角形测试一 正弦定理和余弦定理一、选择题1．B 2．C 3．B 4．D 5．B 提示：4．由正弦定理，得sin C ＝23，所以C ＝60°或C ＝120°， 当C ＝60°时，∵B ＝30°，∴A ＝90°，△ABC 是直角三角形； 当C ＝120°时，∵B ＝30°，∴A ＝30°，△ABC 是等腰三角形. 5．因为A ∶B ∶C ＝1∶2∶3，所以A ＝30°，B ＝60°，C ＝90°，由正弦定理CcB b A a sin sin sin ==＝k ， 得a ＝k ·sin30°＝21k ，b ＝k ·sin60°＝23k ，c ＝k ·sin90°＝k ，所以a ∶b ∶c ＝1∶3∶2. 二、填空题6．362 7．30° 8．等腰三角形 9．2373+ 10．425 提示：8．∵A ＋B ＋C ＝π，∴－cos A ＝cos(B ＋C ).∴2cos B cos C ＝1－cos A ＝cos(B ＋C )＋1， ∴2cos B cos C ＝cos B cos C －sin B sin C ＋1，∴cos(B －C )＝1，∴B －C ＝0，即B ＝C . 9．利用余弦定理b 2＝a 2＋c 2－2ac cos B . 10．由tan A ＝2，得52sin =A ，根据正弦定理，得ABC B AC sin sin =，得AC ＝425. 三、解答题11．c ＝23，A ＝30°，B ＝90°. 12．(1)60°；(2)AD ＝7. 13．如右图，由两点间距离公式，得OA ＝29)02()05(22=-+-，同理得232,145==AB OB .由余弦定理，得cos A ＝222222=⨯⨯-+AB OA OB AB OA ， ∴A ＝45°.14．(1)因为2cos(A ＋B )＝1，所以A ＋B ＝60°，故C ＝120°.(2)由题意，得a ＋b ＝23，ab ＝2，又AB 2＝c 2＝a 2＋b 2－2ab cos C ＝(a ＋b )2－2ab －2ab cos C＝12－4－4×(21-)＝10. 所以AB ＝10. (3)S △ABC ＝21ab sin C ＝21·2·23＝23.测试二 解三角形全章综合练习1．B 2．C 3．D 4．C 5．B 提示：5．化简(a ＋b ＋c )(b ＋c －a )＝3bc ，得b 2＋c 2－a 2＝bc ， 由余弦定理，得cos A ＝212222=-+bc a c b ，所以∠A ＝60°.因为sin A ＝2sin B cos C ，A ＋B ＋C ＝180°， 所以sin(B ＋C )＝2sin B cos C ，即sin B cos C ＋cos B sin C ＝2sin B cos C . 所以sin(B －C )＝0，故B ＝C . 故△ABC 是正三角形. 二、填空题6．30° 7．120° 8．524 9．55 10．3三、解答题11．(1)由余弦定理，得c ＝13；(2)由正弦定理，得sin B ＝13392. 12．(1)由a ·b ＝|a |·|b |·cos 〈a ，b 〉，得〈a ，b 〉＝60°；(2)由向量减法几何意义，知|a |，|b |，|a －b |可以组成三角形，所以|a －b |2＝|a |2＋|b |2－2|a |·|b |·cos 〈a ，b 〉＝7，故|a －b |＝7.13．(1)如右图，由两点间距离公式，得29)02()05(22=-+-=OA ， 同理得232,145==AB OB . 由余弦定理，得,222cos 222=⨯⨯-+=AB OA OB AB OA A所以A ＝45°.故BD ＝AB ×sin A ＝229.(2)S △OAB ＝21·OA ·BD ＝21·29·229＝29. 14．由正弦定理R CcB b A a 2sin sin sin ===，得C Rc B R b A R a sin 2,sin 2,sin 2===. 因为sin 2A ＋sin 2B ＞sin 2C ，所以222)2()2()2(R cR b R a >+， 即a 2＋b 2＞c 2. 所以cos C ＝abc b a 2222-+＞0， 由C ∈(0，π)，得角C 为锐角.15．(1)设t 小时后甲、乙分别到达P 、Q 点，如图，则|AP |＝4t ，|BQ |＝4t ，因为|OA |＝3，所以t ＝43h 时，P 与O 重合. 故当t ∈[0，43]时， |PQ |2＝(3－4t )2＋(1＋4t )2－2×(3－4t )×(1＋4t )×cos60°； 当t ＞43h 时，|PQ |2＝(4t －3)2＋(1＋4t )2－2×(4t －3)×(1＋4t )×cos120°. 故得|PQ |＝724482+-t t (t ≥0).(2)当t ＝h 4148224=⨯--时，两人距离最近，最近距离为2km . 16．(1)由正弦定理R CcB b A a 2sin sin sin ===， 得a ＝2R sin A ，b ＝2R sin B ，c ＝2R sinC . 所以等式c a b C B +-=2cos cos 可化为CR A R BR C B sin 2sin 22sin 2cos cos +⋅-=， 即CA BC B sin sin 2sin cos cos +-=， 2sin A cos B ＋sin C cos B ＝－cos C ·sin B ，故2sin A cos B ＝－cos C sin B －sin C cos B ＝－sin(B ＋C )， 因为A ＋B ＋C ＝π，所以sin A ＝sin(B ＋C )， 故cos B ＝－21， 所以B ＝120°.(2)由余弦定理，得b 2＝13＝a 2＋c 2－2ac ×cos120°， 即a 2＋c 2＋ac ＝13 又a ＋c ＝4， 解得⎩⎨⎧==31c a ，或⎩⎨⎧==13c a .所以S △ABC ＝21ac sin B ＝21×1×3×23＝433.第二章 数列测试三 数列一、选择题1．C 2．B 3．C 4．C 5．B 二、填空题6．(1)12+=n a n (或其他符合要求的答案) (2)2)1(1n n a -+=(或其他符合要求的答案)7．(1)2625,1716,109,54,21 (2)7 8．67 9．151 10．4提示：9．注意a n 的分母是1＋2＋3＋4＋5＝15.10．将数列{a n }的通项a n 看成函数f (n )＝2n 2－15n ＋3，利用二次函数图象可得答案. 三、解答题11．(1)数列{a n }的前6项依次是11，8，5，2，－1，－4；(2)证明：∵n ≥5，∴－3n ＜－15，∴14－3n ＜－1， 故当n ≥5时，a n ＝14－3n ＜0.12．(1)31,313,31092421102-+=++==+n n a n n a a n n ；(2)7932是该数列的第15项. 13．(1)因为a n ＝n －n1，所以a 1＝0，a 2＝23，a 3＝38，a 4＝415；(2)因为a n ＋1－a n ＝[(n ＋1)11+-n ]－(n －n1)＝1＋)1(1+n n又因为n ∈N ＋，所以a n ＋1－a n ＞0，即a n ＋1＞a n .所以数列{a n }是递增数列.测试四 等差数列一、选择题1．B 2．D 3．A 4．B 5．B 二、填空题6．a 4 7．13 8．6 9．6n －1 10．35 提示：10．方法一：求出前10项，再求和即可；方法二：当n 为奇数时，由题意，得a n ＋2－a n ＝0，所以a 1＝a 3＝a 5＝…＝a 2m －1＝1(m ∈N *).当n 为偶数时，由题意，得a n ＋2－a n ＝2，即a 4－a 2＝a 6－a 4＝…＝a 2m ＋2－a 2m ＝2(m ∈N *). 所以数列{a 2m }是等差数列.故S 10＝5a 1＋5a 2＋2)15(5-⨯×2＝35. 三、解答题11．设等差数列{a n }的公差是d ，依题意得⎪⎩⎪⎨⎧=⨯+=+.242344,7211d a d a 解得⎩⎨⎧==.2,31d a ∴数列{a n }的通项公式为a n ＝a 1＋(n －1)d ＝2n ＋1. 12．(1)设等差数列{a n }的公差是d ，依题意得⎩⎨⎧=+=+.5019,30911d a d a 解得⎩⎨⎧==.2,121d a ∴数列{a n }的通项公式为a n ＝a 1＋(n －1)d ＝2n ＋10.(2)数列{a n }的前n 项和S n ＝n ×12＋2)1(-⨯n n ×2＝n 2＋11n ， ∴S n ＝n 2＋11n ＝242，解得n ＝11，或n ＝－22(舍).13．(1)通项a n ＝a 1＋(n －1)d ＝50＋(n －1)×(－0.6)＝－0.6n ＋50.6.解不等式－0.6n ＋50.6＜0，得n ＞84.3. 因为n ∈N *，所以从第85项开始a n ＜0.(2)S n ＝na 1＋2)1(-n n d ＝50n ＋2)1(-n n ×(－0.6)＝－0.3n 2＋50.3n .由(1)知：数列{a n }的前84项为正值，从第85项起为负值， 所以(S n )max ＝S 84＝－0.3×842＋50.3×84＝2108.4.。