2018年高考数学二轮复习专题对点练511-16组合练理!

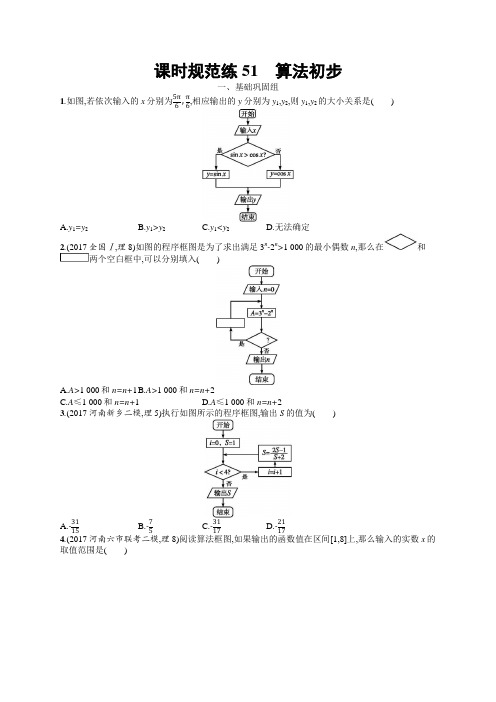
课时规范练51算法初步一、基础巩固组1.如图,若依次输入的x分别为5π,π,相应输出的y分别为y1,y2,则y1,y2的大小关系是()A.y1=y2B.y1>y2C.y1<y2D.无法确定2.(2017全国Ⅰ,理8)如图的程序框图是为了求出满足3n-2n>1 000的最小偶数n,那么在和两个空白框中,可以分别填入()A.A>1 000和n=n+1B.A>1 000和n=n+2C.A≤1 000和n=n+1D.A≤1 000和n=n+23.(2017河南新乡二模,理5)执行如图所示的程序框图,输出S的值为()A.-31B.-7C.-31D.-214.(2017河南六市联考二模,理8)阅读算法框图,如果输出的函数值在区间[1,8]上,那么输入的实数x的取值范围是()A.[0,2)B.[2,7]C.[2,4]D.[0,7]5.执行如图所示的程序框图,如果输入的x,y∈R,那么输出的S的最大值为()A.0B.1C.2D.36.(2017山西晋中一模,理5)执行如图的程序框图,则输出K的值为()A.98B.99C.100D.101 〚导学号21500577〛8.(2017山东,理6)执行两次下图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为()A.0,0B.1,1C.0,1D.1,0 〚导学号21500578〛9.(2017河南焦作二模,理6改编)执行如图所示的程序框图,若输入m=4,t=3,则输出y=.11.(2017北京东城区二模,理6)我国南宋时期的数学家秦九韶(约1202-1261)在他的著作《数书九章》中提出了多项式求值的秦九韶算法.如图所示的算法框图给出了利用秦九韶算法求多项式的一个实例.若输入的n=5,v=1,x=2,则程序框图计算的是()A.25+24+23+22+2+1B.25+24+23+22+2+5C.26+25+24+23+22+2+1D.24+23+22+2+1C.-17,7D.7,-17 〚导学号21500579〛13.(2017河北保定二模,理7)某地区出租车收费办法如下:不超过2公里收7元;超过2公里时,每车收燃油附加费1元,并且超过的里程每公里收2.6元(其他因素不考虑),计算收费标准的程序框图如图所示,则①处应填()A.y=2.0x+2.2B.y=0.6x+2.8C.y=2.6x+2.0D.y=2.6x+2.814.阅读如图所示的程序框图,运行相应的程序,则输出S的值为.三、创新应用组15.(2017河南郑州一中质检一,理5)我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为521,则由此可估计π的近似值为()A.3.119B.3.126C.3.132D.3.151 〚导学号21500580〛 16.(2017山西晋中二模,理7)执行如图程序框图,已知输出的s ∈[0,4],若输入的t ∈[m ,n ],则实数n-m 的最大值为( )A.1B.2C.3D.4课时规范练51 算法初步1.C 由程序框图可知,当输入的x 为5π6时,sin 5π6>cos 5π6成立,所以输出的y 1=sin 5π6=12;当输入的x 为π6时,sin π6>cos π6不成立,所以输出的y 2=cos π6=32,所以y 1<y 2.2.D 因为要求A 大于1000时输出,且程序框图中在“否”时输出,所以“”中不能填入A>1000,排除A,B .又要求n 为偶数,且n 初始值为0,所以“”中n 依次加2可保证其为偶数,故选D .3.C 程序运行如下:i=0,S=1;满足条件i<4,执行循环体,i=1,S=13; 满足条件i<4,执行循环体,i=2,S=-17;满足条件i<4,执行循环体,i=3,S=-913;满足条件i<4,执行循环体,i=4,S=-3117,不满足条件i<4,退出循环,输出S 的值为-3117.故选C .4.D 根据题意,得当x ∈(-2,2)时,f (x )=2x ,∴1≤2x ≤8,∴0≤x ≤3;当x 不在(-2,2)时,f (x )=x+1, ∴1≤x+1≤8,∴0≤x ≤7, ∴x 的取值范围是[0,7].5.C 先画出x ,y 满足的约束条件 x ≥0,y ≥0,x +y ≤1对应的可行域如图中的阴影部分.平移直线l 0:y=-2x.当直线经过点A (1,0)时,y=-2x+S 中截距S 最大,此时S max =2×1+0=2. 与x ≥0,y ≥0,x+y ≤1不成立时S=1进行比较,可得S max =2. 6.B 程序运行如下:K=1,S=0,S=lg2;不满足条件S ≥2,执行循环体,K=2,S=lg2+lg 32=lg3, 不满足条件S ≥2,执行循环体,K=3,S=lg3+lg 43=lg4;…… 观察规律,可得不满足条件S ≥2,执行循环体,K=99,S=lg99+lg10099=lg100=2, 满足条件S ≥2,退出循环,输出K 的值为99.7.A ∵f (x )= (x +1)2,x <0,(x -1)2,x ≥0,∴当x<0时,令(x+1)2=16,解得x=-5; 当x ≥0时,令(x-1)2=16, 解得x=5,故x=±5.8.D 若输入x=7,则b=2(b 2<x ,且x 不能被b 整除)→b=3(b 2>x )→输出a=1;若输入x=9,则b=2(b 2<x ,且x 不能被b 整除)→b=3(b 2=x ,但x 能被b 整除)→输出a=0.故选D . 9.183 运行程序如下:m=4,t=3,y=1,i=3;满足条件i ≥0,执行循环体,y=6,i=2; 满足条件i ≥0,执行循环体,y=20,i=1; 满足条件i ≥0,执行循环体,y=61,i=0; 满足条件i ≥0,执行循环体,y=183,i=-1;不满足条件i ≥0,退出循环,输出y 的值为183.10.3 ∵a=2,b=3,∴a<b ,应把b 的值赋给m ,∴m 的值为3. 11.A n=5,v=1,x=2,i=4,满足条件i ≥0,执行循环体,v=1×2+1=3,i=3; 满足条件i ≥0,执行循环体,v=3×2+1=7,i=2; 满足条件i ≥0,执行循环体,v=7×2+1=15,i=1; 满足条件i ≥0,执行循环体,v=15×2+1=31,i=0; 满足条件i ≥0,执行循环体,v=31×2+1=63,i=-1,不满足条件i ≥0,退出循环,输出v 的值为63,故选A .12.A 因为x<0,所以x=y+3=18,即此时x=18,y=15,输出x-y ,x+y ,即3,33,所以输出的结果为3,33,故选A .13.D 当满足条件x>2时,即里程超过2公里.里程超过2公里时,每车收燃油附加费1元,并且超过的里程每公里收2.6元,即y=2.6(x-2)+7+1=8+2.6(x-2),整理可得y=2.6x+2.8.故选D .14.4 第一次循环:S=8,n=2;第二次循环:S=2,n=3;第三次循环:S=4,n=4,满足条件n>3,结束循环,输出S=4.15.B x 2+y 2+z 2<1表示空间直角坐标系中点(x ,y ,z )到原点的距离小于1,满足x 2+y 2+z 2<1的点在以原点为球心,半径为1的球内.因为x ,y ,z ∈(0,1),所以点(x ,y ,z )落在第一象限内的18球内,它发生的概率为4π3×13×1813=π6.当输出结果为521时,i=1001,m=521,x 2+y 2+z 2<1发生的概率为P=5211000,故5211000≈π6,解得π≈3.126.16.D 由题意,得程序框图的功能是计算并输出分段函数S= 3t ,t <1,4t -t 2,t ≥1的函数值,作出该函数的图象,由题意可得输出的s ∈[0,4],当m=0时,n ∈[2,4],n-m ∈[2,4]; 当n=4时,m ∈[0,2],n-m ∈[2,4]. 所以实数n-m 的最大值为4.。

专题对点练2函数与方程思想、数形结合思想专题对点练第2页一、选择题1.设a>1,若对于任意的x∈[a,2a],都有y∈[a,a2]满足方程log a x+log a y=3,这时a的取值的集合为()A.{a|1<a≤2}B.{a|a≥2}C.{a|2≤a≤3}D.{2,3}答案B解析依题意得y=错误!未找到引用源。

,当x∈[a,2a]时,y=错误!未找到引用源。

.由题意可知错误!未找到引用源。

⊆[a,a2],即有错误!未找到引用源。

a2≥a,又a>1,所以a≥2.故选B.2.椭圆错误!未找到引用源。

+y2=1的两个焦点为F1,F2,过F1作垂直于x轴的直线与椭圆相交,其一交点为P,则|PF2|=()A.错误!未找到引用源。

B.错误!未找到引用源。

C.错误!未找到引用源。

D.4答案C解析如图,令|F1P|=r1,|F2P|=r2,则错误!未找到引用源。

故r2=错误!未找到引用源。

.3.若关于x的方程2sin错误!未找到引用源。

=m在错误!未找到引用源。

上有两个不等实根,则m的取值范围是()A.(1,错误!未找到引用源。

)B.[0,2]C.[1,2)D.[1,错误!未找到引用源。

]答案C解析方程2sin错误!未找到引用源。

=m可化为sin错误!未找到引用源。

, 当x∈错误!未找到引用源。

时,2x+错误!未找到引用源。

,画出函数y=f(x)=sin错误!未找到引用源。

在x∈错误!未找到引用源。

上的图象如图所示:由题意,得错误!未找到引用源。

<1,则m的取值范围是[1,2),故选C.4.函数f(x)是定义在区间(0,+∞)上的可导函数,其导函数为f'(x),且满足xf'(x)+2f(x)>0,则不等式错误!未找到引用源。

的解集为()A.{x|x>-2 011}B.{x|x<-2 011}C.{x|-2 016<x<-2 011}D.{x|-2 011<x<0}答案C解析由xf'(x)+2f(x)>0,则当x∈(0,+∞)时,x2f'(x)+2xf(x)>0,即[x2f(x)]'=x2f'(x)+2xf(x),所以函数x2f(x)为单调递增函数,由错误!未找到引用源。

题型专项训练2选择填空题组合特训(二)(时间:60分钟满分:100分)一、选择题(本大题共8小题,每小题8分,共64分)1.已知全集U=R,A={x|x2-2x<0},B={x|x≥1},则A∪(∁U B)=()A.(0,+∞)B.(-∞,1)C.(-∞,2)D.(0,1)2.椭圆=1的焦距为2,则m的值等于()A.5或-3B.2或6C.5或3 D3.已知一几何体的三视图如图所示,则该几何体的体积为()A B+1C D4.已知x,y满足约束条件则z=3x+y的取值范围为()A.[6,10]B.(-2,10]C.(6,10]D.[-2,10)5.(2017浙江宁波十校联考)已知a,b∈R,则“|a|+|b|>1”是“b<-1”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件6.已知函数f(x)=x2+cos x,f'(x)是函数f(x)的导函数,则f'(x)的图象大致是()7.已知随机变量ξ+η=8,若ξ~B(10,0.4),则E(η),D(η)分别是()A.4和2.4B.2和2.4C.6和2.4D.4和5.68.如图所示,在直三棱柱ABC-A1B1C1中,AB=AA1=2,∠ABC=90°,点E,F分别是棱AB,BB1的中点,当二面角C1-AA1-B为45°时,直线EF和BC1所成的角为()A.45°B.60°C.90°D.120°二、填空题(本大题共6小题,每小题6分,共36分)9.“斐波那契”数列由十三世纪意大利数学家斐波那契发现.数列中的一系列数字常被人们称之为神奇数.具体数列为:1,1,2,3,5,8,…,即从该数列的第三项开始,每个数字等于前两个相邻数字之和.已知数列{a n}为“斐波那契”数列,S n为数列{a n}的前n项和,则S7=.10.复数z=(1+2i)(3-i),其中i为虚数单位,则z的实部是,|z|=.11.若x10-x5=a0+a1(x-1)+a2(x-1)2+…+a10(x-1)10,则a0=,a5=.12.△ABC中,内角A,B,C的对边分别为a,b,c,且b sin A=a cos B,b=3,sin C=2sin A,则a+c=,△ABC面积为.13.(2017浙江杭州高级中学模拟)若向量a,b满足|a|=|2a+b|=2,则a在b方向上投影的最大值是,此时a与b夹角为.14.某科室派出4名调研员到3个学校调研该校高三复习备考近况,要求每个学校至少一名,则不同的分配方案种数为.参考答案题型专项训练2选择填空题组合特训(二)1.C解析由题意得,集合A={x|x2-2x<0}={x|0<x<2},B={x|x≥1},所以∁U B={x|x<1},所以A∪(∁U B)={x|x<2},故选C.2.B解析假设椭圆的焦点在x轴上,则m>4,由焦距2c=2,c=,则c2=m-4,解得m=6,当椭圆的焦点在y轴上时,即0<m<4,由焦距2c=2,c=,则c2=4-m,解得m=2,故m的值为2或6,故选B.3.C解析观察三视图可知,几何体是一个圆锥的与三棱锥的组合体,其中圆锥的底面半径为1,高为1.三棱锥的底面是两直角边分别为1,2的直角三角形,高为1.则几何体的体积V=×π×12×1+×1×2×1=.故选C.4.B解析由约束条件作出可行域如图,化目标函数为y=-3x+z,由图可知,当直线y=-3x+z过点A时,z取最大值,由得A(4,-2),此时z max=3×4-2=10;当直线y=-3x+z过点B时,z取最小值,由解得B(0,-2),故z=-2.综上,z=3x+y的取值范围为(-2,10].5.B解析当a=2,b=0时,满足|a|+|b|>1,但b<-1不成立,即充分性不成立;若b<-1,则|b|>1,则|a|+|b|>1恒成立,即必要性成立.则“|a|+|b|>1”是“b<-1”的必要不充分条件,故选B.6.A解析由于f(x)=x2+cos x,∴f'(x)=x-sin x,∴f'(-x)=-f'(x),故f'(x)为奇函数,其图象关于原点对称,排除B,D;又当x=时,f'-sin-1<0,排除C,只有A适合,故选A.7.A解析∵ξ~B(10,0.4),∴E(ξ)=10×0.4=4,D(ξ)=10×0.4×0.6=2.4,∵η=8-ξ,∴E(η)=E(8-ξ)=4,D(η)=D(8-ξ)=2.4,故选A.8.B解析如图,因为三棱柱ABC-A1B1C1是直三棱柱,∴AA1⊥平面A1B1C1,则A1C1⊥AA1,A1B1⊥AA1,∴∠B1A1C1为二面角C1-AA1-B的平面角,等于45°,∵A1B1=AB=2,∴B1C1=BC=2,以B为原点,分别以BC,BA,BB1所在直线为x,y,z轴建立空间直角坐标系,则B(0,0,0),E(0,1,0),C1(2,0,2),F(0,0,1),∴=(2,0,2),=(0,-1,1),∴cos<>=, ∴的夹角为60°,即直线EF和BC1所成的角为60°,故选B.9.33解析由题意S7=1+1+2+3+5+8+13=33.10.55解析z=(1+2i)(3-i)=5+5i.故实部为5,模为5.11.0251解析当x=1时,可得a0=0,x10-x5=[(x-1)+1]10-[(x-1)+1]5,所以a5==251.12.3解析由b sin A=a cos B及正弦定理,得sin B sin A=sin A cos B,∵A为三角形的内角,∴sin A≠0,∴sin B=cos B,即tan B=,又B为三角形的内角,∴B=;由sin C=2sin A及正弦定理,得c=2a,①∵b=3,cos B=,∴由b2=a2+c2-2ac cos B,得9=a2+c2-ac,②联立①②解得a=,c=2,∴a+c=3.面积S=ac sin B=×2.13.- 解析∵|2a+b|=2,|a|=2,∴|b|2+4a·b+16=4,设a,b的夹角为θ,则|b|2+8|b|cos θ+12=0.∴cos θ=-.∴a在b方向上投影为|a|cos θ=-=-.∵≥2,当且仅当|b|=时等号成立,∴|a|cos θ≤-.所以a在b方向上投影最大值是-,cos θ=-,θ=.14.36解析分两步完成:第一步将4名调研员按2,1,1分成三组,其分法有种;第二步将分好的三组分配到三个学校,其分法有种,所以不同的分配方案种数为=36种,故填36.。

专题对点练9 2.1~2.4组合练(限时90分钟,满分100分)一、选择题(共9小题,满分45分)1.设函数f(x)=则f(f(e))=()A.0B.1C.2D.ln(e2+1)答案 C解析f(e)=ln e=1,所以f(f(e))=f(1)=12+1=2.故选C.2.(2017河南新乡二模,理4)设a=60.4,b=log0.40.5,c=log80.4,则a,b,c的大小关系是()A.a<b<cB.c<b<aC.c<a<bD.b<c<a答案 B解析∵a=60.4>1,b=log0.40.5∈(0,1),c=log80.4<0,∴a>b>c.3.已知函数y=log a(x+c)(a,c为常数,其中a>0,a≠1)的图象如图所示,则下列结论成立的是()A.a>1,c>1B.a>1,0<c<1C.0<a<1,c>1D.0<a<1,0<c<1答案 D解析∵函数单调递减,∴0<a<1,当x=1时,y=log a(1+c)<0,即1+c>1,即c>0,当x=0时,log a(x+c)=log a c>0,即c<1,即0<c<1,故选D.4.(2017山东潍坊二模,理4)函数f(x)=lo cos x<x<的图象大致是()答案 C解析-<x<时,y=cos x是偶函数,并且y=cos x∈(0,1],函数f(x)=lo cos x是偶函数,cos x∈(0,1]时,f(x)≥0.∴四个选项,只有C满足题意.故选C.5.函数y=1+log0.5(x-1)的图象一定经过点()A.(1,1)B.(1,0)C.(2,1)D.(2,0)答案 C解析∵函数y=log0.5x恒过定点(1,0),而y=1+log0.5(x-1)的图象是由y=log0.5x的图象向右平移一个单位,向上平移一个单位得到,∴定点(1,0)平移以后即为定点(2,1),故选C.6.若函数f(x)=的值域为[-1,1],则实数a的取值范围是()A.[1,+∞)B.(-∞,-1]C.(0,1]D.(-1,0)答案 A解析函数f(x)=的值域为[-1,1],当x≤a时,f(x)=cos x∈[-1,1],满足题意;当x>a时,f(x)=∈[-1,1],应满足0<≤1,解得x≥1.∴a的取值范围是[1,+∞).7.已知函数f(x)=,则()A.∃x0∈R,使得f(x)<0B.∀x∈(0,+∞),f(x)≥0C.∃x1,x2∈[0,+∞),使得<0D.∀x1∈[0,+∞),∃x2∈[0,+∞),使得f(x1)>f(x2)答案 B解析由函数f(x)=,知在A中f(x)≥0恒成立,故A错误,B正确;又f(x)=在[0,+∞)上是递增函数,故C错误;在D中,当x1=0时,不存在x2∈[0,+∞)使得f(x1)>f(x2),故D不成立.故选B.8.已知函数f(x)为偶函数,当x≤0时,f(x)为增函数,则“<x<2”是“f[log2(2x-2)]>f”的() 〚导学号16804176〛A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案 D解析由f(x)是偶函数且当x≤0时,f(x)为增函数,则x>0时,f(x)是减函数,故由“f[log2(2x-2)]>f”,得|log2(2x-2)|<=log2,故0<2x-2<,解得1<x<,故“<x<2”是“1<x<”的既不充分也不必要条件,故选D.9.(2017山东烟台一模,理10)已知f(x)=若不等式f(x-1)≥f(x)对一切x∈R恒成立,则实数a的最大值为()〚导学号16804177〛A.B.-1 C.-D.1答案 B解析作出函数f(x)和f(x-1)的图象,当a≥0时,f(x-1)≥f(x)对一切x∈R不恒成立(如图1).图1图2当a<0时,f(x-1)过定点(1,0)(如图2),当x>0时,f(x)=ax2+x的两个零点为x=0和x=-,要使不等式f(x-1)≥f(x)对一切x∈R恒成立,则只需要-≤1,得a≤-1,即a的最大值为-1.二、填空题(共3小题,满分15分)10.已知x≥0,y≥0,且x+y=1,则x2+y2的取值范围是.答案解析x2+y2=x2+(1-x)2=2x2-2x+1,x∈[0,1],所以当x=0或1时,x2+y2取最大值1;当x=时,x2+y2取最小值.因此x2+y2的取值范围为.11.(2017山东潍坊二模,理5改编)已知二次函数f(x)=ax2-2x+c的值域为[0,+∞),则的最小值为.答案 6解析二次函数f(x)=ax2-2x+c的值域为[0,+∞),可得判别式Δ=4-4ac=0,即有ac=1,且a>0,c>0,可得≥2=2×3=6,当且仅当,即有c=,a=3时,取得最小值6.12.对于函数y=f(x),若其定义域内存在不同实数x1,x2,使得x i f(x i)=1(i=1,2)成立,则称函数f(x)具有性质P,若函数f(x)=具有性质P,则实数a的取值范围为.〚导学号16804178〛答案解析由题意知,若f(x)具有性质P,则在定义域内xf(x)=1有两个不同的实数根,∵f(x)=,∴x·=1,即方程x e x=a在R上有两个不同的实数根,设g(x)=x e x,则g'(x)=e x+x e x=(1+x)e x,由g'(x)=0,得x=-1,∴g(x)在(-∞,-1)上递减,在(-1,+∞)上递增,∴当x=-1时,g(x)取到最小值是g(-1)=-,∵x<0,g(x)<0,x>0,g(x)>0,∴当方程x e x=a在R上有两个不同的实数根时,即函数g(x)与y=a的图象有两个交点,由图得-<a<0,∴实数a的取值范围为.三、解答题(共3个题,分别满分为13分,13分,14分)13.(2017辽宁沈阳三模,理21)已知f(x)=e x与g(x)=ax+b的图象交于P(x1,y1),Q(x2,y2)两点.(1)求函数h(x)=f(x)-g(x)的最小值;(2)若PQ的中点为M(x0,y0),求证:f(x0)<a<y0.(1)解h(x)=e x-ax-b,求导得h'(x)=e x-a.当a≤0时,h'(x)=e x-a>0,h(x)在R上为增函数,不满足有两个零点,故不符合题意, 所以a>0,令h'(x)=e x-a=0,解得x=ln a,并且有x∈(-∞,ln a),h'(x)<0;x∈(ln a,+∞),h'(x)>0,故h(x)min=h(ln a)=e ln a-a ln a-b=a-b-a ln a.(2)证明要证f(x0)<a<y0成立,即证,不妨设x2>x1,只需证,令t=x2-x1>0,即为,要证,只需证>t,令F(t)=-t,只需证F(t)>0,求导得F'(t)=-1=)-1>0,∴F(t)在(0,+∞)为增函数,故F(t)>F(0)=0,∴成立;要证,只需证明,令G(t)=,求导得G'(t)=<0,∴G(t)在(0,+∞)为减函数,故G(t)<G(0)=0,∴成立;∴(t>0)成立,即f(x0)<a<y0.14.(2017黑龙江大庆三模,理21)已知函数f(x)=2ln x+x2-ax.(1)当a=5时,求f(x)的单调区间;(2)设A(x1,y1),B(x2,y2)是曲线y=f(x)图象上的两个相异的点,若直线AB的斜率k>1恒成立,求实数a的取值范围;(3)设函数f(x)有两个极值点x1,x2,x1<x2且x2>e,若f(x1)-f(x2)≥m恒成立,求实数m的取值范围.解 (1)当a=5时,f(x)=2ln x+x2-5x,f'(x)=(x>0),令f'(x)>0,解得x>2或0<x<,令f'(x)<0,解得<x<2,∴f(x)的单调递增区间为,(2,+∞);f(x)的单调递减区间为.(2)由题意可知k=>1,∴>0,令g(x)=f(x)-x,则g(x)在(0,+∞)内单调递增,∴g'(x)=f'(x)-1≥0,∴-1≥0在(0,+∞)内恒成立,∴a≤2x+-1在(0,+∞)内恒成立,∵2x+≥4,x=1时取等号,∴a≤3.(3)∵x1+x2=,x1x2=1,∴a=2(x1+x2),x2=,∴f (x1)-f(x2)=(2ln x1+-ax1)-(2ln x2+-ax2)=+2ln ,令=x,则0<x<,h(x)=-x-2ln x,∴h'(x)=-<0,∴h(x)在上单调递减,∴h(x)>h=e2--4,∴m≤e2--4.15.(2017河北武邑中学质检一,理21)已知函数f(x)=ln(1+ax)-(a>0).(1)当a=时,求f(x)的极值;(2)若a∈,f(x)存在两个极值点x1,x2,试比较f(x1)+f(x2)与f(0)的大小;(3)求证:>n!(n≥2,n∈N).(1)解f(x)=ln,定义域⇒x>-2,f'(x)=,∴f(x)在(-2,2)递减,(2,+∞)递增.故f(x)极小值=f(2)=ln 2-1,没有极大值.(2)解f(x)=ln(1+ax)-,x∈,f'(x)=.∵a∈,∴a(1-a)∈,∴-<-.由ax2-4(1-a)=0,得x=±.f(x1)+f(x2)=ln [1+2]+ln [1-2]-,f(x1)+f(x2)=ln[(1-2a)2]+=ln[(1-2a)2]+-2,设t=2a-1,当a∈时,t∈(0,1),∴设f(x1)+f(x2)=g(t)=2ln t+-2,当t∈(0,1)时,g(t)=2ln t+-2,g'(t)=<0,g(t)在t∈(0,1)内递减,g(t)>g(1)=0,即f(x1)+f(x2)>f(0)=0恒成立.(3)证明当t∈(0,1)时,g(t)=2ln t+-2>0恒成立,即ln t+-1>0恒成立,设t=(n≥2,n∈N),即ln+n-1>0,∴n-1>ln n.∴1>ln 2,2>ln 3,3>ln 4,…,n-1>ln n.∴1+2+3+…+(n-1)>ln 2+ln 3+ln 4+…+ln n=ln 2×3×4×…×n=ln(n!),∴>ln(n!),∴>n!(n≥2,n∈N).。

专题对点练21 6.1~6.3组合练(限时90分钟,满分100分)一、选择题(共9小题,满分45分)1.(2017河南新乡二模,理6)已知某居民小区户主人数和户主对户型结构的满意率分别如图1和图2所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取20%的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为()A.100,8B.80,20C.100,20D.80,8答案 A解析样本容量为(150+250+100)×20%=100,∴抽取的户主对四居室满意的人数为100××40%=8.故选A.2.投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为()A.0.648B.0.432C.0.36D.0.312答案 A解析由条件知该同学通过测试,即3次投篮投中2次或投中3次.故P=0.62(1-0.6)+0.63=0.648.3.(2017全国Ⅲ,理3)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是()A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳答案 A解析由题图可知2014年8月到9月的月接待游客量在减少,故A错误.4.(2017北京丰台一模,理7)小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小明的父母至少有一人与他相邻,则不同坐法的总数为()A.60B.72C.84D.96答案 C5.设样本数据x1,x2,…,x10的平均值和方差分别为1和4,若y i=x i+a(a为非零常数,i=1,2,…,10),则y1,y2,…,y10的平均值和方差分别为()A.1+a,4B.1+a,4+aC.1,4D.1,4+a答案 A解析由题意知y i=x i+a(i=1,2,…,10),则(x1+x2+…+x10+10a)=(x1+x2+…+x10)+a=+a=1+a,方差s2=[(x1+a--a)2+(x2+a--a)2+…+(x10+a--a)2]=[(x1-)2+(x2-)2+…+(x10-)2]=s2=4.故选A.6.4名同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为()A. B. C. D.答案 D解析基本事件总数为24=16,周六没有同学参加即4名同学均在周日参加,只有一种情况;同理,周日没有同学参加也只有一种情况.故所求概率为-.故选D.7.(2017山东,理8)从分别标有1,2,…,9的9张卡片中不放回地随机抽取2次,每次抽取1张.则抽到的2张卡片上的数奇偶性不同的概率是()A. B. C. D.答案 C解析从分别标有1,2,…,9的9张卡片中不放回地随机抽取2次,每次抽取1张,共有种不同情况.其中2张卡片上的数奇偶性不同的有()种情况,则抽到的2张卡片上的数奇偶性不同的概率P=.故选C.8.在如图所示的正方形中随机投掷10 000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线的一部分)的点的个数的估计值为() 〚导学号16804211〛附:若X~N(μ,σ2),则P(μ-σ<X≤μ+σ)≈0.682 7,P(μ-2σ<X≤μ+2σ)≈0.954 5.A.2 386B.2 718C.3 414D.4 772答案 C解析由X~N(0,1)知P(-1<X≤1)≈0.682 7,∴P(0≤X≤1)≈×0.682 7≈0.341 4,故阴影部分的面积S≈0.341 4.∴落在阴影部分中点的个数x的估计值满足(古典概型),∴x≈10 000×0.341 4=3 414,故选C.9.(2017全国Ⅰ,理6)(1+x)6展开式中x2的系数为()A.15B.20C.30D.35答案 C解析方法一:(1+x)6=1·(1+x)6+(1+x)6,(1+x)6的展开式中的x2的系数为=15,(1+x)6的展开式中的x2的系数为=15,所以x2的系数为15+15=30.方法二:(1+x)6的二项展开式通项为T r+1=x r,(1+x)6的展开式中含x2的项的来源有两部分,一部分是1×x2=15x2,另一部分是x4=15x2,故(1+x)6的展开式中含x2的项为15x2+15x2=30x2,其系数是30.二、填空题(共3小题,满分15分)10.(2017山东,理11)已知(1+3x)n的展开式中含有x2项的系数是54,则n=.答案 4解析二项展开式的通项T r+1=(3x)r=3r··x r,令r=2,得32·=54,解得n=4.11.(2017浙江,16)从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有种不同的选法.(用数字作答)答案 660解析由题意可得,总的选择方法为种方法,其中不满足题意的选法有种方法,则满足题意的选法有=660种.12.(2017河北石家庄二中模拟,理14)已知(ax+1)5的展开式中各项系数和为243,则的展开式中含x项的系数为.(用数字作答)答案-解析∵(ax+1)5的展开式中各项系数和为243,∴(a+1)5=243,得a=2,∴的展开式的通项为T r+1=-(--)r=-(-1)r-,令5-=1,得r=3,故二项式-的展开式中含x项的系数为-=-.故答案为-.13.(2017北京东城一模,理12)“墨子号”是由我国完全自主研制的世界上第一颗空间量子科学实验卫星,于2016年8月16日发射升空.“墨子号”的主要应用目标是通过卫星中转实现可覆盖全球的量子保密通信.量子通信是通过光子的偏振状态,使用二进制编码,比如,码元0对应光子偏振方向为水平或斜向下45度,码元1对应光子偏振方向为垂直或斜向上45度.如图所示.1信号发出后,我们在接收端将随机选择两种编码方式中的一种来解码,比如,信号发送端如果按编码方式1发送,同时接收端按编码方式1进行解码,这时能够完美解码;信号发送端如果按编码方式1发送,同时接收端按编码方式2进行解码,这时无法获取信息.如果发送端发送一个码元,那么接收端能够完美解码的概率是;如果发送端发送3个码元,那么恰有两个码元无法获取信息的概率是.〚导学号16804212〛答案解析发送端发送一个码元,基本事件总数n=2,接收端能够完美解码包含的基本事件个数m=1,故如果发送端发送一个码元,那么接收端能够完美解码的概率p1=.发送端发送3个码元,恰有两个码元无法获取信息的概率p2=.故答案为.三、解答题(共3个题,分别满分为13分,13分,14分)14.为评估设备M生产某种零件的性能,从设备M生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:经计算,样本的平均值μ=65,标准差σ=2.2,以频率值作为概率的估计值.(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为X,并根据以下不等式进行评判:①P(μ-σ<X≤μ+σ)≥0.682 7.②P(μ-2σ<X≤μ+2σ)≥0.954 5.③P(μ-3σ<X≤μ+3σ)≥0.997 3.评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁.试判断设备M的性能等级.(2)将直径小于等于μ-2σ或直径大于μ+2σ的零件认为是次品.(ⅰ)从设备M的生产流水线上随意抽取2件零件,计算其中次品个数Y的数学期望E(Y); (ⅱ)从样本中随意抽取2件零件,计算其中次品个数Z的数学期望E(Z).解(1)P(μ-σ<X≤μ+σ)=P(62.8<X≤67.2)=0.8≥0.6827,P(μ-2σ<X≤μ+2σ)=P(60.6<X≤69.4)=0.94≤0.9545,P(μ-3σ<X≤μ+3σ)=P(58.4<X≤71.6)=0.98≤0.997 3,因为设备M的数据仅满足一个不等式,所以其性能等级为丙.(2)易知样本中次品共6件,可估计设备M生产零件的次品率为0.06.(ⅰ)由题意可知Y~B,于是E(Y)=2×.(ⅱ)由题意可知Z的分布列为故E(Z)=0×+1×+2×.15.(2016河南许昌、新乡、平顶山二模,理18)某校高二年级共有学生1 000名,其中走读生750名,住宿生250名,现采用分层抽样的方法从该年级抽取100名学生进行问卷调查.根据问卷取得了这100名学生每天晚上有效学习时间(单位:分钟)的数据,按照以下区间分为八组:①[0,30),②[30,60),③[60,90),④[90,120),…得到频率分布直方图(部分)如图.(1)如果把“学生晚上有效时间是否达到两小时”作为是否充分利用时间的标准,对抽取的100名学生,完成下列2×2列联表;并判断是否有95%的把握认为学生利用时间是否充分与走读、住宿有关?(2)若在第①组、第②组、第③组中共抽出3人调查影响有效利用时间的原因,记抽到“有效学习时间少于60分钟”的学生人数为X,求X的分布列和数学期望.参考公式:K2=-,n=a+b+c+d.临界值表:解 (1)把“学生晚上有效时间是否达到两小时”作为是否充分利用时间的标准,对抽取的100名学生,完成2×2列联表如下:K2=-≈5.556.因为K2>3.841,所以有95%的把握认为学生利用时间是否充分与走读、住宿有关.(2)设第i组的频率为P i(i=1,2,…,8),则由图可知P1=×30=,P2=×30=,P3=×30=,∴第①组1人,第②组4人,第③组10人.则X的所有可能取值为0,1,2,3,P(X=i)=-(i=0,1,2,3),∴P(X=0)=,P(X=1)=,P(X=2)=,P(X=3)=.∴X的分布列为E(X)=0×+1×+2×+3×=1.16.(2017宁夏中卫二模,理19)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:万元)对年销售量y(单位:吨)的影响,对近六年的年宣传费x i和年销售量y i(i=1,2,3,4,5,6)的数据作了初步统计,得到如下数据:吨经电脑模拟发现年宣传费x(单位:万元)与年销售量y(单位:吨)之间近似满足关系式y=a·x b(a,b>0),即ln y=b·ln x+ln a,对上述数据作了初步处理,得到相关的值如下表:(1)根据所给数据,求y关于x的回归方程;(2)规定当产品的年销售量y(单位:吨)与年宣传费x(单位:万元)的比值在区间内时认为该年效益良好.现从这6年中任选3年,记其中选到效益良好的数量为ξ,求随机变量ξ的分布列和期望.(其中e为自然对数的底数,e≈2.718 3)附:对于一组数据(u1,v1),(u2,v2),…,(u n,v n),其回归直线·u+中的斜率和截距的最小二乘估计分别为--.解 (1)对y=a·x b(a>0,b>0)两边取对数,得ln y=b·ln x+ln a,令μi=ln x i,v i=ln y i,得v=b·μ+ln a,由所给的数据得=4.1,=3.05,(μi·v i)=(ln x i·ln y i)=75.3,(ln x i)2=101.4, ∴b=--=1,ln a=-b·=3.05-×4.1=1,得a=e,∴y关于x的回归方程为y=e·.(2)由(1)中所求回归方程,得,则x∈(49,81),∴x=58,68,78,∴ξ的所有可能取值为0,1,2,3,P(ξ=0)=,P(ξ=1)=,P(ξ=2)=,P(ξ=3)=,∴ξ的分布列为E(ξ)=0×+1×+2×+3×.。

技法强化训练(一) 函数与方程思想(对应学生用书第159页)题组1 运用函数与方程思想解决数列、不等式等问题1．已知{a n }是等差数列，a 1＝1，公差d ≠0，S n 是其前n 项和，若a 1，a 2，a 5成等比数列，则S 8的值为( ) A ．16 B ．32 C ．64D ．62C [由题意可知a 22＝a 1a 5，即(1＋d )2＝1³(1＋4d )，解得d ＝2， ∴a n ＝1＋(n －1)³2＝2n －1.∴S 8＝ a 1＋a 8 ³82＝4³(1＋15)＝64.]2．若2x ＋5y ≤2－y ＋5－x，则有( ) A ．x ＋y ≥0 B ．x ＋y ≤0 C ．x －y ≤0D ．x －y ≥0B [原不等式可化为2x－5－x≤2－y－5y，构造函数y ＝2x－5－x，其为R 上的增函数，所以有x ≤－y ，即x ＋y ≤0.]3．若关于x 的方程x 2＋2kx －1＝0的两根x 1，x 2满足－1≤x 1＜0＜x 2＜2，则k 的取值范围是( ) 【导学号：68334007】A.⎝ ⎛⎭⎪⎫－34，0B.⎝ ⎛⎦⎥⎤－34，0C.⎝ ⎛⎭⎪⎫0，34 D.⎣⎢⎡⎭⎪⎫0，34 B [构造函数f (x )＝x 2＋2kx －1，因为关于x 的方程x 2＋2kx －1＝0的两根x 1，x 2满足－1≤x 1＜0＜x 2＜2，所以⎩⎪⎨⎪⎧f －1 ≥0，f 0 ＜0，f 2 ＞0，即⎩⎪⎨⎪⎧－2k ≥0，－1＜0，4k ＋3＞0，所以－34＜k ≤0，所以k 的取值范围是⎝ ⎛⎦⎥⎤－34，0.]4．已知数列{a n }满足a 1＝60，a n ＋1－a n ＝2n (n ∈N *)，则a n n的最小值为________．292[由a n ＋1－a n ＝2n ，得 a n ＝(a n －a n －1)＋(a n －1－a n －2)＋…＋(a 2－a 1)＋a 1＝2(n －1)＋2(n －2)＋…＋2＋60 ＝n 2－n ＋60.∴a n n ＝n 2－n ＋60n ＝n ＋60n－1.令f (x )＝x ＋60x－1，易知f (x )在(0,215)上单调递减，在(215，＋∞)上单调递增．又n ∈N *，当n ＝7时，a 77＝7＋607－1＝1027，当n ＝8时，a 88＝8＋608－1＝292.又292＜1027，故a n n 的最小值为292.] 5．已知函数f (x )＝x ln x ＋a ，g (x )＝12x 2＋ax ，其中a ≥0.(1)若曲线y ＝f (x )在点(1，f (1))处的切线与曲线y ＝g (x )也相切，求a 的值； (2)证明：x ＞1时，f (x )＋12＜g (x )恒成立．【导学号：68334008】[解] (1)由f (x )＝x ln x ＋a ，得f (1)＝a ，f ′(x )＝ln x ＋1，所以f ′(1)＝1. 1分所以曲线y ＝f (x )在点(1，f (1))处的切线为y ＝x ＋a －1.因为直线y ＝x ＋a －1与曲线y ＝g (x )也相切，所以两方程联立消元得12x 2＋ax ＝a ＋x －1，即12x 2＋(a －1)x ＋1－a ＝0，3分所以Δ＝(a －1)2－4³12³(1－a )＝0，得a 2＝1.因为a ≥0，所以a ＝1.4分(2)证明：x ＞1时，f (x )＋12＜g (x )恒成立，等价于12x 2＋ax －x ln x －a －12＞0恒成立．令h (x )＝12x 2＋ax －x ln x －a －12，则h (1)＝0且h ′(x )＝x ＋a －ln x －1.6分令φ(x )＝x －ln x －1，则φ(1)＝0且φ′(x )＝1－1x ＝x －1x，8分所以x ＞1时，φ′(x )＞0，φ(x )单调递增， 所以φ(x )＞φ(1)＝0.又因为a ≥0，所以h ′(x )＞0，h (x )单调递增，所以h (x )＞h (1)＝0，所以x ＞1时，12x 2＋ax －x ln x －a －12＞0恒成立，11分 即x ＞1时，f (x )＋12＜g (x )恒成立.12分题组2 利用函数与方程思想解决几何问题6．设抛物线C ：y 2＝3px (p ＞0)的焦点为F ，点M 在C 上，|MF |＝5，若以MF 为直径的圆过点(0,2)，则C 的方程为( )A ．y 2＝4x 或y 2＝8x B ．y 2＝2x 或y 2＝8x C ．y 2＝4x 或y 2＝16xD ．y 2＝2x 或y 2＝16xC [由抛物线的定义可知MF ＝x M ＋3p 4＝5，∴x M ＝5－3p 4，y 2M ＝15p －9p24，故以MF 为直径的圆的方程为(x －x M )(x －x F )＋(y －y M )(y －y F )＝0， 即⎝ ⎛⎭⎪⎫0－5＋3p 4⎝ ⎛⎭⎪⎫0－3p 4＋(2－y M )(2－0)＝0.∴y M ＝2＋15p 8－9p 232＝2＋y 2M 8⇒y M ＝4，p ＝43或163.∴C 的方程为y 2＝4x 或y 2＝16x .]7．(2017²宁波市镇海中学高三模拟考试)在直三棱柱A 1B 1C 1­ABC 中，∠BAC ＝π2，AB ＝AC ＝AA 1＝1，已知G 和E 分别为A 1B 1和CC 1的中点，D 与F 分别为线段AC 和AB 上的动点(不包括端点)，若GD ⊥EF ，则线段DF 的长度的取值范围为( )【导学号：68334009】A.⎣⎢⎡⎭⎪⎫55，1 B.⎣⎢⎡⎦⎥⎤55，1 C.⎝⎛⎭⎪⎫255，1 D.⎣⎢⎡⎭⎪⎫255，1 A [建立如图所示的空间直角坐标系，则A (0,0,0)，E ⎝ ⎛⎭⎪⎫0，1，12，G ⎝ ⎛⎭⎪⎫12，0，1，设F (x,0,0)，D (0，y,0)，则GD →＝⎝ ⎛⎭⎪⎫－12，y ，－1，EF →＝⎝ ⎛⎭⎪⎫x ，－1，－12，x ，y ∈(0,1)．由于GD ⊥EF ，所以x ＋2y －1＝0，x ＝1－2y ∈(0,1)，解得0＜y ＜12.DF ＝x 2＋y 2＝5y 2－4y ＋1＝5⎝ ⎛⎭⎪⎫y －252＋15，当且仅当y ＝25时，线段DF 长度的最小值是55，当y ＝0时，线段DF 的最大值是1，由于不包括端点，故y ＝0不能取，所以线段DF 的长度的取值范围是⎣⎢⎡⎭⎪⎫55，1，故选A.] 8．已知椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率e ＝32，并且经过定点P ⎝ ⎛⎭⎪⎫3，12.(1)求椭圆E 的方程；(2)问：是否存在直线y ＝－x ＋m ，使直线与椭圆交于A ，B 两点，且满足OA →²OB →＝125？若存在，求出m 的值；若不存在，请说明理由. 【导学号：68334010】[解] (1)由e ＝c a ＝32且3a 2＋14b2＝1，c 2＝a 2－b 2， 解得a 2＝4，b 2＝1，即椭圆E 的方程为x 24＋y 2＝1.4分(2)设A (x 1，y 1)，B (x 2，y 2)，由⎩⎪⎨⎪⎧x 24＋y 2＝1，y ＝－x ＋m⇒x 2＋4(m －x )2－4＝0⇒5x 2－8mx ＋4m 2－4＝0.(*) 所以x 1＋x 2＝8m 5，x 1x 2＝4m 2－45，8分y 1y 2＝(m －x 1)(m －x 2)＝m 2－m (x 1＋x 2)＋x 1x 2＝m 2－85m 2＋4m 2－45＝m 2－45，由OA →²OB →＝125得(x 1，y 1)²(x 2，y 2)＝125，即x 1x 2＋y 1y 2＝125，4m 2－45＋m 2－45＝125，m ＝±2.又方程(*)要有两个不等实根，所以Δ＝(－8m )2－4³5(4m 2－4)＞0，解得－5＜m ＜5，所以m ＝±2.12分9．如图1，直三棱柱ABC ­A ′B ′C ′中，AC ＝BC ＝5，AA ′＝AB ＝6，D ，E 分别为AB 和BB ′上的点，且AD DB ＝BE EB ′＝λ.图1(1)求证：当λ＝1时，A ′B ⊥CE ；(2)当λ为何值时，三棱锥A ′­CDE 的体积最小，并求出最小体积． [解] (1)证明：∵λ＝1，∴D ，E 分别为AB 和BB ′的中点. 1分又AA ′＝AB ，且三棱柱ABC ­A ′B ′C ′为直三棱柱， ∴平行四边形ABB ′A ′为正方形，∴DE ⊥A ′B . 2分 ∵AC ＝BC ，D 为AB 的中点，∴CD ⊥AB . 3分 ∵三棱柱ABC ­A ′B ′C ′为直三棱柱， ∴CD ⊥平面ABB ′A ′，∴CD ⊥A ′B ， 4分 又CD ∩DE ＝D ，∴A ′B ⊥平面CDE . ∵CE ⊂平面CDE ，∴A ′B ⊥CE .6分(2)设BE ＝x ，则AD ＝x ，DB ＝6－x ，B ′E ＝6－x .由已知可得C 到平面A ′DE 的距离即为△ABC 的边AB 所对应的高h ＝AC 2－⎝ ⎛⎭⎪⎫AB 22＝4， 8分 ∴V A ′­CDE ＝V C ­A ′DE ＝13(S 四边形ABB ′A －S △AA ′D －S △DBE －S △A ′B ′E )²h＝13⎣⎢⎡⎦⎥⎤36－3x －12 6－x x －3 6－x ²h ＝23(x 2－6x ＋36)＝23[(x －3)2＋27](0＜x ＜6)，14分 ∴当x ＝3，即λ＝1时，V A ′­CDE 有最小值18. 15分技法强化训练(二) 数形结合思想(对应学生用书第160页)题组1 利用数形结合思想解决方程的根或函数零点问题 1．方程|x 2－2x |＝a 2＋1(a ＞0)的解的个数是( )【导学号：68334011】A ．1B ．2C ．3D ．4B [∵a ＞0，∴a 2＋1＞1. 而y ＝|x 2－2x |的图象如图，∴y ＝|x 2－2x |的图象与y ＝a 2＋1的图象总有2个交点．]2．已知函数f (x )＝|log 2|x ||－⎝ ⎛⎭⎪⎫12x，则下列结论正确的是( )A ．f (x )有三个零点，且所有零点之积大于－1B ．f (x )有三个零点，且所有零点之积小于－1C ．f (x )有四个零点，且所有零点之积大于1D ．f (x )有四个零点，且所有零点之积小于1＝⎝ ⎛⎭⎪⎫12x的图象， A [在同一坐标系中分别作出f 1(x )＝|log 2|x ||与f 2(x )如图所示，由图象知f 1(x )与f 2(x )有三个交点，设三个交点的横坐标从左到右分别是x 1，x 2，x 3，因为f ⎝ ⎛⎭⎪⎫－12＜0，f ⎝ ⎛⎭⎪⎫－14＞0，所以－12＜x 1＜－14，同理12＜x 2＜1,1＜x 3＜2，即－1＜x 1x 2x 3＜－18，即所有零点之积大于－1.]3．设函数f (x )的定义域为R ，f (－x )＝f (x )，f (x )＝f (2－x )，当x ∈[0,1]时，f (x )＝x 3，则函数g (x )＝|cos(πx )|－f (x )在⎣⎢⎡⎦⎥⎤－12，52上的所有零点的和为( )A ．7B ．6C ．3D ．2A [函数g (x )＝|cos(πx )|－f (x )在⎣⎢⎡⎦⎥⎤－12，52上的零点为函数h (x )＝|cos(πx )|与函数f (x )的交点的横坐标．因为f (－x )＝f (x )，f (x )＝f (2－x )，所以函数f (x )为关于x ＝1对称的偶函数，又因为当x ∈[0,1]时，f (x )＝x 3，则在平面直角坐标系内画出函数h (x )＝|cos(πx )|与函数f (x )在⎣⎢⎡⎦⎥⎤－12，52内的图象，如图所示，由图易得两函数图象共有7个交点，不妨设从左到右依次为x 1，x 2，x 3，x 4，x 5，x 6，x 7，则由图易得x 1＋x 2＝0，x 3＋x 5＝2，x 4＝1，x 6＋x 7＝4，所以x 1＋x 2＋x 3＋x 4＋x 5＋x 6＋x 7＝7，即函数g (x )＝|cos(πx )|－f (x )在⎣⎢⎡⎦⎥⎤－12，52上的零点的和为7，故选A.]4．若函数f (x )＝a ＋sin x 在[π，2π]上有且只有一个零点，则实数a ＝________.【导学号：68334012】1 [函数f (x )＝a ＋sin x 在[π，2π]上有且只有一个零点，即方程a ＋sin x ＝0在[π，2π]上只有一解，即函数y ＝－a 与y ＝sin x ，x∈[π，2π]的图象只有一个交点，由图象可得a ＝1.]5．已知函数f (x )＝⎩⎪⎨⎪⎧x 3，x ≤a ，x 2，x ＞a ，若存在实数b ，使函数g (x )＝f (x )－b 有两个零点，则a 的取值范围是________．(－∞，0)∪(1，＋∞) [函数g (x )有两个零点，即方程f (x )－b ＝0有两个不等实根，则函数y ＝f (x )和y ＝b 的图象有两个公共点．①若a ＜0，则当x ≤a 时，f (x )＝x 3，函数单调递增；当x ＞a 时，f (x )＝x 2，函数先单调递减后单调递增，f (x )的图象如图(1)实线部分所示，其与直线y ＝b 可能有两个公共点．②若0≤a ≤1，则a 3≤a 2，函数f (x )在R 上单调递增，f (x )的图象如图(2)实线部分所示，其与直线y ＝b 至多有一个公共点．③若a ＞1，则a 3＞a 2，函数f (x )在R 上不单调，f (x )的图象如图(3)实线部分所示，其与直线y ＝b 可能有两个公共点． 综上，a ＜0或a ＞1.]题组2 利用数形结合思想求解不等式或参数范围6．若不等式log a x ＞sin 2x (a ＞0，a ≠1)对任意x ∈⎝ ⎛⎭⎪⎫0，π4都成立，则a 的取值范围为( )A.⎝⎛⎭⎪⎫0，π4B.⎝⎛⎭⎪⎫π4，1C.⎝⎛⎭⎪⎫π4，π2D ．(0,1)A [记y1＝log a x (a ＞0，a ≠1)，y 2＝sin 2x ，原不等式即为y 1＞y 2，由题意作出两个函数的图象，如图所示，知当y 1＝log a x 的图象过点A ⎝ ⎛⎭⎪⎫π4，1时，a ＝π4，所以当π4＜a ＜1时，对任意x ∈⎝⎛⎭⎪⎫0，π4都有y 1＞y 2.]7．函数f (x )是定义域为{x |x ≠0}的奇函数，且f (1)＝1，f ′(x )为f (x )的导函数，当x ＞0时，f (x )＋xf ′(x )＞1x，则不等式xf (x )＞1＋ln|x |的解集是( )【导学号：68334013】A ．(－∞，－1)∪(1，＋∞)B ．(－∞，－1)C ．(1，＋∞)D ．(－1,1)A [令g (x )＝xf (x )－ln|x |，则g (x )是偶函数， 且当x ＞0时，g ′(x )＝f (x )＋xf ′(x )－1x＞0，∴g (x )在(0，＋∞)上单调递增．故不等式xf (x )＞1＋ln|x |⇔g (|x |)＞g (1)， ∴|x |＞1，解得x ＞1或x ＜－1.故选A.]8．若不等式|x －2a |≥12x ＋a －1对x ∈R 恒成立，则a 的取值范围是________．⎝ ⎛⎦⎥⎤－∞，12 [作出y ＝|x －2a |和y ＝12x ＋a －1的简图，依题意知应有2a ≤2－2a ，故a ≤12.]9．已知函数f (x )＝⎩⎪⎨⎪⎧|lg x |，0＜x ≤10，－12x ＋6，x ＞10.若a ，b ，c 互不相等，且f (a )＝f (b )＝f (c )，则abc 的取值范围是________．(10,12) [作出f (x )的大致图象．由图象知，要使f (a )＝f (b )＝f (c )，不妨设a ＜b ＜c ， 则－lg a ＝lg b ＝－12c ＋6.∴lg a ＋lg b ＝0，∴ab ＝1， ∴abc ＝c .由图知10＜c ＜12，∴abc ∈(10,12)．]10．(2017²杭州市高三年级第二学期教学质量检测)设函数f (x )＝⎩⎪⎨⎪⎧2cos π2x ，|x |≤1，x 2－1，|x |＞1，若|f (x )＋f (x ＋l )－2|＋|f (x )－f (x ＋l )|≥2(l ＞0)对任意实数x 都成立，则l 的最小值为________. 【导学号：68334014】23 [作出函数f (x )的图象如图，要使原不等式对任意实数x 都成立，由不等式|a |＋|b |≥|a ±b |得|f (x )＋f (x ＋l )－2|＋|f (x )－f (x ＋l )|≥|[f (x )＋f (x ＋l )－2]±[f (x )－f (x ＋l )]|≥2，化简得⎩⎪⎨⎪⎧|2f x －2|≥2，|2f x ＋l －2|≥2，即⎩⎪⎨⎪⎧f x ≥2，f x ＋l ≥2对任意实数恒成立，当x ＝－3时，f (－3＋l )≥2，l ＞0，则l －3≥3，l ≥23，故l 的最小值是2 3.]题组3 利用数形结合解决解析几何问题11．已知圆C ：(x －3)2＋(y －4)2＝1和两点A (－m,0)，B (m,0)(m ＞0)．若圆C 上存在点P ，使得∠APB ＝90°，则m 的最大值为( ) A ．7 B ．6 C ．5D ．4B [根据题意，画出示意图，如图所示，则圆心C 的坐标为(3,4)，半径r ＝1，且|AB |＝2m ，因为∠APB ＝90°，连接OP ，易知|OP |＝12|AB |＝m .要求m 的最大值，即求圆C 上的点P 到原点O 的最大距离．因为|OC |＝32＋42＝5，所以|OP |max ＝|OC |＋r ＝6，即m 的最大值为6.]12．(2017²杭州高级中学高三最后一模)已知双曲线C ：x 2a 2－y 2b2＝1的右顶点为A ，O 为坐标原点，以A为圆心的圆与双曲线C 的某一条渐近线交于两点P ，Q ，若∠PAQ ＝π3且OQ →＝5OP →，则双曲线C 的离心率为( )【导学号：68334015】A.213 B ．2C.72D ．3A [由图知△APQ 是等边三角形，设PQ 的中点为H ，圆的半径为r ，则AH ⊥PQ ，AH ＝32r ，PQ ＝r ，由题易知，点P ，Q 在原点O 的同侧，因为OQ →＝5OP →，所以OP ＝14r ，PH ＝12r ，即OH ＝14r ＋12r ＝34r ，所以tan ∠HOA ＝AH OH ＝233，即b a ＝233，b 2a 2＝c 2－a 2a 2＝43，从而得e ＝c a ＝213，故选A.]13．已知P 是直线l ：3x ＋4y ＋8＝0上的动点，PA ，PB 是圆x 2＋y 2－2x －2y ＋1＝0的两条切线，A ，B 是切点，C 是圆心，则四边形PACB 面积的最小值为________． 22 [从运动的观点看问题，当动点P 沿直线3x ＋4y ＋8＝0向左上方或右下方无穷远处运动时，直角三角形PAC 的面积S Rt △PAC ＝12|PA |²|AC |＝12|PA |越来越大，从而S 四边形PACB 也越来越大；当点P 从左上、右下两个方向向中间运动时，S 四边形PACB变小，显然，当点P 到达一个最特殊的位置，即CP 垂直于直线l 时，S 四边形PACB 应有唯一的最小值， 此时|PC |＝|3³1＋4³1＋8|32＋42＝3， 从而|PA |＝|PC |2－|AC |2＝2 2.所以(S 四边形PACB )min ＝2³12³|PA |³|AC |＝2 2.]14．已知过原点的动直线l 与圆C 1：x 2＋y 2－6x ＋5＝0相交于不同的两点A ，B . (1)求圆C 1的圆心坐标；(2)求线段AB 的中点M 的轨迹C 的方程；(3)是否存在实数k ，使得直线L ：y ＝k (x －4)与曲线C 只有一个交点？若存在，求出k 的取值范围；若不存在，说明理由. 【导学号：68334016】[解] (1)圆C 1的方程x 2＋y 2－6x ＋5＝0可化为(x －3)2＋y 2＝4，所以圆心坐标为(3,0). (2)设A (x 1，y 1)，B (x 2，y 2)(x 1≠x 2)，M (x 0，y 0)，则x 0＝x 1＋x 22，y 0＝y 1＋y 22.由题意可知直线l 的斜率必存在，设直线l 的方程为y ＝tx . 将上述方程代入圆C 1的方程，化简得(1＋t 2)x 2－6x ＋5＝0.5分由题意，可得Δ＝36－20(1＋t 2)＞0(*)，x 1＋x 2＝61＋t 2，所以x 0＝31＋t 2，代入直线l 的方程，得y 0＝3t1＋t2. 6分因为x 20＋y 20＝9 1＋t 2 2＋9t 2 1＋t 2 2＝9 1＋t 21＋t 2 2＝91＋t 2＝3x 0，所以⎝⎛⎭⎪⎫x 0－322＋y 20＝94. 由(*)解得t 2＜45，又t 2≥0，所以53＜x 0≤3.所以线段AB 的中点M 的轨迹C 的方程为⎝ ⎛⎭⎪⎫x －322＋y 2＝94⎝ ⎛⎭⎪⎫53＜x ≤3. 8分图，D ⎝ ⎛⎭⎪⎫53，253，(3)由(2)知，曲线C 是在区间⎝ ⎛⎦⎥⎤53，3上的一段圆弧．如E 53，－253，F (3,0)，直线L 过定点G (4,0).11分 联立直线L 的方程与曲线C 的方程，消去y 整理得(1＋k 2)x 2－(3＋8k 2)x ＋16k 2＝0.令判别式Δ＝0，解得k ＝±34，由求根公式解得交点的横坐标为x H ，I ＝125∈⎝ ⎛⎦⎥⎤53，3.由图可知：要使直线L 与曲线C 只有一个交点，则k ∈[k DG ，k EG ]∪{k GH ，k GI }，即k ∈⎣⎢⎡⎦⎥⎤－257，257∪⎩⎨⎧⎭⎬⎫－34，34. 15分技法强化训练(三) 分类讨论思想(对应学生用书第161页)题组1 由概念、法则、公式引起的分类讨论1．已知数列{a n }的前n 项和S n ＝P n－1(P 是常数)，则数列{a n }是( )【导学号：68334017】A ．等差数列B ．等比数列C ．等差数列或等比数列D ．以上都不对D [∵S n ＝P n－1，∴a 1＝P －1，a n ＝S n －S n －1＝(P －1)Pn －1(n ≥2)．当P ≠1且P ≠0时，{a n }是等比数列； 当P ＝1时，{a n }是等差数列；当P ＝0时，a 1＝－1，a n ＝0(n ≥2)，此时{a n }既不是等差数列也不是等比数列．]2．已知函数f (x )＝⎩⎪⎨⎪⎧－x 2＋ax ，x ≤1，2ax －5，x ＞1.若存在x 1，x 2∈R ，且x 1≠x 2，使得f (x 1)＝f (x 2)成立，则实数a 的取值范围是( ) 【导学号：68334018】A ．(－∞，2)B ．(－∞，4)C ．[2,4]D ．(2，＋∞)B [当－a－2＜1，即a ＜2时，显然满足条件；当a ≥2时，由－1＋a ＞2a －5得2≤a ＜4， 综上可知a ＜4.]3．已知函数f (x )的定义域为(－∞，＋∞)，f ′(x )为f (x )的导函数，函数y ＝f ′(x )的图象如图1所示，且f (－2)＝1，f (3)＝1，则不等式f (x 2－6)＞1的解集为( )图1A ．(－3，－2)∪(2,3)B ．(－2，2)C ．(2,3)D ．(－∞，－2)∪(2，＋∞)A [由导函数图象知，当x ＜0时，f ′(x )＞0， 即f (x )在(－∞，0)上为增函数，当x ＞0时，f ′(x )＜0，即f (x )在(0，＋∞)上为减函数，又不等式f (x 2－6)＞1等价于f (x 2－6)＞f (－2)或f (x 2－6)＞f (3)，故－2＜x 2－6≤0或0≤x 2－6＜3，解得x ∈(－3，－2)∪(2,3)．]4．已知实数m 是2,8的等比中项，则曲线x 2－y 2m＝1的离心率为( )A. 2B.32C. 5D.5或32D [由题意可知，m 2＝2³8＝16，∴m ＝±4. (1)当m ＝4时，曲线为双曲线x 2－y 24＝1.此时离心率e ＝ 5.(2)当m ＝－4时，曲线为椭圆x 2＋y 24＝1.此时离心率e ＝32.] 5．设等比数列{a n }的公比为q ，前n 项和S n >0(n ＝1,2,3，…)，则q 的取值范围是________. (－1,0)∪(0，＋∞) [因为{a n }是等比数列，S n >0，可得a 1＝S 1>0，q ≠0. 当q ＝1时，S n ＝na 1>0；当q ≠1时，S n ＝a 1 1－q n1－q>0，即1－q n1－q >0(n ∈N *)，则有⎩⎪⎨⎪⎧1－q >0，1－q n>0 ①或⎩⎪⎨⎪⎧1－q <0，1－q n<0，②由①得－1<q <1，由②得q >1.故q 的取值范围是(－1,0)∪(0，＋∞)．]6．若x ＞0且x ≠1，则函数y ＝lg x ＋log x 10的值域为________． (－∞，－2]∪[2，＋∞) [当x ＞1时，y ＝lg x ＋1lg x ≥2lg x ²1lg x＝2，当且仅当lg x ＝1，即x ＝10时等号成立；当0＜x ＜1时，y ＝lg x ＋1lg x ＝－⎣⎢⎡⎦⎥⎤ －lg x ＋⎝ ⎛⎭⎪⎫－1lg x ≤－2－lg x ²1 －lg x ＝－2，当且仅当lg x ＝1lg x ，即x ＝110时等号成立．∴y ∈(－∞，－2]∪[2，＋∞)．]题组2 由参数变化引起的分类讨论7．已知集合A ＝{x |1≤x ＜5}，C ＝{x |－a ＜x ≤a ＋3}．若C ∩A ＝C ，则a 的取值范围为( )A.⎝ ⎛⎦⎥⎤－32，－1B.⎝⎛⎦⎥⎤－∞，－32C ．(－∞，－1]D.⎝ ⎛⎭⎪⎫－32，＋∞C [因为C ∩A ＝C ，所以C ⊆A .①当C ＝∅时，满足C ⊆A ，此时－a ≥a ＋3，得a ≤－32；②当C ≠∅时，要使C ⊆A ，则⎩⎪⎨⎪⎧－a ＜a ＋3，－a ≥1，a ＋3＜5，解得－32＜a ≤－1.由①②得a ≤－1.]8．已知不等式组⎩⎪⎨⎪⎧x ＋y ≤1，x －y ≥－1y ≥0，所表示的平面区域为D ，若直线y ＝kx －3与平面区域D 有公共点，则k 的取值范围为( ) 【导学号：68334020】 A ．[－3,3]B.⎝ ⎛⎦⎥⎤－∞，－13∪⎣⎢⎡⎭⎪⎫13，＋∞C ．(－∞，－3]∪[3，＋∞)D.⎣⎢⎡⎦⎥⎤－13，13 C [满足不等式组的平面区域如图中阴影部分所示．∵y ＝kx －3过定点(0，－3)，∴当y ＝kx －3过点C (1,0)时，k ＝3；当y ＝kx －3过点B (－1,0)时，k ＝－3.∴k ≤－3或k ≥3时，直线y ＝kx －3与平面区域D 有公共点，故选C.] 9．已知函数f (x )＝(a ＋1)ln x ＋ax 2＋1，试讨论函数f (x )的单调性． [解] 由题意知f (x )的定义域为(0，＋∞)，1分 f ′(x )＝a ＋1x ＋2ax ＝2ax 2＋a ＋1x.2分 ①当a ≥0时，f ′(x )>0，故f (x )在(0，＋∞)上单调递增. 4分 ②当a ≤－1时，f ′(x )<0，故f (x )在(0，＋∞)上单调递减. 6分 ③当－1<a <0时，令f ′(x )＝0，解得x ＝－a ＋12a， 7分则当x ∈⎝⎛⎭⎪⎫0，－a ＋12a 时，f ′(x )>0； 当x ∈⎝⎛⎭⎪⎫－a ＋12a ，＋∞时，f ′(x )<0. 故f (x )在⎝⎛⎭⎪⎫0，－a ＋12a 上单调递增， 在⎝⎛⎭⎪⎫－a ＋12a ，＋∞上单调递减.10分综上，当a ≥0时，f (x )在(0，＋∞)上单调递增； 当a ≤－1时，f (x )在(0，＋∞)上单调递减； 当－1<a <0时，f (x )在⎝⎛⎭⎪⎫0，－a ＋12a 上单调递增，在⎝⎛⎭⎪⎫－a ＋12a ，＋∞上单调递减.题组3 根据图形位置或形状分类讨论10．已知中心在坐标原点，焦点在坐标轴上的双曲线的渐近线方程为y ＝±34x ，则双曲线的离心率为( ) A.54B.53C.54或53D.35或45C [若双曲线的焦点在x 轴上，则b a ＝34，e ＝ca＝1＋⎝ ⎛⎭⎪⎫b a 2＝54；若双曲线的焦点在y 轴上，则b a ＝43，e ＝c a＝1＋⎝ ⎛⎭⎪⎫b a 2＝53，故选C.] 11．正三棱柱的侧面展开图是边长分别为6和4的矩形，则它的体积为________.【导学号：68334021】43或833[若侧面矩形的长为6，宽为4，则V ＝S 底³h ＝12³2³2³sin 60°³4＝4 3.若侧面矩形的长为4，宽为6，则V ＝S 底³h ＝12³43³43³sin 60°³6＝833.] 12．已知中心在原点O ，左焦点为F 1(－1,0)的椭圆C 的左顶点为A ，上顶点为B ，F 1到直线AB 的距离为77|OB |.图2(1)求椭圆C 的方程；(2)若椭圆C 1的方程为：x 2m 2＋y 2n 2＝1(m ＞n ＞0)，椭圆C 2的方程为：x 2m 2＋y 2n2＝λ(λ＞0，且λ≠1)，则称椭圆C 2是椭圆C 1的λ倍相似椭圆．如图2，已知C 2是椭圆C 的3倍相似椭圆，若椭圆C 的任意一条切线l 交椭圆C 2于两点M ，N ，试求弦长|MN |的取值范围. 【导学号：68334022】[解] (1)设椭圆C 的方程为x 2a 2＋y 2b2＝1(a ＞b ＞0)，∴直线AB 的方程为x －a ＋yb＝1，∴F 1(－1,0)到直线AB 的距离d ＝|b －ab |a 2＋b 2＝77b ，2分a 2＋b 2＝7(a －1)2，又b 2＝a 2－1，解得a ＝2，b ＝3， 3分 故椭圆C 的方程为x 24＋y 23＝1.4分(2)椭圆C 的3倍相似椭圆C 2的方程为x 212＋y 29＝1，5分①若切线l 垂直于x 轴，则其方程为x ＝±2，易求得|MN |＝2 6. 6分②若切线l 不垂直于x 轴，可设其方程y ＝kx ＋b ， 将y ＝kx ＋b 代入椭圆C 的方程， 得(3＋4k 2)x 2＋8kbx ＋4b 2－12＝0，7分∴Δ＝(8kb )2－4(3＋4k 2)(4b 2－12)＝48(4k 2－3－b 2)＝0，即b 2＝4k 2＋3，(*)8分记M ，N 两点的坐标分别为(x 1，y 1)，(x 2，y 2)．将y ＝kx ＋b 代入椭圆C 2的方程，得(3＋4k 2)x 2＋8kbx ＋4b 2－36＝0， 9分 此时x 1＋x 2＝－8kb 3＋4k ，x 1x 2＝4b 2－363＋4k ，|x 1－x 2|＝43 12k 2＋9－b 23＋4k ， 10分∴|MN |＝1＋k 2³43 12k 2＋9－b 23＋4k2＝461＋k23＋4k2＝261＋13＋4k2. ∵3＋4k 2≥3，∴1＜1＋13＋4k 2≤43， 即26＜261＋13＋4k2≤4 2. 综合①②得：弦长|MN |的取值范围为[26，42]. 15分技法强化训练(四) 转化与化归思想(对应学生用书第162页)题组1 正与反的相互转化1．若某公司从五位大学毕业生甲、乙、丙、丁、戊中录用三人，这五人被录用的机会均等，则甲或乙被录用的概率为( ) A.15B.35 C.710D.910D [甲或乙被录用的对立面是甲、乙均不被录用，故所求事件的概率为1－110＝910.]2．若二次函数f (x )＝4x 2－2(p －2)x －2p 2－p ＋1在区间[－1,1]内至少存在一个值c ，使得f (c )＞0，则实数p 的取值范围为________. 【导学号：68334023】⎝ ⎛⎭⎪⎫－3，32 [如果在[－1,1]内没有值满足f (c )＞0，则⎩⎪⎨⎪⎧f －1 ≤0，f 1 ≤0⇒⎩⎪⎨⎪⎧p ≤－12或p ≥1，p ≤－3或p ≥32⇒p ≤－3或p ≥32，取补集为－3＜p ＜32，即为满足条件的p 的取值范围．故实数p 的取值范围为⎝⎛⎭⎪⎫－3，32.]3．若椭圆x 22＋y 2＝a 2(a ＞0)与连接两点A (1,2)，B (3,4)的线段没有公共点，则实数a 的取值范围为________．⎝ ⎛⎭⎪⎫0，322∪⎝ ⎛⎭⎪⎫822，＋∞ [易知线段AB 的方程为y ＝x ＋1，x ∈[1,3]，由⎩⎪⎨⎪⎧y ＝x ＋1，x 22＋y 2＝a 2，得a 2＝32x 2＋2x ＋1，x ∈[1,3]，∴92≤a 2≤412.又a ＞0， ∴322≤a ≤822. 故当椭圆与线段AB 没有公共点时，实数a 的取值范围为⎝ ⎛⎭⎪⎫0，322∪⎝ ⎛⎭⎪⎫822，＋∞.]4．已知点A (1,1)是椭圆x 2a 2＋y 2b2＝1(a >b >0)上一点，F 1，F 2是椭圆的两焦点，且满足|AF 1|＋|AF 2|＝4.(1)求椭圆的两焦点坐标；(2)设点B 是椭圆上任意一点，当|AB |最大时，求证：A ，B 两点关于原点O 不对称．[解] (1)由椭圆定义，知2a ＝4，所以a ＝2.所以x 24＋y 2b＝1.2分 把A (1,1)代入，得14＋1b 2＝1，得b 2＝43，所以椭圆方程为x 24＋y 243＝1.4分所以c 2＝a 2－b 2＝4－43＝83，即c ＝263.故两焦点坐标为⎝ ⎛⎭⎪⎫－263，0，⎝ ⎛⎭⎪⎫263，0.6分(2)反证法：假设A ，B 两点关于原点O 对称，则B 点坐标为(－1，－1)，7分此时|AB |＝22，而当点B 取椭圆上一点M (－2,0)时，则|AM |＝10，所以|AM |>|AB |. 从而知|AB |不是最大，这与|AB |最大矛盾，所以命题成立. 15分题组2 主与次的相互转化5．设f (x )是定义在R 上的单调递增函数，若f (1－ax －x 2)≤f (2－a )对任意a ∈[－1,1]恒成立，则x 的取值范围为________. 【导学号：68334024】 (－∞，－1]∪[0，＋∞) [∵f (x )是R 上的增函数， ∴1－ax －x 2≤2－a ，a ∈[－1,1]．①①式可化为(x －1)a ＋x 2＋1≥0，对a ∈[－1,1]恒成立． 令g (a )＝(x －1)a ＋x 2＋1，则⎩⎪⎨⎪⎧g －1 ＝x 2－x ＋2≥0，g 1 ＝x 2＋x ≥0，解得x ≥0或x ≤－1.即实数x 的取值范围是(－∞，－1]∪[0，＋∞)．]6．已知函数f (x )＝x 3＋3ax －1，g (x )＝f ′(x )－ax －5，其中f ′(x )是f (x )的导函数．对满足－1≤a ≤1的一切a 的值，都有g (x )＜0，则实数x 的取值范围为________．⎝ ⎛⎭⎪⎫－23，1 [由题意，知g (x )＝3x 2－ax ＋3a －5， 令φ(a )＝(3－x )a ＋3x 2－5，－1≤a ≤1. 对－1≤a ≤1，恒有g (x )＜0，即φ(a )＜0，∴⎩⎪⎨⎪⎧φ 1 ＜0，φ －1 ＜0，即⎩⎪⎨⎪⎧3x 2－x －2＜0，3x 2＋x －8＜0，解得－23＜x ＜1.故当x ∈⎝ ⎛⎭⎪⎫－23，1时，对满足－1≤a ≤1的一切a 的值，都有g (x )＜0.] 7．对于满足0≤p ≤4的所有实数p ，使不等式x 2＋px ＞4x ＋p －3成立的x 的取值范围是________． (－∞，－1)∪(3，＋∞) [设f (p )＝(x －1)p ＋x 2－4x ＋3， 则当x ＝1时，f (p )＝0，所以x ≠1.f (p )在0≤p ≤4上恒正，等价于⎩⎪⎨⎪⎧f 0 ＞0，f 4 ＞0，即⎩⎪⎨⎪⎧x －3 x －1 ＞0，x 2－1＞0，解得x ＞3或x ＜－1.]8．已知函数f (x )＝13x 3＋⎝ ⎛⎭⎪⎫a 2－43x 2＋⎝ ⎛⎭⎪⎫43－23a x (0＜a ＜1，x ∈R )．若对于任意的三个实数x 1，x 2，x 3∈[1,2]，都有f (x 1)＋f (x 2)＞f (x 3)恒成立，求实数a 的取值范围.【导学号：68334025】[解] 因为f ′(x )＝x 2＋⎝ ⎛⎭⎪⎫a －83x ＋⎝ ⎛⎭⎪⎫43－23a ＝⎝ ⎛⎭⎪⎫x －23(x ＋a －2)，2分 所以令f ′(x )＝0，解得x 1＝23，x 2＝2－a .3分由0＜a ＜1，知1＜2－a ＜2.所以令f ′(x )＞0，得x ＜23或x ＞2－a ；4分令f ′(x )＜0，得23＜x ＜2－a ，所以函数f (x )在(1,2－a )上单调递减，在(2－a,2)上单调递增.5分所以函数f (x )在[1,2]上的最小值为f (2－a )＝a6(2－a )2，最大值为max{f (1)，f (2)}＝max ⎩⎨⎧⎭⎬⎫13－a 6，23a .6分 因为当0＜a ≤25时，13－a 6≥23a ；7分 当25＜a ＜1时，23a ＞13－a6，8分由对任意x 1，x 2，x 3∈[1,2]，都有f (x 1)＋f (x 2)＞f (x 3)恒成立，得2f (x )min ＞f (x )max (x ∈[1,2])． 所以当0＜a ≤25时，必有2³a 6(2－a )2＞13－a 6，12分结合0＜a ≤25可解得1－22＜a ≤25；当25＜a ＜1时，必有2³a 6(2－a )2＞23a ，结合25＜a ＜1可解得25＜a ＜2－ 2.综上，知所求实数a 的取值范围是1－22＜a ＜2－ 2. 15分。

课时规范练16 定积分与微积分基本定理一、基础巩固组1.给出如下命题:① b a -1d x= ba d t=b-a (a ,b 为常数,且a<b );② 0-1 1-x 2d x= 10 1-x 2d x=π4;③ a -a f (x )d x=2 a0f (x )d x (a>0). 其中正确命题的个数为( )A.0B.1C.2D.32.(2017安徽合肥模拟)由曲线f (x )= x 与y 轴及直线y=m (m>0)围成的图形的面积为83,则m 的值为( ) A.2 B.3 C.1 D.83.(2017广东广州质检)定积分 2-2|x 2-2x|d x=( ) A.5 B.6 C.7 D.8 4.(2017广东汕头考前冲刺,理4)若a= 20x d x ,则二项式 ax x5展开式中含x 2项的系数是() A.80 B.640 C.-160 D.-405.(2017河北邯郸一模,理8)如图,在边长为2的正方形ABCD 中,M 是AB 的中点,则过C ,M ,D 三点的抛物线与CD 围成的阴影部分的面积是( )A.23B.43C.5D.8 〚导学号21500716〛6.若函数f (x )=x m +ax 的导函数为f'(x )=2x+1,则 21f (-x )d x 的值为( )A.56 B.12C.23D.16 7.(2017河南焦作二模,理4)在区间 0,π2 上任选两个数x 和y ,则事件“y<sin x ”发生的概率为( )A .22B .1-42C .42D .1-228.曲线y=x 2与直线y=x 所围成的封闭图形的面积为 .9.一列火车在平直的铁轨上行驶,由于遇到紧急情况,火车以速度v (t )=5-t+55(t 的单位:s,v 的单位:m/s)紧急刹车至停止.在此期间火车继续行驶的距离是 m .10.已知函数f (x )=ax 2+c (a ≠0),若 10f (x )d x=f (x 0),0≤x 0≤1,则x 0的值为 .二、综合提升组11.(2017北京东城区二模,理6)若a= 20(1-2x )d x ,则二项式 1x 2+a 6的常数项是( ) A.240 B.-240 C.-60 D.6012.某物体在力F (x )= 10,0≤x ≤2,3x +4,x >2(单位:N)的作用下沿与力F (x )相同的方向运动了4 m,则力F (x )所做的功为 ( )A.44 JB.46 JC.48 JD.50 J13.(2017安徽黄山二模,理7)已知a=10(x2-1)d x,b=1-log23,c=cos5π,则a,b,c的大小关系是()A.a<b<cB.c<a<bC.a<c<bD.b<c<a14.图中阴影部分的面积是()A.16B.18C.20D.2215.若函数f(x)在R上可导,f(x)=x3+x2f'(1),则20f(x)d x=.三、创新应用组16.(2017河南洛阳三模,理5)已知数列{a n}为等差数列,且a2 016+a2 018=24-x2d x,则a2 017的值为()A.π2B.2πC.π2D.π〚导学号21500717〛17.已知函数f(x)=ax3+b(a≠0),若2f(x)d x=2f(x0),则x0等于()A.±2B.3C.-23 D.2课时规范练16 定积分与微积分基本定理1.B 由于 ba -1d x=a-b , ba d t=b-a ,所以①错误;由定积分的几何意义知, 0-1 1-x 2d x 和 10 1-x 2d x 都表示半径为1的圆面积的14,所以都等于π4,所以②正确;只有当函数f (x )为偶函数时,才有 a-a f (x )d x=2 a 0f (x )d x ,所以③错误,故选B . 2.AS= m 20(m- x)d x= mx -23x 32 0m 2=m 3-23m 3=83,解得m=2.3.D ∵|x 2-2x|= x 2-2x ,-2≤x <0,-x 2+2x ,0≤x ≤2,∴ 2-2|x 2-2x|d x= 0-2(x 2-2x )d x+ 20(-x 2+2x )d x= 13x 3-x 2 -20+ -13x 3+x 2 02=8. 4.Aa= 20x d x=12x 2 02=12×4=2,则二项式 ax x 5即 2xx 5, 易求得二项式展开式中x 2项的系数为80,故选A .5.D 由题意,建立如图所示的坐标系,则D (2,1).设抛物线方程为y 2=2px (p>0),将D (2,1)代入,可得p=14,∴y= 12x , ∴S=2 20 12x d x= 2·23x 32 02=83,故选D .6.A 由于f (x )=x m+ax 的导函数为f'(x )=2x+1,所以f (x )=x 2+x ,于是 21f (-x )d x= 21(x 2-x )d x= 13x 3-12x 2 12=56. 7.C 在区间 0,π2 上任选两个数x 和y ,点(x ,y )构成的区域的面积为π24,满足y<sin x 的点(x ,y )构成的区域的面积为 π20sin x d x=(-cos x ) 0π2=1,所以所求的概率为4π2.故选C .8.16 曲线y=x 2与直线y=x 所围成的封闭图形如图中阴影部分所示,由 y =x ,y =x 2,解得x=0或x=1,所以S=10(x-x 2)d x= 12x 2-13x 3 01=12−13=16.9.55ln 11 令5-t+551+t =0,由t>0,得t=10,即经过的时间为10 s .行驶的距离s= 100 5-t +55t +1 d t= 5t -12t 2+55ln (t +1) 010 =55ln 11.10.33 ∵ 10f (x )d x= 10(ax 2+c )d x= 13ax 3+cx 01=13a+c=f (x 0)=a x 02+c , ∴x 02=13,x 0=± 33.又0≤x 0≤1,∴x 0= 33.11.D a= 20(1-2x )d x=(x-x 2) 02=2-22=-2,易求二项式 12x 2-2x6展开式中的常数项为60,故选D . 12.B 力F (x )所做的功为 2010d x+ 42(3x+4)d x=20+26=46(J). 13.B ∵a= 10(x 2-1)d x= 1x 3-x 01=1-1=-2≈-0.667, b=1-log 23=1-lg3lg2≈-0.58,c=cos 5π6=- 32≈-0.866,∴c<a<b ,故选B . 14.B15.-4 因为f (x )=x 3+x 2f'(1),所以f'(x )=3x 2+2xf'(1).所以f'(1)=3+2f'(1),解得f'(1)=-3. 所以f (x )=x 3-3x 2.故 20f (x )d x= 20(x 3-3x 2)d x= x 44-x 3 02=-4. 16.A 20 4-x 2d x 表示以原点为圆心,以2为半径的圆的面积的四分之一,则a 2 016+a 2 018= 20 4-x 2d x=π.∵数列{a n }为等差数列,∴a 2 017=12(a 2 016+a 2 018)=π2,故选A .17.B ∵ 20f (x )d x= 20(ax 3+b )d x= 14ax 4+bx 02=4a+2b ,∴4a+2b=2(a x 03+b ),解得x 0= 23,故选B .。

专题对点练1选择、填空题的解法专题对点练第1页一、选择题1.方程ax2+2x+1=0至少有一个负根的充要条件是()A.0<a≤1B.a<1C.a≤1D.0<a≤1或a<0答案C解析当a=0时,x=-错误!未找到引用源。

,符合题意,排除A,D;当a=1时,x=-1,符合题意,排除B.故选C.2.设f(x)=ln x,0<a<b,若p=f(错误!未找到引用源。

),q=f错误!未找到引用源。

,r=错误!未找到引用源。

[f(a)+f(b)],则下列关系式中正确的是()A.q=r<pB.q=r>pC.p=r<qD.p=r>q答案C解析f(x)=ln x是增函数,根据条件不妨取a=1,b=e,则p=f(错误!未找到引用源。

)=ln错误!未找到引用源。

,q=f错误!未找到引用源。

>f(错误!未找到引用源。

)=错误!未找到引用源。

,r=错误!未找到引用源。

·[f(1)+f(e)]=错误!未找到引用源。

.在这种特例情况下满足p=r<q,所以选C.3.(2016河北衡水中学一模,理3)在等差数列{a n}中,错误!未找到引用源。

是一个与n无关的常数,则该常数的可能值的集合为()A.{1}B.错误!未找到引用源。

C.错误!未找到引用源。

D.错误!未找到引用源。

答案B解析∵错误!未找到引用源。

是一个与n无关的常数,∴结合选项令错误!未找到引用源。

=1, 则数列{a n}是一个常数列,满足题意;令错误!未找到引用源。

,设等差数列的公差为d,则a n=错误!未找到引用源。

a2n=错误!未找到引用源。

(a n+nd),∴a n=nd,即a1+(n-1)d=nd,化简,得a1=d,也满足题意;错误!未找到引用源。

=0,则a n=0,a2n=0,不满足题意.故选B.4.若(1+mx)6=a0+a1x+a2x2+…+a6x6,且a1+a2+a3+…+a6=63,则实数m的值为()A.1B.-1C.-3D.1或-3答案D解析令x=0,则a0=1;令x=1,故(1+m)6=a0+a1+a2+…+a6.∵a1+a2+…+a6=63,∴(1+m)6=64=26.∴m=1或m=-3.5.已知定义在R上的函数f(x)满足:对任意实数x,都有f(1+x)=f(1-x),且f(x)在(-∞,1]上单调递增.若x1<x2,且x1+x2=3,则f(x1)与f(x2)的大小关系是()A.f(x1)<f(x2)B.f(x1)=f(x2)C.f(x1)>f(x2)D.不能确定答案C解析由f(1+x)=f(1-x)知,函数y=f(x)的图象关于直线x=1对称.又f(x)在(-∞,1]上单调递增,所以f(x)在[1,+∞)上单调递减.设点A(x1,0),B(x2,0),因为x1<x2,且x1+x2=3,则点A在点B的左侧,且AB的中点坐标为错误!未找到引用源。

[组合练一]单独成册一、选择题1．集合A＝{x|－2≤x≤2}，B＝{y|y＝x，0≤x≤4}，则下列关系正确的是() A．A⊆∁R B B．B⊆∁R AC．∁R A⊆∁R B D．A∪B＝R解析：依题意得B＝{y|0≤y≤2}，因此B⊆A，∁R A⊆∁R B，选C.答案：C2．(2017·河南八市联考)复数z＝3＋i1＋i＋3i在复平面内对应的点所在的象限为()A．第一象限B．第二象限C．第三象限D．第四象限解析：z＝3＋i1＋i＋3i＝(3＋i)(1－i)(1＋i)(1－i)＋3i＝4－2i2＋3i＝2－i＋3i＝2＋2i，故z在复平面内对应的点在第一象限，故选A. 答案：A3．函数f(x)＝1x＋ln|x|的图象大致为()解析：因为f(1)＝1，排除A项；当x>0时，f(x)＝1x＋ln x，f′(x)＝－1x2＋1x＝x－1x2，所以当0<x<1时，f′(x)<0，f(x)单调递减，当x>1时，f′(x)>0，f(x)单调递增，排除D项，又f(－1)＝－1，所以排除C项，故选B.答案：B4．已知直线l ，m ，平面α，l ⊄α且m ∥α，则“l ∥m ”是“l ∥α”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分也不必要条件解析：利用线面平行的判定和性质判断充分性和必要性．若l ⊄α，m ∥α，l ∥m ，则l ∥α，所以充分性成立；反之，若l ∥α，l ⊄α，m ∥α，则l ，m 的位置关系不确定，可能平行、相交或异面，所以必要性不成立，故“l ∥m ”是“l ∥α”的充分不必要条件，故选A. 答案：A5．(2017·湖南东部五校联考)函数f (x )＝⎩⎨⎧2e x －1，x ＜2，log 3(x 2－1)，x ≥2，则不等式f (x )＞2的解集为( ) A ．(－2,4)B ．(－4，－2)∪(－1,2)C ．(1,2)∪(10，＋∞)D ．(10，＋∞)解析：当x ＜2时，令2e x －1＞2，解得1＜x ＜2；当x ≥2时，令log 3(x 2－1)＞2，解得x ＞10，故选C. 答案：C6．(2017·重庆模拟)某几何体的三视图如图所示，则该几何体的体积为( )A.23 B.43 C.53D.73解析：依题意，题中的几何体是由一个直三棱柱与一个三棱锥所组成的，其中该直三棱柱的底面是一个直角三角形(直角边长分别为1,2)、高为1；该三棱锥的底面是一个直角三角形(直角边长分别为1,2)、高为1，因此该几何体的体积为12×2×1×1＋13×12×2×1×1＝43，选B. 答案：B7．已知双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的一条渐近线的方程是y ＝32x ，且双曲线的一个焦点在抛物线y 2＝47x 的准线上，则双曲线的方程为( ) A.x 221－y 228＝1 B.x 24－y 23＝1 C.x 228－y 221＝1D.x 23－y 24＝1解析：双曲线的渐近线方程是y ＝±b a x ，所以b a ＝32，抛物线的准线方程为x ＝－7，所以c ＝7，由a 2＋b 2＝c 2，可得a 2＝4，b 2＝3，故选B. 答案：B8．(2017·赣州摸底)甲、乙、丙3名教师安排在10月1日至5日的5天中值班，要求每人值班一天且每天至多安排一人，其中甲不在10月1日值班且丙不在10月5日值班，则不同的安排方法有( ) A ．36种 B ．39种 C ．42种D ．45种解析：当甲安排在10月2日值班时，则丙可以安排在1,3,4日中某一天，乙可以在剩余的3日中选一天，有C 13C 13＝9种排法，同理可得甲安排在10月3日，4日中的一天值班时，有C 13C 13＋C 13C 13＝18种排法；当甲安排在10月5日值班时，有A 24＝12种排法，所以不同的安排方法有9＋18＋12＝39种，故选B.答案：B 二、填空题9．已知n ＝∫e 611x d x ，那么(x 2－1x )n 的展开式中的常数项为________．解析：n ＝⎠⎛ 1e 61x d x ＝ln x | e 61＝ln e 6－ln 1＝6－0＝6，(x 2－1x )6的通项公式为T r ＋1＝C r 6(x 2)6－r ·(－1x)r ＝C r 6(－1)r x12－3r，令12－3r ＝0，得r ＝4，故展开式中的常数项为T 5＝C 46(－1)4＝15.答案：1510．(2017·东北三省四市模拟)在某次数学考试中，甲、乙、丙三名同学中只有一个人得了优秀．当他们被问到谁得到了优秀时，丙说：“甲没有得优秀．”乙说：“我得了优秀．”甲说：“丙说的是真话．”事实证明：在这三名同学中，只有一人说的是假话，那么得优秀的同学是________．解析：分析题意只有一人说假话可知，甲与丙必定说的都是真话，故说假话的只有乙，即乙没有得优秀，甲也没有得优秀，得优秀的是丙． 答案：丙11．(2016·广西模拟)已知在三角形ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，面积S ＝a 2－(b －c )2，b ＋c ＝8，则S 的最大值是________．解析：因为S ＝a 2－(b －c )2，所以12bc sin A ＝－(b 2＋c 2－a 2)＋2bc ，所以12bc sin A＝2bc －2bc cos A ，所以sin A ＝4(1－cos A )，所以sin A ＝817，所以S ＝12bc sin A ＝417bc ≤417⎝ ⎛⎭⎪⎫b ＋c 22＝6417. 答案：641712．已知函数f (x )＝⎩⎪⎨⎪⎧x ln x ，x ≥1，ln xx，0<x <1，对于正数x ，有x ＝f ⎝ ⎛⎭⎪⎫1x ＋2 017＋f⎝ ⎛⎭⎪⎫1x ＋2 016＋…＋f ⎝ ⎛⎭⎪⎫1x ＋1＋f (x )＋f (x ＋1)＋…＋f (x ＋2 017)，则x ＝________. 解析：当x >1时，f (x )＝x ln x ，则0<1x <1，所以f ⎝ ⎛⎭⎪⎫1x ＝ln 1x1x ＝－x ln x ，所以f (x )＋f⎝ ⎛⎭⎪⎫1x ＝0，x ＝f ⎝ ⎛⎭⎪⎫1x ＋2 017＋f ⎝ ⎛⎭⎪⎫1x ＋2 016＋…＋f ⎝ ⎛⎭⎪⎫1x ＋1＋f (x )＋f (x ＋1)＋…＋f (x ＋2 017)＝f (x )．又f (1)＝0，所以当x ≥1时，x ＝f (x )＝x ln x ，所以ln x ＝1，所以x ＝e>1，符合题意；当0<x<1时，0<x＝f(x)＝ln xx<0，矛盾，故x＝e.答案：e。