电工技术第3章 习题解答
- 格式:ppt
- 大小:328.50 KB
- 文档页数:18

第三章直流电路3.1闭合电路欧姆定律填空题1、闭合电路由两部分组成,一部分是电路,另一部分是电路。
外电路上的电阻称为电阻,内电路上的电阻称为电阻。
2、负载上的电压等于电源的电压,也等于电源的电动势减去电源的内压降,即U=E-Ir。
选择题1、用万用表测得全电路中的端电压为0,这说明()A外电路断路 B外电路短路 C外电路上电流比较小 D电源内阻为零2、用电压表测得电源端电压为电源的电动势E,这说明()A 外电路断路B 外电路短路C 电源内阻为零D无法判断3、电源电动势为2V,内电阻是0.1Ω,当外电路断路时电路中的电流和端电压分别为()A、0A,2VB、20A,2VC、20A ,0VD、0V ,0V4、在闭合电路中,负载电阻减少,则端电压将()。
A、增大B、减小C、不变D、不能确定5、一直流电源,开路时测得其端电压为6V,短路时测得其短路电流为30A,则该电源的电动势E和内阻r分别为()。
A、6V,0.5ΩB、16V,0.2ΩC、6V,0.2Ω判断题1、全电路中,在开路状态下,开路电流为零,电源的端电压也为零。
()2、短路电流很大,要禁止短路现象。
()3、短路状态下,电源内阻的压降为零。
()4、当外电路开路时,电源的端电压等于零()计算题1、如图所示,电源电动势E=4.5V,内阻r=0.5Ω,外接负载R=4Ω,则电路中的电流I=? 电源的端电压U=?电路的内压降U=?2.如下图,已知电源电动势E=110V,r=1Ω,负载R=10Ω,求:(1)电路电流;(2)电源端电压;(3)负载上的电压降;(4)电源内阻上的电压降。
3.如下图所示,已知E=5V,r=1Ω,R1=14Ω,R2=20Ω,R3=5Ω。
求该电路电流大小应为多少?R2两端的电压是多少?4.如图所示电路中,已知E=12V,r=1Ω,负载R=99Ω。
求开关分别打在1、2、3位置时电压表和电流表的读数5、如图所示,E=220V,负载电阻R为219Ω,电源内阻r为1Ω,试求:负载电阻消耗的功率P负、电源内阻消耗功率P内及电源提供的功率P。
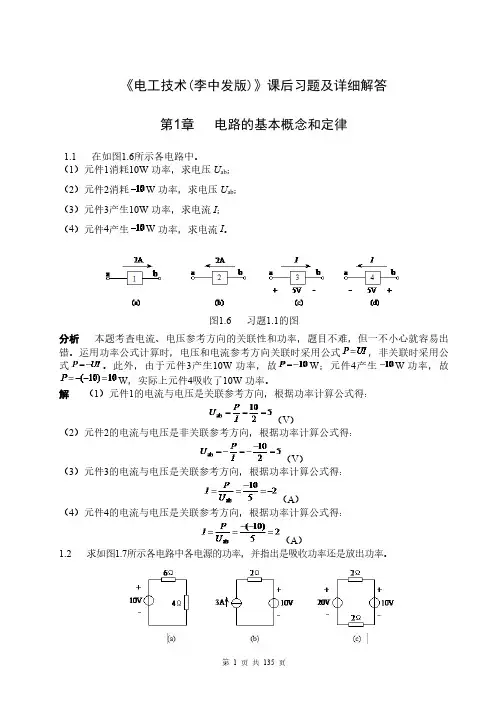

第3章单相正弦电路分析已知正弦电压(V)、(V),则u1与u2的相位差为,是否正确?为什么?分析讨论相位差问题时应当注意,只有同频率正弦量才能对相位进行比较。
这是因为只有同频率正弦量在任意时刻的相位差是恒定的,能够确定超前、滞后的关系,而不同频率正弦量的相位差是随时间变化的,无法确定超前、滞后的关系,因此不能进行相位的比较。
解不正确。
因为u1的角频率为ω,而u2的角频率为2ω,两者的频率不同,相位差随时间变化,无法确定超前、滞后的关系,因此不能进行相位的比较。
已知某正弦电流的有效值为10 A,频率为50 Hz,初相为45°。
(1)写出该电流的正弦函数表达式,并画出波形图;(2)求该正弦电流在s时的相位和瞬时值。
解(1)由题设已知正弦电流的有效值A,频率Hz,初相。
由频率f可得角频率ω为:(rad/s)所以,该电流的正弦函数表达式为:(A)波形图如图所示。
(2)s时的相位为:(rad)瞬时值为:(A)已知正弦电流(A)、(A),试求i1与i2的振幅、频率、初相、有效值和相位差,并画出其波形图。
解i1与i2的振幅分别为:(A)(A)频率分别为:(Hz)初相分别为:有效值分别为:(A)(A)i1与i2的相位差为:说明i1超前i2。
波形图如图所示。
图习题解答用图图习题解答用图设,,试计算、、AB、。
分析复数可用复平面上的有向线段、代数型、三角函数型和指数型(极坐标型)等形式表示。
复数的加减运算就是将实部和虚部分别进行加减,因而采用代数型比较方便。
复数的乘法运算就是将模相乘而辐角相加,复数的除法运算就是将模相除而辐角相减,因而采用指数型(极坐标型)比较方便。
解写出下列各正弦量所对应的相量,并画出其相量图。
(1)(mA)(2)(A)(3)(V)(4)(V)分析用相量来表示正弦量,就是用一个复数来反映正弦量的振幅(或有效值)和初相,即用相量的模来代表正弦量的振幅(或有效值),用相量的辐角来代表正弦量的初相。


第3章 正弦交流电路的稳态分析本章的主要任务是学习正弦量、正弦交流电路和相量法的基本概念、正弦交流电路的稳态分析与计算、正弦交流电路功率的概念和计算。
在此基础上理解和掌握功率因数提高的意义,和谐振的概念。
本章基本要求(1) 正确理解正弦量和正弦交流电路概念; (2) 正确理解相量法引入的意义;(3) 正确理解有功功率和功率因数的概念; (4) 掌握相量法;(5) 掌握电路定律的相量形式和元件约束方程的相量形式; (6) 分析计算正弦稳态电路; (7) 了解功率因数提高的意义; (8) 了解谐振的概念。
本章习题解析3-1 已知正弦电压和电流的三角函数式,试用有效值相量表示它们,并画出它们的相量图。
(1))20sin(210 +=t i ωA ,)60sin(2150 +=t u ωV (2))20sin(28 -=t i ωA ,)45sin(2120 -=t u ωV (3))30sin(25 +=t i ωA ,)90sin(2100 +=t u ωV解 (1)︒∠=2010IA ,︒∠=60150U V ,相量图如图3-1(a )所示。
(2))20(10︒-∠=IA ,)45(120︒-∠=U V ,相量图如图3-1(b )所示 (3)︒∠=305IA ,︒∠=90100U V ,相量图如图3-1(c )所示3-2 已知电压、电流的相量表示式,试分别用三角函数式、波形图及相量1+j (a )1+(b )1+j(c )图3-1图表示它们。
(1)4030j U+= V ,43j I += A (2)100=UV ,43j I -= A (3)V 10045 j e U=,A 44j I +=解 (1))13.53(504030︒∠=+=j U=︒+︒13.53sin 5013.53cos 50j ,V )13.53(543︒∠=+=j I=︒+︒13.53sin 513.53cos 5j ,A 波形图相量图如图3-2(a )所示。

习题3.1 某三相同步发电机,三相绕组连接成星形时的线电压为10.5kV ,若将它连接成三角形,则线电压是多少?若连接成星形时,B 相绕组的首末端接反了,则3 个线电压的有效值 U AB 、U BC 、U CA 各是多少?解:三相绕组连接成星形时U L =3U P ,线电压为10.5kV ,则每相绕组的电压为6.06kV ,若连接成三角形U L =U P ,则线电压为6.06kV 。
若连接成星形时,B 相绕组的首末端接反了,则B 相相电压的相位与原来的相差1800, 根据相量计算可得U AB =6.06 kV 、U BC =6.06 kV 、U CA =10.5 kV 。
3.2 题3.2 图所示的三相对称电路,线电压U L =380V ,每相负载Z = 6+j8Ω,试求相电压、相电流和线电流,并画出电压和电流的相量图。
题3.2 图解:由题意:负载作星接U l =3U p 因U l =380V ,则U a =U b =U c = = 220 (V )设U a = 220/0°(V )因相电流即线电流,其大小为:.220/0°I A == 22/−53°(A) 6 + j 8.I B = 22/−173ο(A).I C = 22/67°(A) 此时的相量图略。
3.3 有一电源和负载都是星形连接的对称三相电路,已知电源相电压为220V ,负载每相阻抗Z = Ω10 ,试求负载的相电流和线电流。
3 380第3 章三相交流电路习题解答77解:负载的相电压等于电源的相电压:U p = 220(V)U P 220(A)I l = I p = = = 22Z 103.4 已知星形联接的对称三相负载,每相阻抗为40∠25°(Ω);对称三相电源的线电压为380V。
求: 负载相电流,并绘出电压、电流的相量图。
解:UAB =380VZ=40∠25°Ω(1)三相对称电源接入三相对称负载令U A =220∠0°V则相线电流I A =U A /Z=5.5∠-25°VI B =5.5∠-145°VI c =5.5∠95°V(2) 矢量图如图所示。

第三章直流电路3.1闭合电路欧姆定律填空题1、闭合电路由两部分组成,一部分是电路,另一部分是电路。
外电路上的电阻称为电阻,内电路上的电阻称为电阻。
2、负载上的电压等于电源的电压,也等于电源的电动势减去电源的内压降,即U=E-Ir。
选择题1、用万用表测得全电路中的端电压为0,这说明()A外电路断路 B外电路短路 C外电路上电流比较小 D电源内阻为零2、用电压表测得电源端电压为电源的电动势E,这说明()A 外电路断路B 外电路短路C 电源内阻为零D无法判断3、电源电动势为2V,内电阻是0.1Ω,当外电路断路时电路中的电流和端电压分别为()A、0A,2VB、20A,2VC、20A ,0VD、0V ,0V4、在闭合电路中,负载电阻减少,则端电压将()。
A、增大B、减小C、不变D、不能确定5、一直流电源,开路时测得其端电压为6V,短路时测得其短路电流为30A,则该电源的电动势E和内阻r分别为()。
A、6V,0.5ΩB、16V,0.2ΩC、6V,0.2Ω判断题1、全电路中,在开路状态下,开路电流为零,电源的端电压也为零。
()2、短路电流很大,要禁止短路现象。
()3、短路状态下,电源内阻的压降为零。
()4、当外电路开路时,电源的端电压等于零()计算题1、如图所示,电源电动势E=4.5V,内阻r=0.5Ω,外接负载R=4Ω,则电路中的电流I=? 电源的端电压U=?电路的内压降U=?2.如下图,已知电源电动势E=110V,r=1Ω,负载R=10Ω,求:(1)电路电流;(2)电源端电压;(3)负载上的电压降;(4)电源内阻上的电压降。
3.如下图所示,已知E=5V,r=1Ω,R1=14Ω,R2=20Ω,R3=5Ω。
求该电路电流大小应为多少?R2两端的电压是多少?4.如图所示电路中,已知E=12V,r=1Ω,负载R=99Ω。
求开关分别打在1、2、3位置时电压表和电流表的读数5、如图所示,E=220V,负载电阻R为219Ω,电源内阻r为了1Ω,试求:负载电阻消耗的功率P负、电源内阻消耗功率P内及电源提供的功率P。


(1)Z =(6+j8);(2)U =50 30V,I =2 30�A; (3)U =100 30V,I =4 40�A3.3.1在图图3.6(教材图图3.01)所示 电路中,已知 R = 100 & , L = 31.8 mH,C = 318 ∝ F, 求电源的频率和电压分别为50 Hz 、100 V 和1 000 Hz ,100 V 两种情况下,开关S合向 a 、b 、c 位置时电流表的读数,并 计算各元件中的有功功率和无功功率。
3.4.1在图3.7(教材图3.02)所示电路中,三个照明相同,R = X C = X L ,试问接于交流电源上时,照明灯的亮度有什么不同?若该接到电压相同的直流电源上,稳定后,与接交流电 源时相比,各照明灯的亮度有什么变化?3.4.2求串联交流电路中下列三种情况下电路中的 R 和 X 各为多少?指出电路的性质和电压对电流的相位差• •� • •�时,电路中的电流为2mA ,电容电压U C 滞后于电源电压U 60 3.4.5电流如图3.9(教材图•3.03)求:()I 和U 1、U 2;(2)改变Z 2为何3.4.3将一个电感线圈接到 20 V 直流电源时,通过的电 流为1A ,将此线圈该接于2 000Hz 、20 V 的电源时,电流为 0.8 A 。
求该线圈的电阻 R 和电感 L 。
3.4.4一个 R 、C 串联电路,当输入电压为1 000 Hz 、12V • •,求 R 和 C 。
图3.9图3.03 所示, 1 = (6 + j8) & , Z 2 = j10 & ,U S = 15 0� V • • •(1(2 值时,电路中的电流最大,这时的电流 是多少? 图3.99�V ,U 1超前于U 90,超前于I 30�,求U 1和U 2。
•••3.4.6在图3.10(教材图3.04)所示电路中,已知 U =220 �3.5.1电路如图3.12(教材图3.05)•Z 1 = (2 + j2) & , Z 2 = (3 + j3) & , I S = 5 0�• •求各支路电流 I 1 、I 2和理想电流源的端电压。

第3章习题答案3.2.1 选择题1.晶体管能够放大的外部条件是___C______。
(a) 发射结正偏,集电结正偏 (b) 发射结反偏,集电结反偏(c) 发射结正偏,集电结反偏2.当晶体管工作于饱和状态时,其__A_______。
(a) 发射结正偏,集电结正偏 (b) 发射结反偏,集电结反偏(c) 发射结正偏,集电结反偏3. 测得晶体管三个电极的静态电流分别为0.06mA,3.66mA和3.6mA。
则该管的为___C______。
(a) 40 (b) 50 (c) 604.反向饱和电流越小,晶体管的稳定性能___A______。
(a) 越好 (b) 越差 (c) 无变化5.温度升高,晶体管的电流放大系数b___A______。
(a) 增大 (b) 减小 (c) 不变6.温度升高,晶体管的管压降|UBE|__B_______。
(a) 升高 (b) 降低 (c) 不变7.对PNP型晶体管来说,当其工作于放大状态时,__C______极的电位最低。
(a) 发射极 (b) 基极 (c) 集电极8.温度升高,晶体管输入特性曲线____B____。
(a) 右移 (b) 左移 (c) 不变9.温度升高,晶体管输出特性曲线___A_____。
(a) 上移 (b) 下移 (c) 不变10.温度升高,晶体管输出特性曲线间隔___C_____。
(a) 不变 (b) 减小 (c) 增大11.晶体管共射极电流放大系数b随集电极电流iC___B_____。
(a) 不变化 (b) 有一定变化 (c) 无法判断12.当晶体管的集电极电流时,下列说法正确的是__C_____。
(a) 晶体管一定被烧毁 (b) 晶体管的(c) 晶体管的一定减小13.对于电压放大器来说,___B____越小,电路的带负载能力越强。
(a) 输入电阻 (b) 输出电阻 (c) 电压放大倍数14.在单级共射放大电路中,若输入电压为正弦波形,则输出与输入电压的相位___B____。

第三章 电路的暂态分析含有电感或电容储能元件的电路,在换路时会出现暂态过程。
本章研究了暂态过程中电压与电流的变化规律。
主要内容:1.暂态过程的基本概念。
2.换路定则:在换路瞬间,电容电流和电感电压为有限值的情况下,电容电压 和电感电流在换路前后的瞬间保持不变。
3.RC 电路的零输入响应、零状态响应和全响应。
4.RL 电路的零输入响应、零状态响应和全响应。
5.一阶线性电路暂态分析的三要素法:一阶线性电路在直流激励下的全响应零、 输入响应和零状态响应都可以用三要素法τte f f f t f -+∞-+∞=)]()0([)()(来求出。
6.暂态过程的应用:对于RC 串联电路,当输入矩形脉冲,若适当的选择参数 和输出,可构成微分电路或积分电路。
[练习与思考]解答3-1-1什么是稳态?什么是暂态?解:当电路的结构、元件参数及激励一定时,电路的工作状态也就一定,且电流和电压为某一稳定的值,此时电路所处的工作状态就称为稳定状态,简称为稳态。
在含有储能元件的电路中,当电路的发生换路时,由于储能元件储的能量的变化,电路将从原来的稳定状态经历一定时间变换到新的稳定状态,这一变换过程称为过渡过程,电路的过渡过程通常是很短的,所以又称暂态过程。
3-1-2什么是暂态过程?产生暂态过程的原因是什么?解:含有储能元件的电路从一个稳态转变到另一个稳态的所需的中间过程称为电路的暂态过程(过渡过程)。
暂态过程产生的内因是电路中含有储能元件,外因是电路发生换路。
3-2-1 初始值和稳态值分别是暂态过程的什么时刻的值?解:初始值是暂态过程的+=0t 时刻的值,稳态值是暂态过程的∞=t 时刻的值。
3-2-2 如何求暂态过程的初始值?解:求暂态过程初始值的步骤为:⑴首先画出换路前-=0t 的等效电路,求出-=0t 时刻电容电压)0(-C u 和电感电流)0(-L i 的值。
对直流电路,如果换路前电路处于稳态,则电容相当于开路,电感相当于短路。
第3章电路的暂态过程一、思考题解答3.1 思考题【思3.1.1】电路在换路前储能元件没有储能,则在t=0-和t=0+的电路中,可将电容元件视为短路,电感元件视为开路。
如果换路前储能元件已有储能,且电路已处于稳态,则在t=0-电路中,电容元件视为开路,电感元件视为短路。
在t=0+电路中,电容元件可用一理想电压源代替,其电压为u C(0-);电感元件可用一理想电流源代替,其电流为i L(0-)。
【思3.1.2】根据换路定律可知,开关S断开瞬间电容器的电压值不能突变,则在t=0+时的等效电路可简化为如图3-2所示的电路。
u C(0+)=u C(0-)=112+×6=2V,i2(0+)=0,i1(0+)=i C(0+)=622-=2A【思3.1.3】根据换路定律可知,开关S断开瞬间电感的电流值不能突变,则在t=0+时的等效电路可简化为如图3-3所示的电路。
i L(0+)=i L(0-)=42=2A,U V=R V×i L(0+)=-2500×2=-5kV图3-2 思考题3.1.2的0+电路图图3-3 思考题3.1.3的0+电路图【思3.1.4】根据换路定律可知,开关S闭合瞬间电容器的电压值不能突变,则在t=0+时的等效电路可简化为如图3-4(a)所示的电路。
(1) i1(0+)=0,i(0+)=i2(0+)=100Au R1(0+)=100×1=100V,u R2(0+)=u C(0+)=0第3章 电路的暂态过程• 1 •1(2) i (∞)=i 1(∞)=100199+=1A ,i 2(∞)=0 u R1(∞)=1×1=1V ,u R2(∞)=u C (∞)=99×1=99 V(3) 根据换路定律可知,当S 闭合瞬间电感的电流值不能突变,则在t =0+时的等效电路可简化为如图3-4(b)所示的电路。
i 2(0+)=0,i (0+)=i 1(0+)=100199+=1A u R1(0+)=1×1=1V ,u R2(∞)=u L (0+)=99×1=99 V S 闭合后电路达到稳态时,i 1(∞)=0,i (∞)=i 2(∞)=1001=100A u R1(∞)=100×1=100V ,u R2(∞)=u C (∞)=(a) (b) 图3-4 思考题3.1.4的0+电路图【思3.1.5】i L (0+)=i L (0-)=013E R R R ++=12222++=2Au C (0+)=u C (0-)=2×2=4Vt =0+时的等效电路如图3-5所示,可得12=2×[2+i C (0+)]+2×i C (0+)+4 所以,i C (0+)=124422--+=1A ,u L (0+)=12-2×(2+1)-2×2=2V【思3.1.6】(1) 根据换路定律可知,开关S 闭合瞬间电容器可视为短路,各电感可视为开路。
第三章 正弦交流电路三、习题详解3-1 试计算下列正弦量的周期、频率和初相:(1))30314(sin 5 +t (2))60(cos 8+πt解 (1)周期 s 02.050131422==π=ωπ=T 频率 Hz 5002.011===T f初相 ︒=300ϕ(2)周期 s 222=ππ=ωπ=T频率 Hz 5.0211===T f初相 ︒=1500ϕ3-2 试计算下列各正弦量间的相位差:(1)A )30(sin 5)(1+ω=t t iA )30(sin 4)(2-ω=t t i(2)V )1520(cos 5)(1+=t t uV )3010(sin 8)(2-=t t u(3)V )45(sin 30)(+ω=t t uA )30(sin 40)(-ω=t t i解 (1)60303021=--=-=)(ϕϕϕ (2) 角频率不同,比较无意义。
(3) ︒=︒--︒=-=75)30(4521ϕϕϕ注意 ①通常只对同频率的两个正弦量才能做相位比较。
②求相位差时要将两个正弦量用相同的sin 函数或cos 函数表示。
③求相位差时,两个正弦量表达式前均带正号。
3-3 已知正弦量 30j 220e U =和A I3j 4--= ,试分别用三角函数式、正弦波形及相量图表示它们。
解 (1)30j 220e U= 三角函数式 )30sin(2220︒+ω=t u2t︒-30330︒图3-1题3-3正弦波形(2) A 3j 4--=I三角函数式 A )43a r c t g s i n (25π-+ω=t i 正弦波形,相量图可参照(1)答案画出。
注意 习惯上常取初相绝对值小于180°。
3-4 写出下列正弦量的相量表示式(1)A cos 25t i ω=(2)V )45314(cos 2125-=t u(3)A )605(sin 10--=t i解 (1)A cos 25t i ω=A t t t t i )90sin(25)90sin(25)90sin(25cos 25︒+=︒--=-︒==ωωωωA 905︒∠=∴I(2)V )45314(cos 2125-=t u)4531490sin(2125)45314(cos 2125︒+-︒=-=t t u)135314sin(2125)314135sin(2125︒--=-︒=t t )45314sin(2125)180135314sin(2125︒+=︒+︒-=t tV 45125︒∠=∴U(3)A )605(sin 10--=t iA )1205sin(10)180605sin(10)605(sin 10︒+=︒+︒-=--=t t t iA 12025︒∠=∴I注意 ①不能认为电流相量I等于正弦量i. 即≠I i. ②以余弦函数表示的正弦电流都要将其化为正弦表达式,再写出相量。
第三章三相电路一、单相选择题1.三相对称绕组在空间位置上应彼此相差(B )A 、60°电角度;B 、120°电角度;C 、180°电角度;D 、360°电角度。
2.三相对称电路是指(C )A 、三相电源对称的电路;B 、三相负载对称的电路;C 、三相电源和三相负载均对称的电路-D 、三相电源对称和三相负载均不对称的电路。
3. 有“220V 、100W ”“220V 、25W ”白炽灯两盏,串联后接入220V 交流电源,其亮度情况是(B )A 、100W 灯泡最亮;B 、25W 灯泡最亮;C 、两只灯泡一样亮;D 、100W 和25W 都不亮。
4.三相四线制供电线路,已知作星形联接的三相负载中U 相为纯电阻,V 相为纯电感,W 相为纯电容,通过三相负载的电流均为10安培,则中线电流为(A )A 、30安;B 、10安;C 、27.32安。
5. 在某对称星形连接的三相负载电路中,已知线电压u t AB = V 3802sin ,则C 相电压有效值相量C U 为( A )A 、22090VB 、38090VC 、22090VD 、903806.星型连接的三相对称负载,接于三相对称电源上,线电流与相电流之比为( C )。
A 、3B 、2C 、1D 、337. 额定电压为220 V 的照明负载接于线电压为380 V 的三相四线制电源时,必须接成( A) 形。
A 、B 、C 、Y 和都可以D 、Y 和都不可以8.当三相交流发电机的三个绕组连接成星形时,若线电压V t u BC)180sin(2380,则相电压Cu ( D )。
A 、V t )30sin(2220B 、V t )30sin(2380C 、Vt)120sin(2380D 、2202sin(30)t o9.有一对称三相电动势,若U 相电动势为V tu U )314sin(311则V 相和W 相电动势分别为(A)A 、V t u V t u W V )3314sin(311)3314sin(311B 、V t u V t u W V )3314sin(311)3314sin(311C 、V t u V t u W V )6314sin(311)6314sin(311D 、Vtu Vtu WV)6314sin(311)6314sin(31110.在三相交流电路中,三相堆成负载星形连接,三个线电流均为4A ,则中线电流为( A )。
第三章 正弦交流电路三、习题详解3-1 试计算下列正弦量的周期、频率和初相:(1))30314(sin 5 +t (2))60(cos 8 +πt解 (1)周期 s 02.050131422==π=ωπ=T 频率 Hz 5002.011===T f 初相 ︒=300ϕ(2)周期 s 222=ππ=ωπ=T 频率 Hz 5.0211===T f初相 ︒=1500ϕ3-2 试计算下列各正弦量间的相位差:(1)A )30(sin 5)(1 +ω=t t iA )30(sin 4)(2 -ω=t t i(2)V )1520(cos 5)(1 +=t t uV )3010(sin 8)(2 -=t t u (3)V )45(sin 30)( +ω=t t uA )30(sin 40)( -ω=t t i 解 (1) 60303021=--=-=)(ϕϕϕ(2) 角频率不同,比较无意义。
(3) ︒=︒--︒=-=75)30(4521ϕϕϕ注意 ①通常只对同频率的两个正弦量才能做相位比较。
②求相位差时要将两个正弦量用相同的sin 函数或cos 函数表示。
③求相位差时,两个正弦量表达式前均带正号。
3-3 已知正弦量 30j 220e U =和A I3j 4--= ,试分别用三角函数式、正弦波形及相量图表示它们。
解 (1)30j 220e U= 三角函数式 )30sin(2220︒+ω=t u2t︒-30330︒图3-1题3-3正弦波形(2) A 3j 4--=I三角函数式 A )43a r c t g s i n (25π-+ω=t i 正弦波形,相量图可参照(1)答案画出。
注意 习惯上常取初相绝对值小于180°。
3-4 写出下列正弦量的相量表示式(1)A cos 25t i ω=(2)V )45314(cos 2125 -=t u (3)A )605(sin 10 --=t i 解 (1)A cos 25t i ω=A t t t t i )90sin(25)90sin(25)90sin(25cos 25︒+=︒--=-︒==ωωωωA 905︒∠=∴I(2)V )45314(cos 2125 -=t u)4531490sin(2125)45314(cos 2125︒+-︒=-=t t u )135314sin(2125)314135sin(2125︒--=-︒=t t )45314sin(2125)180135314sin(2125︒+=︒+︒-=t tV 45125︒∠=∴U(3)A )605(sin 10 --=t iA )1205sin(10)180605sin(10)605(sin 10︒+=︒+︒-=--=t t t iA 12025︒∠=∴I注意 ①不能认为电流相量I等于正弦量i. 即≠I i. ②以余弦函数表示的正弦电流都要将其化为正弦表达式,再写出相量。
第三章 电路的暂态分析3.2.1 图3.01所示各电路在换路前都处于稳态,试求换路后其中电流i 的初始值(0)i +和稳态值()i ∞。
(b)(a)(c)(d)图3.01解: (a )A 5.1265.0)0(5.0)0(21)0(=×===−++L L i i i A 326)(==∞i(b )02662)0(62)0(6)0(=−=−−=−=++c c u u iA 5.1226)(=+=∞i (c )A 6)0()0(==−+i i A 0)(=∞i(d )A 75.04364)0(622)0(6)0(=−=−=+−=−++c c u u iA 12226)(=++=∞i3.4.1 在图3.07(a)的电路中,u 为一阶跃电压,如图3.07(b)所示,试求3i 和c u 。
设V 1)0(c =−u 。
(a)图3.07(b)解:s 102)(331312−×=++=C R R R R R τV 22224)(C =+×=∞u V 1)0()0(C C ==−+u u V 2)(500C t e t u −−=mA 75.0)(1)(4)0(31131312322323213=+++++++=+R R R R R R R R R R R R R R R R i mA 144)(3==∞imA 25.01)(5003t e t i −−=3.4.2 电路如图3.08所示,求0t ≥时(1)电容电压C u ,(2)B 点电位B v 和(3)A 点电位A v 的变化规律。
换路前电路处于稳态。
Sk 10图3.08解:(1)求0≥t 时的电容电压C uV 15255)6(0)0()0(C =×+−−==−+C u uV 5.1525510)6(6)(C =×++−−=∞u[]s 1044.010100105//)2510(6123−−×=×××+=τ故V 5.05.1)5.11(5.1)(66103.21044.0C t t e et u ×−×−−=−+=−t =0_时k 10t =0+时+6V Ωk 10(2)求0≥t 时的B 点电位B v注意,+=0t 时,由于电容中存在电流,0CC ≠=dtdu Ci 因此,10K 和5K 电阻中的电流不等。