微波射频学习笔记8.RLC谐振电路
- 格式:doc
- 大小:729.50 KB
- 文档页数:2

RLC串联谐振电路电路的研究RLC串联谐振电路是一种常用的电路结构,在电路中,电感(L),电容(C)和电阻(R)依次相连,形成一个串联电路。
该电路的谐振频率是指在该频率下,电感与电容产生的阻抗相等,电路中的电流可以达到最大值。
谐振频率可以根据电感、电容和电阻的数值计算得出。
RLC串联谐振电路的重要性在于其在信号处理和滤波器设计中的广泛应用。
谐振电路可以在特定频率下增强或阻止特定频率的信号,从而实现信号的选择性放大或抑制。
因此,了解和研究RLC串联谐振电路的工作原理、性质和特点对于电子工程师和电路设计师至关重要。
首先,研究RLC串联谐振电路的工作原理是必不可少的。
在谐振频率下,电感和电容的产生的阻抗相等,电路中的电流可以达到最大值。
这是因为在谐振频率下,电感和电容的阻抗具有相反的相位,可以抵消彼此。
而电阻对电路中的电流没有影响。
其次,研究RLC串联谐振电路的频率响应特性也是重要的。
频率响应是指电路对不同频率信号的响应程度。
在谐振频率附近,电路的频率响应表现为一个较为尖锐的共振峰,这意味着对谐振频率附近的信号具有较高的放大和传递能力。
而在谐振频率两侧,电路的频率响应衰减,对信号的传递能力较弱。
进一步,研究RLC串联谐振电路的品质因数也是重要的。
品质因数是指电路的质量或品质衡量指标,决定了电路的频率选择性和能量损耗。
品质因数可以通过电路的谐振频率与谐振曲线的带宽之比计算得出。
品质因数越大,电路的频率选择性越好,能量损耗越小。
此外,研究RLC串联谐振电路的稳定性和幅频特性也是重要的内容之一、稳定性是指电路对输入信号的幅度和相位变化的响应程度。
稳定性好的电路可以保持输入信号的形状和幅度,减少失真。
幅频特性表示电路的放大或衰减程度随频率变化的情况。
了解电路的幅频特性可以帮助设计者选择合适的频率范围,实现期望的信号处理效果。
最后,研究RLC串联谐振电路还需要关注电路中的各个元件的选取、参数的计算和电路的实际应用。

rlc电路谐振实验报告RLC电路是一种典型的振荡电路,也叫作可变阻抗指数电路。
RLC 电路中,R表示电阻,L表示电感,C表示电容。
它是一个非常重要的电路,广泛应用于信号滤波、频率分离的过程中。
RLC电路谐振实验是研究RLC电路谐振特性的实验,它可以让我们了解到RLC电路在谐振情况下的响应特征,从而更加深入地理解RLC电路的工作原理。
二、实验原理RLC电路的谐振特性是由它内部的高频振荡来实现的。
当RLC电路处于谐振情况时,就会出现低频振荡,从而产生持续的电压或电流振荡。
谐振点就是指在电路谐振时,电路输出的相位角和频率与输入的相位角和频率完全相同的情况。
在这种情况下,电路的反馈能力最大,能够达到最大反馈。
三、实验步骤实验步骤:1.制恒功率曲线:使用电脑绘制RLC电路的恒功率曲线,了解电路响应特性。
2.算谐振频率:计算由电感L、电容C和线性电阻R组成的RLC 电路的谐振频率。
3.率变换:调整谐振电路中的电阻或电感,改变谐振频率。
4.据采集:采集谐振状态下电路的输入信号与输出信号的时域信号图和频域信号图,以了解谐振电路的振荡行为。
四、实验结果1.功率曲线:由实验结果可知,RLC电路的恒功率曲线在谐振点处有最大反馈响应,表现出谐振现象。
2.率变换:由实验结果可知,调整RLC电路中的电阻或电感,可以改变谐振的频率。
3.域信号图:谐振状态下,电路的内部信号与外界输入信号同步,在时域信号图中表现出低频振荡的现象。
4.域信号图:谐振状态下,电路的内部信号与外界输入信号同步,在频域信号图中可看到谐振频率的高增益峰值。
五、结论从上述实验结果可以看出,RLC电路的恒功率曲线反映出它在谐振状态下的响应特性,由实验结果也可以了解到,调整RLC电路的电阻或电感可以改变谐振频率,谐振状态下,电路的内部信号与外界输入信号同步,在时域和频域信号图中都可以看到谐振频率的响应特性。
本实验证明,RLC电路可以实现低频振荡,并可以调节电路频率,达到满足应用需求的谐振特性。


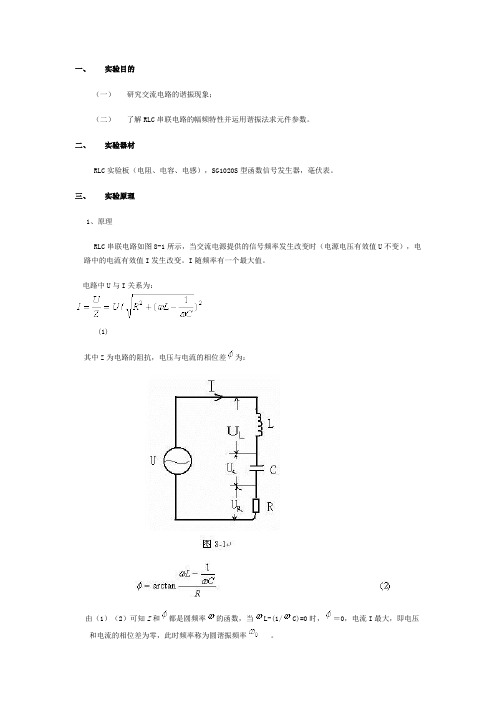
一、实验目的(一)研究交流电路的谐振现象;(二)了解RLC串联电路的幅频特性并运用谐振法求元件参数。
二、实验器材RLC实验板(电阻、电容、电感),SG1020S型函数信号发生器,毫伏表。
三、实验原理1、原理RLC串联电路如图8-1所示,当交流电源提供的信号频率发生改变时(电源电压有效值U不变),电路中的电流有效值I发生改变。
I随频率有一个最大值。
电路中U与I关系为: (1) 其中Z为电路的阻抗,电压与电流的相位差为:由(1)(2)可知Z和都是圆频率的函数,当L-(1/C)=0时,=0,电流I最大,即电压和电流的相位差为零,此时频率称为圆谐振频率。
=(3)RLC串联电路中,对I和频率f(f=)可以作一曲线,如图8-2,可以看到当时,I有一极大值。
(在实验中测量时,一般测量电阻两端电压,因为电阻两端电压和电路中I的变化是同步的。
)常用Q值标志谐振电路的性能,Q称为电路的品质因数,定义为谐振时电感上的电压U L和总电压U之比。
(4)由(4)式可知,串联谐振时,电容或电感上的电压是电源电压的Q倍。
因为Q往往是>>1的,所以U C 和U L可以比U大得多,因此串联谐振又称为电压谐振。
Q值还标志着电路的频率选择性,即谐振峰的尖锐程度。
通常规定I值为最大值I max的时的两点f1和f2频率之差为“通频带宽度”(图3)。
根据定义,=f2-f1=f0/Q (5)可见,Q值越大,带宽就越小,谐振曲线也就越尖锐。
当L=1/C时,=0 。
电流i与电压u的相位一致,电路达到谐振,R两端电压最大。
四、仪器描述1.毫伏表的使用仪器面板见图8-4(1)将“测量范围”开关放在最大量程,接通电源,预热5分钟。
(2)将两根输入线短路,然后使测量范围开关置于最小档,调节“零点校准”旋钮使电表指示为零。
(3)根据被测电压的大小,将“测量范围”开关放在所需量程,去掉短路线,即可进行测量。
2、信号发生器的使用见实验七五、实验步骤1、打开毫伏表电源,调整毫伏表零点。
RLC 串联谐振电路目的及要求:(1)设计电路(包括参数的选择)(2) 不断改变函数信号发生器的频率,测量三个元件两端的电压,以验证幅频特性。
(3)不断改变函数信号发生器的频率,利用示波器观察端口电压与电流相位,以验证发生谐振时的频率与电路参数的关系。
(4)用波特图示仪观察幅频特性 (5)得出结论进行分析并写出仿真体会。
二、工作原理:(1) RLC 串联电路(图 4-7-1)的阻抗是电源角频率ω的函数,即ϕωω<=⎪⎭⎫ ⎝⎛-+=Z C L J R Z 1当01=-CL ωω 时,电路处于串联谐振状态,谐振角频率为 LCo 1=ω谐振频率为 f LCf o π21=显然,谐振频率仅与元件 L 、C 的数值有关,而与电阻R 和激励电源的角频率ω无关。
当ω<ωo 时,电路呈容性,阻抗角φ<0;当ω>ωo 时,电路呈感性,阻抗角φ<0。
(2) 电路处于谐振状态时的特性① 由于回路总电抗X O =ωo-1/ωoC=0,因此,回路阻抗|Z 0|为最小值,整个回路相当于一个纯电阻电路,激励电源的电压与回路的响应电流同相位。
② 由于感抗ωoL 容抗1/ωoC 相等,所以电感上的电压U L ’与电容上的电压U C ’数值相等,相位相差1800。
电感上的电压(或电容 上的电压)与激励电压之比称为品质因数Q ,即:③ RC LR C R L U U U U Q O O S C S L =====ωω1L 和 C 为定值的条件下,Q 值仅仅决定于回路电阻 R 的大小。
③在激励电压(有效值)不变的情况下,回路中的电流I=U S /R 为最大值。
三、实验内容1、测量 RLC 串联电路响应电流的幅频特性曲线的U L (ω)、U C (ω)曲线 实验电路如图2-3所示。
确定元件R 、L 、C 的数值之后,保持正弦信号发生器输出电压 Us (有效值)不变,测量不同频率时的U R 、U L 和U C 。
第1篇一、RLC串联谐振电路的基本原理RLC串联谐振电路由电阻R、电感L和电容C三个元件组成。
当电路中电压或电流的频率发生变化时,电路的阻抗Z也会随之变化。
当电路的阻抗Z达到最小值时,电路处于谐振状态,此时的频率称为谐振频率。
二、谐振频率的计算1. 谐振频率的定义谐振频率是指RLC串联电路在谐振状态下,电路的阻抗Z达到最小值时的频率。
在谐振状态下,电路的电流I与电压U之间的相位差为0,即电流和电压同相位。
2. 谐振频率的计算公式RLC串联电路的谐振频率可以通过以下公式计算:\[ f_0 = \frac{1}{2\pi\sqrt{LC}} \]其中,\( f_0 \)表示谐振频率,L表示电感,C表示电容。
三、谐振频率的影响因素1. 电感L和电容C谐振频率与电感L和电容C的乘积成反比。
当电感L或电容C增大时,谐振频率会减小;反之,当电感L或电容C减小时,谐振频率会增大。
2. 电阻R电阻R对谐振频率没有直接影响,但会影响电路的品质因数Q。
品质因数Q定义为:\[ Q = \frac{f_0}{\Delta f} \]其中,\( \Delta f \)表示谐振曲线的带宽。
当电阻R增大时,品质因数Q减小,电路的带宽增大,谐振频率基本不变。
四、谐振频率在实际应用中的重要性1. 选择合适的谐振频率在实际应用中,选择合适的谐振频率可以提高电路的性能。
例如,在无线通信、信号传输等领域,通过选择合适的谐振频率,可以减小信号损耗,提高传输效率。
2. 提高电路的稳定性在电路设计和分析过程中,通过调整电感L和电容C的值,可以使电路在特定的频率下达到谐振状态,从而提高电路的稳定性。
3. 优化电路性能通过调整谐振频率,可以优化电路的性能。
例如,在滤波器设计中,通过选择合适的谐振频率,可以实现对特定频率信号的滤波。
五、总结RLC串联谐振电路的谐振频率是电路设计和分析中的一个重要参数。
通过掌握谐振频率的计算方法、影响因素以及在实际应用中的重要性,有助于我们更好地进行电路设计和优化。
RLC谐振
一、关于谐振的各种解释:
1. 当外力作用频率与系统固有振荡频率相同或很接近时,振幅急剧增大的现象。
产生谐振时的频率称“谐振频率”。
2. 包含电容和电感及电阻元件的无源一端口网络,其端口可能呈现容性、感性及电阻性,当电路端口的电压U和电流I,出现同相位,电路呈电阻性时。
称之为谐振现象,这样的电路,称之为谐振电路。
3. 谐振的实质是电容中的电场能与电感中的磁场能相互转换,此增彼减,完全补偿。
电场能和磁场能的总和时刻保持不变,电源不必与电容或电感往返转换能量,只需供给电路中电阻所消耗的电能。
4. 在物理学里,有一个概念叫共振,当驱动力的频率和系统的固有频率相等时,系统受迫振动的振幅最大,这种现象叫共振。
电路里的谐振其实也是这个意思:当电路中激励的频率等于电路的固有频率时,电路的电磁振荡的振幅也将达到峰值。
以上各种解释都是正确的,只是从不同角度的解读。
二、RLC谐振电路
谐振是正弦电路中可能发生的一种特殊现象。
由于回路在谐振状态下呈现某些特征,因此在工程中特别是电子技术中有着广泛的应用,但在电力系统中却常要加以防止。
1.串联谐振电路/电压谐振
当电路内平均存储的磁能和电能相等时,产生谐振,即容抗=感抗:谐振频率f0=1/(2πLC);
角频率ω0=2πf0;
品质因数Q值=1/(ω0RC),损耗低意味着Q值高,Q值高,频率选择
性越好,通带越窄,带外抑制越好;
带宽BW=f0/Q,所以Q值高意味着带宽窄;
此电路上,电感和电容电压远远大于回路电压,U L和U C=QU回路。
此谐振,电路阻抗最小,且为纯电阻,Z0=R。
谐振频率点f0,此时电容电感抵消,对外相当于一条导线,相当于短路。
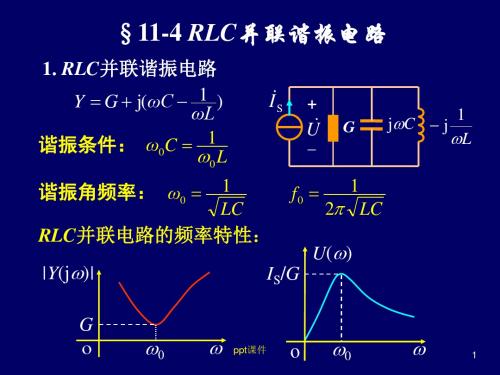
2.并联谐振电路/电流谐振
或
(图上G应该不是写错了,似乎这个电路也叫GLC并联电路,都是对的,但LC
一定要并联)
当电压和电流同相时,产生谐振:
谐振频率f0=1/(2πLC);
角频率ω0=2πf0;
品质因数Q值=1/(ω0RC),损耗低意味着Q值高,Q值高,频率选择性越好,通带越窄,带外抑制越好;
带宽BW=f0/Q,所以Q值高意味着带宽窄;
此电路上,电感和电容电流远远大于回路电压,I L和I C=QI回路。
此谐振,回路导纳最小,且为纯电导,回路阻抗最大,Z0=L/RC。