112数学建模与数学实验实验指导书

数学建模课程设计指导书课程名称：《数学建模》课程设计时间：两周开课学期：第五学期课程设计目的：通过对《数学建模与数学实验》的学习，使学生初步了解数学建模的过程与思想。

在课程结束后，进行课程设计其目的是培养学生综合运用所学知识和技能、独立分析和解决问题的能力，提高学生的数学修养与素质，增强学生学习的兴趣，加强学生的科学研究的训练；通过课程设计的开展，既能巩固同学们所学专业知识、又能培养其独立设计能力、还能提高其综合运用知识的能力，同时进一步锻炼科技论文写作的能力，为毕业设计奠定良好的基础。

具体要求：1.每位同学独立完成一个小的题目，并提交一篇建模论文。

若对较大的题目（简称大题），也可以每二到三人组成一组，一起共同完成。

大题的题目一般来自近年来的全国大学生数学建模竞赛、美国大学生数学建模竞赛、全国研究生数学建模竞赛、国内高校竞赛的题目。

2.论文的主要项目及要求是：摘要（针对所研究问题，采用了什么方法，建立了什么模型，得到什么结果）。

问题的提出（按你的理解对所给题目作更清晰的表达）。

问题的分析（根据问题性质，你打算建立什么样的模型）。

模型假设（有些假设需作必要的解释）。

模型设计（对出现的数学符号必须有明确的定义）。

模型解法与结果。

模型结果的分析和检验，包括误差分析、稳定性分析等。

模型的优缺点及改进方向。

必要的计算机程序。

3.文档格式：统一制作模板，每组在完成设计后需要装订。

根据要求，使用A4纸装订，装订顺序为：课程设计论文封面，课程设计任务书、摘要、正文（包括问题的提出、问题的分析、模型假设、符号说明、模型建立、模型求解、结果分析）、参考文献、附录等。

4.每位同学都要按照数学建模竞赛的要求，广泛调研、查找资料，对问题进行深入分析，要特别注意创新性思想，不得抄袭别人成果，一旦发现，将直接记不及格。

5.学生在作题期间，可以与指导教师进行深入讨论，研究方案。

6.评阅依据：假设的合理性、模型的创造性、结果的正确性、文字表述的清晰程度。

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==数学建模实验指导书篇一：数学建模实验指导书《数学实验》实验指导书实验一：matlab编程基础学时：2学时实验目的：熟悉matlab编程实验内容：1. f(x)的定义如下：?x2?x?6,x?0且x??4?f(x)??x2?5x?6,0?x?10,x?2且x?32?x?x?1,其它?写一个函数文件f(x)实现该函数，要求参数x可以是向量。

2. 用起泡法对10个数由小到大排序. 即将相邻两个数比较,将小的调到前头.3. 有一个4?5矩阵,编程求出其最大值及其所处的位置.4. 编程求?n!n?1205. 一球从100米高度自由落下,每次落地后反跳回原高度的一半,再落下. 求它在第10次落地时,共经过多少米?第10次反弹有多高? 6. 有一函数 f ( x , y ) ? x 2 xy? 2 y ,写一程序,输入自变量的值,输出函数值. ? sin7. 写一个函数rs=f(s)，对传进去的字符串变量s，删除其中的小写字母，然后将原来的大写字母变为小写字母，得到rs返回。

例如s=”aBcdE,Fg?”，则rs=”be,f?”。

提示：可利用find函数和空矩阵。

实验二：matlab函数拟合学时：2学时实验目的：掌握用matlab进行函数拟合的方法。

实验内容：根据美国人口从1790年到1990年间的人口数据（如下表），确定人口指数增长模型（Logistic模型）中的待定参数，估计出美国201X年的人口，同时画出拟合效果的图形。

表1 美国人口统计数据提示：rtx(t)?xe 0指数增长模型：Logistic模型：x?t??xm?x?1??m?1?e?rt?x0?可参考拟合函数：a=lsqcurvefit('example_curvefit_fun',a0,x,y);实验三：用matlab求解微分方程（组）学时：2学时实验目的：掌握用matlab求微分方程和微分方程组的数值解的方法。

第一章数学软件简介第一节 MatLab简介及基本运算一、MatLab简介MATLAB名字由MATrix和 LABoratory 两词的前三个字母组合而成。

那是20世纪七十年代后期的事：时任美国新墨西哥大学计算机科学系主任的Cleve Moler教授出于减轻学生编程负担的动机，为学生设计了一组调用LINPACK和EISPACK库程序的“通俗易用”的接口，此即用FORTRAN编写的萌芽状态的MATLAB。

经几年的校际流传，在Little的推动下，由Little、Moler、Steve Bangert合作，于1984年成立了MathWorks公司，并把MATLAB正式推向市场。

从这时起，MATLAB的内核采用C语言编写，而且除原有的数值计算能力外，还新增了数据图视功能。

MATLAB以商品形式出现后，仅短短几年，就以其良好的开放性和运行的可靠性，使原先控制领域里的封闭式软件包（如英国的UMIST，瑞典的LUND和SIMNON，德国的KEDDC）纷纷淘汰，而改以MATLAB为平台加以重建。

在时间进入20世纪九十年代的时候，MATLAB 已经成为国际控制界公认的标准计算软件。

在欧美大学里，诸如应用代数、数理统计、自动控制、数字信号处理、模拟与数字通信、时间序列分析、动态系统仿真等课程的教科书都把MATLAB作为内容。

这几乎成了九十年代教科书与旧版书籍的区别性标志。

在那里，MATLAB是攻读学位的大学生、硕士生、博士生必须掌握的基本工具。

在国际学术界，MATLAB已经被确认为准确、可靠的科学计算标准软件。

在许多国际一流学术刊物上，（尤其是信息科学刊物），都可以看到MATLAB的应用。

在设计研究单位和工业部门，MATLAB被认作进行高效研究、开发的首选软件工具。

如美国National Instruments公司信号测量、分析软件LabVIEW，Cadence公司信号和通信分析设计软件SPW等，或者直接建筑在MATLAB之上，或者以MATLAB为主要支撑。

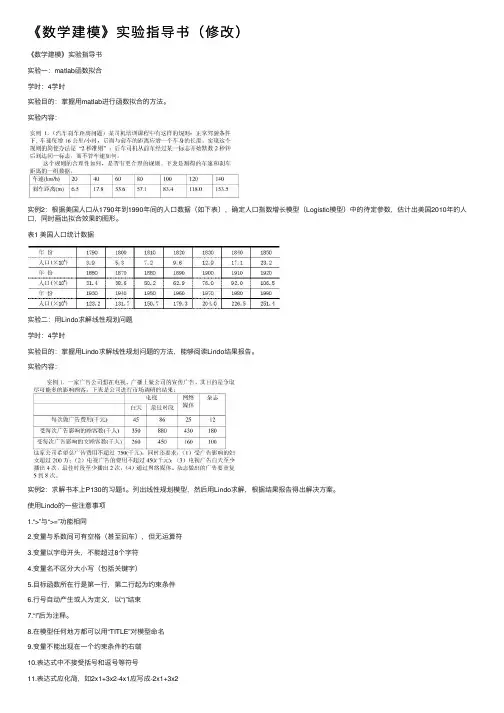
《数学建模》实验指导书（修改）《数学建模》实验指导书实验⼀：matlab函数拟合学时：4学时实验⽬的：掌握⽤matlab进⾏函数拟合的⽅法。

实验内容：实例2：根据美国⼈⼝从1790年到1990年间的⼈⼝数据（如下表），确定⼈⼝指数增长模型（Logistic模型）中的待定参数，估计出美国2010年的⼈⼝，同时画出拟合效果的图形。

表1 美国⼈⼝统计数据实验⼆：⽤Lindo求解线性规划问题学时：4学时实验⽬的：掌握⽤Lindo求解线性规划问题的⽅法，能够阅读Lindo结果报告。

实验内容：实例2：求解书本上P130的习题1。

列出线性规划模型，然后⽤Lindo求解，根据结果报告得出解决⽅案。

使⽤Lindo的⼀些注意事项1.“>”与“>=”功能相同2.变量与系数间可有空格（甚⾄回车），但⽆运算符3.变量以字母开头，不能超过8个字符4.变量名不区分⼤⼩写（包括关键字）5.⽬标函数所在⾏是第⼀⾏，第⼆⾏起为约束条件6.⾏号⾃动产⽣或⼈为定义，以“)”结束7.“!”后为注释。

8.在模型任何地⽅都可以⽤“TITLE”对模型命名9.变量不能出现在⼀个约束条件的右端10.表达式中不接受括号和逗号等符号11.表达式应化简，如2x1+3x2-4x1应写成-2x1+3x212.缺省假定所有变量⾮负，可在模型“END”语句后⽤“FREE name”将变量name的⾮负假定取消13.可在“END”后⽤“SUB”或“SLB”设定变量上下界。

例如：“sub x1 10”表⽰“x1<=10”14.“END”后对0-1变量说明：INT n或INT name15.“END”后对整数变量说明：GIN n或GIN name实验四：⽤Lingo求解⾮线性规划问题学时：2学时实验⽬的：掌握⽤Lingo求解⾮线性规划问题的⽅法。

实验内容：求解书本上P132的习题6、7。

列出⾮线性规划模型，然后⽤Lingo求解，根据结果报告得出解决⽅案。

基础实验一 数列极限与函数极限一、实验目的从刘徽的割圆术、裴波那奇数列研究数列的收敛性并抽象出极限的定义；理解数列收敛的准则；理解函数极限与数列极限的关系。

二、实验材料1.1割圆术中国古代数学家刘徽在《九章算术注》方田章圆田术中创造了割圆术计算圆周率。

刘徽先注意到圆内接正多边形的面积小于圆面积；其次，当将边数屡次加倍时，正多边形的面积增大，边数愈大则正多边形面积愈近于圆的面积。

“割之弥细，所失弥少。

割之又割以至不可割，则与圆合体而无所失矣。

”这几句话明确地表明了刘徽的极限思想。

以表示单位圆的圆内接正123-⨯n 多边形面积，则其极限为圆周率。

用下列Mathematica 程序可以从量和形两个角度考察数列{}的收敛情况：m=2;n=15;k=10;For[i=2,i<=n,i++, l[i_]:=N[2*Sin[Pi/(3*2^i)],k];(圆内接正123-⨯n 多边形边长) s[i_]:=N[3*2^(i-1)*l[i]*Sqrt[1-(l[i])^2/4],k];(圆内接正123-⨯n 多边形面积) r[i_]:=Pi-s[i]; d[i_]:=s[i]-s[i-1];Print[i," ",r[i]," ",l[i]," ",s[i]," ",d[i]] ]t=Table[{i,s[i]},{i,m,n}](数组)ListPlot[t](散点图)1.2裴波那奇数列和黄金分割由2110;1;0--+===n n n F F F F F 有著名的裴波那奇数列}{n F 。

如果令nn n F F R 11--=，由递推公式可得出 11111/11---+=+=+=n n n n n n n R F F F F F R ，]251251[5111++⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛+=n n n F ； 215lim lim 1-==+∞→∞→n nn n n F F R 。

《数学建模与数学实验》课程公共课教学大纲一、课程名称：数学建模与数学实验（Mathematical Modeling and MathematicalExperiment ）二、学时与学分：30学时三、适用专业：全校各专业（除艺术系）四、课程教材：《数学建模与数学实验》（第2版）赵静，旦琦编著，高等教育出版社，2003年。

五、参考教材：1. 萧树铁主编，姜启源等编著，大学数学《数学实验》，高等教育出版社，1999年;2.胡良剑，丁晓东等著，《数学实验使用MA TLAB》，上海科学技术出版社，2001年;3. 姜启源，谢金星等编，《数学模型》，高等教育出版社，2003年；4. 李海涛，邓樱等编，《MATLAB程序设计与教程》，高等教育出版社，2002年.六、开课单位：数理教学部七、课程的性质、目的和任务“数学实验”是近几年来才开设的一门新兴课程，它以实际问题为载体，把数学建模、数学知识、数学软件和计算机应用有机地结合，容知识性、启发性、实用性和实践性于一体，特别强调学生的主体地位，在教师的引导下，用学到的数学知识和计算机技术，借助适当的数学软件，分析、解决一些经过简化的实际问题。

该课程的引入，是数学教学体系、内容和方法改革的一项有益的尝试。

开设本课程的目的是使学生掌握数学实验的基本思想和方法。

从实际问题出发，借助计算机，通过学生亲自设计和动手，体验解决问题的全过程，从实验中去探索、学习和发现数学规律，充分调动学生学习的主动性。

培养学生的创新意识，运用所学知识，建立数学模型，使用计算机并利用数学软件解决实际问题的能力，最终达到提高学生数学素质和综合能力的目的。

该课程主要讲授一些最常用的解决实际问题的方法及其MATLAB软件实现，包括数值计算、优化方法、统计计算、图论及网络优化方法等。

我们还将介绍一些大型的数学建模案例，这些案例主要取材于最近几年的全国大学生数学建模竞赛试题。

总之学生通过该课程的学习，要求他们掌握数学建模的全过程；掌握对各种数学模型如何选择合适的数学方法和数学软件去解决它；掌握数学数值软件的强大的运算功能、图形功能以及开发应用功能。

数学建模实验指导书Experiment Instruction Book Of Mathematical Modeling数学与信息科学学院2008年2月前言数学建模实验是数学建模课程的一个重要组成部分，实验的设置是为了配合课堂教学，使学生亲自实践建模、求解、解释和结果分析的全过程，进一步掌握和理解课堂教学内容，培养动手能力，提高他们分析问题和解决问题能力。

同时，通过上机练习，也可以提高应用数学软件和计算机技术的能力。

实验一指导实验项目：初等模型实验实验目的：1．实践参数估计及多项式拟合的方法；2．学习掌握用数学软件包进行参数估计和多项式拟合的问题。

实验内容：1．建模实例，汽车刹车距离问题等； 2．编程计算 实例1．（汽车刹车距离问题）某司机培训课程中有这样的规则：正常驾驶条件下, 车速每增16公里/小时，后面与前车的距离应增一个车身的长度。

实现这个规则的简便办法是 “2秒准则” ：后车司机从前车经过某一标志开始默数2秒钟后到达同一标志，而不管车速如何。

这个规则的合理性如何，是否有更合理的规则。

下表是测得的车速和刹车距离的一组数据。

实验方法与步骤：1．建立模型刹车距离的拟合多项式为v k v k d 221+=2．Matlab 计算求解 建立M 文件exp1.m v=[20:20:140]/3.6; v2=v.^2; x=[v;v2]‟;d=[6.5,17.8,33.6,57.1,83.4,118,153.5]‟; a=x\d; dd=x*a;ddd=[6.5,17.8,33.6,57.1,83.4,118,153.5]; b=polyfit(v,ddd,2) y=polyval(b,v)plot(v,ddd,‟ro ‟,v,dd,‟b ‟) t=y./vy = 6.2024 17.7571 34.5643 56.6238 83.9357 116.5000 154.3167t =1.1164 1.5981 2.0739 2.5481 3.0217 3.4950 3.96813．结果分析.0.02+=0851vvd6617实验一问题：举重比赛按照运动员的体重分组，在一些合理、简化的假设下建立比赛成绩与体重之间的关系。

《数学建模》实验指导书目录实验一Matlab概述与简单计算4课时实验二符号函数及其微积分2课时实验三多元函数及其微积分2课时实验四无穷级数及曲线拟合2课时实验五线性代数2课时实验六数理统计2课时实验七优化问题的matlab求解2课时实验八MATLAB编程基础4课时实验一Matlab概述与简单计算【实验学时】4学时【实验目的和要求】实验目的: 熟悉Matlab工作界面, 掌握Matlab的基本命令与基本函数, 掌握Matlab的基本赋值与运算。

经过具体实例, 掌握Matlab的基本使用方法。

实验要求:1.掌握Matlab的一些基本操作命令和基本函数;2.掌握Matla的基本赋值与有运算。

【实验步骤】1．熟练Matlab软件的进入与运行方式及工作界面; 2．MATLAB基本命令与基本函数使用;3．MATLAB的基本赋值与运算。

【实验主要仪器及材料】WindowsXP计算机、Matlab软件【实验内容】1.显示当前日期, 并在屏幕上显示当年度各月的月历;fix(clock)结果: ans =12 1 21 2 212.56.3osin-48+ocosln24sind(48)+cosd(24)-log(3.56)结果: ans =0.38693. 25.3=x+-xxy)8ln,22=53(lnx=3.25;y=2*(log(3*x+8))^2-5*log(x) 结果: y =10.65394.输入矩阵, 并求矩阵的行列式值和逆矩阵。

⎪⎪⎪⎭⎫ ⎝⎛---924613312 a=[2 -1 3;3 1 -6;4 -2 9]; det(a) inv(a) 结果: ans =15ans =-0. 0. 0.-3.4000 0.4000 1.4000 -0.6667 0 0.3333实验二符号函数及其微积分【实验学时】2学时【实验目的和要求】实验目的: 掌握符号函数的基本运算、二维图形的绘制。

实验要求:1.掌握符号函数计算;2.掌握二维图形的各种绘制命令。

《数学建模与实验》实验指导书⒈目的计算机的应用在数学建模的教学中占有重要地位，在为解决实际问题而建立数学模型的过程中、对所建模型的检验以及大量的数值计算中，都必需用到计算机。

《数学建模与实验》的实验课的目的和任务是通过实验培养并提高学生的数学建模能力和计算机应用能力。

⒉实验任务分解通过一些实例初步掌握建立数学模型的方法，实验任务可分解为：初等建模，确定性连续模型，确定性离散模型，随机性模型。

在各个具体任务中，练习运用数值计算软件Matlab 进行数学实验，对问题中的各有关变量进行分析、计算，给出分析和预测结果。

⒊实验环境介绍计算机房⒋实验时数16学时实验一⒈实验目的与要求通过对具体实例的分析，学会运用初等数学建立数学模型的方法，掌握Matlab的基本使用方法和Matlab中编程方法及M文件的编写。

⒉实验内容初等代数建模，图形法建模，静态随机性模型，量纲分析法建模等。

学习和练习数值计算软件Matlab的基本方法。

⒊思考题1)在超市购物时你注意到大包装商品比小包装商品便宜这种现象了吗。

比如洁银牙膏50g装的每支1.50元，120g装的每支3.00元，二者单位重量的价格比是1.2:1。

试用比例方法构造模型解释这个现象。

2)动物园里的成年热血动物靠饲养的食物维持体温基本不变，在一些合理、简化的假设下建立动物的饲养食物量与动物的某个尺寸之间的关系。

3)原子弹爆炸的速度v与空气密度ρ、粘滞系数μ和重力加速度g有关，其中粘滞系数的定义是：运动物体在流体中受的摩擦力与速度梯度和接触面积的乘积成正比，比例系数为粘滞系数。

用量纲分析方法给出速度v的表达式。

4)掌握Matlab的基本使用方法，并试解以下问题：(1)至少用3种方法解线性方程组Ax = b，如矩阵除法、求逆矩阵法、矩阵三角分解法等。

(2)用几种方法画简单函数的图形，并练习：考虑如何画坐标轴;在一个坐标系中画多条函数曲线; 用subplot画多幅图形; 图上加注各种标记等。