下载文档原格式
F检验的假设、对F值的判断、对F值的概率值的判断。
T检验的假设、对t值的判断、对t值的概率值的判断。
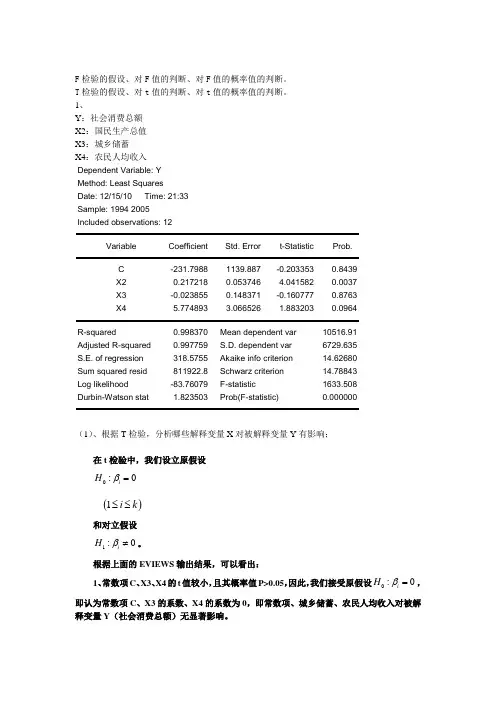
1、Y：社会消费总额X2：国民生产总值X3：城乡储蓄X4：农民人均收入Dependent Variable: YMethod: Least SquaresDate: 12/15/10 Time: 21:33Sample: 1994 2005Included observations: 12Variable Coefficient Std. Error t-Statistic Prob.C -231.7988 1139.887 -0.203353 0.8439X2 0.217218 0.053746 4.041582 0.0037X3 -0.023855 0.148371 -0.160777 0.8763X4 5.774893 3.066526 1.883203 0.0964R-squared 0.998370 Mean dependent var 10516.91 Adjusted R-squared 0.997759 S.D. dependent var 6729.635 S.E. of regression 318.5755 Akaike info criterion 14.62680 Sum squared resid 811922.8 Schwarz criterion 14.78843 Log likelihood -83.76079 F-statistic 1633.508 Durbin-Watson stat 1.823503 Prob(F-statistic) 0.000000（1）、根据T检验，分析哪些解释变量X对被解释变量Y有影响；在t检验中，我们设立原假设0:0iHβ= ()1i k≤≤和对立假设1:0iHβ≠。
根据上面的EVIEWS输出结果，可以看出：1、常数项C、X3、X4的t值较小，且其概率值P>0.05，因此，我们接受原假设0:0iHβ=，即认为常数项C、X3的系数、X4的系数为0，即常数项、城乡储蓄、农民人均收入对被解释变量Y（社会消费总额）无显著影响。
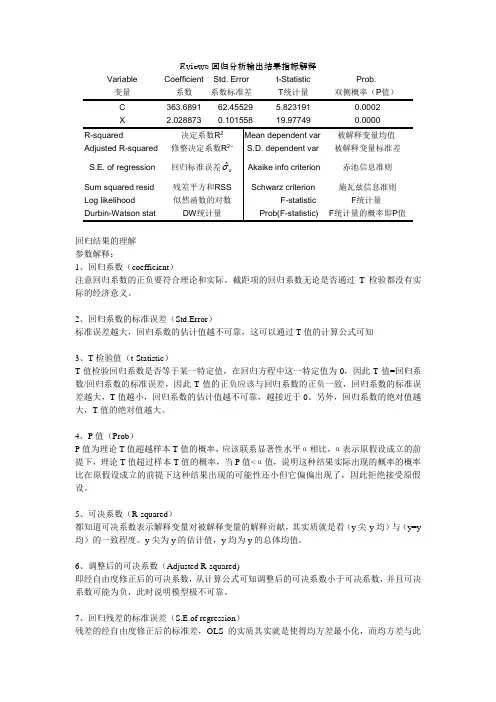
Eviews回归分析输出结果指标解释Variable 变量Coefficient系数Std. Error系数标准差t-StatisticT统计量Prob.双侧概率（P值）C 363.6891 62.45529 5.823191 0.0002回归结果的理解参数解释：1、回归系数（coefficient）注意回归系数的正负要符合理论和实际。
截距项的回归系数无论是否通过T检验都没有实际的经济意义。
2、回归系数的标准误差（Std.Error）标准误差越大，回归系数的估计值越不可靠，这可以通过T值的计算公式可知3、T检验值（t-Statistic）T值检验回归系数是否等于某一特定值，在回归方程中这一特定值为0，因此T值=回归系数/回归系数的标准误差，因此T值的正负应该与回归系数的正负一致，回归系数的标准误差越大，T值越小，回归系数的估计值越不可靠，越接近于0。
另外，回归系数的绝对值越大，T值的绝对值越大。
4、P值（Prob）P值为理论T值超越样本T值的概率，应该联系显著性水平α相比，α表示原假设成立的前提下，理论T值超过样本T值的概率，当P值<α值，说明这种结果实际出现的概率的概率比在原假设成立的前提下这种结果出现的可能性还小但它偏偏出现了，因此拒绝接受原假设。
5、可决系数（R-squared）都知道可决系数表示解释变量对被解释变量的解释贡献，其实质就是看（y尖-y均）与（y=y 均）的一致程度。
y尖为y的估计值，y均为y的总体均值。
6、调整后的可决系数（Adjusted R-squared)即经自由度修正后的可决系数，从计算公式可知调整后的可决系数小于可决系数，并且可决系数可能为负，此时说明模型极不可靠。
7、回归残差的标准误差（S.E.of regression）残差的经自由度修正后的标准差，OLS的实质其实就是使得均方差最小化，而均方差与此的区别就是没有经过自由度修正。
8、残差平方和（Sum Squared Resid）见上79、对数似然估计函数值（Log likelihood）首先，理解极大似然估计法。
eviews实验报告总结eviews实验报告总结篇一：Evies实验报告实验报告一、实验数据：1994至201X年天津市城镇居民人均全年可支配收入数据 1994至201X年天津市城镇居民人均全年消费性支出数据 1994至201X年天津市居民消费价格总指数二、实验内容：对搜集的数据进行回归，研究天津市城镇居民人均消费和人均可支配收入的关系。
三、实验步骤：1、百度进入“中华人民共和国国家统计局”中的“统计数据”，找到相关数据并输入Exc el，统计结果如下表1：表11994年--201X年天津市城镇居民消费支出与人均可支配收入数据2、先定义不变价格（1994=1）的人均消费性支出（Yt）和人均可支配收入（Xt）令：Yt=cn sum/priceXt=ine/pri ce 得出Yt与Xt的散点图，如图1.很明显，Yt和X t服从线性相关。
图1 Yt和Xt散点图3、应用统计软件EVies完成线性回归解：根据经济理论和对实际情况的分析也都可以知道，城镇居民人均全年耐用消费品支出Yt依赖于人均全年可支配收入Xt的变化，因此设定回归模型为 Yt=β0+β?Xt﹢μt（1）打开E Vies软件，首先建立工作文件， Fil e rkfile ,然后通过bject建立 Y、X系列，并得到相应数据。
（2）在工作文件窗口输入命令：l s y c x,按E nter键，回归结果如表2 ：表2 回归结果根据输出结果，得到如下回归方程：Y t=977.908+0.670Xt s=(172.3797) (0.0122) t=(5.673) (54.950) R2=0.995385 Adjust ed R2=0.995055 F-sta tistic=3019.551 残差平方和Sum sq uared resi d =1254108回归标准差S.E.f regressi n=299.2978（3）根据回归方程进行统计检验：拟合优度检验由上表2中的数分别为0.995385和0.995055，计算结果表明，估计的样本回归方程较好地拟合了样本观测值。
Eviews回归分析输出结果指标解释Variable Coefficie Std。
Error t-Statistic Prob.X2。
0288730。
10155819。
977490。
0000回归结果的理解参数解释：1、回归系数（coefficient）注意回归系数的正负要符合理论和实际。
截距项的回归系数无论是否通过T检验都没有实际的经济意义。
2、回归系数的标准误差(Std。
Error）标准误差越大，回归系数的估计值越不可靠,这可以通过T值的计算公式可知3、T检验值（t-Statistic)T值检验回归系数是否等于某一特定值，在回归方程中这一特定值为0，因此T值=回归系数/回归系数的标准误差,因此T值的正负应该与回归系数的正负一致,回归系数的标准误差越大，T值越小，回归系数的估计值越不可靠，越接近于0。
另外，回归系数的绝对值越大,T值的绝对值越大。
4、P值（Prob）P值为理论T值超越样本T值的概率，应该联系显著性水平α相比，α表示原假设成立的前提下，理论T值超过样本T值的概率，当P值<α值，说明这种结果实际出现的概率的概率比在原假设成立的前提下这种结果出现的可能性还小但它偏偏出现了,因此拒绝接受原假设。
5、可决系数（R—squared）都知道可决系数表示解释变量对被解释变量的解释贡献，其实质就是看（y尖-y均）与(y=y均）的一致程度。
y尖为y的估计值，y均为y的总体均值。
6、调整后的可决系数(Adjusted R—squared）即经自由度修正后的可决系数，从计算公式可知调整后的可决系数小于可决系数，并且可决系数可能为负，此时说明模型极不可靠。
7、回归残差的标准误差（S。
E。
of regression）残差的经自由度修正后的标准差，OLS的实质其实就是使得均方差最小化，而均方差与此的区别就是没有经过自由度修正.8、残差平方和（Sum Squared Resid)见上79、对数似然估计函数值（Log likelihood）首先,理解极大似然估计法。
Eviews格兰杰因果关系检验结果说明Eviews格兰杰因果关系检验结果说明一、经济变量之间的因果性问题计量经济模型的建立过程，本质上是用回归分析工具处理一个经济变量对其他经济变量的依存性问题，但这并不是暗示这个经济变量与其他经济变量间必然存在着因果关系。
由于没有因果关系的变量之间常常有很好的回归拟合，把回归模型的解释变量与被解释变量倒过来也能够拟合得很好，因此回归分析本身不能检验因果关系的存在性，也无法识别因果关系的方向。
假设两个变量，比如国内生产总值GDP和广义货币供给量M，各自都有滞后的分量GDP(-1)，GDP(-2)…，M(-1)，M(-2)，…，显然这两个变量都存在着相互影响的关系。
但现在的问题是:究竟是M引起GDP的变化，还是GDP引起M的变化，或者两者间相互影响都存在反馈，即M引起GDP的变化，同时GDP也引起M的变化。
这些问题的实质是在两个变量间存在时间上的先后关系时，是否能够从统计意义上检验出因果性的方向，即在统计上确定GDP是M的因，还是M是GDP的因，或者M和GDP互为因果。
因果关系研究的有趣例子是回答“先有鸡还是先有蛋”的问题。
1988年有两位学者Walter N. Thurman和Mark E. Fisher用美国1930——1983年鸡蛋产量(EGGS)和鸡的产量(CHICKENS)的年度数据，对此问题进行了统计研究。
他们运用格兰杰的方法检验鸡和蛋之间的因果关系，结果发现，鸡生蛋的假设被拒绝，而蛋生鸡的假设成立，因此，蛋为因，鸡为果，也就是先有蛋。
他们并建议作其他诸如“谁笑在最后谁笑得最好”、“骄傲是失败之母”之类的格兰杰因果检验。
二、格兰杰因果关系检验经济学家开拓了一种可以用来分析变量之间的因果的办法，即格兰杰因果关系检验。
该检验方法为2003年诺贝尔经济学奖得主克莱夫?格兰杰(Clive W. J. Granger)所开创，用于分析经济变量之间的因果关系。
他给因果关系的定义为“依赖于使用过去某些时点上所有信息的最佳最小二乘预测的方差。
Eviews回归分析输出结果指标解释Variable 变量Coefficient系数Std. Error系数标准差t-Statistic Prob.双侧概率（P值）C 363.6891 62.45529 5.823191 0.0002七年级英语期末考试质量分析一、试卷分析：本次试卷的难易程度定位在面向大多数学生。
该份试卷紧扣教材，突出重点，注重对基础知识和基本技能的考查。
二、题型分析：1．单项选择单项选择题共15道小题，知识覆盖面较广，重点、难点和疑点比较突出，注重能力考查。
考查以动词为主，兼顾其它词类，并考查句法和语言点。
考查的方式突出了语境。
2．完形填空文章对学生的语言理解能力和综合运用能力提出了较高的要求，重点突出了对单复数和语言点的考查。
3．阅读理解本大题包括五篇文章，安排较合理，难度适中，既有日常生活的题材，又有表格图片解说，符合新课程的要求，体现新课程的理念。
根据《新课程标准》五级有关读的目标描述，问题符合“能找出文章中的主题，理解故事的情节…”等目标描述。
阅读体现新课标所倡导的任务型教学的理念。
通过阅读短文，主要考查学生根据所获取的信息解决实际问题的能力。
阅读的难度不很大，完成任务的环节也比较简洁。
4．书面表达书面表达中仿写与课本内容有着极大的相似之处，是对教材的深加工，做到了学以致用。
创新写作紧扣《课程标准》要求，结合《课程标准》有关写的目标描述，考查了学生综合应用语言的能力。
三、典型错误分析第一大题单项填空中，错误率较高。
主要问题是对单词没理解透，平时讲过的语法没记住，不能灵活应用。
交际运用失分较多，主要是课文掌握不到位。
书面表达中考生的主要错误有：1）在完成句子时不尊重原句的中文意思，改变了句意；2）不会用英语思考，用英语表达的能力较差；3）思路不清晰。
4）语言的基本功不扎实，病句较多；（5）书写习惯不好，卷面不整洁。
书面表达部分中常见错误形式：1．时态错误。
a.时态混淆 b.时态前后不一致 c. 主谓不一致2. 句子结构错误。
EViews图像及结果分析EViews软件提供了序列(Series)和序列组(Group)等对象的各种视图、统计分析方法和过程。
当序列对象中输入数据后，就可对序列对象中输入的数据进行统计分析，并且可以通过图、表等形式进行描述。
本章将介绍序列和序列组对象图形的生成和描述性统计量及其检验。
4.1 图形对象图形(Graph)对象可以形成序列和序列组等对象的各种视图，如线图(Line)、散点图(Scatter)以及饼图(Pie)等。
通过图形可以进一步观察和分析数据的变化趋势和规律。
下面介绍图形对象的基本操作。
4.1.1 图形(Graph)对象的生成图形对象也是工作文件中的基本对象之一。
要生成图形对象需首先打开序列对象窗口或序列组对象窗口，选择对象窗口工具栏中的“View”|“Graph”选项。
选择的对象类型不同，将弹出不同的窗口。
如果在序列对象窗口下选择“View”|“Graph”选项，将弹出如图4-1所示的界面。
图4-1 序列窗口下图形对象的生成此时“Graph”弹出的菜单中有6种图形可供选择。
“Line”表示生成的是折线图，如图4-2所示，其横轴表示时间或序列的顺序，纵轴表示序列对象观测值的大小。
“Area”表示生成面积图，其图形的形状与“Line”(折线图)相同，不同的是“Area”(面积图)曲线下方是被填满的，而“Line”(折线图)下方是空白。
图4-2 “Line”折线图“Bar”表示为条形图，用条状的高度表示观测值的大小。
“Spike”表示尖峰图，由竖线组成，每根竖线的高度代表观测值的大小。
“Seasonal Stacked Line”表示生成的是季节性堆叠图，“Seasonal Split Line”表示生成的是季节性分割线。
如果在序列组(群)对象窗口下选择“View”|“Graph”选项，将弹出如图4-3所示的界面。
这里有9种图形可供选择。
其前4种与上面讲述的相同。
图4-3 序列组(群)窗口下图对象的生成其中，“Scatter”表示生成散点图。
在“Scatter”弹出的菜单中有5个选项，分别是“Simple Scatter”(简单散点图)、“Scatter with Regression”(带有回归线的散点图)、“Scatter with Nearest Neighbor Fit”(近邻匹配散点图)、“Scatter with Kernel Fit”(核心匹配散点图)、“XY Pairs”(XY成对散点图)。
当序列组中包含两个序列对象时，第一个序列对象的观测值构成散点图的横坐标，第二个序列对象的观测值构成散点图的纵坐标，如图4-4所示。
当序列组中有三个以上的序列对象时，第一个序列对象构成散点图的横坐标，其余序列对象构成散点图的纵坐标。
图4-4 简单散点图(“Simple Scatter”)“XY line”表示X与Y的折线图，横纵坐标分别表示两个序列对象的观测值。
“Error Bar”表示误差长条图，“High-Low”表示高低图，“Pie”表示饼图。
另外，在序列组(群)对象窗口下还可通过选择“View”|“Multiple Graphs”选项来生成图形。
此时图形显示在不同的坐标系中，即每个序列对象各形成一个图形，并显示在同一个窗口中。
除上面介绍的在序列对象窗口中生成图对象外，还可以通过选择EViews主菜单中的“Quick”|“Graph”选项来生成。
在“Graph”的菜单中选择图的类型，将弹出图4-5所示的文本框。
在文本框内输入序列或序列组的名称，例如“fdi”，然后单击“OK”按钮，即可打开相应的图。
此时所生成的图对象未被命名，单击图对象窗口中的“Name”按钮即可命名。
图4-5 生成图对象的文本框4.1.2 图形的冻结在上面所介绍的两种图对象生成方法中，通过“Quick”|“Graph”选项生成图形对象，单击图对象窗口工具栏中的“Name”选项，在弹出的对话框中输入该对象的名称，单击“OK”按钮后该对象即可被保存，并在工作文件窗口中显示图对象的图标。
但直接在序列对象窗口中形成的图形未被保存，当序列对象中的观测值发生改变时，或当前工作文件的样本范围发生变化时，图形也将随之改变。
如果要保留所建立的图形，使之不随样本及观测值的改变而发生变化，则可以通过序列对象窗口中的“Freeze”键来冻结图形。
EViews软件将被冻结的图形以一个图(Graph)对象的形式保存在工作文件中。
当选择序列对象窗口中的“Freeze”键时，会弹出图对象窗口。
其中有几个键值得关注，一个是“AddText”功能键，通过它可以将文字显示在图形中，并且可以选择显示的位置。
一个是“Line/Shade”功能键，通过它可以改变图形的背景颜色，横纵坐标轴的线条类型和颜色等。
还有一个是“Remove”功能键，可以用来删除图形中的一些附加要素。
例如，将在图形中所建立的文字删除，应首先用鼠标单击所需删除的内容，使其被选中，然后单击“Remove”键，则文字即被删除。
用同样的方法也可以删除为图形所设置的颜色等。
4.1.3 图形的复制如果需要将图形保存到其他文件中，例如放在Word文档中，则选择图对象窗口中的“Proc”|“Copy”选项，然后在弹出的对话框中单击“OK”按钮。
或者将鼠标移动到图形上，右击，在弹出的快捷菜单中选择“Copy”命令。
再打开需要粘贴的文件，进行粘贴即可。
4.2 描述性统计量EViews软件中包含一些基本的描述性统计量，有直方图、均值、方差、协方差、自相关等。
本节主要介绍序列和序列组对象窗口下的描述性统计量及其检验。
4.2.1 描述性统计量概述序列窗口下的描述性统计量和序列组窗口下的描述性统计量有所不同。
在序列窗口下有4种描述性统计量，分别是“Histogram and Stats”(直方图和统计量)、“Stats Table”(统计表)、“Stats by Classification”(分类统计量)和“Boxplots by Classification”(箱线图/箱尾图分类)。
序列组窗口下有3种描述性统计量，分别是“Common Sample”(普通样本)、“Individual Samples”(个体样本)和“Boxplots”(箱线图/箱尾图)。
下面分别进行详细介绍。
(1) 序列窗口下的描述性统计量在序列(Series)对象窗口下选择工具栏中的“View”|“Descriptive Statistics”(描述性统计量)选项，将出现4个选项。
第一个选项是“Histogram and Stats”(直方图和统计量)，能显示序列对象的直方图和描述性统计量的值。
下面以建立好的序列对象“fdi”为例来进行说明。
如图4-6所示，图的左侧显示的是该序列对象的直方图，为观测值的频率分布。
右侧分三个部分，最上面显示的是序列对象的名称、样本的范围和样本数量。
中间部分显示的是各统计量的值。
其中，“Mean”表示均值，即序列对象观测值的平均值；“Median”表示中位数，即从小到大排列的序列对象观测值的中间值，是对序列分布中心的一个大致估计；“Maximum”和“Minimum”表示的是该序列观测值中的最大值和最小值；“Std.Dev”表示标准差，用来衡量序列观测值的离散程度。
其计算公式为∑=--=N i x x N i 1)(112σ (4-1)式中，σ为标准差，N 为样本观测值个数，x i 是样本观测值，x 为样本均值。
图4-6 序列对象“fdi ”的直方图分布形状和相关统计量的描述“Skewness ”表示偏度，用来衡量观测值分布偏离均值的状况。
其计算公式为31ˆ1∑=⎪⎭⎫ ⎝⎛-=N i x x N S i σ (4-2)式中，σˆ是变量方差的有偏估计。
当S =0时，序列的分布是对称的，如正态分布；当S >0时，序列分布为右偏；当S <0时，序列分布为左偏。
例如图4-6中的偏度为1.422 500>0，所以我国的外商直接投资(fdi)的分布是不对称的，为右偏分布形态。
“Kurtosis ”表示峰度，用来衡量序列分布的凸起状况。
其计算公式为41ˆ1∑=⎪⎭⎫ ⎝⎛-=N i x x N K i σ (4-3)正态分布的K 值为3，当K >3时，序列对象的分布凸起程度大于正态分布的凸起程度；当K <3时，序列对象的分布凸起程度要比正态分布小。
例如，图4-6中的峰度为4.898 917 >3，外商直接投资(fdi)的分布呈尖峰状态。
最下方是JB(Jarque-Bera)统计量及其相应的概率(Probability)。
JB 统计量用来检验序列观测值是否服从正态分布，该检验的零假设为样本服从正态分布。
在零假设下，JB 统计量服从χ2(2)分布。
根据第1章所介绍的假设检验，P(Probability)值为拒绝原假设所犯第Ⅰ类错误的概率。
在本例中P 值接近于0，因而可在1%的显著性水平下拒绝零假设，即序列不服从正态分布。
第二个选项是“Stats Table ”(统计表)，它将描述性统计量值通过电子表格的形式显示在对象窗口中。
第三个选项是“Stats by Classification”(分类统计量)，它将样本分为若干组后再对各组观测值分别进行描述统计。
选择此项后将弹出如图4-7所示的对话框，其中包括三部分内容。
在左边“Statistics”选项中勾选需要显示的统计量，其中“# of NAs”为无观测个数，“Observations”为观测值个数。
在“Series/Group for classify”中输入需分类的序列或序列组对象名称，右侧“Output Layout”为输出结果的显示形式。
选择好后单击“OK”按钮即可。
图4-7 “Stats by Classification”(分类统计量)对话框第四个选项是“Boxplots by Classification”(分类箱线图/箱尾图)，将序列分布按照箱线图/箱尾图进行分类。
箱线图(Boxplot)也称为箱尾图，是利用数据统计量来描述数据的一种方法，它可以粗略地看出数据是否具有对称性，分布的分散程度等。
图4-8所示为fdi序列的分类箱线图。
图4-8 fdi序列对象的分类箱线图(“Boxplots by Classification”)(2) 序列组窗口下的描述性统计量在序列组(Group)对象窗口下选择工具栏中的“View”| “Descriptive Statistics”(描述性统计量)选项，将弹出3个选项。
第一个选项是“Common Sample”(普通样本)，选择该项将得到含有均值、中位数、最大/小值等统计量的一张电子表格。
“Common Sample”要求各序列对象的样本范围相同，不能含有NA符(空值)。
