第二章一元线性回归案例分析

一元线性回归模型案例分析一元线性回归是最基本的回归分析方法，它的主要目的是寻找一个函数能够描述因变量对于自变量的依赖关系。

在一元线性回归中，我们假定存在满足线性关系的自变量与因变量之间的函数关系，即因变量y与单个自变量x之间存在着线性关系，可表达为：y=β0+ β1x (1)其中，β0和β1分别为常量，也称为回归系数，它们是要由样本数据来拟合出来的。

因此，一元线性回归的主要任务就是求出最优回归系数和平方和最小平方根函数，从而评价模型的合理性。

下面我们来介绍如何使用一元线性回归模型进行案例分析。

数据收集：首先，研究者需要收集自变量和因变量之间关系的相关数据。

这些数据应该有足够多的样本观测值，以使统计分析结果具有足够的统计力量，表示研究者所研究的关系的强度。

此外，这些数据的收集方法也需要正确严格，以避免因相关数据缺乏准确性而影响到结果的准确性。

模型构建：其次，研究者需要利用所收集的数据来构建一元线性回归模型。

即建立公式（1），求出最优回归系数β0和β1，即最小二乘法拟合出模型方程式。

模型验证：接下来，研究者需要对所构建的一元线性回归模型进行验证，以确定模型精度及其包含的统计意义。

可以使用F检验和t检验，以检验回归系数β0和β1是否具有统计显著性。

另外，研究者还可以利用R2等有效的拟合检验统计指标来衡量模型精度，从而对模型的拟合水平进行评价，从而使研究者能够准确无误地判断其研究的相关系数的统计显著性及包含的统计意义。

另外，研究者还可以利用偏回归方差分析（PRF），这是一种多元线性回归分析技术，用于计算每一个自变量对相应因变量的贡献率，使研究者能够对拟合模型中每一个自变量的影响程度进行详细的分析。

模型应用：最后，研究者可以利用一元线性回归模型进行应用，以实现实际问题的求解以及数据挖掘等功能。

例如我们可以使用这一模型来预测某一物品价格及销量、研究公司收益及投资、检测影响某一地区经济发展的因素等。

综上所述，一元线性回归是一种利用单变量因变量之间存在着线性关系来拟合出回归系数的回归分析方法，它可以应用于许多不同的问题，是一种非常实用的有效的统计分析方法。

一元线性回归模型案例分析一、研究的目的要求居民消费在社会经济的持续发展中有着重要的作用。

居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长，而且这也是人民生活水平的具体体现。

改革开放以来随着中国经济的快速发展，人民生活水平不断提高，居民的消费水平也不断增长。

但是在看到这个整体趋势的同时，还应看到全国各地区经济发展速度不同，居民消费水平也有明显差异。

例如，2002年全国城市居民家庭平均每人每年消费支出为6029.88元, 最低的黑龙江省仅为人均4462.08元，最高的上海市达人均10464元，上海是黑龙江的2.35倍。

为了研究全国居民消费水平及其变动的原因，需要作具体的分析。

影响各地区居民消费支出有明显差异的因素可能很多，例如，居民的收入水平、就业状况、零售物价指数、利率、居民财产、购物环境等等都可能对居民消费有影响。

为了分析什么是影响各地区居民消费支出有明显差异的最主要因素，并分析影响因素与消费水平的数量关系，可以建立相应的计量经济模型去研究。

二、模型设定我们研究的对象是各地区居民消费的差异。

居民消费可分为城市居民消费和农村居民消费，由于各地区的城市与农村人口比例及经济结构有较大差异，最具有直接对比可比性的是城市居民消费。

而且，由于各地区人口和经济总量不同，只能用“城市居民每人每年的平均消费支出”来比较，而这正是可从统计年鉴中获得数据的变量。

所以模型的被解释变量Y 选定为“城市居民每人每年的平均消费支出”。

因为研究的目的是各地区城市居民消费的差异，并不是城市居民消费在不同时间的变动，所以应选择同一时期各地区城市居民的消费支出来建立模型。

因此建立的是2002年截面数据模型。

影响各地区城市居民人均消费支出有明显差异的因素有多种，但从理论和经验分析，最主要的影响因素应是居民收入，其他因素虽然对居民消费也有影响，但有的不易取得数据，如“居民财产”和“购物环境”；有的与居民收入可能高度相关，如“就业状况”、“居民财产”；还有的因素在运用截面数据时在地区间的差异并不大，如“零售物价指数”、“利率”。

第二章 一元线性回归模型典型例题分析例1、令kids 表示一名妇女生育孩子的数目,educ 表示该妇女接受过教育的年数.生育率对教育年数的简单回归模型为μββ++=educ kids 10（1）随机扰动项μ包含什么样的因素?它们可能与教育水平相关吗？（2)上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗？请解释.例2．已知回归模型μβα++=N E ，式中E 为某类公司一名新员工的起始薪金（元），N 为所受教育水平（年).随机扰动项μ的分布未知，其他所有假设都满足。

如果被解释变量新员工起始薪金的计量单位由元改为100元，估计的截距项与斜率项有无变化?如果解释变量所受教育水平的度量单位由年改为月,估计的截距项与斜率项有无变化？例3．对于人均存款与人均收入之间的关系式t t t Y S μβα++=使用美国36年的年度数据得如下估计模型，括号内为标准差：)011.0()105.151(067.0105.384ˆtt Y S +=2R ＝0.538 023.199ˆ=σ(1）β的经济解释是什么？(2）α和β的符号是什么？为什么？实际的符号与你的直觉一致吗?如果有冲突的话,你可以给出可能的原因吗？（3)对于拟合优度你有什么看法吗? （4）检验统计值？例4．下列方程哪些是正确的？哪些是错误的？为什么？⑴ y x t n t t =+=αβ12,,, ⑵ y x t n t t t =++=αβμ12,,,⑶ y x t n t t t=++= ,,,αβμ12⑷ ,,,y x t n t t t =++=αβμ12 ⑸ y x t n t t =+= ,,,αβ12 ⑹ ,,,y x t n t t =+=αβ12⑺ y x t n t t t =++= ,,,αβμ12 ⑻ ,,,y x t n t tt =++=αβμ12其中带“＾”者表示“估计值”.例5．对于过原点回归模型i i i u X Y +=1β ,试证明∑=∧221)(iu XVar σβ例6、对没有截距项的一元回归模型i i i X Y μβ+=1称之为过原点回归（regression through the origin ）。

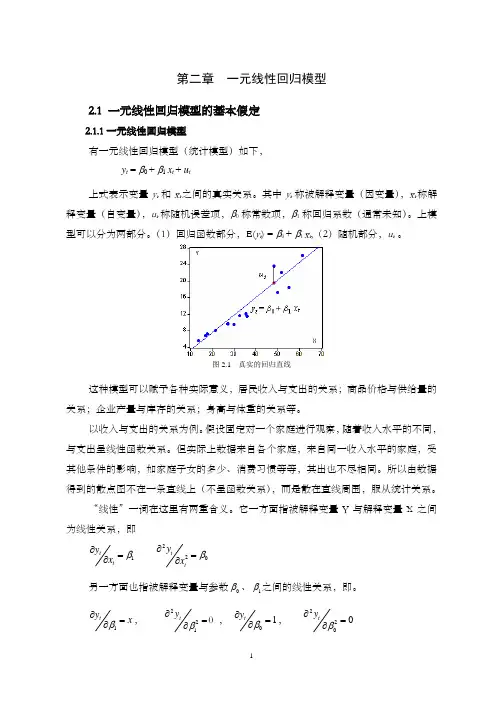
第二章 一元线性回归模型2.1 一元线性回归模型的基本假定2.1.1一元线性回归模型有一元线性回归模型（统计模型）如下， y t = β0 + β1 x t + u t上式表示变量y t 和x t 之间的真实关系。

其中y t 称被解释变量（因变量），x t 称解释变量（自变量），u t 称随机误差项，β0称常数项，β1称回归系数（通常未知）。

上模型可以分为两部分。

（1）回归函数部分，E(y t ) = β0 + β1 x t ,（2）随机部分，u t 。

图2.1 真实的回归直线这种模型可以赋予各种实际意义，居民收入与支出的关系；商品价格与供给量的关系；企业产量与库存的关系；身高与体重的关系等。

以收入与支出的关系为例。

假设固定对一个家庭进行观察，随着收入水平的不同，与支出呈线性函数关系。

但实际上数据来自各个家庭，来自同一收入水平的家庭，受其他条件的影响，如家庭子女的多少、消费习惯等等，其出也不尽相同。

所以由数据得到的散点图不在一条直线上（不呈函数关系），而是散在直线周围，服从统计关系。

“线性”一词在这里有两重含义。

它一方面指被解释变量Y 与解释变量X 之间为线性关系，即1tty x β∂=∂220tt y x β∂=∂另一方面也指被解释变量与参数0β、1β之间的线性关系，即。

1ty x β∂=∂，221ty β∂=∂0 ，1ty β∂=∂，2200ty β∂=∂2.1.2 随机误差项的性质随机误差项u t 中可能包括家庭人口数不同，消费习惯不同，不同地域的消费指数不同，不同家庭的外来收入不同等因素。

所以在经济问题上“控制其他因素不变”是不可能的。

随机误差项u t 正是计量模型与其它模型的区别所在，也是其优势所在，今后咱们的很多内容，都是围绕随机误差项u t 进行了。

回归模型的随机误差项中一般包括如下几项内容： （1）非重要解释变量的省略， （2）数学模型形式欠妥， （3）测量误差等，（4）随机误差（自然灾害、经济危机、人的偶然行为等）。

⼀元线性回归分析—内容提要与案例⼀元线性回归分析—内容提要与案例⼀.回归分析的基本概念1.函数关系与相关关系【相关关系】指变量之间确实存在的，但在数量上表现为不确定的相互依存关系.例如，⼈的体重y与⾝⾼x有关，⼀般⽽⾔，较⾼的⼈体重较重，但同样⾝⾼的⼈体重却不会完全相同；⼜如居民的储蓄存款额y与他的收⼊x有关，但同样收⼊的⼈储蓄存款额也不会相同.【函数关系】指变量之间确实存在的，且在数量上表现为确定性的相互依存关系.例如，圆的⾯积S与半径R有关，⼀旦半径R确定，则⾯积S可通过函数2=)fπ(RR求出，即2R=.Sπ函数关系往往通过具有不确定性的相关关系表现出来，⽽完全的相关关系必定是函数关系.2.相关关系的种类⑴按相关的⽅向划分【正相关】指两个变量按照相同的趋势变化.或者说某个现象的数量增加，另⼀个现象的数量也增加的现象.【负相关】指两个变量按照相反的趋势变化.或者说某个现象的数量增加，另⼀个现象的数量反⽽减少的现象.【零相关】指两个变量在数量上完全独⽴，在⼀定的形式下，互不影响，互不相⼲的关系.严格的讲，零相关不是“不相关”，因为事物的联系是绝对的，⽽独⽴是相对的，只有在某种形式下它才能互不影响，互不相⼲.⑵按相关形式划分【线性相关】指两个变量之间呈线性关系的相关.【⾮线性相关】指两个变量之间呈⾮线性关系的相关关系.⑶按变量多少划分【单相关】指两个变量之间的相关关系.【复相关】指两个以上的变量之间的相关关系.【偏相关】指在多个变量相关的场合，考察其中两个变量的相关关系（假定其他变量不变）.⑷按相关性质划分【真实相关】变量之间具有内在联系的相关关系.【虚假相关】变量之间只是表⾯存在、⽽实质上并没有内在联系的相关关系. 3.回归分析的⼀般概念“回归”⼀词由英国统计学家道尔顿提出.道尔顿在研究⼈的⾝⾼问题时，发现⽗母的⾝⾼与⼦⼥的⾝⾼有⼀定关系，⽗母⾼的⼦⼥反⽽矮⼀些，⽗母矮的⼦⼥反⽽⾼⼀些，他称这种返祖现象为回归.此后，回归分析泛指遵循道尔顿研究问题的思想和⽅法的⼀类统计分析⽅法.【回归分析的⽬的】建⽴变量之间相关关系的具体的数学表达形式，并藉此来探讨对因变量的预测问题.这不仅依赖变量之间相关程度的度量（需要相关分析的辅助），更依赖变量之间真实相关性的存在.然⽽，现象之间是否存在真实相关，必须根据有关专业领域的学科理论来确定.因此，回归分析必须要在定性分析前提下进⾏，不能进⾏纯数量的计算.⼆. ⼀元线性回归分析1.⼀元线性回归模型【模型的理论假设】设x 是⾃变量（⾮随机变量，其值是可以控制或精确测量），y 是因变量（随机变量，对给定的x 值不能事先确定y 的取值），则⼀元线性回归模型的理论假设是),0(~ ,2σεεβαN x y ++=.【模型的建⽴】求线性函数x Ey βα+=的经验回归⽅程x yβα+= 其中y是Ey 的统计估计，βα?,?分别是βα,的的统计估计，称为回归系数. 【模型的数据结构】设数据对n i y x i i ,,2,1 ),,( =是对变量对),(y x 的观测数据，则i i i x y εβα++=，称为⼀元样本回归⽅程，其中),0(~2σεN i ，n i ,,2,1 =且各个i ε相互独⽴. 2.模型参数α与β的最⼩⼆乘估计【参数估计的准则】定义（诸i y 回归到直线x Ey βα+=时的误差平⽅和）2112)())?((),(∑∑==--=-=ni i i ni i i x y yE y Q βαβα，求βα,使得 ),(min )?,?(,βαβαβαQ Q =，称βα,称为模型参数βα,的最⼩⼆乘估计，称 ii x y βα+= 为因变量(1,2,,)i y i n =的回归拟合值，简称回归值或拟合值.称i i i e y y=- 为因变量(1,2,,)i y i n =的残差.【参数估计的算法】记??=n y y y y=n x x x X 1 1121，???? ??=βα??A ，则⼀元线性回归的数据模型为XA y =，这是⼀个不相容线性⽅程组，当n X rank <=2)(时，其最⼩⼆乘解为()y X XX A T T 1-=.可以证明21)?( var , )?(σβββxxl E ==并且)0(?>=k kr xyβ. 221)?( var , )?(σααα???? ?+==xx l x n E ，其中∑==ni i x n x 11，∑=-=ni i xx x x l 12)(. 3.回归⽅程的显著性检验【显著性检验基本定理】定义∑=-=ni i y y SST 12)( ─总偏差平⽅和，⾃由度1-=n f T .∑=-=n i i y ySSR 12)?( ─回归平⽅和，⾃由度1=T f . ∑=-=ni i i yy SSE 12)?( ─残差平⽅和，⾃由度2-=n f T .则有⑴ SSE SSR SST +=. ⑵)2(~22-n SSEχσ⑶ SSE 与β相互独⽴. 【显著性检验基本⽅法】⑴⽅差分析（F 检验）检验假设0：H 变量y 对变量x 不存在线性相关关系（即0=β）.检验统计量及其分布在0H 为真时，SSR 与SSE 相互独⽴，)1(~2χSSR ，于是检验统计量)2,1(~)2/(--=n F n SSE SSRF .检验的显著性概率))2,1((F n F P p >-=.决策准则在显著性⽔平α下，当p >α时拒绝0H ，即认为回归⽅程有显著意义. ①当01.0⑵拟合程度测定可决系数（测定回归直线对各个观测点的拟合程度的统计量)SSTSSRr =2. 可决系数的解释① ]1,0[2∈r ，2r 的值越⼤（⼩），表明回归直线对各个观测点的拟合程度越⾼（低）；若12=r ，即0=SSE ，表明y 对x ⼏乎有确定的线性函数关系；若02=r ，即0=SSR ，表明y 对x 完全没有线性相关关系.② 2r r ±=的统计意义是数据向量T n y y y)?,,?,?(21 与T n y y y ),,,(21 的相关系数，其正负号与回归系数β的正负号相同. ⑶估计的标准误差定义2-=n SSEs 为变量y 对x 的最⼩⼆乘回归的估计标准误差.显然，s 的值越⼩，表明回归直线对各个观测点的拟合程度越⾼.注意，)2/(2-=n SSE s 是2σ的⽆偏估计. 4.利⽤回归⽅程进⾏预测【点预测】设0x 是⾃变量x 的预测值，则因变量y 的预测值为00?bx a y+=，是ε++=00bx a y的⽆偏估计.近似-，2-=n SSEs .因此，⑴ 0y 的0.95预测置信区间近似为)2? ,2?(00s y s y+-. ⑵ 0y 的0.99预测置信区间近似为)3? ,3?(00s y s y+-. 5.应⽤范例【例题1】我们知道营业税税收总额 y 与社会商品零售总额x 有关.为能从社会商品零售总额去预测税收总额，需要了解两者的关系.现收集了如下九组数据(表1).表1 社会商品零售总额与税收总额（单位：亿元）序号社会商品零售总额x营业税税收总额y1 2142.08 177.303.93 5.963 4 5 6 7 8 9 204.68242.88316.24341.99332.69389.29453.407.859.8212.5015.5515.7916.3918.45【⼀元线性回归的基本步骤·M A T L A B实现】⑴绘制数据散点图，直观分析建⽴⼀元线性回归模型的可⾏性clear,clfx=[142.08,177.30,204.68,242.88,316.24,341.99,332.69,389.29,453.40]';y=[3.93,5.96,7.85,9.82,12.50,15.55,15.79,16.39,18.45]';plot(x,y,'.'),lsline⑵求出⼀元线性回归模型参数的最⼩⼆乘估计X=[ones(length(x),1),x]; %构造系数矩阵aANDb=inv(X'*X)*X'*y %求模型参数aANDb =-2.26100.0487即求出的回归⽅程为x-=..2+261y049.0注释求模型参数的MATLAB计算也可⽤命令ab=(X'*X)\(X'*y).⑶对求出的回归⽅程进⾏F检验①计算各偏差平⽅和yy=-2.26+0.048678.*x; %计算模型模拟值ST=sum((y-mean(y)).^2); %计算总偏差平⽅和SR=sum((yy-mean(y)).^2); %计算回归平⽅和SE=sum((y-yy).^2); %计算剩余平⽅和②计算⽅差和F统计量的值VR=SR; %计算回归⽅差FE=length(x)-2; %计算SE的⾃由度VE=SE/FE; %计算剩余⽅差F=VR/VE; %计算F统计量的值③计算检验的显著性概率p值p=1-fcdf(F,1,FE);④判断回归⽅程的显著性if p<0.01h='**'; %⾼度显著elseif 0.01<=p<0.05h='*'; %显著elseh='[ ]'; %不显著⑤报告检验结果Name={'⽅差来源';'回归';'剩余';'总和'};SS={'偏差平⽅和';SR;SE;ST};FD={'⾃由度';1;FE;1+FE};FF={'F值';F;[];[]};PP={'p值';p;[];[]};XZX={'显著性';h;[];[]};ANOVA=[Name,SS,FD,FF,PP,XZX]ANOVA =Columns 1 through 4'⽅差来源' '偏差平⽅和 ' '⾃由度 ' '⽅差''回归' [ 203.4102] [ 1] [203.4102]'剩余' [ 7.9204] [ 7] [ 1.1315]'总和' [ 211.3284] [ 8] []Columns 5 through 7'F值' 'p值' '显著性'[179.7728] [3.0103e-006] '**'[] [] [][] [] []注释为⽅便今后的使⽤，已经将上述指令汇编为m函数⽂件b y k l r，调⽤这个函数即可⾃动完成上述全部⼯作. clearx=[142.08,177.30,204.68,242.88,316.24,341.99,332.69,389.29,453.40]';y=[3.93,5.96,7.85,9.82,12.50,15.55,15.79,16.39,18.45]';[aANDb,RR,VE,ANOVA]=byklr(x,y)aANDb =-2.26100.0487RR =0.9625VE =1.1315ANOVA =Columns 1 through 4'⽅差来源' '偏差平⽅和' ' ⾃由度 ' ' F值 ''剩余' [ 7.9204] [ 7] []'总和' [ 211.3284] [ 8] []Columns 5 through 6'p值 ' '显著性 '[3.0103e-006] '**'[] [][] []]关于这个函数的使⽤⽅法，可通过M A T L A B系统的在线帮助得到，运⾏下⾯的命令即可.doc byklr⑷利⽤回归⽅程进⾏预测现预测社会商品零售总额x=300亿元时的营业税的平均税收总额.①点预测YCDx=300;YCZy=aANDb(1)+aANDb(2)*YCDx;DYC=[{'预测点:',YCDx};{'预测值:',YCZy}]DYC ='预测点:' [ 300]'预测值:' [12.3423]即当社会商品零售总额为300亿元时营业税平均税收总额的预测值为12.3423亿元.②区间预测求社会商品零售总额为300亿元时营业税平均税收总额的概率为0.95（或0.99）的预测区间ALPHA=0.95;if ALPHA==0.95bykZXBJ=2*sqrt(VE);elseif ALPHA==0.99bykZXBJ=3*sqrt(VE);endQJYC=[{'置信⽔平:',ALPHA};{'预测下限:',YCZy-bykZXBJ};{'预测上限:',YCZy+bykZXBJ}]QJYC ='置信⽔平:' [ 0.9500]'预测下限:' [10.0794]'预测上限:' [14.6053]注释为⽅便今后的使⽤，已经将上述预测指令也汇编为m 函数⽂件b y k l r d o ，调⽤这个函数即可⾃动完成上述全部⼯作. [DYC,QJYC]=byklrdo(aANDb,VE,300,0.99)'预测点:' [ 300] '预测值:' [12.3423] QJYC ='置信⽔平:' [ 0.9900] '预测下限:' [ 9.1512] '预测上限:' [15.5335]doc byklrdo【线性回归分析·S t a t i s t i c s T o o l b o x 解决⽅案】1、S t a t i s t i c s T o o l b o x 线性回归分析函数介绍【函数名称】 regress 【函数功能】多元线性回归模型 ),0(~ ,2I N X y σεεβ+= 的建模分析. 【调⽤格式】b=regress(y,X)[b,bint,r,rint,stats]=regress(y,X)[b,bint,r,rint,stats]=regress(y,X,alpha) 【参数说明】输⼊参数X –p 元线性模型⾃变量的n 个观测值的n ×p 矩阵. y -p 元线性模型因变量的n 个观测值的n ×1向量. alpha –显著性⽔平(默认为0.05)，1-alpha 为区间估计的置信⽔平. 输出参数b -模型系数β的最⼩⼆乘估计值.bint -模型系数β的100(1-alpha)%置信区间.r -模型拟合残差.rint -模型拟合残差的100(1-alpha)%置信区间.stats -包含R2统计量、⽅差分析的F统计量的值、⽅差分析的显著性概率p值和2 的估计值.2、例题1（社会商品零售总额与税收总额问题）的r e g r e s s函数建模与分析X=[ones(length(x),1),x];[b,bint,r,rint,states]=regress(y,X)b =-2.26100.0487bint =-4.8794 0.35750.0401 0.0573r =-0.7251-0.40960.14760.2581-0.63291.16371.8564-0.2988rint =-2.7785 1.3282-2.7189 1.8997-2.2875 2.5828-2.2551 2.7714-3.1075 1.8417-1.0851 3.41250.0718 3.6410-2.6678 2.0702-2.9448 0.2258states =0.9625 179.7711 0.0000 1.1315如果需要对残差进⾏更直观的观察，可调⽤rcoplot函数，绘制按案例号排序的残差及其置信区间的误差条图.如rcoplot(r,rint)其中r和rint是regress函数的输出参数.。

⼀元线性回归模型案例第⼆章⼀元线性回归模型案例⼀、中国居民⼈均消费模型从总体上考察中国居民收⼊与消费⽀出的关系。

表2.1给出了1990年不变价格测算的中国⼈均国内⽣产总值（GDPP）与以居民消费价格指数（1990年为100）所见的⼈均居民消费⽀出（CONSP）两组数据。

1) 建⽴模型，并分析结果。

输出结果为：对应的模型表达式为：201.1070.3862CONSP GDPP =+(13.51) (53.47) 20.9927,2859.23,0.55R F DW ===从回归估计的结果可以看出，拟合度较好，截距项和斜率项系数均通过了t 检验。

中国⼈均消费增加10000元，GDP 增加3862元。

⼆、线性回归模型估计表2.2给出⿊龙江省伊春林区1999年16个林业局的年⽊材采伐量和相应伐⽊剩余物数据。

利⽤该数据（1）画散点图；（2）进⾏OLS 回归；（3）预测。

表2.2 年剩余物y 和年⽊材采伐量x 数据（1）画散点图先输⼊横轴变量名，再输⼊纵轴变量名得散点图（2）OLS估计弹出⽅程设定对话框得到输出结果如图：由输出结果可以看出，对应的回归表达式为：0.76290.4043t t yx =-+ (-0.625) (12.11)20.9129,146.7166, 1.48R F DW === （3）x=20条件下模型的样本外预测⽅法⾸先修改⼯作⽂件范围将⼯作⽂件范围从1—16改为1—17确定后将⼯作⽂件的范围改为包括17个观测值，然后修改样本范围将样本范围从1—16改为1—17打开x的数据⽂件，利⽤Edit+/-给x的第17个观测值赋值为20将Forecast sample选择区把预测范围从1—17改为17—17，即只预测x=20时的y的值。

由上图可以知道，当x=20时，y的预测值是7.32，yf的分布标准差是2.145。

三、表2.3列出了中国1978—2000年的参政收⼊Y和国内⽣产总值GDP的统计资料。

一元线性回归模型案例一元线性回归是统计学中常用的一种回归分析方法，用于研究一个自变量和一个因变量之间的线性关系。

在本文中，我们将通过一个实际案例来介绍一元线性回归模型的应用和分析过程。

案例背景：假设我们是某家电商平台的数据分析师，我们希望通过用户的年龄来预测其在平台上的消费金额。

我们收集了100位用户的年龄和其在平台上的消费金额的数据，现在我们希望利用一元线性回归模型来分析这些数据，以便更好地了解用户消费行为。

数据分析：首先，我们需要对收集到的数据进行初步的分析。

我们可以使用散点图来观察年龄和消费金额之间的关系。

通过观察散点图，我们可以初步判断年龄和消费金额之间是否存在线性关系，以及线性关系的方向和强度。

模型建立：在确认了年龄和消费金额之间存在线性关系后，我们可以建立一元线性回归模型。

模型的基本形式为，Y = β0 + β1X + ε，其中Y表示因变量（消费金额），X表示自变量（年龄），β0和β1分别表示截距和斜率，ε表示误差项。

我们需要通过最小二乘法来估计β0和β1的值，从而建立回归方程。

模型评价：建立回归模型后，我们需要对模型进行评价。

我们可以通过计算回归方程的拟合优度R^2来评价模型的拟合程度，R^2的取值范围为0到1，值越接近1表示模型拟合得越好。

此外，我们还可以利用残差分析来检验模型的假设是否成立，以及检验模型的稳健性和可靠性。

预测分析：最后，我们可以利用建立的回归模型进行预测分析。

通过输入不同年龄的值，我们可以利用回归方程来预测用户在平台上的消费金额。

预测分析可以帮助电商平台更好地了解不同年龄段用户的消费特点，从而制定针对性的营销策略和服务方案。

结论：通过以上一元线性回归模型的应用分析，我们可以得出结论，用户的年龄和在平台上的消费金额之间存在一定的线性关系，通过建立回归模型，我们可以对用户的消费金额进行预测和分析。

这对于电商平台来说具有重要的参考价值，可以帮助平台更好地了解用户消费行为，从而提升用户体验和增加销售额。