一元线性回归案例spss

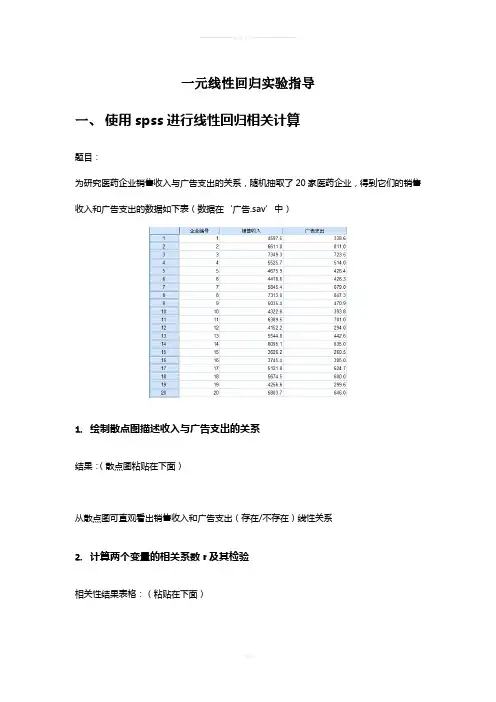
一元线性回归实验指导一、使用spss进行线性回归相关计算题目：为研究医药企业销售收入与广告支出的关系，随机抽取了20家医药企业，得到它们的销售收入和广告支出的数据如下表（数据在‘广告.sav’中）1.绘制散点图描述收入与广告支出的关系结果：（散点图粘贴在下面）从散点图可直观看出销售收入和广告支出（存在/不存在）线性关系2.计算两个变量的相关系数r及其检验相关性结果表格：（粘贴在下面）从结果中可看出，销售收入与广告支出的相关系数为（），双侧检验的P值（），r在0.01显著性水平下（），表明销售收入与广告支出之间（存在/不存在）线性关系。

3.一元线性回归分析计算回归分析；并输出标准化残差的pp图和直方图分析输出的结果：模型汇总表格：（粘贴在下面）这个表格给出相关系数R=（）以及标准估计的误差（）方差分析（ANOVA）表格：（粘贴在下面）这个表格给出回归模型的方差分析表，包括回归平方和SSR、回归均方MSR、残差平方和SSE、残差均方MSE、总平方和SST和总均方MST，F值129.762以及P值（），此处p 值（），说明回归的线性关系（显著/不显著）系数表格：（粘贴在下面）上面这个表格给出的是参数估计和检验的有关内容，包括回归方程的常数项、非标准化回归系数、常数项和回归系数检验的统计量t和显著性水平sig，以及回归系数的%95置信区间从此表可以得出销售收入与广告支出的估计方程为（）。

回归系数（）表示广告支出每变动1万元，销售收入平均变动（）万元。

4.残差的检验从上面的输出结果中可得到标准化残差的标准pp图和直方图（粘贴在下面）同时在数据表格中出现残差以及估计值和区间的上下界，其中PRE_1为点估计值；RES_1为非标准化残差；ZRE_1为标准化残差；LMCI_1和UMCI_1表示平均值的置信区间（均值的预测区间）；LICI_1和UICI_1表示个别值的预测区间的上界和下界；下面绘制非标转化残差图：（粘贴在下面）从残差图上可以看出，各个残差随机分布于0轴两侧，没有任何固定模式，这表明在销售收入与广告支出的一元线性回归中，线性假定以及等方差的假定成立。

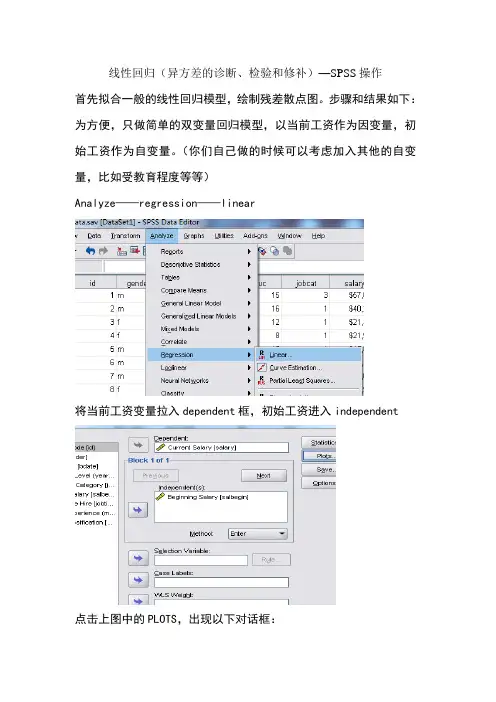
线性回归（异方差的诊断、检验和修补）—SPSS操作首先拟合一般的线性回归模型，绘制残差散点图。

步骤和结果如下：为方便，只做简单的双变量回归模型，以当前工资作为因变量，初始工资作为自变量。

（你们自己做的时候可以考虑加入其他的自变量，比如受教育程度等等）Analyze——regression——linear将当前工资变量拉入dependent框，初始工资进入independent点击上图中的PLOTS，出现以下对话框：以标准化残差作为Y轴，标准化预测值作为X轴，点击continue，再点击OK第一个表格输出的是模型拟合优度2R，为。

调整后的拟合优度为.第二个是方差分析，可以说是模型整体的显着性检验。

F统计量为，P值远小于，故拒绝原假设，认为模型是显着的。

第三个是模型的系数，constant代表常数项，初始工资前的系数为，t检验的统计量为，通过P值，发现拒绝原假设，认为系数显着异于0。

以上是输出的残差对预测值的散点图，发现存在喇叭口形状，暗示着异方差的存在，故接下来进行诊断，一般需要诊断异方差是由哪个自变量引起的，由于这里我们只选用一个变量作为自变量，故认为异方差由唯一的自变量“初始工资”引起。

接下来做加权的最小二乘法，首先计算权数。

Analyze——regression——weight estimation再点击options，点击continue，再点击OK，输出如下结果：由于结果比较长，只贴出一部分，第二栏的值越大越好。

所以挑出来的权重变量的次数为。

得出最佳的权重侯，即可进行回归。

Analyze——regression——linear继续点击save，在上面两处打勾，点击continue，点击ok这是输出结果，和之前同样的分析方法。

接下需要绘制残差对预测值的散点图，首先通过transform里的compute计算考虑权重后的预测值和残差。

以上两个步骤后即可输出考虑权重后的预测值和残差值然后点击graph，绘制出的散点图如下：。

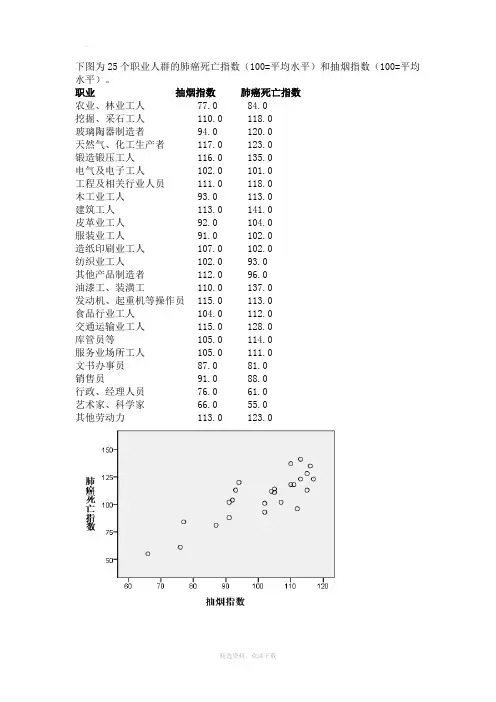
下图为25个职业人群的肺癌死亡指数（100=平均水平）和抽烟指数（100=平均水平）。

职业抽烟指数肺癌死亡指数农业、林业工人77.0 84.0挖掘、采石工人110.0 118.0玻璃陶器制造者94.0 120.0天然气、化工生产者117.0 123.0锻造锻压工人116.0 135.0电气及电子工人102.0 101.0工程及相关行业人员111.0 118.0木工业工人93.0 113.0建筑工人113.0 141.0皮革业工人92.0 104.0服装业工人91.0 102.0造纸印刷业工人107.0 102.0纺织业工人102.0 93.0其他产品制造者112.0 96.0油漆工、装潢工110.0 137.0发动机、起重机等操作员115.0 113.0食品行业工人104.0 112.0交通运输业工人115.0 128.0库管员等105.0 114.0服务业场所工人105.0 111.0文书办事员87.0 81.0销售员91.0 88.0行政、经理人员76.0 61.0艺术家、科学家66.0 55.0其他劳动力113.0 123.0散点图呈线性关系令Y=肺癌死亡指数，X=抽烟指数，做线性回归分析如下：表2中R=0.839 表示两变量高度相关R方=0.703 表示拟合较好，散点相对集中于回归线表3中sig.<0.05 则自变量与因变量具有显著的线性关系，即可以用回归模型表示表4中自变量sig.<0.05 则自变量对因变量的线性影响是显著的由此得到抽烟指数及肺癌死亡指数的一元回归方程：Y=-24.421+1.301X即抽烟指数每变动一个单位则肺癌死亡指数平均变动1.301个单位Welcome !!! 欢迎您的下载，资料仅供参考！。

SPSS实现一元线性回归分析实例2009-12-14 15:311、准备原始数据。

为研究某一大都市报开设周日版的可行性，获得了34种报纸的平日和周日的发行量信息(以千为单位)。

数据如图1所示。

SPSS17.0图12、判断是否存在线性关系。

制作直观散点图：（1）SPSS：菜单Analyze/Regression/linear Regression,如图2所示：图2 （2）打开对话框如图3图3图3中，Dependent是因变量，Independent是自变量，分别将左栏中的sunday选入因变量，daily选入自变量，newspaper作为标识标签选入case labels.(3)点击图3对话框中的plots按钮，如图4所示：图4将因变量DEPENTENT 选入Y:，自变量 ZPRED 选入X: continue 返回上级对话框。

单击主对话框OK.便生成散点图如图5所示：图5从以上散点图可看出，二者变量之间关系趋势呈线性关系。

2、回归方程菜单Analyze/Regression/linear Regression，在图3对话框的右边单击statistics如图6所示：图6regression coefficient回归系数，estimates估计值，confidence intervals level:95%置信区间，model fit拟合模型。

点击continue返回主对话框，单击OK.结果如图7、图8所示：图7图7中第一个图是变量的输入与输出，从图下的提示可知所有变量均输入与输出，没有遗漏。

图7中的第二图是模型总和R值，R平方值，R调整后的平方值，及标准误。

图8图8中第一图为方差统计图，包括回归平方和，自由度，方程检验F值及P值。

图8第二图为回归参数图，从图中可知，constant为回归方程截距，即13.836，回归系数为1.340，标准误分别为：35.804和0.071，及t检验值和95%的置信区间的最大值和最小值。

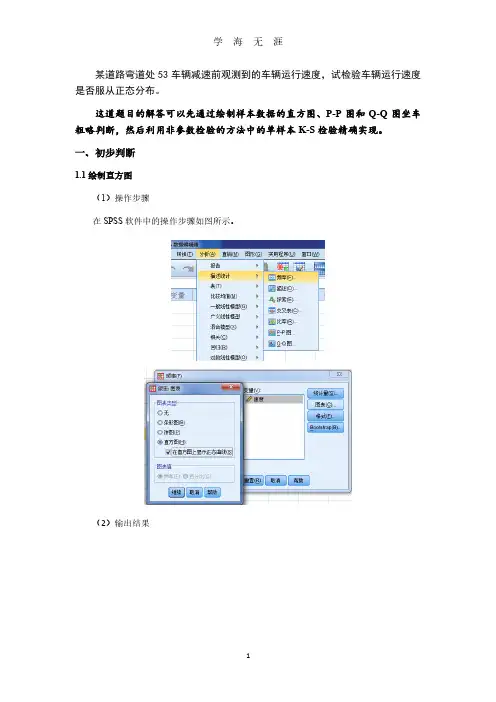
某道路弯道处53车辆减速前观测到的车辆运行速度，试检验车辆运行速度是否服从正态分布。

这道题目的解答可以先通过绘制样本数据的直方图、P-P图和Q-Q图坐车粗略判断，然后利用非参数检验的方法中的单样本K-S检验精确实现。

一、初步判断1.1绘制直方图（1）操作步骤在SPSS软件中的操作步骤如图所示。

（2）输出结果通过观察速度的直方图及其与正态曲线的对比，直观上可以看到速度的直方图与正太去线除了最大值外，整体趋势与正态曲线较吻合，说明弯道处车辆减速前的运行速度有可能符合正态分布。

1.2绘制P-P图（1）操作步骤在SPSS软件中的操作步骤如图所示。

（2）结果输出根据输出的速度的正态P-P 图，发现速度均匀分布在正态直线的附近，较多部分与正态直线重合，与直方图的结果一致，说明弯道处车辆减速前的运行速度可能服从正态分布。

二、单样本K-S 检验2.1单样本K-S 检验的基本思想K-S 检验能够利用样本数据推断样本来自的总体是否服从某一理论分布，是一种拟合优的检验方法，适用于探索连续型随机变量的分布。

单样本K-S 检验的原假设是：样本来自的总体与指定的理论分布无显著差异，即样本来自的总体服从指定的理论分布。

SPSS 的理论分布主要包括正态分布、均匀分布、指数分布和泊松分布等。

单样本K-S 检验的基本思路是：首先，在原假设成立的前提下，计算各样本观测值在理论分布中出现的累计概率值F(x)，；其次，计算各样本观测值的实际累计概率值S(x)；再次，计算实际累计概率值与理论累计概率值的差D(x)；最后，计算差值序列中的最大绝对值差值，即）（）（i i x F x S max D −=通常，由于实际累计概率为离散值，因此D 修正为：）（）（1i i x F x S max D −=−D 统计量也称为K-S 统计量。

在小样本下，原假设成立时，D 统计量服从Kolmogorov 分布。

在大样本下，原假设成立时，D n 近似服从K(x)分布：当D 小于0时，K(x)为0；当D 大于0时，）2-（exp ）1-（）（22x j x K j ∑∞−∞==容易理解，如果样本总体的分布与理论分粗的差异不明显，那么D 不应较大。

SPSS一元线性回归分析例题（体检数据中的体重和肺活量的分析）某单位对12名女工进行体检，体检项目包括体重(kg)和肺活量(L)，数据如下：X(体重：kg) 42.00 42.00 46.00 46.00 46.00 50.0050.00 50.00 52.00 52.00 58.00 58.00Y(肺活量：L) 2.55 2.20 2.75 2.40 2.80 2.813.41 3.10 3.46 2.85 3.50 3.00用x表示体重，y表示肺活量，建立数据文件。

利用一元线性回归分析描述其关系。

基本操作提示：Step 1 建立数据文件，并打开该数据文件。

Step 2 选择菜单Analyz e→Regressio n→Linear，打开主对话框。

在“Dependent”(因变量)列表框中选择变量“肺活量”，作为线性回归分析的被解释变量；在“Independent”(自变量)列表框中选择变量“体重”，作为解释变量。

Step 3 单击“Statistics”按钮，在打开的对话框中，依次选择“Estimates”(显示回归系数的估计值)、“Confidence intervals”、“Model fit”(模型拟合)、“Descriptives”、“Casewise diagnostic”(个案诊断)和“All Cases”选项。

选择完毕后，单击“Continue”按钮，返回主对话框。

Step 4 单击“Plots”(图形)按钮，在打开的主对话框中，选择“DEPENDENT”(因变量)作为y轴变量，“*ZPRED”(标准化预测值)作为x轴变量；并在“Standardized Residual Plots”(标准化残差图)中选择“Histogram”(直方图)和“Normal probabilityplot”(正态概率图，即P-P图)选项。

选择完毕后，单击“Continue”按钮，返回主对话框。

Step 5 单击“Save”(保存)按钮，在打开的主对话框中，在“Predicted Values”(预测值)选项区域中选择“Unstandardized”和“S. E. ofmean predictions”(预测值均数的标准误差)选项；“PredictionIntervals”(预测区间)选项区域中选择“Mean”和“Individual”选项；“Residuals”(残差)选项区域中选择“Unstandardized”选项。

回归分析例题SPSS求解过程（一）1、一元线性回归SPSS求解过程：判别：xy202.0173.2ˆˆˆ1+=+=ββ，且x与y的线性相关系数为R=0.951，回归方程的F检验值为75.559，对应F值的显著性概率是0.000<0.05,表示线性回归方程具有显著性，当对应F值的显著性概率>0.05,表示回归方程不具有显著性。

每个系数的t检验值分别是3.017与8.692，对应的检验显著性概率分别为：0.017（<0.05）和0.000（<0.05），即否定0H，也就是线性假设是显著的。

二、一元非线性回归SPSS求解过程：1、Y与X的二次及三次多项式拟合：所以，二次式为：2029.07408.00927.6xxY-+=三次式为：320046.01534.07068.1118.4xxxY+-+=2、把Y与X的关系用双曲线拟合：作双曲线变换：xVyU1,1==判别：V U 131.0082.0-=，x V y U 1,1==，V 与U 的相关系数为R=0.968，回归方程系数的F 检验值为196.227，对应F 值的显著性概率是0.000（<0.05）,表示线性回归方程具有显著性 ，每个系数的t 检验值分别是440514与14.008，对应的检验显著性概率分别为：0.000（<0.05）和0.000（<0.05），即否定0H ，也就是线性假设是显著的。

3、把Y 与X 的关系用倒指数函数拟合：x bae Y =，则x b a Y 1ln ln +=令U1=LN （Y ），V1=V=1/x,有 U1=c+bV1.判别：V U 111.1458.21-=，x V y U /1,ln 1==，V 与1U 的相关系数为R=0.979，回归方程的F 检验值为303.190，对应F 值的显著性概率是0.000（<0.05）,表示线性回归方程具有显著性 ，每个系数的t 检验值分别是195.221与-17.412，对应的检验显著性概率分别为：0.000（<0.05）和0.000（<0.05），即否定0H ，也就是线性假设是显著的。

第六节线性回归分析的SPSS操作本节内容主要介绍如何确定并建立线性回归方程。

包括只有一个自变量的一元线性回归和和含有多个自变量的多元线性回归。

为了确保所建立的回归方程符合线性标准，在进行回归分析之前，我们往往需要对因变量与自变量进行线性检验。

也就是类似于相关分析一章中讲过的借助于散点图对变量间的关系进行粗略的线性检验，这里不再重复。

另外，通过散点图还可以发现数据中的奇异值，对散点图中表示的可能的奇异值需要认真检查这一数据的合理性。

一、一元线性回归分析1．数据以本章第三节例3的数据为例，简单介绍利用SPSS如何进行一元线性回归分析。

数据编辑窗口显示数据输入格式如下图7-8（文件7-6-1.sav）：图7-8：回归分析数据输入2．用SPSS进行回归分析，实例操作如下：2.1.回归方程的建立与检验（1）操作①单击主菜单Analyze / Regression / Linear…，进入设置对话框如图7-9所示。

从左边变量表列中把因变量y选入到因变量（Dependent）框中，把自变量x选入到自变量（Independent）框中。

在方法即Method一项上请注意保持系统默认的选项Enter，选择该项表示要求系统在建立回归方程时把所选中的全部自变量都保留在方程中。

所以该方法可命名为强制进入法（在多元回归分析中再具体介绍这一选项的应用）。

具体如下图所示：图7-9 线性回归分析主对话框②请单击Statistics…按钮，可以选择需要输出的一些统计量。

如Regression Coefficients(回归系数)中的Estimates，可以输出回归系数及相关统计量，包括回归系数B、标准误、标准化回归系数BETA、T值及显著性水平等。

Model fit 项可输出相关系数R，测定系数R2，调整系数、估计标准误及方差分析表。

上述两项为默认选项，请注意保持选中。

设置如图7-10所示。

设置完成后点击Continue返回主对话框。

线性回归分析的SPSS操作本节内容主要介绍如何确定并建立线性回归方程。

包括只有一个自变量的一元线性回归和和含有多个自变量的多元线性回归。

为了确保所建立的回归方程符合线性标准，在进行回归分析之前，我们往往需要对因变量与自变量进行线性检验。

也就是类似于相关分析一章中讲过的借助于散点图对变量间的关系进行粗略的线性检验，这里不再重复。

另外，通过散点图还可以发现数据中的奇异值，对散点图中表示的可能的奇异值需要认真检查这一数据的合理性。

一、一元线性回归分析1．数据以本章第三节例3的数据为例，简单介绍利用SPSS如何进行一元线性回归分析。

数据编辑窗口显示数据输入格式如下图7-8（文件7-6-1.sav）：图7-8：回归分析数据输入2．用SPSS进行回归分析，实例操作如下：2.1.回归方程的建立与检验（1）操作①单击主菜单Analyze / Regression / Linear…，进入设置对话框如图7-9所示。

从左边变量表列中把因变量y选入到因变量（Dependent）框中，把自变量x选入到自变量（Independent）框中。

在方法即Method一项上请注意保持系统默认的选项Enter，选择该项表示要求系统在建立回归方程时把所选中的全部自变量都保留在方程中。

所以该方法可命名为强制进入法（在多元回归分析中再具体介绍这一选项的应用）。

具体如下图所示：图7-9 线性回归分析主对话框②请单击Statistics…按钮，可以选择需要输出的一些统计量。

如Regression Coefficients(回归系数)中的Estimates，可以输出回归系数及相关统计量，包括回归系数B、标准误、标准化回归系数BETA、T值及显著性水平等。

Model fit项可输出相关系数R，测定系数R2，调整系数、估计标准误及方差分析表。

上述两项为默认选项，请注意保持选中。

设置如图7-10所示。

设置完成后点击Continue返回主对话框。

图7-10：线性回归分析的Statistics选项图7-11：线性回归分析的Options选项回归方程建立后，除了需要对方程的显著性进行检验外，还需要检验所建立的方程是否违反回归分析的假定，为此需进行多项残差分析。

南昌航空大学经济管理学院学生实验报告实验课程名称：统计学实验时间 2012.12.24 班级学号 11091125 姓名戴文琦成绩实验地点 G804实验性质： □基础性 ■综合性 □设计性实验项目名 称一元线性回归分析指导老师王秀芝一、实验目的：掌握用SPSS 软件进行一元线性回归分析。

二、实验要求：在《中国统计年鉴》中选择合适的数据进行一元线性回归分析（注明数据来源）。

注意回归分析要有经济意义。

三、实验结果及主要结论根据该表进行拟合优度检验。

由于判定系数（0.983）较接近1，因此，认为拟合优度较高，被解释变量可以被模型解释的部分较多，不能被解释的部分较少。

由表中数据，被解释变量的SST 为2.462×107，SSR 为2.379×107，SSE 为835127.295，MSR 为2.379×107，MSE 为167025.459，F 统计量的观测值为142.428，对应的概率P 值近似为0。

根据表中数据进行回归方程的显著性检验。

如果显著性水平α为0.05，由于概率P 值小于显著性水平α，应拒绝回归方程显著性检验的原假设（β1＝0），认为回归系数不为0，被解释变量与解释变量的线性关系显著，可建立线性模型。

根据表中数据进行回归系数的显著性检验。

可以看出，如果显著性水平α为0.05，变量回归系数显著性t 检验的概率远远小于显著性水平α，因此拒绝原假设（β1＝0），认为回归系数与0存在显著差异，即不为0。

根据上述结果写出的一元线性回归方程如下1：x y214.0858.2437ˆ+= 原数据：按收入等级分城镇居民家庭平均每人全年现金消费支出 (2011年)Model SummaryModel R R Square Adjusted R Square Std. Error of theEstimate 1.983a.966.959408.68748a. Predictors: (Constant), 现金消费支出 (元)ANOVA bModel Sum of Squares df Mean Square F Sig.1 Regression 2.379E7 1 2.379E7 142.428 .000aResidual 835127.295 5 167025.459 Total 2.462E7 6a. Predictors: (Constant), 现金消费支出 (元)b. Dependent Variable: 食品 Coefficients aModelUnstandardizedCoefficients Standardized CoefficientstSig.BStd. ErrorBeta1(Constant) 2437.858 349.6876.972.001现金消费支出(元).214.018.98311.934 .000a. Dependent Variable: 食品1未考虑异方差问题。

回归分析一．实验描述：中国民航客运量的回归模型。

为了研究我国民航客运量的变化趋势及其成因，我们以民航客运量作为因变量Y，以国民收入（X1)、消费额（X2）、铁路客运量（X3）、民航航线里程（X4）、来华旅游入境人数（X5）、为主要影响因素。

数据如下表。

试建立Y与X1--X5之间的多元线性回归模型。

二．实验过程描述及实验结果(1)该表格中输出了5个自变量和1个因变量的一般统计结果，包括各自变量与因变量的平均值，标准差和个案数16。

该表格中列出了各个变量之间的相关性，从该表格可以看出因变量Y和自变量X1之间的相关系数为0.989，相关性最大,。

因变量Y与自变量X3之间相关系数为0.227，相关性最小。

(3)该表格输出的是被引入或从回归方程中被剔出的各变量。

说明进行线性回归分析时所采用的方法是全部引入法Enter。

因变量为Y。

(4)该表格输出的是常用统计量。

从该表看出相关性系数R为0.999，判定系数R2为0.998，调整的判定系数为0.997，回归估计的标准误差为49.49240。

该表格输出的是方差分析表。

从这部分结果看出：统计量F为1.128E3;相伴概率值小于0.01，拒绝原假设说明多个自变量与因变量Y之间存在线性回归关系。

Sum of Squares一栏中分别代表回归平方和(1.382E7)，残差平方和(24494.981)以及总平方和(1.384E7)，df为自由度。

判定系数R2=0.99855。

该表格为回归系数分析。

其中Unstandardized Coefficients为非标准化系数，Standardized Coefficients为标准化系数，t为回归系数检验统计量，sig为相伴概率值。

由表知t检验的相伴概率值均小于0.01，拒绝原假设，说明个变量与因变量之间均有显著线性相关关系。

从表格中可以看出该多元线性回归方程为：y=450.909+0.354 X1-0.561 X2-0.007 X3+21.578 X4+0.435 X5该表格为残差统计结果表。