11.1.2三角形的高中角平分线同步练习题(二)

人教版八年级数学上册11.1.2三角形的高、中线与角平分线同步训练一、选择题（共10小题，3*10=30）1．过△ABC的顶点A，作BC边上的高，以下作法正确的是()2．下列说法中正确的是()A．三角形的三条高都在三角形内B．直角三角形只有一条高C．锐角三角形的三条高都在三角形内D．三角形每一边上的高都小于其他两边3．如图，在△ABC中有四条线段DE，BE，EF，FG，其中有一条线段是△ABC的中线，则该线段是()A．线段DE B．线段BE C．线段EF D．线段FG4．若AD是△ABC的中线，下列结论错误的是()A．AB＝BC B．BD＝DCC．AD平分BC D．BC＝2DC5．如图，已知P是△ABC的重心，连接AP并延长交BC于点D，若△ABC的面积为20，则△ADC 的面积为()A．10 B．8 C．6 D．56. 如图，D ，E 分别是△ABC 的边AC ，BC 的中点，那么下列说法中不正确的是( )A ．DE 是△BCD 的中线B ．BD 是△ABC 的中线C ．AD ＝DC ，BE ＝ECD ．AD ＝EC ，DC ＝BE7．如图，CD ，CE ，CF 分别是△ABC 的高、角平分线、中线，则下列各式中错误的是( )A ．AB ＝2BF B ．∠ACE ＝12∠ACB C ．AE ＝BE D ．CD ⊥BE8．如图，AD ，BE ，CF 依次是△ABC 的高、中线和角平分线，下列表达式中错误的是( )A ．AE ＝CEB ．∠ADC ＝90°C ．∠CAD ＝∠CBED ．∠ACB ＝2∠ACF9．三角形一边上的中线一定可以把原三角形分成两个( )A ．形状相同的三角形B ．面积相等的三角形C ．直角三角形D ．周长相等的三角形10．如图，在△ABC 中，CD 平分∠ACB 交AB 于点D ，过点D 作DE ∥BC 交AC 于点E.若∠A ＝54°，∠B ＝48°，则∠CDE 的大小为( )A ．44°B ．40°C ．39°D ．38°二．填空题（共8小题，3*8=24）11．如图，线段AD 叫做△ABC 的边BC 上的_______，则∠ADB ＝∠ADC ＝________．12. 如图，以CF 为高的三角形是_______________________________．13．如图，在△ABC 中，AD ⊥BC ，垂足为D.若BC ＝5，AD ＝2，则△ABC 的面积为________．14．如图，AD ，BE ，CF 是△ABC 的三条中线，则AB ＝2________，BD ＝________，AE ＝12________．15．如图②，AE 平分∠BAC ，交BC 于点E.若∠BAE ＝50°，则∠CAE ＝________，∠CAB ＝________．16．如图，AD ⊥BC 于点D ，那么图中以AD 为高的三角形有________个.17．如图，在△ABC 中，∠1＝∠2，点G 为AD 的中点，延长BG 交AC 于点E ，F 为AB 上一点，且CF⊥AD于点H，下列说法正确的有________个.①AD是△ABE的角平分线；②BE是△ABD的边AD上的中线；③CH是△ACD的边AD上的高．18．如图，在△ABC中，CD是△ABC的角平分线，DE∥BC，交AC于点E，若∠ACB＝60°，则∠EDC＝__________．三．解答题（共7小题，46分）19．(6分) 在△ABC中，∠ACB是钝角，AD是BC边上的高．若AD＝2，BD＝3，CD＝1，求△ABC 的面积．20．(6分)如图所示，已知AD是△ABC的边BC上的中线．(1)作出△ABD的边BD上的高．(2)若△ABD的面积为6，且BD边上的高为3，求BC的长21．(6分) 如图，已知△ABC.(1)画中线AD；(2)画△ABD的高BE及△ACD的高CF.22．(6分) 如图，AD是∠CAB的平分线，DE∥AB，DF∥AC，EF交AD于点O. DO是∠EDF的平分线吗？如果是，请给予证明；如果不是，请说明理由．23．(6分)如图，D是△ABC中BC边上一点，DE∥AC交AB于点E，若∠EDA＝∠EAD，试说明AD是△ABC的角平分线．24．(8分)如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC＝8 cm2，求阴影部分的面积S阴影．25．(8分) 在等腰三角形ABC中，一腰AC上的中线BD将该三角形的周长分成9cm和15cm两部分，求这个三角形的腰长和底边长．参考答案1-5ACBAA 6-10DCCBC11. 高，90°12. △ABC，△BCF和△AFC13. 514. AF(BF)，CD，AC15. 50°，100°16. 617. 118. 30°19. 解：∵BD＝3，CD＝1，∴BC＝3－1＝2.∴S△ABC＝12BC·AD＝12×2×2＝2.20. 解：(1)如图所示．AM为△ABD的边BD上的高．(2)∵AD是△ABC的边BC上的中线，△ABD的面积为6，∴△ABC的面积为12.∵BD边上的高AM为3，∴BC＝12×2÷3＝8.21. 解：(1)中线AD如图．(2)△ABD的高BE及△ACD的高CF如图．22. 解：DO是∠EDF的平分线．证明：∵AD是∠CAB的平分线，∴∠EAD＝∠FAD.∵DE∥AB，DF∥AC，∴∠EDA＝∠FAD，∠FDA＝∠EAD.∴∠EDA＝∠FDA.∴DO是∠EDF的平分线．23. 解：∵DE∥AC，∴∠EDA＝∠CAD.∵∠EDA＝∠EAD，∴∠CAD＝∠EAD，∴AD是△ABC的角平分线．24. 解：∵D是边BC的中点，∴S△ABD＝S△ACD＝12S△ABC＝12×8＝4(cm2)，∵E是AD的中点，∴S△BDE＝12S△ABD＝2 cm2，S△CDE＝12S△ACD＝2 cm2，∴S△BEC＝S△BDE＋S△CDE＝4 cm2，又∵F 是CE 的中点，∴S 阴影＝12S △BEC ＝2 cm 2 25. 解：设腰长为x cm.①当腰长与腰长的一半是9 cm 时，x ＋12x ＝9， 解得x ＝6.∴底边长为15－12×6＝12(cm)． ∵6＋6＝12，∴6 cm ，6 cm ，12 cm 不能组成三角形．②当腰长与腰长的一半是15 cm 时，x ＋12x ＝15， 解得x ＝10.∴底边长为9－12×10＝4(cm)． ∵10＋4＞10，∴10 cm ，10 cm ，4cm 能组成三角形． 综上所述，三角形的腰长为10 cm ，底边长为4 cm.。

11.1.2 三角形的高、中线与角平分线1.关于三角形的高、中线与角平分线,下列说法正确的是( ).A.都是直线B.都是射线C.都是线段D.可以是射线,也可以是线段2.如图,已知BD 是△ABC 的中线,AB=5,BC=3,则△ABD 和△BCD 的周长的差是( ).A.2B.3C.6D.不能确定3.如图,AD 是△ABC 的角平分线,AE 是△ABD 的角平分线.若∠BAC=80°,则∠EAD 的度数是( ).A.20°B.30°C.45°D.60°4.如图,AM 是△ABC 的中线,△ABC 的面积为4 cm2,则△ABM 的面积为( ).A.8 cm2B.4 cm2C.2 cm2D.以上答案都不对5.如果一个三角形的三条高的交点在三角形的内部,那么该三角形是三角形.(填“锐角”“直角”或“钝角”)6.如图,线段AD,CE 分别是△ABC 中边BC,AB 上的高.若AD=10,CE=9,AB=12,则BC= .7.如图,在△ABC 中,AB=AC,线段AD 是△ABC 的中线,△ABC 的周长为34 cm,△ABD 的周长为30 cm,求AD 的长.8.如图,已知AD,AE 分别是△ABC 的高和中线,AB=6 cm,AC=8 cm,BC=10 cm,∠CAB=90°.试求:(1)AD 的长;(2)△ABE 的面积;(3)△ACE 和△ABE 的周长的差.9.如图,D 是△ABC 的边AC 上一点,过点D 作DE∥AB 交BC 于点E.若∠DBE=∠BDE,试说明线段BD 是△ABC 的角平分线.10.有一块三角形优良品种试验基地如图所示,由于引进四个品种进行对比试验,需将这块土地分成面积相等的四块,请你制定出两种以上的划分方案以供选择,并画图说明.★11.如图,线段AD 是△ABC 的角平分线,DE∥AC 交AB 于点E,EF∥AD 交BC 于点F,试问线段EF 是△BED 的角平分线吗?为什么?答案与解析夯基达标1.C2.A 因为BD 是△ABC 的中线,所以AD=CD.所以△ABD 与△BCD 的周长的差是(AB+BD+AD)-(BC+CD+BD)=AB+BD+AD-BC-CD-BD=AB+AD-BC-CD=5-3=2.3.A4.C 三角形的中线将三角形分成面积相等的两部分.5.锐角6.10.8 SABC =1·BC ·AD=1·AB ·CE ,△ 2 2则 BC=A ·C = 12×9=10.8.A 107.解 ∵点 D 是线段 BC 的中点,∴BC=2BD.∵AB=AC ,△ABC 的周长为 34 cm,∴2AB+2BD=34 cm,即 AB+BD=17 cm .①∵△ABD 的周长为 30 cm,即 AB+BD+AD=30 cm,②∴由②-①,得 AD=13 cm .培优促能8.解 (1)S ABC =1AB ·AC=1×6×8=24(cm 2),△ 2 2所以 S ABC =1AD ·BC=24,即 AD=4.8 cm .△ 2(2)S ABE =1BE ·AD=1 1 �� ·AD=1BC ·AD=12 cm 2.△ 2 2 2 4(3)将△ACE 和△ABE 的周长分别记为 C △ACE 和 C △ABE ,则 C △ACE -C △ABE =AC+CE+AE-(AB+BE+AE )=AC-AB=8-6=2(cm).9. 解 ∵DE ∥AB ,∴∠BDE=∠ABD.又∠BDE=∠DBE ,∴∠ABD=∠DBE,即线段BD 是△ABC 的角平分线.10.解答案不唯一,如方案一:如图①,在BC 上取点D,E,F,使BD=DE=EF=CF,连接AD,AE,AF. 方案二:如图②,分别取AB,BC 的中点D,E,连接AE,DE,再取AE 的中点F,连接FC.方案三:如图③,分别取BC 的中点D,CD 的中点E,AB 的中点F,连接AD,AE,DF.方案四:如图④,分别取BC 的中点D,AB 的中点E,AC 的中点F,连接AD,DE,DF.①②③④创新应用11.解线段EF 是△BED 的角平分线.理由如下:如图,∵线段AD 是△ABC 的角平分线,∴∠1=∠2.∵EF∥AD,∴∠1=∠3,∠4=∠ADE. ∵DE∥AC,∴∠2=∠ADE,∴∠2=∠4,∴∠3=∠4.故线段EF 是△BED 的角平分线.。

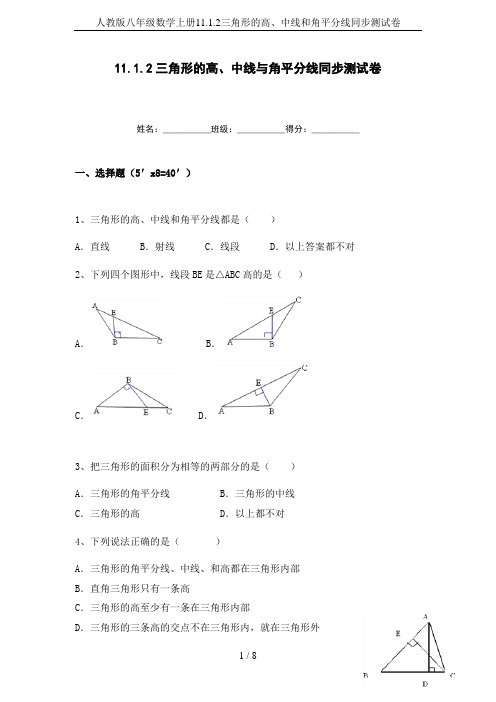
11.1.2三角形的高、中线与角平分线同步测试卷姓名：___________班级：___________得分：___________一、选择题（5′x8=40′）1、三角形的高、中线和角平分线都是（）A．直线B．射线 C．线段D．以上答案都不对2、下列四个图形中，线段BE是△ABC高的是（）A．B．C．D．3、把三角形的面积分为相等的两部分的是（）A．三角形的角平分线B．三角形的中线C．三角形的高D．以上都不对4、下列说法正确的是（）A．三角形的角平分线、中线、和高都在三角形内部B．直角三角形只有一条高C．三角形的高至少有一条在三角形内部D．三角形的三条高的交点不在三角形内，就在三角形外5、如图，AD,CE 是△ABC 的两条高，已知AD=10，CE=9，AB=12，则BC 的长是（ ）A ．10B ．10.8C ．12D ．156、如图，在△ABC 中，已知点D 、E 、F 分别是BC 、AD 、CE 的中点， 且S △ABC =4，S △BEF =（ ）A. 2B. 1C. 21D. 417、如图：在△ABC 中，BE 、CD 分别是AC 、AB 边上的中线，BE 与CD 相交于点O ，则 ( )A. B.C. D.8、如图,在△ABC 中,点D,E,F 分别在三边上,E 是AC 的中点,AD,BE,CF 交于一点G,BD ＝2DC,S △BDG ＝8,S △AGE ＝3,则S △ABC ＝( )A ．25B ．30C ．35D ．40二、填空题（5′x4=20′）9、①三角形的三条角平分线交于一点，这点到三条边的距离相等；②三角形的三条中线交于一点；③三角形的三条高线所在的直线交于一点；④三角形的三条边的垂直平分线交于一点，这点到三个顶点的距离相等．以上说法中正确的是_________________．10、如图，△ABC中，AB=AC，∠BAC和∠ACD的平分线相交于点D，∠ADC=130°，则∠BAC的度数________．11、如图，已知BE、CF是△ABC的角平分线，BE、CF相交于D，若，则等于________.12、如图，已知AD为△ABC的中线，AB=10cm，AC=7cm，△ACD的周长为19cm，则△ABD的周长为________.第10题第11题第12题三、解答题（10′x4=40′）13、已知：如图，在中，．（1）求作：的角平分线（2）在（1）的条件下，若，，求的长．14、在Rt△ABC中，∠ACB=90°，CD是AB边上的高，AB=10cm，BC=8cm，AC=6cm，（1）求CD的长；（2）若AE是BC边上的中线，求△ABE的面积．15、如图所示，三亚有三个车站A、B、C成三角形，一辆公共汽车从B站前往到C站。

11.1.2三角形的高、中线与角平分线同步练习(时间120分钟,满分150分)一、选择题：本大题共12个小题，每小题4分，共48分． 1.三角形的角平分线、中线、高线都是（ ）A.线段B.射线C.直线D.以上都有可能 2. 下列说法正确的是（ ）A ．三角形三条高都在三角形内B ．三角形三条中线相交于一点C ．三角形的三条角平分线可能在三角形内，也可能在三角形外D ．三角形的角平分线是射线 3.至少有两条高在三角形内部的三角形是（ ）A. 锐角三角形B. 钝角三角形C. 直角三角形D.都有可能 4.不一定在三角形内部的线段是（ ）（A ）三角形的角平分线 （B ）三角形的中线 （C ）三角形的高 （D ）三角形的中位线 5.可以把一个三角形分成面积相等的两部分的线段是（ ）A ．三角形的高B ．三角形的角平分线C ．三角形的中线D ．无法确定 7．在三角形中，交点一定在三角形内部的有（ ）①三角形的三条高线 ②三角形的三条中线 ③三角形的三条角平分线 ④三角形的外角平分线．A ．①②③④B ．①②③C ．①④D ．②③8.如果一个三角形三条高的交点恰是三角形的一个顶点，那么这个三角形是 （ ） A. 锐角三角形 B. 直角三角形 C.钝角三角形 D.不能确定 9．画△ABC 中AB 边上的高，下列画法中正确的是（ ）A B C D10. 如图,D,E 分别是△ABC 的边AC,BC 的中点,则下列说法不正确的是( )A.DE 是△BCD 的中线B.BD 是△ABC 的中线C.AD=DC,BD=ECD.∠C 的对边是DE11.如图3所示,在△ABC 中,已知点D, E,F 分别为边BC,AD,CE 的中点, 且S △ABC =4cm 2,则S 阴影等于( )A.2cm 2B.1cm 2C.12cm 2 D.14cm 212.在△ABC 中，D 是BC 上的点，且BD:CD=2:1,S △ACD =12,那么S △ABC 等于（ ）A. 30B. 36C. 72D.24二、填空题：本大题共6小题，每小题4分，共24分．13. 照相机的支架是三条腿，这是利用了三角形的_________． 14.如图，在△ABC 中，BC 边上的高是 ，在△AEC 中，AE 边上的高是 ，EC 边上的高是 . 15.如图所示，CD 是△ABC 的中线，AC =9cm ，BC =3cm ，那么△ACD 和△BCD 的周长差是___________cm ． 16.在ABC ∆中,2,3AC cm BC cm ==,则ABC ∆的高AD 与BE 的比是FE（第11题） D CBA（第10题）17.如图所示：（1）在△ABC 中，BC 边上的高是_____（2）在△AEC 中，AE 边上的高是_____． 18．如图所示，在△ABC 中，AD ⊥BC ，BE ⊥AC ，BC=12，AC=8，AD=6，则BE的长 ．三、解答题：本大题共2个小题，每小题7分，共14分． 19.如图,在⊿ABC 中画出高线AD 、中线BE 、角平分线CF .20.在△ABC 中,AB=AC,AD 是中线,△ABC 的周长为34cm,△ABD 的周长为30cm, 求AD 的长.四、解答题：本大题共4个小题，每小题10分，共40分21.如图，已知：在三角形ABC 中，∠C=90º,CD 是斜边AB 上的高，AB=5,BC=4,AC=3,求高CD 的长度.22.在等腰三角形ABC 中，AB=AC ，一腰上的中线BD 将这个等腰三角形的周长分为15和6两部分，求该等腰三角形的腰长及底边长．ABC（第17题） （第15题） E FDCBA（第14题） （第18题）23.（1）如图，在△ABC中，D、E分别是BC、AD的中点，S△ABC=4cm2，求S△ABE．（2）如图，S△ABC=1,且D是BC的中点，AE:EB=1:2,求△ADE的面积.EDCBA24.如图，在直角三角形ABC中，∠ACB=90°，CD是AB边上的高，AB=13cm，BC=12cm，AC=5cm，求：（1）△ABC的面积；（2）CD的长；（3）作出△ABC的边AC上的中线BE，并求出△ABE的面积；（4）作出△BCD的边BC边上的高DF，当BD=11cm 时，试求出DF的长。

前言：
该同步训练习题由多位一线国家特级教师针对当前最新的热点、考点、重点、难点、知识点，精心编辑而成。

以高质量的同步训练习题助力考生查漏补缺，在原有基础上更进一步。

（最新精品同步训练习题）
11．1.2 三角形的高、中线与角平分线
[学生用书P5]
1．下列说法不正确的是( )
A．三角形的中线在三角形的内部
B．三角形的角平分线在三角形的内部
C．三角形的高在三角形的内部
D．三角形必有一高线在三角形的内部
2．三角形的下列线段中，能将三角形的面积分成相等的两部分的是( ) A．中线 B．角平分线
C．高 D．以上答案均正确
3．如图11-1-13，在△ABC中，BD为角平分线，BE为中线．如果AC＝12 cm，则AE＝__ __；如果∠ABC＝80°，则∠ABD＝__ _．
图11-1-13
4．[2016·丹阳期中]如图11-1-14，AD⊥BC于D，那么图中以AD为高的三角形有__ _个．
图11-1-14
5．如图11-1-15，已知△ABC，过点A画△ABC的角平分线AD，中线AE和高线AF.
图11-1-15
6．如图11-1-16，已知在△ABC中，CF，BE分别是AB，AC边上的中线，若AE＝2，AF＝3，且△ABC的周长为15，求BC的长．
图11-1-16
7．如图11-1-17所示，已知AD是△ABC的边BC上的中线．
(1)作出△ABD的边BD上的高；
(2)若△ABC的面积为10，求△ADC的面积；
(3)若△ABD的面积为6，且BD边上的高为3，求BC的长．。

11.1.2 三角形的高、中线与角平分线提高拓展题中考链接答案及解题思路初中数学公式大全1 过两点有且只有一条直线2 两点之间线段最短3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中，垂线段最短7 平行公理经过直线外一点，有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行，这两条直线也互相平行9 同位角相等，两直线平行10 内错角相等，两直线平行11 同旁内角互补，两直线平行12 两直线平行，同位角相等13 两直线平行，内错角相等14 两直线平行，同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180 °18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 平行四边形判定定理 1 两组对角分别相等的四边形是平行四边形21 平行四边形判定定理 2 两组对边分别相等的四边形是平行四边形22 平行四边形判定定理 3 对角线互相平分的四边形是平行四边形23 平行四边形判定定理 4 一组对边平行相等的四边形是平行四边形24 矩形性质定理 1 矩形的四个角都是直角25 矩形性质定理 2 矩形的对角线相等26 矩形判定定理 1 有三个角是直角的四边形是矩形27 矩形判定定理 2 对角线相等的平行四边形是矩形28 菱形性质定理 1 菱形的四条边都相等29 菱形性质定理 2 菱形的对角线互相垂直，并且每一条对角线平分一组对角30 菱形面积= 对角线乘积的一半，即S= （a×b ）÷231 菱形判定定理1 四边都相等的四边形是菱形32 菱形判定定理2 对角线互相垂直的平行四边形是菱形33 正方形性质定理1 正方形的四个角都是直角，四条边都相等34 正方形性质定理 2 正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角35 定理1 关于中心对称的两个图形是全等的36 定理2 关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分37 逆定理如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称38 等腰梯形性质定理等腰梯形在同一底上的两个角相等。

11.1.2三角形的高、中线与角平分线一、选择题1.画△ABC中AB边上的高，下列画法中正确的是（）A．B．C．D．2．下列说法正确的是（）A．三角形三条高都在三角形内B．三角形三条中线相交于一点C．三角形的三条角平分线可能在三角形内，也可能在三角形外D．三角形的角平分线是射线3.如图，已知BD是△ABC 的中线，AB=5，BC=3，△ABD和△BCD的周长的差是（）A．2 B．3 C．6 D．不能确定（第3题）（第4题）（第6题）（第7题）4.如图，△ABC中∠C=90°，CD⊥AB，图中线段中可以作为△ABC的高的有（）A．2条 B．3条 C．4条 D．5条5．在△ABC中，AD为中线，BE为角平分线，则在以下等式中：①∠BAD=∠CAD；②∠ABE=∠CBE；③BD=DC；④AE=EC．正确的是（）A．①②B．③④C．①④D．②③6.王师傅用4根木条钉成一个四边形木架，如图．要使这个木架不变形，他至少还要再钉上几根木条？（ ）A ．0根B ．1根C ．2根D ．3根7.如图，工人师傅砌门时，常用木条EF 固定矩形门框ABCD ，使其不变形，这种做法的根据是（ ）A ．两点之间线段最短B ．矩形的对称性C ．矩形的四个角都是直角D ．三角形的稳定性8.三角形的高线是（ ） A ．直线B ．线段C ．射线D ．三种情况都可能 二、填空题9.如图，在△ABC 中，∠ACB=90°，CD ⊥AD ，垂足为点D ，有下列说法：①点A 与点B 的距离是线段AB 的长；②点A 到直线CD 的距离是线段AD 的长；③线段CD 是△ABC 边AB 上的高；④线段CD 是△BCD 边BD 上的高． 上述说法中，正确的个数为_________个10.如图，△ABC 的角平分线AD 、中线BE 相交于点O ，则①AO 是△ABE 的角平分线；②BO 是△ABD 的中线；③DE 是△ADC 的中线；④ED 是△EBC 的角平分线的结论中正确的有_________.11．如图，小明的父亲在院子的门板上钉了一个加固板，从数学角度看，这样做的原因是______________________．（第9题） （第10题） （第11题） （第12题）12.如图所示，CD 是△ABC 的中线，AC=9cm ，BC=3cm ，那么△ACD 和△BCD 的周长差是___________cm ．13.AD 是△ABC 的一条高，如果∠BAD=65°，∠CAD=30°，则∠BAC=______．14.如图，在△ABC 中，AC ⊥BC ，CD ⊥AB 于点D ．则图中共有_____个直角三角形．15.如图，在△ABC 中，BD 是角平分线，BE 是中线，若AC=24cm ，则AE=cm ，若∠ABC=72°，则∠ABD=_____度． 16.如图所示：（1）在△ABC 中，BC 边上的高是_____；（2）在△AEC 中，AE 边上的高是_____．17.三角形一边上的中线把三角形分成的两个三角形的面积关系为_____.18.如图，在△ABC 中，CD 平分∠ACB ，DE ∥AC ，DC ∥EF ，则与∠ACD 相等角有_____个．三、解答题19．如图，AD 是△ABC 的角平分线，过点D 作直线DF ∥BA ，交△ABC 的外角平分线AF 于点F ，DF 与AC 交于点E ．求证：DE=EF ．（第18题）（第16题） （第19题）（第14题） （第15题）20.若等腰三角形一腰上的中线分周长为１２cm和１５cm两部分，求这个等腰三角形的底边和腰的长.21.如图：（1）画出△ABC的BC边上的高线AD；（2）画出△ABC的角平分线CE．第21题22.△ABC中，AD⊥BC，AE平分∠BAC交BC于点E ．（1）∠B=30°，∠C=70°，求∠EAD的大小．（2）若∠B＜∠C，则2∠EAD与∠C-∠B是否相等？若相等，请说明理由．第22题23.已知△ABC中，∠ACB=90°，CD为AB边上的高，BE平分∠ABC，分别交CD、AC于点F、E，求证：∠CFE=∠CEF ．第23题一、选择题 1.C 2.B 3.A 4.B 5.D 6.B 7.D 8.B二、填空题9.4 10.2 11.利用三角形的稳定性使门板不变形． 12..6 13.95°或35° 14.3 15.12,36 16.AB,CD 17.相等 18.4三、解答题19.证明：∵AD 是△ABC 的角平分线，AF 平分△ABC 的外角，∴∠1=∠2，∠3=∠4，∵DF ∥BA ，∴∠4=∠ADE ，∠1=∠F∴∠3=∠ADE ，∠2=∠F∴DE=EA EF=EA∴DE=EF20.在ＡＢＣ∆中，ＡＢ＝ＡＣ，ＢＤ是中线，设ＡＢ＝x,BC=y.(1)当AB+AD=12时，则⎪⎪⎩⎪⎪⎨⎧=+=+15211221x y x x ，解得,118⎩⎨⎧==y x ∴三角形三边的长为８，８，１１； （２）当AB+AD=1５时，则⎪⎪⎩⎪⎪⎨⎧=+=+12211521x y x x ，解得,y x ⎩⎨⎧==710∴三角形三边的长为１０，１０，７； 经检验，两种情况均符合三角形的三边关系.∴三角形三边的长分别为８，８，１１或１０，１０，７.21. 解：（1）如图所示：AD 即为所求；（2）如图所示：CE 即为所求．22.解：（1）∵∠B=30°，∠C=70°∴∠BAC=180°-∠B-∠C=80°∵AE 是角平分线，∴∠EAC=21∠BAC=40°∵AD 是高，∠C=70°∴∠DAC=90°-∠C=20°∴∠EAD=∠EAC-∠DAC=40°-20°=20°；（2）由（1）知，∠EAD=∠EAC-∠DAC=21∠BAC-（90°-∠C ）① 把∠BAC=180°-∠B-∠C 代入①，整理得∠EAD=21∠C-21∠B ，∴2∠EAD=∠C-∠B ．23.证明： ∵∠ACB=90°， ∴∠1+∠3=90°，∵CD ⊥AB ，∴∠2+∠4=90°，又∵BE 平分∠ABC ，∴∠1=∠2，∴∠3=∠4，∵∠4=∠5，∴∠3=∠5，即∠CFE=∠CEF ．。

人教版八年级数学上册《11.1.2三角形的高、中线与角平分线》同步测试题及答案班级：姓名：一、单选题1．如图，在△ABC中，∠C＝90°，∠B＝30°，根据尺规作图保留的痕迹，判断下列结论错误的是（）A．AD是∠BAC的平分线B．AD=BDC．AD=2CD D．2S△ABD =3S△ACD2．如图是一块不规则的四边形地皮ABCO，各顶点坐标分别为A(−2,6)，B(−5,4)，C(−7,0)，O(0,0)（图上一个单位长度表示10米），则这块地皮的面积是（）m2．A．25 B．250 C．2500 D．22003．如图，每个小正方形边长均为1，则下列图中的三角形（阴影部分）与图中△ABC面积相等的是（）A．B．C．D．4．如图，在Rt△ABC 中，∠ACB=90°， CD 是AB边上的高，若 AC=3， AB=5则CD=( )A．2 B．2.4 C．3 D．√155．如图所示的网格是正方形网格，点A，B，C，D是网格线交点，则下列关于△ABC的面积与△BCD 的面积的大小说法正确的是（）A．S△ABC>S△BCD B．S△ABC=S△BCDC．S△ABC<S△BCD D．无法比较6．如图，在四边形ABCD中∠A=90°，AD=2，BC=4，对角线BD平分∠ABC，则△BCD的面积为（）A．3 B．4 C．5 D．67．如图，已知∠ACB=90°，BC=8，AC=6，AB=10，点D在线段AB上运动，线段CD的最短距离是（）A．4.8 B．4 C．5.8 D．5 8．ABCD是边长为1的正方形，△BPC是等边三角形，则△BPD的面积为()A．14B．√3−14C．18D．2√3−189．下列命题正确的是（）A．三角形的一个外角大于任何一个内角B．三角形的三条高都在三角形内部C．三角形的一条中线将三角形分成两个三角形面积相等D．两边和其中一边的对角相等的三角形全等10．下列说法中，正确的个数为（）①三角形的高、中线、角平分线都是线段②三角形的外角大于任意一个内角③△ABC中，∠A＝2∠B＝3∠C，则△ABC是直角三角形④若a、b、c均大于0，且满足a+b＞c，则长为a、b、c的三条线段一定能组成三角形A．1 B．2 C．3 D．411．如图，在△ABC中，AD是角平分线，DE⊥AB于点E，DF⊥AC于点F，DE=2，AC=4则△ADC 的面积为．12．如图，在平面直角坐标系中，已知点A(−3,−1)，B(1,3)，C(2,−3)，则三角形ABC的面积为．13．如图，在矩形ABCD中，AB＝5，AD＝3，动点P满足3S△PAB＝S矩形ABCD，则点P到A、B两点距离之和PA＋PB的最小值为.14．已知一次函数y=32x+m和y=−12x+n的图象都经过点A(−2,0)，且与y轴分别交于B，C两点，则△ABC的面积为．15．已知a b=35，则b+2ab−2a=．16．如图△ABC中AD是高，AE、BF是角平分线，它们相交于点O，∠BAC=50°，∠C=70°求∠DAC，∠AOB．17．三角形ABC在直角坐标系中，且A(0,4)，B(−2,0)，C(3,−5)，将三角形ABC向下平移2个单位，再向左平移4个单位得到三角形A1B1C1，求三角形A1B1C1的面积．18．如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B＝70°，∠C＝30°.（1）则∠BAE＝；（2）求∠DAE的度数.参考答案1．答案D2．答案C3．答案A4．答案B5．答案B6．答案B7．答案A8．答案B9．答案C10．答案A11．答案412．答案1413．答案√4114．答案415．答案−1116．答案∠DAC=20°17．答案1518．答案（1）40°（2）解：∵AD⊥BC∴∠ADC=90°∴∠DAC＝90°-∠C＝60°∴∠DAE＝∠DAC-∠EAC＝20°.。

人教版八年级数学上册《11.1.2三角形的高、中线与角平分线》测试题及答案班级：姓名：一、选择题1．下列说法：①三角形的一个外角等于这个三角形的两个内角的和；②三角形中最小的锐角不能大于60°；③三角形任意两个内角的和大于第三个内角；④三角形一边上的高小于这个三角形的其他两边；⑤直角三角形只有一条高．其中正确的个数为（）A．1个B．2个C．3个D．4个2．如图，在△ABC中，AB＝AC，∠BAC＝36°，以点C为圆心，以BC为半径作弧交AC于点D，再分别以B，D为圆心，以大于12BD的长为半径作弧，两弧相交于点P，作射线CP交AB于点E，连接DE．以下结论不正确的是（）A．∠BCE＝36°B．BC＝AEC．BEAC=√5−12D．S△AECS△BEC=√5+123．如图，△ABC中∠ACB=75°，将△ABC绕点C顺时针方向旋转一定角度得到△EDC．若点D恰好落在AB边上，且AD=CD，则∠E的度数为（）A．20°B．25°C．30°D．35°4．在△ABC中AB=AC，点D在AC上，且BD=BC=AD，取AB边上的中点E，连接DE，则∠ADE=（）°．A．18 B．36 C．54 D．725．下列命题中，真命题的是（）A．三角形的一个外角大于任何一个内角B．三角形的三条角平分线交于一点，且这一点到三角形的三个顶点距离相等C．同旁内角互补D．若a1，a2，a3都是正数，且a1+a2+a3=1，那么这三个数中至少有一个大于或等于136．如图，把等腰直角三角形ABC的直角顶点和另外一个顶点分别放在矩形纸片的两条对边上，已知∠1=20°，则∠2的度数为（）A．55°B．60°C．65°D．75°7．如图，直线a∥b，若∠1=24°，∠A=42°，则∠2等于（）A．66°B．70°C．42°D．30°8．如图，在△ABC中，∠BAC和∠ABC的平分线AE，BF相交于点O，AE交BC于E，BF交AC于F，过点O作OD⊥BC于D，下列三个结论：①∠AOB=90°+12∠C；②当∠C=60°时AF+BE=AB；③若OD=a，AB+BC+CA=2b则S△ABC=2ab．其中正确的是（）A．①②B．②③C．①②③D．①③9．如图，△ABC中，BD是∠ABC的角平分线DE∥BC，交AB于E,∠A=60°,∠BDC=95°，则∠BED的度数是（）A．95°B．100°C．105°D．110°10．等腰三角形一个外角为100°，则它的顶角为（）A．40°B．80°C．100°D．80°或20°二、填空题11．如图，在△ABC中，AD平分∠BAC，点E在射线BC上EF⊥AD于F，∠B=40°，∠ACE=72°则∠E 的度数为.12．如图，在△ABC中，AD是△ABC的角平分线，F在射线AD上，FE⊥BC于E，∠C=80°，∠B=36°则∠F=度．13．如图，在△ABC中，BAC=108°，将△ABC绕点A逆时针旋转得到△ADE，若点D恰好落在BC边上，且DC=DA，则∠E的度数为°．14．如图把三角形ABC沿DE折叠，使点B落在点B′处∠1=24°，∠2=80°，则∠B′=度．15．如图，在△ABC中，将△ABC沿直线m翻折，点B落在点D的位置，若∠1−∠2=60°，则∠B 的度数是．16．如图，在△ABC中AB=AC，点D在AC上，且BC=CD=AD，则∠A=．三、解答题17．生活中到处都存在着数学知识，只要同学们学会用数学的眼光观察生活，就会有许多意想不到的收获，下面两幅图都是由同一副三角板拼合得到的：（1）如图1，请你计算出的∠ABC的度数．（2）如图2，若AE∥BC，请你计算出∠AFD的度数．18．如图，D是△ABC的BC边上一点∠B=∠BAD，∠ADC=70∘，∠BAC=80∘．求：（1）∠B的度数；（2）∠C的度数．19．△ABC中，AD是∠BAC的角平分线，AE是△ABC的高．（1）如图1，若∠B=40°，∠C=60°，求∠DAE的度数；（2）如图2，∠B<∠C由(1)的计算结果，你能发现△DAE与∠C−∠B的数量关系吗？写出这个关系式，并加以证明；（3）如图3，∠B=30°，∠C=70°延长AB到点G，∠BAD和∠CBG的角平分线交于点F、请直接写出∠F的度数______．20．如图，△ABC中AB=AC，AB的垂直平分线交AC于P点．（1）若∠A=35°，求∠BPC的度数（2）若AB=5cm，BC=3cm，求△PBC的周长？21．陕西省的地势南北高、中间低，有高原、山地、平原和盆地等多种地形．某工程队现需穿过某座大山修一条隧道AB，如图，为了测量隧道AB的长度，在山的另一侧水平地面上取了一点C，在隧道BA的延长线上取了点D，测量得知∠CAD−∠C=90°，AC=500米，BC=140米，请你求出隧道AB的长．22．如图，在△ABC中∠1=∠B,∠2=∠C,∠DAC=40°，求∠B的度数．参考答案1．答案A2．答案C3．答案D4．答案C5．答案D6．答案C7．答案A8．答案A9．答案D10．答案D11．答案34°12．答案2213．答案2714．答案2815．答案30°16．答案36°17．答案（1）∠ABC＝75°（2）∠AFD＝75°18．答案（1）35°（2）65°19．答案（1）∠DAE=10°（2）∠DAE=12(∠C−∠B)（3）55°20．答案（1）∠BPC=70°（2）周长为8cm21．答案隧道AB的长为480米22．答案35°。

人教版八年级上册数学11.1.2三角形的高、中线与角平分线同步练习一、单选题1．如图，在△ABC中，AD、CE是中线，若四边形BDFE的面积是6，则△ABC的面积为（）A．12B．15C．18D．242．如图，线段AD把ABC分成面积相等的两部分，则线段AD是（）A．ABC的中线B．ABC的高C．ABC的角平分线D．以上都不对3．如图，A、B、C分别是DB、EC、F A的中点，若△DEF的面积为21，那么△ABC 的面积是（）A．6B．5C．4D．34．如图，在△ABC中，BP平分△ABC，AP BP于点P，连接PC，若△P AB的面积为26cm，△PBC的面积为2cm．8cm，则△P AC的面积为（）2A ．2B ．2.5C ．3D ．4 5．如图，已知AM 是△ABC 的中线，点P 是AC 边上一动点，若△ABC 的面积为10，AC =4，则MP 的最小值为（ ）A ．5B ．2.5C ．1.4D ．1.25 6．如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是( ) A ．锐角三角形 B ．钝角三角形 C ．直角三角形 D ．不能确定 7．如图,AD 、BE 、CF 是△ABC 三边的中线，若S △ABC =12，则图中的阴影部分的面积是( )A ．3B ．4C ．5D ．6 8．如图，AD ，AE ，AF 分别是ABC 的中线，角平分线，高，下列各式中错误的是（ ）A ．2BC CD =B ．12BAE BAC ∠=∠ C ．90AFB ∠=︒D ．AE CE =二、填空题9．如图，在△ABC 中，D 是BC 上的一点，且BC ＝4BD ，E 是AC 的中点，BE 与AD 相交于点F ，若△BDF 的面积为1，则△ABC 的面积为_________.10．如图，△ABC 的面积为25cm 2，BP 平分△ABC ，过点A 作AP △BP 于点P ，则△PBC 的面积为________；11．如图，△ABC 的中线BD 、CE 相交于点F ，若四边形AEFD 的面积为6，则△CBF 的面积为_________．12．如图，点D 是ABC ∆的边BC 上任意一点，点E 、F 分别是线段AD 、CE 的中点，且ABC ∆的面积为40，则∆BEF 的面积=_________．13．如图，在ABC 中，点D 、E 、F 分别在三边上，E 是AC 的中点，AD 、BE 、CF 交于一点G ，2BD DC =，8,3BGD AGE S S ==，则ABC 的面积是_________．14．已知：如图所示，在△ABC 中，点D ，E ，F 分别为BC ，AD ，CE 的中点，且232cm ABC S =，则阴影部分的面积为______2cm ．15．如图，在ABC ∆中，点D 在BC 上，点E 是AD 的中点，点F 在BE 上，且2EF BF =，若5∆=BCF S ，则ABC S ∆=________．16．如图，在ABC 中，G 是边BC 上任意一点，D 、E 、F 分别是AG 、BD 、CE 的中点，48ABC S =△，则DEF S △的值为______．三、解答题17．如图， △ABC 中，AE ，CD 是△ABC 的两条高，AB ＝4，CD ＝2 （1）请画出AE ，CD ；（2）求△ABC 的面积；（3）若AE ＝3，求BC 的长．18．如图，在ABC 中（AB BC >），2AC BC =，BC 边上的中线AD 把ABC 的周长分成60和40两部分，求AC 和AB 的长．19．如图所示，AD，CE是△ABC的两条高，AB＝6cm，BC＝12cm，CE＝9cm．（1）求△ABC的面积；（2）求AD的长．20．如图，已知AD、AE分别是ABC的高和中线，ABE△的面积2=，12cmAB=．求：CAB∠=︒，6cm4.8cmAD=，90（1）BC的长；（2）ABC的周长．参考答案：1．C2．A3．D4．A5．B6．C7．B8．D9．2010．212.5cm11．612．1013．3014．815．3016．617．（2）4；（3）8 318．48AC=，28AB=19．（1）27；（2）4.520．（1）10cmBC=；（2）ABC的周长=24cm．答案第1页，共1页。