08_2007年高考数学试题知识汇编圆锥曲线

2008年高考数学试题分类汇编圆锥曲线一． 选择题：1.（福建卷11)又曲线22221x y a b==（a ＞0,b ＞0）的两个焦点为F 1、F 2,若P为其上一点，且|PF 1|=2|PF 2|,则双曲线离心率的取值范围为BA.(1,3)B.(]1,3C.(3,+∞)D.[)3,+∞2.（海南卷11）已知点P 在抛物线y 2 = 4x 上，那么点P 到点Q （2，－1）的距离与点P 到抛物线焦点距离之和取得最小值时，点P 的坐标为（ A ） A. （41，－1） B. （41，1）C. （1，2）D. （1，－2）3.(湖北卷10)如图所示，“嫦娥一号”探月卫星沿地月转移轨道飞向月球，在月球附近一点P 轨进入以月球球心F 为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在P 点第二次变轨进入仍以F 为一个焦点的椭圆轨道Ⅱ绕月飞行，最终卫星在P 点第三次变轨进入以F 为圆心的圆形轨道Ⅲ绕月飞行，若用12c 和22c 分别表示椭轨道Ⅰ和Ⅱ的焦距，用12a 和22a 分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长，给出下列式子：①1122a c a c +=+; ②1122a c a c -=-; ③1212c a a c >; ④11c a ＜22ca . 其中正确式子的序号是BA. ①③B. ②③C. ①④D. ②④4.（湖南卷8）若双曲线22221x y a b-=（a ＞0,b ＞0）上横坐标为32a 的点到右焦点的距离大于它到左准线的距离，则双曲线离心率的取值范围是( B )A.(1,2)B.(2,+∞)C.(1,5)D. (5,+∞)5.（江西卷7）已知1F 、2F 是椭圆的两个焦点，满足120MF MF ⋅=的点M 总在椭圆内部，则椭圆离心率的取值范围是CA ．(0,1)B ．1(0,]2 C．(0,2 D．[26.（辽宁卷10）已知点P 是抛物线22y x =上的一个动点，则点P 到点（0，2）的距离与P 到该抛物线准线的距离之和的最小值为（ A ） AB ．3 CD ．927.（全国二9）设1a >，则双曲线22221(1)x y a a -=+的离心率e 的取值范围是（ B ） A．B．C ．(25)，D．(28.（山东卷(10)设椭圆C 1的离心率为135，焦点在X 轴上且长轴长为26.若曲线C 2上的点到椭圆C 1的两个焦点的距离的差的绝对值等于8，则曲线C 2的标准方程为A（A ）1342222=-y x (B)15132222=-y x(C)1432222=-y x (D)112132222=-y x9.（陕西卷8）双曲线22221x y a b-=（0a >，0b >）的左、右焦点分别是12F F ，，过1F 作倾斜角为30的直线交双曲线右支于M 点，若2MF 垂直于x 轴，则双曲线的离心率为（ B ） ABCD．3AB-CD-10.（四川卷12）已知抛物线2:8C y x =的焦点为F ，准线与x 轴的交点为K ，点A 在C 上且AK =，则AFK ∆的面积为( B )（Ａ）4 （Ｂ）8 （Ｃ）16 （Ｄ）3211.（天津卷（7）设椭圆22221x y m n+=（0m >，0n >）的右焦点与抛物线28y x=的焦点相同，离心率为12，则此椭圆的方程为B （A ）2211216x y += （B ）2211612x y += （C ）2214864x y += （D ）2216448x y += 12.（浙江卷7）若双曲线12222=-by a x 的两个焦点到一条准线的距离之比为3：2,则双曲线的离心率是D（A ）3 （B ）5 （C ）3 （D ）513.（浙江卷10）如图，AB 是平面a 的斜线段，A 为斜足，若点P 在平面a 内运动，使得△ABP 的面积为定值，则动点P 的轨迹是B（A ）圆 （B ）椭圆 （C ）一条直线 （D ）两条平行直线14.（重庆卷(8)已知双曲线22221x y a b-=（a ＞0,b ＞0）的一条渐近线为y =kx (k ＞0),离心率e ,则双曲线方程为C（A ）22x a －224y a =1(B)222215x y a a-=(C)222214x y b b-=(D)222215x y b b-=二． 填空题：1.（海南卷14）过双曲线221916x y -=的右顶点为A ，右焦点为F 。

【2012年高考试题】一、选择题1.【2012高考真题浙江理8】如图，F1,F2分别是双曲线C：22221x ya b-=（a,b＞0）的左、右焦点，B是虚轴的端点，直线F1B与C的两条渐近线分别交于P,Q两点，线段PQ的垂直平分线与x轴交与点M，若|MF2|=|F1F2|,则C的离心率是B【答案】B2.【2012高考真题新课标理8】等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线xy162=的准线交于,A B两点，AB=；则C的实轴长为（）()A ()B ()C 4 ()D 83.【2012高考真题新课标理4】设12F F 是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点，P 为直线32ax =上一点，12PF F ∆是底角为30的等腰三角形，则E 的离心率为（ ）()A 12 ()B 23 ()C 34 ()D 45【答案】C【解析】因为12PF F ∆是底角为30的等腰三角形，则有PF F F 212=,，因为02130=∠F PF ，所以0260=∠D PF ,0230=∠DPF ，所以21222121F F PF D F ==，即c c c a =⨯=-22123，所以c a 223=，即43=a c ，所以椭圆的离心率为43=e ，选C. 4.【2012高考真题四川理8】已知抛物线关于x 轴对称，它的顶点在坐标原点O ，并且经过点0(2,)M y 。

若点M 到该抛物线焦点的距离为3，则||OM =（ ）A 、、、4 D 、 【答案】B【解析】设抛物线方程为22y px =，则点(2,M ±Q 焦点,02p ⎛⎫⎪⎝⎭，点M 到该抛物线焦点的距离为3，∴ 22492p P ⎛⎫-+= ⎪⎝⎭， 解得2p =，所以OM ==.5.【2012高考真题山东理10】已知椭圆2222:1(0)x y C a b a b +=>>双曲线221x y -=的渐近线与椭圆C 有四个交点，以这四个焦点为顶点的四边形的面积为16，则椭圆C 的方程为（A ）22182x y += （B ）221126x y += （C ）221164x y += （D ）221205x y +=6.【2012高考真题湖南理5】已知双曲线C ：22x a -22y b=1的焦距为10 ，点P （2,1）在C 的渐近线上，则C 的方程为A ．220x -25y =1 B.25x -220y =1 C.280x -220y =1 D.220x -280y =1【答案】A【解析】设双曲线C ：22x a -22y b=1的半焦距为c ，则210,5c c ==.又C 的渐近线为b y x a =±，点P （2,1）在C 的渐近线上，12ba∴=，即2a b =.又222c a b =+，a ∴=∴C 的方程为220x -25y =1.7.【2012高考真题福建理8】已知双曲线22214x y b-=的右焦点与抛物线y 2=12x 的焦点重合，则该双曲线的焦点到其渐近线的距离等于8.【2012高考真题安徽理9】过抛物线24y x =的焦点F 的直线交抛物线于,A B 两点，点O 是原点，若3AF =，则AOB ∆的面积为（ ）()A ()B ()C ()D 【答案】C【解析】设(0)AFx θθπ∠=<<及BF m =；则点A 到准线:1l x =-的距离为3，得：1323cos cos 3θθ=+⇔=又232cos()1cos 2m m m πθθ=+-⇔==+，AOB ∆的面积为113sin 1(3)22232S OF AB θ=⨯⨯⨯=⨯⨯+⨯=。

历年高考圆锥曲线2000年：（10）过原点的直线与圆相切，若切点在第三象限，则该直03422=+++x y x 线的方程是（ ）（A ） （B ） （C ）（D ）x y 3=x y 3-=x 33x 33-（11）过抛物线的焦点F 作一条直线交抛物线于P 、Q 两点，若线()02>=a ax y段PF 与FQ 的长分别是、，则等于（ ）p q qp 11+（A ）（B ）（C ） （D ）a 2a21a 4a4（14）椭圆的焦点为、，点P 为其上的动点，当为钝角14922=+y x 1F 2F 21PF F ∠ 时，点P 横坐标的取值范围是________。

（22）（本小题满分14分）如图，已知梯形ABCD 中，点E 分有向线段所成的比为，CD AB 2=AC λ双曲线过C 、D 、E 三点，且以A 、B 为焦点。

当时，求双曲线离心率4332≤≤λ的取值范围。

e 2004年3．过点（－1，3）且垂直于直线的直线方程为（ ）032=+-y x A ．B ．C ．D ．12=-+y x 052=-+y x 052=-+y x 072=+-y x 8．已知圆C 的半径为2，圆心在轴的正半轴上，直线与圆C 相切，则圆x 0443=++y x C 的方程为（ ）A ．B ．03222=--+x y x 0422=++x y x C ．D ．3222=-++x y x 0422=-+x y x 8．（理工类）已知椭圆的中心在原点，离心率，且它的一个焦点与抛物线21=e 的焦点重合，x y 42-= 则此椭圆方程为（ ）A ．B ．13422=+y x 16822=+y x C ．D ．1222=+y x 1422=+y x 22．（本小题满分14分）双曲线的焦距为2c ，直线过点（a ，0）和（0，b ），且点)0,1(12222>>=-b a by a x l （1，0）到直线的距离与点（－1，0）到直线的距离之和求双曲线的离心率e l l .54c s ≥的取值范围.2005年：9．已知双曲线的焦点为，点在双曲线上且则点1222=-y x 12,F F M 120,MF MF ⋅= 到M 轴的距离为（x ）A ．B ．CD435310．设椭圆的两个焦点分别为过作椭圆长轴的垂线交椭圆于点P ，若△为12,,F F 2F 12F PF等腰直角三角形，则椭圆的离心率是（）A B C ．D 2121、（理工类）（本小题满分12分）设，两点在抛物线上，是的垂直平分线。

年高考数学试题知识分类大全圆锥曲线LG GROUP system office room 【LGA16H-LGYY-LGUA8Q8-LGA162】2007年高考数学试题汇编圆锥曲线重庆文（12）已知以F 1（2,0），F 2（2,0）为焦点的椭圆与直线043=++y x 有且仅有一个交点，则椭圆的长轴长为（A ）23（B ）62（C ）72（D ）24（21）（本小题满分12分，（Ⅰ）小问4分，（Ⅱ）小问8分）如题（21）图，倾斜角为a 的直线经过抛物线x y 82=的焦点F ，且与抛物线交于A 、B 两点。

题（21）图（Ⅰ）求抛物线的焦点F 的坐标及准线l 的方程；（Ⅱ）若a 为锐角，作线段AB 的垂直平分线m 交x 轴于点P ，证明|FP|-|FP|cos2a 为定值，并求此定值。

（21）（本小题12分）（Ⅰ）解：设抛物线的标准方程为px y 22=，则82=p ，从而.4=p 因此焦点)0,2(p F 的坐标为（2，0）. 又准线方程的一般式为2p x -=。

从而所求准线l 的方程为2-=x 。

答（21）图（Ⅱ）解法一：如图（21）图作AC ⊥l ，BD ⊥l ，垂足为C 、D ，则由抛物线的定义知 |FA |=|FC |,|FB |=|BD |.记A 、B 的横坐标分别为x x x z ，则 |FA |＝|AC |＝4cos ||22cos ||2+=++=+a FA p p a FA p x x 解得aFA cos 14||-=， 类似地有a FB FB cos ||4||-=，解得aFB cos 14||+=。

记直线m 与AB 的交点为E ，则aaa a FB FA FB FA FA AE FA FE 2sin cos 4cos 14cos 1421|)||(|212||||||||||||=⎪⎭⎫ ⎝⎛+--=-=+-=-= 所以aa FE FP 2sin 4cos ||||==。

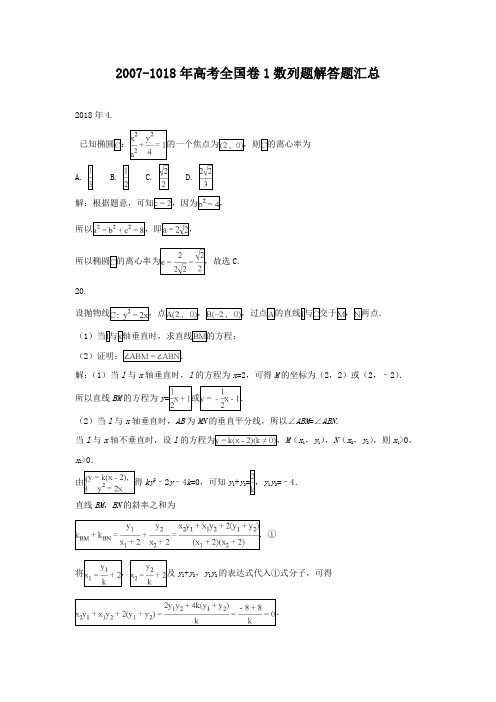
2007-1018年高考全国卷1数列题解答题汇总2018年4.C.解：根据题意，可知所以椭圆 C.20.设抛物线，过点的直线（1轴垂直时，求直线（2解：（1）当l与x轴垂直时，l的方程为x=2，可得M的坐标为（2，2）或（2，–2）．所以直线BM的方程为y（2）当l与x轴垂直时，AB为MN的垂直平分线，所以∠ABM=∠ABN．当l与x轴不垂直时，设l的方程为M（x1，y1），N（x2，y2），则x1>0，x2>0．ky2–2y–4k=0，可知y1+y2y1y2=–4．直线BM，BN的斜率之和为将，及y1+y2，y1y2的表达式代入①式分子，可得所以k BM +k BN =0，可知BM ，BN 的倾斜角互补，所以∠ABM =∠ABN ． 综上，∠ABM =∠ABN ．点评：该题考查的是有关直线与抛物线的问题，涉及到的知识点有直线方程的两点式、直线与抛物线相交的综合问题、关于角的大小用斜率来衡量，在解题的过程中，第一问求直线方程的时候，需要注意方法比较简单，需要注意的就是应该是两个，关于第二问，在做题的时候需要先将特殊情况说明，一般情况下，涉及到直线与曲线相交都需要联立方程组，之后韦达定理写出两根和与两根积，借助于斜率的关系来得到角是相等的结论.2017年5．已知F 是双曲线C ：x 2-23y =1的右焦点，P 是C 上一点，且PF 与x 轴垂直，点A 的坐标是(1,3).则△APF 的面积为 A ．13B ．12C ．23D ．3 2答案:D 12．设A 、B 是椭圆C ：2213x y m+=长轴的两个端点，若C 上存在点M 满足∠AMB =120°，则m的取值范围是A ．(0,1][9,)+∞B ．[9,)+∞C ．(0,1][4,)+∞D ．[4,)+∞答案:A20．（12分）设A ，B 为曲线C ：y =24x 上两点，A 与B 的横坐标之和为4.（1）求直线AB 的斜率；（2）设M 为曲线C 上一点，C 在M 处的切线与直线AB 平行，且AM ⊥BM ，求直线AB 的方程.20.（12分）解：（1）设A （x 1，y 1），B （x 2，y 2），则12x x ≠，2114x y =，2224x y =，x 1+x 2=4，于是直线AB 的斜率12121214y y x x k x x -+===-.（2）由24x y =，得2xy'=.设M （x 3，y 3），由题设知312x=，解得32x =，于是M （2，1）.设直线AB 的方程为y x m =+，故线段AB 的中点为N （2,2+m ），|MN |=|m +1|.将y x m =+代入24x y =得2440x x m --=.当16(1)0m ∆=+>，即1m >-时，1,22x =±从而12||AB x x -=.由题设知||2||AB MN =，即2(1)m =+，解得7m =. 所以直线AB 的方程为7y x =+.2016年5.答案:B 20.在直角坐标系xOy 中，直线)0(:≠=t t y l 交y 轴于点M ，交抛物线)0(2:2>=p px y C 于点P ，M 关于点P 的对称点为N ，连结ON 并延长交C 于点H .（II ）除H 以外，直线MH 与C 是否有其它公共点？说明理由.解析：（Ⅰ）由已知得，. ),0(t M ),2(2t pt P又为关于点的对称点，故，的方程为，代入整理得，解得，，因此. 所以为的中点，即. （Ⅱ）直线与除以外没有其它公共点.理由如下： 直线的方程为，即.代入得，解得，即直线与只有一个公共点，所以除以外直线与没有其它公共点.2015年5、已知椭圆E 的中心为坐标原点，离心率为，E 的右焦点与抛物线的焦点重合，是C 的准线与E 的两个交点，则（A ） （B ） （C ） （D ） 答案:B16.已知是双曲线的右焦点，P 是C 左支上一点， ，当周长最小时，该三角形的面积为 ． 答案:20.已知过点且斜率为k 的直线l 与圆C ：交于M ，N 两点. （I ）求k 的取值范围；（II ）若，其中O 为坐标原点，求. 解：（I ）由题设，可知直线的方程为. 因为与C 交于两点，所以.N M P ),(2t p t N ON x t p y =px y 22=0222=-x t px 01=x p t x 222=)2,2(2t pt H N OH 2||||=ON OH MH C H MH x tp t y 2=-)(2t y p tx -=px y 22=04422=+-t ty y t y y 221==MH C H MH C 122:8C y x =,A B AB =36912F 22:18y C x -=(A APF ∆()1,0A ()()22231x y -+-=12OM ON ⋅=MN l 1y kx =+l 1解得所以k 的取值范围为. ……5分 （II ）设.将代入方程，整理得.所以.. 由题设可得=12，解得k=1，所以的方程是y=x+1. 故圆心C 在上，所以.2014年4.已知双曲线的离心率为2，则 A. 2 B. C. D. 1 答案:D10.已知抛物线C ：的焦点为F,A(x 0,y 0)是C 上一点，，则x 0=（ ） A. 1 B. 2 C. 4 D. 8 答案:C 20已知点，圆:，过点的动直线与圆交于两点，线段的中点为，为坐标原点.k 44(33-()1122,,(,)M x y N x y 1y kx =+22(2)(3)1x y -+-=22(1)4(1)70k x k x +-++=1212224(1)7,11k x x x x k k ++==++1212OM ON c x y y ⋅=+()()2121211kx xk x x =++++()24181k k k+=++()24181k k k+=++l l2MN =)0(13222>=-a y a x =a 2625x y =2x F A 045=)2,2(P C 0822=-+y y x P l C B A ,AB M O(1)求的轨迹方程；（2）当时，求的方程及的面积 解：（1）方法一：圆的方程可化为，所以，圆心为，半径为4， 设，则， 由题设知，故，即由于点在圆的内部，所以的轨迹方程是……………6分方法二：圆的方程可化为，所以，圆心为，半径为4， 设，设， 则 所以化简得，，即 所以的轨迹方程是（2）方法一： 由（1）可知的轨迹是以点为半径的圆由于，故在线段的垂直平分线上，又在圆上，从而因为的斜率为3，所以的斜率为， 所以的方程为 又，到的距离为，所以的面积为 M OM OP =l POM ∆C 22(4)16x y +-=(0,4)C (,)M x y (,4),(2,2)CM x y MP x y =-=--0CM MP ⋅=(2)(4)(2)0x x y y -+--=22(1)(3)2x y -+-=P C M 22(1)(3)2x y -+-=C 22(4)16x y +-=(0,4)C (,)M x y 24,2AB CM y y k k x x --==-24,2AB CM y y k k x x--==-2412AB CM y y k k x x--==--222680x y x y +--+=22(1)(3)2x y -+-=M 22(1)(3)2x y -+-=M (1,3)N ||||OP OM =O PM P N ON PM ⊥ON l 13-l 1833y x =-+||||OM OP ==O l ,||55PM =POM ∆165方法二：依题意，，因为 所以，M 也在上所以 两式相减，得，即，此方程也就是的方程 由（1）知，的轨迹方程是，设此方程的圆心为，则 所以 又所以 到的距离所以， 综上所述，的方程为，的面积为2013年4已知双曲线C ：(a＞0，b ＞0)的离心率为，则C 的渐近线方程为( )．A ．y ＝B ．y ＝C ．y ＝D ．y ＝±x 解：∵，即.∵c 2＝a 2＋b 2，∴.∴.∵双曲线的渐近线方程为，∴渐近线方程为.故选C.||OP =||||OM OP ==228x y +=222282680x y x y x y ⎧+=⎪⎨+--+=⎪⎩26160x y --+=1833y x =-+l M 22(1)(3)2x y -+-=N (1,3)N d =||NP ==||MP ==O l h =11625POM S ∆==l 1833y x =-+POM ∆1652222=1x y a b-214x ±13x ±12x±e =c a =2254c a =2214b a =12b a =by x a=±12y x =±8．O 为坐标原点，F 为抛物线C ：y 2＝的焦点，P 为C 上一点，若|PF |＝则△POF的面积为( )．A ．2B ．．．4 解：利用|PF |＝x P ＝∴y P ＝.∴S △POF ＝|OF |·|y P |＝故选C. 21．已知圆M ：(x ＋1)2＋y 2＝1，圆N ：(x －1)2＋y 2＝9，动圆P 与圆M 外切并且与圆N 内切，圆心P 的轨迹为曲线C. (1)求C 的方程；(2)l 是与圆P ，圆M都相切的一条直线，l 与曲线C 交于A ，B两点，当圆P 的半径最长时，求|AB |.解：由已知得圆M 的圆心为M (－1,0)，半径r 1＝1；圆N 的圆心为N (1,0)，半径r 2＝3.设圆P 的圆心为P(x ，y )，半径为R .(1)因为圆P与圆M 外切并且与圆N 内切，所以|PM |＋|PN |＝(R ＋r 1)＋(r 2－R )＝r 1＋r 2＝4.由椭圆的定义可知，曲线C 是以M ，N 为左、右焦点，长半轴长为2(左顶点除外)，其方程为(x ≠－2)． (2)对于曲线C 上任意一点P (x ，y )，由于|PM |－|PN |＝2R －2≤2，所以R ≤2，当且仅当圆P 的圆心为(2,0)时，R ＝2.所以当圆P 的半径最长时，其方程为(x －2)2＋y 2＝4. 若l 的倾斜角为90°，则l 与y 轴重合，可得|AB |＝若l 的倾斜角不为90°，由r 1≠R 知l 不平行于x 轴，设l 与x 轴的交点为Q ，则，可求得Q (－4,0)，所以可设l ：y ＝k (x ＋4)． 由l 与圆M ＝1，解得k ＝当k ＝时，将，并整理得7x 2＋8x －8＝0，解得x 1,2＝， 所以|AB ||x 2－x 1|＝.当k ＝时，由图形的对称性可知|AB |＝.综上，|AB |＝|AB |＝.2012年4.设F 1、F 2是椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点，P 为直线x =3a2上一点，△F 1PF 2是底角P x =±1222=143x y +1||||QP RQM r =44y x =+22=143x y +1874-187187为30°的等腰三角形，则E 的离心率为（ ） （A ）12 （B ）23 （C ）34 （D ）45答案:C 10等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线y 2=16x 的准线交于A ，B 两点，|AB|=43，则C 的实轴长为（A ） 2 （B ）2 2 （C ）4 （D ）8 答案:C 20．（本小题满分12分）设抛物线C ：x 2=2py (p >0)的焦点为F ，准线为l ，A 为C 上一点，已知以F 为圆心，FA 为半径的圆F 交l 于B ，D 两点。

四川理21．（本小题满分12分）设椭圆22221x y a b +=（0a b >>）的左、右焦点分别为12F F ，，离心率e =，右准线为l ，M N ，是l 上的两个动点，120FM F N =． （Ⅰ）若 1225F M F N ==，求a b ，的值；（Ⅱ）证明：当MN 取最小值时，12FM F N +与12F F 共线．21．解：由222a b c -=与2c e a ==，得222a b =． 10F ⎛⎫ ⎪⎪⎝⎭，，20F ⎫⎪⎪⎝⎭，，l 的方程为x =． 设12))M y N y ，，， 则113F M y ⎛⎫= ⎪⎪⎝⎭，，222F N y ⎛⎫= ⎪⎪⎝⎭，， 由120FM F N =得 212302y y a =-<． ①（Ⅰ）由1225F MF N === ②= ③ 由①、②、③三式，消去12y y ，，并求得24a =．故2a =，b ==． （Ⅱ）22222121212121212()22246MNy y y y y y y y y y y y a =-=+---=-=≥，当且仅当122y y a =-=或212y y =-=时，MN 取最小值． 此时，12121212322(22)(220)222F M F N a y a y a y y a F F ⎛⎫⎛⎫+=+=+== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，，，，．故12FM F N +与12F F 共线． 广东文B 卷20．（本小题满分14分）设0b >，椭圆方程为222212x y b b +=，抛物线方程为28()x y b =-．如图6所示，过点(02)F b +，作x 轴的平行线，与抛物线在第一象限的交点为G ，已知抛物线在点G 的切线经过椭圆的右焦点1F ．（1）求满足条件的椭圆方程和抛物线方程；（2）设A B ，分别是椭圆长轴的左、右端点，试探究在抛物线上是否存在点P ，使得ABP △为直角三角形？若存在，请指出共有几个这样的点？并说明理由（不必具体求出这些点的坐标）．20．解：（1）由28()x y b =-得218y x b =+ 当2y b =+时，4x =±，G ∴点的坐标为(42)b +，14y x '=，4|1x y ='= 过点G 的切线方程为(2)4y b x -+=-，即2y x b =+-， 令0y =得2x b =-，1F ∴点的坐标为(20)b-，； 由椭圆方程得1F 点的坐标为(0)b ，， 2b b ∴-=，即1b =，因此所求的椭圆方程及抛物线方程分别为2212x y +=和28(1)x y =-． （2）过A 作x 轴的垂线与抛物线只有一个交点P ， ∴以PAB ∠为直角的Rt ABP △只有一个， 同理以PBA ∠为直角的Rt ABP △只有一个；若以APB ∠为直角，设P 点的坐标为2118x x ⎛⎫+ ⎪⎝⎭，，则A B ，坐标分别为(由22212108AB AB x x ⎛⎫=-++= ⎪⎝⎭得421510644x x +-=， 关于2x 的一元二次方程有一解，x ∴有二解，即以APB ∠为直角的Rt ABP △有二个； 因此抛物线上共存在4个点使ABP △为直角三角形．全国卷2文科11．设ABC △是等腰三角形，120ABC ∠=，则以A B ，为焦点且过点C 的双曲线的离心图6率为（ ） A ．221+ B ．231+ C ． 21+ D ．31+15．已知F 是抛物线24C y x =：的焦点，A B ，是C 上的两个点，线段AB 的中点为(22)M ，，则ABF △的面积等于 ．15．2全国卷2文科 22．（本小题满分12分）设椭圆中心在坐标原点，(20)(01)A B ，，，是它的两个顶点，直线)0(>=k kx y 与AB 相交于点D ，与椭圆相交于E 、F 两点． （Ⅰ）若6ED DF =，求k 的值； （Ⅱ）求四边形AEBF 面积的最大值．22．（Ⅰ）解：依题设得椭圆的方程为2214x y +=， 直线AB EF ，的方程分别为22x y +=，(0)y kx k =>． ····································· 2分 如图，设001122()()()D x kx E x kx F x kx ，，，，，，其中12x x <， 且12x x ，满足方程22(14)4k x +=，故21x x =-=．①由6ED DF =知01206()x x x x -=-，得021215(6)77x x x x =+==； 由D 在AB 上知0022x kx +=，得0212x k=+． 所以212k =+ 化简得2242560k k -+=， 解得23k =或38k =． ······················································································ 6分（Ⅱ）解法一：根据点到直线的距离公式和①式知，点E F，到AB的距离分别为1h==，2h==·······················································9分又AB==AEBF的面积为121()2S AB h h=+1525(14k=+==≤当21k=，即当12k=时，上式取等号．所以S的最大值为 ························ 12分解法二：由题设，1BO=，2AO=．设11y kx=，22y kx=，由①得2x>，21y y=->，故四边形AEBF的面积为BEF AEFS S S=+△△222x y=+ ····································································································9分===当222x y =时，上式取等号．所以S的最大值为 ······································· 12分全国卷I 文科14．已知抛物线21y ax =-的焦点是坐标原点，则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 ．14．12全国卷I 文科15．在ABC △中，90A ∠=，3tan 4B =．若以A B ，为焦点的椭圆经过点C ，则该椭圆的离心率e = ．15．12全国卷I 文科 22．（本小题满分12分）（注意：在试题卷上作答无效．．．．．．．．．） 双曲线的中心为原点O ，焦点在x 轴上，两条渐近线分别为12l l ，，经过右焦点F 垂直于1l 的直线分别交12l l ，于A B ，两点．已知OA AB OB 、、成等差数列，且BF 与FA 同向． （Ⅰ）求双曲线的离心率；（Ⅱ）设AB 被双曲线所截得的线段的长为4，求双曲线的方程．22．解：（1）设OA m d =-，AB m =，OB m d =+ 由勾股定理可得：222()()m d m m d -+=+ 得：14d m =，tan b AOF a ∠=，4tan tan 23AB AOB AOF OA ∠=∠== 由倍角公式∴22431ba b a =⎛⎫- ⎪⎝⎭，解得12b a =则离心率e =（2）过F 直线方程为()ay x c b=-- 与双曲线方程22221x y a b-=联立将2a b =，c 代入，化简有22152104x x b b-+=124x =-=将数值代入，有4=解得3b =最后求得双曲线方程为：221369x y -=． 全国理II14．已知抛物线21y ax =-的焦点是坐标原点，则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 ．14．2 全国理II15．在ABC △中，AB BC =，7cos 18B =-．若以A B ，为焦点的椭圆经过点C ，则该椭圆的离心率e = ．15．38全国理II 21．（本小题满分12分）（注意：在试题卷上作答无效．．．．．．．．．） 双曲线的中心为原点O ，焦点在x 轴上，两条渐近线分别为12l l ，，经过右焦点F 垂直于1l 的直线分别交12l l ，于A B ，两点．已知OA AB OB 、、成等差数列，且BF 与FA 同向． （Ⅰ）求双曲线的离心率；（Ⅱ）设AB 被双曲线所截得的线段的长为4，求双曲线的方程． 21．解（Ⅰ）设双曲线方程为22221(00)x y a b a b-=>>，，右焦点为(0)(0)F c c >，，则222c a b =+．不妨设10l bx ay -=：，20l bx ay +=：， 则b FA b ⨯==，OA OF a =．因为222AB OA OB +=，2OB AB OA =-， 所以222(2)AB OA AB OA +=-， 于是得4tan 3AB AOB OA∠==． 又BF 与FA 同向，故12AOF AOB ∠=∠， 所以22tan 41tan 3AOF AOF ∠=-∠．解得1tan 2AOF∠=，或tan 2AOF ∠=-（舍去）．因此12ba =，2ab =，c ==．所以双曲线的离心率2ce a ==． （Ⅱ）由2a b =知，双曲线的方程可化为22244x y b -=．① 由1l 的斜率为12，c =知，直线AB 的方程为2()y x =-．② 将②代入①并化简，得2215840x b --=． 设AB 与双曲线的两交点的坐标分别为1122()()x y x y ，，，，则12x x +=，2128415b x x =．③AB 被双曲线所截得的线段长12l x x =-=将③代入④，并化简得43bl =，而由已知4l =，故36b a ==，． 所以双曲线的方程为221369x y -=． 全国卷2理科（+选修II ）9．设1a >，则双曲线22221(1)x y a a -=+的离心率e 的取值范围是（ ）A ．B ．C ．(25)，D ．(2全国卷2理科（+选修II ）15．已知F 是抛物线24C y x =：的焦点，过F 且斜率为1的直线交C 于A B ，两点．设FA FB >，则FA 与FB 的比值等于 ．15．3+全国卷2理科（+选修II ） 21．（本小题满分12分）设椭圆中心在坐标原点，(20)(01)A B ，，，是它的两个顶点，直线)0(>=k kx y 与AB 相交于点D ，与椭圆相交于E 、F 两点． （Ⅰ）若6ED DF =，求k 的值； （Ⅱ）求四边形AEBF 面积的最大值．21．（Ⅰ）解：依题设得椭圆的方程为2214x y +=， 直线AB EF ，的方程分别为22x y +=，(0)y kx k =>． ····································· 2分 如图，设001122()()()D x kx E x kx F x kx ，，，，，，其中12x x <，且12x x ，满足方程22(14)4k x +=， 故21x x =-=．①由6ED DF =知01206()x x x x -=-，得021215(6)77x x x x =+==； 由D 在AB 上知0022x kx +=，得0212x k=+．所以212k =+ 化简得2242560k k -+=，解得23k =或38k =． ······················································································ 6分 （Ⅱ）解法一：根据点到直线的距离公式和①式知，点E F ，到AB 的距离分别为1h ==，2h ==······················································· 9分又AB ==AEBF 的面积为121()2S AB h h =+ 1525(14k =+==≤当21k =，即当12k =时，上式取等号．所以S 的最大值为 ························ 12分 解法二：由题设，1BO =，2AO =．设11y kx =，22y kx =，由①得20x >，210y y =->， 故四边形AEBF 的面积为BEF AEF S S S =+△△222x y =+ ···································································································· 9分===当222x y =时，上式取等号．所以S 的最大值为 ······································· 12分 江苏卷12.在平面直角坐标系中，椭圆2222x y a b+=1( a b >>0)的焦距为2，以O 为圆心，a 为半径的圆，过点2,0a c ⎛⎫⎪⎝⎭作圆的两切线互相垂直，则离心率e = ▲ ． ? ?【解析】设切线PA 、PB 互相垂直，又半径OA 垂直于PA ，所以△OAP 是等腰直角三角形，故2a c =，解得2c e a ==．【答案】2山东理 22．（本小题满分14分）如图，设抛物线方程为22(0)x py p =>，M 为直线2y p =-上任意一点，过M 引抛物线的切线，切点分别为A B ，．（Ⅰ）求证：A M B ，，三点的横坐标成等差数列；（Ⅱ）已知当M 点的坐标为(22)p -，时，AB =（Ⅲ）是否存在点M ，使得点C 关于直线AB 的对称点D 在抛物线22(0)x py p =>上，其中，点C 满足OC OA OB =+（O 为坐标原点）．若存在，求出所有适合题意的点M 的坐标；若不存在，请说明理由．22．（Ⅰ）证明：由题意设221212120(2)22x x A x B x x x M x p p p ⎛⎫⎛⎫<- ⎪ ⎪⎝⎭⎝⎭，，，，，，．由22x py =得22x y p=，得x y p '=，所以1MA x k p =，2MB xk p=． 因此直线MA 的方程为102()x y p x x p+=-， 直线MB 的方程为202()x y p x x p+=-． 所以211102()2x x p x x p p+=-，①222202()2x xp x x p p+=-．② 由①、②得121202x x x x x +=+-， 因此1202x x x +=，即0122x x x =+．所以A M B ，，三点的横坐标成等差数列．（Ⅱ）解：由（Ⅰ）知，当02x =时，将其代入①、②并整理得：2211440x x p --=，2222440x x p --=，所以12x x ，是方程22440x x p --=的两根， 因此124x x +=，2124x x p =-，又222101221222ABx x x x x p p k x x p p-+===-，所以2AB k p=．由弦长公式得AB ==又AB = 所以1p =或2p =，因此所求抛物线方程为22x y =或24x y =．（Ⅲ）解：设33()D x y ，，由题意得1212()C x x y y ++，， 则CD 的中点坐标为12312322x x x y y y Q ++++⎛⎫⎪⎝⎭，， 设直线AB 的方程为011()x y y x x p-=-， 由点Q 在直线AB 上，并注意到点121222x x y y ++⎛⎫⎪⎝⎭，也在直线AB 上，代入得033x y x p=．若33()D x y ，在抛物线上，则2330322x py x x ==，因此30x =或302x x =．即(00)D ，或2022x D x p ⎛⎫ ⎪⎝⎭，．（1）当00x =时，则12020x x x +==，此时，点(02)M p -，适合题意．（2）当00x ≠，对于(00)D ，，此时2212022x x C x p ⎛⎫+ ⎪⎝⎭，，2212022CDx x pk x +=221204x x px +=， 又0AB x k p=，AB CD ⊥， 所以22220121220144AB CDx x x x x k k p px p ++===-， 即222124x x p +=-，矛盾．对于20022x D x p ⎛⎫ ⎪⎝⎭，，因为2212022x x C x p ⎛⎫+ ⎪⎝⎭，，此时直线CD 平行于y 轴，又00AB x k p=≠， 所以直线AB 与直线CD 不垂直，与题设矛盾， 所以00x ≠时，不存在符合题意的M 点．综上所述，仅存在一点(02)M p -，适合题意．山东文13．221412x y -= 山东文22．解：（Ⅰ）由题意得2ab ⎧=⎪⎨=又0a b >>，解得25a =，24b =．因此所求椭圆的标准方程为22154x y +=． （Ⅱ）（1）假设AB 所在的直线斜率存在且不为零，设AB 所在直线方程为(0)y kx k =≠，()A A A x y ，．解方程组22154x y y kx ⎧+=⎪⎨⎪=⎩，，得222045A x k =+，2222045A k y k =+， 所以22222222202020(1)454545AAk k OA x y k k k +=+=+=+++．设()M x y ，，由题意知(0)MO OA λλ=≠，所以222MO OA λ=，即2222220(1)45k x y kλ++=+， 因为l 是AB 的垂直平分线， 所以直线l 的方程为1y x k=-， 即x k y=-， 因此22222222222220120()4545x y x y x y x y x yλλ⎛⎫+ ⎪+⎝⎭+==++， 又220x y +≠， 所以2225420x y λ+=，故22245x y λ+=．又当0k =或不存在时，上式仍然成立．综上所述，M 的轨迹方程为222(0)45x y λλ+=≠． （2）当k 存在且0k ≠时，由（1）得222045Ax k =+，2222045A k y k=+， 由221541x y y x k ⎧+=⎪⎪⎨⎪=-⎪⎩，，解得2222054M k x k =+，222054M y k =+， 所以2222220(1)45AAk OA x y k +=+=+，222280(1)445k AB OA k +==+，22220(1)54k OM k+=+． 解法一：由于22214AMB S AB OM =△ 2222180(1)20(1)44554k k k k++=⨯⨯++ 2222400(1)(45)(54)k k k +=++ 22222400(1)45542k k k +⎛⎫+++ ⎪⎝⎭≥222221600(1)4081(1)9k k +⎛⎫== ⎪+⎝⎭， 当且仅当224554k k +=+时等号成立，即1k =±时等号成立，此时AMB △面积的最小值是409AMB S =△．当0k =，140229AMB S =⨯=>△． 当k不存在时，140429AMB S ==>△．综上所述，AMB △的面积的最小值为409． 解法二：因为222222111120(1)20(1)4554k k OAOMk k +=+++++2224554920(1)20k k k +++==+， 又22112OA OMOAOM+≥，409OA OM ≥，当且仅当224554k k +=+时等号成立，即1k =±时等号成立，此时AMB △面积的最小值是409AMB S =△． 当0k =，140229AMB S =⨯=>△．当k不存在时，140429AMB S ==>△．综上所述，AMB △的面积的最小值为409．福建文12．双曲线22221x y a b-=(00)a b >>，的两个焦点为F 1，F 2，若P 为其上一点，且|PF 1|=2|PF 2|，则双曲线离心率的取值范围为（ ） A ．(1，3)B ．(]13，C ．(3，+∞)D ．[)3+∞，福建文 22．（本小题满分14分）如图，椭圆C ：22221(0)x y a b a b+=>>的一个焦点为F （1，0），且过点(20)，． （Ⅰ）求椭圆C 的方程；（Ⅱ）若AB 为垂直于x 轴的动弦，直线l ：4x =与x 轴交 于点N ，直线AF 与BN 交于点M ．（ⅰ）求证：点M 恒在椭圆C 上；（ⅱ）求AMN △面积的最大值．22．本小题主要考查直线与椭圆的位置关系、轨迹方程、不等式等基本知识，考查运算能力和综合解题能力．满分14分． 解法一：（Ⅰ）由题设2a =，1c =，从而2223b a c =-=．所以椭圆C 的方程为22143x y +=． （Ⅱ）（ⅰ）由题意得(10)F ，，(40)N ，，设()A m n ，，则()(0)B m n n -≠，，22143m n +=．……① AF 与BN 的方程分别为：(1)(1)0n x m y ---=，(4)(4)0n x m y -+-=．设00()M x y ，，则有0000(1)(1)0(4)(4)0n x m y n x m y ---=⎧⎨-+-=⎩， ②，③由②，③得05825m x m -=-，0325ny m =-由于222222(58)3434(25)(25)x y m n m m -+=+-- 2222(58)34(25)(25)m n m m -=+-- 222(58)124(25)m n m -+=- 222(58)3694(25)m m m -+-=- 1=．所以点M 恒在椭圆C 上．（ⅱ）设AM 的方程为1x ty =+，代入22143x y +=得22(34)690t y ty ++-=．设11()A x y ，，22()M x y ，，则有：122634t y y t -+=+，122934y y t -=+212333t y y +-==． 令234(4)t λλ+=≥，则1231y y λ--===因为4λ≥，1104λ<≤，所以当114λ=，即4λ=，0t =时， 12y y -有最大值3，此时AM 过点F ．AMN △的面积12121322AMN S FN y y y y =-=-△有最大值92． 解法二：（Ⅰ）同解法一．（Ⅱ）（ⅰ）由题意得(10)F ，，(40)N ，， 设()A m n ，，则()(0)B m n n -≠，，22143m n +=．……① AF 与BN 的方程分别为：(1)(1)0n x m y ---=，……②(4)(4)0n x m y -+-=．……③由②，③得：当52x ≠时，5825x m x -=-，325yn x =-．……④ 由④代入①，得221(0)43x y y +=≠． 当52x =时，由②，③得：3(1)023(4)0.2n m y n m y ⎧--=⎪⎪⎨⎪-++=⎪⎩，解得00n y =⎧⎨=⎩，，与0n ≠矛盾．所以点M 的轨迹方程为221(0)43x y y +=≠，即点M 恒在椭圆C 上． （ⅱ）同解法一．福建理11．双曲线22221x y a b-=(00)a b >>，的两个焦点为F 1，F 2，若P 为其上一点，且|PF 1|=2|PF 2|，则双曲线离心率的取值范围为（ ） A ．(1，3)B ．(]13，C ．(3，+∞)D ．[)3+∞，福建理21．（本小题满分12分）如图，椭圆22221(0)x y a b a b+=>>的一个焦点是F （1，0），O 为坐标原点．（Ⅰ）已知椭圆短轴的两个三等分点与一个焦点构成正三角形，求椭圆的方程；（Ⅱ）设过点F 的直线l 交椭圆于A ，B 两点．若直线l 绕点F 任意转动，恒有222OA OB AB +<，求a 的取值范围．21想，考查运算能力和综合解题能力．满分12分． 解法一：（Ⅰ）设M ，N 为短轴的两个三等分点，因为△MNF 为正三角形， 所以OF =， 即123b，解得b 2214a b =+=，因此，椭圆方程为22143x y +=．（Ⅱ）设1122()()A x y B x y ，，，．(ⅰ)当直线 AB 与x 轴重合时，22222224(1)OA OB a AB a a +==>，，因此，恒有222OA OB AB +<． （ⅱ）当直线AB 不与x 轴重合时，设直线AB 的方程为：1x my =+，代入22221x y a b+=，整理得22222222()20a b m y b my b a b +++-=，所以222212122222222b m b a b y y y y a b m a b m-+=-=++，． 因为恒有222OA OB AB +<，所以∠AOB 恒为钝角． 即11221212()()0OA OB x y x y x x y y ==+<，，恒成立．2121212121212(1)(1)(1)()1x x y y my my y y m y y m y y +=+++=++++222222222222(1)()21m b a b b m a b m a b m +-=-+++22222222220m a b b a b a a b m -+-+=<+．又a 2+b 2m 2>0，所以22222220m a b b a b a -+-+<对m ∈R 恒成立， 即2222222a b m a a b b >-+对m ∈R 恒成立．当m ∈R 时，222a b m 最小值为0，所以22220a a b b -+<．2222a a b b <-，2224(1)a a b b <-=，因为a >0，b >0，所以a <b 2，即210a a -->，解得12a >或12a <(舍去)，即12a +>，综合（i ）（ii ），a 的取值范围为12⎛⎫++ ⎪ ⎪⎝⎭∞．解法二：（Ⅰ）同解法一， （Ⅱ）解：（i ）当直线l 垂直于x 轴时，x =1代入22222221(1)1A y b a y a b a-+==，． 因为恒有|OA |2+|OB |2<|AB |2，222(1)4A A y y+<，21Ay >，即21a a->1，解得a >a <(舍去)，即a >． （ii ）当直线l 不垂直于x 轴时，设11()A x y ，，22()B x y ，．设直线AB 的方程为y =k (x -1)代入22221x y a b+=，得(b 2+a 2k 2)x 2-2a 2k 2x + a 2 k 2-a 2 b 2=0，故22222212122222222a k a k a b x x x x b a k b a k -+==++，因为恒有|OA |2+|OB |2<|AB |2，所以x 21+y 21+ x 22+ y 22<( x 2-x 1)2+(y 2-y 1)2， 得x 1x 2+ y 1y 2<0恒成立．x 1x 2+ y 1y 2= x 1x 2+k 2(x 1-1) (x 2-1)=(1+k 2) x 1x 2-k 2(x 1+x 2)+ k 222222222222222222222222222()(1)a k a b a k a a b b k a b k k k b a k b a k b a k--+-=+-+=+++． 由题意得（a 2-a 2 b 2+b 2）k 2-a 2 b 2<0对k ∈R 恒成立．①当a 2-a 2 b 2+b 2>0时，不合题意；②当a 2-a 2 b 2+b 2=0时，a =12+； ③当a 2-a 2 b 2+b 2<0时，a 2-a 2(a 2-1)+ (a 2-1)<0，a 4-3a 2 +1>0，解得a 2>a 2>，a >，因此a ．综合（i ）（ii ），a 的取值范围为⎫+⎪⎪⎝⎭∞．辽宁文6．设P 为曲线C ：223y x x =++上的点，且曲线C 在点P 处切线倾斜角的取值范围为04π⎡⎤⎢⎥⎣⎦，，则点P 横坐标的取值范围为（ ） A ．112⎡⎤--⎢⎥⎣⎦，B ．[]10-，C ．[]01，D ．112⎡⎤⎢⎥⎣⎦，辽宁文11．已知双曲线22291(0)y m x m -=>的一个顶点到它的一条渐近线的距离为15，则m =（ ） A ．1 B ．2 C ．3 D ．4辽宁文 21．（本小题满分12分）在平面直角坐标系xOy 中，点P 到两点(0，(0的距离之和等于4，设点P 的轨迹为C ．（Ⅰ）写出C 的方程；（Ⅱ）设直线1y kx =+与C 交于A ，B 两点．k 为何值时OA ⊥OB ？此时AB 的值是多少？21．本小题主要考查平面向量，椭圆的定义、标准方程及直线与椭圆位置关系等基础知识，考查综合运用解析几何知识解决问题的能力．满分12分． 解：（Ⅰ）设P （x ，y ），由椭圆定义可知，点P 的轨迹C 是以(0(0为焦点，长半轴为2的椭圆．它的短半轴1b ==，故曲线C 的方程为2214y x +=． ······································································· 4分 （Ⅱ）设1122()()A x y B x y ，，，，其坐标满足2214 1.y x y kx ⎧+=⎪⎨⎪=+⎩， 消去y 并整理得22(4)230k x kx ++-=， 故1212222344k x x x x k k +=-=-++，． ····························································· 6分 OA OB ⊥，即12120x x y y +=．而2121212()1y y k x x k x x =+++，于是222121222223324114444k k k x x y y k k k k -++=---+=++++． 所以12k =±时，12120x x y y +=，故OA OB ⊥． ················································ 8分 当12k =±时，12417x x +=，121217x x =-．(AB x ==而22212112()()4x x x x x x -=+-23224434134171717⨯⨯=+⨯=， 所以465AB =． ····················································································· 12分 辽宁理6．设P 为曲线C ：223y x x =++上的点，且曲线C 在点P 处切线倾斜角的取值范围为04π⎡⎤⎢⎥⎣⎦，，则点P 横坐标的取值范围为（ ） A ．112⎡⎤--⎢⎥⎣⎦，B ．[]10-，C ．[]01，D ．112⎡⎤⎢⎥⎣⎦，辽宁理10．已知点P 是抛物线22y x =上的一个动点，则点P 到点（0，2）的距离与P 到该抛物线准线的距离之和的最小值为（ ） A．2B ．3CD ．92辽宁理 20．（本小题满分12分）在直角坐标系xOy 中，点P到两点(0，，(0的距离之和等于4，设点P 的轨迹为C ，直线1y kx =+与C 交于A ，B 两点． （Ⅰ）写出C 的方程；（Ⅱ）若OA ⊥OB ，求k 的值；（Ⅲ）若点A 在第一象限，证明：当k >0时，恒有|OA |>|OB |．20．本小题主要考查平面向量，椭圆的定义、标准方程及直线与椭圆位置关系等基础知识，考查综合运用解析几何知识解决问题的能力．满分12分． 解：（Ⅰ）设P （x ，y ），由椭圆定义可知，点P 的轨迹C是以(0(0为焦点，长半轴为2的椭圆．它的短半轴1b ==，故曲线C 的方程为2214y x +=． ······································································· 3分 （Ⅱ）设1122()()A x y B x y ，，，，其坐标满足2214 1.y x y kx ⎧+=⎪⎨⎪=+⎩， 消去y 并整理得22(4)230k x kx ++-=， 故1212222344k x x x x k k +=-=-++，． ····························································· 5分 若OA OB ⊥，即12120x x y y +=．而2121212()1y y k x x k x x =+++，于是22121222233210444k k x x y y k k k +=---+=+++， 化简得2410k -+=，所以12k =±． ································································· 8分 （Ⅲ）2222221122()OA OB x y x y -=+-+22221212()4(11)x x x x =-+--+12123()()x x x x =--+ 1226()4k x x k -=+．因为A 在第一象限，故10x >．由12234x x k =-+知20x <，从而120x x ->．又0k >， 故220OA OB ->，即在题设条件下，恒有OA OB >． ································································ 12分安徽文14．已知双曲线2212x y n n--=1n = ．14．4安徽文 22．（本小题满分14分）已知椭圆2222:1(0)x y C a b a b+=＞＞，其相应于焦点(20)F ，的准线方程为4x =． （Ⅰ）求椭圆C 的方程；（Ⅱ）已知过点1(20)F -，倾斜角为θ的直线交椭圆C 于A B ，两点．求证：22cos AB =-θ；（Ⅲ）过点1(20)F -，作两条互相垂直的直线分别交椭圆C 于点A B ，和D E ，，求AB DE +的最小值．22．本题主要考查直线的方程、椭圆的方程和性质、直线与椭圆的位置关系等知识．考查数形结合的数学思想以及运算能力和综合解题能力．本小题满分14分． 解：（Ⅰ）由题意得：222224c ac a b c =⎧⎪⎪=⎨⎪⎪=+⎩，，．∴ 2284a b ⎧=⎪⎨=⎪⎩，．∴椭圆C 的方程为22184x y +=． （Ⅱ）方法一：由（I ）知，1(20)F -，是椭圆C的左焦点，离心率2e =， 设l 为椭圆的左准线，则l ：4x =-．作1AA l ⊥于1A ，1BB l ⊥于1B ，l 与x 轴交于点H （如图）． 点A 在椭圆上，11||||2AP AA ∴=11|||cos )2F H AF θ=+1||cos AF θ=．1||AF ∴=同理1||BF =．第（22）题图11||||||AB AF BF∴=+=+=方法二：当π2θ≠时，记tankθ=，则(2)AB y k x=+：，将其代入方程2228x y+=．得2222(12)88(1)0k x k x k+++-=．设1122()()A x yB x y，，，，则12x x，是此二次方程的两个根．2122812kx xk∴+=-+，21228(1)12kx xk-=+．||AB===22)12kk+==+．①22tankθ=，代入①式得2||2cosABθ=-．②当π2θ=时，||AB=2||2cosABθ∴=-．（Ⅲ）设直线AB的倾斜角为θ，由于DE AB⊥，由（Ⅱ）可得，||||AB DE==22222||||12cos2sin2sin cos2sin24AB DEθθθθθ+=+==--++．当π4θ=或3π4θ=时，||||AB DE +取得最小值3．安徽理22． (本小题满分13分)设椭圆22221(0)x y C a b a b+=>>：过点M，且左焦点为1(F ． （Ⅰ）求椭圆C 的方程；（Ⅱ）当过点(41)P ，的动直线l 与椭圆C 相交于两不同点A ，B 时，在线段AB 上取点Q ，满足AP QB AQ PB =．证明：点Q 总在某定直线上．22．本题主要考查直线、椭圆的方程及几何性质、线段的定比分点公式等基础知识、基本方法和分析问题、解决问题的能力．本小题满分13分． 解：（Ⅰ）由题意：2222222211c a b c a b ⎧=⎪⎪+=⎨⎪⎪=-⎩，，．解得2242a b ==，． 所求椭圆方程为22142x y +=． （Ⅱ）方法一：设点Q A B ，，的坐标分别为1122()()()x y x y x y ，，，，，，由题设知AP PB AQ QB ，，，均不为零，记AP AQ PBQBλ==．则0λ>且1λ≠．又A P B Q ，，，四点共线，从而AP PB AQ QB λλ=-=，． 于是12124111x x y y λλλλ--==--，．121211x x y y x y λλλλ++==-+，．从而22212241x x x λλ-=-， ………………① 2221221y y y λλ-=-．…………………② 又点A B ，在椭圆C 上，即221124x y +=，………………③222224x y +=，………………④①2+⨯②并结合③，④得424x y +=．即点()Q x y ，总在定直线220x y +-=上． 方法二：设点()Q x y ，，11()A x y ，，22()B x y ，，由题设， PA PB AQ QB ，，，均不为零 且PA PB AQQB=，又P A Q B ，，，四点共线，可设PA AQ PB BQ λλ=-=，（01λ≠±，）．于是 114111x yx y λλλλ--==--，， ① 224111x y x y λλλλ++==++，． ②由于11()A x y ，22()B x y ，在椭圆C 上，将①、②分别代入C 的方程2224x y +=，整理得222(24)4(22)140x y x y λλ+--+-+=． ③ 222(24)4(22)140x y x y λλ+-++-+=． ④④-③，得8(22)0x y λ+-=．0λ≠，220x y ∴+-=．即点()Q x y ，总在定直线220x y +-=上．湖北文10．如图所示，“嫦娥一号”探月卫星沿地月转移轨道飞向月球，在月球附近一点P 变轨进入以月球球心F 为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在P 点第二次变轨进入仍以F 为一个焦点的椭圆轨道Ⅱ绕月飞行，最终卫星在P 点第三次变轨进入以F 为圆心的圆形轨道Ⅲ绕月飞行，若用12c 和22c 分别表示椭圆轨道Ⅰ和Ⅱ的焦距，用12a 和22a 分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长，给出下列式子：①1122a c a c +=+；②1122a c a c -=-；③1212c a a c >；④11c c <22c a ． 其中正确式子的序号是（ ）A ．①③B ．②③C ．①④D ．②④湖北文20．(本小题满分13分)已知双曲线22221(00)x y C a b a b-=>>：，的两个焦点为1(20)F -，，2(20)F ，，点(3P 在双曲线C 上．（Ⅰ）求双曲线C 的方程；（Ⅱ）记O 为坐标原点，过点(02)Q ，的直线l 与双曲线C 相交于不同的两点E F ，，若OEF △的面积为l 的方程．20．本小题主要考查双曲线的定义、标准方程、直线和双曲线位置关系等平面解析几何的基础知识，考查待定系数法、不等式的解法以及综合运用数学知识进行推理运算的能力． （满分13分）（Ⅰ）解法1：依题意，由224a b +=，得双曲线方程为222221(04)4x y a a a-=<<-．将点(3代入上式，得229714a a-=-． 解得218a =（舍去）或22a =，故所求双曲线方程为22122x y -=． 解法2：依题意得，双曲线的半焦距2c =．122a PF PF =-== 22a ∴=，2222b c a =-=．∴双曲线C 的方程为22122x y -=． （Ⅱ）解法1：依题意，可设直线l 的方程为2y kx =+，代入双曲线C 的方程并整理， 得22(1)460k x kx ---=． ①直线l 与双曲线C 相交于不同的两点E F ，，222110(4)46(1)0k k k k k ≠±⎧⎧-≠⎪⎪∴⇔⎨⎨<<∆=-+⨯->⎪⎪⎩⎩，，，(1)(11)(13)k ∴∈--，，． ②设1122()()E x y F x y ，，，，则由①式得12241k x x k +=-，12261x x k =--，于是EF ==22212122223()411k x x x x k k-=+-=+-． 而原点O 到直线l 的距离d =2222211223122111OEFk S d EF kk kk -∴==+=--+△． 若OEFS =△，即422201k k k=⇔--=-，解得k = 满足②．故满足条件的直线l 有两条，其方程分别为2y =+和2y =+ 解法2：依题意，可设直线l 的方程为2y kx =+，代入双曲线C 的方程并整理， 得22(1)460k x kx ---=． ①。

2007年高考数学试题汇编圆锥曲线重庆文（12）已知以F 1（2,0），F 2（2,0）为焦点的椭圆与直线043=++y x 有且仅有一个交点，则椭圆的长轴长为（A ）23（B ）62（C ）72（D ）24（21）（本小题满分12分，（Ⅰ）小问4分，（Ⅱ）小问8分） 如题（21）图，倾斜角为a 的直线经过抛物线x y 82=的焦点F ，且与抛物线交于A 、B 两点。

（Ⅰ）求抛物线的焦点F 的坐标及准线l 的方程；（Ⅱ）若a 为锐角，作线段AB 的垂直平分线m 交x 轴于点P ，证明|FP|-|FP|cos2a 为定值，并求此定值。

重庆理（16）过双曲线422=-y x 的右焦点F 作倾斜角为0105的直线，交双曲线于P 、Q 两点，则|FP||FQ|的值为__________.(22) (本小题满分12分)如图，中心在原点O 的椭圆的右焦点为F （3，0），右准线l 的方程为x = 12。

（1）求椭圆的方程；（2）在椭圆上任取三个不同点321,,P P P ，使133221FP P FP P FP P ∠=∠=∠，证明||1||1||1321FP FP FP ++为定值，并求此定值。

浙江文（10）已知双曲线22221x y a b-= (0,0)a b >>的左、右焦点分别为F 1、F 2，P 是准线上一点，且PF 1⊥P F 2，｜P F 1｜⋅｜P F 2 ｜＝4ab ，则双曲线的离心率是23XOFY2P 1P3Pl(21)(本题15分)如图，直线y ＝kx ＋b 与椭圆2214x y +=交于A 、B 两点，记△AOB 的面积为S ．(I)求在k ＝0，0＜b ＜1的条件下，S 的最大值； （Ⅱ)当｜AB ｜＝2，S ＝1时，求直线AB 的方程． 浙江理（9）已知双曲线22221(00)x y a b a b-=>>，的左、右焦点分别为1F ，2F ，P 是准线上一点，且12PF PF ⊥，124PF PF ab =g ，则双曲线的离心率是（）Ｂ．Ｃ．2Ｄ．3天津文（7）设双曲线22221(00)x y a b a b-=>>，24y x =的准线重合，则此双曲线的方程为（ ）Ａ．2211224x y -=Ｂ．2214896x y -= Ｃ．222133x y -=Ｄ．22136x y -= （22）（本小题满分14分）设椭圆22221(0)x y a b a b+=>>的左、右焦点分别为12F F A ，，是椭圆上的一点，212AF F F ⊥，原点O到直线1AF 的距离为113OF ．（Ⅰ）证明a =；（Ⅱ）求(0)t b ∈，使得下述命题成立：设圆222xy t +=上任意点00()M x y ，处的切线交椭圆于1Q ，2Q 两点，则12OQ OQ ⊥．天津理22．（本小题满分14分）设椭圆22221(0)x y a b a b+=>>的左、右焦点分别为12F F A ，，是椭圆上的一点，212AF F F ⊥，原点O到直线AF 的距离为1OF ．（Ⅰ）证明a =；（Ⅱ）设12Q Q ，为椭圆上的两个动点，12OQ OQ ⊥，过原点O 作直线12Q Q 的垂线OD ，垂足为D ，求点D 的轨迹方程． 四川文（5）如果双曲线2242x y -＝1上一点P 到双曲线右焦点的距离是2,那么点P 到y 轴的距离是(A)364 (B)362(C)62(D)32(10)已知抛物线y=x 2+3上存在关于直线x+y=0对称的相异两点A 、B ，则|AB|等于A.3B.4C.32 D.42解析：选C ．设直线AB 的方程为y x b =+，由22123301y x x x b x x y x b⎧=-+⇒++-=⇒+=-⎨=+⎩，进而可求出AB 的中点11(,)22M b --+，又由11(,)22M b --+在直线0x y +=上可求出1b =，∴220xx +-=，由弦长公式可求出AB ==线的位置关系．自本题起运算量增大．（21）(本小题满分12分)求F 1、F 2分别是椭圆2214x y +=的左、右焦点. （Ⅰ）若r 是第一象限内该数轴上的一点，221254PF PF +=-u u u r u u u u r ，求点P 的作标； （Ⅱ）设过定点M （0，2）的直线l 与椭圆交于同的两点A 、B ，且∠ADB 为锐角（其中O 为作标原点），求直线l 的斜率k 的取值范围. 四川理20）（本小题满分12分）设1F 、2F 分别是椭圆1422=+y x 的左、右焦点. （Ⅰ）若P 是该椭圆上的一个动点，求1PF ·2PF 的最大值和最小值; （Ⅱ）设过定点)2,0(M 的直线l 与椭圆交于不同的两点A 、B ，且∠AOB 为锐角（其中O 为坐标原点），求直线l 的斜率k 的取值范围.18、已知双曲线22145x y -=，则以双曲线中心为焦点，以双曲线左焦点为顶点的抛物线方程为_____ 21、已知半椭圆()222210x y x a b +=≥与半椭圆()222210y x x b c +=≤组成的曲线称为“果圆”，其中222,0,0a b c a b c =+>>>，012,,F F F 是对应的焦点。

（2008-2020）高考数学分类汇编全国1卷（理）-圆锥曲线一、选择填空题1（2008）．已知抛物线21y ax =-的焦点是坐标原点，则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 ．2（2008）．在ABC △中，AB BC =，7cos 18B =-．若以A B ，为焦点的椭圆经过点C ，则该椭圆的离心率e = ．3(2008)设双曲线22221x y a b-=（a ＞0,b ＞0）的渐近线与抛物线y=x 2 +1相切，则该双曲线的离心率等于（A （B ）2 （C （D4(2009)（12）已知椭圆C: 2212x y +=的又焦点为F ，右准线为L ，点A L ∈,线段AF 交C 与点B 。

若3FA FB =,则AF =5(2010)（9）已知1F 、2F 为双曲线22:1C χγ-=的左、右焦点，点在P 在C 上，12F PF ∠=60°，则P 到χ轴的距离为（A （B （C （D6(2010)（16）已知F 是椭圆C 的一个焦点，B 是短轴的一个端点，线段BF 的延长线交C 于点D ，且2BF FD =，则C 的离心率为 。

7(2011)（14）在平面直角坐标系xOy 中，椭圆C 的中心为原点，焦点12,F F 在x 轴。

过1F 的直线L 交C 于,A B 两点，且2ABF 的周长为16，那么C 的方程为 。

8（2012）（4）设12,F F 是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点，P 为直线32ax =上的一点，21F PF ∆是底角为30的等腰三角形，则 E 的离心率为(A) 12 (B) 23 (C) 34 (D) 459（2012）（8）等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线216y x =的准线交于,A B 两点， ||AB =，则C 的实轴长为（A （B ）（C ）4 （D ）810（2013）10.已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为(3,0)F ，过点F 的直线交椭圆于,A B 两点。

2007年高考数学试题汇编圆锥曲线重庆文（12）已知以F 1（2,0），F 2（2,0）为焦点的椭圆与直线043=++y x 有且仅有一个交点，则椭圆的长轴长为（A ）23（B ）62（C ）72（D ）24（21）（本小题满分12分，（Ⅰ）小问4分，（Ⅱ）小问8分）如题（21）图，倾斜角为a 的直线经过抛物线x y 82=的焦点F ，且与抛物线交于A 、B 两点。

题（21）图 （Ⅰ）求抛物线的焦点F 的坐标及准线l 的方程；（Ⅱ）若a 为锐角，作线段AB 的垂直平分线m 交x 轴于点P ，证明|FP|-|FP|cos2a 为定值，并求此定值。

（21）（本小题12分）（Ⅰ）解：设抛物线的标准方程为px y 22=，则82=p ，从而.4=p 因此焦点)0,2(pF 的坐标为（2，0）.又准线方程的一般式为2p x -=。

从而所求准线l 的方程为2-=x 。

答（21）图（Ⅱ）解法一：如图（21）图作AC ⊥l ，BD ⊥l ，垂足为C 、D ，则由抛物线的定义知 |F A |=|FC |,|FB |=|BD |.记A 、B 的横坐标分别为x x x z ，则 |F A |＝|AC |＝4cos ||22cos ||2+=++=+a FA p p a FA p x x 解得aFA cos 14||-=， 类似地有a FB FB cos ||4||-=，解得aFB cos 14||+=。

记直线m 与AB 的交点为E ，则aaa a FB FA FB FA FA AE FA FE 2sin cos 4cos 14cos 1421|)||(|212||||||||||||=⎪⎭⎫ ⎝⎛+--=-=+-=-=所以a a FE FP 2sin 4cos ||||==。

故8sin sin 2·4)2cos 1(sin 42cos ||||222==-=-aa a aa FP FP 。

解法二：设),(A A y x A ，),(B B y x B ，直线AB 的斜率为a k tan =，则直线方程为)2(-=x k y 。