13.4最短路径问题

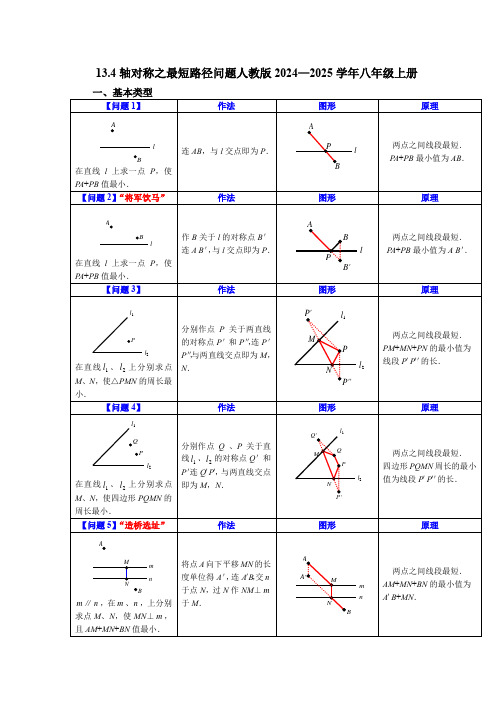
13.4轴对称之最短路径问题人教版2024—2025学年八年级上册二、例题讲解例1.如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC，已知线段AB＝4，DE＝2，BD＝8，设CD＝x．（1）用含x的代数式表示AC+CE的长；（2）请问点C满足什么条件时，AC+CE最小？最小为多少？（3）根据（2）中的规律和结论，请构图求代数式的最小值．变式1.如图，C为线段BD上一动点，分别过点B，D作AB⊥BD，ED⊥BD，连结AC，EC，已知AB＝5，DE＝1，BD＝8．（1）请问点C什么位置时AC+CE的值最小？最小值为多少？（2）设BC＝x，则AC+CE可表示为，请直接写出的最小值为．例2.如图，直线l是一条河，P，Q是两个村庄，欲在l上的某处修建一个水泵站，向P，Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（）A．B．C．D．变式1.如图，在⊥ABC中，BA＝BC，BD平分⊥ABC，交AC于点D，点M、N 分别为BD、BC上的动点，若BC＝10，⊥ABC的面积为40，则CM+MN的最小值为．变式2.如图，等腰三角形ABC的底边BC长为8，面积是24，腰AC的垂直平分线EF分别交AC，AB于E，F点，若点D为BC边的中点，点M为线段EF 上一动点，则⊥CDM的周长的最小值为（）A．7B．8C．9D．10变式3.如图，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点．（1）点D的坐标为；（2）若E为边OA上的一个动点，当⊥CDE的周长最小时，求点E的坐标．例3.如图，⊥AOB内一点P，P1，P2分别是P关于OA、OB的对称点，P1P2交OA于点M，交OB于点N．若⊥PMN的周长是6cm，则P1P2的长为（）A．6cm B．5cm C．4cm D．3cm变式1.已知点P在⊥MON内．如图1，点P关于射线OM的对称点是G，点P 关于射线ON的对称点是H，连接OG、OH、OP．（1）若⊥MON＝50°，求⊥GOH的度数；（2）如图2，若OP＝6，当⊥P AB的周长最小值为6时，求⊥MON的度数．变式2.如图，⊥MON＝45°，P为⊥MON内一点，A为OM上一点，B为ON上一点，当⊥P AB的周长取最小值时，⊥APB的度数为（）A．45°B．90°C．100°D．135°变式3.如图，⊥AOB＝30°，P是⊥AOB内的一个定点，OP＝12cm，C，D分别是OA，OB上的动点，连接CP，DP，CD，则⊥CPD周长的最小值为．变式4.如图，在五边形中，⊥BAE＝140°，⊥B＝⊥E＝90°，在边BC，DE上分别找一点M，N，连接AM，AN，MN，则当⊥AMN的周长最小时，求⊥AMN+⊥ANM 的值是（）A．100°B．140°C．120°D．80°例4.如图，在⊥ABC中，AB＝AC，⊥A＝90°，点D，E是边AB上的两个定点，点M，N分别是边AC，BC上的两个动点．当四边形DEMN的周长最小时，⊥DNM+⊥EMN的大小是（）A．45°B．90°C．75°D．135°变式1.如图，在平面直角坐标系中，已知点A（0，1），B（4，0），C（m+2，2），D（m，2），当四边形ABCD的周长最小时，m的值是（）A．B．C．1D．变式2.如图，在四边形ABCD中，⊥B＝90°，AB⊥CD，BC＝3，DC＝4，点E 在BC上，且BE＝1，F，G为边AB上的两个动点，且FG＝1，则四边形DGFE 的周长的最小值为．例5.如图，⊥AOB＝20°，点M、N分别是边OA、OB上的定点，点P、Q分别是边OB、OA上的动点，记⊥MPQ＝α，⊥PQN＝β，当MP+PQ+QN最小时，则β﹣α的值为（）A．10°B．20°C．40°D．60°变式1.如图，∠AOB＝20°，M，N分别为OA，OB上的点，OM＝ON＝3，P，Q分别为OA，OB上的动点，求MQ+PQ+PN的最小值。