常见概率分布期望方差以及分布图汇总

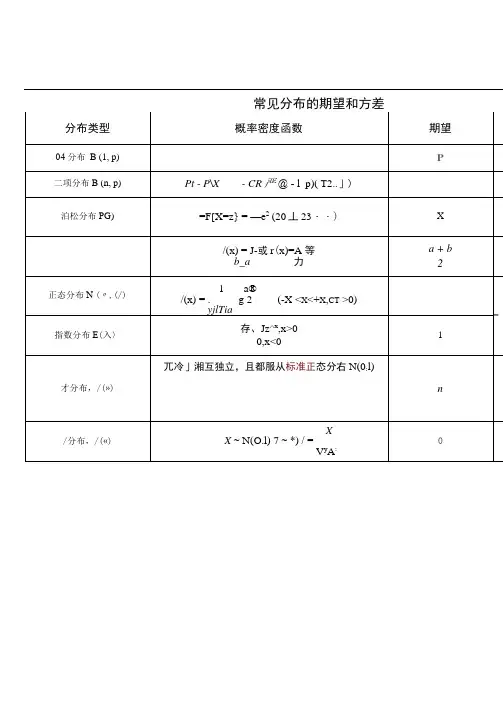
常见分布的期望和方差概率与数理统计重点摘要1、正态分布的计算： VF(x) P(X x)(X) o2、 随机变量函数的概率密度： X 是服从某种分布的随机变量，求 Y f(X)的概率密度: f y (y) f x (x)[h(y)] h'(y)。

(参见 P66〜72)x y3、 分布函数F(x,y) f (u, v)dudv 具有以下基本性质：⑴、是变量x , y 的非降函数;⑵、0 F(x,y) 1，对于任意固定的x , y 有：F( ,y) F(x, )0 ； ⑶、F(x,y)关于x右连续，关于y 右连续;⑷、对于任意的(x i , yj,(X 2, y 2), X i X 2, y i y ，有下述不等式成立:为一维正态分布4、一个重要的分布函数1:F(x,y)2f(x,y)F(x,y)x y62 , 2(x24)( y 9)5、二维随机变量的边缘分布：边缘概率密度：f x (X ) f Y (y)f (x, y)dy f (x, y)dxx y 、 (— arctan-)(— arctan‘)的概率 密度为2 3xF x (x) F(x,)[边缘分布函数：yF Y (y) F( ,y) y[f(u,y)dy]du二维正态分布的边缘分布 f(x,v)dx]dv6随机变量的独立性：若F(x,y) F X (x)F Y (y)则称随机变量X , Y 相互独立。

简称X 与Y 独立7、两个独立随机变量之和的概率密度：f Z (z) f X (x)f Y (z x)dx f Y (y)f X (z y)dy 其中 Z = X + Y 8、两个独立正态随机变量的线性组合仍服从正态分布，即2 2 2 2Z aX bY: N(a 1 b 2,a 1 b 2 。

9、期望的性质：…( 3)、E(X Y) E(X) E(Y) ； (4)、若 X , 丫 相互独立，则E(XY) E(X)E(Y) O10、方差： D(X) E(X 2) (E(X))2 O若 X , 丫不相关，则 D(X Y) D(X) D(Y),否则 D(X Y) D(X) D(Y) 2Cov(X,Y), D(X Y) D(X) D(Y) 2Cov(X,Y)称：X 与丫不相关。

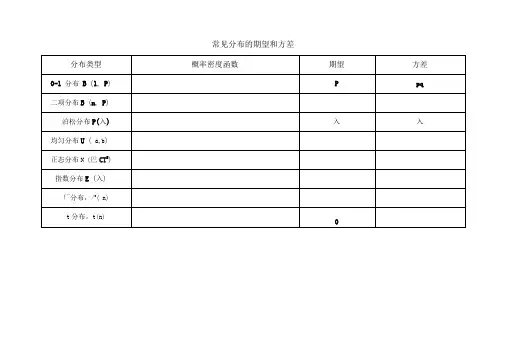
常见分布的期望和方差概率与数理统计重点摘要X — 41、 正态分布的计算： F(x) = p(x 兰x)=e ( ------ )。

c2、 随机变量函数的概率密度：X 是服从某种分布的随机变量， 求丫 = f(X)的概率密度：f Y (y)= f x (x)[h(y)]|h'(y)|。

(参见P66〜_ x y3、分布函数F(x,y)=f f f(u,v)dudv 具有以下基本性质:0<F(x,y)<1，对于任意固定的 x , y 有：F^,y) = F(x^)=0 ;对于任意的(x i , y i ), (x 2, y 2), X i<:x 2,y i<y 2，有下述不等式成立:r 24、一个重要的分布函数： F(x,y)=l&+arcta n 与Q+arcta n')的概率密度为：f (x, y)=丄 F (x, y) = 2 22兀亠 2 2 2 3 c x c y 兀(x + 4)(y +9)5、二维随机变量的边缘分布:f x (x) = J*f(x, y)dy边缘概率密度：tf Y (y) = Lcf(x,y)dxx -beF X (x^F(x^^ f J f f (u,y)dy]du边缘分布函数： '4； 二维正态分布的边缘分布为一维正态分布。

⑴、 是变量x , y 的非降函数;⑵、 ⑶、 F(x,y)关于x 右连续，关于y 右连续;⑷、yF Y(y)=F(P,y) = UJf(x,v)dx]dv随机变量的独立性：若 F(x, y) =F x (x)F Y (y)则称随机变量X ，Y 相互独立。

简称X 与Y 独立。

两个独立正态随机变量的线性组合仍服从正态分布，即 Z=aX+b Y L N(a 已卄巴^务；+b 2cr 2)o13、k 阶原点矩：vk=E(X k)，k 阶中心矩：4k =E[(X-E(X))k] o16、独立同分布序列的中心极限定理:6、 7、 两个独立随机变量之和的概率密度：f z (z) = J f x (x)f Y (z-x)dx= J f Y (y)f x (z-y)dy 其中Z = X + YJ-oC9、 期望的性质: (3)、EX Y )EX( )EY()；(4)、若 X ，Y 相互独立，则 E(XY) = E(X)E(Y) o10、方差： D(X ) =E(X 2)-(E(X))2o若 X , Y 不相关，贝y D(X + Y) = D(X) + D(Y),否贝U D(X + Y) = D(X)+D(Y) + 2Cov(X,Y),D(X -Y) = D(X) +D(Y) -2Cov(X,Y)11、协方差：Cov(X,Y) =E[(X -E(X))(Y-E(Y))]，若 X , Y 独立，则 Cov(X,Y) = 0，此时称：X 与 Y 不相关。

概率论与数理统计：六大基本分布及其期望和方差绪论：概率论中有六大常用的基本分布，大致可分成两类：离散型（0-1分布、二项分布、泊松分布），连续型（均匀分布、指数分布、正态分布）。

补充：在进入正文之前先讲一下期望和均值的一些区别：期望和均值都具有平均的概念，但期望是指的随机变量总体的平均值，而均值则是指的从总体中抽样的样本的平均值，即前者是理想的均值，而后者则是实际观测出来的数据的均值。

例如：对于一个六面的骰子，其期望E = （1+2+3+4+5+6）/ 6 = 3.5。

然后掷5次骰子，每次掷的点数分别为1,3,5,5,1，则平均值为（1+3+5+5+1）/ 5 = 3。

可以发现两者并不相等。

方差（variance）：方差是各个数据与平均数之差的平方的平均数，方差度量了随机变量与期望（也可说均值）之间的偏离程度。

标准差为方差的开根号。

协方差（Covariance）：用于衡量两个变量之间的误差，而方差是协方差的特殊情况，即当两个变量相同的情况。

其公式如下：，表示含义为：E（∑（“X与其均值之差” * “Y与其均值之差”））当协方差为正时：表示两变量正相关（即同时变大变下）。

当协方差为负时：表示两变量负相关（即你变大，我变小，反之亦然）。

当协方差为0时：两变量相互独立。

相关系数：其公式如下，表示的含义为用X和Y的协方差除以X 和Y的标准差。

所以相关系数也可以看成协方差，一种剔除两个变量量纲影响，标准化后的特殊协方差。

正文：1、0-1分布已知随机变量X，其中P{X=1} = p，P{X=0} = 1-p，其中 0 < p< 1，则成X服从参数为p的0-1分布。

其中期望为E（X） = p 方差D（X） = p（1-p）；2、二项分布n次独立的伯努利实验（伯努利实验是指每次实验有两种结果，每种结果概率恒定，比如抛硬币）。

其中期望E（X） = np 方差D（X） = np（1-p）；3、泊松分布表示单位时间内某稀有事件发生k次的概率，其公式为其中方差和期望均为，详细了解请☞戳4、均匀分布若连续型随机变量X具有概率密度，则称X在（a，b）上服从均匀分布其中期望E（X） = （a+b）/ 2 ，方差D（X） = （b-a）^2 / 12。

创卫人人有责
本文是关于初二叙事作文的创卫人人有责，感谢您的阅读！
创建文明城市不是高大上，创建文明城市就是要从点滴小事做起，聚“点滴小事”成“文明大事”。

3月15日下午，我们小区以“创建国家卫生县城、人人有责人人受益”为主题的创卫公益活动隆重举行。

创建国家卫生城市，我们一家都去当了志愿者。

3月15日上午8：30---12:00、下午13:30---18:00，我们一家与40名志愿者叔叔阿姨，在社工部主任的带领下，协助交警维护交通秩序、摆放整齐非机动车、劝阻行人抽烟、捡垃圾烟头、清除野广告、发放宣传创卫知识手册，用实际行动支持创卫工作。

创建文明城市关键是要从点滴小事做起。

事事文明了，人人文明了，文明城市创建才能成功。

为迎接创建卫生城市工作，进一步营造人人支持创建、个个参与创建的浓厚氛围，3月16日，我们市里消防支队组织志愿者开展道路卫生“大扫除”活动。

上午，志愿者们走出营区，清理道路两边草坪上的垃圾并对路边草坪进行浇水，清理草坪垃圾，志愿者们积极认真，哪怕是一片纸屑，一个烟头，一块塑料，都绝不放过，不知不觉一个小时过去了，道路旁边的草坪也变得清洁、干净，过路行人赞不绝口。

表现出了崭新的风貌，战士们深刻体会到“精神文明建设”不是一句口号，而是与自己的工作息息相关。

创建卫生城市不是过了这几天检查，而是为了卫生文明深入人心，从每时每刻做起，从我们身边做起，从小事做起………
本文来自于互联网，仅供参考和阅读。

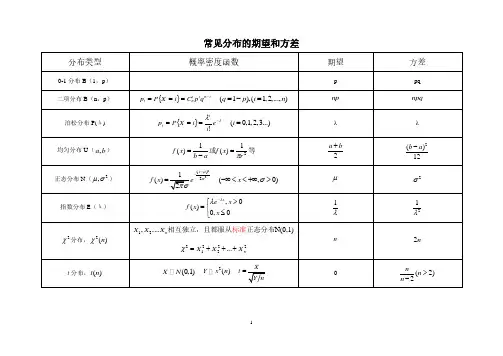
常见的概率分布离散分布0-1分布(伯努利分布)它的分布律为：\[P\{X=k\}=p^k(1-p)^{1-k}, k=0,1, (0<p<1)\]0-1分布记作：\(X \sim b(1,p)\)期望：\(E(X)=p\)⽅差:\(D(X)=p(1-p)\)常⽤的场景：新⽣婴⼉性别的登记，招⽣考试的录取，产品的是否合格，硬币的正反⾯。

⼆项分布⼆项分布为\(n\)重伯努利实验的概率分布。

分布律为：\[P\{X=k\}=\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k},k=0,1,2,...,n,(0<p<1)\]\[\sum\limits_{k=0}^{n}P\{X=k\}=\sum\limits_{k=0}^{n}\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}=(p+1-p)^n=1\]⼆项分布记作：\( X \sim b(n,p)\)期望：\(E(X)=np\)⽅差:\(D(X)=np(1-p)\)常⽤的场景：⽐如⼀个⼈射击\(n\)次，其中\(k\)次命中的概率，抽查50台设备，其中10台出故障的概率等等。

从下⾯的图中，我们可以看到命中次数先增加，到了3达到最⼤，之后⼜逐渐减少，⼀般来说，对于固定的\(n,p\)，都具有这⼀性质。

（1）当\(（n+1）p\)不为整数时，⼆项概率\(P\{X=k\}\)在\(k=[(n+1)p]\)时达到最⼤值；（2）当\(（n+1）p\)为整数时，⼆项概率\(P\{X=k\}\)在\(k=(n+1)p,k=(n+1)p-1\)时达到最⼤值。

%每轮射击10次，命中概率0.3，射击10000轮，x中返回的是每轮中命中的次数x=binornd(10,0.3,10000,1);%bin的数⽬为10hist(x,10);N=100;p=0.4;k=0:N;%事件发⽣k次的概率pdf=binopdf(k,N,p);%事件发⽣不⼤于k次的概率cdf=binocdf(k,N,p);plotyy(k,pdf,k,cdf);grid on;多项分布多项式分布是⼆项式分布的扩展，在多项式分布所代表的实验中，⼀次实验会有多个互斥结果，⽽⼆项式分布所代表的实验中，⼀次实验只有两个互斥结果。