当前位置：文档之家 › 中考二次函数压轴题PPT优秀课件

中考二次函数压轴题PPT优秀课件

  • 格式：ppt
  • 大小：1.32 MB
  • 文档页数：52

下载文档原格式

  / 52

合集下载

中考二次函数压轴题PPT

中考二次函数压轴题PPT


∴ 点 F 到 AC 的距离为 9 × = ， 4
又∵ AC=
=3 ，
∴ △ ACE 的最大面积=×3 × = ，此时 E 点坐标为（ 5 ，﹣ 3 ）．
24
9
7、（2013•曲靖压轴题）如图，在平面直角坐标系 xOy 中，直线 y=x+4 与坐标轴分别交 于 A、B 两点，过 A、B 两点的抛物线为 y=﹣x2+bx+c．点 D 为线段 AB 上一动点，过 点 D 作 CD⊥x 轴于点 C，交抛物线于点 E． （1）求抛物线的解析式． （2）当 DE=4 时，求四边形 CAEB 的面积． （3）连接 BE，是否存在点 D，使得△ DBE 和△ DAC 相似？若存在，求此点 D 坐标； 若不存在，说明理由．
解得
，
所以，直线 AC 的解析式为 y=x﹣1，
∵ y=x2﹣4x+3=（x﹣2）2﹣1，
∴ 抛物线的对称轴为直线 x=2，
当 x=2 时，y=2﹣1=1，
∴ 抛物线对称轴上存在点 D（2，1），使△ BCD 的周长最小；
8
（3）如图，设过点 E 与直线 AC 平行线的直线为 y=x+m，联立， 消掉 y 得，x2﹣5x+3﹣m=0， △ =（﹣5）2﹣4×1×（3﹣m）=0，
7
解：（1）∵ 抛物线 y=ax2+bx+3 经过点 A（1，0），点 C（4，3），
∴
，解得
，
所以，抛物线的解析式为 y=x2﹣4x+3；
（2）∵ 点 A、B 关于对称轴对称， ∴ 点 D 为 AC 与对称轴的交点时△ BCD 的周长最小， 设直线 AC 的解析式为 y=kx+b（k≠0），则，
S 四边形 CAEB=S△ ACE+S 梯形 OCEB﹣S△ BCO= ×2×6+ （6+4）×2﹣ ×2×4=12．
2025年中考数学复习专题 二次函数综合题复习课件(48张PPT)

2025年中考数学复习专题 二次函数综合题复习课件(48张PPT)

∴当m≤x≤4＋m或x≥8＋m时，y的值随x值的增大而减小，
∴当8≤x≤9时，y的值随x值的增大而减小，结合函数图象，得m的取值范围：
①m≤8且4＋m≥9，得5≤m≤8，
②8＋m≤8，得m≤0，由题意知m＞0，
∴m≤0不符合题意，舍去，
综上所述，m的取值范围是5≤函数y＝x2－2ax＋3a,顶点坐标为(m，n).
1．(2022·贵阳第24题12分)已知二次函数y＝ax2＋4ax＋b.
(1)求二次函数图象的顶点坐标(用含a，b的代数式表示)；
(2)在平面直角坐标系中，若二次函数的图象与x轴交于A，B两点，AB＝6，
且图象过(1，c)，(3，d)，(－1，e)，(－3，f)四点，判断c，d，e，f的大小，
并说明理由；
∴OP′＝OB·tan∠OBP′＝3× 3 ＝3 3 ，∴CP′＝3 3 －3，
综上所述，线段CP的长为3－ 3 或3 3 －3.
(3)当a≤x≤a＋1时，二次函数y＝x2＋bx＋c的最小值为2a，求a的值．
【分层分析】分对称轴x＝1在a到a＋1范围的右侧、中间和左侧三种情况，
结合二次函数的性质求解可得．
∴点B的坐标为(3，0)，代入y＝x2＋bx＋c，得
1 − + = 0,
= −2,
ቊ
解得ቊ
9 + 3 + = 0,
= −3,
∴二次函数的解析式为y＝x2－2x－3.
(2)连接BC，若点P在y轴上时，BP和BC的夹角为15°，求线段CP的长度；
【分层分析】分点P在点C上方和下方两种情况，先求出∠OBP的度数，再
在x轴下方部分与桥拱OBA在平静水面中的倒影组成一个新函数图象．将
新函数图象向右平移m(m＞0)个单位长度，平移后的函数图象在8≤x≤9时，
中考二次函数压轴题解题通法PPT课件

中考二次函数压轴题解题通法PPT课件


6
方程总有固定根问题
• 可以通过解方程的方法求出该固定根
已知关于的方程（mx2 3(m 1)x 2m 3 0 为实数），
求证：无论为何值，方程总有一个固定的根。
解：当 m 0 时， x 1
x1
当 m 0 时，
2
3 m
、x2
1
m3
2
0
，x
3m
1
2m
，
综上所述无论:m 为何值，方程总有一个固
19
２、“平行于y轴的动线段长度的最大值”的问题
2020/3/23
20
3、求一个已知点关于一条已知直线的对称点的坐标 问题Leabharlann 2020/3/2321
4、“抛物线上是否存在一点，使之到定直线的距离 最大”的问题
2020/3/23
22
5.常数问题
2020/3/23
23
6.“在定直线（常为抛物线的对称轴，或x轴或y轴或其它的定 直线）上是否存在一点，使之到两定点的距离之和最小”的 问题
2020/3/23
2
两点间的距离公式
AB yA yB 2 xA xB 2
2020/3/23
3
中点坐标
• 线段的中点的坐标为：
xA xB ，yA yB 2 2
2020/3/23
4
一元二次方程有整数根问题
解题步骤如下：① 用和参数的其他要求确定
参数的取值范围 ② 解方程，求出方程的根
2020/3/23
28
10、“定四边形面积的求解”问题
• 有两种常见解决的方案： • 方案（一）：连接一条对角线，分成两个三角形面积之和； • 方案（二）：过不在x轴或y轴上的四边形的一个顶点，向
精品课件-《二次函数》中考总复习PPT课件

精品课件-《二次函数》中考总复习PPT课件


(D ) B.x > a
b
C.x < a
b
D.x < a
b
a <0,b <0
7、若抛物线y=ax2+3x+1与x轴有两
个交点，则a的取值范围是 ( D )
A.a＞0
B.a＞
4 9
C.a＞ 9
4
D.a＜ 9 且a≠0
4
练习：
1、已知抛物线 y＝x²-mx+m-1.
(1)若抛物线经过坐标系原点，则m__=__1__；
2，函数 y(m2m2)xm22 当m取何值时，
（1）它是二次函数？ （2）它是反比例函数？
（1）若是二次函数，则 m2 22 且m2m20
∴当 m 2时，是二次函数。
（2）若是反比例函数，则 m2 21且m2m20
∴当 m 1 时，是反比例函数。
驶向胜利的彼 岸
小结：
1. 二次函数y=ax²+bx+c(a,b,c是常数,a≠0)的几 种不同表示形式:
特别注意：在实际问题中画函数的图像时要注意自变量的取值范围，若图像是直线， 则 画图像时只取两个界点坐标来画（包括该点用实心点，不包括该点用空心圈);若是二次 函数的图像，则除了要体现两个界点坐标外，还要取上能体现图像特征的其它一些点
3、二次函数y=x2-x-6的图象顶点坐标是_（_—_12_，_-_—2_45）___ 对称轴是__x_=_—12_____。
x
A
B
C
√D
小结：双图象的问题，寻找自相矛盾的地方。即由一个图象得 出字母的取值范围，再去检验这个字母的符号是否适合另一个
图象
3、画二次函数y=x2-x-6的图象，顶点坐标是（__—12_，__-—2_45_）___
中考二次函数复习课件【优质PPT】

中考二次函数复习课件【优质PPT】


x=2，y最大值=3
练习 根据下列条件，求二次函数的解析式。
(1)、图象经过(-1，3)， (1，3) ， (2，6) 三点；
(2)、图象的顶点(2，3)， 且经过点(3，1) ；
(3)、图象经过(0，0)， (12，0) ，且最高点
的纵坐标是3 。
顶点(6，3）
解法一设解析式为y=a(x-0)(x-12)
令y=1.4,则-0.2x2+3.2=1.4
B x解得x=-3或x=3 ∴M(-3,1.4),N(3,1.4) ∴MN=6 20 答：横向活动范围是6米。
练习、已知二次函数y=ax2-5x+c的图象如图。
(1)、当x为何值时，y随x的增大而增大; (2)、当x为何值时，y<0。 (3)、求它的解析式和顶点坐标y ；
(3)、图象经过(0，0)， (12，0) ，且最高点 的纵坐标是3 。
2021/10/10
14
5一.待般定式系数y法=a求x解2+b析x式+c (a≠0) 顶点式 y=a(x-h)2+k (a≠0)
交点式 y=a(x-x1)(x-x2) (a≠0)
6–
3–
-2 -1
12
练习 根据下列条件，求二次函数的解析式。
二次函数的图象是一条 对称轴平行于 y 轴．
抛物线
，它是 轴
对称图形，其
2021/10/10
2
y 3.二次函数的图象及性质y
0
x
0
x
抛物线 顶点坐标 对称轴 开口方向
y=ax2+bx+c(a>0)
b 2a
,
4acb2 4a
直线x b
2a
2020年河南中考复习专题八 二次函数压轴题_课件(共37张PPT)

2020年河南中考复习专题八 二次函数压轴题_课件(共37张PPT)

(3)点Q是线段BD上异于B，D的动点，过点Q作QF⊥x轴于点F，交抛物线于 点G，当△QDG为直角三角形时，直接写出点Q的坐标．
2．(2019·洛阳三模)在平面直角坐标系中，直线y＝ x－2与x轴交于点B， 与y轴交于点C，二次函数y＝ x2＋bx＋c的图象经过B，C两点，且与x轴的 负半轴交于点A.
(1)求该抛物线的解析式；
(2)若直线y＝－ x＋m将△AOC的面积分成相等的两部分，求m的值；
(3)点B是该二次函数图象与x轴的另一个交点，点D是直线x＝2上位于x轴 下方的动点，点E是第四象限内该二次函数图象上的动点，且位于直线x ＝2右侧．若以点E为直角顶点的△BED与△AOC相似，求点E的坐标．
1．(2020·原创)如图，抛物线y＝ax2＋bx＋c关于直线x＝1对称，
与坐标轴交于A，B，C三点，且AB＝4，点D
在抛物线上，直
线l是一次函数y＝kx－2(k≠0)的图象，点O是坐标原点．
(1)求抛物线的解析式；
(2)若直线l平分四边形OBDC的面积，求k的值；
(3)在抛物线上是否存在一点P，使得点Q在x轴上，点M在坐标平面 内，四边形CQPM是正方形，若存在，求点P的横坐标；若不存在， 请说明理由
(1)求b，c的值； (2)直线l与x轴交于点P. ①如图1，若l∥y轴，且与线段AC及抛物线分别相交于点E，F，点C关于直 线x＝1的对称点为D，求四边形CEDF面积的最大值； ②如图2，若直线l与线段BC相交于点Q，当△PCQ∽△CAP时，求直线l的表 达式．
1．(2019·四川泸州)如图，在平面直角坐标系xOy中，已知二次函数y＝ ax2＋bx＋c的图象经过点A(－2，0)，C(0，－6)，其对称轴为直线x＝2.
(1)求抛物线的解析式；
中考二次函数压轴题省名师优质课赛课获奖课件市赛课一等奖课件

中考二次函数压轴题省名师优质课赛课获奖课件市赛课一等奖课件

1．（2023•遵义）如图，已知抛物线y=ax2+bx+c（a≠0）旳图象经过原点O，交x轴于点A ，其顶点B旳坐标为（3，﹣ )
（1）求抛物线旳函数解析式及点A旳坐标； （2）在抛物线上求点P，使S△POA=2S△AOB； （3）在抛物线上是否存在点Q，使△AQO与△AOB相同？假如存在，祈求出Q点旳坐标； 假如不存在，请阐明理由．
（1）请观察题中旳表格和图象，用所学过旳一次函数、反百分比函数或二次函数旳有关知识，分别
直接写出y1，y2与x之间旳函数关系式； （2）请你求出该企业去年哪个月用于污水处理旳费用W（元）最多，并求出这个最多费用；
（3）今年以来，因为自建污水处理设备旳全方面运营，该企业决定扩大产能并将全部污水全部本身
5．（2023•重庆）企业旳污水处理有两种方式，一种是输送到污水厂进行集中处理，另一 种是经过企业旳本身设备进行处理．某企业去年每月旳污水量均为12023吨，因为污水厂
处于调试阶段，污水处理能力有限，该企业投资自建设备处理污水，两种处理方式同步进 行．1至6月，该企业向污水厂输送旳污水量y1（吨）与月份x（1≤x≤6，且x取整数）之间 满足旳函数关系如下表：
4．（2023•株洲）如图，一次函数
分别交y轴、x轴于A、B两点，抛物线y=﹣x2+bx+c过A、B两点． （1）求这个抛物线旳解析式； （2）作垂直x轴旳直线x=t，在第一象限交直线AB于M，交这个抛 物线于N．求当t取何值时，MN有最大值？最大值是多少？ （3）在（2）旳情况下，以A、M、N、D为顶点作平行四边形，求 第四个顶点D旳坐标．
7．（2023•湛江）如图，在平面直角坐标系中，直角三角形AOB旳顶点A、B分别落在坐 标轴上．O为原点，点A旳坐标为（6，0），点B旳坐标为（0，8）．动点M从点O出发． 沿OA向终点A以每秒1个单位旳速度运动，同步动点N从点A出发，沿AB向终点B以每秒 个 单位旳速度运动．当一种动点到达终点时，另一种动点也随之停止运动，设动点M、N 运动旳时间为t秒（t＞0）．（1）当t=3秒时．直接写出点N旳坐标，并求出经过O、A、 N三点旳抛物线旳解析式；
2020年中考数学二模复习之二次函数中考压轴题(26张PPT)【精美版】

2020年中考数学二模复习之二次函数中考压轴题(26张PPT)【精美版】


利 用 铅 垂 线 求 面 积
2020年中考数学二模复习之二次函数 中考压 轴题（2 6张PPT ）【精 美版】
四.逐问突破（2）→铅垂线
2020年中考数学二模复习之二次函数 中考压 轴题（2 6张PPT ）【精 美版】
“类铅垂线”问题
利 用 铅 垂 线 求 面 积
2020年中考数学二模复习之二次函数 中考压 轴题（2 6张PPT ）【精 美版】
本题不直接考察，而是利用铅垂线与已知直线的“几何关联”来求解 2.16-17连续考察平行四边形存在性，18年等腰三角形存在性，19年再次 考察“平行四边形存在性”的可能大，而且平行四边形难度也较大，正符合 “150分”下难度提升的大形势
2020年中考数学二模复习之二次函数 中考压 轴题（2 6张PPT ）【精 美版】
2020年中考数学二模复习之二次函数 中考压 轴题（2 6张PPT ）【精 美版】
四.逐问突破（3）→存在性
直接探讨“等腰三角形存在性”
等 腰 三 角 形
2020年中考数学二模复习之二次函数 中考压 轴题（2 6张PPT ）【精 美版】
2020年中考数学二模复习之二次函数 中考压 轴题（2 6张PPT ）【精 美版】
2020年中考数学二模复习之二次函数 中考压 轴题（2 6张PPT ）【精 美版】
四.逐问突破（3）→存在性
利用“平行四边形”性质求解
平 行 四 边 形
2020年中考数学二模复习之二次函数 中考压 轴题（2 6张PPT ）【精 美版】
2020年中考数学二模复习之二次函数 中考压 轴题（2 6张PPT ）【精 美版】
四.逐问突破（3）→存在性
利用“等腰三角形”求点
等 腰 三 角 形
2020年中考数学二模复习之二次函数 中考压 轴题（2 6张PPT ）【精 美版】
初三数学复习《二次函数》(专题复习)PPT课件

初三数学复习《二次函数》(专题复习)PPT课件


面积问题
面积问题
在二次函数中，可以通过求函数与坐标轴的交点来计算图形的面积。例如，当函数与x轴交于两点时 ，可以计算这两点之间的面积；当函数与y轴交于一点时，可以计算这一点与原点之间的面积。这些 方法在解决实际问题时非常有用，例如在计算利润、产量等方面。
求解方法ቤተ መጻሕፍቲ ባይዱ
求出二次函数与x轴和y轴的交点坐标，然后根据这些坐标计算图形的面积。对于更复杂的问题，可能 需要使用积分或其他数学方法来求解。
05
综合练习与提高
基础练习题
巩固基础 覆盖全面 由浅入深
基础练习题主要针对二次函数的基本概念、性质和公 式进行设计，旨在帮助学生巩固基础知识，提高解题的 准确性和速度。
基础练习题应涵盖二次函数的各个方面，包括开口方 向、顶点坐标、对称轴、与坐标轴的交点等，确保学生 对二次函数有全面的了解。
题目难度应从易到难，逐步引导学生深入理解二次函 数，从简单的计算到复杂的综合题，逐步提高学生的解 题能力。
初三数学复习《二次函数》(专题复习)ppt课 件
目录 Contents
• 二次函数的基本概念 • 二次函数的解析式 • 二次函数的图像与性质 • 二次函数的实际应用 • 综合练习与提高
01
二次函数的基本概念
二次函数的定义
总结词
理解二次函数的定义是掌握其性 质和图像的基础。
详细描述
二次函数是形式为$f(x) = ax^2 + bx + c$的函数，其中$a, b, c$是 常数，且$a neq 0$。这个定义表 明二次函数具有两个变量$x$和 $y$，并且$x$的最高次数为2。
03
二次函数的图像与性质
开口方向
总结词：根据二次项系数a的正负判断开口方向 a>0时，开口向上
中考数学复习---二次函数考点归纳与典型例题讲解PPT课件

中考数学复习---二次函数考点归纳与典型例题讲解PPT课件


【解析】解：（1）设 y 与 x 之间的函数关系式为 y kx b （ k 0 ），根据题意，得：
12k 14k
b b
90 80
，解得
k b
5 150
，∴
y
与
x
之间的函数关系式为
y
5x
150（10≤x≤15，
且 x 为整数）；
（2）根据题意，得：w (x 10)(5x 150) 5x2 200x 1500 5(x 20)2 500 ，
舍去）；
Байду номын сангаас
函数的应用
（2）∵ a 3 ，∴ C(0, 3) ，∵ SABP SABC .∴ P 点的纵坐标为±3，
把 y 3 代入 y x2 2x 3 得 x2 2x 3 3 ，解得 x 0 或 x 2 ，
把 y 3 代入 y x2 2x 3 得 x2 2x 3 3 ，解得 x 1 7 或 x 1 7 ， ∴ P 点的坐标为 (2,3) 或 (1 7, 3) 或 (1 7, 3) ．
得 810 40x=0 ，解得 x 20.25 ．∴排队人数最多时是 490 人，全部考生都完成体温检测
需要 20.25 分钟．
（3）设从一开始就应该增加 m 个检测点，根据题意，得12 20(m 2) 810 ，解得 m 1 3 ． 8
∵ m 是整数，∴ m 1 3 的最小整数是 2．∴一开始就应该至少增加 2 个检测点． 8
【点睛】此题主要考查二次函数的图像与性质，解题的关键是熟知待定系数法的应用．
本课结束
2、函数动点问题 （1）函数压轴题主要分为两大类：一是动点函数图像问题；二是与动点、存在点、相似等有关的二次函数 综合题． （2）解答动点函数图像问题，要把问题拆分，分清动点在不同位置运动或不同时间段运动时对应的函数表 达式，进而确定函数图像；解答二次函数综合题，要把大题拆分，做到大题小做，逐步分析求解，最后汇总 成最终答案． （3）解决二次函数动点问题，首先要明确动点在哪条直线或抛物线上运动，运动速度是多少，结合直线或 抛物线的表达式设出动点的坐标或表示出与动点有关的线段长度，最后结合题干中与动点有关的条件进行计 算．
2020年中考数学考前专题复习——二次函数压轴专题 课件(共22张PPT)

2020年中考数学考前专题复习——二次函数压轴专题 课件(共22张PPT)


类型三 特殊三角形存在性问题
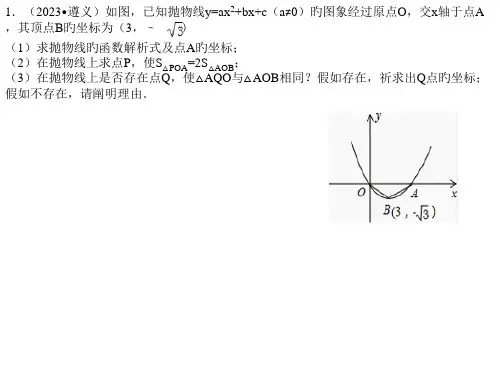
1. 如图，抛物线y＝x 2＋bx＋c（c＜0）与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，顶点 为D，且OB＝OC＝3．点E为线段BD上的一个动点，EF⊥x轴于F．
（1）求抛物线的解析式；
（2）是否存在点E，使△ECF为直角三角形？若存在，求点E的坐标；若不存在，请说明理由．
当x b 时, y最大值为 4ac b2
2a
4a
3、求解析式的三种方法
1、一般式：已知抛物线上的三点，通常设解析式为
_y_=__a_x_2_+_b_x_+__c_(a__≠_0)
2,顶点式：已知抛物线顶点坐标（h, k），通常
设抛物线解析式为__y__=_a_(_x_-_h_)_2+__k_(_a≠0)
变式一：
2. 如图，抛物线y＝x²＋(m＋2)x＋4的顶点C在x轴正半轴上，直线y＝x＋2与抛物线交于A，B两点 (点A在点B的左侧)． (1)求抛物线的函数表达式； (2)点P是抛物线上一点，若S△PAB＝2S△ABC，求点P的坐标； (3)将直线AB上下平移，平移后的直线y＝x＋t与抛物线交于A′、B′两点(A′在B′的左侧)，当 以点A′、B′、(2)中第二象限的点P为顶点的三角形是直角三角形时，求t的值．
A： y (x 4)2 6 C: y (x 2)2 2
B: y (x 4)2 2 D： y (x 1)2 3
5.二次函数与一元二次方程和不等式的关系
当b2 4ac 0时,方程ax2 bx c 0a 0有两个不相等的实数根；
x1,2 b
b2 4ac .
2a
当b2 4ac 0时,方程ax2 bx c 0a 0有两个相等的实数根:

中考专题复习 二次函数压轴题PPT


1 a b
中考┃ 代数计算题
a－3 例 3 [2014· 凉山州] 先化简，再求值： 2 ÷(a＋2－ 3a －6a 5 )，其中 a2＋3a－1＝0. a－2
【例题分层探究】 (1)分式运算中的除法一般转化为什么运算？ (2)必须知道未知字母的值时才能进行化简求值吗？
(1)在分式运算中的除法一般转化为乘法运算． (2)在进行化简时，若化去一些字母，可在已知其他字 母值的情况下求值；若能将条件中的关于字母的代数式整 体代入， 也可在不求未知字母的值的情况下直接代入求值．
1 3a（a＋3） 1 ＝ . 3（a2＋3a） 1 当 a2＋3a－1＝0，即 a2＋3a＝1 时，原式＝ . 3
中考┃ 代数计算题
（2011•泸州）计算： 计算：
探究三
泸州中考 代数的计算题
1.(2011年) 计算： 2.(2012年) 3.(2013年) 计算：
1 2 4.(2014年) 计算： 12 4sin 60 ( 2) ( ) 2
【解题方法点析】 在进行分式的化简求值时，有时可以不用求出未知字 母的值，而直接用整体代入的方法求得．
0
泸州中考┃ 代数计算题
．
探究三
．
泸州中考 代数的计算题
其中：
1.(2015年先化简，再求值) ：
2.(2016年) ： 3.(2016年先化简，再求值) ：
其中：a= 4.(2016年化简) ：
泸州中考┃ 代数计算题
代数的计算和化解题方法总结：
【解题方法点析】 熟记特殊锐角三角函数值，理解并掌握一个数的绝对值、 整数指数幂、 算术平方根的求法是解答实数与三角函数计算题 的关键．在计算过程中，先按照运算顺序进行分割，然后同时 计算可简化计算过程．

2019【中考语文】初三九年级数学复习课件：解答题专题—二次函数压轴题(一)(共28张PPT)


时与抛物线的交点坐标即为所求.
解：存在. ∵抛物线的解析式y=-x2+2x+3=-(x-1)2+4, ∴P(1,4),如解图②,过点P且与BC平行的直线与抛物线的交
点Q1，即为所求Q点之一，
∴可得直线BC为y＝-x+3， ∴过点P且与BC平行的直线l1为y=-x+b,将 点P(1，4)代入得l1的解析式为y＝-x+5， y＝-x+5 x2＝1 x1＝2 由 y＝-x2+2x+3 ，解得 ， ， 例2题解图② y2＝4 y1＝3 ∴点Q1的坐标为(2，3).
PD，PF的长，进而求出即可；(3)根据题意当P，E，F三点
共线时，PE＋PF最小，进而得出P点坐标以及利用△PDE的 面积可以等于4到13之间的所有整数，在面积为12时，a的 值有两个，进而得出答案． 【自主解答】
1 2 (1)抛物线的解析式为y＝－ 8 x ＋8.
(2)猜想正确．
1 2 理由：设P(x，－ x ＋8)， 8 1 则PF＝8－(－ x2＋8)＝ 1 x2. 8 8
∴“好点”共有11个．
二、典例精讲
类型二 面积问题
例2：如图，已知抛物线y=-x2+bx+c与x轴交于A(-1，0)， B(3，0)两点，与y轴交于点C，抛物线的对称轴与抛物线交
于点P、与直线BC相交于点M，连接PB.
(1)求该抛物线的解析式； (2)在(1)中位于第一象限内的抛物线上是否存在点D，使得 △BCD的面积最大？若存在，求出D点坐标及△BCD面积 的最大值；若不存在，请说明理由；
∵直线PM为直线x＝1，直线BC的解析式为y＝-x+3， ∴M(1，2). 设PM与x轴交于E点， ∵PM＝EM＝2，

初中数学华东师大九年级下册第章二次函数-二次函数压轴题修改版PPT


建立关系式 并计算
根据平行四边形的 性质或抛物线的对 称性·相似三角形的 性质·直角三角形的 性质等等建立方程 （组）的方法求解。
2017年成都
Part 6
类型 六
平行四边形存在性问题
在四川中考中： 广安、巴中，宜宾（2016,2017）
等地作为压轴题。
满分技巧
一般知道三点然后求第四点坐标这类题，进行分类讨论作为边或对 角线利用平行四边形对边平行且相等或对角线的性质，再结合抛物 线的对称性画出满足题意的图形。
类型 三
三角形形状及相似存在性问题
在2019年四川中考中： 成都市、泸州市、等作为压轴
题出现。
满分技巧
直角三角形 存在问题
①先确定直角的顶点 ②利用两点距离公式 得到三边平方建立方 程 ③利用与已知直角三 角形相似 ④腰或底分类，两定 点画圆
三角形相似 存在问题
①假设结论成立 ，找 出对应边，角进行分类 讨论 ②设未知数，求边长， 直接或间接设所求点的 坐标 ③建立关系式，并计算， 由相似性质得方程从而 求出点
预祝大家2020年 中考取得理想的成绩！
江安县汉安初级中学校 邓尚斌
Part 1
类型 一
线段数量关系与最值问题
在2019年四川中考中：
绵阳24 南充25 广安26 内江28 眉山26
满分技巧
2.两线一点型
1.一线两点型
2018年宜宾第二问题
2019年广安第二问题
2019年内江第二问题
Part 2
类型 二
面积数量关系与最值问题
在2019年四川中考中： 绵阳 攀枝花 内江 达州 乐山 泸州等
初中数学函数涉及到的常用公式或结论
初中数学函数涉及到的常用公式或结论
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

，解得：
，
故直线 AC 解析式为 y=﹣ x+3，
与抛物线解析式联立解得：
或
，
则点 D 坐标为（1， ）；
5
（3）存在，分两种情况考虑： ①当点 M 在 x 轴上方时，如答图 1 所示： 四边形 ADMN 为平行四边形，DM∥ AN，DM=AN， 由对称性得到 M（3， ），即 DM=2，故 AN=2，
10
解：（1）在直线解析式 y=x+4 中，令 x=0，得 y=4；令 y=0，得 x=﹣4， ∴ A（﹣4，0），B（0，4）． ∵ 点 A（﹣4，0），B（0，4）在抛物线 y=﹣x2+bx+c 上，
∴
，
解得：b=﹣3，c=4， ∴ 抛物线的解析式为：y=﹣x2﹣3x+4．
（2）设点 C 坐标为（m，0）（m＜0），则 OC=﹣m，AC=4+m． ∵ OA=OB=4，∴ ∠ BAC=45°， ∴ △ ACD 为等腰直角三角形，∴ CD=AC=4+m， ∴ CE=CD+DE=4+m+4=8+m， ∴ 点 E 坐标为（m，8+m）． ∵ 点 E 在抛物线 y=﹣x2﹣3x+4 上， ∴ 8+m=﹣m2﹣3m+4，解得 m=﹣2． ∴ C（﹣2，0），AC=OC=2，CE=6，
课程标题 二次函数综合题
1
二次函数压轴题设想
Ø第（1）问是求直线或抛物线的解析式 Ø第（2）（3）问是抛物线与几何结合 的问题
常见形式有以下类型
2
抛物线与几何结合常见形式：
①四点构成的四边形是平行四边形
四点构成的四 ②四点构成的四边形是菱形
边形
③四点构成的四边形是正方形
④四点构成的四边形是矩形
⑧求四边形的面积或最大面积
⑤以某三点构成的三角形与某个三角形 相似
三点构成的三 ⑥某三点构成等腰三角形 角形 ⑥某三点构成直角三角形
⑦某三角形的面积或最大面积
⑨两线段的和最小 两线段的和
⑩三角形的周长最小
直线与圆的位 置关系
⑾过某三点的圆与某条直线的位置关系
求点的坐标 或最大面积
证明
3
2、（2013•昆明压轴题）如图，矩形 OABC 在平面直角坐标系 xOy 中，点 A 在 x 轴的正半轴上，点 C 在 y 轴的正半轴上，OA=4，OC=3，若抛物线的顶点在 BC 边上，且抛物线经过 O，A 两点，直线 AC 交抛物线于点 D． （1）求抛物线的解析式； （2）求点 D 的坐标； （3）若点 M 在抛物线上，点 N 在 x 轴上，是否存在以 A，D，M，N 为顶点 的四边形是平行四边形？若存在，求出点 N 的坐标，△ ACE 的面积最大，此时 x= 5 ，y=﹣ 3 ，
2
4
∴ 点 E 的坐标为（ 5 ，﹣ 3 ）， 24
设过点 E 的直线与 x 轴交点为 F，则 F（ ，0），∴ AF= ﹣1= 9 ， 4
∵ 直线 AC 的解析式为 y=x﹣1，
∴ ∠ CAB=45°，
7
解：（1）∵ 抛物线 y=ax2+bx+3 经过点 A（1，0），点 C（4，3），
∴
，解得
，
所以，抛物线的解析式为 y=x2﹣4x+3；
（2）∵ 点 A、B 关于对称轴对称， ∴ 点 D 为 AC 与对称轴的交点时△ BCD 的周长最小， 设直线 AC 的解析式为 y=kx+b（k≠0），则，
4
解：（1）设抛物线顶点为 E，根据题意 OA=4，OC=3，得：E（2，3）， 设抛物线解析式为 y=a（x﹣2）2+3，
将 A（4，0）坐标代入得：0=4a+3，即 a= 3 ， 4
则抛物线解析式为 y= 3 （x﹣2）2+3= 3 x2+3x；
4
4
（2）设直线 AC 解析式为 y=kx+b（k≠0），则
∴ 点 F 到 AC 的距离为 9 × = ， 4
又∵ AC=
=3 ，
∴ △ ACE 的最大面积=×3 × = ，此时 E 点坐标为（ 5 ，﹣ 3 ）．
24
9
7、（2013•曲靖压轴题）如图，在平面直角坐标系 xOy 中，直线 y=x+4 与坐标轴分别交 于 A、B 两点，过 A、B 两点的抛物线为 y=﹣x2+bx+c．点 D 为线段 AB 上一动点，过 点 D 作 CD⊥x 轴于点 C，交抛物线于点 E． （1）求抛物线的解析式． （2）当 DE=4 时，求四边形 CAEB 的面积． （3）连接 BE，是否存在点 D，使得△ DBE 和△ DAC 相似？若存在，求此点 D 坐标； 若不存在，说明理由．
解得
，
所以，直线 AC 的解析式为 y=x﹣1，
∵ y=x2﹣4x+3=（x﹣2）2﹣1，
∴ 抛物线的对称轴为直线 x=2，
当 x=2 时，y=2﹣1=1，
∴ 抛物线对称轴上存在点 D（2，1），使△ BCD 的周长最小；
8
（3）如图，设过点 E 与直线 AC 平行线的直线为 y=x+m，联立， 消掉 y 得，x2﹣5x+3﹣m=0， △ =（﹣5）2﹣4×1×（3﹣m）=0，
S 四边形 CAEB=S△ ACE+S 梯形 OCEB﹣S△ BCO= ×2×6+ （6+4）×2﹣ ×2×4=12．
∴ N1（2，0），N2（6，0）； ②当点 M 在 x 轴下方时，如答图 2 所示：
过点 D 作 DQ⊥x 轴于点 Q，过点 M 作 MP⊥x 轴于点 P，可得△ ADQ≌ △ NMP， ∴ MP=DQ= ，NP=AQ=3，
将 yM=﹣ 代入抛物线解析式得：﹣ =﹣ x2+3x，
解得：xM=2﹣ 或 xM=2+ ， ∴ xN=xM﹣3=﹣ ﹣1 或 ﹣1， ∴ N3（﹣ ﹣1，0），N4（ ﹣1，0）． 综上所述，满足条件的点 N 有四个：N1（2，0），N2（6，0），N3（﹣
﹣1，0），N4（
6
﹣1，0）．
5、（2013•新疆压轴题）如图，已知抛物线 y=ax2+bx+3 与 x 轴交于 A、B 两 点，过点 A 的直线 l 与抛物线交于点 C，其中 A 点的坐标是（1，0），C 点 坐标是（4，3）． （1）求抛物线的解析式； （2）在（1）中抛物线的对称轴上是否存在点 D，使△ BCD 的周长最小？若 存在，求出点 D 的坐标，若不存在，请说明理由； （3）若点 E 是（1）中抛物线上的一个动点，且位于直线 AC 的下方，试求 △ ACE 的最大面积及 E 点的坐标．