高斯定理[4]

三、高斯定理(Gauss theorem )
高斯简介 高斯（Carl Friedrich Gauss 1777~1855）
高斯长期从事于数学并将数学应用于物理学、 天文学和大地测量学等领域的研究，主要成就： (1)物理学和地磁学：关于静电学、温差电和 摩擦电的研究、利用绝对单位（长度、质量和时 间）法则量度非力学量以及地磁分布的理论研究。 (2)光学 ：利用几何学知识研究光学系统近 轴光线行为和成像，建立高斯光学。 (3)天文学和大地测量学中：如小行星轨道的 德国数学家、 计算，地球大小和形状的理论研究等。 天文学家和物理 (4)试验数据处理：结合试验数据的测算，发 学家。高斯在数 展了概率统计理论和误差理论，发明了最小二乘 学上的建树颇丰， 法，引入高斯误差曲线。 有“数学王子” (5)高斯还创立了电磁量的绝对单位制。 15 美称。
i内 i内
e
• 闭合曲面上各点的场强 E 是闭合面内、外全部电荷共同
q
i内
产生的合场强，而非仅由闭合面内电荷所产生。
E 表面
q
i内

q
i外
• 闭合面外的电荷对总通量无贡献。 • 高斯定理适用于静电场和运动电荷的电场，是电磁场基 本规律之一。 • 静电场是有源场。电力线起始于正电荷，终止于负电荷 。
轴对称分布：包 括无限长均匀带 电的直线，圆柱 面，圆柱壳等；
无限大平面电荷： 包括无限大的均 匀带电平面，平 板等。
步骤：
1.进行对称性分析，即由电荷分布的对称性，分析场强分 布的对称性，判断能否用高斯定理来求电场强度的分布 （常见的对称性有球对称性、轴对称性、面对称性等）； 2.根据场强分布的特点，作适当的高斯面，要求： ①待求场强的场点应在此高斯面上， ②穿过该高斯面的电通量容易计算。 一般地，高斯面各面元的法线矢量n与E平行或垂直，n与 E平行时，E的大小要求处处相等，使得E能提到积分号外 面； 3.计算电通量和高斯面内所包围的电荷的代数和，最后由高 斯定理求出场强。

证明方法
高斯定理的证明通常基于库仑定律、电场线性质和微积分等 基本原理。通过选择适当的闭合曲面和运用微积分中的高斯 公式，可以推导出高斯定理。
推导过程
首先，根据库仑定律，电场线从正电荷发出，终止于负电荷 或无穷远处。然后，通过选取适当的闭合曲面，将电荷包围 在其中，运用高斯公式和高斯定理的推导过程，最终得到高 斯定理的数学表述。
要点一
总结词
高斯定理在其他领域也有广泛的应用，如电场、量子力学 、光学等。
要点二
详细描述
高斯定理在电场中可以用来计算电场的分布和强度，以及 电通量的计算等问题。在量子力学中，高斯定理可以用来 研究波函数的性质和演化。在光学中，高斯定理可以用来 研究光场的分布和强度，以及光通量的计算等问题。
05
高斯定理的扩展和深化
磁场中的应用
总结词
高斯定理在磁场中也有广泛的应用，它可以 帮助我们理解和计算磁场的分布和强度。
详细描述
在磁场中，高斯定理可以用来计算球形区域 内磁场的分布和强度，通过球面上的磁场强 度的积分可以得到球内的磁场。此外，高斯 定理还可以用来研究磁场线的闭合性质，以 及磁通量的计算等问题。
其他领域的应用
引力场中的应用
总结词
高斯定理在引力场中也有重要的应用，它可以帮助我们理解和计算引力场的分布和强度。
详细描述
在引力场中，高斯定理可以用来计算球形区域内物质的质量分布，通过球面上的引力场强度的积分可以得到球内 的质量。此外，高斯定理还可以用来研究引力场的空间分布，通过球面上的引力场强度的分布，可以推导出球内 引力场的分布情况。
高斯定理的应用条件
适用范围
高斯定理适用于任何线性、非自相互作用、电荷连续分布的电场。对于非线性、 自相互作用或离散分布的电荷，高斯定理可能不适用。

∫
思考： 电量分布 均匀？ 圆环、圆 弧？
[例4] 平行板电容器两板间的电势差 解：平行板电容器内部的场强为 两板间的电势差
ΔU =
( )
+
σ E= ε0
σ
r E d
σ
∫) (
r r E dl
=
∫ )Edl = (
+
( )
E
∫ )dl (
+
( )
r r E , dl
方向一致
均匀场
ΔU = Ed
r dl
R1
λ2 λ1
U2 U1
当R1 <r<R2时,
U2 =
λ1 R2 = ln 2πε 0 r
∫
R2
p
∫
R2
r
λ1 dr 2πε 0 r
R1 O

R2
当r>R2时
U3 =
= ∫
r
R2
λ 1 + λ 2 dr λ 1 + λ 2 R2 = ln 2πε 0 r 2πε 0 r
∫
R2
r r E dl
p
v v = ∫ E dr
4) 电势叠加原理 Ui = 1 qi 4πε0 ri
对点电荷系有
U P = ∫ E d l = ∫ E1 d l + ∫ E2 d l + L + ∫ Ek d l + L = U P1 + U P 2 + L + U Pk + L = ∑U pi
P P P P
∞
∞
∞
∞
对连续带电体有 U = P
∞
如图
R ∞

①待求场强的场点应在此高斯面上，
②穿过该高斯面的电通量容易计算。
一般地，高斯面各面元的法线矢量n与E平行或垂直， n与E平行时，E的大小要求处处相等，使得E能提到 积分号外面；
3.计算电通量和高斯面内所包围的电荷的代数和， 最后由高斯定理求出场强。
高斯定理的应用
高斯定理的应用举例
条件： 电荷分布具有较高的空间对称性 1. 均匀带电球面的电场 2. 均匀带电球体的电场 3. 均匀带电无限大平面的电场 4.均匀带电无限长直线的电场 5. 均匀带电无限长圆柱面的电场 6. 均匀带电球体空腔部分的电场
轴对称分布：包 括无限长均匀带 电的直线，圆柱 面，圆柱壳等；
无限大平面电荷： 包括无限大的均 匀带电平面，平 板等。
步骤：
1.进行对称性分析，即由电荷分布的对称性，分 析场强分布的对称性，判断能否用高斯定理来求 电场强度的分布（常见的对称性有球对称性、轴 对称性、面对称性等）； 2.根据场强分布的特点，作适当的高斯面，要求：
•当闭合曲面上各点 E =时0，通过闭合曲面的电通量 反之e , 0
不一定成立. •高斯定理中所说的闭合曲面，通常称为高斯面。
电通量计算
四、高斯定律应用举例
当场强分布具有某种特殊的对称性时，应用高斯定 理能比较方便求出场强。求解的关键是选取适当的 高斯面。常见的具有对称性分布的源电荷有：
球对称分布：包括 均匀带电的球面， 球体和多层同心球 壳等
强分布
S
解：以带电直导线为轴，作一个通过P
点，高为h的圆筒形封闭面为高斯面 S。
eSEdS
h
O
E
rp
侧 面 E d S 上 E d S 下 E d S
其中上、下底面的电场强度方向与面平行，

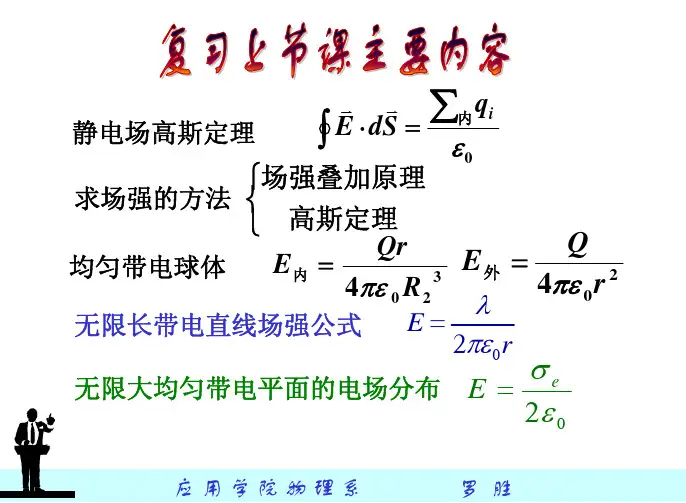
电场的高斯定理及其应用1. 高斯定理的背景高斯定理，也称为高斯电场定理，是电磁学中的基本定律之一。

它描述了电场通过任意闭合曲面的电通量与该闭合曲面内部的总电荷之间的关系。

这个定理是由德国数学家和物理学家卡尔·弗里德里希·高斯在19世纪初期提出的。

高斯定理在电磁学、物理学和工程学等领域有着广泛的应用。

2. 高斯定理的数学表述高斯定理的数学表述如下：对于任意闭合曲面S，电场通过S的电通量（记作ΦE）与曲面S内部的总电荷（记作q）之间存在以下关系：ΦE = ∫∫S E·dA = q / ε₀其中，E是电场强度，dA是曲面元素的面积向量，ε₀是真空的电介质常数（也称为电常数），其值约为8.85×10^-12 C2/N·m2。

3. 高斯定理的物理意义高斯定理的物理意义可以从两个方面来理解：（1）电场线与闭合曲面的关系：高斯定理说明，对于任意闭合曲面S，电场线通过S的电通量等于曲面S内部的总电荷。

这意味着，无论曲面S如何选择，只要它是闭合的，电场线穿过它的总通量都与曲面内部的电荷有关，而与曲面的形状和位置无关。

（2）电场的分布与电荷的关系：高斯定理表明，电场是通过闭合曲面的电通量的度量，而电通量与曲面内部的总电荷成正比。

这意味着，电场的强度和分布与曲面内部的电荷量有关，而与曲面的具体形状和位置无关。

4. 高斯定理的应用高斯定理在电场分析和计算中有着广泛的应用，下面列举几个常见的应用例子：（1）计算静电场中的电荷分布：通过高斯定理，可以计算静电场中某个闭合曲面内的电荷分布。

只需测量通过该曲面的电通量，然后根据电通量与电荷的关系，可以确定曲面内部的电荷量。

（2）设计电容器和绝缘材料：在电容器和绝缘材料的设计中，高斯定理可以用来分析电场的分布和电荷的积累。

通过合理选择闭合曲面的形状和位置，可以优化电场分布，提高电容器的性能和绝缘材料的可靠性。

（3）研究电磁波的传播：在研究电磁波的传播过程中，高斯定理可以用来分析电磁波在不同介质中的电场分布和电荷的变化。

高斯定理表达式及其物理意义
高斯定理：在一个封闭的曲面上，任意一点外部电荷的积分等于曲面内部电荷的积分。

高斯定理是由德国数学家卡尔·马克斯·费马于1813年发现的，它是电动势的基本定理，是研究电场的基础。

它有着极其重要的物理意义，是电磁理论的基础。

高斯定理的物理意义是：在一个封闭的曲面上，任意一点外部电荷的积分等于曲面内部电荷的积分。

高斯定理是一个重要的数学定理，它的公式表达为：∮⃗E⋅d⃗s=q/ε，其中，∮⃗E⋅d⃗s是曲面上某一点外电荷的电场积分，q是曲面内部电荷的总量，ε是介电常数。

这一定理可以用来研究电场及其相关问题，可以用来计算电场的强度、电势等。

换句话说，高斯定理告诉我们，在一个封闭的曲面上，外部电荷的积分等于曲面内部电荷的积分，这一定理是计算电场强度、电势等问题的重要依据。

高斯定理还可以用来研究磁场及相关问题，它可以用来计算磁场的强度、磁势等。

其公式表达为：∮⃗B⋅d⃗s=μq/ε，其中，∮⃗B⋅d⃗s是曲面上某一点外磁荷的磁场积分，μ是磁导率，q是曲面内部磁荷的总量，ε是介电常数。

高斯定理可以用来研究电场、磁场的强度、电势、磁势等，它的物
理意义是：在一个封闭的曲面上，任意一点外部电荷或磁荷的积分等于曲面内部电荷或磁荷的积分。

高斯定理是电磁理论的基础，是研究电磁场的重要依据。

q1
q1 + q 2
ε0
∫∫ E ⋅ dS = ε
S3
q2
0
四 利用高斯定律求静电场的分布 四 利用高斯定律求静电场的分布
高斯定理的一个重要应用，是用来计算带电体周围电场的电 场强度。实际上，只有在场强分布具有一定的对称性时，才 能比较方便应用高斯定理求出场强。求解的关键是选取适当 的高斯面。常见的具有对称性分布的源电荷有：
S
q
2、 高斯定理：
通过任意闭合 曲面S的电通量 S面包围的 电荷的代数和
r r 1 若S内的电荷是连续分布： Φ e = E ⋅ dS = ∫ ρ ⋅ dV ∫ ε
oV
r r 1 即：Φ e = ∫ E ⋅ dS =
εo
∑q
S内
i
用电通量表示的电场与场源电荷关系的规律。
说明
1º 定理中E是所取的封闭面S（高斯面）上的场强， 它是由全部电荷（S内、外）共同产生的合场强。 2º Φe只决定于S面包围的电荷，S面外的电荷对Φe 无贡献。 3° 高斯定律的物理意义： 给出了静电场的重要性质 ——静电场是有源场 ∑ qi > 0 Φ e > 0 电场线穿出 正负电荷就是场源 ∑ qi < 0 Φ e < 0 电场线穿入
σ E = 2ε 0
+σ
E= σ 2ε o
−σ
均匀场 r
E
讨论： +σ − σ
E = 0 E= σ E = 0 εo
+σ
+σ
−σ −σ
E = σ E=0 E = σ εo εo
E = σ E=0 E = σ εo εo
例6.11 求均匀带电球面的电场分布。 r r 1 Φe = ∫ E ⋅ dS = 设半径为R，电量为+q。 εo 解：取以r为半径的同心高斯球面S

电场的高斯定理的内容
电场的高斯定理是电场学中的一条基本定理，它描述了电场通过一个闭合曲面的总电通量与该闭合曲面内电荷的关系。

具体来说，高斯定理表明，通过一个闭合曲面的电场总通量等于该闭合曲面内所有电荷的代数和与真空介电常数的乘积。

设闭合曲面为S，电场矢量为E，闭合曲面内的电荷分布为ρ，则根据高斯定理有公式：
∮S E·dS = 1/ε0 ∫∫∫V ρ dV
其中，∮S表示对闭合曲面S的面积分，E·dS表示电场E沿曲面S的方向的分量与面积元素dS的点积，∫∫∫V表示对闭合曲面内的体积V进行体积分，ρ表示电荷密度，ε0表示真空介电常数。

根据高斯定理，当闭合曲面内没有电荷时，即所有电荷的代数和为零（或称为等效于零电荷），则通过闭合曲面的电场总通量为零；当闭合曲面内存在电荷时，通过闭合曲面的电场总通量与该闭合曲面内电荷的代数和成正比，且与真空介电常数成反比。

通过高斯定理，我们可以简化求解电场的问题，将复杂的分布电荷情况转化为求闭合曲面内电荷的代数和，从而简化计算。

高斯定理在电场和电荷分布的研究中具有广泛的应用，为分析和解决与电场有关的问题提供了有力的工具。

1
4π0
q r3
rdS
e
S de
q
q
dS
S 4π0r 2
4π0r 2
dS q
S
0
Φe 与r 无关q ，也就是说，无论高斯面多大，总 电通量都为 0 ，即通过各球面的电力线总条数相 等。 说明点电荷的电力线可以延伸到无限远处。 9
2. 点电荷在任意封闭曲面内
穿过球面S1和S2的电场线，必定也穿 过闭合曲面S。所以穿过任意闭合曲
e ES cos 或 e E S
S cos
(3) 非均匀电场强度电通量
de E dS
通过任一曲面S 的电通量：
e de EdS
S
S
5
思考题：电场线与电通量的区别
(4) 任意闭合曲面的电通量：
e d e E dS
S
S
一个闭合曲面把整个空间分割成两部分： 内部空间和外部空间
外法线矢量：指向曲面外部空间的法线矢量 内法线矢量：指向曲面内部空间的法线矢量
S2
S
E
面 S的电通量必然为q/ 0 ，即
q S1
Φe
s
Ev dSv
q
0
• 点电荷为-q时，通过任意闭合曲面的电通量
Φe
S
Ev
dSv
q
0
电场线是穿入闭合曲面的。
10
3. 任意闭合曲面S包围多个点电荷q1、q2、…、qn 根据电通量的定义和电场强度的叠加原理，其电通
量可以表示为
Φe
E
S
dS
(E1
其实高斯定理不仅适用于静电场，还可用于变化的电 场，比库仑定律更广泛，是Maxwell方程组之一
16

详解高斯定理高斯定理（Gauss theorem），矢量分析的重要定理之一。

它给出，矢量场通过任意闭合曲面的通量（面积分）等于该矢量场的散度在闭合曲面所包围体积内的积分（体积分）。

如果通量恒为零，则矢量场是无源场亦称无散场；如果通量可以不为零，则矢量场是有源场亦称有散场。

高斯定理是比较、区别各种矢量场特征的重要手段之一。

在静电学中，表明在闭合曲面内的电荷之和与产生的电场在该闭合曲面上的电通量积分之间的关系。

高斯定律（Gauss' law）表明在闭合曲面内的电荷分布与产生的电场之间的关系。

高斯定律在静电场情况下类比于应用在磁场学的安培定律，而二者都被集中在麦克斯韦方程组中。

因为数学上的相似性，高斯定律也可以应用于其它由平方反比律决定的物理量，例如引力或者辐照度。

穿过一封闭曲面的电通量与封闭曲面所包围的du电荷量成正比。

换一种说法就是，电场强度在一封闭曲面上的面积分与封闭曲面所包围的电荷量成正比。

由于磁力线总是闭合曲线，因此任何一条进入一个闭合曲面的磁力线必定会从曲面内部出来，否则这条磁力线就不会闭合起来了。

如果对于一个闭合曲面，定义向外为正法线的指向，则进入曲面的磁通量为负，出来的磁通量为正，那么就可以得到通过一个闭合曲面的总磁通量为0。

这个规律类似于电场中的高斯定理，因此也称为高斯定理。

高斯定理的适用范围：1、高斯定理适用于任何静电场。

2、高斯定律（Gauss“law）表明在闭合曲面内的电荷分布与产生的电场之间的关系。

高斯定律在静电场情况下类比于应用在磁场学的安培定律，而二者都被集中在麦克斯韦方程组中。

3、因为数学上的相似性，高斯定律也可以应用于其它由平方反比律决定的物理量，例如引力或者辐照度。

非均匀电场强度电通量
dS dS en dΦe E dS
en
E dS
E
dS

E
Φe dΦe E cosdS s Φe E dS s
E ds EdS cos 0 E ds EdS cos 0
球对称分布：包 括均匀带电的球 面，球体和多层 同心球壳等
轴对称分布：包 括无限长均匀带 电的直线，圆柱 面，圆柱壳等；
无限大平面电荷： 包括无限大的均匀 带电平面，平板等。
关键：选取高斯面
电场分布的对称性分析 选取适当的高斯面
一般原则是： ①高斯面要通过所求场强的点 ②高斯面上（部分面上）各点的E(大小)=常量； 且 方向与曲面处处成 一定的角度，即 cos 为定值,从而使积分简化为: e E cosdS E cos dS
取长 L 的同轴圆柱面，加上底、下底构成高斯面 S
S

dq
L
r
P
' dE dE
o dq
'
' dE dE
E dS E dS
S 上
下
E dS
侧
E dS

上
E cos

2
dS E cos
下

2
dS E cos 0 dS
闭合曲面
闭合曲面的电场强度通量
E
S
Φe E dS E cosdS
S S
dΦe E dS
dS
E
解： e E ds E ds E ds E ds

电学高斯定理全文共四篇示例，供读者参考第一篇示例：电学高斯定理是电学领域中的重要定理之一，它描述了电场的性质与电荷之间的关系。

高斯定理的提出者是德国数学家卡尔·弗里德里希·高斯，他在通过对电场分析的基础上，发现了电场的一种非常有用的特性，这就是高斯定理。

电学高斯定理是电场理论的基石之一，它提供了一种简单而优雅的方法来计算静电场中的电荷分布和电场强度。

高斯定理描述了一个有无限小体积的闭合曲面，其内部电荷的总电量等于曲面上的电荷总和乘以一个常数，即真空介电常数乘以电场的通量。

高斯定理的数学形式如下：\[\oint\limits_S \vec{E} \cdot d\vec{A} =\frac{Q_{enc}}{\varepsilon_0}\]\(\oint\limits_S \vec{E} \cdot d\vec{A}\)表示电场强度在闭合曲面S上的通量，\(d\vec{A}\)表示曲面元素的面积微元，它与曲面的法线方向一致，\(Q_{enc}\)表示闭合曲面S内部的电荷总量，\(\varepsilon_0\)表示真空介电常数。

高斯定理的物理意义在于，它告诉我们，一个闭合曲面的电场通量只取决于曲面内部的电荷分布，与曲面的具体形状和大小无关。

这使得高斯定理成为了电场分布的计算利器，在许多问题的求解中起到了至关重要的作用。

举个简单的例子来说明高斯定理的应用。

假设我们有一个均匀带电的无限长线段，电荷密度为\(\lambda\)，现在我们希望确定距离这个线段距离为r处的电场强度。

我们可以选取一个半径为r的闭合球面，这个球面的中心位于线段上，利用高斯定理可以得到线段上的电荷等于球面包围电荷的总和，即：\[Q_{enc} = \lambda \cdot 2\pi r\]根据高斯定理，我们可以得到球面上的电场通量等于：如果我们假设球面上的电场强度与球面法线方向垂直，并且与球面上的法向面积元素大小相等，那么可以将上式简化为：解得电场强度为：这就是距离带电线段距离为r处的电场强度。

求 电场强度分布。 解 电场强度垂直带电平面, 选取 垂直带电面的圆柱形高斯面 S e E dS E dS E dS E dS
侧 左底 右底

0
左底
E dS E dS
右底
0 E1S E2 S
• q 在球心处，球面电通量为
dS
e E dS EdS E dS
S
S
S

q 4 π 0r
2
4π r
2
q
q
r
0
穿过球面的电力线条数为 q/ 0
• q 在任意闭合面内，电通量为 • q 在闭合面外，电通量为
e q / 0
e 0
穿出、穿入闭合面电力线条数相等
5.4 电通量
一、电力线（电场线） E
dN
高斯定理
场强方向沿电力线切线方 向，场强大小取决于电力 线的疏密
+
-
dS
dN E dS
• 电力线起始于正电荷
（或无穷远处），终止 于负电荷（或无穷远 处）。 • 电力线不相交。
二、电通量
穿过任意曲面的电力线条 数称为通过该面的电通量 1. dS 面元的电通量

E 由所有电荷决定，但 e EdS 与外部电荷无关,只
取决于内部电荷。
0
q1

0
q2

0
q3

1
0
q内
静电场高斯定理
1 e E dS
S
0
q内
真空中的任何静电场中，穿过任一闭合曲面的电通量，等
于该曲面所包围的电荷电量的代数和乘以 1 0

通量仅由面内电荷决定。
27
3、高斯定理的意义 1 e E dS
S
0
q
i
i
(1) 说明静电场是有源场，源即电荷。
q 0, e 0 , 电场线从+q 出发，+q 是源头； q 0, e 0 , 电场线止于 - q ， - q 是尾闾。
(2) 高斯定理不仅适用于静电场， 亦适用于运动电荷的电场和随时间变 化的电场，是电磁场基本定理之一。
其中， E ：电场强度， P ：电极化强度
18
其中， 0 —— 真空中的介电常数 12 ( 8.854 10 F / m)(电容率) —— 介质的介电常数 ( 0 r ) (电容率) r —— 介质的相对介电常数 ( 1 e )(相对电容率)
e
利用高斯定理求场强 E 比较方便。
(2) 常见的具有对称性分布的电荷系统：
1） 球对称（球体，球面）；
2） 柱对称（无限长柱体，无限长柱面）； 3） 面对称（无限大平板，无限大平面）。
30
(3) 求电场分布的步骤：
1) 分析带电系统的对称性； 2) 选合适的高斯面：使面上场强的大小处处 相等(或部分 相等，部分为零），场强的方 向与曲面正交或平行。 3) 利用高斯定理求场强。
—— 介质的电极化率
0
SI单位： r 、e ：(纯数)
、 0 ：C2/Nm2
(F/m)
19
介 真空 空气
质
r
1 1.00059
变压器油
瓷
2.24
68
玻璃
钛酸钡
510
103104
20
性质
(1) D是辅助物理量, E 才是真实物理量。 (2) D是一个包含了场与介质极化两种性质的量。 (3) D 线只由自由电荷决定。

0
z
2 rhE h 0
E
2 0 r
+
+
r h
+
+o
x+
E
y en
35
例4 无限大均匀带电平面的电场强度
无限大均匀带电平面，单位面积上的电荷，即电
r 荷面密度为 ， 求距平面为 处的电场强度.
解 对称性分析：E垂直平面
选取闭合的柱形高斯面
E
dS
S＇
S
0 底面积
2S＇E S＇
E
S＇
0
S＇ E
10
规定：法线的正方向为指向闭合曲面的外侧。
例1 如图所示 ，有一
个三棱柱体放置在电场强度 E 200i N C1的匀强电
场中 . 求通过此三棱柱体的 电场强度通量 .
y
o
z
E
x
11
解 Φe Φe前 Φe后
Φe左 Φe右 Φe下
Φe前 Φe后 Φe下
s
E
dS
0
y
P
N
ezn
o
M
en
E
en
= 0，不一定面内无电荷，有可能面内电荷等量异号。 = 0，不一定高斯面上各点的场强为 0。
25
qi 0 e 0
表明电力线从正电荷发出，穿出闭合曲面, 所以正电荷是静电场的源头。
qi 0 e 0
表明有电力线穿入闭合曲面而终止于负电荷， 所以负电荷是静电场的尾。
静电场是有源场
26
球壳 . 求球壳内外任意点的电场强
度. 解（1）0 r R
E dS 0 S1
E0
（2） r R
r S +

解： （1）自由电荷所产生旳场强（在真空中）为
E0
σ0 ε0
9.0 106 8.85 1012
1.02 106 V/m
(2)
由
E
E0 εr
εσrε00
σ0 ε
可知电介质内的场强为
E
σ0 ε
9.0 106 3.5 1011
2.57 105
V/m
（3）极化电荷面密度为：
0
0
3.5 1011 8.85 1010 3.5 1011
有电介质时旳高斯定理得（注意导体中
D=0）：
D dS S2
D dS
右底面
D1 A
A
与前面的式子相比较， 有D1 D2
+ +
S2
利用 D1 1E1 ，D2 2 E2 ，可求得：
E1
1
r1 0
,
E2
2
r 2 0
（2）正、负两极板间旳电势差为：
U
E1d1
E2d2
(d1 1
E1 E2
S D dS D S 0 S
D＝ 0
E1
D
1
0 0 r
E2
D
0
0 0
U
E1
d 2
E2
d 2
0d 2 0 r
0d 2 0
0d 0
r 1 2 r
3 5 U0
C1
Q1 U1
2 r 0 S
d
C2
Q2 U2
2 0 S
d
C1，C2串联：
C
C1C2 C1 C2
5 3 C0
由前面知：
例6、同轴电缆半径分别为R1和R2，其间充斥电介质 r1,，r2 ，

r<R
电量 ∑ qi = 0 由高斯定理 电量
P
r>R
∑q
i
= lλ
由高斯定理
E=0
λ E = 2π ε0 r
关于电通量
高斯定理的练习 1 Φ e = ∫ E • ds = ∑ qi
s
ε0
教材：P164 例1 P169 例2 P170例3 例4 P190 5-2 5-14 5-15 5-17 5-18 5-19 5-20 5-21
例.如图所示，一个带电量为 q 的点电荷位于正立方体的 A 角 上，则通过侧面 abcd 的电场 强度通量等于：
a
d
A
q
（A）q /6ε0 ; （B）q /12ε0 ； （C）q /24ε0 ; （D）q /36ε0 .
q
●q
●q
c
b
位于中 心 位于一顶点
过每一面的通量
[C] 若将此电荷移到正方体的一个顶点上，则通过整个正 方体表面的电场强度通量为 。q 8ε 0
3 r ρ 4 π 高斯定理 E 4 πr 2 = ε0 3
∑ qi ε0
ρr qr q 场强大小 E = = 场强大小 E = 3 4 πε 0 r 2 3ε 0 4 πε 0 R
q
∴E =
q e 2 r 4π ε0 r
r≥R
r≤R
oo RR
1 qr e, E= 3 r 4π ε0 R
5-4
电场强度通量
电场中的高斯定理
Eb
一．电场线（电场的图示法） c b 1、 E 方向：切线 E ∆N E a 2、 电场强度大小 E = ∆S a ⊥ 性质：不闭合；不相交； 定义：面积矢量 起于正、止于负。 S = Sn n 为面积的法向 闭合曲面的方向: 由曲面内指向曲面外 n n n n