磁场中的高斯定理.
- 格式:pdf
- 大小:77.17 KB
- 文档页数:5

磁场高斯定理
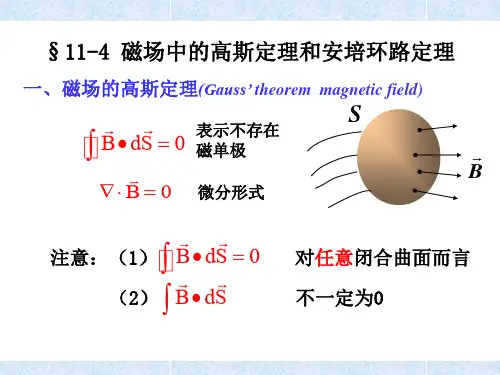
磁场的高斯定理是磁场理论中的一个重要定律,它表述为:磁场中通过任一封闭曲面的磁通量一定为零。
这里,磁通量表示的是通过某个曲面的磁感线的数量,磁感线是用来表示磁场分布的线。
高斯定理告诉我们,不论磁场如何分布,无论曲面如何取向,只要它是封闭的,通过这个曲面的磁通量总是为零。
这个定理反映了磁场的无源性质。
在磁场中,没有类似于电荷这样的源,磁场线是闭合的,从一处出发的磁场线会形成闭合回路,不会像电场线那样从一个正电荷出发终止于一个负电荷。
因此,磁场线不会从一个地方出发而终止于另一处,这就意味着磁场线不会穿越一个封闭的曲面,导致磁通量恒为零。
与静电场的高斯定理相比,磁场的高斯定理体现了磁场的本质差异。
在静电场中,由于电荷的存在,电场线会从正电荷出发终止于负电荷,因此,通过一个封闭曲面的电通量可以不为零。
而磁场的高斯定理表明磁场是无源的,不存在孤立的磁荷,磁场线总是闭合的。
这个定理在磁场的实际应用中具有重要意义,例如在电磁感应、磁场的能量传递等方面都是基于磁场的高斯定理的原理。
通过理解和应用磁场的高斯定理,我们可以更好地理解和预测磁场的行为和作用。
1。



磁场的高斯定理表达式及其物理意义
高斯定理是物理学中最重要的定理之一,它是了解和研究磁场的重要基础。
高斯定理表达式被记作Phi(φ=)div B,其中φ是称为磁智的标量场函数,B代表磁场矢量。
简而言之,高斯定理可以说是一条用标量变量来描述磁场矢量大小和方向的定理。
高斯定理的物理意义在于表明,任何一个磁场矢量的总收入(即磁智的总和)等于该磁场矢量离开所在区域的总产出(即磁智的总和)。
这是在集中于磁力线构造中得出的,其中磁力线是由围绕磁场产生和维护的磁场中出现的“线”现象。
既然这个定理反映了磁力线的物理性质,那么我们也可以得出这样的结论:一个区域内的磁场矢量不能有总的流动,因为它的总收入和总产出必须相等。
因此,高斯定理的结果揭示了磁力线的构造,以及磁场的分布特性,是磁场研究的重要理论依据。
高斯定理对于了解磁场扩散、收集和聚集的基本规律有着重要的价值,从而有助于我们正确控制和保护磁场。
因此,高斯定理为高等学校中物理学习提供了一个基本的理论基础,是可解释和预测磁场分布和行为的重要方法。

恒定磁场高斯定理公式
恒定磁场高斯定理:
1. 定义:恒定磁场高斯定理是物理学中一种物理学定理,其主要涉及
到磁场如何影响物体,及磁场是如何分布的。
2. 原理:恒定磁场高斯定理称为「磁产生定律」,这个定律表明:磁
场的强度、施加力的大小和物体的深度之间的关系是简单的高斯模型,即在空间上,磁场的强度衰减率满足高斯型模型,而不是简单的正弦
型模型。
3. 应用:恒定磁场高斯定理常用来描述磁场的强度分布,如果一个磁
场内没有任何外部质量或电流的影响,那么磁场的强度衰减率将满足
高斯型模型。
这一定律经常用于测量磁场的强度,以了解地磁场的强
度分布和磁场方位,以及估计电磁散射层的厚度。
4. 公式:恒定磁场高斯定理的数学公式表述为,若将物体的中心视为
原点,则磁场的强度B随着距离r的变化满足:
$$B(r)=\frac{B_0}{1+\left(\frac{2c}{r}\right)^2}$$
其中,B_0为物体中间磁力线的平均强度,而c是磁场到物体中心的距离。
5. 参考:E.W Jorry曾表明恒定磁场高斯定理,这个定律经常被用于研究地磁场和大气层。
6. 总结:测量磁场强度及分布与恒定磁场高斯定理有关,它给出了磁场强度衰减率满足高斯型模型的物理定律,广泛的应用于地磁方位、磁场强度分布和电磁散射层厚度估计等等方面。



磁高斯定理
磁高斯定理(Maxwell's theorem)是磁力学的重要定理,由英国
物理学家乔治·马克斯韦(George Maxwell)于1865年提出。
它解释
了磁场的电流和旋转矢量之间的关系,是磁力学最根本的定律。
磁高斯定理可以用数学形式来表示:∇ × B = μ0J,其中B为
磁场,J为电流密度,μ0为真空磁导率(μ0=4π×10-7H/m),∇是
矢量求导运算符号。
这个定理描述了一个简单的物理现象:电流的旋
转产生了磁场,所以它是磁力学的基础。
磁高斯定理非常重要,可以解释各种电磁相关的现象。
它提供了
一种理解电磁学中电流向量、磁场强度和磁矢量之间关系的方法。
马
克斯韦在提出它的定理后,将电磁学理论推向了一个新的高度。
此外,磁高斯定理也可以用来解决电磁学中各种实际问题。
例如,它可以解释磁场强度的变化情况,从而帮助我们探索和分析电磁学现象。
总之,磁高斯定理是电磁学的基石,是磁力学的重要定理。
它不
仅能够精确地描述电磁学上的实际现象,而且可以结合其它电磁学定律,来求解一些复杂的实际问题。

电场磁场的高斯定理
《电场磁场的高斯定理》
一、什么是高斯定理
高斯定理(Gauss's law)是18世纪德国物理学家克劳德·高斯(K.F.Gauss)发现的一个重要的定理,它表明电场强度的实际场值可以由有限增量内所包围的电荷和与荷量有关的容量而确定,在物理学中占据着重要的位置。
高斯定理可以简单地表示为:
在任何闭合面上,电场总积分(即电势差)与体积内的电荷数量之比,等于这个闭合面上每平方厘米所受的电荷数量,即:
(电场总积分/电荷数量)=(每平方厘米所受的电荷数量).
二、高斯定理的应用
高斯定理可以用来计算多种电场的属性,例如可以用来求取电场强度、电容器的电容及等离子体的电荷分布等等。
1、计算电场和电势:
由高斯定理,可以简便地确定电荷分布所产生的电场和电势,如果知道电荷量,则可以用高斯定理直接确定场强,也可以利用高斯定理求得某一特定点上的电势。
2、计算电容:
利用高斯定理,也可以用来计算电容器中两个电极之间的电容。
当两个具有不同电荷的电极放入同一个介质中,电容器新形成了一种特殊的电场,在电容器电极上可以产生一定的电势差。
三、结论
高斯定理是物理学中经典的定理,它是用来描述电场的重要定理。
它主要描述的是在任何闭合面上,电场总积分与体积内的电荷数量之比,等于这个闭合面上每平方厘米所受的电荷数量。
应用高斯定理,可以计算电场的属性,也可以用来求取电容器的电容。
磁场中的高斯定理公式
磁场中的高斯定理公式:∮EdS=(∑Q)/ε0,高斯定理也称为高斯通量理论,或称作散度定理、高斯散度定理、高斯-奥斯特罗格拉德斯基公式、奥氏定理或高-奥公式。
在静电学中,表明在闭合曲面内的电荷之和与产生的电场在该闭合曲面上的电通量积分之间的关系。
高斯定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。
高斯定律在静电场情况下类比于应用在磁场学的安培定律,而二者都被集中在麦克斯韦方程组中。
因为数学上的相似性,高斯定律也可以应用于其它由平方反比律决定的物理量,例如引力或者辐照度。
磁场的高斯定理,说明高斯定律(gauss' law),属物理定律。
在静电场中,穿过任一封闭曲面的电场强度通量只与封闭曲面内的电荷的代数和有关,且等于封闭曲面的电荷的代数和除以真空中的电容率。
该定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。
静电场中通过任意闭合曲面(称高斯面)s 的电通量等于该闭合面内全部电荷的代数和除以真空中的电容率,与面外的电荷无关。
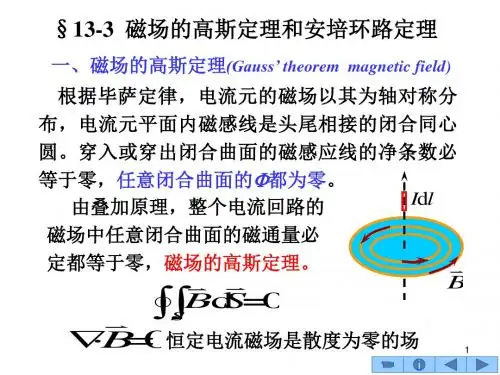
物理定律由于磁力线总是闭合曲线,因此任何一条进入一个闭合曲面的磁力线必定会从曲面内部出来,否则这条磁力线就不会闭合起来了。
如果对于一个闭合曲面,定义向外为正法线的指向,则进入曲面的磁通量为负,出来的磁通量为正,那么就可以得到通过一个闭合曲面的总磁通量为0。
这个规律类似于电场中的高斯定理,因此也称为高斯定理。
与静电场中的高斯定理相比较,两者有著本质上的区别。
在静电场中,由于自然界中存有着单一制的电荷,所以电场线存有起点和终点,只要闭合面内有净余的也已(或负)电荷,沿着闭合面的电通量就不等于零,即为静电场就是有源场;而在磁场中,由于自然界中没单独的磁极存有,n极和s极就是无法拆分的,磁感线都就是无头无尾的滑动线,所以通过任何闭合面的磁通量必等于零。
特别要强调两点: 1.关于电场线的方向的规定:电场线上每一点的切线方向就是该点电场的方向。
2.关于电场线的疏密的规定:电场线在某处的疏密要反映电场强度的大小,即在电场中通过某一点的电场线的数密度与该点电场强度的大小呈正相关,即: e=dn/ds,其中ds是在电场中的某一点取一个通过该点的且与电场线垂直的微分面,dn就是穿过该面ds的电场线的根数。
高斯定理来源于库仑定律,依赖场强共振原理,只有当电场线密度等同于场强悍小时场线通量就可以与场强通量等同于,并统一遵守高斯定理。
高斯面上的实际场强就是其内外所有电荷产生的场强共振而变成的合场强。
但利用高斯面所求出的场强则仅仅就是分析高斯面上场强原产时所牵涉的电荷在高斯面上产生的合场强,而不涵盖未牵涉的电荷所产生的场强。