人教版六年级数学上册分数除法《例2》导学案
- 格式:doc
- 大小:77.00 KB
- 文档页数:2

人教版数学六年级上册分数除法导学案(精选3篇)〖人教版数学六年级上册分数除法导学案第【1】篇〗教学目标:1、通过画线段图引导学生分析并归纳一个数除以分数的计算法则.2、能运用法则,正确迅速地计算分数除法.3、培养学生抽象思维能力.4、让学生通过探索知识,从而获得知识,体验成功的乐趣,树立学习的自信心.教学重点:分析并归纳一个数除以分数的计算法则.教学难点:理解一个数除以分数的算理.教具准备:多媒体课件教学方法:讨论交流。
教学过程:一、复习导入1、计算:5/6÷10 3/5÷3 15/16÷20 40/39÷26(说一说,你在计算中如何尽量避免错误的产生在计算中要注意什么 )2、胜利路长1000米,东东走完全程用了20分钟,东东平均每分钟行多少米(独立解答并且说明解题依据)3、2/3小时有()个1/3小时,1小时有()个1/3小时.二、新授:1、教学例3:小明2/3小时走了2km,小红5/12小时走了5/6 km,谁走得快些师:已知什么生:已知小明和小红各自的时间和对应的路程.师:问题求什么生:求谁走的快些.师:求谁走得快些就是比较什么生:就是比较谁的速度快.师:你能根据题意列出算式吗生:2÷2/3 5/6÷5/122、除数是分数的除法计算方法的探究:引导学生画线段图分析:师:2/3里有几个1/3 2/3小时走了2 km,能不能求出1/3小时走多少千米生:2/3里有2个1/3,求1/3小时走了多少千米可以用2 km÷2,也就是2km×1/2;师:2 km÷2得到的1km,有什么具体的含义是线段图上的哪一段生:略师:1小时里有几个1/3小时,能求1小时行多少千米了吗生:2×1/2×3=2×3/2=3 km.指导学生观察:2÷2/3=2×1/2×3=2×3/2=3(提示:观察2÷2/3=2×3/2这一步)师:这儿把除法转化成什么运算来计算除以2/3=生:把除法转化为法来计算,除以2/3等于以3/2.师:你能用自己的语言叙述整数除以分数的计算方法吗(有语言叙述,用字母表示等都行,只要是正确的都肯定学生的结论)师:请你观察上面和算式,怎样把除法转化成为乘法来进行计算你能说出转化的要点吗生:1,被除数没有变化;2,除号变乘号;3,除数变成了它的倒数.3、学生独立计算5/6÷5/12 订正并板书:4、让学生根据分数除法的意义检验后作答.三、练习:1、31页做一做第1题和第2题的后两个小题.(做完1题后,让学生把每个算式完整地读一遍,然后再完成第2题,第二题要求学生要写出计算过程.)2、练习八第2题的后4个小题.(在学生完成此题时,教师指导好思维慢的学生先算出乘法算式的积,再找出两题之间的关系)四、全课小结:1、今天我们共同研究了什么知识?2、你能用一句完整的话来说一说今天的主要内容吗?3、你认为在完成课后作业时,应该从哪些方面尽量避免错误的产生?五、作业练习:练习八第3,4题.六、板书设计2÷=2××3=2×(3)、分数除法的计算练习课〖人教版数学六年级上册分数除法导学案第【2】篇〗一、说教材我说课的内容是人教版小学数学六年级上册第34的内容:分数四则混合运算。

《分数除法》单元分析一、课标要求正确地、比较熟练地进行分数除法计算。
掌握分数整数除以分数,分数除以分数的计算法则能熟练进行加法和除法,减法和除法的混合运算. 并能应用运算定律进行简便运算. 正确解答简单的分数乘、除法应用题。
二、教材分析本单元的教学内容有:倒数的认识,分数除以整数,整数除以分数,分数除以分数分数除法的应用,整理与复习。
地位和作用分数除法的计算实际是转化成分数乘法的计算。
掌握分数除法的计算有两方面的作用,一方面巩固分数乘法,另一方面它给我们学习带来一种学习方法-------转化方法。
也交给同学们处理事情的方法。
当我们遇到新的问题,不妨回头看看以前的知识,学会应用旧知识解决新问题,有山重水复疑无路,柳暗花明又一村的感觉。
三、三维目标知识与技能:理解倒数的意义,掌握求倒数的方法。
理解分数除以整数的意义,利用已有知识理解和探索分数除以整数的算理和算法。
掌握一个数除以分数的计算方法,并能正确计算。
运用分数乘除法的计算方法解决分数连除、分数乘除混合的运算。
会用方程解决“已知一个数的几分之几的是多少,求这个数”的实际问题。
通过对比练习,掌握分数乘、除法应用题的联系和区别,正确解答简单的分数乘、除法应用题。
过程与方法:通过倒数的认识,在掌握求倒数的方法中学会把分数除法转化成分数乘法。
通过对比练习,掌握分数乘、除法应用题的联系和区别,正确解答简单的分数乘、除法应用题。
通过实践运用,选择合理的方法正确计算分数除以整数通过相互交流、相互评价,培养学生的分析、判断、推理能力和反思意识,进一步渗透转化的数学思想。
参与数学活动过程中,提高计算能力。
通过相互交流、相互评价,培养学生的分析、判断、推理能力,进一步渗透转化的数学思想。
培养学生的分析、判断、推理能力情感态度价值观:通过倒数的认识,在掌握求倒数的方法中学会把分数除法转化成分数乘法。
在对比练习,掌握分数乘、除法应用题的联系和区别,正确解答简单的分数乘、除法应用题。
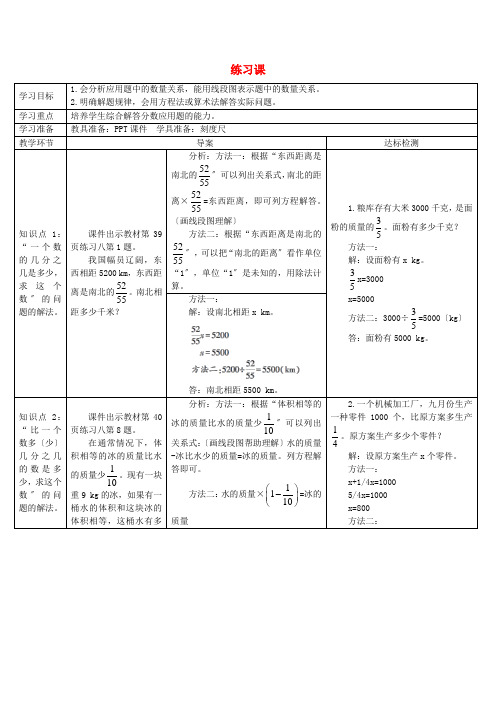
练习课学习目标1.会分析应用题中的数量关系,能用线段图表示题中的数量关系。
2.明确解题规律,会用方程法或算术法解答实际问题。
学习重点培养学生综合解答分数应用题的能力。
学习准备教具准备:PPT课件学具准备:刻度尺教学环节导案达标检测知识点1:“一个数的几分之几是多少,求这个数〞的问题的解法。
课件出示教材第39页练习八第1题。
我国幅员辽阔,东西相距5200 km,东西距离是南北的5255。
南北相距多少千米?分析:方法一:根据“东西距离是南北的5255〞可以列出关系式,南北的距离×5255=东西距离,即可列方程解答。
〔画线段图理解〕方法二:根据“东西距离是南北的5255〞,可以把“南北的距离〞看作单位“1〞,单位“1〞是未知的,用除法计算。
1.粮库存有大米3000千克,是面粉的质量的35。
面粉有多少千克?方法一:解:设面粉有x kg。
35x=3000x=5000方法二:3000÷35=5000〔kg〕答:面粉有5000 kg。
方法一:解:设南北相距x km。
答:南北相距5500 km。
知识点2:“比一个数多〔少〕几分之几的数是多少,求这个数〞的问题的解法。
课件出示教材第40页练习八第8题。
在通常情况下,体积相等的冰的质量比水的质量少110。
现有一块重9 kg的冰,如果有一桶水的体积和这块冰的体积相等,这桶水有多分析:方法一:根据“体积相等的冰的质量比水的质量少110〞可以列出关系式:〔画线段图帮助理解〕水的质量-冰比水少的质量=冰的质量。
列方程解答即可。
方法二:水的质量×1110⎛⎫-⎪⎝⎭=冰的质量2.一个机械加工厂,九月份生产一种零件1000个,比原方案多生产14。
原方案生产多少个零件?解:设原方案生产x个零件。
方法一:x+1/4x=10005/4x=1000x=800方法二:重?1000÷(1+1/4)=1000÷5/4=800〔个〕答:原方案生产800个零件。

分数除法应用题(二)导学案介休市义安镇沙堡小学王治伟姓名小组评价学习目标:1、在理解数量关系的基础上学会列方程解答稍复杂的分数应用题,能用列方程的方法解决一些简单的实际问题。
2、经历“做数学”“用数学”的活动过程,体验分析、判断、推理的学习方法。
3、感受数学思考的条理性,体会数学知识的逻辑之美,激发学习数学的兴趣。
学习难点:找等量关系学习重点:分析数量关系。
学习过程:一、自主学习5,吃了多少千克?(1)小红家买来一袋大米重40千克,吃了81、分析题目中的单位“1”2、分析题目中的等量关系3、根据题意绘制线段图。
列式解答:(2)根据题意写出代数式1。
那么西瓜比苹果重()1、苹果有x kg,西瓜的质量比苹果重4kg,西瓜得()kg1,鸭比鸡少()只,鸭2、鸡有鸡有y只,鸭的数量比鸡少3有()只。
二、合作探究:1,航模小组例2:美术小组有25人,美术小组的人数比航模小组多4有多少人?(1)这道题中单位“1”是(2)画出线段图:(3)根据题意写出等量关系式:(4)列方程解答:解:设有x人。
1,美思考:(1)航模小组有20人,美术小组的人数比航模小组多4术小组有多少人?1,航模小组(2)美术小组有24人,美术小组的人数比航模小组少4有多少人?以上两题与“例2”比较,你发现了什么?三、课堂练习:3。
张大爷养的鸡比鸭多5(1)鸭有500只,鸡有多少只?(2)鸡有800只,鸭有多少只?(3)鸡比鸭多300只,鸭有多少只?四、小结:今天我们学习了用方程解稍复杂的分数应用题,在解题时关键是什么?。

人教版数学六年级上册分数除法导学案(精选3篇)〖人教版数学六年级上册分数除法导学案第【1】篇〗教学目标:1、引导学生在具体的情景中借助已有的经验理解分数除法的意义并掌握分数除法的计算方法,能正确计算分数除以整数.2、通过富有启发性的问题情景和探索性的学习活动,引导学生主动参与,独立思考,合作交流,形成计算技能.3、在教学中渗透转化的思想,让学生充分感受转化的美妙与魅力.教学重点:1、分数除法意义的理解;2、分数除以整数的算法的探究.教学难点:分数除以整数的算法的探究.教学准备:例1的教学挂图;平均分成5份的长方形纸一张.多媒体课件。
教学方法:自主探究。
教学过程:一、创设情景导入:同学们,你们去过超市购物吗(去过)你去买了一些什么东西呢你有没有过相同的东西买几件的时候能不能举个例(指名让学生举例并用算式表示求该例的总价)二、新授:(一)分数除法的意义1、出示例1的教学挂图,让学生看图观察图意,指名口答图意和应该怎样列式.2、上面的问题能改编成用除法计算的问题吗 (学生独立思考,口答问题和列式)3、100g=()kg,你能将上面的问题改成用kg作单位的吗 (引导学生将整数乘除法应用题改变成分数乘除法应用题)4、引导学生观察比较整数乘除法的问题和改写后的问题,分析得出整数除法和分数除法的联系以及分数除法的意义.5、练习:(巩固加深对意义的理解)课本28页做一做.学生独立练习,订正时让学生说明为什么这样填.(二)、分数除以整数1、小组学习活动:活动⑴把这张纸的4/5平均分成2份,每份是这张长方形纸的几分之几活动⑵把这张纸的4/5平均分成3份,每份是这张长方形纸的几分之几[活动要求]先独立动手操作,再在组内交流:通过折纸操作和计算,你发现了什么规律你有什么问题要提出来2、汇报学习结果:活动1学生甲,把4/5平均分成2份,就是把4个1/5平均分成2份,1份就是2个1/5,就是2/5;用算式表示是:4/5÷2=(4÷2)/5=2/5 学生乙、把4/5平均分成2份,每份就是4/5的1/2,就是4/5×1/2;用算式表示是:4/5×1/2=4/10=2/5;学生丙、我发现了计算4/5÷2时,可以用分子4÷2作分子,分母不变;学生丁、我发现分数除以整数可能转化成乘法来计算,也就是乘以这个整数的倒数;活动2:学生甲,4要平均分成3份,不能直接分,我先找出4和3的最小公倍数12,把4分成12份,再把12份平均分成3份,算式可以用4/5÷3表示,4不能够被3整除,这道题我不知道怎样计算;学生乙:我的分法与前面的同学相同,不同的是:我在计算4/5÷3时,我把4/5÷3转化成4/5×1/3来计算,因为,把4/5平均分成3份,就是求4/5的1/3是多少.讨论:1、从折纸实验和计算来看,你发现计算分数除以整数可以怎样计算2、整数可以为0吗小结并板书:分数除以一个不等于0的整数,等于分数乘以这个整数的倒数.三、练习1、把3/5平均分成4份,每份是多少;什么数乘6等于3/202、如果a是一个不等于0的自然数,1/3÷a等于多少 1/a÷3等于多少你能用一个具体的数检验上面的结果吗四、作业练习:÷3 ÷3 ÷20 ÷5 ÷10 ÷6五、总结1、今天我们学习了哪些内容?(分数除法的意义及分数除以整数的计算法则)2、谁来把这两部分内容说一说?六、板书设计:分数除法——分数除以整数例1每盒水果糖重100g,3盒重多少g 例2把一张纸的4/5平均分成2份,每份是这张纸100×3=300g→1/10×3=3/10g 的几分之几3盒水果糖重300g,每盒子重多少g 4/5÷2=(4÷2)/5=2/5 4/5÷2=4/5×1/2=2/5300÷3=100g→3/10÷3=1/10g 如果把这张纸的4/5平均分成3份,每份是300g水果糖,100g装1盒,可以装几盒这张纸的几分之几300÷100=3(盒)→3/10÷1/10=3(盒) 4/5÷3=4/5×1/3=4/15 除以一个不等于0的整数,等于分数乘以这个整数的倒数.(2)、一个数除以分数〖人教版数学六年级上册分数除法导学案第【2】篇〗练习目标:1、在理解分数除法算理的基础上,正确熟练地进行分数除法的计算;2、运用所学的分数除法的知识,解决相应的实际问题.练习重难点:正确熟练地计算分数除法。
人教版数学六年级上册分数除法导学案(推荐3篇)〖人教版数学六年级上册分数除法导学案第【1】篇〗教学要求:1、使学生认识分数除法应用题的特点,能根据应用题的特点理解解题思路和解题方法,学会解答已知一个数的几分之几是多少求这个数的应用题。
2、进一步培养学生自主探索问题解决的能力和分析、推理和判断等思维能力,提高解答应用题的能力。
教学重难点:分数除法应用题的特点及解题思路和解题方法。
教学过程:一:复习1、根据条件说出把哪个数量看作单位1。
(1)棉田的面积占全村耕地面积的2/5。
(2)小军的体重是爸爸体重的3/8。
(3)故事书的本数占图书总数的1/3。
(4)汽车速度相当于飞机速度的1/5。
2、找单位1,并说出数量关系式。
(1)白兔的只数占总只数的2/5。
(2)甲数正好是乙数的3/8。
(3)男生人数的1/3恰好和女生同样多。
3、一个儿童体重35千克,他体内所含水分占体重的4/5,他体内的水分有多少千克?集体订正时,让学生分析数量关系,说出把哪个数量看作单位1,并说出解答这个问题的数量关系式,即:体重4/5=体内水分的重量。
同学们都能正确分析和解答分数乘法应用题,分数除法应用题又如何解答呢?今天这节课我们就一起来研究。
(板书课题:分数除法应用题)二、新授1、教学例1。
一个儿童体内所含的水分有28千克,占体重的4/5。
这个儿童体重有多少千克?(1)指名读题,说出已知条件和问题。
(2)共同画图表示题中的条件和问题。
(3)分析数量关系式提问:根据水份占体重的`4/5,可以得到什么数量关系式?学生回答后,教师说明:例1和复习题的第二个已知条件相同,因此单位1相同,数量关系式也相同,都是把体重看作单位1,数量关系式是:体重4/5=体内水分的重量。
根据学生的回答,把线段图进一步完善。
提问:根据题目的条件,我们已经找到了这一题的数量关系式:体重4/5=体内水分的重量。
现在已知体内水分的重量,要求儿童体重有多少千克,可以用什么方法解答?(引导学生说出用方程解答。
《一个数除以分数》导学单
班级:六年级 姓名: 小组:
学习目标:
1、通过画线段图分析并归纳一个数除以分数的计算法则。
能运用法则,正确迅速地计算分数除法。
2、通过探索知识,从而获得知识,体验成功的乐趣,树立学习的自信心。
学习重点:通过画线段图分析并归纳一个数除以分数的计算法则。
学习难点:能运用法则,正确迅速地计算分数除法。
课时安排:2课时
学习过程:
〖自主学习〗
【学法指导】请同学们自学课本第31-32页,独立思考完成自主学习任务,并把自己遇到的或生成的问题记下来。
你们可要动脑筋,多思考哦!
一、轻松准备:
1、计算下面各题。
10
9÷3= 83÷2= 98÷4= 75÷5= 分数除以整数等于分数乘( )。
2、只列式不计算:
(1)小明3
2小时走了2㎞,平均每小时走多少千米?
(2)小红12
5小时走了65㎞,平均每小时走多少千米?
二、自主预习:
自学教材P31例2题,并填写下面的空。
1、已知( ),求( )?求谁走得快些?就是比较( )
2、你能根据题意列出算式吗?
小组长评价: 学科长评价: 教师评价(抽查): 〖合作探究〗
【学法指导】请同学们在预习的基础上,小组讨论交流下面的问题;小组长负责组织讨论后派出代表,进行全班交流展示。
看谁最棒哟!。
第3课时分数混合运算课题分数混合运算课型新授课设计说明本节课是在学生已经掌握了分数的加、减、乘、除及整数混合运算的基础上进行教学的,本课时的教学设计有以下几个特点:1.重内容,重形式。
在复习准备阶段,精心设计练习题内容,在高效复习旧知的同时,激发学生的学习兴趣。
2.重探究,重归纳。
在教学例3的环节中,不但要重视引导学生在解决问题中体会、理解除加、除减混合运算的运算顺序,而且重视个例分析,重视归纳总结相关规律。
3.重联系,重迁移。
有效利用已有的整数混合运算的基础,巧妙地引导学生把原有知识迁移到分数混合运算中来,使学生通过分析、尝试,理解并掌握分数混合运算的顺序。
学习目标1.进一步掌握分数除法的计算方法,能够正确迅速地计算两、三步计算的分数混合运算题,提高计算分数混合运算的能力。
2.体会数学与生活的联系,提高学生运用知识解决实际问题的能力。
3.通过练习,培养学生观察、类推的思维能力和灵活计算的能力。
学习重点掌握分数四则混合运算的运算顺序并能正确解答关于分数四则混合运算的问题。
学习难点分数混合运算的运算顺序学习准备教具准备:PPT课件课时安排1课时教学环节导案学案达标检测一、复习导入。
(7分钟)1.说出运算顺序,不用计算。
(18+7)×488+30÷5350-25×260÷(77-65)2.导入新知,今天我们来学习分数混合运算。
1.口答运算顺序:第1题,先算加法,再算乘法。
第2题,先算除法,再算加法。
第3题,先算乘法,再算减法。
第4题,先算减法,再算除法。
2.明确本节课的学习内容。
1.回顾整数混合运算的运算顺序。
先算乘除、后算加减,有括号的要先算括号里面的。
二、探究新知。
(20分钟)1.课件出示教材第33页例3。
(1)分析题意,明确题中的各个数量的意义。
(2)指导学生在小组内讨论、交流解题思路。
(3)尝试列式。
2.探究有小括号的分数乘除混合运算的运算顺序。
(1)课件出示算式,小组讨论计算方法。
2 分 数 除 法投我以桃,报之以李。
《诗经·大雅·抑》 翰辰学校 李道友组长(1)分数除以整数预习指南:1.借助图形理解分数除以整数的意义并掌握其计算方法并能正确地进行计算。
2.通过学习进一步理解数学的转化思想。
1.写出下面各数的倒数。
1 0.45 100 512452.教材第30页例1。
(1)(3)如果把这张纸的45平均分成3份,每份是这张纸的几分之几?45÷3=( )×( )=( )3.先看清左右两题之间的关系,再写出得数。
4.芳芳将45m 长的丝带剪成同样长的8段,每段丝带有多长? 每日口算4.7+2.3= 4.5×2= 7.5-2.5= 7.2×0.8= (14+13)×24= 24.06+0.4= 38-13=(56-15)×30=(2)一个数除以分数预习指南:1.借助线段图理解分数除法的算理并掌握算法。
2.在理解分数除法算理的过程中进一步体会知识之间的内在联系。
1.计算。
910÷3= 38÷2= 89÷4= 57÷6=2.教材第31页例2。
小明: 小红:23小时走了2km,23小时里有( )个13小时,求1个13小时走了多少千米,就是求2km 的12是多少,即( )×12=1(km)。
1小时里有3个13小时,1个13小时走1km,3个13小时就走( )×( )m,列式解答为:2÷23=2×12×3=2×(12×3)=2×32 =( )(km)5个112小时走56km,把56平均分成5份,求一份是多少,就是求56的( )是多少,即56×( ) , 再乘12就是1小时走的路程,列式解答为56÷512=56×15×12=56×(15×12)=56×125=( )(km)( )>( ) ( )走得快些。