2008年北京市中学生数学竞赛高一年级初赛试题及答案

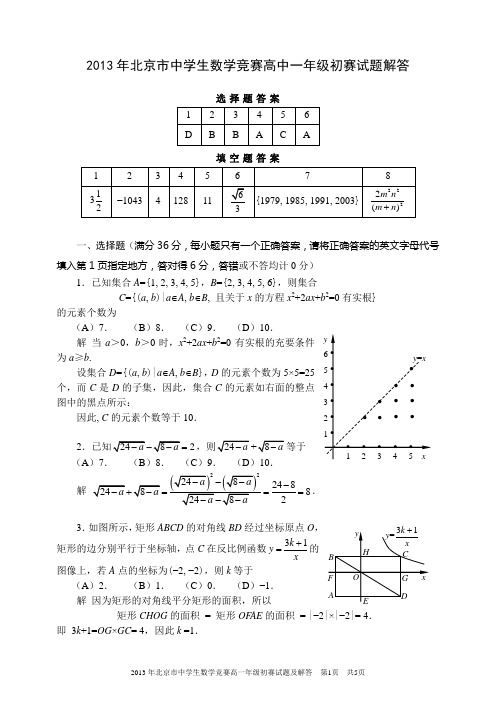
2013年北京市中学生数学竞赛高中一年级初赛试题解答选择题答案填空题答案一、选择题（满分36分，每小题只有一个正确答案，请将正确答案的英文字母代号填入第1页指定地方，答对得6分，答错或不答均计0分）1．已知集合A={1, 2, 3, 4, 5}，B={2, 3, 4, 5, 6}，则集合C={(a, b)|a∈A, b∈B, 且关于x的方程x2+2ax+b2=0有实根}的元素个数为（A）7．（B）8．（C）9．（D）10．解当a＞0，b＞0时，x2+2ax+b2=0有实根的充要条件为a≥b.设集合D={(a,b)|a∈A, b∈B}，D的元素个数为5×5=25个，而C是D的子集，因此，集合C的元素如右面的整点图中的黑点所示：因此, C的元素个数等于10．22=（A）7．（B）8．（C）9．（D）10．解2224882--===．3．如图所示，矩形ABCD的对角线BD经过坐标原点O，矩形的边分别平行于坐标轴，点C在反比例函数31kyx+=的图像上，若A点的坐标为(−2, −2)，则k等于（A）2．（B）1．（C）0．（D）−1．解因为矩形的对角线平分矩形的面积，所以矩形CHOG的面积= 矩形OF AE的面积= |−2|×|−2|= 4．即3k+1=OG×GC= 4，因此k =1．4．定义在R 上的偶函数f (x )，满足f (x+1)=−f (x )，且在区间[−1, 0]上递增，则 （A）(3)(2)f f f <<． （B）(2)(3)f f f <<． （C）(3)(2)f f f <<． （D）(2)(3)f f f <<．解 根据题意f (x )=−f (x+1) =−[−f (x+2)]= f (x+2)，因为f (x )是偶函数，即f (a )= f (−a )， 则(3)(1)(1)f f f ==-，(2)(0)f f =，((22)f f f f ===． 而 −12＜0，f (x )在区间[−1, 0]上递增，所以(3)(2)f f f <<．5．由1开始的连续n 个正整数相乘，简记为n !=1×2×…×n ， 如3!=1×2×3=6，10!=1×2×3×4×5×6×7×8×9×10=3628800等等，则12345672!3!4!5!6!7!8!++++++等于（A ）719720．（B ）50395040．（C ）4031940320．（D ）4032140320．解 因为1111!!!(1)!!n n n n n n n -=-=--，所以 12345672!3!4!5!6!7!8!++++++ 213141516171812!2!3!3!4!4!5!5!6!6!7!7!8!8!⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+-+-+- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭111111*********!2!3!3!4!4!5!5!6!6!7!7!8!⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+-+-+- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ 1140319118!4032040320=-=-=．6．如图，正方形ABCD 内接于⊙O ，P 为劣弧CD 上一点，P A交BD 于点M ，PB 交AC 于点N ，记∠P AC =θ，若MN ⊥P A ，则2cos 2θ−tan θ的值等于 （A ）1． （B． （C ）12． （D． 解 ∵ 四边形ABCD 是正方形，∴ ∠ACB =45º，DB ⊥AC ， ∴ ∠APB =∠ACB =45º， ∵ MN ⊥P A ，∴ ∠MNP =∠APB =45º，∴ MP =MN ．∵ AC 为圆的直径，∴∠APC =90º，∴P 、M 、O 、C 四点共圆．∴ AM ·AP = AO ·AC ．因此2cos 2θ − tan θ 222AO MN AM AM =⋅-222AO AM MNAM⋅-⋅= 2AO AC AM MN AM ⋅-⋅=2AM AP AM MN AM⋅-⋅= AP MN AM -=1AP PM AM-==．二、填空题（满分64分，每小题8分，请将答案填入第1页指定地方） 1．求222222235753sin 30sin 35sin 40sin 45sin 50sin 55sin 60tan 36tan 39tan 42tan 45tan 48tan 51tan 54++++++⨯⨯⨯⨯⨯⨯ 的值．解 注意到sin 2α+sin 2(90º−α)= sin 2α+cos 2α=1，sin 245º=12，n 为正整数时，tan n α×tan n (90º−α)= tan n α×cot n α=(tan α×cot α)n =1，tan45º=1，则222222235753s i n 30s i n 35s i n 40s i n 45s i n 50s i n 55s i n 60t a n 36t a n 39t a n 42t a n 45t a n 48t a n 51t a n 54++++++⨯⨯⨯⨯⨯⨯ 3.5=．2．f (x )是定义在R 上的奇函数，当x ≥0时，f (x )=2x +2x +b (b 为常数)，求f (−10)的值．解 因为f (x )为定义在R 上的奇函数，所以f (0)=0，即20+2×0+b =0，得b =−1．由奇函数的性质f (−x )=−f (x )，有若x ＜0，即−x ＞0，则−f (x )= f (−x )=2−x −2x −1， 即f (x )= −2−x +2x +1 (x ＜0)． 所以f (−10)= −210−2×10+1= −1043．3．若实数x , y , z44x y z +-=，试确定(5x +3y −3z )2013的末位数字．解 易见x ≥7，则≥4，而4x y z+-≥0，又x , y , z满足方程44x y z +-=，且4x y z+-=0． 所以 x =7，x +y −z =0，(5x +3y −3z )2013 =142013，这个数的末位数字为4．4．如右图，正方形ABCD 被分成了面积相等的8个三角形，如果AGABCD 面积的值．解 过F 作KL//DC ，取AB 的中点N ，延长GN 交AH 于P ， 设正方形ABCD 的边长为a ，由于△DCI 、△ABH 的面积都是正方形ABCD 面积的18，所以CI =BH =14BC =4a ． 由△ADF 的面积=△DCL 的面积的2倍，得AB C D EFGIH ABCDE F P IH L KG N11222AD KF CD CI ⨯=⨯⨯ 所以KF =2CI 1.2a =所以F 为DI 中点． 易见，E 是AF 的中点，由△F AG 、△FHG 的面积相等，可得AP=PH ，即FP 为△F AH 的一条中线，因此F 、P ，N 是一条直线．同理可证，HG 的延长线必过AE 的中点E ，所以HE 为△F AH 的另一条中线，中线FP 与HE 的交点G 为△F AH 的重心，12GP FG =． 注意FP 为梯形AHID 的中位线，FP//BC ，所以 132224a aHI AD aFP ++===，所以134a GP FP ==，所以3488a a a GN GP PN =+=+=．而AN =2a ，根据勾股定理，有22223252864a a a AG ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭，即2255064a =，所以a 2=128．5．已知实数m 、n 满足m −nm 2−3n 2为质数．若m 2−3n 2的最大值为a ，最小值为b ．试确定a −b 的值．解 设m 2−3n 2=p （p 为质数） ① 由m −nm= n ， ②把②式代入①式得n )2−3n 2= p ，整理得2n 2−+p −10=0， ∴ Δ=40−8p +80≥0，∴ p ≤15．∴ p 的最大值a =13，最小值b =2 ， ∴ a −b =11．6．在△ABC 的边BC 上有一点D ，∠ADB 是锐角，P 、Q 分别是△ABD 、△ACD 的外心，且四边形APDQ 面积是△ABC 面积的34．求sin ∠ADB 的值． 解 连结PQ ，易证△AQP ≌△DQP ， 由已知得38AQP ABCS S ∆∆=， 易证：△APQ ∽△ABC ，所以2AQP ABCS AQ S AC ∆∆⎛⎫= ⎪⎝⎭，所以AQ AC =． 连结QC ，作QH ⊥AC 于H ，则11112222ADB ACD CAD AD CD ADC AQC AQH ∠=∠+∠=+==∠=∠． 所以 sin ∠ADB = sin ∠AQH == 7．S (x )表示自然数x 的数字和，试确定方程x +S (x )+S (S (x ))=2013的解集． 解 显然x ＜2013，而S (x )最大为28，S (S (x ))最大为10，因此x 最小为2013−38=1975．因此1975≤x ＜2013，容易试验得x =2003，S (2003)=5，S (S (2003))=5，2003+5+5=2013； x =1991，S (1991)=20，S (S (1991))=2，1991+20+2=2013； x =1985，S (1985)=23，S (S (1985))=5，1985+23+5=2013； x =1979，S (1979)=26，S (S (1979))=8，1979+26+8=2013． 除此之外的x 都不满足方程，所以解集是{1979, 1985, 1991, 2003}．8．直角△ABC 中，内切圆⊙O 切斜边AB 于D ，切BC 于E ，切CA 于F ，作DK ⊥AC 于K ，DP ⊥BC 于P ，已知AD =m ，BD =n ，试确定矩形CKDP 的面积（用m ，n 来表示）．解 设内切圆半径为r ，连接OD ，OE ，OF ，如图，则OD =OE =OF = r ．由切线长定理得AD =AF =m ，BD =BE =n ，CE =CF =r ．设△ABC 的半周长为p ，面积为S ，则p =r +m +n ，所以 ()()2r m r n S ++=．即 2S =r 2+rm +rn +mn =r (r +m +n )+mn =rp +mn ． 因为S =rp ，代入上式得 S = mn ． 因为DK //BC ，所以 △ADK ∽△ABC ，所以 223222()()()ADKABC m m m nS S mn m n m n m n ∆∆=⨯=⨯=+++， 同理可得223222()()()BDPABC n n mn S S mn m n m n m n ∆∆=⨯=⨯=+++， 因此，矩形CKDP 的面积 = 33222222()()()m n mn m n mn m n m n m n --=+++．。

2008年全国高中数学联合竞赛加试（A 卷）一、（本题满分50分）如题一图，给定凸四边形A B C D ，180B D ∠+∠< ，P 是平面上的动点，令()f P PA BC PD CA PC AB =⋅+⋅+⋅．（Ⅰ）求证：当()f P 达到最小值时，P A B C ,,,四点共圆； （Ⅱ）设E 是A B C ∆外接圆O 的 AB 上一点，满足：32A E A B=，31B C E C=-，12E C B E C A ∠=∠，又,DA DC 是O 的切线，2AC =，求()f P 的最小值．二、（本题满分50分）设()f x 是周期函数，T 和1是()f x 的周期且01T <<．证明： （Ⅰ）若T 为有理数，则存在素数p ，使1p是()f x 的周期；（Ⅱ）若T 为无理数，则存在各项均为无理数的数列{}n a 满足110n n a a +>>> (1,2,)n =⋅⋅⋅，且每个(1,2,)n a n =⋅⋅⋅都是()f x 的周期．三、（本题满分50分）设0k a >，1,2,,2008k = ．证明：当且仅当200811k k a =>∑时，存在数列{}n x 满足以下条件：（ⅰ）010n n x x x +=<<，1,2,3,n = ； （ⅱ）lim n n x →∞存在；（ⅲ）20082007111n n k n k k n k k k x x a x a x -+++==-=-∑∑，1,2,3,n = ．2008年全国高中数学联合竞赛加试（A 卷）试题参考答案及评分标准说明：1．评阅试卷时，请严格按照本评分标准的评分档次给分；2．如果考生的解答方法和本解答不同，只要思路合理、步骤正确，在评卷时可参考本评分标准适当划分档次评分，10分为一个档次，不要增加其他中间档次．一、（本题满分50分）如题一图，给定凸四边形A B C D ，180B D ∠+∠< ，P 是平面上的动点，令()f P PA BC PD CA PC AB =⋅+⋅+⋅．（Ⅰ）求证：当()f P 达到最小值时，P A B C ,,,四点共圆； （Ⅱ）设E 是A B C ∆外接圆O 的 AB 上一点，满足：32A E A B=，31B C E C=-，12E C B E C A ∠=∠，又,DA DC 是O 的切线，2AC =，求()f P 的最小值．[解法一] （Ⅰ）如答一图1，由托勒密不等式，对平面上的任意点P ，有PA BC PC AB PB AC ⋅+⋅≥⋅． 因此 ()f P PA BC PC AB PD CA =⋅+⋅+⋅P B C A P D C A ≥⋅+⋅()PB PD CA =+⋅．因为上面不等式当且仅当,,,P A B C 顺次共圆时取等号，因此当且仅当P在A B C ∆的外接圆且在A C 上时， ()()f P PB PD CA =+⋅． …10分又因PB PD BD +≥，此不等式当且仅当,,B P D 共线且P 在BD 上时取等号．因此当且仅当P 为A B C ∆的外接圆与BD 的交点时，()f P 取最小值min ()f P AC BD =⋅．故当()f P 达最小值时，,,,P A B C 四点共圆． …20分 （Ⅱ）记E C B α∠=，则2E C A α∠=，由正弦定理有sin 23sin 32AE ABαα==，从而3sin 32sin 2αα=，即33(3sin 4sin )4sin cos αααα-=，所以答一图123343(1cos )4cos 0αα---=，整理得243cos 4cos 30αα--=， …30分 解得3cos 2α=或1cos 23α=-（舍去），故30α= ，60ACE ∠= ．由已知31B C E C=-=()sin 30sin E A C E A C∠-∠,有sin(30)(31)sin EAC EAC ∠-=-∠，即31sin cos (31)sin 22EAC EAC EAC ∠-∠=-∠，整理得231s i n c o s22EAC EAC -∠=∠，故1t a n 2323EAC ∠==+-，可得75EAC ∠=， …40分 从而45E ∠= ，45DAC DCA E ∠=∠=∠= ，A D C ∆为等腰直角三角形．因2AC =，则1C D =．又A B C ∆也是等腰直角三角形，故2BC =，212212cos1355BD =+-⋅⋅= ，5BD =． 故min ()5210f P BD AC =⋅=⋅=． …50分 [解法二] （Ⅰ）如答一图2，连接BD 交A B C ∆的外接圆O 于0P 点（因为D在O 外，故0P 在BD 上）．过,,A C D 分别作000,,P A P C P D 的垂线，两两相交得111A B C ∆，易知0P 在AC D ∆内，从而在111A B C ∆内，记A B C ∆之三内角分别为x y z ，，，则0180AP C y z x ∠=︒-=+，又因110B C P A ⊥，110B A P C ⊥，得1B y ∠=，同理有1A x ∠=，1C z ∠=， 所以111A B C ∆∽A B C ∆． …10分设11B C BC λ=，11C A C A λ=，11A B AB λ=，则对平面上任意点M ，有 000()()f P P A B C P D C A P C A Bλλ=⋅+⋅+⋅ 01101101P A B C P D C A P C A B =⋅+⋅+⋅ 1112AB C S ∆=11111M A B C M D C A M C A B≤⋅+⋅+⋅ ()MA BC MD CA MC AB λ=⋅+⋅+⋅ ()f M λ=， 从而 0()()f P f M ≤． 由M 点的任意性，知0P 点是使()f P 达最小值的点．由点0P 在O 上，故0,,,P A B C 四点共圆． …20分（Ⅱ）由（Ⅰ），()f P 的最小值 11102()A B Cf P S λ∆=2ABC S λ∆=，记E C B α∠=，则2E C A α∠=，由正弦定理有s i n 23s i n 32AE ABαα==，从而3s i n 32s i n 2αα=，即33(3sin 4sin )4sin cos αααα-=，所以23343(1cos )4cos 0αα---=，整理得243cos 4cos 30αα--=， …30分 解得3cos 2α=或1cos 23α=-（舍去），故30α= ，60ACE ∠= ． 由已知31B C E C=-=()sin 30sin E A C E A C∠-∠,有sin(30)(31)sin EAC EAC∠-=-∠ ，即31sin cos (31)sin 22EAC EAC EAC ∠-∠=-∠，整理得231s i n c o s22EAC EAC -∠=∠，故1t a n 2323EAC ∠==+-，可得75EAC ∠=， …40分 所以45E ∠=︒，A B C ∆为等腰直角三角形，2AC =，1ABC S ∆=，因为145AB C ∠=︒，1B 点在O 上，190AB B ∠=︒，所以11B BD C 为矩形，1112212cos1355B C BD ==+-⋅⋅︒=，故52λ=，所以m in 5()21102f P =⋅⋅=． …50分答一图2[解法三] （Ⅰ）引进复平面，仍用,,A B C 等代表,,A B C 所对应的复数．由三角形不等式，对于复数12,z z ，有 1212z z z z +≥+，当且仅当1z 与2z （复向量）同向时取等号．有 P A B C P C A B P A B C P C A B⋅+⋅≥⋅+⋅， 所以 ()()()()A P CBC P B A --+-- ()()()()A P C B C P B A ≥--+-- （1） P C A B C B P A=-⋅-⋅+⋅+⋅ ()()B P C A P B A C =--=⋅ ，从而 P A B C P C A B P D C A ⋅+⋅+⋅ P B A C P D A C≥⋅+⋅ ()PB PD AC =+⋅BD AC ≥⋅． （2） …10分（1）式取等号的条件是复数 ()()A P C B --与()()C P B A -- 同向，故存在实数0λ>，使得 ()()()(A P C B C P B A λ--=--， A P B A C P C Bλ--=--，所以 a r g ()a r g ()A PB AC P C B--=--， 向量PC 旋转到PA 所成的角等于BC 旋转到AB所成的角，从而,,,P A B C 四点共圆．（2）式取等号的条件显然为,,B P D 共线且P 在BD 上．故当()f P 达最小值时P 点在A B C ∆之外接圆上，,,,P A B C 四点共圆． …20分（Ⅱ）由（Ⅰ）知min ()f P BD AC =⋅． 以下同解法一．二、（本题满分50分）设()f x 是周期函数，T 和1是()f x 的周期且01T <<．证明： （Ⅰ）若T 为有理数，则存在素数p ，使1p是()f x 的周期；（Ⅱ）若T 为无理数，则存在各项均为无理数的数列{}n a 满足110n n a a +>>> (1,2,)n =⋅⋅⋅，且每个(1,2,)na n =⋅⋅⋅都是()f x 的周期．[证] （Ⅰ）若T 是有理数，则存在正整数,m n 使得n T m=且(,)1m n =，从而存在整数,a b ，使得1m a n b +=． 于是11m a nba bT ab T m m+==+=⋅+⋅是()f x 的周期． …10分 又因01T <<，从而2m ≥．设p 是m 的素因子，则m pm '=，m *'∈N ，从而11m p m'=⋅是()f x 的周期． …20分（Ⅱ）若T 是无理数，令111a T T ⎡⎤=-⎢⎥⎣⎦，则101a <<，且1a 是无理数，令 21111a a a ⎡⎤=-⎢⎥⎣⎦， ……111n n n a a a +⎡⎤=-⎢⎥⎣⎦，……． …30分由数学归纳法易知n a 均为无理数且01n a <<．又111n n a a ⎡⎤-<⎢⎥⎣⎦，故11n n n a a a ⎡⎤<+⎢⎥⎣⎦，即111n n n n a a a a +⎡⎤=-<⎢⎥⎣⎦．因此{}n a 是递减数列． …40分最后证：每个n a 是()f x 的周期．事实上，因1和T 是()f x 的周期，故111a T T ⎡⎤=-⎢⎥⎣⎦亦是()f x 的周期．假设k a 是()f x 的周期，则111k k k a a a +⎡⎤=-⎢⎥⎣⎦也是()f x 的周期．由数学归纳法，已证得na 均是()f x 的周期． …50分三、（本题满分50分）设0k a >，1,2,,2008k = ．证明：当且仅当200811k k a =>∑时，存在数列{}n x 满足以下条件：（ⅰ）010n n x x x +=<<，1,2,3,n = ； （ⅱ）lim n n x →∞存在；（ⅲ）20082007111n n kn k k n kk k x x ax ax -+++==-=-∑∑，1,2,3,n = ．[证] 必要性：假设存在{}n x 满足（ⅰ），（ⅱ），（iii ）．注意到（ⅲ）中式子可化为 2008111()n n k n k n k k x x a x x -++-=-=-∑，n ∈*N ，其中00x =．将上式从第1项加到第n 项，并注意到00x =得 11122220082008()()()n n n n x a x x a x x a x x +++=-+-++-． …10分由（ⅱ）可设lim n n b x →∞=，将上式取极限得1122200820()()()b a b x a b x a b x =-+-++-20081122200820081()k k b a a x a x a x ==⋅-+++∑20081k k b a =<⋅∑，因此200811k k a =>∑． …20分充分性：假设200811k k a =>∑．定义多项式函数如下：20081()1kkk f s as ==-+∑，[0,1]s ∈，则()f s 在[0,1]上是递增函数，且(0)10f =-<，20081(1)10kk f a==-+>∑．因此方程()0f s =在[0,1]内有唯一的根0s s =，且001s <<，即0()0f s =． …30分 下取数列{}n x 为01nkn k x s==∑，1,2,n = ，则明显地{}n x 满足题设条件（ⅰ），且10011n nkn k s s x ss +=-==-∑．因001s <<，故10l i m 0n n s+→∞=，因此1000lim lim11n n n n s s sx s s +→∞→∞-==--，即{}n x 的极限存在，满足（ⅱ）． …40分最后验证{}n x 满足（ⅲ），因0()0f s =，即2008011k k k a s ==∑，从而20082008200810001111()()nk n n k n n k k k n kn kk k k x x s a s s a s a x x +-++-===-====-∑∑∑．综上，存在数列{}n x 满足（ⅰ），（ⅱ），（ⅲ）． …50分。

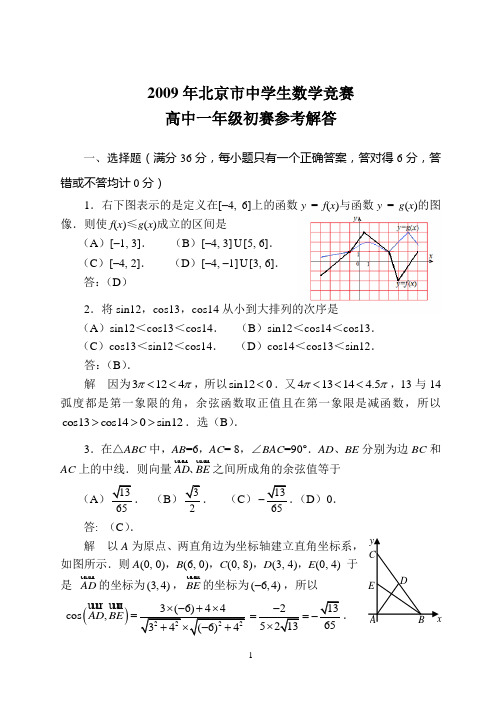
2009年北京市中学生数学竞赛 高中一年级初赛参考解答一、选择题（满分36分，每小题只有一个正确答案，答对得6分，答错或不答均计0分）1．右下图表示的是定义在[–4, 6]上的函数y = f (x )与函数y = g (x )的图像．则使f (x )≤g (x )成立的区间是（A ）[–1, 3]． （B ）[–4, 3] [5, 6]． （C ）[–4, 2]． （D ）[–4, –1] [3, 6]． 答：（D ）2．将sin12，cos13，cos14从小到大排列的次序是（A ）sin12＜cos13＜cos14． （B ）sin12＜cos14＜cos13． （C ）cos13＜sin12＜cos14． （D ）cos14＜cos13＜sin12． 答：（B ）．解 因为3124ππ<<，所以sin120<．又41314 4.5ππ<<<，13与14弧度都是第一象限的角，余弦函数取正值且在第一象限是减函数，所以cos13cos140sin12>>>．选（B ）．3．在△ABC 中，AB =6，AC = 8，∠BAC =90°．AD 、BE 分别为边BC 和AC 上的中线．则向量AD BE、之间所成角的余弦值等于 （A）65． （B）2． （C）65-．（D ）0． 答: （C ）．解 以A 为原点、两直角边为坐标轴建立直角坐标系，如图所示．则A (0, 0)，B (6, 0)，C (0, 8)，D (3, 4)，E (0, 4) 于是 AD 的坐标为(3,4)，BE的坐标为(6,4)-，所以()cos ,AD BE ===4．log 2sin12π+ log 2sin6π+ log 2sin512π等于 （A ）–3． （B ）–1． （C ）1． （D ）3．答：（A ）解 2225l o g s i n l o g si n l o g s i n 12612πππ++ =215log sin sin 12212ππ⎛⎫⋅⋅ ⎪⎝⎭=21log sin cos 21212ππ⎛⎫⋅ ⎪⎝⎭=21log 2sin cos 41212ππ⎛⎫⋅⋅ ⎪⎝⎭2211log sin log 3468π⎛⎫===- ⎪⎝⎭．5. 对于函数2(0)()2(0)x bx c x f x x ⎧++≥=⎨-<⎩，f (4)=f (0)，f (1)= –1，则方程f (x )= x的解的个数为（A ）0． （B ）1． （C ）2． （D ）3． 答：（D ）．解 由f (4) = f (0)，f (1)= −1，得16+4b +c = c ，1+b +c = −1，解得b = −4，c = 2．所以242(0)()2(0)x x x f x x ⎧-+≥=⎨-<⎩， 其图像如右图所示，共3个解．6．a 为参数，函数2283()()3()3x a x a f x x a x a -+--=+--是偶函数，则a 可取值的集合是（A ）{}0,5．（B ）{}2,5-．（C ）{5,2}-．（D ）{}1,2009． 答：（C ）．解 如果函数2283()()3()3x a x a f x x a x a -+--=+--是偶函数，则f (–a )=f (a )， 即28322323a a a a a a +--+⋅=⋅．所以，要么a =0，要么8+a −3a = a −2+a 2．若取a =0，函数28()(33)x x f x x --=-不是偶函数．故a ≠0．若8+a −3a = a −2+a 2，则a =−5，或a =2，此时，函数2323()(5)3(5)3x xf x x x +-=---+和22()(2)3(2)3x x f x x x +-=+- 都是偶函数．二、填空题（满分64分，每小题8分） 1. 依次排列的正数1235960,,,,,b b b b b 满足35960241235859b b b b b b b b b b ===== ， 试确定11501260log ()b b bb b 的值．答：30． 解 设35960241235859b b b b b q b b b b b ====== ，所以 23575859213141581591601b b q b b q b b q b b q b b q b b q ====== ，，，，，， 则 11501260l o g ()b b bb b =1049110159111log ()b q b q b q b q b q ⋅⋅⋅⋅=2104916001591log ()b q b q ++++=2591259301log ()30b q b q =．2．已知sin(α+β)=0.8，cos(α–β)=0.3，求(sin α–cos α) (sin β–cos β)的值． 答：−0.5．解 (sin α–cos α) (sin β–cos β)=(cos αcos β+sin αsin β) – (sin αcos β+cos αsin β) =cos(α–β) − sin(α+β) = 0.3−0.8 = −0.5．3．如果四边形ABCD 顶点的坐标依次为A (1,2)，B (2,5)，C (7,3)，D (5,1)，求四边形ABCD 的面积．答：13.5.解 如图，在坐标平面上作点A ，B，C ，D ，围绕所得到的四边形ABCD 作外接长方形,其顶点为M (1, 1)，N (1, 5)，P (7, 5)，T (7, 1)，四边形ABCD 则是从长方形MNPT 中去掉△AMD 、△ANB 、△BPC 、△CTD 得到的图形，易知S MNPT =24，S △AMD =2，S △ANB =1.5，S △BPC =5，S △CTD =2，因此，S ABCD =24−(2+1.5+5+2)=13.5．4．[x ] 表示不超过x 的最大整数，若[log 36]+ [log 37]+ [log 38]+…+ [log 3(n –1)]+ [log 3n ]=2009，试确定正整数n 的值． 答：474.解 ∵[log 36]= [log 37]= [log 38]=1，∴[log 36]+ [log 37]+ [log 38]=3， ∵[log 39]=[log 310]=…=[log 326]=2，∴[log 39]+ [log 310]+…+[log 326]=36， ∵[log 327]=[log 328]=…=[log 380]=3，∴[log 327]+[log 328]+…+[log 380]=162， ∵[log 381]=[log 382]=…=[log 3242]=4，∴[log 381]+[log 382]+…+[log 3242]=648， 又∵3+36+162+648=849=2009−1160＜2009，[log 3243]=[log 3244]=…=[log 3728]=5，[log 3243]+[log 3244]+…+[log 3728]=2430＞1160，∴243＜243728.n <<n ＜728．由于849+5×(n –242)=2009，解得n =474．5．在△ABC 中，AB =BC ＞AC ，AH 与AM 分别为BC 上的高线和中线，38AMH ABC S S ∆∆=．试确定cos ∠BAC 的值． 答：cos ∠BAC =14． 解 在△ABC 中，AB =BC ＞AC ，AH ⊥BC ，BM =MC ，作BD ⊥AC 于D ． 设AB =BC =a ，则S △ABC =12AH ·BC =12AH ·a ，且S △AMH =12AH ·MH ，因为38AMH ABC S S ∆∆=，所以132,182AH MHAH a ⋅=⋅所以MH =38a ，HC =MC −MH =12a –38a =18a ．设∠BAC =β，则∠BCA =β．由Rt △BCD 得DC = a cos β．在△ABC 中，AC =2 DC =2 a cos β．由Rt △ACH 得cos β=HC AC =182cos aa β，即cos 2β=116．由于β是锐角, 所以cos β=14．6．函数f (x )=2x 2−2x −1和g (x )=−5x 2+2x +3的图像交于两个点，通过这两个交点的直线方程为y =ax +b ．求a –b 的值．答：−1．解 函数f (x )= 2x 2−2x −1和g (x )=–5x 2+2x +3的图像两个交点的坐标是方程组22221523y x x y x x ⎧=--⎨=-++⎩的两个解，因此 7y =5(2x 2−2x –1)+2(−5x 2+2x +3)=−6x +1所以图形的两个交点在直线y =6177x -+上，即6177a b =-=，，a –b = −1．7．已知6027位数2009abcabcabcabc abc 个是91的倍数．求三位数abc 的最小值与最大值的和． 答：1092．解 由于91=7×13，1001=7×11×13，所以91|1001.而abcabc =1001×abc ，所以91|abcabc ．已知2009abcabcabcabc abc 个被91整除，而2009abcabcabcabc abc 个=21004abcabcabcabc abc ⨯ 个×1001+abc ，又21004abcabcabcabc abc ⨯ 个被91整除，所以abc 被91整除．能被91整除的三位数最小为182，最大为910，所以abc 的最小值与最大值的和=182+910=1092．8. 如图，在菱形ABCD 中，∠ABC =120°，BCP 是BC 延长线上向远离点C 方向运动的一个动点，AP 交CD 于点E ，联结BE 并延长交DP 于点Q ．如果动点P 在初始位置时∠QBP =15°，在终止位置时∠QBP =35°，试确定P 的曲线段的长度．答：43π．解 连接BD ，作△ABD 的外接圆交AP 于F ，连接BF , DF , FC 和CQ ，易知∠DFB =∠DFP =∠BFP =120°， ∠BFE =∠ECP =120°，所以B , F , E , C 四点共圆，B CP所以∠1=∠2，由于∠DFP=∠DCP=120°，所以D, F, C, P四点共圆，所以∠2=∠3，因此∠1=∠3，所以B, C, Q, D四点共圆．即点Q在△BCD的外接圆上．易知，当P在BC延长线上由C向外运动时，Q在△BCD的外接圆的 CD 上从点C起沿逆时针方向运动．△BCD是边长为它的外接圆半径为263=，所以外接圆周长为2π×6=12π．由于Q在△BCD的外接圆上运动的圆周角等于35°−15°=20°，所以Q在△BCD的外接圆上运动的弧为40°，是整个圆周的19，所以，动点P运动时Q走过的这段曲线12Q Q的长度为12493ππ=．2009年北京市中学生数学竞赛高中一年级初赛参考答案选择题答案填空题答案。

2008年全国高中数学联合竞赛一试试题一、选择题(本题满分36分，每小题6分)1.函数f (x )=5−4x +x 22−x在(−∞,2)上的最小值是()A.0 B.1 C.2 D.3解答f (x )=2−x +12−x⩾2，等号成立时x =1.所以选C .2.设A =[−2,4),B ={x |x 2−ax −4⩽0}，若B ⊆A ，则实数a 的取值范围为()A.[−1,2)B.[−1,2]C.[0,3]D.[0,3)解答设f (x )=x 2−ax −4，依题意f (x )=0的两根x 1,x 2∈[−2,4).由于∆=a 2+16>0，于是 f (−2)=2a ⩾0,f (4)=12−4a >0,a 2∈[−2,4)⇒a ∈[0,3).所以选D .3.甲、乙两人进行乒乓球比赛，约定每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为23，乙在每局中获胜的概率为13，且各局胜负相互独立，则比赛停止时已打局数ξ的期望Eξ为()A.24181 B.26681 C.27481 D.670243解答由于比赛不满6局时胜者比对方多2分，则比赛局数只能是2,4,6.其中2局分胜负的情况为甲或乙胜2局；4局分胜负的情况为甲或乙胜3局负1局，且负的1局在前2局.于是需要比赛6局的情况是在前4局中，甲或乙在1,2局和3,4局中均为1胜1负.相应分布列为局数ξ246概率P (23)2+(13)2C 12·13(23)3+C 12·23(13)34(13)2(23)2于是Eξ=2×59+4×2081+6×1681=26681.所以选B .4.若三个棱长均为整数(单位：cm )的正方体的表面积之和为564cm 2，则这三个正方体的体积之和为()A.764cm 3或586cm 3B.764cm 3C.586cm 3或564cm 3D.586cm 3解答设三个正方体的棱长分别为a,b,c ，则6(a 2+b 2+c 2)=564⇒a 2+b 2+c 2=94.由于(3k ±1)2≡1(mod 3)，于是a,b,c 中必有2个数为3的倍数，不妨设为a,b .检验得32+62=45⇒c =7；32+92=90⇒c =2.从而a 3+b 3+c 3=586或764.所以选A .5.方程组 x +y +z =0,xyz +z =0,xy +yz +xz +y =0的有理数解(x,y,z )的个数为()A.1B.2C.3D.4解答xyz +z =z (xy +1)=0⇒z =0或xy =−1.当z =0时， x +y =0,xy +y =y (x +1)=0⇒ x =0,y =0或 x =−1,y =1.当xy =−1时， (x +y )2=y −1,xy =−1⇒(y −1y )2=y −1⇒y 2+1y 2=y +1⇒y 4−y 3−y 2+1=(y −1)(y 3−y −1)=0.由于y 3−y −1=0没有有理根，则y =1⇒x =−1.于是有理解(x,y,z )的个数为2，所以选B .6.设△ABC 的内角A 、B 、C 所对的边a 、b 、c 成等比数列，则sin A cot C +cos A sin B cot C +cos B的取值范围是()A.(0,+∞) B.(0,√5+12)C.(√5−12,√5+12) D.(√5−12,+∞)解答设等比数列a,b,c 的公比为q ，则b =aq,c =aq 2.于是 a +b >c,b +c >a ⇒ q 2−q −1<0,q 2+q −1>0⇒√5−12<q <√5+12.sin A cot C +cos A sin B cot C +cos B =sin A cos C +cos A sin C sin B cos C +cos B sin C =sin (A +C )sin (B +C )=sin B sin A =b a =q ∈(√5−12,√5+12).所以选C .二、填空题(本题满分54分，每小题9分)7.设f (x )=ax +b ，其中a,b 为实数，f 1(x )=f (x ),f n +1(x )=f (f n (x ))，n =1,2,···，若f 7(x )=128x +381，则a +b =.解答f 2(x )=a (ax +b )+b =a 2x +ab +b =a 2x +b (1−a 2)1−a ，f 3(x )=a (a 2x +ab +b )+b =a 3x +a 2b +ab +b =a 3x +b (1−a 3)1−a ，···，f 7(x )=a 7x +b (1−a 7)1−a =128x +381⇒a =2,b =3.所以a +b =5.8.设f (x )=cos 2x −2a (1+cos x )的最小值为−12，则a =.解答设t =cos x ∈[−1,1]，则f (x )=2t 2−1−2a (1+t )=2t 2−2at −2a −1=2(t −a 2)2−a 22−2a −1.于是 a 2∈[−1,1],−a 22−2a −1=−12或 a 2>1,1−4a =−12或 a 2<−1,1=−12.解得a =−2±√3(−2−√3舍去).所以a =−2+√3.9.将24个志愿者名额分配给3所学校，则每校至少有一个名额且各校名额互不相同的分配方法共有种.解答将24个志愿者名额分配给3所学校，每校至少有一个名额的分配方法有C 223=253种；3所学校名额相同的分配方法有1种；有且仅有2所学校名额相同的分配方法(即满足2x +z =24且x =z 的正整数解)有10×3=30种.所以3所学校名额互不相同的分配方法共有253−1−30=222种.10.设数列{a n }的前n 项和S n 满足：S n +a n =n −1n (n +1),n =1,2,···，则通项a n =.解答S n +a n =2S n −S n −1=n −1n (n +1)=2n +1−1n ⇒2(S n −1n +1)=S n −1−1n ⇒数列{S n −1n +1}是公比为12的等比数列，且S 1−12=−12，于是S n −1n +1=−(12)n ⇒S n =1n +1−(12)n (n ∈N ∗).所以a n =S n −S n −1=1n +1−(12)n −1n +(12)n −1=(12)n −1n (n +1).11.设f (x )是定义在R 上的函数，若f (0)=2008，且对任意x ∈R ，满足f (x +2)−f (x )⩽3·2x ,f (x +6)−f (x )⩾63·2x ，则f (2008)=.解答f (2008)=f (0)+[f (2)−f (0)]+[f (4)−f (2)]+···+[f (2008)−f (2006)]⩽2008+3(20+22+···+22006)=2008+41004−1=22008+2007；f (2004)=f (0)+[f (6)−f (0)]+[f (12)−f (6)]+···+[f (2004)−f (1998)]⩾2008+63(20+26+···+21998)=2008+64334−1=22004+2007，又 f (x +6)−f (x )⩾63·2x ,f (x )−f (x +2)⩾−3·2x⇒f (x +6)−f (x +2)⩾60·2x ⇒f (2008)−f (2004)⩾60·22002⇒f (2008)⩾f (2004)+60·22002=64·22002+2007=22008+2007.所以f (2008)=22008+2007.12.一个半径为1的小球在一个内壁棱长为4√6的正四面体容器内可向各个方向自由运动，则该小球永远不可能接触到的容器内壁的面积是.解答如图，小球O 是正四面体P −DEF 的内切球.设AC 的中点为G ，作OM ⊥P G 于M .则有r =1⇒P O =3⇒P M =2√2=13P G ，同理AN =2√2=13AF ⇒MN =2√6.于是小球在正四面体一个面内能接触到的区域是以MN 为边长的正三角形及内部，其面积为正四面体一个面面积的14.所以该小球永远不可能接触到的容器内壁的面积为正四面体表面积的34，即S =34×4×√34×(4√6)2=72√3.三、解答题(本题满分60分，每小题20分)13.已知函数f (x )=|sin x |的图像与直线y =kx (k >0)有且仅有三个交点，交点的横坐标的最大值为α，求证：cos αsin α+sin 3α=1+α24α.解答如图，直线y =kx (k >0)与f (x )=|sin x |的图像相切于点A (α,−sin α)(π<α<3π2)，由于(−sin x )′=−cos x，于是有−sin αα=−cos α⇒α=tan α.所以cos αsin α+sin 3α=cos α2sin 2αcos α=12sin 2α=1+tan 2α4tan α=1+α24α.14.解不等式log 2(x 12+3x 10+5x 8+3x 6+1)<1+log 2(x 4+1).解答解析一：原不等式⇒x 12+3x 10+5x 8+3x 6+1<2(x 4+1)⇒x 12+3x 10+5x 8+3x 6−2x 4−1<0⇒(x 4+x 2−1)(x 8+2x 6+4x 4+x 2+1)<0⇒x 4+x 2−1<0⇒0⩽x 2<√5−12⇒x ∈(− √5−12, √5−12).解析二：原不等式⇒x 12+3x 10+5x 8+3x 6+1<2(x 4+1)⇒x 12+3x 10+3x 8+x 6+2(x 8+x 6)<2x 4+1⇒x 6+3x 4+3x 2+1+2(x 2+1)<2x 2+1x 6⇒(x 2+1)3+2(x 2+1)<(1x 2)3+2x 2⇒x 2+1<1x 2⇒x 4+x 2−1<0⇒0⩽x 2<√5−12⇒x ∈(− √5−12, √5−12).15.如图，P 是抛物线y 2=2x 上的动点，点B 、C 在y 轴上，圆(x −1)2+y 2=1内切于△P BC ，求△P BC 面积的最小值.解答如图，设P (2t 2,2t ),M (1,0)，过P 的直线y −2t =k (x −2t 2)与圆M 相切，则有|k (1−2t 2)+2t |√1+k2=1⇒4t 2(t 2−1)k 2−4t (2t 2−1)k +4t 2−1=0设直线P B,P C 的斜率为k 1,k 2，于是y B =2t −2t 2k 1,y C =2t −2t 2k 2，S △P BC =12·2t 2|y B−y C |=2t 4|k 1−k 2|=2t 4·√16t 2(2t 2−1)2−16t 2(t 2−1)(4t 2−1)4t 2(t 2−1)=2t 2·|t |√(2t 2−1)2−(t 2−1)(4t 2−1)t 2−1=2t 4t 2−1=2(t 4−1+1t 2−1)=2(t 2+1+1t 2−1)=2(t 2−1+1t 2−1+2)⩾2(2+2)=8，等号成立时t 2=2⇒t =±√2.所以△P BC 面积的最小值是8.。

北京市中学生数学竞赛高中一年级初赛试题参考解答选择题答案填空题答案一、选择题1．集合A={2, 0, 1, 7}，B={x| x2−2∈A, x−2∉A}，则集合B的所有元素之积为（A）36．（B）54．（C）72．（D）108．答：A．解：由x2−2∈A，可得x2=4，2，3，9，即x=±2，，±3．又因为x−2∉A，所以x≠2，x≠3，故x= −2，，，−3．因此，集合B={−2, , , , −3}．所以，集合B的所有元素的乘积等于(−2)()(−3)=36．2．已知锐角△ABC的顶点A到它的垂心与外心的距离相等，则tan(2BAC∠)=（A．（B）2．（C）1．（D答：A．解：作锐角△ABC的外接圆，这个圆的圆心O在形内，高AD，CE相交于点H，锐角△ABC的垂心H也在形内．连接BO交⊙O于K，BK为Oe的直径. 连接AK，CK．因为AD，CE是△ABC的高，∠KAB，∠KCB是直径BK上的圆周角，所以∠KAB=∠KCB=90°．于是KA//CEKC//AD，因此AKCH是平行四边形．所以KC =AH =AO =12BK ． 在直角△KCB 中，由KC =12BK ，得∠BKC =60°，所以∠BAC =∠BKC =60°． 故tan(2BAC∠)= tan30°=3．3．将正奇数的集合{1, 3, 5, 7, …}从小到大按第n 组2n −1个数进行分组：{1}，{3, 5, 7}，{9, 11, 13, 15, 17}，…，数2017位于第k 组中，则k 为（A ）31． （B ）32． （C ）33． （D ）34． 答：B.解：数2017是数列a n = 2n −1的第1009项．设2017位于第k 组，则1+3+5+…+(2k −1)≥1009，且1+3+5+…+(2k −3)＜1009．即k 是不等式组221009(1)1009k k ⎧≥⎨-<⎩的正整数解，解得k =32，所以2017在第32组中． 4．如图，平面直角坐标系x -O -y 中，A , B 是函数y =1x在第I 象限的图象上两点，满足∠OAB =90°且AO = AB ，则等腰直角△OAB 的面积等于（A ）12． （B ）2． （C） （D答：D ．解：依题意，∠OAB =90°且AO = AB ，∠AOB =∠ABO =45°．过点A 做y 轴垂线交y 轴于点C ，过点B 做y 轴平行线，交直线CA 于点D ． 易见△COA ≌△DAB ．设点A (a , 1a )，则点B (a +1a , 1a − a )．因为点B 在函数y =1x 的图象上，所以(a +1a )(1a− a )=1，即21a− a 2=1． 因此S △ABC =12OA 2=12(21a + a 2) =12= 5．已知f (x ) = x 5 + a 1x 4 + a 2x 3 + a 3x 2 + a 4x + a 5，且当m =1, 2, 3, 4时，f (m )=2017m ，则f (10)−f (−5)=（A ）71655． （B ）75156． （C ）75615． （D ）76515．答：C ．解：因为 当m =1, 2, 3, 4时，f (m )=2017m ，所以1, 2, 3, 4是方程f (x )−2017x =0的四个实根，由于5次多项式f (x )−2017x 有5个根，设第5个根为p ，则f (x )−2017x = (x −1)(x −2)(x −3)(x −4)(x −p )即 f (x ) = (x −1)(x −2)(x −3)(x −4)(x −p )+2017x ．所以f (10)=9×8×7×6(10−p )+2017×10，f (−5)=−6×7×8×9(5+p )−2017×5， 因此f (10)− f (−5)=15(9×8×7×6+2017)=75615．6．已知函数2||,,()42,.x x a f x x ax a x a ≤⎧=⎨-+>⎩若存在实数m ，使得关于x 的方程f (x )=m有四个不同的实根，则a 的取值范围是（A ）17a >． （B ）16a >． （C ）15a >． （D ）14a >．答：D ．解：要使方程f (x )=m 有四个不同的实根，必须使得y =m 的图像与y =f (x )的图像有4个不同的交点．而直线与y =|x |的图像及二次函数的图像交点都是最多为两个，所以y =m 与函数y =|x |, x ≤a 的图像和y =x 2−4ax +2a , x ＞a 的图像的交点分别都是2个．而存在实数m ，使y =m 与y =|x |, x ≤a 的图像有两个交点，需要a ＞0，此时0＜m ≤a ；又因为y =x 2−4ax +2a , x ＞a 顶点的纵坐标为242(4)4a a ⨯-，所以，要y =m 与y =x 2−4ax +2a ,x ＞a 的图像有两个交点，需要m ＞242(4)4a a ⨯-．因此y =m 的图像与y =f (x )的图像有4个不同的交点需要满足：0＜m ≤a 且m ＞242(4)4a a ⨯-，解得14a >．二、填空题1. 用[x ]表示不超过x 的最大整数，设S =++++L ，求的值．答：24．解：因为12≤1, 2, 3＜22，所以1,2，因此1===，共3个1；同理，22≤4, 5, 6, 7, 8＜32，因此，2=====，共5个2；又32≤9, 10, 11, 12, 13, 14, 15＜42，因此3===K ，共7个3；依次类推，4=====K ，共9个4；5=====K ，共11个5；6=====K ，共13个6；7=====K ，共15个7；8=====K ，共17个8；9=====K ，共19个9.S= (++)+(++++)+…+(++L ) = 1×3+2×5+3×7+4×9+5×11+6×13+7×15+8×17+9×19=615．因为242=576＜615=S ＜625=252，即2425，所以，．2．确定(201721log 2017×201741log 2017×201781log 2017×2017161log 2017×2017321log 2017)15的值．答：8．解：原式=(20172017log 2×20172017log 4×20172017log 8×20172017log 16×20172017log 32)15=(2×4×8×16×32)15= (21×22×23×24×25)15=(21+2+3+4+5)15=(215)15=23=8．3．已知△ABC 的边ABBCCA厘米，求△ABC 的面积． 答：9.5平方厘米．解：注意到13=32+22，29=52+22，34=52+32，作边长为5厘米的正方形AMNP ，分成25个1平方厘米的正方形网格，如图．根据勾股定理，可知，AB厘米，BCCA米，因此△ABC 的面积可求．△ABC 的面积=5×5−12×3×5−12×2×5−12×2×3=9.5（平方厘米）．4.设函数()f x =的最大值为M ，最小值为N ，试确定M +N的值．答：2．解：由已知得()1f x =+因为NA M BP)())(())]x x x x ++-=---=22ln(()1())ln10x x -+--==，所以()))x x -=-，因此，)x +是奇函数．进而可判定，函数22)()1x x g x x ++=+为奇函数．则g (x )的最大值M 1和最小值N 1满足M 1+N 1= 0． 因为M =M 1+1，N = N 1+1，所以 M + N = 2．5．设A 是数集{1, 2, …, 2017}的n 元子集，且A 中的任意两个数既不互质，又不存在整除关系，确定n 的最大值．答：504．解：在数集{1, 2, …, 2017}中选取子集，使得子集中任意两个数不互质，最大的子集是偶数集{2, 4, …, 2016}共1008个元素，但其中，有的元素满足整除关系，由于1010的2倍是2020，所以集合A ={1010, 1012, 1014, …, 2016}中，任意两个数既不互质，又不存在整除关系，A 中恰有504个元素．事实上504是n 的最大值．因为若从{1009, 1011, …, 2017}中任取一个奇数，会与A 中的与它相邻的偶数互质；若从{1, 2, 3, …, 1008}中任取一数，则它的2倍在A 中，存在整除关系．6．如图，以长为4厘米的线段AB 的中点O 为圆心、2厘米为半径画圆，交AB 的中垂线于点E 和F . 再分别以A 、B 为圆心，4厘米为半径画圆弧交射线AE 于点C ，交射线BE 于点D . 再以E 为圆心DE 为半径画圆弧»DC，求这4条实曲线弧连接成的“卵形”¼AFBCDA 的面积．（圆周率用π表示，不取近似值）答：(12−)π−4平方厘米．解：半圆(O , 2)的面积=12π×22=2π．因为AO=OB =2，所以AB=AC=BD =4，AE =BE，ED =EC =4−． 又∠AEB =∠CED =90°，∠EAB =∠EBA =45°，因此，扇形BAD 的面积=扇形ACB 的面积=18π×42=2π，△AEB 的面积=12×4×2=4，直角扇形¼EDC的面积=14π(4−2)2= 6π−π， 卵形¼AFBCDA 的面积 = 半圆(O , 2)的面积+扇形BAD 的面积+扇形ACB 的面积 −△AEB 的面积+直角扇形¼EDC的面积B FADCEO= 2π+2×2π−4+6π−4π = (12−)π−4（平方厘米）．7. 已知22()1005000x f x x x =-+，求f (1)+f (2)+…+f (100)的值．答：101．解：设g (x ) = x 2−100x +5000，则g (100−x ) = (100−x )2−100(100−x )+5000=1002−200x +x 2−1002+100x +5000= x 2−100x +5000= g (x )， 即 g (k ) = g (100−k )．所以 f (k ) + f (100−k ) =22(100)()(100)k k g k g k -+- =22(100)()k k g k +-=2， 又 f (50) =2250=150100505000-⨯+， f (100)22100==2.1001001005000-⨯+ 所以， f (1)+ f (2)+…+ f (100)= (f (1)+ f (99))+ (f (2)+ f (98))+…+ (f (49)+ f (51))+ f (50)+ f (100) = 2×49+1+2=101．8．如图，在锐角△ABC 中，AC = BC = 10，D 是边AB 上一点，△ACD 的内切圆和△BCD 的与BD 边相切的旁切圆的半径都等于2，求AB 的长．答：解：线段AB 被两圆与AB 的切点及点D 分成四段，由于两圆半径相等，再根据切线长定理，可知中间两段相等，于是可将这四段线段长度分别记为a , b , b , c ，由于圆O 2的切线长CE = CG ，所以BC +a = CD +b = (AC −c +b )+b ，而AC = BC ，所以a +c = 2b ．由等角关系可得△AO 1F ∽△O 2BE ，得12O F BEAF O E=，即22ac =，由此推出ac = 4． 分别计算△BCD 和△ACD 的面积：12(),2BCD S BC CD BD ∆=⨯+-12()2ACD S AC CD AD ∆=⨯++所以24ACD BCD S S AD BD AB a c b b ∆∆-=+==++=. ①又设由C 引向AB 的高为h ，可得1()2ACD BCD S S c a h ∆∆-=-=② 由①、②两式可得DACBD A C B EG FO 1 O 2 · a b b c·4b =将a +c = 2b ，ac = 4代入，化简得42251000b b -+=解得b 2=5或b 2=20，即b b ，（负根舍）．于是，AB = a +c +2b = 4b ，或AB若AB ，△ABC 为钝角三角形，不合题设△ABC 是锐角三角形的要求．所以AB 的长为．。

2008年全国高中数学联合竞赛一试试题（A 卷）一、选择题（本题满分36分，每小题6分）1．函数254()2x x f x x-+=-在(,2)-∞上的最小值是 （ ）A ．0B ．1C ．2D ．32．设[2,4)A =-，2{40}B x x ax =--≤，若B A ⊆，则实数a 的取值范围为 （ ） A ．[1,2)- B ．[1,2]- C ．[0,3] D ．[0,3)3．甲乙两人进行乒乓球比赛，约定每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或打满6局时停止．设甲在每局中获胜的概率为23，乙在每局中获胜的概率为13，且各局胜负相互独立，则比赛停止时已打局数ξ的期望E ξ为 （ ） A. 24181 B. 26681 C. 27481D. 6702434．若三个棱长均为整数（单位：cm ）的正方体的表面积之和为564 cm 2，则这三个正方体的体积之和为 （ ） A. 764 cm 3或586 cm 3 B. 764 cm 3 C. 586 cm 3或564 cm 3 D. 586 cm 35．方程组0,0,0x y z xyz z xy yz xz y ++=⎧⎪+=⎨⎪+++=⎩的有理数解(,,)x y z 的个数为 （ ） A. 1 B. 2 C. 3 D. 46．设ABC ∆的内角A B C ,,所对的边,,a b c 成等比数列，则sin cot cos sin cot cos A C AB C B++的取值范围是（ ）A. (0,)+∞B.C.D. )+∞二、填空题（本题满分54分，每小题9分）题15图7．设()f x ax b =+，其中,a b 为实数，1()()f x f x =，1()(())n n f x f f x +=，1,2,3,n =L ，若7()128381f x x =+，则a b += .8．设()cos 22(1cos )f x x a x =-+的最小值为12-，则a = ．9．将24个志愿者名额分配给3个学校，则每校至少有一个名额且各校名额互不相同的分配方法共有 种．10．设数列{}n a 的前n 项和n S 满足：1(1)n n n S a n n -+=+，1,2,n =L ，则通项n a = ．11．设()f x 是定义在R 上的函数，若(0)2008f = ，且对任意x ∈R ，满足 (2)()32x f x f x +-≤⋅，(6)()632x f x f x +-≥⋅，则)2008(f = ．12．一个半径为1的小球在一个内壁棱长为46的正四面体容器内可向各个方向自由运动，则该小球永远不可能接触到的容器内壁的面积是 ．．三、解答题（本题满分60分，每小题20分）13．已知函数|sin |)(x x f =的图像与直线y kx = )0(>k 有且仅有三个交点，交点的横坐标的最大值为α，求证：2cos 1sin sin 34ααααα+=+．14．解不等式121086422log (3531)1log (1)x x x x x ++++<++．15．如题15图，P 是抛物线22y x =上的动点，点B C ,在y 轴上，圆22(1)1x y -+=内切于PBC ∆，求PBC ∆面积的最小值．2008年全国高中数学联合竞赛一试参考答案及评分标准（A卷）说明：1．评阅试卷时，请依据本评分标准．选择题只设6分和0分两档，填空题只设9分和0分两档；其他各题的评阅，请严格按照本评分标准的评分档次给分，不要增加其他中间档次．2．如果考生的解答方法和本解答不同，只要思路合理、步骤正确，在评卷时可参考本评分标准适当划分档次评分，解答题中5分为一个档次，不要增加其他中间档次．一、选择题（本题满分36分，每小题6分）1．函数254()2x x f x x-+=-在(,2)-∞上的最小值是 （ C ）A ．0B ．1C ．2D ．3[解] 当2x <时，20x ->，因此21(44)1()(2)22x x f x x x x +-+==+---2≥2=，当且仅当122x x=--时上式取等号．而此方程有解1(,2)x =∈-∞，因此()f x 在(,2)-∞上的最小值为2．2．设[2,4)A =-，2{40}B x x ax =--≤，若B A ⊆，则实数a 的取值范围为 （ D ） A ．[1,2)- B ．[1,2]- C ．[0,3] D ．[0,3) [解] 因240x ax --=有两个实根12a x =22a x =故B A ⊆等价于12x ≥-且24x <，即22a ≥-且42a ，解之得03a ≤<．3．甲乙两人进行乒乓球比赛，约定每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或打满6局时停止．设甲在每局中获胜的概率为23，乙在每局中获胜的概率为13，且各局胜负相互独立，则比赛停止时已打局数ξ的期望E ξ为 （ B ）A.24181 B. 26681 C. 27481 D. 670243 [解法一] 依题意知，ξ的所有可能值为2，4，6.设每两局比赛为一轮，则该轮结束时比赛停止的概率为22215()()339+=．若该轮结束时比赛还将继续，则甲、乙在该轮中必是各得一分，此时，该轮比赛结果对下轮比赛是否停止没有影响．从而有5(2)9P ξ==， 4520(4)()()9981P ξ===，2416(6)()981P ξ===，故520162662469818181E ξ=⨯+⨯+⨯=．[解法二] 依题意知，ξ的所有可能值为2，4，6.令k A 表示甲在第k 局比赛中获胜，则k A 表示乙在第k 局比赛中获胜． 由独立性与互不相容性得12125(2)()()9P P A A P A A ξ==+=， 1234123412341234(4)()()()()P P A A A A P A A A A P A A A A P A A A A ξ==+++332112202[()()()()]333381=+=，1234123412341234(6)()()()()P P A A A A P A A A A P A A A A P A A A A ξ==+++2221164()()3381==，故520162662469818181E ξ=⨯+⨯+⨯=．4．若三个棱长均为整数（单位：cm ）的正方体的表面积之和为564 cm 2，则这三个正方体的体积之和为 （ A ） A. 764 cm 3或586 cm 3 B. 764 cm 3 C. 586 cm 3或564 cm 3 D. 586 cm 3[解] 设这三个正方体的棱长分别为,,a b c ，则有()2226564a b c ++=，22294a b c ++=，不妨设110a b c ≤≤≤<，从而2222394c a b c ≥++=，231c >．故610c ≤<．c 只能取9，8，7，6．若9c =，则22294913a b +=-=，易知2a =，3b =，得一组解(,,)(2,3,9)a b c =． 若8c =，则22946430a b +=-=，5b ≤．但2230b ≥，4b ≥，从而4b =或5．若5b =，则25a =无解，若4b =，则214a =无解．此时无解．若7c =，则22944945a b +=-=，有唯一解3a =，6b =．若6c =，则22943658a b +=-=，此时222258b a b ≥+=，229b ≥．故6b ≥，但。