偏微分方程求解 复变函数的积分
- 格式:pdf
- 大小:1.60 MB
- 文档页数:129


一.复变函数积分计算方法:
1. 线积分法,udy vdx i vdy udx z f c c c ++-=⎰⎰⎰
)( 2. 参数方程法,就是将积分线段分成几段,每一段尽可能简单,并且可以用一个参数式表达出来。
参考课本37页例3.1(2) 3. 原函数法,要用此方法必须保证函数f(z)在单连通区域D 内解析,求出f(z)的原函数G
(z ),则)z ()z ()(00G G dt t f z z -=⎰
4. 柯西积分公式,)z (2z -z z)(00
if dz f c π=⎰,用这种方法的关键是找出函数)z (f ,有时候要进行一些变形。
二.课本难点
课本47页例3.10(2) 他在解答过程中,有一步是令2)z ()z (i e f z +=,开始看的时候很难看明白是为什么,后来细心一想,原来他用了一个很巧妙的变换:
2
2222)()z /()])(z [()1z (111i z i e i z i e dz e z c z c z c -+=-+=+⎰⎰⎰ 这样就可以凑成柯西积分公式的形式,令2)z ()z (i e f z +=,就可以轻松使用柯西积分公式求出答案。
作业题很多都要用到这个技巧。
三.错误更正
课本55页作业6(3)的答案是i e π,课本答案e π是错误的。
四.规律总结
在做作业过程中,我找到以下两个公式:
ishz iz =sin
ithz iz =tan
特别是z=1的时候,有sini=ish1,tani=ith1
上面的公式根据定义就可以证明。


复变函数积分方法总结[键入文档副标题]acer[选取日期]复变函数积分方法总结数学本就灵活多变,各类函数的排列组合会衍生多式多样的函数新形势,同时也具有本来原函数的性质,也会有多类型的可积函数类型,也就会有相应的积分函数求解方法。
就复变函数: z=x+iy i²=-1 ,x,y 分别称为z 的实部和虚部,记作x=Re(z),y=Im(z)。
arg z =θ₁ θ₁称为主值 -π<θ₁≤π ,Arg=argz+2k π 。
利用直角坐标和极坐标的关系式x=rcos θ ,y=rsin θ,故z= rcos θ+i rsin θ;利用欧拉公式e i θ=cos θ+isin θ。
z=re i θ。
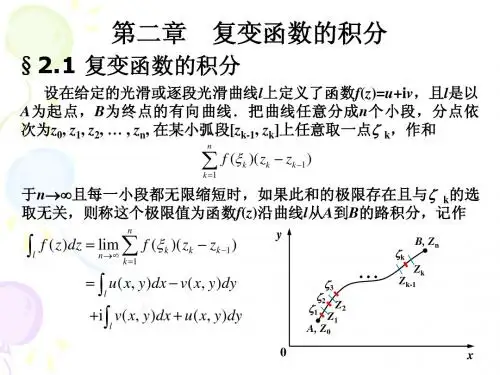
1.定义法求积分:定义:设函数w=f(z)定义在区域D 内,C 为区域D 内起点为A 终点为B 的一条光滑的有向曲线,把曲线C 任意分成n 个弧段,设分点为A=z 0 ,z 1,…,z k-1,z k ,…,z n =B ,在每个弧段z k-1 z k (k=1,2…n)上任取一点ξk 并作和式S n =∑f(ξk )n k−1(z k -z k-1)= ∑f(ξk )n k−1∆z k 记∆z k = z k - z k-1,弧段z k-1 z k 的长度 δ=max 1≤k≤n {∆S k }(k=1,2…,n),当 δ→0时,不论对c 的分发即ξk 的取法如何,S n 有唯一的极限,则称该极限值为函数f(z)沿曲线C 的积分为:∫f(z)dz c=lim δ 0∑f(ξk )nk−1∆z k设C 负方向(即B 到A 的积分记作) ∫f(z)dz c−.当C 为闭曲线时,f(z)的积分记作∮f(z)dz c(C 圆周正方向为逆时针方向) 例题:计算积分1)∫dz c 2) ∫2zdz c ,其中C 表示a 到b 的任一曲线。
(1) 解:当C 为闭合曲线时,∫dz c=0.∵f(z)=1 S n =∑f(ξk)n k−1(z k -z k-1)=b-a ∴lim n 0Sn =b-a,即1)∫dz c=b-a. (2)当C 为闭曲线时,∫dz c =0. f(z)=2z;沿C 连续,则积分∫zdz c 存在,设ξk =z k-1,则∑1= ∑Z n k−1(k −1)(z k -z k-1) 有可设ξk =z k ,则∑2= ∑Z n k−1(k −1)(z k -z k-1)因为S n 的极限存在,且应与∑1及∑2极限相等。


复变函数积分计算公式一、复变函数的积分定义复变函数f(z)的积分定义为:∫f(z)dz = ∫[u(x, y)dx - v(x, y)dy] + i∫[u(x, y)dy + v(x, y)dx]其中,u(x,y)和v(x,y)为复变函数f(z)的实部和虚部分别对x和y 的偏导数。
1.第一类曲线积分公式设C是定义在[a,b]上的光滑曲线,而f(z)是C上的复变函数,则复变函数f(z)沿C的积分表示为:∫f(z)dz = ∫f(z(t))z'(t)dt其中,z(t)表示C上的参数方程,z'(t)表示z(t)对t的导数。
2.第二类曲线积分公式设C是封闭的简单光滑曲线,内部有有向单位法向量n,并设f(z)是C内的解析函数,则复变函数f(z)沿C的积分表示为:∫f(z)dz = 2πi Res[f(z), a]其中,a表示C内的任意一个孤立奇点,Res[f(z), a]表示f(z)在a 处的留数。
3.圆弧积分公式对于参数方程z(t) = a + re^(it),其中t∈[θ1, θ2],a为圆心,r为半径,则复变函数f(z)沿圆弧C的积分表示为:∫f(z)dz = ∫f(a + re^(it))ire^(it)dt4.辐角积分公式设f(z)是C所在区域的解析函数,它在z=a处有极点,则复变函数f(z)沿C的积分表示为:∫f(z)dz = i∫R[f(z) - f(a)]dz其中,C是以a为圆心的环形曲线,R是C所围成的圆环区域。
5.亚纯函数积分公式设f(z)是C所在区域的亚纯函数,它在z=a处有一级极点∫f(z)dz = 2πiI(C, a)其中,I(C,a)为C围绕a的索引。
三、复变函数积分计算技巧1.选择适当的路径进行积分,常常选择直线、弧线或封闭曲线。
2.利用柯西-黎曼条件和柯西-黎曼方程进行变量转换和求导。
3.利用留数定理计算包括奇点与不同路径的积分。
4.利用对称性和奇偶性简化积分计算。

复变函数课后答案复变函数是数学中的一个重要的分支,它将实变函数的概念引入到复数域中。
复变函数的研究对于科学和工程领域有着广泛的应用,因此学习复变函数是数学学生的必修课程之一。
在学习过程中,课后习题是一个不可或缺的重要环节。
本文将为读者提供复变函数课后答案,希望可以帮助大家在学习上得到更好的理解和掌握。
一、Cauchy-Riemann方程Cauchy-Riemann方程是研究复变函数的基础。
它是一个关于函数的实部和虚部的偏微分方程组。
具体而言,设$f(z)=u(x,y)+iv(x,y)$是一个复变函数,其中$x,y\in\mathbb{R}$是实数,$z=x+iy$是一个复数,那么Cauchy-Riemann方程可以表示为:$$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y},\quad\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}$$当且仅当复变函数满足Cauchy-Riemann方程时,它才是解析的。
此外,如果$f(z)$是解析的,则它在一个开放的区域内是无限可微的。
这是我们在复分析中经常使用的重要性质。
二、复积分复积分是计算复变函数的积分的一种方法。
与实变函数中的积分不同的是,复变函数的积分是在复平面上的路径上取值的。
具体而言,设$f(z)$是一个在复平面上连续的函数,$C$是一条连接$z_0$和$z_1$的可求长曲线,则$f(z)$沿着$C$的积分定义为:$$\int_Cf(z)dz=\int_C [u(x,y)dx-v(x,y)dy]+i\int_C [u(x,y)dy+v(x,y)dx] $$其中,$u(x,y)$和$v(x,y)$分别是$f(z)$的实部和虚部。
如果$\int_Cf(z)dz=0$,则称$f(z)$沿着$C$是可积的。
三、Laurent级数在复分析中,我们经常需要将一个复变函数表示为一个Laurent 级数的形式,这个级数包含一部分关于$z$的负次幂,并且它可以用于计算发生奇点的复变函数。

复变函数积分方法总结[键入文档副标题]acer[选取日期]复变函数积分方法总结数学本就灵活多变,各类函数的排列组合会衍生多式多样的函数新形势,同时也具有本来原函数的性质,也会有多类型的可积函数类型,也就会有相应的积分函数求解方法。
就复变函数: z=x+iy i²=-1 ,x,y 分别称为z 的实部和虚部,记作x=Re(z),y=Im(z)。
arg z =θ₁ θ₁称为主值 -π<θ₁≤π ,Arg=argz+2k π 。
利用直角坐标和极坐标的关系式x=rcos θ ,y=rsin θ,故z= rcos θ+i rsin θ;利用欧拉公式e i θ=cos θ+isin θ。
z=re i θ。
1.定义法求积分:定义:设函数w=f(z)定义在区域D 内,C 为区域D 内起点为A 终点为B 的一条光滑的有向曲线,把曲线C 任意分成n 个弧段,设分点为A=z 0 ,z 1,…,z k-1,z k ,…,z n =B ,在每个弧段z k-1 z k (k=1,2…n)上任取一点ξk 并作和式S n =∑f(ξk )n k−1(z k -z k-1)= ∑f(ξk )n k−1∆z k 记∆z k = z k - z k-1,弧段z k-1 z k 的长度 δ=max 1≤k≤n {∆S k }(k=1,2…,n),当 δ→0时,不论对c 的分发即ξk 的取法如何,S n 有唯一的极限,则称该极限值为函数f(z)沿曲线C 的积分为:∫f(z)dz c=lim δ 0∑f(ξk )nk−1∆z k设C 负方向(即B 到A 的积分记作) ∫f(z)dz c−.当C 为闭曲线时,f(z)的积分记作∮f(z)dz c(C 圆周正方向为逆时针方向) 例题:计算积分1)∫dz c 2) ∫2zdz c ,其中C 表示a 到b 的任一曲线。
(1) 解:当C 为闭合曲线时,∫dz c=0.∵f(z)=1 S n =∑f(ξk)n k−1(z k -z k-1)=b-a ∴lim n 0Sn =b-a,即1)∫dz c=b-a. (2)当C 为闭曲线时,∫dz c =0. f(z)=2z;沿C 连续,则积分∫zdz c 存在,设ξk =z k-1,则∑1= ∑Z n k−1(k −1)(z k -z k-1) 有可设ξk =z k ,则∑2= ∑Z n k−1(k −1)(z k -z k-1)因为S n 的极限存在,且应与∑1及∑2极限相等。


复变函数积分计算|z|=2的内部有两个奇点,z=±i,而且都是一阶极点.原式=2πi[Res(f(z),i)+Res(f(z),-i)]=2πi[lim(z→i)sinz/(z+i)+lim(z→-i)sinz/(z-i)]=2πi(sini/2i+sin(-i)/(-2i))=2πi*2sini/2i=2πi*[e^(i*i)-e^(-i*i)]/2i²=π/i*(1/e-e)设f(z)=(z^10)/(z-3)。
∴f(z)有一个一阶极点z1=3,但z1不在丨z丨=1内。
故,f(z)在丨z丨=1的留数Res[f(z),z1]=0。
∴由柯西积分定理,有原式=(2πi)Res[f(z),z1]=0。
设f(z)=1/[(z^2)(z-1)(z+4)],∵(z^2)(z-1)(z+4)=0,则z1=0、z2=1、z3=-4,其中z1是二阶极点、z2、z3是一阶极点。
∴丨z丨=3内,f(z)有两个极点z1、z2。
故,由柯西积分定理,原式=(2πi){Res[f(z),z1]+Res[f(z),z2]}。
而,Res[f(z),z1]=lim(z→z1)[(z^2)f(z)]'=-{(2z+3)/[(z-1)(z+4)]^2}丨(z=0)=-3/16、Res[f(z),z2]=lim(z→z2)(z-z2)f(z)=1/5。
∴原式=πi/40。
扩展资料:复变函数论在应用方面,涉及的面很广,有很多复杂的计算都是用它来解决的。
比如物理学上有很多不同的稳定平面场,所谓场就是每点对应有物理量的一个区域,对它们的计算就是通过复变函数来解决的。
比如俄国的茹柯夫斯基在设计飞机的时候,就用复变函数论解决了飞机机翼的结构问题,他在运用复变函数论解决流体力学和航空力学方面的问题上也做出了贡献。
复变函数论不但在其他学科得到了广泛的应用,而且在数学领域的许多分支也都应用了它的理论。
它已经深入到微分方程、积分方程、概率论和数论等学科,对它们的发展很有影响。
复变函数的积分例题及解析例题1:计算复变函数 f(z) = z^3 的积分∮ γ f(z) dz,其中γ为以原点为圆心、半径为R的逆时针方向正向的圆周。
解析:根据复变函数的积分定义,可以将复变函数积分转化为对参数t的实函数积分。
即∮ γ f(z) dz = ∫ f(γ(t)) γ'(t) dt。
对于本题中的γ(t) = Rcos(t) + iRsin(t),γ'(t) = -Rsin(t) + iRcos(t)。
因此:∮ γ f(z) dz = ∫ [Rcos(t) + iRsin(t)]^3 [-Rsin(t) +iRcos(t)] dt= ∫[(R^3cos^3(t) + 3Rcos^2(t)iRsin(t) +3Rcos(t)i^2R^2sin^2(t) + i^3R^3sin^3(t))(-Rsin(t) + iRcos(t))]dt= ∫[-R^4cos^3(t)sin(t) - 3R^2cos^2(t)sin^2(t) +3R^2cos(t)sin^3(t) - iR^4cos(t)sin^3(t) + iR^2cos(t)sin^2(t) - iRsin^4(t) + R^4cos^4(t) + 3R^2cos^3(t)sin^2(t) -3R^2cos(t)sin^4(t) + iR^4cos^3(t)sin(t) - iR^2cos^3(t)sin(t) +iR^4cos(t)sin^3(t)] dt= ∫[-4R^4cos^3(t)sin(t) - 3R^2cos^2(t)sin^2(t) +6R^2cos(t)sin^3(t) - 3R^2cos(t)sin^4(t) + R^4cos^4(t) +6R^2cos^3(t)sin^2(t) + i(R^4cos(t)sin^3(t) - R^2cos(t)sin^2(t) + R^4cos^3(t)sin(t) - R^2cos^3(t)sin(t))] dt对上式分别对t进行积分,积分得到:∮ γ f(z) dz = ∫[-4R^4cos^3(t)sin(t)] dt -∫[3R^2cos^2(t)sin^2(t)] dt + ∫[6R^2cos(t)sin^3(t)] dt -∫[3R^2cos(t)sin^4(t)] dt + ∫[R^4cos^4(t)] dt +∫[6R^2cos^3(t)sin^2(t)] dt + i[∫(R^4cos(t)sin^3(t)) dt -∫(R^2cos(t)sin^2(t)) dt + ∫(R^4cos^3(t)sin(t)) dt -∫(R^2cos^3(t)sin(t)) dt]=0-0+0-0+π*R^4/2+0+i[0-0+0-0]=π*R^4/2因此,复变函数f(z)=z^3在以原点为圆心、半径为R的逆时针方向正向的圆周上的积分值为π*R^4/2例题2:计算复变函数 f(z) = e^z 的积分∮ γ f(z) dz,其中γ为沿单位圆的逆时针方向正向的圆周。
复变函数积分的几种计算方法
陈静;贠书杰
【期刊名称】《河南机电高等专科学校学报》
【年(卷),期】2013(000)002
【摘要】复变函数积分是复变函数的重要内容。
文章对复变函数积分的计算方法
进行归纳,以典型例题加以说明。
主要包括积分曲线的参数方程法、牛顿-莱布尼兹公式、柯西积分定理及公式、高阶导数公式、留数定理等计算方法。
【总页数】4页(P21-23,55)
【作者】陈静;贠书杰
【作者单位】河南机电高等专科学校,河南新乡453000;河南机电高等专科学校,河南新乡453000
【正文语种】中文
【中图分类】O174.55
【相关文献】
1.复变函数积分计算方法的探讨 [J], 黄隽
2.浅谈复变函数中积分的计算方法 [J], 焦晶晶;
3.关于复变函数积分的计算方法探讨 [J], 薛宾;
4.复变函数与积分变换教学中几种思维习惯的培养 [J], 曾婷;李俊锋;
5.复变函数中闭路积分的计算方法 [J], 周畅;段耀勇
因版权原因,仅展示原文概要,查看原文内容请购买。