最新湘教版九年级数学(下)同步练习 试题及答案 2.3 垂径定理

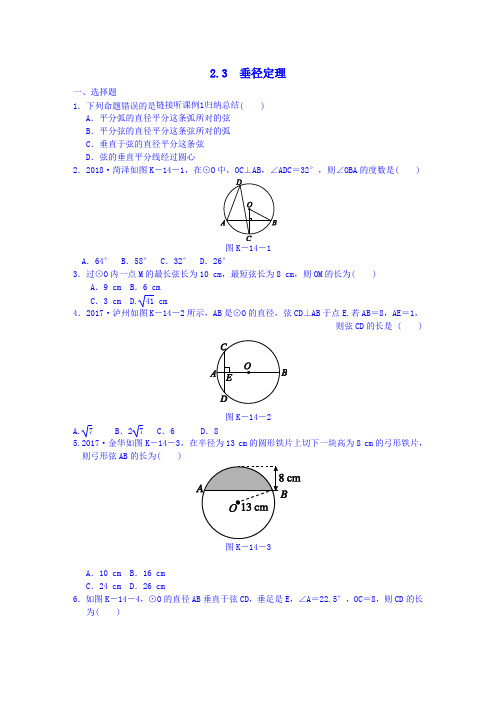
2.3 垂径定理一、选择题1．下列命题错误的是链接听课例1归纳总结( )A．平分弧的直径平分这条弧所对的弦B．平分弦的直径平分这条弦所对的弧C．垂直于弦的直径平分这条弦D．弦的垂直平分线经过圆心2．2018·菏泽如图K－14－1，在⊙O中，OC⊥AB，∠ADC＝32°，则∠OBA的度数是( )图K－14－1A．64° B．58° C．32° D．26°3．过⊙O内一点M的最长弦长为10 cm，最短弦长为8 cm，则OM的长为( )A．9 cm B．6 cmC．3 cm D.41 cm4．2017·泸州如图K－14－2所示，AB是⊙O的直径，弦CD⊥AB于点E.若AB＝8，AE＝1，则弦CD的长是 ( )图K－14－2A.7 B．27 C．6 D．85.2017·金华如图K－14－3，在半径为13 cm的圆形铁片上切下一块高为8 cm的弓形铁片，则弓形弦AB的长为( )图K－14－3A．10 cm B．16 cmC．24 cm D．26 cm6．如图K－14－4，⊙O的直径AB垂直于弦CD，垂足是E，∠A＝22.5°，OC＝8，则CD的长为( )图K－14－4A．4 2B．8 2C．8D．167．如图K－14－5，在等边三角形ABC中，AB，AC都是⊙O的弦，OM⊥AB，ON⊥AC，垂足分别为M，N，如果MN＝1，那么△ABC的面积为( )图K－14－5A．3 B. 3 C．4 D.3 38．2017·襄阳模拟⊙O的半径为5 cm，弦AB∥CD，AB＝6 cm，CD＝8 cm，则AB和CD间的距离是( )图K－14－6A．7 cm B．8 cmC．7 cm或1 cm D．1 cm二、填空题9．如图K－14－6，OD是⊙O的半径，弦AB⊥OD于点E，若∠O＝70°，则∠A＋∠C＝________°. 10．如图K－14－7，在⊙O中，弦AB的长为8，圆心O到AB的距离为3.若P是AB上的一动点，则OP的取值范围是________．图K－14－711．2017·孝感已知半径为2的⊙O中，弦AC＝2，弦AD＝2 2，则∠COD的度数为________．三、解答题12．已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C，D(如图K－14－8所示)．(1)求证：AC＝BD；(2)若大圆的半径R＝10，小圆的半径r＝8，且圆心O到直线AB的距离为6，求AC的长.链接听课例2归纳总结图K－14－813．如图K－14－9所示，在正方形网格图中建立平面直角坐标系，一条圆弧经过网格点A(0，2)，B(4，2)，C(6，0)，解答下列问题：(1)请在图中确定该圆弧所在圆圆心D的位置，并写出点D的坐标为________；(2)连接AD，CD，求⊙D的半径(结果保留根号)．图K－14－914．如图K－14－10，已知AB是⊙O的直径，弦CD⊥AB于点E，点M在⊙O上，∠M＝∠D.(1)判断BC，MD的位置关系，并说明理由；(2)若AE＝16，BE＝4，求线段CD的长；(3)若MD恰好经过圆心O，求∠D的度数．图K－14－1015．如图K－14－11，有一拱形公路桥，圆弧形桥拱的水面跨度AB＝80米，桥拱到水面的最大高度为20米．(1)求桥拱的半径；(2)现有一艘宽60米，船舱顶部为长方形并高出水面9米的轮船要经过这里，这艘轮船能顺利通过吗？并说明理由．图K－14－11素养提升探究性问题如图K－14－12，在半径为5的扇形AOB中，∠AOB＝90°，C是弧AB上的一个动点(不与点A，B重合)，OD⊥BC，OE⊥AC，垂足分别为D，E.(1)当BC＝6时，求线段OD的长．(2)探究：在△DOE中是否存在长度保持不变的边？如果存在，请指出并求其长度；如果不存在，请说明理由．图K－14－121．B2．[解析] D ∵OC ⊥AB ，∴AC ︵＝BC ︵.∠ADC 是AC ︵所对的圆周角，∠BOC 是BC ︵所对的圆心角，∴∠BOC ＝2∠ADC ＝64°，∴∠OBA ＝90°－∠BOC ＝90°－64°＝26°.故选D.3．[解析] C 由题意知，最长的弦为直径，最短的弦为垂直于直径的弦，如图所示．直径ED ⊥AB 于点M ，则ED ＝10 cm ，AB ＝8 cm ，由垂径定理知M 为AB 的中点， ∴AM ＝4 cm.∵半径OA ＝5 cm ，∴OM 2＝OA 2－AM 2＝25－16＝9， ∴OM ＝3(cm)． 4．B5．[解析] C 如图，过点O 作OD ⊥AB 于点C ，交⊙O 于点D.∵CD ＝8 cm ，OD ＝13 cm ，∴OC ＝5 cm. 又∵OB ＝13 cm ，∴在Rt △BCO 中，BC ＝OB 2－OC 2＝12 cm ，∴AB ＝2BC ＝24 cm.6．[解析] B ∵∠A ＝22.5°，∴∠BOC ＝2∠A ＝45°.∵⊙O 的直径AB 垂直于弦CD ，∴CE ＝DE ，△OCE 为等腰直角三角形，∴CE ＝22OC ＝4 2，∴CD ＝2CE ＝8 2.故选B. 7．[解析] B ∵OM ⊥AB ，ON ⊥AC ，垂足分别为M ，N ， ∴M ，N 分别是AB ，AC 的中点， ∴MN 是等边三角形ABC 的中位线． ∵MN ＝1，∴AB ＝AC ＝BC ＝2MN ＝2， ∴S △ABC ＝12×2×2×sin60°＝2×32＝ 3.8．C9．[答案] 55[解析] 连接OB.∵OA ＝OB ，∴∠A ＝∠ABO.又∵OD 是⊙O 的半径，弦AB ⊥OD 于点E ，∠AOD ＝70°， ∴AD ︵＝BD ︵，∠AOB ＝140°，∴∠C ＝12∠AOD ＝35°，∠A ＝∠ABO ＝20°，∴∠A ＋∠C ＝55°.故答案是55.10．[答案] 3≤OP≤5[解析] 连接OA ，作OC ⊥AB 于点C ，则AC ＝12AB ＝4.由勾股定理，得OA ＝AC 2＋OC 2＝5，则OP 的取值范围是3≤OP≤5.11．[答案] 150°或30°[解析] 如图所示，连接OC ，过点O 作OE ⊥AD 于点E.∵OA ＝OC ＝AC ，∴∠OAC ＝60°.∵AD ＝2 2，OE ⊥AD ，∴AE ＝2，OE ＝OA 2－AE 2＝2，∴∠OAD ＝45°，∴∠CAD ＝∠OAC ＋∠OAD ＝105°或∠CAD ＝∠OAC －∠OAD ＝15°，∴∠COD ＝360°－2×105°＝150°或∠COD ＝2×15°＝30°.故答案为150°或30°.12．解：(1)证明：过点O 作OE ⊥AB 于点E ，则CE ＝DE ，AE ＝BE ， ∴AE －CE ＝BE －DE ， 即AC ＝BD.(2)连接OA ，OC ，由(1)可知OE ⊥AB 且OE ⊥CD ， ∴CE ＝OC 2－OE 2＝82－62＝2 7，AE ＝OA 2－OE 2＝102－62＝8， ∴AC ＝AE －CE ＝8－2 7.13．(1)确定点D 的位置略 (2，－2) (2)⊙D 的半径为2 5 14．解：(1)BC ∥MD.理由：∵∠M ＝∠D ，∠M ＝∠C ， ∴∠D ＝∠C ，∴BC ∥MD. (2)∵AE ＝16，BE ＝4， ∴OB ＝16＋42＝10，∴OE ＝10－4＝6.连接OC ，如图①. ∵CD ⊥AB ，∴CE ＝12CD.在Rt △OCE 中，∵OE 2＋CE 2＝OC 2，即62＋CE 2＝102，∴CE ＝8，∴CD ＝2CE ＝16.(3)如图②，∵∠M ＝12∠BOD ，∠M ＝∠D ，∴∠D ＝12∠BOD.又∵AB ⊥CD ，∴∠D ＝13×90°＝30°.15．解：(1)如图①，设E 是桥拱所在圆的圆心，过点E 作EF ⊥AB 于点F ，延长EF 交⊙E 于点D ，则F 是AB 的中点，AF ＝FB ＝12AB ＝40米，EF ＝ED －FD ＝AE －DF.由勾股定理知AE 2＝AF 2＋EF 2＝AF 2＋(AE －DF)2.设⊙E 的半径是r ，则r 2＝402＋(r －20)2， 解得r ＝50.即桥拱的半径为50米．①②(2)这艘轮船能顺利通过这座拱桥． 理由：如图②，设MN 与DE 交于点G ， GM ＝30米．在Rt △GEM 中，GE ＝EM 2－GM 2＝502－302＝40(米)． ∵EF ＝50－20＝30(米)，∴GF ＝GE －EF ＝40－30＝10(米)． ∵10米＞9米，∴这艘轮船能顺利通过这座拱桥．[素养提升]解：(1)∵OD ⊥BC ，∴BD ＝12BC ＝12×6＝3.∵∠BDO ＝90°，OB ＝5，BD ＝3，∴OD ＝OB 2－BD 2＝4， 即线段OD 的长为4.(2)存在，DE 的长度保持不变．理由：连接AB ，如图． ∵∠AOB ＝90°，OA ＝OB ＝5， ∴AB ＝OB 2＋OA 2＝5 2. ∵OD ⊥BC ，OE ⊥AC ，∴D 和E 分别是线段BC 和AC 的中点， ∴DE ＝12AB ＝5 22，其长度保持不变．。

*2.3 垂径定理知识点 垂径定理1．如图2－3－1，在半径为5 cm 的⊙O 中，弦AB ＝6 cm ，OC ⊥AB 于点C ，则OC 的长为( )图2－3－1A ．3 cmB ．4 cmC ．5 cmD ．6 cm2．如图2－3－2，AB 是⊙O 的直径，CD 为弦，CD ⊥AB 于点E ，则下列结论中不一定成立的是( )图2－3－2A ．∠COE ＝∠DOEB ．CE ＝DEC ．OE ＝BED .BD ︵＝BC ︵3．2019·金华如图2－3－3，在半径为13 cm 的圆形铁片上切下一块高为8 cm 的弓形铁片，则弓形弦AB 的长为( )图2－3－3A ．10 cmB ．16 cmC ．24 cmD ．26 cm4．2019·大连如图2－3－4，在⊙O 中，弦AB ＝8 cm ，OC ⊥AB ，垂足为C ，OC ＝3 cm ，则⊙O 的半径为________ cm .图2－3－45．如图2－3－5，AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ，连接AC.若∠CAB ＝22.5°，CD ＝8 cm ，则⊙O 的半径为________cm .图2－3－56．如图2－3－6，CD 是⊙O 的直径，AB 是⊙O 的弦，AB ⊥CD ，垂足为M ，根据以上条件，请写出三个正确的结论(含90°的角除外)：①________，②________，③________．图2－3－67．赵州桥是我国建筑史上的一大创举，它距今约1400年，历经无数次洪水冲击和8次地震却安然无恙．如图2－3－7，若桥跨度AB 约为40米，主拱高CD 约为10米，则桥弧AB 所在圆的半径R ＝________米．图2－3－78．2019·衡阳模拟如图2－3－8，⊙O 的半径为5，P 是弦AB 延长线上的一点，连接OP ，若OP ＝8，∠P ＝30°，则弦AB 的长为________．图2－3－89．如图2－3－9，在以点O 为圆心的两个同心圆中，大圆的弦AB 交小圆于点C ，D ，求证：AC ＝BD.图2－3－910．教材习题2.3A组第2题变式如图2－3－10，AB是⊙O的弦，C，D是直线AB上两点，并且OC＝OD.求证：AC＝BD.图2－3－1011．2019·菏泽如图2－3－11，在⊙O中，OC⊥AB，∠ADC＝32°，则∠OBA的度数是()图2－3－11A．64°B．58°C．32°D．26°12．如图2－3－12所示，⊙O的直径CD＝10 cm，AB是⊙O的弦，AM＝BM，OM∶OC＝3∶5，则AB的长为()图2－3－12A．8 cm B.91 cmC．6 cm D．2 cm13．2019·牡丹江在半径为20的⊙O中，弦AB＝32，点P在弦AB上，且OP＝15，则AP＝________.图2－3－1314．如图2－3－13，在平面直角坐标系中，点O为坐标原点，点P在第一象限，⊙P与x轴交于O，A两点，点A的坐标为(6，0)，⊙P的半径为13，则点P的坐标为________．15．如图2－3－14，⊙O的直径AB和弦CD相交于点E，AE＝2，EB＝6，∠DEB＝30°，求弦CD的长．图2－3－1416．如图2－3－15，AB是⊙O的直径，弦CD⊥AB于点E.点M在⊙O上，MD恰好经过圆心O，连接MB.(1)若CD＝16，BE＝4，求⊙O的直径；(2)若∠M＝∠D，求∠D的度数．图2－3－1517．如图2－3－16，有两条公路OM，ON相交成30°角，沿公路OM方向离点O80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时，在以P为圆心，50米长为半径的圆形区域内都会受到卡车噪声的影响，且卡车P与学校A的距离越近噪声影响越大．若一重型运输卡车P沿道路ON方向行驶的速度为18千米/时．(1)求对学校A的噪声影响最大时卡车P与学校A的距离；(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间是多少分钟．图2－3－16教师详解详析1．B 2.C3．C [解析] 如图，在Rt △OCB 中，OC ＝5 cm ，OB ＝13 cm ，根据勾股定理，得BC ＝OB 2－OC 2＝132－52＝12(cm)．∵OC ⊥AB ，∴AB ＝2BC ＝24 cm.4．55．4 2 [解析] 连接OC ，如图所示．∵AB 是⊙O 的直径，弦CD ⊥AB ，∴CE ＝DE ＝12CD ＝4 cm. ∵OA ＝OC ，∴∠A ＝∠OCA ＝22.5°.∵∠COE 为△AOC 的外角，∴∠COE ＝45°，∴△COE 为等腰直角三角形，∴OC ＝2CE ＝4 2 cm ，故答案为4 2.6．答案不唯一，如：①AM ＝BM ，②AD ＝BD ，③∠A ＝∠B7．258．6 [解析] 过点O 作OC ⊥AB 于点C ，连接OA ，如图，则AC ＝BC ，∵OP ＝8，∠P ＝30°，∴OC ＝4.在Rt △OAC 中，OA ＝5，OC ＝4，∴AC ＝OA 2－OC 2＝3，∴AB ＝2AC ＝6.9．证明：过圆心O 作OE ⊥AB 于点E ，在大圆O 中，OE ⊥AB ，∴AE ＝BE .在小圆O 中，OE ⊥CD ，∴CE ＝DE ，∴AE －CE ＝BE －DE ，即AC ＝BD .10．证明：过点O 作OE ⊥AB ，垂足为E ，则AE ＝BE .∵OC ＝OD ，OE ⊥AB ，∴CE ＝DE .∴CE －AE ＝DE －BE ，即AC ＝BD .11．D [解析] 由垂径定理，得AC ︵＝BC ︵，∴∠O ＝2∠D ＝64°，∴∠OBA ＝90°－64°＝26°.12．A [解析] 如图所示，连接OA .∵⊙O 的直径CD ＝10 cm ，∴⊙O 的半径为5 cm ，即OA ＝OC ＝5 cm.∵OM ∶OC ＝3∶5，∴OM ＝3 cm.∵AM ＝BM ，∴AB ⊥CD .在Rt △AOM 中，AM ＝52－32＝4(cm)，∴AB ＝2AM ＝2×4＝8(cm)．故选A.13．7或25 [解析] 作OC ⊥AB 于点C ，∴AC ＝12AB ＝16，OC ＝OA 2－AC 2＝12.又OP ＝15，∴PC ＝OP 2－OC 2＝9，当点P 在线段AC 上时，AP 1＝16－9＝7，当点P 在线段BC 上时，AP 2＝16＋9＝25.故答案为7或25.14．(3，2) [解析] 如图，过点P 作PB ⊥OA 于点B ，连接PO .∵点A 的坐标为(6，0)，∴OB ＝3，在Rt △POB 中，PO ＝13，OB ＝3，∴由勾股定理求得PB ＝2，∴点P 的坐标是(3，2)．15．解：过点O 作OF ⊥CD ，交CD 于点F ，连接OD ，则F 为CD 的中点，即CF ＝DF .∵AE ＝2，EB ＝6，∴AB ＝AE ＋EB ＝2＋6＝8，∴OA ＝4，∴OE ＝OA －AE ＝4－2＝2.在Rt△OEF 中，∵∠OEF ＝30°，∴OF ＝12OE ＝1.在Rt △ODF 中，OF ＝1，OD ＝4，根据勾股定理，得DF ＝OD 2－OF 2＝15，则CD ＝2DF ＝2 15.16．解：(1)∵AB 是⊙O 的直径，弦CD ⊥AB ，CD ＝16，∴DE ＝12CD ＝8.∵BE ＝4，∴OE ＝OB －BE ＝OD －4.在Rt △OED 中，OE 2＋DE 2＝OD 2，即(OD －4)2＋82＝OD 2，解得OD ＝10，∴⊙O 的直径是20.(2)∵弦CD ⊥AB ，∴∠OED ＝90°，∴∠EOD ＋∠D ＝90°.∵∠M ＝∠D ，∠EOD ＝2∠M ，∴∠BOD ＋∠D ＝2∠M ＋∠D ＝3∠D ＝90°，∴∠D ＝30°.17．解：(1)如图，过点A 作AD ⊥ON 于点D ，∵∠NOM ＝30°，AO ＝80米，∴AD ＝40米，即对学校A 的噪声影响最大时卡车P 与学校A 的距离为40米．(2)如图，以A 为圆心，50米长为半径画圆，交ON 于B ，C 两点，∵AD ⊥BC ，∴BD ＝CD ＝12BC .在Rt △ABD 中，AB ＝50米，AD ＝40米，由勾股定理，得BD ＝AB 2－AD 2＝502－402＝30(米)，故BC ＝2×30＝60(米)，即重型运输卡车在经过BC 时对学校产生噪声影响．∵重型运输卡车的速度为18千米/时，即1800060＝300(米/分)， ∴重型运输卡车经过BC 时需要60÷300＝0.2(分)．答：卡车P 沿道路ON 方向行驶一次给学校A 带来噪声影响的时间为0.2分钟．。

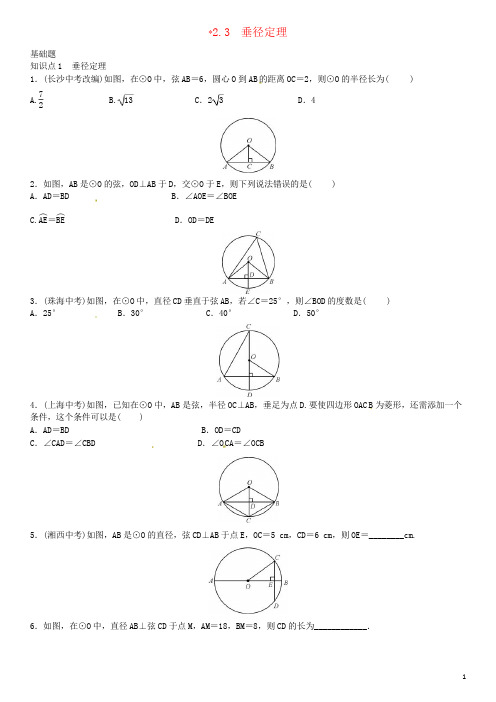
2*2.3垂径定理基础题知识点1垂径定理1．(长沙中考改编)如图，在⊙O中，弦AB＝6，圆心O到AB的距离OC＝2，则⊙O的半径长为()7A. B.13C．23D．42．如图，AB是⊙O的弦，OD⊥AB于D，交⊙O于E，则下列说法错误的是()A．AD＝BD B．∠AOE＝∠BOE︵︵C.AE＝BE D．OD＝DE3．(珠海中考)如图，在⊙O中，直径CD垂直于弦AB，若∠C＝25°，则∠BOD的度数是()A．25°B．30°C．40°D．50°4．(上海中考)如图，已知在⊙O中，AB是弦，半径OC⊥AB，垂足为点D.要使四边形OAC B为菱形，还需添加一个条件，这个条件可以是()A．AD＝BD B．OD＝CDC．∠CAD＝∠CBD D．∠O CA＝∠OCB5．(湘西中考)如图，AB是⊙O的直径，弦CD⊥AB于点E，OC＝5cm，CD＝6cm，则OE＝________cm.6．如图，在⊙O中，直径AB⊥弦CD于点M，AM＝18，BM＝8，则CD的长为____________．7．如图，已知AB是⊙O的弦，半径OA＝20cm，∠AOB＝120°，求△AOB的面积．知识点2垂径定理的实际应用8．一条排水管的截面如图所示．已知排水管的截面圆半径OB＝10，截面圆圆心O到水面的距离OC是6，则水面宽AB是()A．16B．10C．8D．69．(邵阳中考)如图所示，某窗户是由矩形和弓形组成，已知弓形的跨度AB＝3m，弓形的高EF＝1m，现计划安装︵玻璃，请帮工程师求出AB所在圆O的半径r.O中档题10．如图，⊙O的直径AB垂直于弦CD，垂足是E，∠A＝22.5°，OC＝4，CD的长为()A．22B．4C．42D．811．如图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为()A．2cm B.3cmC．23cm D．25cm12．已知⊙O的半径为13cm，弦AB∥CD，AB＝24cm，CD＝10cm，则AB，CD之间的距离为()A．17cm B．7cmC．12cm D．17cm或7cm13．如图，以点P为圆心的圆弧与x轴交于A，B两点，点P的坐标为(4，2)，点A的坐标为(2，0)，则点B的坐标为____________．14．(黔东南中考)如图，AD是⊙O的直径，弦BC⊥AD于E，AB＝BC＝12，则OC＝____________.15．高速公路的隧道和桥梁最多．如图是一个隧道的横截面，若它的形状是以为圆心的圆的一部分，路面A B＝10米，净高CD＝7米，求此圆的半径OA长．16．(湖州中考)已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C，D(如图所示)．(2)若大圆的半径R＝10，小圆的半径r＝8，且圆心O到直线AB的距离为6，求AC的长．综合题17．已知∠MAN＝30°，O为边AN上一点，以O为圆心，2为半径作⊙O，交AN于D，E两点，设AD＝x.当x为何值时，⊙O与AM相交于B，C两点，且∠BOC＝90°？2 2228m.8772参考答案1．B 2.D 3.D 4.B 5.4 6.2417．作OC⊥AB于点C，则有AC＝CB，∠AOC＝∠AOB＝60°.在△R t AOC中，OA＝20cm，∴AC＝103cm，OC＝10cm.∴AB＝203cm.1∴△AOB的面积为AB·OC＝1003(cm2)．8．A9．由题意知OA＝OE＝r.∵EF＝1，∴OF＝r－1.11∵OE⊥AB，∴AF＝AB＝×3＝1.5.在△R t OAF中，OF2＋AF2＝OA2，即(r－1)2＋1.52＝r2.1313解得r＝.即圆O的半径为10．C11.C12.D13.(6，0)14.4315．CD⊥AB，由垂径定理得AD＝5米，设圆的半径为r米．在△R t ADO中，由勾股定理得OD2＋AD2＝OA2，即(7－r)2＋52＝r2.37解得r＝.37答：此圆的半径OA长为米．16．(1)证明：过点O作OE⊥AB于点E.则CE＝DE，AE＝BE.∴AE－CE＝BE－DE，即AC＝BD.(2)连接OA，OC.由(1)可知，OE⊥AB且OE⊥CD，∴CE＝OC2－OE2＝82－62＝27.AE＝OA2－OE2＝102－62＝8.∴AC＝AE－CE＝8－27.17．作OF⊥BC于点F.∵∠BOC＝90°，OB＝OC＝2，∴∠OBC＝45°，BC＝OB2＋OC2＝2 2.1∵OF⊥BC，∴BF＝BC＝2，∠BOF＝45°.∴∠OBF＝∠BOF.∴OF＝BF＝ 2.∵∠MAN＝30°，∴OA＝2OF＝2 2.∴AD＝22－2.即当x＝22－2时，∠BOC＝90°.。

2.3 垂径定理1.如图，AB是⊙O的弦，CD是⊙O的直径，CD⊥AB，垂足为E，则可推出的相等关系是___________.2.圆中一条弦把和它垂直的直径分成3 cm和4 cm两部分，则这条弦弦长为__________.3.判断正误.(1)直径是圆的对称轴; (2)平分弦的直径垂直于弦.4.圆O的半径OA=6,OA的垂直平分线交圆O于B、C,那么弦BC的长等于___________.二、课中强化(10分钟训练)1.圆是轴对称图形，它的对称轴是______________.2.如图，在⊙O中，直径MN垂直于弦AB，垂足为C，图中相等的线段有__________，相等的劣弧有______________.第2题图第3题图3.如图，弦AB的长为24 cm，弦心距OC=5 cm，则⊙O的半径R=__________ cm.4.如图所示，直径为10 cm的圆中，圆心到弦AB的距离为4 cm.求弦AB的长.三、课后巩固(30分钟训练)1.如图,⊙O的半径OA=3,以点A为圆心,OA的长为半径画弧交⊙O于B、C,则BC 等于( )A.32B.33C.223D.233第1题图第2题图2.如图24-1-2-6，AB是⊙O的弦，半径OC⊥AB于点D，且AB=8 cm，OC=5 cm，则OD的长是( )A.3 cmB.2.5 cmC.2 cmD.1 cm3.⊙O半径为10，弦AB=12，CD=16，且AB∥CD.求AB与CD之间的距离.4.如图所示，秋千链子的长度为3 m，静止时的秋千踏板(大小忽略不计)距地面0.5 m.秋千向两边摆动时，若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°，则秋千踏板与地面的最大距离约为多少？5. “五段彩虹展翅飞”，我省利用国债资金修建的，横跨南渡江的琼州大桥如图(1)已于今年5月12日正式通车，该桥的两边均有五个红色的圆拱，如图(1).最高的圆拱的跨度为110米，拱高为22米，如图(2),那么这个圆拱所在圆的直径为___________米.6.如图，要把破残的圆片复制完整，已知弧上三点A、B、C.(1)用尺规作图法，找出弧BAC所在圆的圆心O；(保留作图痕迹，不写作法)(2)设△ABC为等腰三角形，底边BC=10 cm，腰AB=6 cm，求圆片的半径R；(结果保留根号)(3)若在(2)题中的R满足n＜R＜m(m、n为正整数)，试估算m和n的值.7.⊙O的直径为10，弦AB的长为8，P是弦AB上的一个动点，求OP长的取值范围.思路分析：求出OP长的最小值和最大值即得范围，本题考查垂径定理及勾股定理.该题创新点在于把线段OP看作是一个变量，在动态中确定OP的最大值和最小值.事实上只需作OM⊥AB，求得OM即可.考点综合专题：一元二次方程与其他知识的综合◆类型一一元二次方程与三角形、四边形的综合1．(雅安中考)已知等腰三角形的腰和底的长分别是一元二次方程x2－4x＋3＝0的根，则该三角形的周长可以是（）A．5 B．7 C．5或7 D．102．(广安中考)一个等腰三角形的两条边长分别是方程x2－7x＋10＝0的根，则该等腰三角形的周长是（）A．12 B．9C．13 D．12或93．(罗田县期中)菱形ABCD的一条对角线长为6，边AB的长是方程x2－7x ＋12＝0的一个根，则菱形ABCD的周长为（）A．16 B．12 C．16或12 D．244．(烟台中考)等腰三角形边长分别为a，b，2，且a，b是关于x的一元二次方程x2－6x＋n－1＝0的两根，则n的值为（）A．9 B．10C．9或10 D．8或105．(齐齐哈尔中考)△ABC的两边长分别为2和3，第三边的长是方程x2－8x ＋15＝0的根，则△ABC的周长是．6．(西宁中考)若矩形的长和宽是方程2x2－16x＋m＝0(0＜m≤32)的两根，则矩形的周长为．【方法8】7．已知一直角三角形的两条直角边是关于x的一元二次方程x2＋(2k－1)x ＋k2＋3＝0的两个不相等的实数根，如果此直角三角形的斜边是5，求它的两条直角边分别是多少．【易错4】◆类型二一元二次方程与函数的综合8．(泸州中考)若关于x的一元二次方程x2－2x＋kb＋1＝0有两个不相等的实数根，则一次函数y＝kx＋b的大致图象可能是（）9．(安顺中考)若一元二次方程x2－2x－m＝0无实数根，则一次函数y＝(m ＋1)x＋m－1的图象不经过（）A．第四象限B．第三象限C．第二象限D．第一象限10．(葫芦岛中考)已知k、b是一元二次方程(2x＋1)(3x－1)＝0的两个根，且k＞b，则函数y＝kx＋b的图象不经过（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限11．(广元中考)从3，0，－1，－2，－3这五个数中抽取一个数，作为函数y ＝(5－m 2)x 和关于x 的一元二次方程(m ＋1)x 2＋mx ＋1＝0中m 的值．若恰好使函数的图象经过第一、三象限，且使方程有实数根，则满足条件的m 的值是 ．12．(甘孜州中考)若函数y ＝－kx ＋2k ＋2与y ＝kx (k ≠0)的图象有两个不同的交点，则k 的取值范围是 ． .◆类型三 一元二次方程与二次根式的综合13．(达州中考)方程(m －2)x 2－3－mx ＋14＝0有两个实数根，则m 的取值范围为（ ）A ．m ＞52B ．m ≤52且m ≠2C ．m ≥3D ．m ≤3且m ≠214．(包头中考)已知关于x 的一元二次方程x 2＋k －1x －1＝0有两个不相等的实数根，则k 的取值范围是 ．考点综合专题：一元二次方程与其他知识的综合1．B 2.A 3.A 4.B 5.86．16 解析：设矩形的长和宽分别为x 、y ，根据题意得x ＋y ＝8，所以矩形的周长为2(x ＋y)＝16.7．解：∵一元二次方程x 2＋(2k －1)x ＋k 2＋3＝0有两个不相等的实数根，∴Δ>0，∴(2k －1)2－4(k 2＋3)>0，即－4k －11>0，∴k<－114，令其两根分别为x 1，x 2，则有x 1＋x 2＝1－2k ，x 1·x 2＝k 2＋3，∵此方程的两个根分别是一直角三角形的两条直角边，且此直角三角形的斜边长为5，∴x 21＋x 22＝52，∴(x 1＋x 2)2－2x 1·x 2＝25，∴(1－2k)2－2(k 2＋3)＝25，∴k 2－2k －15＝0，∴k 1＝5，k 2＝－3，∵k<－114，∴k ＝－3, ∴把k ＝－3代入原方程得到x 2－7x ＋12＝0，解得x 1＝3，x 2＝4，∴直角三角形的两直角边分别为3和4.8．B9．D 解析：∵一元二次方程x 2－2x －m ＝0无实数根，∴Δ＜0，∴Δ＝4－4×1×(－m)＝4＋4m ＜0，∴m ＜－1，∴m ＋1＜1－1，即m ＋1＜0，m －1＜－1－1，即m －1＜－2，∴一次函数y ＝(m ＋1)x ＋m －1的图象不经过第一象限．故选D.10．B 11.－2 12.k>－12且k ≠013．B 14.k ≥1。

2.3 垂径定理知|识|目|标1．通过圆的对称性折叠操作，理解垂径定理．2．通过对垂径定理的理解，采用转化和对称思想解决有关直角三角形的计算与证明问题．3．在掌握垂径定理的基础上，能应用垂径定理解决实际生活中的问题.目标一理解垂径定理例1 教材补充例题如图2－3－1所示的图形中，哪些图形能得到AE＝BE的结论，哪些不能，为什么？①②③④图2－3－1【归纳总结】理解垂径定理的“三点注意”：(1)这里的垂径可以是直径、半径或过圆心的直线(线段)，其本质是“过圆心”；(2)垂径定理中的弦为直径时，结论仍然成立；(3)平分弦所对的两条弧，是指平分弦所对的劣弧和优弧，不要漏掉优弧．目标二能运用垂径定理进行计算或推理证明例2 教材补充例题如图2－3－2，⊙O的半径为17 cm，弦AB∥CD，AB＝30 cm，CD＝16 cm，圆心O位于AB，CD的上方，求AB和CD之间的距离．图2－3－2【归纳总结】垂径定理中常用的两种辅助线：(1)若已知圆心，则作垂直于弦的直径；(2)若已知弦、弧的中点，则作弦、弧中点的连线或连半径等．目标三能利用垂径定理解决实际问题例3 教材补充例题赵州桥是我国建筑史上的一大创举，它距今约1400年，历经无数次洪水冲击和8次地震却安然无恙．如图2－3－3，若桥跨度AB 约为40米，主拱高CD 约为10米，则桥弧AB 所在圆的半径R ＝________米．图2－3－3图2－3－4【归纳总结】1．垂径定理基本图形的四变量、两关系：(1)四变量：如图2－3－4，弦长a ，圆心到弦的距离d ，半径r ，弧的中点到弦的距离(弓形高)h ，这四个变量知任意两个可求其他两个．(2)两关系：①⎝ ⎛⎭⎪⎫a 22＋d 2＝r 2；②h ＋d ＝r.2．垂径定理在应用中常作的辅助线： 作垂线，连半径，构造直角三角形． 3．垂径定理在应用中常用的技巧： 设未知数，根据勾股定理列方程．知识点 垂径定理垂径定理：垂直于弦的直径平分这条____，并且平分________________． [点拨] (1)平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧． (2)弦的垂直平分线经过圆心，并且平分弦所对的两条弧．(3)平分弦所对的一条弧的直径垂直平分弦，并且平分弦所对的另一条弧．已知CD 是⊙O 的一条弦，作直径AB ，使AB ⊥CD ，垂足为E ，若AB ＝10，CD ＝8，求BE 的长． 解：如图2－3－5，连接OC ，则OC ＝5.图2－3－5∵AB 是⊙O 的直径，AB ⊥CD ， CD ＝8， ∴CE ＝12CD ＝4.在Rt △OCE 中，OE ＝OC 2－CE 2＝3， ∴BE ＝OB ＋OE ＝5＋3＝8.以上解答完整吗？若不完整，请进行补充．教师详解详析【目标突破】例1 解：①②能，③④不能．理由略． 例2 [解析] 如图，过圆心O 作弦AB 的垂线，易证它也与弦CD 垂直，由垂径定理知AE ＝BE ，CF ＝DF ，根据勾股定理可求OE ，OF 的长，进而可求出AB 和CD 之间的距离．解：如图，过点O 作OE ⊥AB 于点E ，交CD 于点F ，连接OA ，OC.∵AB ∥CD ，∴OF ⊥CD. 在Rt △OAE 中，∵OA ＝17 cm ，AE ＝BE ＝12AB ＝15 cm ，∴OE ＝172－152＝8(cm)．同理可求OF ＝172－82＝15(cm)． ∵圆心O 位于AB ，CD 的上方， ∴EF ＝OF －OE ＝15－8＝7(cm)． 即AB 和CD 之间的距离是7 cm. 例3 [答案] 25[解析] 根据垂径定理，得AD ＝12AB ＝20米．在Rt △AOD 中，根据勾股定理，得R 2＝202＋(R－10)2，解得R ＝25(米)． 【总结反思】[小结] 知识点 弦 弦所对的两条弧 [反思] 不完整．补充：若垂足E 在线段OA 上，则BE ＝OB ＋OE ＝5＋3＝8； 若垂足E 在线段OB 上， 则BE ＝OB －OE ＝5－3＝2. 综上所述，BE 的长为8或2. 其长度保持不变．。

xx学校xx学年xx学期xx 试卷姓名:_____________ 年级:____________ 学号:______________ 题型选择题填空题简答题xx题xx题xx题总分得分一、xx题（每空xx 分，共xx分）试题1:如图，在⊙O中，弦AB＝6，圆心O到AB的距离OC＝2，则⊙O的半径长为( ) A. B. C．2 D．4试题2:．如图，AB是⊙O的弦，OD⊥AB于D，交⊙O于E，则下列说法错误的是( ) A．AD＝BD B．∠AOE＝∠BOEC.＝ D．OD＝DE试题3:．如图，在⊙O中，直径CD垂直于弦AB.若∠C＝25°，则∠BOD的度数是( ) 评卷人得分A．25° B．30° C．40° D．50°试题4:如图，AB是⊙O的弦，半径OC⊥AB于点D.若⊙O的半径为5，AB＝8，则CD的长是( )A．2 B．3 C．4 D．5试题5:如图，AB是⊙O的直径，弦CD⊥AB于点E，OC＝5 cm，CD＝6 cm，则OE＝ cm.试题6:如图，在⊙O中，直径AB垂直弦CD于点M，AM＝18，BM＝8，则CD的长为．试题7:如图，AB是⊙O的直径，弦CD⊥AB于点E，点M在⊙O上，MD恰好经过圆心O，连接MB.若CD＝16，BE＝4，求⊙O的直径．试题8:一条排水管的截面如图所示．已知排水管的截面圆半径OB＝10，截面圆圆心O到水面的距离OC是6，则水面宽AB是 )A．16B．10C．8D．6试题9:如图所示，某窗户是由矩形和弓形组成，已知弓形的跨度AB＝3 m，弓形的高EF＝1 m，现计划安装玻璃，请帮工程师求出所在圆O的半径r.试题10:下列说法正确的是( )A．过弦的中点的直径平分弦所对的两条弧B．弦的垂直平分线平分它所对的两条弧，但不一定过圆心C．过弦的中点的直径垂直于弦D．平分弦所对的两条弧的直径平分弦试题11:如图，将半径为2 cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为( )A．2 cm B. cm C．2 cm D．2 cm试题12:如图，AB是⊙O的直径，弦CD交AB于点P，AP＝2，BP＝6，∠APC＝30°.则CD的长为( )A. B．2 C．2 D．8试题13:如图，以点P为圆心的圆弧与x轴交于A，B两点，点P的坐标为(4，2)，点A的坐标为(2，0)，则点B的坐标为．试题14:如图，△ABC内接于⊙O，AB为⊙O的直径，∠CAB＝60°，弦AD平分∠CAB.若AD＝6，则AC＝．试题15:已知⊙O的半径为10 cm，AB，CD是⊙O的两条弦，AB∥CD，AB＝16 cm，CD＝12 cm，则弦AB和CD之间的距离是 cm.试题16:如图，⊙O为锐角△ABC的外接圆，半径为5.(1)用尺规作图作出∠BAC的平分线，并标出它与劣弧BC的交点E；(保留作图痕迹，不写作法)(2)若(1)中的点E到弦BC的距离为3，求弦CE的长．试题17:如图，CD为⊙O的直径，弦AB交CD于点E，连接BD，OB.(1)求证：△AEC∽△DEB；(2)若CD⊥AB，AB＝8，DE＝2，求⊙O的半径．试题18:如图，已知∠MAN＝30°，O为边AN上一点，以O为圆心，2为半径作⊙O，交AN于D，E两点，设AD＝x.当x为何值时，⊙O与AM相交于B，C两点，且∠BOC＝90°？试题19:已知：如图，A，B，C，D是⊙O上的点，∠1＝∠2，AC＝3 cm.(1)求证：＝；(2)求BD的长．试题20:A，B是⊙O上的两个定点，P是⊙O上的动点(P不与A，B重合)，我们称∠APB是⊙O上关于点A，B的滑动角．已知∠APB 是⊙O上关于点A，B的滑动角．(1)若AB是⊙O的直径，则∠APB＝90°；(2)如图，若⊙O的半径是1，AB＝，求∠APB的度数．试题21:如图，AB是⊙O的直径，C，D两点在⊙O上．若∠C＝45°.(1)求∠ABD的度数；(2)若∠CDB＝30°，BC＝3，求⊙O的半径．试题22:如图，A，P，B，C是圆上的四个点，∠APC＝∠CPB＝60°，AP，CB的延长线相交于点D.(1)求证：△ABC是等边三角形；(2)若∠PAC＝90°，AB＝2，求PD的长．试题23:如图，一圆弧形桥拱的圆心为E，拱桥的水面跨度AB＝80米，桥拱到水面的最大高度为20米．求：(1)桥拱的半径；(2)现水面上涨后水面跨度为60米，求水面上涨的高度为多少米？试题24:．已知△ABC，以AB为直径的⊙O分别交AC，BC于点D，E，连接ED.若ED＝EC.(1)求证：AB＝AC；(2)若AB＝4，BC＝2，求CD的长．试题25:如图，在△ABC中，AB＝BC＝2，以AB为直径的⊙O分别交BC，AC于点D，E，且点D为BC的中点．(1)求证：△ABC为等边三角形；(2)求DE的长；(3)在线段AB的延长线上是否存在一点P，使△PBD≌△AED，若存在，请求出PB的长；若不存在，请说明理由．试题1答案:B试题2答案:D试题3答案:D试题4答案:A试题5答案:4试题6答案:24试题7答案:解：∵AB⊥CD，CD＝16，∴CE＝DE＝8.设OB＝x，∵BE＝4，∴x2＝(x－4)2＋82.解得x＝10.∴⊙O的直径是20.试题8答案:A试题9答案:解：由题意，知OA＝OE＝r.∵EF＝1，∴OF＝r－1.∵OE⊥AB，∴AF＝AB＝×3＝1.5.在Rt△OAF中，OF2＋AF2＝OA2，即(r－1)2＋1.52＝r2.解得r＝.∴圆O的半径为 m.试题10答案:D试题11答案:C试题12答案:C提示：过点O作OH⊥PD于H，连接OD.AP＝2，BP＝6，则AO＝BO＝4，则PO＝2，又∠OPH＝∠APC＝30°，∴OH＝1，OD ＝OB＝4，在Rt△HOD中，HD＝＝，∴CD＝2HD＝2.试题13答案:(6，0)试题14答案:2试题15答案:2或14试题16答案:解：(1)画图如图所示．(2)∵AE平分∠BAC，∴＝.连接OE，OC，EC，则OE⊥BC于点F，EF＝3.在Rt△OFC中，由勾股定理可得，FC＝＝＝.在Rt△EFC中，由勾股定理可得，CE＝＝＝.试题17答案:解：(1)证明：根据“同弧所对的圆周角相等”，得∠A＝∠D，∠C＝∠ABD，∴△AEC∽△DEB.(2)∵CD⊥AB，O为圆心，∴BE＝AB＝4.设⊙O的半径为r，∵DE＝2，则OE＝r－2.∴在Rt△OEB中，由勾股定理，得OE2＋EB2＝OB2，即(r－2)2＋42＝r2，解得r＝5.∴⊙O的半径为5.试题18答案:解：过点O作OF⊥BC于点F.∵∠BOC＝90°，OB＝OC＝2，∴∠OBC＝45°，BC＝＝2.∵OF⊥BC，∴BF＝BC＝，∠BOF＝45°.∴∠OBF＝∠BOF.∴OF＝BF＝.∵∠MAN＝30°，∴OA＝2OF＝2.∴AD＝2－2，即当x＝2－2时，∠BOC＝90°.试题19答案:解：(1)证明：∵∠1＝∠2，∴＝，∴＋＝＋. ∴＝.(2)∵＝，∴AC＝BD.∵AC＝3 cm，∴BD＝3 cm.试题20答案:解：连接OA，OB，AB.∵⊙O的半径是1，即OA＝OB＝1，又∵AB＝，∴OA2＋OB2＝AB2.由勾股定理的逆定理可得，∠AOB＝90°. ∴∠APB＝∠AOB＝45°.试题21答案:解：(1)连接AD.∵∠BCD＝45°，∴∠DAB＝∠BCD＝45°.∵AB是⊙O的直径，∴∠ADB＝90°.∴∠ABD＝45°.(2)连接AC.∵AB是⊙O的直径，∴∠ACB＝90°.∵∠CAB＝∠CDB＝30°，BC＝3，∴AB＝6.∴⊙O的半径为3.试题22答案:解：(1)证明：∵A，P，B，C是圆上的四个点，∴∠ABC＝∠APC，∠CPB＝∠BAC.∵∠APC＝∠CPB＝60°，∴∠ABC＝∠BAC＝60°.∴∠ACB＝60°.∴△ABC是等边三角形．(2)∵△ABC是等边三角形，∴∠ACB＝60°，AC＝AB＝BC＝2.∵∠PAC＝90°，∴∠DAB＝∠D＝30°.∴BD＝AB＝2.∵四边形APBC是圆内接四边形，∠PAC＝90°，∴∠PBC＝∠PBD＝90°.在Rt△PBD中，PD＝＝＝4.试题23答案:解：(1)过点E作EF⊥AB于点F，延长EF交圆于点D，则由题意得DF＝20. 由垂径定理知，点F是AB的中点，AF＝FB＝AB＝40米，EF＝ED－FD＝AE－DF，由勾股定理知，AE2＝AF2＋EF2＝AF2＋(AE－DF)2. 设圆的半径是r，则r2＝402＋(r－20)2，解得r＝50.即桥拱的半径为50米．(2)设水面上涨后水面跨度MN为60米，MN交ED于H，连接EM，则MH＝NH＝MN＝30米，∴EH＝＝40(米)．∵EF＝50－20＝30(米)，∴HF＝EH－EF＝10米．试题24答案:解：(1)证明：∵ED＝EC，∴∠EDC＝∠C.∵∠EDC＋∠ADE＝180°，∠ADE＋∠B＝180°，∴∠EDC＝∠B.∴∠B＝∠C.∴AB＝AC.(2)连接AE，∵AB为直径，∴AE⊥BC.由(1)知，AB＝AC，∴BE＝CE＝BC＝.在△ABC与△EDC中，∵∠C＝∠C，∠CDE＝∠B，∴△ABC∽△EDC.∴＝.∴CE·CB＝CD·CA.∵AC＝AB＝4，∴×2＝4CD.∴CD＝.试题25答案:解：(1)证明：连接AD.∵AB是⊙O的直径，∴∠ADB＝90°.∵点D是BC的中点，∴AD是线段BC的垂直平分线．∴AB＝AC.∵AB＝BC，∴AB＝BC＝AC.∴△ABC为等边三角形．(2)连接BE.∵AB是直径，∴∠AEB＝90°. ∴BE⊥AC.∵△ABC是等边三角形，∴AE＝EC，即E为AC的中点．∵D是BC的中点，故DE为△ABC的中位线，∴DE＝AB＝×2＝1.(3)存在点P使△PBD≌△AED，由(1)(2)知，BD＝ED，∵∠BAC＝60°，DE∥AB，∴∠AED＝120°. ∵∠ABC＝60°，∴∠PBD＝120°.∴∠PBD＝∠AED.要使△PBD≌△AED，只需PB＝AE＝1.。

亲爱的同学：这份试卷将再次记录你的自信、沉着、智慧和收获，我们一直投给你信任的目光……学习资料专题2.3 垂径定理知|识|目|标1．通过圆的对称性折叠操作，理解垂径定理．2．通过对垂径定理的理解，采用转化和对称思想解决有关直角三角形的计算与证明问题．3．在掌握垂径定理的基础上，能应用垂径定理解决实际生活中的问题.目标一理解垂径定理例1 教材补充例题如图2－3－1所示的图形中，哪些图形能得到AE＝BE的结论，哪些不能，为什么？①②③④图2－3－1【归纳总结】理解垂径定理的“三点注意”：(1)这里的垂径可以是直径、半径或过圆心的直线(线段)，其本质是“过圆心”；(2)垂径定理中的弦为直径时，结论仍然成立；(3)平分弦所对的两条弧，是指平分弦所对的劣弧和优弧，不要漏掉优弧．目标二能运用垂径定理进行计算或推理证明例2 教材补充例题如图2－3－2，⊙O的半径为17 cm，弦AB∥CD，AB＝30 cm，CD＝16 cm，圆心O位于AB，CD的上方，求AB和CD之间的距离．图2－3－2【归纳总结】垂径定理中常用的两种辅助线：(1)若已知圆心，则作垂直于弦的直径；(2)若已知弦、弧的中点，则作弦、弧中点的连线或连半径等．目标三 能利用垂径定理解决实际问题例3 教材补充例题赵州桥是我国建筑史上的一大创举，它距今约1400年，历经无数次洪水冲击和8次地震却安然无恙．如图2－3－3，若桥跨度AB 约为40米，主拱高CD 约为10米，则桥弧AB 所在圆的半径R ＝________米．图2－3－3图2－3－4【归纳总结】1．垂径定理基本图形的四变量、两关系：(1)四变量：如图2－3－4，弦长a ，圆心到弦的距离d ，半径r ，弧的中点到弦的距离(弓形高)h ，这四个变量知任意两个可求其他两个．(2)两关系：①⎝ ⎛⎭⎪⎫a 22＋d 2＝r 2；②h ＋d ＝r. 2．垂径定理在应用中常作的辅助线：作垂线，连半径，构造直角三角形．3．垂径定理在应用中常用的技巧：设未知数，根据勾股定理列方程．知识点 垂径定理垂径定理：垂直于弦的直径平分这条____，并且平分________________．[点拨] (1)平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧．(2)弦的垂直平分线经过圆心，并且平分弦所对的两条弧．(3)平分弦所对的一条弧的直径垂直平分弦，并且平分弦所对的另一条弧．已知CD 是⊙O 的一条弦，作直径AB ，使AB ⊥CD ，垂足为E ，若AB ＝10，CD ＝8，求BE 的长． 解：如图2－3－5，连接OC ，则OC ＝5.图2－3－5∵AB 是⊙O 的直径，AB ⊥CD ，CD ＝8，∴CE ＝12CD ＝4. 在Rt △OCE 中，OE ＝OC 2－CE 2＝3，∴BE ＝OB ＋OE ＝5＋3＝8.以上解答完整吗？若不完整，请进行补充．教师详解详析【目标突破】例1 解：①②能，③④不能．理由略．例2 [解析] 如图，过圆心O 作弦AB 的垂线，易证它也与弦CD 垂直，由垂径定理知AE ＝BE ，CF ＝DF ，根据勾股定理可求OE ，OF 的长，进而可求出AB 和CD 之间的距离．解：如图，过点O 作OE ⊥AB 于点E ，交CD 于点F ，连接OA ，OC.∵AB ∥CD ，∴OF ⊥CD. 在Rt △OAE 中，∵OA ＝17 cm ，AE ＝BE ＝12AB ＝15 cm ， ∴OE ＝172－152＝8(cm)．同理可求OF ＝172－82＝15(cm)．∵圆心O 位于AB ，CD 的上方，∴EF ＝OF －OE ＝15－8＝7(cm)．即AB 和CD 之间的距离是7 cm.例3 [答案] 25[解析] 根据垂径定理，得AD ＝12AB ＝20米．在Rt △AOD 中，根据勾股定理，得R 2＝202＋(R －10)2，解得R ＝25(米)．【总结反思】[小结] 知识点 弦 弦所对的两条弧[反思] 不完整．补充：若垂足E 在线段OA 上，则BE ＝OB ＋OE ＝5＋3＝8；若垂足E 在线段OB 上，则BE ＝OB －OE ＝5－3＝2.综上所述，BE 的长为8或2.其长度保持不变．。

*2.3 垂径定理知识要点垂径定理(教材P60习题T1变式)如图，在⊙O中，半径OD垂直于弦AB，垂足为C，OD＝13cm，AB＝24cm，则CD＝______.分析：由垂径定理得AC＝12AB＝12cm.连接OA，由半径相等，得OA＝OD＝13cm.在Rt△AOC中，利用勾股定理可求OC的长，最后用CD＝OD－OC即可求出CD的长．方法点拨：解题的方法是作辅助线构造直角三角形，运用勾股定理、垂径定理解答．如图是一个隧道的横截面，若它的形状是以O为圆心的圆的一部分，路面AB＝12米，净高CD＝9米，则此圆的半径OA为 ( )A．6米 B.132米 C．7米 D.152米分析：设⊙O的半径为r米，则OA＝r米，OD＝(9－r)米．∵AB＝12米，CD⊥AB，∴AD＝12AB＝12×12＝6(米)．在Rt△AOD中，由勾股定理得OA2＝AD2＋OD2，即可得到关于r的方程，解出方程即可求出⊙O的半径长．方法点拨：构造直角三角形，结合垂径定理和勾股定理，可以解决计算弦长、半径、弦到圆心的距离、同心圆的相关线段等问题．1．如图，DC是⊙O的直径，弦AB⊥CD于点F，连接BC、BD，则下列结论错误的是( )A．AF＝BF B．OF＝CFC.AC︵＝BC︵D．∠DBC＝90°2．如图，在⊙O 中，AB 为弦，OC ⊥AB ，垂足为C ，若AO ＝5cm ，OC ＝3cm ，则弦AB 的长为______cm.3．如图所示，是一根水平放置的圆柱形输水管道的横截面，其中有水部分水面宽0.8m ，最深处水深0.2m ，则此输水管道的直径是________m.参考答案: 要点归纳知识要点：平分 平分 DB BN ︵ BM ︵相等 典例导学 例1 8 例2 B 当堂检测1．B 2.8 3.1。