2018年中考数学真题分类汇编(第三期)专题34投影与视图试题(含解析)

2017-2018年中考数学专题复习题：投影与视图、选择题1. 图中三视图对应的几何体是2. 如图是由若干小正方体组成的几何体的俯视图，小正方形中的数字表示该位置小正方体的个数，这个几何体的主视图是3. 如图，上下底面为全等的正六边形礼盒，其正视图与侧视图均由矩形构成，正视图中大矩形边长如图所示，侧视图中包含两全等的矩形，如果用彩色胶带如图包扎礼盒，所需胶带长度至少为I IA. B. C. D.3112—60cm -—20cm M CE正视图侧视图A. 320 cmB. 讥IH .- ;C. 4 1, 一二’D. 480 cm4. 如图，一个正方体切去一个三棱锥后所得几何体的俯视图是A.5. 有一圆柱形的水池，已知水池的底面直径为 4米，水面离池口 2米，水池内有一小青蛙，它每天晚上都会浮在水面上赏月，则它能观察到的最大视角为如图，直立于地面上的电线杆 AB 在阳光下落在水平地面和坡面上的影子分别是 BC CD 测得BC=6米， = -米，二 二:二FC'，在D 处测得电线杆顶端 A 的仰角为:Ej ，则电线杆AB 的高度为，A. 2+ 2逅B. 4+ 2V3C. 2+D.4+8. 在阳光下，一名同学测得一根长为 1米的垂直地面的竹竿的影长为1七米，同时另一名同学测量树的高度时，发现树的影 子不全落在地面上，有一部分落在教学楼的第一级台阶上,6.如图所示，在房子外的屋檐E 处安有一台监视器,a一 一 -邛1■ 口 口FA B CA. _ -.1B. A BFDC.四边形 BCEDD. - -5；7.测得此影子长为米，一级台阶高为）d米，如图所示，若此时落在地面上的影长为丄丄］米，则树高为I IA. ■> -■ ■米B. 8 米C. .1 =米D. 12 米9. 如图所示，右面水杯的杯口与投影面平行，投影线的方向如箭头所示，它的正投影图是I .10. 圆桌面•桌面中间有一个直径为：.4-;的圆洞I正上方的灯泡I看作一个点I发出的光线照射平行于地面的桌面后，在地面上形成如图所示的圆环形阴影，已知桌面直径为_.?：■，桌面离地面1m若灯泡离地面3m则地面圆环形阴影的面积是（）A. 1.1. A1 1. ■B.丄，‘C.D. 0.72rm:、填空题11.如图，光源P在横杆AB的正上方,I' ^「，」3 = 1.;，「二二•：；「，则AB离地面的距离为12.如图，圆桌面正上方的灯泡发出的光线照射桌面后，在地面上形成阴影圆形»已知灯泡距离地面2 4 ;，桌面距离地面■I “桌面厚度不计算「，若桌面的面积是一.J：'-，则地面上体的俯视图的周长是 _______ ，面积是 _______15. 如图，AB 和DE 是直立在地面上的两根立柱，-F 二F 米，某一时刻 AB 在阳光下的投影3 ? = ：■米，在测量AB 的投影时，同时测量出DE 在阳光下的投影长为 6米，则 DE 的长为 _______ 16. 如图，在一面与地面垂直的围墙的同侧有一根高13米的旗杆AB 和一根高度未知的电线杆CD 它们都与地面垂直，为了侧得电线杆的高度，数学兴趣小组的同学进 行了如下测量.某一时刻，在太阳光照射下，旗杆落在围墙上的影子EF 的长度为3米,落在地面上的影子 BF 的长为8 米,而电信杆落在围墙上的影子 GH 的长度为:-2 米，落在地面上的银子 DH 的长为6米，依据这些数据，该小组的同学计算出了电 线杆的高度是的阴影面积是 ______ m 町13.如图是某几何体的三视图，根据图中数据，求得该几何体的表面积为 ______ .1 !r1 ■ ■ 1 ■ ■ ■ ■ ■ ■14.如图，正三棱柱的底面周长为15,截去一个底面周长为 6的正三棱柱，所得几何__________________ 米・地面的距离CD = ________19. ___________________________________________________________ 桌面上放两件物体，它们的三视图图，则这两个物体分别是 _____________________________ ，它们的位置20.桌上放着一个三棱锥和一个圆柱体， 如图的三幅图分别是从哪个方向看的？按图填17. 如图是王芳同学某一天观察到的一棵树在不同时刻的影子,请你把它们按时间先后顺序进行排列是 ________18.墙壁D 处有一盏灯如图，小明站在A 处测得他的影长与身长相等都为1三「，小明向墙壁走1m 到B 处发现影子刚好落在 A 点，则灯泡与厂□王观圈旗杆电遙杆(A) (B)是 ______21. 如图，校园内有一棵与地面垂直的树，数学兴趣小组两次测量它在地面上的影子，第一次是阳光与地面成亠卩角时，第二次是阳光与地面成 :< 角时，两次测量的影长相差8米，求树高AB多少米，结果保留根号・22. 如图，是住宅区内的两幢楼，它们的高-F = L"：=■■ j ，两楼间的距离现需了解甲楼对乙楼的采光的影响情况..当太阳光与水平线的夹角为•工角时，求甲楼的影子在乙楼上有多高|精确到1 : > .厂1 ；若要甲楼的影子刚好不落在乙楼的墙上，此时太阳与水平线的夹角为多少度?23. 某兴趣小组开展课外活动如图，小明从点M出发以］三米秒的速度，沿射线MN方向匀速前进，2秒后到达点B,此时他（4#）在某一灯光下的影长为MB继续按原速行走2秒到达点D,此时他在同一灯光下的影子GD仍落在其身后，并测得这个影长GD为1 1米，然后他将速度提高到原来的一上倍，再行走2秒到达点F,此时点A, C, E三点共线..请在图中画出光源0点的位置，并画出小明位于点F时在这个灯光下的影长- J 不写画法；•求小明到达点F时的影长FH的长.■---------------------------------------M B G D F N24.如图是一个密封纸盒的三视图，请你根据图中数据计算这个密封纸盒的表面积结果保留根号【答案】J D 1 解：在A - _ "1中，：山 £T |J在丁_.匸〕中，'in 厂AB AB 如&'——^，答：树高AB 为4.-米.22.解：I 如图，延长0B 交DC 于E,作严丄_卫，交AB 于F ,在- 中,1. 2. C 3. C 4. D 5. C 6. D 7. B 8. 9. D 10. D11.12.13. (225 + 25 v 1?) T14. 13； Ml415. 10m16. 1117. B A 、C D18.4.Srn19. 长方体和圆柱；圆柱在前，长方体在后20. 左面、上面、正面21.= :: } ，一 匚二 I 二：口 ,设5-=.，则?5= : . • 根据勾股定理知'二.,. 2.「 「:小"■,:1 j-. 负值舍去, 八'二川;•因此，-—. - •（勻当甲幢楼的影子刚好落在点 C 处时，一 为等腰三角形，因此，当太阳光与水平线夹角为 芟，时，甲楼的影子刚好不落在乙楼的墙上.23.解：|如图，点0和FH 为所作；M B G D K F H M'.■ ■- ' — — '「一 ； . ，4 二一.=,；二二一 ♦一.二'2= - E-，设 -5 = II.二三二二 I ：'，作；■■-:于K 如图，I ■ ■.",_ j.\ 2、s _；「［ -■,V CD//OK,J 8OX 耐JT'•，即卩二——ffJC OK l.^rDK由注得"亠，解得H,.-m「,_三“_二即'■':OJC KK ffFM5 E答：小明到达点F时的影长FH的长为24. 解：根据该密封纸盒的三视图知道它是一个六棱柱,其高为12cm底面边长为5cm其侧面积为丨＜，密封纸盒的上、下底面的面积和为：「「_「. -匚：”」，其表面积为-。

2018中考数学分类汇编--投影与视图（有解析）2018中考数学试题分类汇编：考点38投影与视图一．选择题（共45小题）1．（2018广安）下列图形中，主视图为①的是（）A．B．C．D．【分析】主视图是从物体的正面看得到的图形，分别写出每个选项中的主视图，即可得到答案．【解答】解：A、主视图是等腰梯形，故此选项错误；B、主视图是长方形，故此选项正确；C、主视图是等腰梯形，故此选项错误；D、主视图是三角形，故此选项错误；故选：B．2．（2018眉山）下列立体图形中，主视图是三角形的是（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得图形的主视图．【解答】解：A、C、D主视图是矩形，故A、C、D不符合题意；B、主视图是三角形，故B正确；故选：B．3．（2018泰州）下列几何体中，主视图与俯视图不相同的是（）A．正方体B．四棱锥C．圆柱D．球【分析】根据主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形进行分析．【解答】解：四棱锥的主视图与俯视图不同．故选：B．4．（2018昆明）下列几何体的左视图为长方形的是（）A．B．C．D．【分析】找到个图形从左边看所得到的图形即可得出结论．【解答】解：A．球的左视图是圆；B．圆台的左视图是梯形；C．圆柱的左视图是长方形；D．圆锥的左视图是三角形．故选：C．5．（2018桂林）如图所示的几何体的主视图是（）A．B．C．D．【分析】根据主视图是从正面看到的图形，可得答案．【解答】解：从正面看下面是一个长方形，如图所示：故C选项符合题意，故选：C．6．（2018湘潭）如图所示的几何体的主视图是（）A．B．C．D．【分析】找出从几何体的正面看所得到的图形即可．【解答】解：该几何体的主视图是三角形，故选：C．7．（2018常德）把图1中的正方体的一角切下后摆在图2所示的位置，则图2中的几何体的主视图为（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看是一个等腰三角形，高线是虚线，故选：D．8．（2018长春）下列立体图形中，主视图是圆的是（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：A、圆锥的主视图是三角形，故A不符合题意；B、圆柱的柱视图是矩形，故B错误；C、圆台的主视图是梯形，故C错误；D、球的主视图是圆，故D正确；故选：D．9．（2018扬州）如图所示的几何体的主视图是（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看第一层是两个小正方形，第二层左边一个小正方形，第三层左边一个小正方形，故选：B．10．（2018新疆）如图是由三个相同的小正方体组成的几何体，则该几何体的左视图是（）A．B．C．D．【分析】细心观察图中几何体中正方体摆放的位置，根据左视图是从左面看到的图形判定则可．【解答】解：从左边看竖直叠放2个正方形．故选：C．11．（2018资阳）如图是由四个相同的小正方体堆成的物体，它的正视图是（）A．B．C．D．【分析】找到从正面看所得到的图形即可．【解答】解：从正面看可得从左往右2列正方形的个数依次为2，1，故选：A．12．（2018十堰）今年“父亲节”佳佳给父亲送了一个礼盒，该礼盒的主视图是（）A．B．C．D．【分析】找出从几何体的正面看所得到的图形即可．【解答】解：由图可得，该礼盒的主视图是左边一个矩形，右面一个小正方形，故选：C．13．（2018黄石）如图，该几何体的俯视图是（）A．B．C．D．【分析】找到从几何体的上面所看到的图形即可．【解答】解：从几何体的上面看可得，故选：A．14．（2018江西）如图所示的几何体的左视图为（）A．B．C．D．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：从左边看是上大下小等宽的两个矩形，矩形的公共边是虚线，故选：D．15．（2018香坊区）如图的几何体是由五个小正方体组合而成的，则这个几何体的左视图是（）A．B．C．D．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：从左边看第一层是两个正方形，第二层是左边一个正方形，故选：D．16．（2018泸州）如图是一个由5个完全相同的小正方体组成的立体图形，它的俯视图是（）A．B．C．D．【分析】根据从上面看得到的图形是俯视图，可得答案．【解答】解：从上面看第一列是两个小正方形，第二列是一个小正方形，第三列是一个小正方形，故选：B．17．（2018广州）如图所示的几何体是由4个相同的小正方体搭成的，它的主视图是（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看第一层是三个小正方形，第二层右边一个小正方形，故选：B．18．（2018宁波）如图是由6个大小相同的立方体组成的几何体，在这个几何体的三视图中，是中心对称图形的是（）A．主视图B．左视图C．俯视图D．主视图和左视图【分析】根据从上边看得到的图形是俯视图，可得答案．【解答】解：从上边看是一个田字，“田”字是中心对称图形，故选：C．19．（2018娄底）如图所示立体图形的俯视图是（）A．B．C．D．【分析】找到从上面看所得到的图形即可，注意所有的看到的棱都应表现在俯视图中．【解答】解：从上边看立体图形得到俯视图即可得立体图形的俯视图是，故选：B．20．（2018泰安）如图是下列哪个几何体的主视图与俯视图（）A．B．C．D．【分析】直接利用主视图以及俯视图的观察角度结合结合几何体的形状得出答案．【解答】解：由已知主视图和俯视图可得到该几何体是圆柱体的一半，只有选项C符合题意．故选：C．21．（2018荆门）某几何体由若干个大小相同的小正方体搭成，其主视图与左视图如图所示，则搭成这个几何体的小正方体最少有（）A．4个B．5个C．6个D．7个【分析】由主视图和左视图确定俯视图的形状，再判断最少的正方体的个数．【解答】解：由主视图和左视图可确定所需正方体个数最少时俯视图为：，则搭成这个几何体的小正方体最少有5个．故选：B．22．（2018襄阳）一个几何体的三视图如图所示，则这个几何体是（）A．B．C．D．【分析】由主视图和左视图确定是柱体，锥体还是球体，再由俯视图确定具体形状．【解答】解：根据主视图和左视图为矩形判断出是柱体，根据俯视图是三角形可判断出这个几何体应该是三棱柱．故选：C．23．（2018贵阳）如图是一个几何体的主视图和俯视图，则这个几何体是（）A．三棱柱B．正方体C．三棱锥D．长方体【分析】根据三视图得出几何体为三棱柱即可．【解答】解：由主视图和俯视图可得几何体为三棱柱，故选：A．24．（2018恩施州）由若干个完全相同的小正方体组成一个立体图形，它的左视图和俯视图如图所示，则小正方体的个数不可能是（）A．5B．6C．7D．8【分析】直接利用左视图以及俯视图进而分析得出答案．【解答】解：由左视图可得，第2层上至少一个小立方体，第1层一共有5个小立方体，故小正方体的个数最少为：6个，故小正方体的个数不可能是5个．故选：A．25．（2018武汉）一个几何体由若干个相同的正方体组成，其主视图和俯视图如图所示，则这个几何体中正方体的个数最多是（）A．3B．4C．5D．6【分析】易得这个几何体共有2层，由俯视图可得第一层立方体的个数，由主视图可得第二层立方体的可能的个数，相加即可．【解答】解：结合主视图和俯视图可知，左边上层最多有2个，左边下层最多有2个，右边只有一层，且只有1个．所以图中的小正方体最多5块．故选：C．26．（2018包头）如图，是由几个大小相同的小立方块所搭几何体的俯视图，其中小正方形中的数字表示在该位置的小立方块的个数，则这个几何体的主视图是（）A．B．C．D．【分析】由俯视图知该几何体共2列，其中第1列前一排1个正方形、后1排2个正方形，第2列只有前排2个正方形，据此可得．【解答】解：由俯视图知该几何体共2列，其中第1列前一排1个正方形、后1排2个正方形，第2列只有前排2个正方形，所以其主视图为：故选：C．27．（2018金华）一个几何体的三视图如图所示，该几何体是（）A．直三棱柱B．长方体C．圆锥D．立方体【分析】根据三视图的形状可判断几何体的形状．【解答】解：观察三视图可知，该几何体是直三棱柱．故选：A．28．（2018黔南州）如图的几何体是由四个大小相同的正方体组成的，它的俯视图是（）A．B．C．D．【分析】找到从上面看所得到的图形即可．【解答】解：从上面可看到从上往下2行小正方形的个数为：2，1，并且下面一行的正方形靠左，故选C．29．（2018随州）如图是一个由4个相同正方体组成的立体图形，它的左视图是（）A．B．C．D．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：从左边看第一层是两个小正方形，第二层左边一个小正方形，故选：D．30．（2018哈尔滨）六个大小相同的正方体搭成的几何体如图所示，其俯视图是（）A．B．C．D．【分析】俯视图有3列，从左到右正方形个数分别是2，1，2．【解答】解：俯视图从左到右分别是2，1，2个正方形．故选：B．31．（2018郴州）如图是由四个相同的小正方体搭成的立体图形，它的主视图是（）A．B．C．D．【分析】找到几何体的上面看所得到的图形即可．【解答】解：从几何体的上面看可得，故选：B．32．（2018沈阳）如图是由五个相同的小立方块搭成的几何体，这个几何体的左视图是（）A．B．C．D．【分析】细心观察图中几何体中正方体摆放的位置，根据左视图是从左面看到的图形判定则可．【解答】解：从左边看，从左往右小正方形的个数依次为：2，1．左视图如下：故选：D．33．（2018深圳）图中立体图形的主视图是（）A．B．C．D．【分析】根据主视图是从正面看的图形解答．【解答】解：从正面看，共有两层，下面三个小正方体，上面有两个小正方体，在右边两个．故选：B．34．（2018临安区）小明从正面观察如图所示的两个物体，看到的是（）A．B．C．D．【分析】分别找出四个选项中图形是从哪个方位看到的，此题得解．【解答】解：A、从上面看到的图形；B、从右面看到的图形；C、从正面看到的图形；D、从左面看到的图形．故选：C．35．（2018潍坊）如图所示的几何体的左视图是（）A．B．C．D．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：从左边看是两个等宽的矩形，矩形的公共边是虚线，故选：D．36．（2018聊城）如图所示的几何体，它的左视图是（）A．B．C．D．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：用左边看是等宽的上下两个矩形，上边的矩形小，下边的矩形大，两矩形的公共边是虚线，故选：D．37．（2018曲靖）如图所示的支架（一种小零件）的两个台阶的高度和宽度相等，则它的左视图为（）A．B．C．D．【分析】找到从左面看所得到的图形即可，注意所有的看到的棱都应表现在视图中．【解答】解：从左面看去，是两个有公共边的矩形，如图所示：故选：D．38．（2018湖州）如图所示的几何体的左视图是（）A．B．C．D．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：从左边看是一个圆环，故选：D．39．（2018菏泽）如图是两个等直径圆柱构成的“T”形管道，其左视图是（）A．B．C．D．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：从左边看如图，故选：B．40．（2018嘉兴）下列几何体中，俯视图为三角形的是（）A．B．C．D．【分析】根据从上边看得到的图形是俯视图，可得答案．【解答】解：A、俯视图是圆，故A不符合题意；B、俯视图是矩形，故B不符合题意；C、俯视图是三角形，故C符合题意；D、俯视图是四边形，故D不符合题意；故选：C．41．（2018安徽）一个由圆柱和圆锥组成的几何体如图水平放置，其主（正）视图为（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看上边是一个三角形，下边是一个矩形，故选：A．42．（2018怀化）下列几何体中，其主视图为三角形的是（）A．B．C．D．【分析】找出四个选项中几何体的主视图，由此即可得出结论．【解答】解：A、圆柱的主视图为矩形，∴A不符合题意；B、正方体的主视图为正方形，∴B不符合题意；C、球体的主视图为圆形，∴C不符合题意；D、圆锥的主视图为三角形，∴D符合题意．故选：D．43．（2018自贡）下面几何的主视图是（）A．B．C．D．【分析】主视图是从物体正面看所得到的图形．【解答】解：从几何体正面看，从左到右的正方形的个数为：2，1，2．故选B．44．（2018遂宁）如图，5个完全相同的小正方体组成了一个几何体，则这个几何体的主视图是（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看第一层是三个小正方形，第二层中间一个小正方形，．故选：D．45．（2018温州）移动台阶如图所示，它的主视图是（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看是三个台阶，故选：B．二．填空题（共5小题）46．（2018青岛）一个由16个完全相同的小立方块搭成的几何体，其最下面一层摆放了9个小立方块，它的主视图和左视图如图所示，那么这个几何体的搭法共有10种．【分析】先根据主视图确定每一列最大分别为4，2，3，再根据左视确定每一行最大分别为4，3，2，总和要保证为16，还要保证俯视图有9个位置．【解答】解：设俯视图有9个位置分别为：由主视图和左视图知：①第1个位置一定是4，第6个位置一定是3；②一定有2个2，其余有5个1；③最后一行至少有一个2，当中一列至少有一个2；根据2的排列不同，这个几何体的搭法共有10种：如下图所示：故答案为：10．47．（2018东营）已知一个圆锥体的三视图如图所示，则这个圆锥体的侧面积为20π．【分析】先利用三视图得到底面圆的半径为4，圆锥的高为3，再根据勾股定理计算出母线长l为5，然后根据圆锥的侧面积公式：S侧=πrl代入计算即可．【解答】解：根据三视图得到圆锥的底面圆的直径为8，即底面圆的半径r为4，圆锥的高为3，所以圆锥的母线长l==5，所以这个圆锥的侧面积是π×4×5=20π．故答案为：20π48．（2018孝感）如图是一个几何体的三视图（图中尺寸单位：cm），根据图中数据计算，这个几何体的表面积为16πcm2．【分析】由主视图和左视图确定是柱体，锥体还是球体，再由俯视图确定具体形状，确定圆锥的母线长和底面半径，从而确定其表面积．【解答】解：由主视图和左视图为三角形判断出是锥体，由俯视图是圆形可判断出这个几何体应该是圆锥；根据三视图知：该圆锥的母线长为6cm，底面半径为2cm，故表面积=πrl+πr2=π×2×6+π×22=16π（cm2）．故答案为：16π．49．（2018白银）已知某几何体的三视图如图所示，其中俯视图为正六边形，则该几何体的侧面积为108．【分析】观察该几何体的三视图发现该几何体为正六棱柱，然后根据提供的尺寸求得其侧面积即可．【解答】解：观察该几何体的三视图发现该几何体为正六棱柱，其底面边长为3，高为6，所以其侧面积为3×6×6=108，故答案为：108．50．（2018齐齐哈尔）三棱柱的三视图如图所示，已知△EFG中，EF=8cm，EG=12cm，∠EFG=45°．则AB的长为4cm．【分析】根据三视图的对应情况可得出，△EFG中FG上的高即为AB的长，进而求出即可．【解答】解：过点E作EQ⊥FG于点Q，由题意可得出：EQ=AB，∵EF=8cm，∠EFG=45°，∴EQ=AB=×8=4（cm）．故答案为：4．。

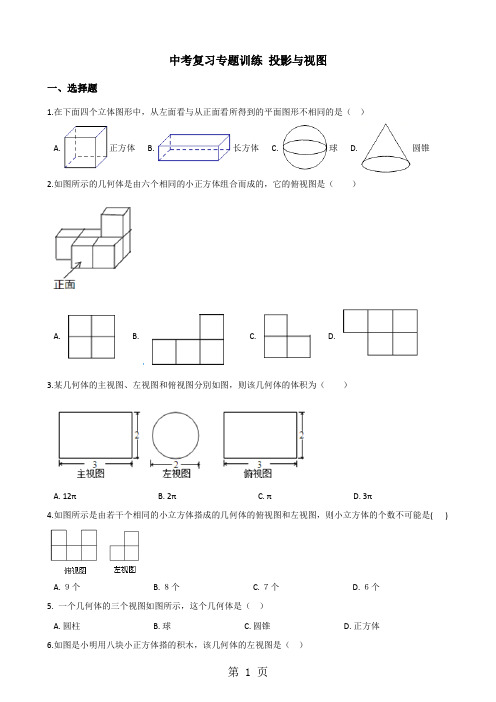
中考复习专题训练投影与视图一、选择题1.在下面四个立体图形中，从左面看与从正面看所得到的平面图形不相同的是（）A. 正方体B. 长方体C. 球D. 圆锥2.如图所示的几何体是由六个相同的小正方体组合而成的，它的俯视图是（）A. B. C. D.3.某几何体的主视图、左视图和俯视图分別如图，则该几何体的体积为（）A. 12πB. 2πC. πD. 3π4.如图所示是由若干个相同的小立方体搭成的几何体的俯视图和左视图，则小立方体的个数不可能是( )A. ９个B. ８个C. ７个D. ６个5. 一个几何体的三个视图如图所示，这个几何体是（）A. 圆柱B. 球C. 圆锥D. 正方体6.如图是小明用八块小正方体搭的积木，该几何体的左视图是（）A. B. C. D.7.小明拿一个等边三角形木框在太阳下玩耍，发现等边三角形木框在地面上的投影不可能是（）A.B.C.D.8.如图所示，该几何体的俯视图是（）A. B. C. D.9.某同学画出了如图所示的几何体的三种视图，其中正确的是（）A. ①②B. ①③C. ②③D. ②10.灯光下的两根小木棒A和B，它们竖立放置时的影子长分别为l A和l B，若l A＞l B．则它们的高度为h A和h B满足（）A. h A＞h BB. h A＜h BC. h A≥h BD. 不能确定二、填空题11.用一些大小相同的小正方体搭成一个几何体，使得从正面和上面看到的这个几何体的形状如图所示，那么，组成这个几何体的小正方体的块数至少为________．12.大双、小双兄弟二人的身高相同，可是在灯光下，哥哥大双的影子比弟弟小双的影子短，这是因为________ ．13.下面四幅图是两个物体不同时刻在太阳光下的影子，按照时间的先后顺序是________ ．14.（2019•江西模拟）如图是某几何体的三视图，根据图中数据，求得该几何体的体积为 ________．15.由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示，俯视图的方格中的字母和数字表示该位置上小立方体的个数，求x=________ ，y=________ ．16.如图是两棵小树在同一时刻的影子，请问它们的影子是在________ 光线下形成的（填“灯光”或“太阳”）．17.如图是一个由若干个正方体搭建而成的几何体的主视图与左视图，那么下列图形中可以作为该几何体的俯视图的序号是：________ （多填或错填得0分，少填酌情给分）．18.如图是由几块相同的小正方体搭成的立体图形的三视图，则这个立体图形中小正方体共有________ 块．三、解答题19.某自由下落的物体在灯光下的影子为AB，试确定灯源m的位置，并画出站在底面上的小明的应在EF．（保留作图痕迹，不写作法）20.如图，花丛中有一路灯杆AB，在灯光下，大华在D点处的影长DE=3米，沿BD方向行走到达G点，DG=5米，这时大华的影长GH=5米．如果大华的身高为2米，求路灯杆AB的高度．21.如图，AB和DE是直立在地面上的两根立柱，已知AB=5m，某一时刻AB在太阳光下的影子长BC=3m．（1）在图中画出此时DE在太阳光下的影子EF；（2）在测量AB的影子长时，同时测量出EF=6m，计算DE的长．22.如图，一种某小区的两幢10层住宅楼间的距离为AC=30m，由地面向上依次为第1层、第2层、…、第10层，每层高度为3m．假设某一时刻甲楼在乙楼侧面的影长EC=h，太阳光线与水平线的夹角为α．（1）用含α的式子表示h（不必指出α的取值范围）；（2）当α=30°时，甲楼楼顶B点的影子落在乙楼的第几层？若α每小时增加15°，从此时起几小时后甲楼的影子刚好不影响乙楼采光？参考答案一、选择题B D D A A A BC B D二、填空题11.812.哥哥比弟弟更靠近灯13.C→D→A→B14.70π15.1或2；316.灯光17.①②③18.9三、解答题19.解：如图：20.解：∵CD∥AB，∴△EAB∽△ECD，∴=，即=①，∵FG∥AB，∴△HFG∽△HAB，∴=，即=②，由①②得=，解得BD=7.5，∴=，解得：AB=7．答：路灯杆AB的高度为7m．21.（1）解：如图所示：EF即为所求（2）解：由题意可得：，解得：DE=10，答：DE的长为10m22.（1）解：过点E作EH⊥AB于H，由题意四边形ACEH是矩形，∴EH=AC=30，AH=CE=h，∠BEH=α，∴BH=30﹣h，在Rt△BEH中，tan∠BEH= ，∴30﹣h=30tanα，∴h=30﹣30tanα．（2）解：当α=30°时，h=30﹣30× ≈12.7，∵12.7÷3=4.2，∴B点的影子落在乙楼的第五层，当B点的影子落在乙楼C处时，甲楼的影子刚好不影响乙楼采光，此时AB=AC=30，△ABC是等腰直角三角形，∴∠ACB=45°，∴=1（小时），∴从此时起1小时后甲楼的影子刚好不影响乙楼采光．。

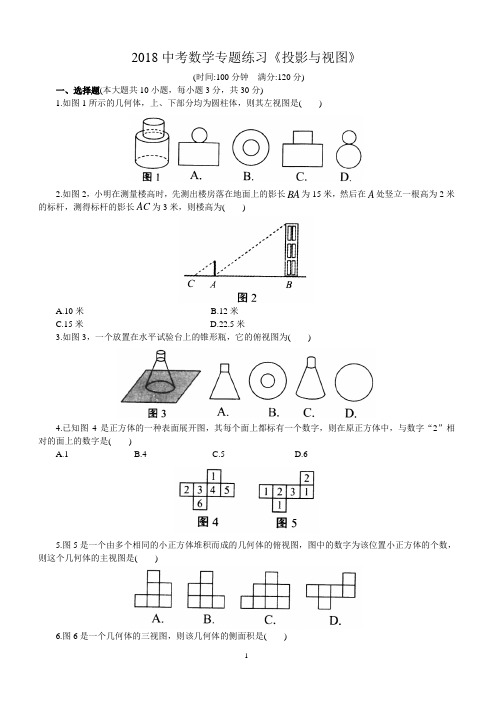
2018中考数学专题练习《投影与视图》(时间:100分钟满分:120分)一、选择题(本大题共10小题，每小题3分，共30分)1.如图1所示的几何体，上、下部分均为圆柱体，则其左视图是( )2.如图2，小明在测量楼高时，先测出楼房落在地面上的影长BA为15米，然后在A处竖立一根高为2米的标杆，测得标杆的影长AC为3米，则楼高为( )A.10米B.12米C.15米D.22.5米3.如图3，一个放置在水平试验台上的锥形瓶，它的俯视图为( )4.已知图4是正方体的一种表面展开图，其每个面上都标有一个数字，则在原正方体中，与数字“2”相对的面上的数字是( )A.1B.4C.5D.65.图5是一个由多个相同的小正方体堆积而成的几何体的俯视图，图中的数字为该位置小正方体的个数，则这个几何体的主视图是( )6.图6是一个几何体的三视图，则该几何体的侧面积是( )A. 213πB. 10πC. 20πD. 413π7.下列几何体是由4个相同的小正方体搭成的，其中左视图与俯视图相同的是()8.一个几何体由n 个大小相同的小正方体搭成，其左视图、俯视图如图7所示，则n 的值最小是( )A.5B.7C.9D.109一个几何体的主视图和俯视图如图8所示，若这个几何体最多有a 个小正方体组成，最少有b 个小正方体组成，则a b +等于( )A.10B.11C.12D.1310.如图9，空心卷筒纸的高度为12 cm ，外径(直径)为10 cm ，内径为4 cm ，在比例尺为1:4的三视图中，其主视图的面积是( )A.214πcm 2 B. 2116πcm 2C. 30cm 2D. 7.5cm 2二、填空题(本大题共5小题，每小题4分，共20分)11.图10是由若干个棱长为1的小正方体组合而成的一个几何体的三视图，则这个几何体的表面积是 .12.如图11，在放映幻灯时，通过光源把幻灯片上的图形放大到屏幕上，若光源到幻灯片的距离为20 cm ，到屏幕的距离为60 cm ，且幻灯片中图形的高度为6 cm ，则屏幕上图形的高度为 cm.13.从棱长为2的正方体毛坯的一角挖去一个棱长为1的小正方体，得到一个如图12所示的零件，则这个零件的表面积是 .14.三棱柱的三视图如图13所示，在EFG ∆中，8EF =cm ，12EG =cm ，30EGF ∠=︒，则AB 的长为 cm.15.如图14，一个几何体的三视图是两个矩形和一个扇形，则这个几何体的表面积为 .三、解答题(本大题共7个小题，共70分)16. ( 8分)图15是一个包装纸盒的三视图(单位:cm)，求制作一个该包装纸盒所需纸板的面积.17. (10分)如图16，某居民小区内A ，B 两楼之间的距离30MN =米，两楼的高度都是20米，A 楼在B 楼的正南，B 楼窗户朝南，B 楼内一楼住户的窗台离小区地面的距离2DN =米，窗户高 1.8CD =米.当正午时刻太阳光线与地面成30º角时，A 楼的影子是否影响B 楼的一楼住户采光?若影响，挡住该住户窗户多高?若不影响，请说明理由. (参考数据:2 1.414≈3 1.732≈5 2.236≈)18.(10分)小明想利用太阳光测量楼高，他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下:如图17，小明边移动边观察，发现站到点E 处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠，且高度恰好相同，此时，测得小明落在墙上的影子高度 1.2CD =米，0.8CE =米，30CA =米(点A ，E ，C 在同一条直线上).已知小明的身高EF 是1.7米，请你帮小明求出楼高AB (结果精确到0.1米)19. (10分)如图18，该小组发现8米高的旗杆DE的影子EF落在了包含一圆弧形小桥在内的路上，于是他们开展了测算小桥所在圆的半径的活动.小刚的身高为1.6米，测得其影长为2.4米，同时测得EG的长为3米，HF的长为1米，测得拱高(弧GH的中点到弦GH的距离，即MN的长)为2米，求小桥所在圆的半径.20. (10分)如图19，若要在宽度AD为20米的城南大道的两边安装路灯，路灯的灯臂BC的长为2米，且与灯柱AB成120º角，路灯采用圆锥形灯罩，灯罩的轴线CO与灯臂BC垂直，当灯罩的轴线CO通过公路路面的中心线时照明效果最好，此时，路灯的灯柱AB的高度应该设计为多少米?(结果保留根号)21. (10分)如图20，为了测量路灯(P点)距地面的高度，身高为1.8米的小强站在A点，在路灯下的头部的影子落在M处，测得影长是5米，向路灯的方向前进15米，到达点B处，在路灯下的头部的影子落在N处，测得影长是1.25米，根据以上数据你能否帮助小强计算路灯的高度以及小强原来站的位置A处到路灯的距离?22. (12分)如图21，某兴趣小组开展课外活动，A，B两地相距12米，小明从点A出发沿AB方向匀速前进，2秒后到达点D，此时他(CD)在某一灯光下的影长为AD，继续按原速行走2秒到达点F，此时他在同一灯光下的影子仍落在其身后，并测得这个影长为1.2米，然后他将速度提高到原来的1.5倍，再行走2秒到达点H ，此时他(GH )在同一灯光下的影长为BH (点C ，E ，G 在同一条直线上).(1)请在图中画出光源O 点的位置，并画出位于点F 时在这个灯光下的影长FM (不写画法). (2)求小明原来的速度.参考答案1. C2. A3. B4. B5. C6. A7. C8. B9. C 10. D 11. 22 12. 18 13. 24 14. 615. 1512π+16. 由俯视图，可得上、下底面均是正六边形. ∴俯视图的面积是15375365222⨯⨯⨯=(cm 2). ∴包装纸盒的侧面是6个正方形， ∴侧面积是265150⨯= (cm 2).∴一个该包装纸盒的表面积是(753150)cm 2.17.如图8，设光线FE 影响到B 楼的E 处.作EG FM ⊥于G .由题意，知30EG MN ==米，30FEG ∠=︒.∴30tan 303017.32FG =⨯︒==≈ (米). ∴2017.32 2.68MG FM GF =-=-= (米).∵2DN =米， 1.8CD =米， ∴ 2.6820.68ED =-=(米).∴A 楼影子影响到B 楼的一楼住户采光，挡住该户窗户0.68米. 18.过点D 作DH AB ⊥，分别交AB ，EF 于点G ，H .∴ 1.2EH AG CD ===米，0.8DH CE ==米，30DG CA ==米. ∵//EF AB ，∴FH DHBG DG=. 由题意，知 1.7 1.20.5FH EF EH =-=-=米). ∴0.50.830BG =. 解得18.75BG =米.∴18.75 1.219.9520.0AB BG AG =+=+=≈(米). ∴楼高AB 约为20.0米.19.由相似，得 1.62.4DE EF =， 解得12EF =米.∵3EG =米，1HF =米， ∴8GH EF EG HF =--=米.由垂径定理，得142GM GH ==米已知2MN =米，设半径OG R =，则2OM R =-. 在Rt OMG ∆中，由勾股定理，得222OM MG OG +=. ∴222(2)4R R -+=.解得5R =.∴小桥所在圆的半径为5米.20.如图9，分别延长OC ，AB 相交于点P .∵120ABC ∠=︒， ∴60PBC ∠=︒.∵90OCB A ∠=∠=︒， ∴30P ∠=︒.∵20AD =米，∴1102OA AD ==米. ∵2BC =米，∴在Rt CPB ∆中，tan 60PC BC =︒=g 24PB BC ==米. ∵P P ∠=∠，90PCB A ∠=∠=︒， ∴PCB PAO ∆∆:. ∴PC BCPA OA=. ∴2310103PC OA PA BC ⨯===g 米). ∴(1034)AB PA PB =-=米.∴路灯的灯柱AB 的高度应该设计为(1034)米.21.设小强原来站的位置A 处到路灯的距离是x 米，路灯的高度是h 米.∵90MAC MOP ∠=∠=︒，AMC OMP ∠=∠， ∴MAC MOP ∆∆:.∴MA ACMO OP =， 即 1.8MA x MA h =+.∵5MA =米，∴5 1.85x h=+， 化简可得5 1.8(5)h x =+.同理可得NB BDON OP =， 即 1.25 1.815 1.25x h=-+，化简可得1.25 1.8(13.75)h x =-.∴可得方程组5 1.8(5)1.25 1.8(13.75)h x h x =+⎧⎨=-⎩解得209x h =⎧⎨=⎩.∴小强原来站的位置A 处到路灯的距离是20米，路灯的高度是9米.22.(1)分别延长AC ，BG 相交于点O ，延长OE 交AB 于点M ，如图10，则点O ，FM 即为所求作.(2)设小明原来的速度为x 米/秒，则2AD DF CE x ===米，3FH EG x ==米，(4 1.2)AM x =-米，(124 1.2)BM x =-+米. ∵//CG AB ，∴OCE OAM ∆∆:，OEG OMB ∆∆:.∴CE OE AM OM =，EG OEMB OM =， ∴CE EGAM MB =， 即234 1.213.24x xx x=--，∴220300x x -=，解得1 1.5x =，20x =(不合题意，舍去). 经检验， 1.5x =是原方程的解. ∴小明原来的速度为1.5米/秒.。

1. （2010年浙江省东阳县）张家界国际乡村音乐周活动中，来自中、日、美的三名音乐家准备在同一节目中依次演奏本国的民族音乐，若他们出场先后的机会是均等的，则按“美—日—中”顺序演奏的概率是 （ ） A 、61 B 、 31 C 、 121 D 32【关键词】概率【答案】A 2．（2010年山东省济宁市）某校举行以“保护环境，从我做起”为主题的演讲比赛．经预赛，七、八年级各有一名同学进入决赛，九年级有两名同学进入决赛．前两名都是九年级同学的概率是 .【关键词】事件与概率 【答案】163．（2010年山东省青岛市）一个口袋中装有10个红球和若干个黄球．在不允许将球倒出来数的前提下，为估计口袋中黄球的个数，小明采用了如下的方法：每次先从口袋中摸出10个球，求出其中红球数与10的比值，再把球放回口袋中摇匀．不断重复上述过程20次，得到红球数与10的比值的平均数为0.4．根据上述数据，估计口袋中大约有 个黄球． 【关键词】概率 【答案】154.（2010年福建省晋江市）下列事件中，是确定事件的是( ) . A.打雷后会下雨 B. 明天是睛天 C. 1小时等于60分钟 D.下雨后有彩虹 【关键词】确定事件 【答案】C5.（2010年广东省广州市）从图2的四张印有汽车品牌标志图案的卡片中任取一张，取出印有汽车品牌标志的图案是中心对称称图形的卡片的概率是（ ）图2A ．41B ．21C ．43D ．1【关键词】中心对称图形 概率 【答案】A6.（2010年四川省眉山市）下列说法不正确的是 A ．某种彩票中奖的概率是11000，买1000张该种彩票一定会中奖 B ．了解一批电视机的使用寿命适合用抽样调查C ．若甲组数据的标准差S 甲=0.31，乙组数据的标准差S 乙=0.25，则乙组数据比甲组数据稳定D ．在一个装有白球和绿球的袋中摸球，摸出黑球是不可能事件 【关键词】事件与概率、数据的收集与分析【答案】A7.(2010年浙江省绍兴市)根据第六届世界合唱比赛的活动细则,每个参赛的合唱团在比赛时须演唱4首歌曲.爱乐合唱团已确定了2首歌曲,还需在A ,B 两首歌曲中确定一首,在C ,D 两首歌曲中确定另一首,则同时确定A ,C 为参赛歌曲的概率是_______________. 【答案】41 8（2010年宁德市）下列事件是必然事件的是（ ）． A.随意掷两个均匀的骰子，朝上面的点数之和为6 B.抛一枚硬币，正面朝上C.3个人分成两组，一定有2个人分在一组D.打开电视，正在播放动画片【答案】C9\(2010年滨州).某电视台在2010年春季举办的青年歌手大奖赛活动中,得奖选手由观众发短信投票产生,并对发短信者进行抽奖活动.一万条短信为一个开奖组,设一等奖1名,二等奖3名, 三等奖6名.王小林同学发了一条短信,那么他获奖的概率是 . 【答案】110009.(2010年山东聊城)一个材质均匀的正方体的六个面上分别标有字母A 、B 、C ，其展开图如图所示随机抛掷此正方体，A 面朝上的概率是______________.【关键词】概率【答案】1310、（2010年宁波市）从1－9这九年自然数中任取一个，是2的倍数的概率是（ ） A 、92 B 、94 C 、95 D 、32【关键词】概率【答案】B 11．（2010年山东省济宁市）某校举行以“保护环境，从我做起”为主题的演讲比赛．经预赛，七、八年级各有一名同学进入决赛，九年级有两名同学进入决赛．前两名都是九年级同学的概率是 .【关键词】事件与概率 【答案】1612．(2010年北京崇文区) 在 6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、直角梯形、正方形和圆． 在看不见图形的情况下随机摸出1张，这张卡片上的图形是中心对称图形的概率是（ ）A ．61 B ．31C ．21 D ．32 【关键词】中心对称、概率 【答案】D13.（2010年毕节地区）在盒子里放有三张分别写有整式1a +、2a +、2的卡片，从中随机抽取两张卡片，把两张卡片上的整式分别作为分子和分母，则能组成分式的概率是( )．A .13 B . 23 C . 16 D . 34【关键词】事件的概率和整式的概念 【答案】B 14．（2010年门头沟区）小明要给刚结识的朋友小林打电话，他只记住了电话号码的前5位的顺序，后3位是3，6，8三个数字的某一种排列顺序，但具体顺序忘记了，那么小明第一次就拨通电话的概率是A ．121 B ．61 C ．41D ．31 【关键词】概率 【答案】B 15．（2010浙江省喜嘉兴市）若自然数n 使得三个数的加法运算“n ＋(n ＋1)＋(n ＋2)”产生进位现象，则称n 为“连加进位数”．例如：2不是“连加进位数”，因为2＋3＋4＝9不产生进位现象；4是“连加进位数”，因为4＋5＋6＝15产生进位现象；51是“连加进位数”，因为51＋52＋63＝156产生进位现象．如果从0，1，2，…，99这100个自然数中任取一个数，那么取到“连加进位数”的概率是（ ）A ．0.88B ．0.89C ．0.90D ．0.91 【关键词】概率 【答案】A 16. (2010年浙江省金华)小明的讲义夹里放了大小相同的试卷共12页，其中语文4页、数学2页、英语6页，他随机地从讲义夹中抽出1页，抽出的试卷恰好是数学试卷的概率为（ ）A .21B .31C .61D .121 【关键词】概率 【答案】C10. （2010年益阳市） 有三张大小、形状完全相同的卡片，卡片上分别写有数字1、2、3，从这三张卡片中随机同时抽取两张，用抽出的卡片上的数字组成两位数，这个两位数是偶数的概率是 ． 【关键词】概率 【答案】31 11．（2010山东德州）袋子中装有3个红球和5个白球，这些球除颜色外均相同．在看不到球的条件下，随机从袋中摸出一个球，则摸出白球的概率是_____________． 【关键词】概率 【答案】85 12、不透明的袋子中装有4个红球、3个黄球和5个蓝球，每个球除颜色不同外其它都相同，从中任意摸出一个球，则摸出 ▲ 球的可能性最大 关键词：概率 答案：蓝13．（2010年山东省青岛市）一个口袋中装有10个红球和若干个黄球．在不允许将球倒出来数的前提下，为估计口袋中黄球的个数，小明采用了如下的方法：每次先从口袋中摸出10个球，求出其中红球数与10的比值，再把球放回口袋中摇匀．不断重复上述过程20次，得到红球数与10的比值的平均数为0.4．根据上述数据，估计口袋中大约有 个黄球． 【关键词】概率 【答案】1514．(2010重庆市)在一个不透明的盒子里装有5个分别写有数字－2，－1，0，1，2的小球，它们除数字不同外其余全部相同. 现从盒子里随机取出一个小球，将该小球上的数字作为点P 的横坐标，将该数的平方作为点P 的纵坐标，则点P 落在抛物线y ＝－x 2＋2x ＋5与x 轴所围成的区域内（不含边界）的概率是_____________.解析：点P 的坐标总共有5种可能，而落在抛物线y ＝－x 2＋2x ＋5与x 轴所围成的区域内有（-1，1），（1，1），（2，4）三种，所求的概念为3/5. 答案：3/5.15．（2010年山东省青岛市）“五·一”期间，某书城为了吸引读者，设立了一个可以自由转动的转盘（如图，转盘被平均分成12份），并规定：读者每购买100元的书，就可获得一次转动转盘的机会，如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么读者就可以分别获得45元、30元、25元的购书券，凭购书券可以在书城继续购书．如果读者不愿意转转盘，那么可以直接获得10元的购书券．（1）写出转动一次转盘获得45元购书券的概率；（2）转转盘和直接获得购书券，你认为哪种方式对读者更合算？请说明理由． 【关键词】概率 【答案】解：（1）P （获得45元购书券） =112；（2）12345302515121212⨯+⨯+⨯=（元）. ∵15元＞10元，∴转转盘对读者更合算．16.(2010年安徽省B 卷)20.（本小题满分8分）市种子培育基地用A 、B 、C 三种型号的甜玉米种子共1500粒进行发芽试验，从中选出发芽率高的种子进行推广，通过试验知道，C 型号种子的发芽率为80%．根据试验数据绘制了下面两个不完整的统计图（图1、图2）：（1）C 型号种子的发芽数是_________粒；（2）通过计算说明，应选哪种型号的种子进行推广？（精确到1%）（3）如果将所有已发芽的种子放到一起，从中随机取出一粒，求取到C 型号发芽种子的概率． 【关键词】统计图 概率 【答案】（1）480．（2）A 型号种子数为：1500×30％＝450，发芽率＝450420×100％≈93％． B 型号种子数为：1500×30％＝450，发芽率＝450370×100％≈82％．C 型号种子数发芽率是80％．第18题图∴选A 型号种子进行推广．（3）取到C 型号发芽种子的概率＝480370420480++＝12748．17.(2010年安徽省B 卷)22.（本小题满分10分）有3个完全相同的小球，把它们分别标号为1，2，3，放在一个口袋中，随机地摸出一个小球不放回，再随机地摸出一个小球．（Ⅰ）采用树形图法（或列表法）列出两次摸球出现的所有可能结果； （Ⅱ）求摸出的两个球号码之和等于5的概率． 【关键词】树状图（列表法） 概率 【答案】（Ⅰ）法一：根据题意，可以画出如下的树形图： 从树形图可以看出，摸出两球出现的所有可能结果共有6种； 法二：根据题意，可以列出下表：从上表中可以看出，摸出两球出现的所有可能结果共有6种. （Ⅱ）设两个球号码之和等于5为事件A . 摸出的两个球号码之和等于5的结果有2种，它们是：()()2332，，，.()2163P A ∴==. 18、（2010福建德化）有三张卡片（形状、大小、质地都相同），正面分别写上整式x+1，x ，3。

图形的投影参考答案与试题解析一．选择题（共39小题）1．（2018•扬州）如图所示的几何体的主视图是（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看第一层是两个小正方形，第二层左边一个小正方形，第三层左边一个小正方形，故选：B．2．（2018•十堰）今年“父亲节”佳佳给父亲送了一个礼盒，该礼盒的主视图是（）A． B．C．D．【分析】找出从几何体的正面看所得到的图形即可．【解答】解：由图可得，该礼盒的主视图是左边一个矩形，右面一个小正方形，故选：C．3．（2018•眉山）下列立体图形中，主视图是三角形的是（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得图形的主视图．【解答】解：A、C、D主视图是矩形，故A、C、D不符合题意；B、主视图是三角形，故B正确；故选：B．4．（2018•泰州）下列几何体中，主视图与俯视图不相同的是（）A．正方体B．四棱锥C．圆柱D．球【分析】根据主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形进行分析．【解答】解：四棱锥的主视图与俯视图不同．故选：B．5．（2018•江西）如图所示的几何体的左视图为（）A．B．C．D．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：从左边看是上大下小等宽的两个矩形，矩形的公共边是虚线，故选：D．6．（2018•泸州）如图是一个由5个完全相同的小正方体组成的立体图形，它的俯视图是（）A．B．C．D．【分析】根据从上面看得到的图形是俯视图，可得答案．【解答】解：从上面看第一列是两个小正方形，第二列是一个小正方形，第三列是一个小正方形，故选：B．7．（2018•广州）如图所示的几何体是由4个相同的小正方体搭成的，它的主视图是（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看第一层是三个小正方形，第二层右边一个小正方形，故选：B．8．（2018•宁波）如图是由6个大小相同的立方体组成的几何体，在这个几何体的三视图中，是中心对称图形的是（）A．主视图B．左视图C．俯视图D．主视图和左视图【分析】根据从上边看得到的图形是俯视图，可得答案．【解答】解：从上边看是一个田字，“田”字是中心对称图形，故选：C．9．（2018•娄底）如图所示立体图形的俯视图是（）A． B． C．D．【分析】找到从上面看所得到的图形即可，注意所有的看到的棱都应表现在俯视图中．【解答】解：从上边看立体图形得到俯视图即可得立体图形的俯视图是，故选：B．10．（2018•黔南州）如图的几何体是由四个大小相同的正方体组成的，它的俯视图是（）A．B．C．D．【分析】找到从上面看所得到的图形即可．【解答】解：从上面可看到从上往下2行小正方形的个数为：2，1，并且下面一行的正方形靠左，故选C．11．（2018•泰安）如图是下列哪个几何体的主视图与俯视图（）A．B．C．D．【分析】直接利用主视图以及俯视图的观察角度结合结合几何体的形状得出答案．【解答】解：由已知主视图和俯视图可得到该几何体是圆柱体的一半，只有选项C符合题意．故选：C．12．（2018•随州）如图是一个由4个相同正方体组成的立体图形，它的左视图是（）A．B．C．D．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：从左边看第一层是两个小正方形，第二层左边一个小正方形，故选：D．13．（2018•湘潭）如图所示的几何体的主视图是（）A．B．C．D．【分析】找出从几何体的正面看所得到的图形即可．【解答】解：该几何体的主视图是三角形，故选：C．14．（2018•常德）把图1中的正方体的一角切下后摆在图2所示的位置，则图2中的几何体的主视图为（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看是一个等腰三角形，高线是虚线，故选：D．15．（2018•盐城）如图是由5个大小相同的小正方体组成的几何体，则它的左视图是（）A．B．C．D．【分析】找到从左面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．【解答】解：从左面看易得第一层有1个正方形，第二层有2个正方形，如图所示：．故选：B．16．（2018•潍坊）如图所示的几何体的左视图是（）A．B．C．D．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：从左边看是两个等宽的矩形，矩形的公共边是虚线，故选：D．17．（2018•聊城）如图所示的几何体，它的左视图是（）A．B．C．D．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：用左边看是等宽的上下两个矩形，上边的矩形小，下边的矩形大，两矩形的公共边是虚线，故选：D．18．（2018•湖州）如图所示的几何体的左视图是（）A．B．C．D．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：从左边看是一个圆环，故选：D．19．（2018•菏泽）如图是两个等直径圆柱构成的“T”形管道，其左视图是（）A．B．C．D．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：从左边看如图，故选：B．20．（2018•嘉兴）下列几何体中，俯视图为三角形的是（）A． B．C．D．【分析】根据从上边看得到的图形是俯视图，可得答案．【解答】解：A、俯视图是圆，故A不符合题意；B、俯视图是矩形，故B不符合题意；C、俯视图是三角形，故C符合题意；D、俯视图是四边形，故D不符合题意；故选：C．21．（2018•安徽）一个由圆柱和圆锥组成的几何体如图水平放置，其主（正）视图为（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看上边是一个三角形，下边是一个矩形，故选：A．22．（2018•自贡）下面几何的主视图是（）A．B．C．D．【分析】主视图是从物体正面看所得到的图形．【解答】解：从几何体正面看，从左到右的正方形的个数为：2，1，2．故选B．23．（2018•成都）如图所示的正六棱柱的主视图是（）A．B．C．D．【分析】根据主视图是从正面看到的图象判定则可．【解答】解：从正面看是左右相邻的3个矩形，中间的矩形的面积较大，两边相同．故选：A．24．（2018•广东）如图，由5个相同正方体组合而成的几何体，它的主视图是（）A．B．C．D．【分析】根据主视图是从物体正面看所得到的图形解答即可．【解答】解：根据主视图的定义可知，此几何体的主视图是B中的图形，故选：B．25．（2018•绍兴）有6个相同的立方体搭成的儿何体如图所示，则它的主视图是（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看第一层是三个小正方形，第二层左边一个小正方形，故选：D．26．（2018•永州）如图几何体的主视图是（）A．B．C．D．【分析】依据从该几何体的正面看到的图形，即可得到主视图．【解答】解：由图可得，几何体的主视图是：故选：B．27．（2018•天津）如图是一个由5个相同的正方体组成的立体图形，它的主视图是（）A．B． C．D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看第一层是三个小正方形，第二层右边一个小正方形，第三层右边一个小正方形，故选：A．28．（2018•连云港）如图是由5个大小相同的正方体搭成的几何体，这个几何体的俯视图是（）A．B．C．D．【分析】根据从上面看得到的图形是俯视图，可得答案．【解答】解：从上面看第一列是两个小正方形，第二列是一个小正方形，第三列是一个小正方形，故选：A．29．（2018•温州）移动台阶如图所示，它的主视图是（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看是三个台阶，故选：B．30．（2018•武汉）一个几何体由若干个相同的正方体组成，其主视图和俯视图如图所示，则这个几何体中正方体的个数最多是（）A．3 B．4 C．5 D．6【分析】易得这个几何体共有2层，由俯视图可得第一层立方体的个数，由主视图可得第二层立方体的可能的个数，相加即可．【解答】解：结合主视图和俯视图可知，左边上层最多有2个，左边下层最多有2个，右边只有一层，且只有1个．所以图中的小正方体最多5块．故选：C．31．（2018•金华）一个几何体的三视图如图所示，该几何体是（）A．直三棱柱B．长方体C．圆锥D．立方体【分析】根据三视图的形状可判断几何体的形状．【解答】解：观察三视图可知，该几何体是直三棱柱．故选：A．32．（2018•临沂）如图是一个几何体的三视图（图中尺寸单位：cm），根据图中所示数据求得这个几何体的侧面积是（）A．12cm2B．（12+π）cm2 C．6πcm2D．8πcm2【分析】根据三视图确定该几何体是圆柱体，再计算圆柱体的侧面积．【解答】解：先由三视图确定该几何体是圆柱体，底面半径是2÷2=1cm，高是3cm．所以该几何体的侧面积为2π×1×3=6π（cm2）．故选：C．33．（2018•衡阳）如图是由5个大小相同的小正方体摆成的立体图形，它的主视图是（）A．B．C．D．【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．【解答】解：从正面看易得第一层有3个正方形，第二层有1个正方形，且位于中间．故选：A．34．（2018•宜宾）一个立体图形的三视图如图所示，则该立体图形是（）A．圆柱B．圆锥C．长方体D．球【分析】综合该物体的三种视图，分析得出该立体图形是圆柱体．【解答】解：A、圆柱的三视图分别是长方形，长方形，圆，正确；B、圆锥体的三视图分别是等腰三角形，等腰三角形，圆及一点，错误；C、长方体的三视图都是矩形，错误；D、球的三视图都是圆形，错误；故选：A．35．（2018•威海）如图是某圆锥的主视图和左视图，该圆锥的侧面积是（）A．25πB．24πC．20πD．15π【分析】求得圆锥的底面周长以及母线长，即可得到圆锥的侧面积．【解答】解：由题可得，圆锥的底面直径为8，高为3，∴圆锥的底面周长为8π，圆锥的母线长为=5，∴圆锥的侧面积=×8π×5=20π，故选：C．36．（2018•南通）一个空间几何体的主视图和左视图都是边长为2cm的正三角形，俯视图是一个圆，那么这个几何体的表面积是（）A．πcm2B．3πcm2C．πcm2D．5πcm2【分析】根据三视图的知识可知该几何体为一个圆锥．又已知底面半径可求出母线长以及侧面积、底面积后即可求得其表面积．【解答】解：综合主视图，俯视图，左视图可以看出这个几何体应该是圆锥，且底面圆的半径为1，母线长为2，因此侧面面积为1×π×2=2π，底面积为π×（1）2=π．表面积为2π+π=3π；故选：B．37．（2018•河北）图中三视图对应的几何体是（）A．B．C．D．【分析】首先画出各个图形的三视图，对照给出的三视图，找出正确的答案；或者用排除法．【解答】解：观察图象可知选项C符合三视图的要求，故选：C．38．（2018•济宁）一个几何体的三视图如图所示，则该几何体的表面积是（）A．24+2πB．16+4πC．16+8πD．16+12π【分析】根据三视图知该几何体是一个半径为2、高为4的圆柱体的纵向一半，据此求解可得．【解答】解：该几何体的表面积为2וπ•22+4×4+×2π•2×4=12π+16，故选：D．39．（2018•衢州）由五个大小相同的正方体组成的几何体如图所示，那么它的主视图是（）A．B．C． D．【分析】得到从几何体正面看得到的平面图形即可．【解答】解：从正面看得到3列正方形的个数依次为2，1，1，故选：C．。

2018年中考数学总复习6.3视图与投影精讲试题（河北附
答案）
5 c 第三节视图与投影
,河北五年中考命题规律)
年份题号考查点考查内容分值总分
20188几何体的三视图已知几何体确定主视图33
20188正方体的展开图还原补图将展开图还原成正方体33
20184几何体的三视图已知三视图，确定几何体33
201810正方体展开图的还原将正方体的展开图折叠还原，求正方体上两点的距离33
201826(2)三视图的相关计算以装有液体的正方体容器倾斜放在水平桌面上为背景，计算液体体积33
命题规律视图、立体图形的展开与折叠在中考中一般设置1道题，分值为2～3分，题型以选择题为主，仅2018年在解答题中考查还原三视图并计算体积．分析近五年河北中考试题可以看出，本时常考类型有(1)判断几何体的三视图；(2)视图的相关计算；(3)正方体展开图的还原及相关计算
,河北五年中考真题及模拟)
视图的识别与相关计算
1．(2018河北中考)如图是由相同的小正方体木块粘在一起的几何体，它的主视图是( A )
,A) ,B) ,c) ,D)
2．(2018沧州一模)如图中的三视图所对应的几何体是( B ) ,A) ,B) ,c) ,D)
3．(2018张家口二模)图中几何体的主视图是( A )
,A) ,B) ,c) ,D)。

俯视图左视图主视图111122中考数学分类汇编--投影与视图一、选择题1.一个几何体的三视图如图所示，这个几何体是（ ） A ．棱柱 B ．圆柱 C ．圆锥 D ．球2.如图是由相同小正方体组成的立体图形，它的左视图为（ ）3、（2008四川内江）在一仓库里堆放着若干个相同的正方体货箱，仓库管理员将这堆货箱的三视图画了出来．如图所示，则这堆正方体货箱共有（ ） A ．9箱 B ．10箱 C ．11箱 D ．12箱 4. 水平地面上放着1个球和1个圆柱体，摆放方式如右图所示，其左视图是（ ）5．（2008泰州市）如左下图是一个几何体的三视图，根据图中提供的数据（单位：cm ）可求得这个几何体的体积为（ ）A ． 2cm 3B ．4 cm 3C ．6 cm 3D ．8 cm 36．如图所示的图形是由7个完全相同的小立方体组成的立体图形，这个立体图形的主视力是（ ）正视图 左视图 俯视图A ．B ．C ．D ．左视图 主视图 俯视图 （11题图）7、如图，有一圆心角为120 o、半径长为6cm 的扇形，若将OA 、OB 重合后围成一圆锥侧面，那么圆锥的高是（ ）A ．24cmB ．35cmC ．62cmD ．32cm8.下图※是一种瑶族长鼓的轮廓图，其主视图正确的是（ ）9.某几何体的三视图如图所示，则它是（ ）A ．球体B ．圆柱C ．棱锥D ．圆锥10、如图１，圆柱的左视图是 （ ）Ａ Ｂ Ｃ Ｄ11、（2008山西太原）右图是一个正方体的平面展开图，这个正方体是（ ）俯视图正视图12、（2008湖北武汉）一个无盖的正方体盒子的平面展开图可以是下列图形中的（ ）．Ａ.只有图① Ｂ．图①、图② Ｃ．图②、图③ Ｄ．图①、图③． 13、一几何体的三视图如右，这个几何体是（ ）A.圆锥B.圆柱C. 三棱锥D. 三棱柱14、（2008湖北襄樊）如图5,是一个由若干个相同的小正方体组成的几何体的三视图,则组成这个几何体的小正方体的个数是( )A.7个B.8个C.9个D.10个15、（2008江苏盐城）下列四个几何体中，主视图、左视图、俯视图完全相同的是（ ）A ．圆锥B ．球C ．圆柱D ．三棱柱 16．在生活和生产实践中，我们经常需要运用三视图来描述物体的形状和大小。

第六部分图形的变化6.10 投影和视图【一】知识点清单1、投影平行投影；中心投影；正投影；中心投影、平行投影的区别和联系；视点、视角和盲区（删）2、三视图简单几何体的三视图；简单组合体的三视图；由三视图判断几何体；作图-三视图3、课题学习制作立体模型由三视图判断几何体；立体图形与其三视图、展开图之间的关系【二】分类试题汇编及参考答案与解析一、选择题1．（2018年广西桂林市-第4题-3分）如图所示的几何体的主视图是（）A．B．C．D．【知识考点】简单几何体的三视图．【思路分析】根据主视图是从正面看到的图形，可得答案．【解答过程】解：从正面看下面是一个长方形，如图所示：故C选项符合题意，故选：C．【总结归纳】本题考查了简单组合体的三视图，从正面看得到的图形画出来就是主视图．2．（2018年贵州省黔东南州/黔西南州/黔南州-第2题-3分）如图的几何体是由四个大小相同的正方体组成的，它的俯视图是（）A．B．C．D．【知识考点】简单组合体的三视图．【思路分析】找到从上面看所得到的图形即可．【解答过程】解：从上面可看到从上往下2行小正方形的个数为：2，1，并且下面一行的正方形靠左，故选C．【总结归纳】本题考查了三视图的知识，俯视图是从物体的上面看得到的视图．3．（2018年湖北省襄阳市-第6题-3分）一个几何体的三视图如图所示，则这个几何体是（）A．B．C．D．【知识考点】由三视图判断几何体．【思路分析】由主视图和左视图确定是柱体，锥体还是球体，再由俯视图确定具体形状．【解答过程】解：根据主视图和左视图为矩形判断出是柱体，根据俯视图是三角形可判断出这个几何体应该是三棱柱．故选：C．【总结归纳】此题主要考查了由三视图判断几何体．主视图和左视图的大致轮廓为长方形的几何体为柱体，俯视图为几边形就是几棱柱．4．（2018年湖北省咸宁市-第4题-3分）用4个完全相同的小正方体搭成如图所示的几何体，该几何体的（）A．主视图和左视图相同B．主视图和俯视图相同C．左视图和俯视图相同D．三种视图都相同【知识考点】简单组合体的三视图．【思路分析】分别得出该几何体的三视图进而得出答案．【解答过程】解：如图所示：，故该几何体的主视图和左视图相同．故选：A．【总结归纳】本题考查了三视图的知识，正确把握三视图的画法是解题关键．5．（2018年湖南省娄底市-第7题-3分）如图所示立体图形的俯视图是（）A．B．C．D．【知识考点】简单组合体的三视图．【思路分析】找到从上面看所得到的图形即可，注意所有的看到的棱都应表现在俯视图中．【解答过程】解：从上边看立体图形得到俯视图即可得立体图形的俯视图是，故选：B．【总结归纳】本题考查了三视图的知识，掌握所看的位置，注意所有的看到的棱都应表现在视图中．6．（2018年湖南省湘潭市-第2题-3分）如图所示的几何体的主视图是（）A．B．C．D．【知识考点】简单几何体的三视图．【思路分析】找出从几何体的正面看所得到的图形即可．【解答过程】解：该几何体的主视图是三角形，故选：C．【总结归纳】此题主要考查了简单几何体的三视图，画简单组合体的三视图要循序渐进，通过仔细观察和想象．7．（2018年辽宁省大连市-第5题-3分）一个几何体的三视图如图所示，则这个几何体是（）A．圆柱B．圆锥C．三棱柱D．长方体【知识考点】由三视图判断几何体．【思路分析】由常见几何体的三视图即可判断．【解答过程】解：由三视图知这个几何体是三棱柱，故选：C．【总结归纳】本题主要考查由三视图判断几何体，解题的关键是熟练掌握常见几何体的三视图．8．（2018年辽宁省葫芦岛市-第2题-3分）下列几何体中，俯视图为矩形的是（）A．B．C．D．【知识考点】简单几何体的三视图．【思路分析】根据常见几何体的三视图，可得答案．【解答过程】解：A、圆锥的俯视图是圆，故A不符合题意；B、圆柱的俯视图是圆，故B错误；C、长方体的主视图是矩形，故C符合题意；D、三棱柱的俯视图是三角形，故D不符合题意；故选：C．【总结归纳】本题考查了简单几何体的三视图，熟记常见几何题三视图是解题关键．9．（2018年辽宁省锦州市-第2题-3分）如图，这是由5个大小相同的正方体搭成的几何体，该几何体的左视图（）A．B．C．D．【知识考点】简单组合体的三视图．【思路分析】找到从几何体的左边看所得到的图形即可．【解答过程】解：左视图有2列，每列小正方形数目分别为2，1．故选：A．【总结归纳】此题主要考查了简单几何体的三视图，关键是掌握所看的位置．10．（2018年甘肃省白银市/酒泉市/张掖市/武威市/定西市/陇南市-第14题-4分）已知某几何体的三视图如图所示，其中俯视图为正六边形，则该几何体的侧面积为．【知识考点】由三视图判断几何体；几何体的表面积；正多边形和圆；简单几何体的三视图．【思路分析】观察该几何体的三视图发现该几何体为正六棱柱，然后根据提供的尺寸求得其侧面积即可．【解答过程】解：观察该几何体的三视图发现该几何体为正六棱柱，其底面边长为3，高为6，所以其侧面积为3×6×6=108，故答案为：108．【总结归纳】本题考查了由三视图判断几何体的知识，解题的关键是能够根据三视图判断几何体的形状及各部分的尺寸，难度不大．11．（2018年山东省潍坊市-第3题-3分）如图所示的几何体的左视图是（）A．B．C．D．【知识考点】简单组合体的三视图．【思路分析】根据从左边看得到的图形是左视图，可得答案．【解答过程】解：从左边看是两个等宽的矩形，矩形的公共边是虚线，故选：D．【总结归纳】本题考查了简单组合体的三视图，从左边看得到的图形是左视图，注意看不到而且是存在的线是虚线．12．（2018年山东省济宁市-第9题-3分）一个几何体的三视图如图所示，则该几何体的表面积是（）A．24+2πB．16+4πC．16+8πD．16+12π【知识考点】几何体的表面积；由三视图判断几何体．【思路分析】根据三视图知该几何体是一个半径为2、高为4的圆柱体的纵向一半，据此求解可得．【解答过程】解：该几何体的表面积为2וπ•22+4×4+×2π•2×4=12π+16，故选：D．【总结归纳】本题主要考查由三视图判断几何体，解题的关键是根据三视图得出几何体的形状及圆柱体的有关计算．13．（2018年浙江省嘉兴市舟山市-第1题-3分）下列几何体中，俯视图为三角形的是（）A．B．C．D．【知识考点】简单几何体的三视图．【思路分析】根据从上边看得到的图形是俯视图，可得答案．【解答过程】解：A、俯视图是圆，故A不符合题意；B、俯视图是矩形，故B不符合题意；C、俯视图是三角形，故C符合题意；D、俯视图是四边形，故D不符合题意；故选：C．【总结归纳】本题考查了简单组合体的三视图，从上边看得到的图形是俯视图．14．（2018年浙江省宁波市-第6题-4分）如图是由6个大小相同的立方体组成的几何体，在这个几何体的三视图中，是中心对称图形的是（）A．主视图B．左视图C．俯视图D．主视图和左视图【知识考点】简单组合体的三视图；中心对称图形．【思路分析】根据从上边看得到的图形是俯视图，可得答案．【解答过程】解：从上边看是一个田字，“田”字是中心对称图形，故选：C．【总结归纳】本题考查了简单组合体的三视图，从上边看得到的图形是俯视图，又利用了中心对称图形．二、填空题1．（2018年黑龙江省齐齐哈尔市-第13题-3分）三棱柱的三视图如图所示，已知△EFG中，EF=8cm，EG=12cm，∠EFG=45°．则AB的长为cm．【知识考点】由三视图判断几何体．【思路分析】根据三视图的对应情况可得出，△EFG中FG上的高即为AB的长，进而求出即可．【解答过程】解：过点E作EQ⊥FG于点Q，由题意可得出：EQ=AB，∵EF=8cm，∠EFG=45°，∴EQ=AB=×8=4（cm）．故答案为：4．【总结归纳】此题主要考查了由三视图解决实际问题，根据已知得出EQ=AB是解题关键．三、解答题。