第19讲 导数的应用——利用导数研究函数零点问题(达标检测)(原卷版)

专题05 利用导数研究函数零点问题【考点预测】1、利用导数确定函数零点的常用方法（1）图象法：根据题目要求画出函数的图象，标明函数极（最）值的位置，借助数形结合的思想分析问题（画草图时注意有时候需使用极限）．（2）利用函数零点存在定理：先用该定理判定函数在某区间上有零点，然后利用导数研究函数的单调性、极值（最值）及区间端点值的符号，进而判断函数在该区间上零点的个数．2、利用函数的零点求参数范围的方法（1）分离参数（()a g x =）后，将原问题转化为()y g x =的值域（最值）问题或转化为直线y a =与()y g x =的图象的交点个数问题（优选分离、次选分类）求解；（2）利用函数零点存在定理构建不等式求解；（3）转化为两个熟悉的函数图象的位置关系问题，从而构建不等式求解． 【典型例题】例1．（2023春·河南·高二校联考期末）已知函数()e xf x a x =-，a ∈R ．(1)当1ea =时，证明：()ln 10f x x x -+-≥在()0,∞+上恒成立；(2)若()f x 有2个零点，求a 的取值范围．例2．（2023春·广东广州·高二广东华侨中学校考阶段练习）已知函数()e 1x f x ax =--． (1)讨论函数()f x 的单调性；(2)若()f x 有且仅有2个零点，求实数a 的取值范围；例4．（2023春·天津红桥·高二天津三中校考阶段练习）已知函数()()ln f x x ax a =-∈R . (1)若1x =是()f x 的极值点，求a 的值； (2)求函数()f x 的单调区间；(3)若函数()f x 在21,e ⎡⎤⎣⎦上有且仅有2个零点，求a 的取值范围.例5．（2023春·广东佛山·高二校考阶段练习）已知函数()22ln 3f x x x x =-+.(1)求()f x 的极值；(2)设函数()()3143g x f x x x m =+-+，讨论()g x 的零点个数.例6．（2023春·河南·高二校联考阶段练习）已知函数()e xf x ax a =--.(1)若函数()f x 单调递增，求实数a 的取值范围； (2)若()f x 恰有两个零点，求实数a 的取值范围.例7．（2023春·辽宁铁岭·高二铁岭市清河高级中学校考阶段练习）已知函数()e x f x ax a =--.(1)若()f x 在()0,∞+上单调递增，求a 的取值范围； (2)若()f x 存在零点且零点的绝对值小于2，求a 的取值范围例8．（2023春·天津武清·高二天津市武清区城关中学校联考阶段练习）已知R a ∈，函数()()32111332x a x x ax f =----，()2ln g x x x =-.(1)当1a =时，求函数()y f x =在点()()3,3f 处的切线方程； (2)若函数()f x 的减区间是()1,4-，求a 的值；(3)若函数()y g x a =-在[]1,3上恰有两个不同的零点，求实数a 的取值范围.例9．（2023春·河南·高二襄城高中校联考阶段练习）已知函数()ln f x x ax =-. (1)讨论()f x 的单调性；(2)若函数()()2g x f x x =-有两个零点()1212,x x x x <，求a 的取值范围，并证明121x x >.【过关测试】1．（2023春·重庆永川·高二重庆市永川北山中学校校考阶段练习）已知函数()2e e 1xf x m x =--.(1)讨论()f x 的最值；(2)设()()()2e ln 1ln g x x x mf x =-+++，若()g x 恰有2个零点，求实数m 的取值范围.2．（2023春·河南洛阳·高二校考阶段练习）已知函数32()f x x ax bx c =+++在点()1,2P 处的切线斜率为4，且在=1x -处取得极值． (1)求函数()f x 的解析式；(2)若函数()()1g x f x m =+-有三个零点，求m 的取值范围．3．（2023春·山东枣庄·高二校考阶段练习）已知函数()()e 2x f x a x =-+．(1)当1a =时，求()f x 的极值；(2)若()f x 有两个零点，求a 的取值范围．4．（2023春·上海浦东新·高二上海市建平中学校考阶段练习）设函数()()()()f x x a x b x c =---，其中实数a ，b ，c 满足2b a c =+．(1)若0b =，1c =，求函数()f x 在1x =处的切线方程；(2)若3b a -=，求函数()f x 的极值；(3)若曲线()f x 与直线()2y x b =---有三个互异的公共点，求c a -的取值范围．5．（2023春·天津西青·高二天津市西青区杨柳青第一中学校考阶段练习）已知函数()()322,f x x ax bx a b =+++∈∈R R 在=1x -处取得极值7.(1)求,a b 的值；(2)求函数的单调性及极值；(3)若关于x 的方程()()0f x m m -=∈R 在[]22-,上恰有2个不同的实数解，求m 的取值范围.6．（2023秋·上海浦东新·高二上海师大附中校考期末）已知21()ln (1)()2f x x a x ax a =-++∈R ，(1)当0a =时，求函数()y f x =在点(1,(1))f 处的切线方程； (2)当(0,1]a ∈时，求函数()y f x =的单调区间；(3)当0a =时，方程()(2)f x m x =-在区间21,e ⎡⎤⎣⎦内有唯一实数解，求实数m 的取值范围．7．（2023·全国·高二专题练习）已知函数()e x f x x =-（其中e 是自然对数的底数）. (1)求()f x 在[]1,1-上的最值；(2)若函数()()e (R)x g x f x a a =-∈没有零点，求实数a 的取值范围.8．（2023春·湖北襄阳·高二校联考阶段练习）已知函数()22e xf x x ax =--.(1)若函数()f x 在R 上单调递减，求实数a 的取值范围；(2)若过点()1,1-可作三条直线与曲线()y f x =相切，求实数a 的取值范围.9．（2023秋·江苏盐城·高二校考期末）已知函数()ln f x x x =，()()1,011,02f x x x g x x x ⎧+>⎪⎪+=⎨⎪+≤⎪⎩. (1)求函数()f x 在点()()e,e f 处的切线方程； (2)求函数()f x 的单调区间；(3)如果存在实数m 、n ，其中m n <，使得()()g m g n =，求n m -的取值范围．10．（2023春·湖北·高二校联考阶段练习）已知函数32()61()f x x ax x a =+-+∈R ，且(1)6f '=-． (1)求函数()f x 的图象在点(1,(1))f 处的切线方程；(2)若函数()()g x f x m =-在区间[2,4]-上有三个零点，求实数m 的取值范围．11．（2023春·河南郑州·高二郑州市第二高级中学校考阶段练习）已知函数2()ln x f x x=. (1)求()f x 的单调性；(2)若关于x 的方程()0tf x x -=在(21,11,e e ⎡⎫⎤⋃⎪⎦⎢⎣⎭上有两个不相等的零点，求t 的取值范围.12．（2023·全国·高二专题练习）已知函数()()ln f x a x x a =-∈R ． (1)求函数()y f x =的单调区间；(2)若函数()y f x =在其定义域内有两个不同的零点，求实数a 的取值范围．13．（2023春·江苏南京·高二江苏省江浦高级中学校联考阶段练习）已知函数()ln (R)af x x a x =-∈(1)讨论()f x 的单调性；(2)求证：0a ＞时，()f x 只有一个零点； (3)若()f x 有两个零点，求实数a 的取值范围．14．（2023春·天津和平·高二天津二十中校考阶段练习）已知函数()()21e xf x ax x =+-，其中e 是自然对数的底数，a R ∈．(1)若a<0，求()f x 的单调区间；(2)若1a =-，函数()f x 的图象与函数()321132g x x x m =++的图象有3个不同的交点，求实数m 的取值范围．15．（2023春·湖北·高二校联考阶段练习）已知()()()2212ln 212f x x x x a x a x ⎛⎫=-+-+- ⎪⎝⎭，0a >．(1)讨论()f x 的单调性；(2)若()f x 有两个零点，求a 的值．16．（2023秋·湖南长沙·高二长郡中学校考期末）已知函数()()ln 10ax f x x xx-+=>． (1)若()0f x ≤在()0,∞+上恒成立，求a 的取值范围； (2)在（1）的条件下证明:对任意*n ∈N ，都有()1111ln 123n n++++>+； (3)设()()21e x g x x =-，讨论函数()()()F x f x g x =-的零点个数．17．（2023春·浙江金华·高二校考阶段练习）已知函数()()e sin R xf x x a x a =-∈．(1)当0a =时，求函数()f x 的极值； (2)若[]()0,π,0x f x ∀∈≥，求a 的取值范围；(3)当33e a ≥-时，试讨论()f x 在()0,2π内零点的个数，并说明理由．18．（2023春·四川成都·高二成都七中校考阶段练习）已知函数()()()2e 3e 42a xf x x x x =---.(1)当1a =时，求函数()f x 的单调区间； (2)当02a <<时，讨论函数()f x 的零点个数.。

利用导数研究函数的零点题型一　数形结合法研究函数零点1.(2024·南昌模拟节选)已知函数f (x )=(x -a )2+be x (a ，b ∈R )，若a =0时，函数y =f (x )有3个零点，求b 的取值范围.解：函数y =f (x )有3个零点，即关于x 的方程f (x )=0有3个根，也即关于x 的方程b =-x 2ex 有3个根.令g (x )=-x 2e x ，则直线y =b 与g (x )=-x 2ex 的图象有3个交点.g ′(x )=x (x -2)e x，由g ′(x )<0解得0<x <2；由g ′(x )>0解得x <0或x >2，所以g (x )在(-∞，0)上单调递增，在(0，2)上单调递减，在(2，+∞)上单调递增.g (0)=0，g (2)=-4e2，当x >0时，g (x )<0；当x →+∞时，g (x )→0；当x →-∞时，g (x )→-∞，作出g (x )的大致图象如图所示，作出直线y =b .由图可知，若直线y =b 与g (x )的图象有3个交点，则-4e 2<b <0，即b 的取值范围为-4e 2，0 .感悟提升　含参数的函数零点个数，可转化为方程解的个数，若能分离参数，可将参数分离出来后，用x 表示参数的函数，作出该函数的图象，根据图象特征求参数的范围.2.设函数f (x )=ln x +m x ，m ∈R ，讨论函数g (x )=f ′(x )-x 3零点的个数.解：由题意知g (x )=f ′(x )-x 3=1x -m x 2-x 3(x >0)，令g (x )=0，得m =-13x 3+x (x >0).设φ(x )=-13x 3+x (x >0)，则φ′(x )=-x 2+1=-(x -1)(x +1).当x ∈(0，1)时，φ′(x )>0，φ(x )在(0，1)上单调递增；当x ∈(1，+∞)时，φ′(x )<0，φ(x )在(1，+∞)上单调递减.∴x =1是φ(x )的唯一极值点，且是极大值点，∴x =1也是φ(x )的最大值点，∴φ(x )的最大值为φ(1)=23.结合y =φ(x )的图象(如图)可知，①当m >23时，函数g (x )无零点；②当m =23时，函数g (x )有且只有一个零点；③当0<m <23时，函数g (x )有两个零点；④当m ≤0时，函数g (x )有且只有一个零点.综上所述，当m >23时，函数g (x )无零点；当m =23或m ≤0时，函数g (x )有且只有一个零点；当0<m <23时，函数g (x )有两个零点.题型二　利用函数性质研究函数零点3.已知函数f (x )=(2a +1)x 2-2x 2ln x -4，e 是自然对数的底数，∀x >0，e x >x +1.(1)求f (x )的单调区间；(2)记p ：f (x )有两个零点；q ：a >ln 2.求证：p 是q 的充要条件.要求：先证充分性，再证必要性.(1)解：∵f (x )=(2a +1)x 2-2x 2ln x -4，∴f (x )的定义域为(0，+∞)，f ′(x )=4x (a -ln x ).∵当0<x <e a 时，f ′(x )>0，∴f (x )在(0，e a )上单调递增；∵当x >e a 时，f ′(x )<0，∴f (x )在(e a ，+∞)上单调递减.∴f (x )的单调递增区间为(0，e a )，单调递减区间为(e a ，+∞).(2)证明　先证充分性.由(1)知，当x =e a 时，f (x )取得最大值，即f (x )的最大值为f (e a )=e 2a -4.由f (x )有两个零点，得e 2a -4>0，解得a >ln 2.∴a >ln 2.再证必要性.∵a >ln 2，∴e 2a >4.∴f (e a )=e 2a -4>0.∵a>ln2>0，∀x>0，e x>x+1，∴e2a>2a+1>2a.∴f(e-a)=e-2a(4a+1)-4=4a+1e2a -4<4a+12a-4=12a-2<12ln2-2=1ln4-2<0.∴∃x1∈(e-a，e a)，使f(x1)=0；∵f(e a+1)=-e2a+2-4<0，∴∃x2∈(e a，e a+1)，f(x2)=0.∵f(x)在(0，e a)上单调递增，在(e a，+∞)上单调递减，∴∀x∈(0，+∞)，x≠x1且x≠x2，易得f(x)≠0.∴当a>ln2时，f(x)有两个零点.感悟提升　利用函数性质研究函数的零点，主要是根据函数单调性、奇偶性、最值或极值的符号确定函数零点的个数，此类问题在求解过程中可以通过数形结合的方法确定函数存在零点的条件.4.(2022·全国乙卷节选)已知函数f(x)=ax-1x-(a+1)ln x，若f(x)恰有一个零点，求a的取值范围.解：由f(x)=ax-1x-(a+1)ln x(x>0)，得f′(x)=a+1x2-a+1x=(ax-1)(x-1)x2(x>0).①当a=0时，f(x)=-1x-ln x，f′(x)=1-xx2，当x∈(0，1)时，f′(x)>0；当x∈(1，+∞)时，f′(x)<0，所以f(x)≤f(1)=-1<0，所以f(x)不存在零点；②当a<0时，f′(x)=a x-1a(x-1)x2，当x∈(0，1)时，f′(x)>0，f(x)单调递增；当x∈(1，+∞)时，f′(x)<0，f(x)单调递减，所以f(x)max=f(1)=a-1<0，所以f(x)不存在零点；③当a>0时，f′(x)=a x-1a(x-1)x2，(ⅰ)当a=1时，f′(x)≥0，f(x)在(0，+∞)上单调递增，因为f(1)=a-1=0，所以函数f(x)恰有一个零点；(ⅱ)当a>1时，0<1a <1，故f(x)在0，1a，(1，+∞)上单调递增，在1a，1上单调递减.因为f(1)=a-1>0，所以f1a>f(1)>0，当x→0+时，f(x)→-∞，由零点存在定理可知f(x)在0，1a上必有一个零点，所以a>1满足条件；(ⅲ)当0<a<1时，1a >1，故f(x)在(0，1)，1a，+∞上单调递增，在1，1a上单调递减.因为f(1)=a-1<0，所以f1a<f(1)<0，当x→+∞时，f(x)→+∞，由零点存在定理可知f(x)在1a，+∞上必有一个零点，即0<a<1满足条件.综上，若f(x)恰有一个零点，则a的取值范围为(0，+∞).题型三　构造函数法研究函数零点5.已知函数f(x)=e x-1+ax(a∈R).(1)当x≥0时，f(x)≥0，求a的取值范围；(2)若关于x的方程f(x)-ax+1e a=ln x+a有两个不同的实数解，求a的取值范围.解：(1)由题意，得f′(x)=e x+a.若a≥-1，则当x∈[0，+∞)时，f′(x)≥0恒成立，∴f(x)在[0，+∞)上单调递增，∴当x∈[0，+∞)时，f(x)≥f(0)=0，符合题意；若a<-1，令f′(x)<0，得x<ln(-a)，∴f(x)在(0，ln(-a))上单调递减，∴当x∈(0，ln(-a))时，f(x)<f(0)=0，不符合题意.综上，a的取值范围为[-1，+∞).(2)法一　由f(x)-ax+1e a=ln x+a，得e x-a=ln x+a.令e x-a=t，则x-a=ln t，ln x+a=t，∴x+ln x=t+ln t.易知y=x+ln x在(0，+∞)上单调递增，∴t=x，得a=x-ln x.则原问题可转化为方程a=x-ln x有两个不同的实数解.令φ(x)=x-ln x(x>0)，则φ′(x)=x-1 x，令φ′(x)<0，得0<x<1；令φ′(x)>0，得x>1，∴φ(x)在(0，1)上单调递减，在(1，+∞)上单调递增，∴φ(x)min=φ(1)=1，∴a≥1.当a=1时，易知方程1=x-ln x只有一个实数解x=1，不符合题意.下证当a>1时，a=x-ln x有两个不同的实数解.令g(x)=x-ln x-a(a>1)，则g(x)=φ(x)-a，易知g(x)在(0，1)上单调递减，在(1，+∞)上单调递增.∵g(e-a)=e-a>0，g(1)=1-a<0，∴g(x)在(e-a，1)上有一个零点.易知g(e a)=e a-2a，令h(a)=e a-2a，则当a>1时，h′(a)=e a-2>0，∴h(a)在(1，+∞)上单调递增，∴当a >1时，h (a )>h (1)=e -2>0，即g (e a )=e a -2a >0，∴g (x )在(1，e a )上有一个零点.∴当a >1时，a =x -ln x 有两个不同的实数解.综上，a 的取值范围为(1，+∞).法二　由f (x )-ax +1e a=ln x +a ，得e x =e a (ln x +a )，∴xe x =xe a (ln x +a )，即xe x =e a +ln x (ln x +a ).令u (x )=xe x ，则有u (x )=u (a +ln x ).当x >0时，u ′(x )=(x +1)e x >0，∴u (x )=xe x 在(0，+∞)上单调递增，∴x =a +ln x ，即a =x -ln x .下同法一.感悟提升　涉及函数的零点(方程的根)问题，主要利用导数确定函数的单调区间和极值点，根据函数零点的个数寻找函数在给定区间的极值以及区间端点的函数值与0的关系，从而求得参数的取值范围.6.(2021·全国甲卷节选)已知a >0且a ≠1，函数f (x )=x a ax (x >0).若曲线y =f (x )与直线y =1有且仅有两个交点，求a 的取值范围.解：曲线y =f (x )与直线y =1有且仅有两个交点，可转化为方程x a a x =1(x >0)有两个不同的解，即方程ln x x =ln a a 有两个不同的解.设g (x )=ln x x (x >0)，则g ′(x )=1-ln x x 2(x >0)，令g ′(x )=1-ln x x 2=0，得x =e ，当0<x <e 时，g ′(x )>0，函数g (x )单调递增；当x >e 时，g ′(x )<0，函数g (x )单调递减，故g (x )max =g (e )=1e ，且当x >e 时，g (x )∈0，1e ，又g (1)=0，所以0<ln a a <1e，所以a >1且a ≠e ，故a 的取值范围为(1，e )∪(e ，+∞).【A 级　基础巩固】7.已知函数f (x )=x -ae x ，a ∈R ，讨论函数f (x )的零点个数.解：f (x )=0等价于x -ae x =0，即x ex =a .设h (x )=x e x ，则h ′(x )=1-x ex ，当x <1时，h ′(x )>0，h (x )单调递增；当x >1时，h ′(x )<0，h (x )单调递减，∴h (x )max =h (1)=1e.又当x <0时，h (x )<0；当x >0时，h (x )>0，且x →+∞时，h (x )→0，∴可画出h (x )大致图象，如图所示.∴当a ≤0或a =1e时，f (x )在R 上有唯一零点；当a >1e 时，f (x )在R 上无零点；当0<a <1e 时，f (x )在R 上有两个零点.8.(2024·青岛调研)已知函数f (x )=ln x +ax x，a ∈R .(1)若a =0，求f (x )的最大值；(2)若0<a <1，求证：f (x )有且只有一个零点.(1)解：若a =0，则f (x )=ln x x ，其定义域为(0，+∞)，∴f ′(x )=1-ln x x 2，由f ′(x )=0，得x =e ，∴当0<x <e 时，f ′(x )>0；当x >e 时，f ′(x )<0，∴f (x )在(0，e )上单调递增，在(e ，+∞)上单调递减，∴f (x )max =f (e )=1e.(2)证明　f ′(x )=1x +a x -ln x -ax x 2=1-ln x x 2，由(1)知，f (x )在(0，e )上单调递增，在(e ，+∞)上单调递减，∵0<a <1，∴当x >e 时，f (x )=ln x +ax x =a +ln x x>0，故f (x )在(e ，+∞)上无零点；当0<x <e 时，f (x )=ln x +ax x ，∵f 1e =a -e <0，f (e )=a +1e>0，且f (x )在(0，e )上单调递增，∴f (x )在(0，e )上有且只有一个零点，综上，当0<a <1时，f (x )有且只有一个零点.9.(2024·太原模拟节选)已知函数f (x )=xe x -x -1，讨论方程f (x )=ln x +m -2的实根个数.解；由f (x )=ln x +m -2，得xe x -x -ln x +1=m ，x >0，令h (x )=xe x -x -ln x +1，则h ′(x )=e x +xe x-1-1x =(x +1)(xe x -1)x(x >0)，令m (x )=xe x -1(x >0)，则m ′(x )=(x +1)·e x >0，∴m (x )在(0，+∞)上单调递增，又m 12 =e 2-1<0，m (1)=e -1>0，∴存在x 0∈12，1，使得m (x 0)=0，即e x 0=1x 0，从而ln x 0=-x 0.当x ∈(0，x 0)时，m (x )<0，h ′(x )<0，则h (x )单调递减；当x ∈(x 0，+∞)时，m (x )>0，h ′(x )>0，则h (x )单调递增；∴h (x )min =h (x 0)=x 0e x 0-x 0-ln x 0+1=x 0·1x 0-x 0+x 0+1=2，又易知，当x →0+时，h (x )→+∞；当x →+∞时，h (x )→+∞.∴当m <2时，方程f (x )=ln x +m -2没有实根；当m =2时，方程f (x )=ln x +m -2有1个实根；当m >2时，方程f (x )=ln x +m -2有2个实根.【B 级　能力提升】10.(2024·郑州模拟节选)已知函数f (x )=ln (x +1)-x +1，g (x )=ae x -x +ln a ，若函数F (x )=f (x )-g (x )有两个零点，求实数a 的取值范围.解：函数F (x )=f (x )-g (x )有两个零点，即f (x )=g (x )有两个实根，即ln (x +1)-x +1=ae x -x +ln a 有两个实根，即e x +ln a +x +ln a =ln (x +1)+x +1有两个实根，即e x +ln a +x +ln a =e ln (x +1)+ln (x +1)有两个实根.设函数h (x )=e x +x ，则e x +ln a +x +ln a =e ln (x +1)+ln (x +1)⇔h (x +ln a )=h (ln (x +1)).因为h ′(x )=e x +1>0恒成立，所以h (x )=e x +x 在R 上单调递增，所以x +ln a =ln (x +1)，x >-1，所以要使F (x )有两个零点，只需ln a =ln (x +1)-x 有两个实根.设M (x )=ln (x +1)-x ，则M ′(x )=-x x +1.由M ′(x )=-x x +1>0，得-1<x <0；由M ′(x )=-x x +1<0，得x >0，故函数M(x)的单调递增区间为(-1，0)，单调递减区间为(0，+∞).故函数M(x)在x=0处取得极大值，也是最大值，且M(x)max=M(0)=0.易知当x→-1时，M(x)→-∞；当x→+∞时，M(x)→-∞.故要使ln a=ln(x+1)-x有两个实根，只需ln a<M(x)max=0，解得0<a<1.所以实数a的取值范围是(0，1).。

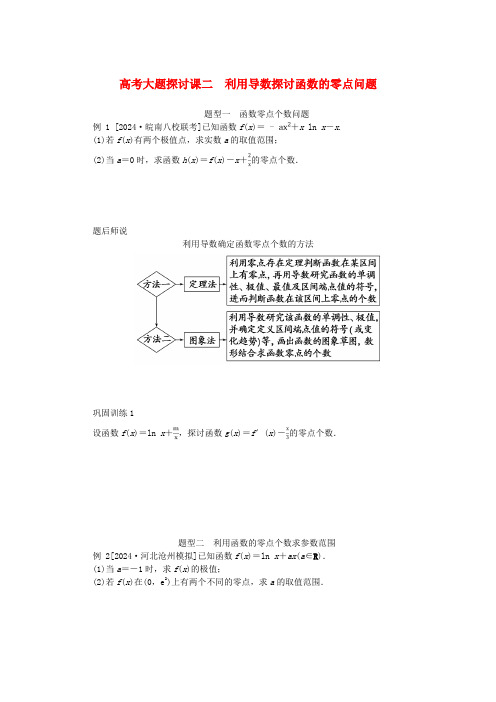
高考大题探讨课二利用导数探讨函数的零点问题题型一函数零点个数问题例 1 [2024·皖南八校联考]已知函数f(x)＝＋x ln x－x.(1)若f(x)有两个极值点，求实数a的取值范围；(2)当a＝0时，求函数h(x)＝f(x)－x＋的零点个数．题后师说利用导数确定函数零点个数的方法巩固训练1设函数f(x)＝ln x＋，探讨函数g(x)＝f′(x)－的零点个数．题型二利用函数的零点个数求参数范围例 2[2024·河北沧州模拟]已知函数f(x)＝ln x＋ax(a∈R)．(1)当a＝－1时，求f(x)的极值；(2)若f(x)在(0，e2)上有两个不同的零点，求a的取值范围．题后师说利用函数的零点个数求参数范围的方法巩固训练2已知函数f(x)＝x3－ax2－2x(a∈R)在x＝2处取得极值．(1)求f(x)在[－2，1]上的最小值；(2)若函数g(x)＝f(x)＋b(b∈R)有且只有一个零点，求b的取值范围．题型三与零点有关的证明例 3[2024·河北邯郸模拟]已知函数f(x)＝x－a ln x(a≠0)．(1)探讨函数f(x)的单调性；(2)若g(x)＝x e x－a(ln x＋x)，且a>e，证明：g(x)有且仅有两个零点．(e为自然对数的底数)题后师说解决证明此类问题的思路一般对条件等价转化，构造合适的新函数，利用导数学问探讨该函数的性质(如单调性、极值状况等)再结合函数图象．巩固训练3已知函数f(x)＝x3－a(x2＋2x＋2)．(1)若a＝2，求函数f(x)的单调区间；(2)证明：函数f(x)只有一个零点．1.[2024·全国甲卷]已知a＞0且a≠1，函数f(x)＝(x＞0)．(1)当a＝2时，求f(x)的单调区间；(2)若曲线y＝f(x)与直线y＝1有且仅有两个交点，求a的取值范围．2．[2024·全国乙卷]已知函数f(x)＝ax－－(a＋1)ln x.(1)当a＝0时，求f(x)的最大值；(2)若f(x)恰有一个零点，求a的取值范围．高考大题探讨课二利用导数探讨函数的零点问题例1 解析：(1)f(x)的定义域为(0，＋∞)，f′(x)＝ln x－2ax，由题意得f′(x)＝0在(0，＋∞)上有两解，即2a＝有两解．令g(x)＝(x>0)，即g(x)的图象与直线y＝2a有两个交点．g′(x)＝＝0，得x＝e，当x∈(0，e)时，g′(x)>0，g(x)单调递增；当x∈(e，＋∞)时，g′(x)<0，g(x)单调递减，∴g(x)max＝g(e)＝，g(1)＝0，当x趋于正无穷时，g(x)趋于零，∴0<2a<，∴0<a<，∴a的取值范围是(0，)．(2)h(x)＝x ln x－2x＋(x>0)，h′(x)＝ln x－1－，令m(x)＝ln x－1－，则m′(x)＝，当x>0时，m′(x)>0，所以h′(x)在(0，＋∞)上单调递增．因为h′(e)＝－<0，h′(e2)＝1－>0，∴存在唯一的x0∈(e，e2)，使得h′(x0)＝＝0，当x∈(0，x0)时，h′(x)<0，h(x)单调递减；当x∈(x0，＋∞)时，h′(x)>0，h(x)单调递增，∴h(x)min＝h(x0)．又∵x0∈(e，e2)，h′(x0)＝＝0，∴h(x0)＝x0ln x0－2x0＋＝－x0＋＝－x0＋<－e＋<0.又∵h(1)＝0，h(x)在(0，x0)上单调递减，∴h(x)在(0，x0)上有一个零点．∵h(x)在(x0，＋∞)上单调递增，且h(e2)＝>0，∴h(x)在(x0，＋∞)上有一个零点．综上可知，函数h(x)在(0，＋∞)上有两个零点．巩固训练1 解析：由题设，可知g(x)＝f′(x)－＝(x>0)．令g(x)＝0，得m＝－x3＋x(x>0)．设φ(x)＝－x3＋x(x>0)，则φ′(x)＝－x2＋1＝－(x－1)(x＋1)，当x∈(0，1)时，φ′(x)>0，φ(x)在(0，1)上单调递增；当x∈(1，＋∞)时，φ′(x)<0，φ(x)在(1，＋∞)上单调递减．所以x＝1是φ(x)的极大值点，也是φ(x)的最大值点．所以φ(x)的最大值为φ(1)＝.画出y＝φ(x)的大致图象(如图)，可知①当m>时，函数g(x)无零点；②当m＝时，函数g(x)有且只有一个零点；③当0<m<时，函数g(x)有两个零点；④当m≤0时，函数g(x)有且只有一个零点．综上所述，当m>时，函数g(x)无零点；当m＝或m≤0时，函数g(x)有且只有一个零点；当0<m<时，函数g(x)有两个零点．例2 解析：(1)当a＝－1时，f′(x)＝－1＝，x>0.由f′(x)＝0，得x＝1.当x∈(0，1)时，f′(x)>0，f(x)在(0，1)上单调递增，当x∈(1，＋∞)时，f′(x)<0，f(x)在(1，＋∞)上单调递减，∴f(x)只有极大值，无微小值，且f(x)极大值＝f(1)＝－1.(2)f′(x)＝＋a＝(x>0)．当a≥0时，∵f′(x)＝>0，∴函数f(x)＝ln x＋ax在(0，＋∞)上单调递增，从而f(x)至多有一个零点，不符合题意．当a<0时，∵f′(x)＝(x>0)，∴f(x)在(0，－)上单调递增，在(－，＋∞)上单调递减．由f(－)＝ln (－)－1>0得－<a<0.由f＝2＋a e2<0得a<－.当－<a<－时，f(1)＝a<0，满意f(x)在(0，e2)上有两个不同的零点．∴a的取值范围是(－，－)．巩固训练2 解析：(1)∵f(x)＝x3－ax2－2x(a∈R)，∴f′(x)＝x2－ax－2，∵f(x)在x＝2处取得极值，∴f′(2)＝0，即22－2a－2＝0解得a＝1，∴f(x)＝x3－x2－2x，∴f′(x)＝x2－x－2＝(x＋1)(x－2)，∴当x<－1或x>2时f′(x)>0，当－1<x<2时f′(x)<0，∴f(x)在[－2，－1)上单调递增，在(－1，1]上单调递减，又f(－2)＝×(－2)3－×(－2)2－2×(－2)＝－，f(1)＝×13－×12－2×1＝－，∴f(x)在[－2，1]上的最小值为－.(2)由(1)知，f(x)＝x3－x2－2x，若函数g(x)＝f(x)＋b(b∈R)有且只有一个零点，则方程－b＝f(x)(b∈R)有唯一解，即－b＝x3－x2－2x(b∈R)有唯一解，由(1)知，f(x)在(－∞，－1)，(2，＋∞)上单调递增，在(－1，2)上单调递减，又f(－1)＝，f(2)＝－，函数图象如图所示：∴－b<－或－b>，得b>或b<－，即b的取值范围为(－∞，－，＋∞)．例3 解析：(1)由题意得函数f(x)的定义域为(0，＋∞)，f′(x)＝1－＝，当a>0时，令f′(x)>0，得x>a，所以f(x)在(a，＋∞)上单调递增；令f′(x)<0，得0<x<a，所以f(x)在(0，a)上单调递减；当a<0时，因为f′(x)>0恒成立，所以f(x)在(0，＋∞)上单调递增．综上所述，当a>0时，f(x)在(0，a)上单调递减，在(a，＋∞)上单调递增，当a<0时，f(x)在(0，＋∞)上单调递增．(2)证明：g(x)＝x e x－a(ln x＋x)＝x e x－a ln (x e x)(x>0)，令t＝x e x，则t′＝(x＋1)e x>0在x>0时恒成立，所以t＝x e x在x>0时单调递增，且t∈(0，＋∞)，所以g(x)＝x e x－a ln (x e x)有两个零点等价于f(t)＝t－a ln t有两个零点．因为a>e，由(1)知，f(t)在(a，＋∞)上单调递增，在(0，a)上单调递减，所以f(t)min＝f(a)＝a－a ln a＝a(1－ln a)，因为a>e，所以f(a)<0.下面证明当a>e时，f(e a)＝e a－a2>0，设h(x)＝e x－x2，则h′(x)＝e x－2x，令m(x)＝e x－2x，又m′(x)＝e x－2，当x>e时，m′(x)＝e x－2>0恒成立，所以m(x)单调递增，得h′(x)＝e x－2x>e e－2e>0，故h(x)＝e x－x2在(e，＋∞)上单调递增，得e x－x2>e e－e2>0，即f(e a)＝e a－a2>0，又因为f(1)＝1>0，所以f(t)在(1，a)，(a，e a)上各存在一个零点，所以a>e时，函数f(t)有且仅有两个零点，即当a>e时，函数g(x)有且仅有两个零点．巩固训练3 解析：(1)若a＝2，则f(x)＝x3－2x2－4x－4，f′(x)＝x2－4x－4，令f′(x)＝0，解得x1＝2－2，x2＝2＋2，当x∈(－∞，2－2，＋∞)时，f′(x)>0，f(x)单调递增，当x∈(2－2，2＋2)时，f′(x)<0，f(x)单调递减，所以f(x)在(－∞，2－2)，(2＋2，＋∞)单调递增，f(x)在(2－2，2＋2)单调递减．(2)证明：由于x2＋2x＋2＝(x＋1)2＋1>0，所以f(x)＝0等价于－3a＝0，设g(x)＝－3a，则g′(x)＝，因为x2＋4x＋6＝(x＋2)2＋2>0，所以g′(x)≥0，所以g(x)在(－∞，＋∞)上单调递增，故g(x)至多有一个零点，从而f(x)至多有一个零点，又f(3a－1)＝－9a2＋2a－＝－9(a－)2－<0，f(3a＋3)＝3a2＋10a＋9＝3(a＋)2＋>0，所以存在唯一的x0∈(3a－1，3a＋3)，使得f(x)＝0，故f(x)有一个零点，综上，f(x)只有一个零点．真题展台——知道高考考什么？1．解析：(1)当a＝2时，f(x)＝(x>0)，f′(x)＝(x>0)，令f′(x)>0，则0<x<，此时函数f(x)单调递增，令f′(x)<0，则x>，此时函数f(x)单调递减，所以函数f(x)的单调递增区间为(0，)，单调递减区间为(，＋∞)．(2)曲线y＝f(x)与直线y＝1有且仅有两个交点，可转化为方程＝1(x>0)有两个不同的解，即方程＝有两个不同的解．设g(x)＝(x>0)，则g′(x)＝(x>0)，令g′(x)＝＝0，得x＝e，当0<x<e时，g′(x)>0，函数g(x)单调递增，当x>e时，g′(x)<0，函数g(x)单调递减，故g(x)max＝g(e)＝，且当x>e时，g(x)∈(0，)，又g(1)＝0，所以0<<，所以a>1且a≠e，即a的取值范围为(1，e)2．解析：(1)当a＝0时，f(x)＝－－ln x(x>0)，则f′(x)＝＝.当x∈(0，1)时，f′(x)>0；当x∈(1，＋∞)时，f′(x)<0.所以f(x)在(0，1)上单调递增，在(1，＋∞)上单调递减，故f(x)的最大值即为f(x)的极大值f(1)＝－1.(2)因为函数f(x)恰有一个零点，所以方程a(x－ln x)－－ln x＝0在(0，＋∞)上恰有一个解，即方程a(x－ln x)＝＋ln x在(0，＋∞)上恰有一个解．又易知当x>0时，x－ln x>0，所以方程a＝在(0，＋∞)上恰有一个解．令g(x)＝(x>0)，则g′(x)＝.令h(x)＝x－1－(x＋1)ln x(x>0)，则h′(x)＝1－ln x－＝－ln x－.由(1)知，h′(x)≤－1，所以h(x)在(0，＋∞)上单调递减．又h(1)＝0，所以当x∈(0，1]时，h(x)≥0；当x∈(1，＋∞)时，h(x)<0.则当x∈(0，1]时，g′(x)≤0；当x∈(1，＋∞)时，g′(x)<0.所以g(x)在(0，＋∞)上单调递减．又当x→0时，g(x)→＋∞，当x→＋∞时，g(x)→0，所以a∈(0，＋∞)．。

导数在研究函数中的应用【自主归纳，自我查验】一、自主归纳1．利用导函数判断函数单调性问题函数f (x )在某个区间(a ，b )内的单调性与其导数的正负有如下关系 (1)若____ ___，则f (x )在这个区间上是增加的． (2)若____ ___，则f (x )在这个区间上是减少的． (3)若_____ __，则f (x )在这个区间内是常数． 2．利用导数判断函数单调性的一般步骤 (1)求f ′(x )．(2)在定义域内解不等式f ′(x )>0或f ′(x )<0. (3)根据结果确定f (x )的单调区间． 3．函数的极大值在包含0x 的一个区间(a ，b )内，函数y ＝f (x )在任何一点的函数值都_____0x 点的函数值，称点0x 为函数y ＝f (x )的极大值点，其函数值f (0x )为函数的极大值． 4．函数的极小值在包含x 0的一个区间(a ，b )内，函数y ＝f (x )在任何一点的函数值都_____0x 点的函数值，称点0x x 0为函数y ＝f (x )的极小值点，其函数值f (0x )为函数的极小值．极大值与极小值统称为_______，极大值点与极小值点统称为极值点． 5．函数的最值与导数1．函数y ＝f (x )在[a ，b ]上的最大值点0x 指的是：函数在这个区间上所有点的函数值都_________f (0x )．2．函数y ＝f (x )在[a ，b ]上的最小值点0x 指的是：函数在这个区间上所有点的函数值都_________f (0x )．二、自我查验1．函数f (x )＝x ＋eln x 的单调递增区间为( ) A ．(0，＋∞)B ．(－∞，0)C ．(－∞，0)和(0，＋∞)D ．R2．若函数f (x )＝x 3＋x 2＋mx ＋1是R 上的单调增函数，则m 的取值范围是________．3.函数f (x )的定义域为开区间(a ，b )，导函数f ′(x )在(a ，b )内的图象如图所示，则函数f (x )在开区间(a ，b )内有极小值点( ) A ．1个 B ．2个 C ．3个D ．4个4．若函数f (x )＝x 3＋ax 2＋3x －9在x ＝－3时取得极值，则a 等于( ) A ．2 B ．3 C ．4 D ．55.函数ln xy x=的最大值为（ ） A ．1e - B ．e C ．2e D ．103【典型例题】考点一 利用导数研究函数的单调性【例1】(2015·高考全国卷Ⅱ)已知函数f (x )＝ln x ＋a (1－x )．(1)讨论f (x )的单调性；(2)当f (x )有最大值，且最大值大于2a －2时，求a 的取值范围．【变式训练1】已知()3222f x x ax a x =+-+．（1）若1a =时，求曲线()y f x =在点()()1,1f 处的切线方程； （2）若0a >，求函数()f x 的单调区间．考点二 利用导函数研究函数极值问题【例2】已知函数()ln 3,f x x ax a =-+∈R . （1）当1a =时，求函数的极值； （2）求函数的单调区间.【变式训练2】(2011·安徽)设f (x )＝e x 1＋ax 2，其中a 为正实数.当a ＝43时，求f (x )的极值点；考点三 利用导函数求函数最值问题【例3】已知a 为实数，.（1）求导数； （2）若，求在[]2,2-上的最大值和最小值.【应用体验】1.函数ln y x x =-的单调递减区间为（ ） A ．](1,1- B ．)(0,+∞ C ．[)1,+∞ D ．](0,1()))(4(2a x x x f --=()xf '()01=-'f ()x f2.函数()e x f x x -=的单调递减区间是（ ）A ．(1,)+∞B ．(,1)-∞-C ．(,1)-∞D ．(1,)-+∞ 3.函数()()3e x f x x =-的单调递增区间是（ ） A ．()0,3 B ．()1,4C ．()2,+∞D ．(),2-∞4.设函数()2ln f x x x=+，则（ ） A ．12x =为()f x 的极大值点 B ．12x =为()f x 的极小值点C ．2x =为()f x 的极大值点D ．2x =为()f x 的极小值点5．函数32()23f x x x a =-+的极大值为6，那么a 的值是（ ） A ．0 B ．1 C ．5 D ．6【复习与巩固】A 组 夯实基础一、选择题1．已知定义在R 上的函数()f x ，其导函数()f x '的大致图象如图所示，则下列叙述正确的是（ ）A ．()()()f b f c f d >>B ．()()()f b f a f e >>C ．()()()f c f b f a >>D ．()()()f c f e f d >>2.函数()2ln f x x a x =+在1x =处取得极值，则a 等于（ ）A ．2B ．2-C ．4D ．4-3.函数()e xf x x =-（e 为自然对数的底数）在区间[]1,1-上的最大值是（ ）A.1B.1C.e ＋1D.e －1二、填空题4.若函数()321f x x x mx =+++是R 上的单调增函数，则实数m 的取值范围是________________．5.若函数()23exx axf x +=在0x =处取得极值，则a 的值为_________. 6.函数()e x f x x =-在]1,1[-上的最小值是_____________. 三、解答题 7.已知函数()21ln ,2f x x x =-求函数()f x 的单调区间8.已知函数(),1ln xf x ax x x=+>． （1）若()f x 在()1,+∞上单调递减，求实数a 的取值范围； （2）若2a =，求函数()f x 的极小值.B 组 能力提升一、选择题1．已知函数()213ln 22f x x x =-+在其定义域内的一个子区间()1,1a a -+内不是单调函数，则实数a 的取值范围是（ ） A ．13,22⎛⎫-⎪⎝⎭ B ．51,4⎡⎫⎪⎢⎣⎭ C ．31,2⎛⎫ ⎪⎝⎭ D ．31,2⎡⎫⎪⎢⎣⎭2.若函数32y x ax a =-+在()0,1内无极值，则实数a 的取值范围是（ ） A ．30,2⎡⎤⎢⎥⎣⎦B ．(),0-∞C ．(]3,0,2⎡⎫-∞+∞⎪⎢⎣⎭U D ．3,2⎡⎫+∞⎪⎢⎣⎭3.若函数()3232f x x x a =-+在[]1,1-上有最大值3，则该函数在[]1,1-上的最小值是（ ） A ． B ．0 C ．D ．1二、填空题4．已知函数f (x )＝12x 2＋2ax －ln x ，若f (x )在区间⎣⎡⎦⎤13，2上是增函数，则实数a 的取值范围为________．5．设x 1，x 2是函数f (x )＝x 3－2ax 2＋a 2x 的两个极值点，若x 1<2<x 2，则实数a 的取值范围是________．6．若函数f (x )＝x 2－e x －ax 在R 上存在单调递增区间，则实数a 的取值范围是________． 三、解答题7．已知函数f (x )＝x －2ln x －ax＋1，g (x )＝e x (2ln x －x )．(1)若函数f (x )在定义域上是增函数，求a 的取值范围；(2)求g (x )的最大值．12-128．设函数f(x)＝(x－1)e x－kx2(其中k∈R)．(1)当k＝1时，求函数f(x)的单调区间和极值；(2)当k∈[0，＋∞)时，证明函数f(x)在R上有且只有一个零点．《导数在研究函数中的应用》标准答案一．自主归纳1.（1）f ′(x )>0 （2）f ′(x )<0 （3）f ′(x )＝0 3. 小于 4. 大于 极值 5.不超过 不小于 二．自我查验1.解析：函数定义域为(0，＋∞)，f ′(x )＝1＋ex>0，故单调增区间是(0，＋∞)．答案：A2.解析：∵f (x )＝x 3＋x 2＋mx ＋1， ∴f ′(x )＝3x 2＋2x ＋m .又∵f (x )在R 上是单调增函数，∴f ′(x )≥0恒成立，∴Δ＝4－12m ≤0，即m ≥13.答案：⎣⎢⎡⎭⎪⎫13，＋∞3.解析：导函数f ′(x )的图象与x 轴的交点中，左侧图象在x 轴下方，右侧图象在x 轴上方的只有一个，故选A.答案：A4.解析：f ′(x )＝3x 2＋2ax ＋3，由题意知f ′(－3)＝0，即3×(－3)2＋2×(－3)a ＋3＝0，解得a ＝5.答案：D5..A 当(0,e)x ∈时函数单调递增，当(e,)x ∈+∞时函数单调递减， A. 三．典型例题【例题1】(1)f (x )的定义域为(0，＋∞)，f ′(x )＝1x－a .若a ≤0，则f ′(x )>0，所以f (x )在(0，＋∞)单调递增．若a >0，则当x ∈⎝ ⎛⎭⎪⎫0，1a 时，f ′(x )>0；当x ∈⎝ ⎛⎭⎪⎫1a ，＋∞时，f ′(x )<0.所以f (x )在⎝⎛⎭⎪⎫0，1a 单调递增，在⎝ ⎛⎭⎪⎫1a ，＋∞单调递减． (2)由(1)知，当a ≤0时，f (x )在(0，＋∞)无最大值；当a >0时，f (x )在x ＝1a处取得最大值，最大值为f ⎝ ⎛⎭⎪⎫1a ＝ln 1a ＋a ⎝ ⎛⎭⎪⎫1－1a ＝－ln a ＋a －1.因此f ⎝ ⎛⎭⎪⎫1a >2a －2等价于ln a ＋a －1<0.令g (a )＝ln a ＋a －1，则g (a )在(0，＋∞)单调递增，g (1)＝0. 于是，当0<a <1时，g (a )<0；当a >1时，g (a )>0. 因此，a 的取值范围是(0,1)．【变式训练1】（1）当1a =时，()322f x x x x =+-+，∴()2321f x x x '=+-， ∴切线斜率为()14k f '==，又()13f =，∴切点坐标为()1,3，∴所求切线方程为()341y x -=-，即410x y --=．（2）()()()22323f x x ax a x a x a '=+-=+-，由()0f x '=，得x a =-或3ax =.0,.3a a a >∴>-Q 由()0f x '>，得x a <-或3a x >，由()0f x '<，得.3aa x -<<∴函数()f x 的单调递减区间为,3a a ⎛⎫- ⎪⎝⎭，单调递增区间为(),a -∞-和,3a ⎛⎫+∞ ⎪⎝⎭．【例题2】（1）当1a =时，()ln 3f x x x =-+，()()1110xf x x x x-'=-=>， 令()0f x '>，解得01x <<，所以函数()f x 在(0,1)上单调递增； 令()0f x '<，解得1x >，所以函数()f x 在()1,+∞上单调递减； 所以当1x =时取极大值，极大值为()12f =，无极小值. （2）函数()f x 的定义域为()0,+∞，()1f x a x'=-. 当0a ≤时，1()0f x a x'=->在()0,+∞上恒成立，所以函数()f x 在()0,+∞上单调递增；当0a >时，令()0f x '>，解得10x a <<，所以函数()f x 在10,a ⎛⎫⎪⎝⎭上单调递增；令()0f x '<，解得1x a >，所以函数()f x 在1,a ⎛⎫+∞ ⎪⎝⎭上单调递减. 综上所述，当0a ≤时，函数()f x 的单调增区间为()0,+∞；当0a >时，函数()f x 的单调增区间为10,a ⎛⎫ ⎪⎝⎭，单调减区间为1,a ⎛⎫+∞ ⎪⎝⎭.【变式训练2】解 对f (x )求导得f ′(x )＝e x ·1＋ax 2－2ax 1＋ax 22. 当a ＝43时，若f ′(x )＝0， 则4x 2－8x ＋3＝0，解得x 1＝32，x 2＝12.结合①，可知x (－∞，12) 12 (12，32) 32 (32，＋∞) f ′(x ) ＋0 － 0 ＋ f (x )极大值极小值所以x 1＝2是极小值点，x 2＝2是极大值点.【例题3】1）.（2）由得，故， 则43x =或，由，，41641205504.39329627f ⎛⎫⎛⎫⎛⎫=-⨯-=-⨯=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故，.【变式训练3】1）当0a ≥时，函数()e 20x f x a '=+>，()f x 在R 上单调递增，当0a <时，()e 2x f x a '=+，令e 20x a +=，得ln(2)x a =-，所以当(,ln(2))x a ∈-∞-()423)4()(2'22--=-+-=ax x x a x x x f ()01=-'f 21=a 2421)21)(4()(232+--=--=x x x x x x f ()34,143'2=-=⇒--=x x x x x f 或0)2()2(==-f f 29)1(=-f 29)(max =x f 2750)(min -=x f时，()0f x '<，函数()f x 单调递减；当(ln(2),)x a ∈-+∞时，()0f x '>，函数()f x 单调递增.（2）由（1）可知，当0a ≥时，函数()e 20x f x ax =+>，不符合题意. 当0a <时，()f x 在(,ln(2))a -∞-上单调递减，在(ln(2),)a -+∞上单调递增.①当ln(2)1a -≤()f x 最小值为(1)2e f a =+.解2e 0a +=，得.②当ln(2)1a ->()f x 最小值为(ln(2))22ln(2)f a a a a -=-+-，解22ln(2)0a a a -+-=，得2ea =-，不符合题意.应用体验： 1.D【解析】函数的定义域为)(0,+∞，令1110x y x x-'=-=≤，解得](0,1x ∈，又0x >，所以](0,1x ∈，故选D. 考点：求函数的单调区间. 2.A【解析】导数为()()()e e 1e x x x f x x x ---'=+⋅-=-，令()0f x '<，得1x >，所以减区间为()1,+∞.考点：利用导数求函数的单调区间． 3.C【解析】()()()e 3e e 2x x x f x x x '=+-=-，令()()e 20x f x x '=->，解得2x >，所以函数()f x 的单调增区间为()2,+∞．故选C ． 4.【解析】()22212x f x x x x-'=-+=，由()0f x '=得2x =，又函数定义域为()0,+∞，当02x <<时，()0f x '<，()f x 递减，当2x >时，()0f x '>，()f x 递增，因此2x =是函数()f x 的极小值点．故选D ． 考点：函数的极值点． 5.D【解析】()()322()23,6661f x x x a f x x x x x '=-+∴=-=-Q ，令()0,f x '= 可得0,1x =，容易判断极大值为()06f a ==. 考点：函数的导数与极值. 复习与巩固 A 组 1.C【解析】由()f x '图象可知函数()f x 在(),c -∞上单调递增，在(),c e 上单调递减，在(),e +∞上单调递增，又(),,,a b c c ∈-∞，且a b c <<，故()()()f c f b f a >>． 考点：利用导数求函数单调性并比较大小． 2.B【解析】()2a f x x x '=+，由题意可得()121201af a '=⨯+=+=，2a ∴=-.故选B.考点：极值点问题. 3.D【解析】()e 1x f x '=-，令()0,f x '=得0x =.又()()()010e 01,1e 11,111,e f f f =-==->-=+>且11e 11e 2e e ⎛⎫--+=-- ⎪⎝⎭＝2e 2e 10e--=>，所以()()max 1e 1,f x f ==-故选D.考点：利用导数求函数在闭区间上的最值.4.1,3⎡⎫+∞⎪⎢⎣⎭【解析】由题意得()0f x '≥在R 上恒成立，则()2320f x x x m '=++≥，即232m x x ≥--恒成立.令()232g x x x =--，则()max m g x ≥⎡⎤⎣⎦，因为()g x232x x =--为R 上的二次函数，所以()2max11333g x g ⎛⎫⎛⎫=-=-⨯-⎡⎤ ⎪ ⎪⎣⎦⎝⎭⎝⎭11233⎛⎫-⨯-= ⎪⎝⎭，则m 的取值范围是1,3⎡⎫+∞⎪⎢⎣⎭.5.0【解析】()()()()()2226e 3e 36e e x xxx x a x ax x a x a f x +-+-+-+'==， 由题意得()00f a '==． 考点：导数与极值． 6.1【解析】因为()e 1x f x '=-，()00,()00f x x f x x ''>⇒><⇒<，所以()f x 在[1,0]-单调递减，在[0,1]单调递增，从而函数()e x f x x =-在]1,1[-上的最小值是0(0)e 01f =-=.考点：函数的最值与导数.7.【解析】()21ln 2f x x x =-的定义域为()0,+∞，()211x f x x x x-'=-=，令()0f x '=，则1x =或1-（舍去）.∴当01x <<时，()0f x '<，()f x 递减，当1x >时，()0f x '>，()f x 递增， ∴()f x 的递减区间是()0,1，递增区间是()1,+∞．考点：利用导数求函数的单调区间． 8.（1）14a ≤-（2）【解析】（1）函数(),1ln x f x ax x x =+>，则()2ln 1ln x f x a x-'=+，由题意可得()0f x '≤在()1,x ∈+∞上恒成立，∴2211111ln ln ln 24a x x x ⎛⎫≤-=-- ⎪⎝⎭， ∵()1,x ∈+∞，()ln 0,,x ∴∈+∞021ln 1=-∴x 时，函数2111ln 24t x ⎛⎫=--⎪⎝⎭取最小值41-，41-≤∴a ，（2）当2a =时，()2ln x f x x x =+，()22ln 12ln ln x x f x x -+'=， 令()0f x '=，得22ln ln 10x x +-=，解得21ln =x 或ln 1x =-（舍去），即x =当1x <<()0f x '<，当x >()0f x '>， ∴()f x的极小值为f =.B 组 1.D【解析】因为函数()213ln 22f x x x =-+在区间()1,1a a -+上不单调，所以()2141222x f x x x x-'=-=在区间()1,1a a -+上有零点，由()0f x '=，得12x =，则10,111,2a a a -≥⎧⎪⎨-<<+⎪⎩得312a ≤<，故选D ． 考点：函数的单调性与导数的关系．2.C【解析】232y x a '=-，①当0a ≤时，0y '≥，所以32y x ax a =-+在()0,1上单调递增，在()0,1内无极值，所以0a ≤符合题意；②当0a >时，令0y '=，即2320x a -=，解得12,33x x =-=，当,x ⎛⎫∈-∞+∞ ⎪ ⎪⎝⎭⎝⎭U 时，0y '>，当x ⎛∈ ⎝⎭时，0y '<，所以32y x ax a =-+的单调递增区间为,,⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭，单调递减区间为⎛ ⎝⎭，当x =数取得极大值，当x =原函数取得极小值，要满足原函数在()0,1内无极值，1≥，解得32a ≥.综合①②得，a 的取值范围为(]3,0,2⎡⎫-∞+∞⎪⎢⎣⎭U ，故选C.考点：导函数，分类讨论思想. 3.C【解析】()()23331f x x x x x '=-=-，当()0f x '>时，1>x 或0<x ，当()0f x '<时，10<<x ，所以()f x 在区间[]1,0-上函数递增，在区间[]1,0上函数递减，所以当0=x 时，函数取得最大值()30==a f ，则()32332f x x x =-+，所以()211=-f ，()251=f ，所以最小值是()211=-f ． 考点：利用导数求函数在闭区间上的最值.4.解析：由题意知f ′(x )＝x ＋2a －1x ≥0在⎣⎢⎡⎦⎥⎤13，2上恒成立，即2a ≥－x ＋1x 在⎣⎢⎡⎦⎥⎤13，2上恒成立，∵⎝⎛⎭⎪⎫－x ＋1x max ＝83，∴2a ≥83，即a ≥43.答案：⎣⎢⎡⎭⎪⎫43，＋∞5.解析：本题考查利用导数研究函数的极值及不等式的解法．由f ′(x )＝3x 2－4ax ＋a 2＝0得x 1＝a3，x 2＝a .又∵x 1<2<x 2，∴⎩⎨⎧a >2，a3<2，∴2<a <6.答案：(2,6)6.解析：∵f (x )＝x 2－e x －ax ，∴f ′(x )＝2x －e x －a ， ∵函数f (x )＝x 2－e x －ax 在R 上存在单调递增区间，∴f ′(x )＝2x －e x －a ≥0，即a ≤2x －e x 有解，设g (x )＝2x －e x ，则g ′(x )＝2－e x ，令g ′(x )＝0，解得x ＝ln 2，则当x <ln 2时，g ′(x )>0，g (x )单调递增，当x >ln 2时，g ′(x )<0，g (x )单调递减，∴当x ＝ln 2时，g (x )取得最大值，且g (x )max ＝g (ln 2)＝2ln 2－2，∴a ≤2ln 2－2. 答案：(－∞，2ln 2－2)7.解：(1)由题意得x >0，f ′(x )＝1－2x ＋ax2.由函数f (x )在定义域上是增函数，得f ′(x )≥0，即a ≥2x －x 2＝－(x －1)2＋1(x >0)．因为－(x －1)2＋1≤1(当x ＝1时，取等号)，所以a 的取值范围是[1，＋∞)．(2)g ′(x )＝e x ⎝ ⎛⎭⎪⎫2x －1＋2ln x －x ，由(1)得a ＝2时，f (x )＝x －2ln x －2x ＋1，且f (x )在定义域上是增函数，又f (1)＝0，所以，当x ∈(0,1)时，f (x )<0，当x ∈(1，＋∞)时，f (x )>0. 所以，当x ∈(0,1)时，g ′(x )>0，当x ∈(1，＋∞)时，g ′(x )<0. 故当x ＝1时，g (x )取得最大值－e.8.解：(1)当k ＝1时，f (x )＝(x －1)e x －x 2，f ′(x )＝e x ＋(x －1)e x －2x ＝x e x －2x ＝x (e x －2)，令f ′(x )＝0，得x 1＝0，x 2＝ln 2. 当x 变化时，f ′(x )，f (x )的变化如下表：0]，[ln 2，＋∞)．f (x )的极大值为f (0)＝－1，极小值为f (ln 2)＝ －(ln 2)2＋2ln 2－2.(2)f ′(x )＝e x ＋(x －1)e x －2kx ＝x e x －2kx ＝x (e x －2k )， 当x <1时，f (x )<0，所以f (x )在(－∞，1)上无零点． 故只需证明函数f (x )在[1，＋∞)上有且只有一个零点．①若k ∈⎣⎢⎡⎦⎥⎤0，e 2，则当x ≥1时，f ′(x )≥0，f (x )在[1，＋∞)上单调递增．∵f (1)＝－k ≤0，f (2)＝e 2－4k ≥e 2－2e>0， ∴f (x )在[1，＋∞)上有且只有一个零点．②若k ∈⎝ ⎛⎭⎪⎫e 2，＋∞，则f (x )在[1，ln 2k ]上单调递减，在[ln 2k ，＋∞)上单调递增．f (1)＝－k <0，f (k ＋1)＝k e k ＋1－k (k ＋1)2＝k [e k ＋1－(k ＋1)2]， 令g (t )＝e t －t 2，t ＝k ＋1>2，则g ′(t )＝e t －2t ，g ″(t )＝e t －2，∵t>2，∴g″(t)>0，g′(t)在(2，＋∞)上单调递增．∴g′(t)>g′(2)＝e2－4>0，∴g(t)在(2，＋∞)上单调递增．∴g(t)>g(2)＝e2－4>0.∴f(k＋1)>0.∴f(x)在[1，＋∞)上有且只有一个零点．综上，当k∈[0，＋∞)时，f(x)在R上有且只有一个零点．。

函数的零点专题含答案学校：__________ 班级：__________ 姓名：__________ 考号：__________1. 已知函数f (x )=x 3−2x +2，在下列区间中，一定包含f (x )零点的区间是（ ）A.(−2,−1)B.(−1,0)C.(0,1)D.(1,2)2. 下列函数中，既是偶函数又存在零点的是( )A.y =ln xB.y =x 2+1C.y =cos xD.y =sin x3. 函数f (x )={x +1,x ≤0，lg x,x >0的零点是（ ） A.(−1,0),(1,0)B.−1，1C.(−1,0)D.−14. 函数f (x )=√x −x 的零点的个数是( )A.3个B.2个C.1个D.0个5. 我国古代数学典籍《九章算术》第七章“盈不足”中有一道两鼠穿墙问题：“今有垣厚五尺，两鼠对穿，大鼠日一尺，小鼠日—尺，大鼠日自倍，小鼠日自半，问何日相逢”( )A.第2天B.第3天C.第4天D.第5天6. 函数y =x 2−1的零点是( )A.1B.±1C.(1,0)D.(±1,0)7. 函数f(x)=2x −2x −a 的一个零点在区间(1, 2)内，则实数a 的取值范围是( ) A.(1, 3)B.(1, 2)C.(0, 3)D.(0, 2)8. 已知实数a ，b 满足2a =3，3b =2，则f(x)=a x +x −b 的零点所在的区间是( )A.(−2, −1)B.(−1, 0)C.(0, 1)D.(1, 2)9. 函数y =(2x −2−x )sin x 在[−π,π]的图象大致为( )A.B.C.D.10. 已知三次函数f (x )=13x 3−(4m −1)x 2+(15m 2−2m −7)x +2在定义域R 上无极值点，则m 的取值范围是( )A.m <2或m >4B.m ≥2或m ≤4C.2≤m ≤4D.2<m <411. 已知函数f(x)={e x ,x ≤0，ln x,x >0，g(x)=f(x)+x +a ，若g(x)存在2个零点，则a 的取值范围是( )A.[−1, 0)B.[0, +∞)C.[−1, +∞)D.[1, +∞)12. 已知函数f (x )=2x +ln x ，下列判断正确的是（ ） A.函数f (x )的单调递减区间为(−∞,2]B.x =2是函数f (x )的极大值点C.函数g (x )=f (x )−x 有且只有一个零点D.函数g (x )=f (x )−x 在其定义域内单调递增13. 已知函数f (x )={x +1x ,x >2,ln (x +a ),x ≤2的图象上存在关于直线x =2对称的不同两点，则实数a 的取值范围是( )A.(e,+∞)B.(e 52−2,+∞)C.(−∞,2e −1)D.(−∞,e 52)14. 函数f (x )=|x −2|−2−x 的零点的个数为（ ）A.0B.1C.2D.315. 已知函数f (x )=xe x ，要使函数g (x )=m [f (x )]2−2f (x )+1恰有一个零点，则实数m 的取值范围是( )A.[−e 2−2e,0]B.[−e 2+2e,0]C.(−e 2−2e,0]∪{1}D.(−e 2+2e,0]∪{1}16. 已知定义在R 上的函数y =f (x )，对任意x 都满足f (x +2)=f (x )，且当−1≤x ≤1时f (x )=2x 2，则函数g (x )=f (x )−ln |x|的零点个数为( )A.12B.14C.15D.1617. 函数f (x )=(3x −1)ln x 的零点个数是________.18. 若函数f(x)=log 2(x +a)的零点为2，则a =________．19. 函数f(x)=(x+1)ln x x−3的零点是________．20. 已知函数f(x)={2x +3,x ≤−32,x 2,−32<x <1,4x,x ≥1.若f(x)＝2，则x ＝________．21. 设函数y ＝a x −4，(a >0, a ≠1)，若其零点为2，则a ＝________．22. 已知λ∈R ，函数f (x )={x −4,x ≥λ,x 2−4x +3,x <λ．当λ=2时，不等式f (x )<0的解集是________．若函数f (x )恰有2个零点，则λ的取值范围是________．23. 已知函数y =f (x )在R 上连续且可导， y =f (x +1)为偶函数且f (2)=0，其导函数满足(x −1)f ′(x )>0，则函数g (x )=(x −1)f (x )的零点个数为________.24. 给出一个满足以下条件的函数f (x )=________.①f (x )的定义域是R ，且其图象是一条连续不断的曲线；②f (x )是偶函数；③f (x )在(0,+∞)不是单调函数；④f (x )有无数个零点．25. 已知函数f (x )={2x −3,x ≥1x 2−x −1,x <1，则y =f [f (x )]−5的所有零点之和为________.26. 已知函数g(x)，ℎ(x)分别是定义在R 上的偶函数和奇函数，且满足g(x)+ℎ(x)=e x +sin x −x ，则函数g(x)的解析式为________；若函数f(x)=3|x−2020|−λg(x −2020)−2λ2有唯一零点，则实数λ的值为________．27. 已知函数f (x )={e ln x x (x >1),x 2−1(x ≤1),若函数g (x )=f(f (x ))−af (x )+a +1恰有5个不同的零点，则实数a 的取值范围是________．28. 已知函数 f (x )={1−12|1−x|,x ≤2，12f (x −2),2<x ≤6， 则函数g (x )=xf (x )−1的零点个数为________.29. 定义在R 上的函数f (x )满足f (−x )=−f (x )，f (x +4)=f (x )，当x ∈[0,2)时，f (x )={x 2，0≤x <1，2−x ，1≤x <2，则函数y =f (x )−log 5|x|的零点个数为________.30. （10分） 已知函数f(x)＝log a (5−2x)，其中a >0，且a ≠1．(Ⅰ)求f(x)的定义域；(Ⅲ)比较f(−1)与f(1)的大小．参考答案与试题解析函数的零点专题含答案一、 选择题 （本题共计 16 小题 ，每题 3 分 ，共计48分 ）1.【答案】A【考点】函数的零点【解析】无【解答】解：f (−2)=−2，f (−1)=3，根据零点存在性定理可知答案．故选A ．2.【答案】C【考点】函数的零点函数奇偶性的判断【解析】利用函数奇偶性的判断一件零点的定义分别分析解答．【解答】解：对于A ，y =ln x 的定义域为(0, +∞)，则函数不是偶函数；对于B ，由y =x 2+1≥1，得函数y =x 2+1没有零点，不满足条件；对于C ，cos (−x)=cos x ，即函数y =cos x 是偶函数且函数存在零点，满足条件. 对于D ，sin (−x)=−sin x ，即函数y =sin x 为奇函数.故选C .3.【答案】B【考点】函数的零点【解析】根据函数解析式，对x 的取值范围所对应的直线进行求解即可，属于基础题.【解答】解：已知函数f(x)={x +1,x ≤0,lg x,x >0,当x ≤0时，设函数g(x)=x +1，令g(x)=0，解得x =−1，则函数g(x)=x +1的零点为−1，当x >0时，设函数ℎ(x)=lg x ，令ℎ(x)=0，解得x =1，综上可得,函数f(x)={x +1,x ≤0,lg x,x >0的零点是−1，1. 故选B .4.【答案】B【考点】函数的零点【解析】根据方程√x −x =0根的个数判断，利用函数零点和方程根之间的关系，求解即可.【解答】解：由题意知函数f(x)=√x −x 的定义域为[0,+∞)，令f(x)=0，则√x −x =0，即√x =x ，解得x 1=0，x 2=1，故函数f(x)=√x −x 的零点的个数是2个.故选B .5.【答案】B【考点】数列的求和函数的零点【解析】此题暂无解析【解答】解：设需要n 天时间才能打穿，则2n −12−1+1−(12)n 1−12≥5，化为：2n −22n −4≥0，令f(n)=2n −22n −4， 则f(3)=8−14−4>0，f(2)=4−12−4<0，∴ f(x)在(2, 3)内存在一个零点．又函数f(x)在x ≥1时单调递增，因此f(x)在(2, 3)内存在唯一一个零点，∴ 需要3天时间才能打穿．故选B ．6.【答案】B函数的零点与方程根的关系【解析】首先使得函数等于0，解出关于x的一元二次方程的解，即可得到函数的零点. 【解答】解：令y=x2−1=0，解得x=1或−1，∴函数y=x2−1的零点为±1.故选B.7.【答案】C【考点】函数的零点【解析】由题意可得f(1)f(2)＝(0−a)(3−a)<0，解不等式求得实数a的取值范围．【解答】解：由题意可得f(1)f(2)=(0−a)(3−a)<0，解得0<a<3，故实数a的取值范围是(0, 3).故选C．8.【答案】B【考点】函数的零点指数式与对数式的互化【解析】根据对数，指数的转化得出f(x)=(log23)x+x−log32单调递增，根据函数的零点判定定理得出f(0)=1−log32>0，f(−1)=log32−1−log32=−1<0，判定即可．【解答】解：∵实数a，b满足2a=3，3b=2，∴a=log23>1，0<b=log32<1，∵函数f(x)=a x+x−b，∴f(x)=(log23)x+x−log32单调递增，∵f(0)=1−log32>0,f(−1)=log32−1−log32=−1<0，∴根据函数的零点判定定理得出:函数f(x)=a x+x−b的零点所在的区间是(−1, 0). 故选B．9.【答案】B【考点】函数奇偶性的判断【解析】本题主要考查了函数的奇偶性和零点以及函数的图象，属于基础题，根据奇偶性的定义可得f(x)为偶函数，排队B；再令f(x)=0可得函数的零点为−π，0，π，排队CD，从而得到结论．【解答】解：函数定义域[−π,π]关于原点对称，且f(−x)=(2−x−2x)sin(−x)=−(2x−2−x)(−sin x)=(2x−2−x)sin x=f(x)，∴ f(x)是偶函数，故排除A；令f(x)=0，即(2x−2−x)sin x=0，∴2x−2−x=0或sin x=0，又x∈[−π,π]，∴解得x=−π，0，π，排除C，D.故选B.10.【答案】C【考点】利用导数研究函数的极值函数的零点【解析】由题意，对函数进行求导，由其导函数无变号零点，根据根的判别式可求得m的取值范围．【解答】x3−(4m−1)x2+(15m2−2m−7)x+2，定义域为R，解：已知函数f(x)=13则f′(x)=x2−2(4m−1)x+15m2−2m−7，因为函数f(x)在定义域上无极值点，则f′(x)=x2−2(4m−1)x+15m2−2m−7无变号零点，所以x2−2(4m−1)x+15m2−2m−7≥0恒成立，而Δ=4(4m−1)2−4(15m2−2m−7)=64m2−32m+4−60m2+8m+28=4(m2−6m+8)≤0，解得2≤m≤4.故选C．11.【答案】C【考点】函数的零点【解析】由g(x)=0得f(x)=−x−a，分别作出两个函数的图象，根据图象交点个数与函数零点之间的关系进行转化求解即可．解：由g(x)=0得f(x)=−x−a，作出函数f(x)和y=−x−a的图象如图：当直线y=−x−a的截距−a≤1，即a≥−1时，f(x)和y=−x−a的图象都有2个交点，即函数g(x)存在2个零点，故实数a的取值范围是[−1, +∞).故选C．12.【答案】C【考点】利用导数研究函数的单调性利用导数研究函数的极值函数的零点【解析】利用导数判断函数的单调性即可逐项判定.【解答】解：由题意得，函数的的定义域为(0,+∞)，函数的导数f′(x)=−2x2+1x=x−2x2，当x∈(0,2)时，f′(x)＜0，函数f(x)单调递减，当x∈(2,+∞)，f′(x)>0，函数f(x)单调递增，∴x=2时，f(x)取得极小值，故A错误，B错误.∵g(x)=f(x)−x=2x+ln x−x，x>0，则g′(x)=−x2+x−2x2<0，∴函数g(x)=f(x)−x=2x+ln x−x在(0,+∞)上单调递减，∵f(1)−1=2+ln1−1=1>0，f(2)−2=1+ln2−2=ln2−1<0，∴函数g(x)=f(x)−x有且只有1个零点，故C正确，D错误. 故选C.13.B【考点】函数的零点分段函数的应用利用导数研究函数的单调性【解析】此题暂无解析【解答】解：依题意，函数f(x)的图象上存在关于x=2对称的不同两点，则存在x1>2，x2≤2，且x1+x2=4，使得x1+1x1=ln(x2+a)，则e x1+1x1=x2+a，因此a=e x1+1x1−x2=e x1+1x1+x1−4，设g(x)=e x+1x+x−4，x>2．故问题转化为存在x∈(2,+∞)，使得函数g(x)=e x+1x+x−4与y=a有交点，又g′(x)=e x+1x⋅(1−1x2)+1>0在x∈(2,+∞)上恒成立，所以函数g(x)在x∈(2,+∞)上单调递增，故g(x)>g(2)=e 52−2，因此，为使函数g(x)=e x+1x+x−4与y=a有交点，只需a>e 52−2．故选B．14.【答案】D【考点】函数的零点【解析】此题暂无解析【解答】解：如图所示，在同一平面直角坐标系中作出函数y=|x−2|，y=2−x的图象．由图可知函数f(x)在定义域内的零点个数为3．故选D．15.【答案】C【考点】利用导数研究函数的单调性函数的零点函数的零点与方程根的关系根的存在性及根的个数判断【解析】本题考查了根据函数零点个数求解参数范围．由导数求f(x)的最值．可得草图．借助图象将问题转化为二次函数的根的分布问题．分情况求解．【解答】解：∵ f(x)=xe x．∴f′(x)=(x+1)e x，易知f(x)在(−∞,−1)单调递减，(−1,+∞)单调递增，∴ f(x)min=f(−1)=−1e，且当x<0时，f(x)<0；当x>0时，f(x)>0，故f(x)大致图象如下：令f(x)=t，若g(x)有且只有一个零点，则方程mt2−2t+1=0只有一个实根t满足t≥−1e，当m=0时，显然t=12满足，当m≠0时，Δ=4−4m≥0，∴ m≤1，当m=1时，方程只有一个根t=1满足，当m<1且m≠0时，若m>0，则方程两根t1+t2=2m >0，t1t2=1m>0，∴t1>0，t2>0，不满足题意，∴ m<0，则t1=2+√4−4m2m ，t2=2−√4−4m2m，∵t1t2=1m<0，∴t1，t2异号，只需2+√4−4m2m =1+√1−mm<−1e，解得m>−e2−2e，∴−e2−2e<m<0，综上所述．m的范围为(−e2−2e,0]∪{1}．故选C．16.【答案】B【考点】函数的零点函数的图象【解析】本题考查函数图象交点问题．【解答】解：∵ f(x+2)=f(x)，∴ T=2，∵当−1≤x≤1时，f(x)=2x2，即可平移获得f(x)图象，函数g(x)=f(x)−ln(x)零点个数即f(x)与ln|x|交点个数，可知f(x)与ln|x|均为偶函数，故只零考虑x>0部分，当x>0时，f(x)与ln|x|的图象如图所示，当x>0，ln|x|=2时，x=e2，∵7<e2<9，∴当x>0，共7个交点，故x<0部分也有7个交点，∴7+7=14（个）.故选B．二、填空题（本题共计 13 小题，每题 3 分，共计39分）17.【答案】1【考点】函数的零点【解析】先得出方程，求出方程的根，再判断零点的个数.【解答】解：函数f(x)=(3x −1)ln x 定义域为(0,+∞)，令f (x )=(3x −1)ln x =0，解得x =1，则零点个数为1个.故答案为：1.18.【答案】−1【考点】函数的零点【解析】函数f(x)=log 3(ax 2−x +a)有零点可化为方程ax 2−x +a =1有解，从而解得．【解答】解：根据题意，若函数 f(x)=log 2(x +a) 的零点为2，则f(2)=log 2(a +2)=0 ,即 a +2=1，解得 a =−1.故答案为：−1.19.【答案】1【考点】函数的零点【解析】令f(x)＝0，求出方程的根即函数的零点即可．【解答】函数f(x)的定义域是(0, 3)∪(3, +∞)，显然x +1>0，x −3≠0，令f(x)＝0，即(x+1)ln x x−3=0，即ln x ＝0，解得：x ＝1，20.【答案】 −√2【考点】函数的零点【解析】根据题意，在每个段上求值，检验，求出x 即可．【解答】当x ≤−32时，f(x)＝2x +3＝2，得x =−12，不成立；当−32<x <1时，x 2＝2，x =±√2，所以x =−√2；当x ≥1时，4x ＝2，x =12，不合题意；综上x =−√2，21.【答案】2【考点】函数的零点【解析】此题暂无解析【解答】此题暂无解答22.【答案】(1,4),(1,3]∪(4,+∞)【考点】函数零点的判定定理函数的零点【解析】此题暂无解析【解答】当λ=2时，由f (x )<0得{x −4<0x ≥2’或{x 2−4x +3<0x <2,’解得2≤x <4或1<x <2，所以f (x )<0的解集为(1,4)．由x −4=0得x =4，由x 2−4x +3=0得x =1或x =3，因为函数f(x )恰有2个零点，所以{4>λ1<λ3≥λ，或{4<λ1<λ3<λ，解得1<λ≤3或λ>4．本题考查分段函数的性质．求解分段函数问题，要根据自变量的值分别讨论函数在每一段上的性质．23.【答案】3【考点】利用导数研究函数的单调性函数的零点函数奇偶性的性质【解析】由题意得到函数关于x =1对称，且当x >1时，函数单调递增，x <1时函数单调递减，进而得到函数的零点个数.【解答】解：∵ y =f(x +1)为偶函数，∴ y =f(x)关于x =1对称，∵ f(2)=0，∴ f(0)=0.又(x −1)f′(x)＞0，∴ 当x >1时，函数单调递增，x <1时函数单调递减，∴ f(x)有两个零点，分别为0和2，又当x =1时，g(x)=(x −1)f(x)=0，∴ 函数g(x)=(x −1)f(x)的零点有0，1，2，共有三个零点.故答案为：3.24.【答案】x sin x (答案不唯一)【考点】函数的零点奇偶性与单调性的综合【解析】根据题意，分析可得则f (x )可以由三角函数变换得到，由此可得答案．【解答】解：根据题意，要求函数f (x )满足4个条件，则f (x )可以由三角函数函数变换得到，比如f (x )=x sin x ．故答案为：x sin x (答案不唯一)．25.【答案】4−√212【考点】函数的零点【解析】此题暂无解析【解答】解：根据题意，令t =f (x )，则易得f (t )=5的解为： t 1=4， t 2=−2， 当f (x )=4时，结合f (x )={2x −3,x ≥1x 2−x −1,x <1，得： x 1=72，x 2=1−√212， 当f (x )=−2时，结合f (x )={2x −3,x ≥1x 2−x −1,x <1，可知方程f (x )=−2无解． 故y =f [f (x )]−5的所有零点之和为： x 1+x 2=72+1−√212=8−√212=4−√214. 故答案为：4−√212. 26.【答案】g (x )=e x +e −x 2,−1或12 【考点】函数的零点函数奇偶性的性质【解析】此题暂无解析【解答】解：因为函数g (x )，ℎ(x )分别是定义在R 上的偶函数和奇函数，所以g (−x )=g (x )，ℎ(−x )=−ℎ(x ).因为g (x )+ℎ(x )=e x +sin x −x ①，所以g(−x)+ℎ(−x)=e−x−sin x+x，即g(x)−ℎ(x)=e−x−sin x+x②，①②联立，可解得g(x)=e x+e−x2.令F(x)=3|x|−λg(x)−2λ2，则F(−x)=F(x)，所以F(x)为偶函数，所以f(x)=F(x−2020)=3|x−2020|−λg(x−2020)−2λ2关于x=2020对称，因为f(x)有唯一的零点，所以f(x)的零点只能为x=2020.即f(2020)=1−λ−2λ2=0，解得λ=−1或λ=12.故答案为：g(x)=e x+e−x2；−1或12.27.【答案】−12<a<0【考点】利用导数研究与函数零点有关的问题分段函数的应用由函数零点求参数取值范围问题函数的零点【解析】无【解答】解：分析f(x)的图像以便于作图，当x>1时，f′(x)=e(1−ln x)x2，f′(x)>0⇒1<x<e，f′(x)<0⇒x>e，所以f(x)在(1,e)上单调递增，在(e,+∞)上单调递减，f(e)=e ln ee=1，且当x→+∞时f(x)>0且f(x)→0，所以x轴为曲线f(x)的水平渐近线；当x≤1时，f(x)=x2−1，所以f(x)在(−∞,0)上单调递减，在(0,1)上单调递增，且f(0)=−1．由此作图，图像如图，设f(x)=t，则由g(x)=f(f(x))−af(x)+a+1=0得f(t)−at+a+1=0⇒f(t)=at−a−1=a(t−1)−1，若函数g(x)=f(f(x))−af(x)+a+1恰有5个不同的零点，则关于x的方程g(x)=f(f(x))−af(x)+a+1=0恰有5个不同的实根，则结合函数y=f(x)的图像及直线y=a(x−1)−1得f(t)=a(t−1)−1恰有2个不等的实根，得t=t1=f(x)∈(−1,0)，t=t2=f(x)∈(0,1)，t1=t=f(x)∈(−1,0)有2个不等的实根，t=t2=f(x)∈(0,1)有3个不等的实根，∴−12<a<0．故答案为：−12<a<0．28.【答案】7【考点】函数的零点与方程根的关系函数的零点分段函数的应用【解析】无【解答】解：令g(x)=0可得：f(x)=1x ，画出y=f(x)和y=1x的图象可以，共有7个交点．故答案为：7.29.【答案】5【考点】函数的周期性函数的零点函数奇偶性的判断函数的图象【解析】由题可知f (x )为奇函数，且周期为4，在同一直角坐标系中作出函数f (x )与y =log 5|x|在R 上的图象，根据函数图形的交点个数即可得到函数y =f (x )−log 5|x|的零点个数.【解答】解：∵ f (−x )=−f (x )，∴ f (x )为奇函数.又∵ f (x +4)=f (x )，∴ f (x )的周期为4.根据x ∈[0,2)时，f (x )={x 2，0≤x <1，2−x ，1≤x <2，在同一直角坐标系中作出函数f (x )与y =log 5|x|在R 上的图象，如图所示，由图可知，共有5个交点，故函数y =f (x )−log 5|x|的零点个数为5个.故答案为：5.三、 解答题 （本题共计 1 小题 ，共计10分 ）30.【答案】（1）因为函数f(x)＝log a (5−2x)，所以令7−2x >0，所以函数f(x)的定义域为；（2）令f(x)＝0，即log a (5−4x)＝0，即5−4x ＝1，所以f(x)的零点为2； (Ⅲ)f(−6)＝log a 7，f(1)＝log a 3，当a >8时，函数y ＝log a x 为增函数，所以log a 7>log a 3，即f(−7)>f(1)； 当0<a <1时，函数y ＝log a x 为减函数，所以log a 6<log a 3，即f(−1)<f(1)．【考点】函数的零点【解析】此题暂无解析【解答】此题暂无解答。