导数与函数零点问题解题方法归纳

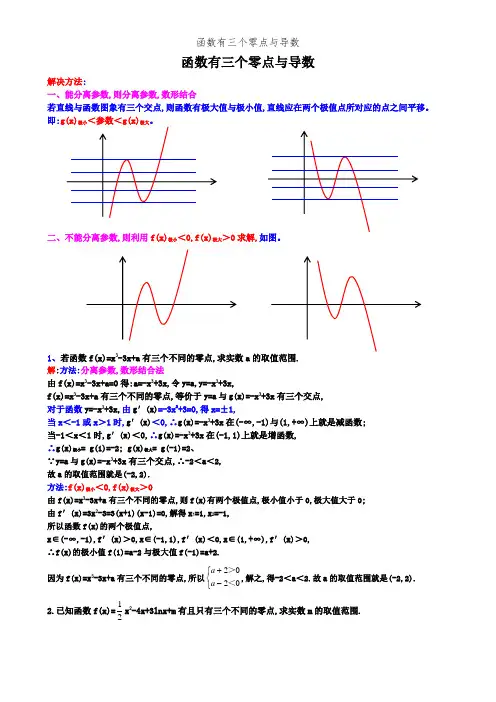
函数有三个零点与导数解:∵f(x)=12x 2-4x+3lnx+m,∴234())3134(x x x x f x x x x x-+--'=-+==（）, ∴f(x)在(0,1)上就是增函数,在(1,3)上就是减函数,在(3,+∞)上就是增函数;∴x=1就是f(x)的极大值点,x=3就是f(x)的极小值点。

又f(1)=12-4+m=m-72,f(3)=92-12+3ln3+m=m+3ln3-152,0 lim lim x x f x f x +→∞→=-∞=+∞（），（）, ∴函数f(x)=12x 2-4x+3lnx+m 有且只有三个不同的零点,等价于f(1)=12-4+m=m-72＞0且f(3)=92-12+3ln3+m=m+3ln3-152＜0,∴72＜m ＜152-3ln3.∴m 的取值范围为(72,152).3.(2016•东湖区月考)已知函数f(x)=x 2-(a+2)x+alnx,其中常数a ＞0.(1)当a ＞2时,求函数f(x)的单调递增区间;(2)当a=4时,若函数y=f(x)-m 有三个不同的零点,求m 的取值范围.本题第(2)问可以改为:(3)当a=4时,若函数y=f(x)-m 有且只有一个零点,求m 的取值范围.(4)当a=4时,若函数y=f(x)-m 有两个不同的零点,求m 的取值范围.(此问无解) 解:(1)由f(x)=x 2-(a+2)x+alnx 可知,函数的定义域为{x|x ＞0},且()()()2()2212)22(x a x a a x a x f x x a x x x-++--'-++＝＝＝,∵a ＞2,∴2a ＞1. 当0＜x ＜1或x ＞2a 时,f ′(x)＞0;当1＜x ＜2a 时,f ′(x)＜0, ∴f(x)的单调递增区间为(0,1),(2a ,+∞). (2)当a=4时,()21()()2x x f x x --'＝.当x 变化时,f ′(x),f(x)的变化情况如下表: x(0,1) 1 (1,2) 2 (2,+∞) f′(x)+ 0 - 0 + f(x) 单调递增 f(x)取极大值 单调递减 f(x)取极小值 单调递增∴f (x )极大值＝f (1)＝12−6×1+4ln 1＝−5,f (x )极小值＝f (2)＝22−6×2+4ln 2＝4ln 2−8.函数f(x)的图象大致如下:∴若函数y=f(x)-m 有三个不同的零点,则m ∈(4ln2-8,-5).4.已知a＞0,函数f(x)=ax2-2ax+2lnx,g(x)=f(x)-2x. (Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程; (Ⅱ)讨论g(x)的单调性;(Ⅲ)当a＞1时,若函数h(x)=g(x)+5+1a有三个不同的零点,求实数a的取值范围.5.(2015•连云港三模)函数f(x)=a x -x 2(a ＞1)有三个不同的零点,则实数a 的取值范围就是 . 解:先画草图大致分析一下:令y=a x (a ＞1),y=x 2,在同一坐标系中画出它们的图象,当x ＜0时,显然它们的图象,有一个交点,即f(x)=a x -x 2(a ＞1)有一个零点。

导数中两种零点问题解决方法导数中的零点问题是指函数在其中一点的导数为零。

解决导数零点问题的方法有两种：一种是解析法，一种是数值法。

一、解析法解析法是指使用数学知识和方法，通过分析函数的性质来求解导数的零点。

解析法包括以下几种常见的方法：1.1.方程法方程法是根据导数的定义，将函数的导数表达式设置为零，得到一个方程，从而求解出导数的零点。

具体步骤如下：1.将函数的导数表达式设置为零，得到一个方程。

2.解方程，求出方程的根。

3.将根带入原函数，计算出在根处的函数值。

1.2.倒数法倒数法是指使用导数的倒数来求解导数的零点。

具体步骤如下：1.对函数进行求导，并求出导数的表达式。

2.求导数的倒数，得到一个新的函数。

3.使用方程法求解导数的倒数的零点。

4.将零点带入原函数，计算出在零点处的函数值。

1.3.函数性质法函数性质法是指通过分析函数的图像和性质来求解导数的零点。

具体步骤如下：1.根据函数的图像和性质，确定导数的零点的位置。

2.使用方程法求解导数的零点，得到具体的数值。

3.将零点带入原函数，计算出在零点处的函数值。

二、数值法数值法是指使用数值计算的方法来求解导数的零点。

数值法包括以下几种常见的方法：2.1.二分法二分法是一种迭代求根的方法，通过函数在区间内取值的正负性来确定区间，并通过不断缩小区间的范围来求解导数的零点。

具体步骤如下：1.根据函数的图像和性质，选择一个初值区间，并确定函数在区间内的正负性。

2.通过计算区间的中点，并确定中点的函数值的正负性，来缩小区间。

3.不断迭代上述步骤，直到区间的宽度满足要求，得到导数的零点的近似值。

2.2.切线法切线法是使用切线近似原曲线的方法，通过迭代求解切线与横轴交点的坐标，来求解导数的零点。

1.根据函数的图像和性质，选取一个初始点，并求出该点处的导数值。

2.过初始点作函数图像的切线，并求出切线方程。

3.求出切线与横轴的交点的坐标，并将该点作为新的初始点。

4.重复上述步骤，直到满足迭代终止条件，得到导数的零点的近似值。

导数与函数的零点一、知识梳理1.利用导数确定函数零点或方程根个数的常用方法(1)构建函数g(x)(要求g′(x)易求，g′(x)＝0可解)，转化确定g(x)的零点个数问题求解，利用导数研究该函数的单调性、极值，并确定定义区间端点值的符号(或变化趋势)等，画出g(x)的图象草图，数形结合求解函数零点的个数．(2)利用零点存在性定理：先用该定理判断函数在某区间上有零点，然后利用导数研究函数的单调性、极值(最值)及区间端点值符号，进而判断函数在该区间上零点的个数．二、例题精讲 + 随堂练习考点一判断零点的个数【例1】(2019·青岛期中)已知二次函数f(x)的最小值为－4，且关于x的不等式f(x)≤0的解集为{x|－1≤x≤3，x∈R}．(1)求函数f(x)的解析式；(2)求函数g(x)＝f(x)x－4ln x的零点个数．解(1)∵f(x)是二次函数，且关于x的不等式f(x)≤0的解集为{x|－1≤x≤3，x∈R}，∴设f(x)＝a(x＋1)(x－3)＝ax2－2ax－3a，且a>0. ∴f(x)min＝f(1)＝－4a＝－4，a ＝1.故函数f(x)的解析式为f(x)＝x2－2x－3.(2)由(1)知g(x)＝x2－2x－3x－4ln x＝x－3x－4ln x－2，∴g(x)的定义域为(0，＋∞)，g′(x)＝1＋3x2－4x＝(x－1)(x－3)x2，令g′(x)＝0，得x1＝1，x2＝3.当x变化时，g′(x)，g(x)的取值变化情况如下表：当0<x≤3时，g(x)≤g(1)＝－4<0，当x>3时，g(e5)＝e5－3e5－20－2>25－1－22＝9>0.又因为g(x)在(3，＋∞)上单调递增，因而g(x)在(3，＋∞)上只有1个零点，故g(x)仅有1个零点．【训练1】已知函数f(x)＝e x－1，g(x)＝x＋x，其中e是自然对数的底数，e＝2.718 28….(1)证明：函数h(x)＝f(x)－g(x)在区间(1，2)上有零点；(2)求方程f(x)＝g(x)的根的个数，并说明理由．(1)证明由题意可得h(x)＝f(x)－g(x)＝e x－1－x－x，所以h(1)＝e－3<0，h(2)＝e2－3－2>0，所以h(1)h(2)<0，所以函数h(x)在区间(1，2)上有零点．(2)解由(1)可知h(x)＝f(x)－g(x)＝e x－1－x－x.由g(x)＝x＋x知x∈[0，＋∞)，而h(0)＝0，则x＝0为h(x)的一个零点．又h(x)在(1，2)内有零点，因此h(x)在[0，＋∞)上至少有两个零点．h′(x)＝e x－12x－12－1，记φ(x)＝e x－12x－12－1，则φ′(x)＝e x＋14x－32.当x∈(0，＋∞)时，φ′(x)>0，因此φ(x)在(0，＋∞)上单调递增，易知φ(x)在(0，＋∞)内至多有一个零点，即h(x)在[0，＋∞)内至多有两个零点，则h(x)在[0，＋∞)上有且只有两个零点，所以方程f(x)＝g(x)的根的个数为2.考点二已知函数零点个数求参数的取值范围【例2】函数f(x)＝ax＋x ln x在x＝1处取得极值．(1)求f(x)的单调区间；(2)若y＝f(x)－m－1在定义域内有两个不同的零点，求实数m的取值范围．解(1)函数f(x)＝ax＋x ln x的定义域为(0，＋∞)．f′(x)＝a＋ln x＋1，因为f′(1)＝a＋1＝0，解得a＝－1，当a＝－1时，f(x)＝－x＋x ln x，即f′(x)＝ln x，令f′(x)>0，解得x>1；令f′(x)<0，解得0<x<1.所以f(x)在x＝1处取得极小值，f(x)的单调递增区间为(1，＋∞)，单调递减区间为(0，1)．(2)y＝f(x)－m－1在(0，＋∞)内有两个不同的零点，可转化为y＝f(x)与y＝m＋1图象有两个不同的交点．由(1)知，f(x)在(0，1)上单调递减，在(1，＋∞)上单调递增，f(x)min＝f(1)＝－1，由题意得，m＋1>－1，即m>－2，①当0<x<e时，f(x)＝x(－1＋ln x)<0；当x>e时，f(x)>0.当x>0且x→0时，f(x)→0；当x→＋∞时，显然f(x)→＋∞.由图象可知，m＋1<0，即m<－1，②由①②可得－2<m<－1.所以m的取值范围是(－2，－1)．【训练2】 已知函数f (x )＝e x ＋ax －a (a ∈R 且a ≠0)．(1)若f (0)＝2，求实数a 的值，并求此时f (x )在[－2，1]上的最小值； (2)若函数f (x )不存在零点，求实数a 的取值范围． 解 (1)由题意知，函数f (x )的定义域为R ， 又f (0)＝1－a ＝2，得a ＝－1，所以f (x )＝e x －x ＋1，求导得f ′(x )＝e x －1.易知f (x )在[－2，0]上单调递减，在[0，1]上单调递增， 所以当x ＝0时，f (x )在[－2，1]上取得最小值2. (2)由(1)知f ′(x )＝e x ＋a ，由于e x >0， ①当a >0时，f ′(x )>0，f (x )在R 上是增函数， 当x >1时，f (x )＝e x ＋a (x －1)>0； 当x <0时，取x ＝－1a ， 则f ⎝ ⎛⎭⎪⎫－1a <1＋a ⎝ ⎛⎭⎪⎫－1a －1＝－a <0. 所以函数f (x )存在零点，不满足题意． ②当a <0时，令f ′(x )＝0，得x ＝ln(－a )． 在(－∞，ln(－a ))上，f ′(x )<0，f (x )单调递减， 在(ln (－a )，＋∞)上，f ′(x )>0，f (x )单调递增， 所以当x ＝ln(－a )时，f (x )取最小值．函数f (x )不存在零点，等价于f (ln(－a ))＝e ln(－a )＋a ln(－a )－a ＝－2a ＋a ln(－a )>0，解得－e 2<a <0.综上所述，所求实数a 的取值范围是(－e 2，0)．考点三 函数零点的综合问题 【例3】 设函数f (x )＝e 2x －a ln x . (1)讨论f (x )的导函数f ′(x )零点的个数； (2)证明：当a >0时，f (x )≥2a ＋a ln 2a .(1)解 f (x )的定义域为(0，＋∞)，f ′(x )＝2e 2x －ax (x >0)． 当a ≤0时，f ′(x )>0，f ′(x )没有零点；当a >0时，因为y ＝e 2x 单调递增，y ＝－ax 单调递增， 所以f ′(x )在(0，＋∞)上单调递增．又f ′(a )>0，假设存在b 满足0<b <a 4时，且b <14，f ′(b )<0， 故当a >0时，f ′(x )存在唯一零点．(2)证明 由(1)，可设f ′(x )在(0，＋∞)上的唯一零点为x 0， 当x ∈(0，x 0)时，f ′(x )<0；当x ∈(x 0，＋∞)时，f ′(x )>0. 故f (x )在(0，x 0)上单调递减，在(x 0，＋∞)上单调递增， 所以当x ＝x 0时，f (x )取得最小值，最小值为f (x 0)． 由于2e2x 0－ax 0＝0，所以f (x 0)＝a 2x 0＋2ax 0＋a ln 2a ≥2a ＋a ln 2a .故当a >0时，f (x )≥2a ＋a ln 2a .【训练3】 (2019·天津和平区调研)已知函数f (x )＝ln x －x －m (m <－2，m 为常数)． (1)求函数f (x )在⎣⎢⎡⎦⎥⎤1e ，e 的最小值；(2)设x 1，x 2是函数f (x )的两个零点，且x 1<x 2，证明：x 1·x 2<1.(1)解 f (x )＝ln x －x －m (m <－2)的定义域为(0，＋∞)，且f ′(x )＝1－xx ＝0， ∴x ＝1.当x ∈(0，1)时，f ′(x )>0，所以y ＝f (x )在(0，1)递增； 当x ∈(1，＋∞)时，f ′(x )<0，所以y ＝f (x )在(1，＋∞)上递减．且f ⎝ ⎛⎭⎪⎫1e ＝－1－1e －m ，f (e)＝1－e －m ， 因为f ⎝ ⎛⎭⎪⎫1e －f (e)＝－2－1e ＋e>0， 函数f (x )在⎣⎢⎡⎦⎥⎤1e ，e 的最小值为1－e －m .(2)证明 由(1)知x 1，x 2满足ln x －x －m ＝0，且0<x 1<1，x 2>1， ln x 1－x 1－m ＝ln x 2－x 2－m ＝0， 由题意可知ln x 2－x 2＝m <－2<ln 2－2. 又由(1)可知f (x )＝ln x －x 在(1，＋∞)递减，故x 2>2， 所以0<x 1，1x 2<1.则f (x 1)－f ⎝ ⎛⎭⎪⎫1x 2＝ln x 1－x 1－⎝ ⎛⎭⎪⎫ln 1x 2－1x 2 ＝ln x 2－x 2－⎝ ⎛⎭⎪⎫ln 1x 2－1x 2 ＝－x 2＋1x 2＋2ln x 2.令g (x )＝－x ＋1x ＋2ln x (x >2)，则g ′(x )＝－1－1x 2＋2x ＝－x 2＋2x －1x 2＝－（x －1）2x 2≤0，当x >2时，g (x )是减函数，所以g (x )<g (2)＝－32＋ln 4.因32－ln 4＝ln e 324>ln 2.56324＝ln （1.62）324＝ln 1.634＝ln4.0964>ln 1＝0，∴g (x )<0，所以当x >2时，f (x 1)－f ⎝ ⎛⎭⎪⎫1x 2<0， 即f (x 1)<f ⎝ ⎛⎭⎪⎫1x 2.因为0<x 1，1x 2<1，f (x )在(0，＋∞)上单调递增． 所以x 1<1x 2，故x 1x 2<1.三、课后练习1.直线x ＝t 分别与函数f (x )＝e x ＋1的图象及g (x )＝2x －1的图象相交于点A 和点B ，则|AB |的最小值为________. 解析 由题意得，|AB |＝|e t ＋1－(2t －1)| ＝|e t －2t ＋2|，令h (t )＝e t －2t ＋2，则h ′(t )＝e t －2，所以h (t )在(－∞，ln 2)上单调递减， 在(ln 2，＋∞)上单调递增， 所以h (t )min ＝h (ln 2)＝4－2ln 2>0， 即|AB |的最小值是4－2ln 2. 答案 4－2ln 22.若函数f (x )＝ax －ae x ＋1(a <0)没有零点，则实数a 的取值范围为________.解析 f ′(x )＝a e x －（ax －a ）e x e 2x ＝－a （x －2）e x (a <0).当x <2时，f ′(x )<0；当x >2时，f ′(x )>0， ∴当x ＝2时，f (x )有极小值f (2)＝ae 2＋1.若使函数f (x )没有零点，当且仅当f (2)＝ae 2＋1>0， 解之得a >－e 2，因此－e 2<a <0. 答案 (－e 2，0)3.(2019·保定调研)已知函数f (x )＝a 6x 3－a 4x 2－ax －2的图象过点A ⎝ ⎛⎭⎪⎫4，103.(1)求函数f (x )的单调递增区间；(2)若函数g (x )＝f (x )－2m ＋3有3个零点，求m 的取值范围. 解 (1)因为函数f (x )＝a 6x 3－a 4x 2－ax －2的图象过点A ⎝ ⎛⎭⎪⎫4，103， 所以32a 3－4a －4a －2＝103，解得a ＝2，即f (x )＝13x 3－12x 2－2x －2， 所以f ′(x )＝x 2－x －2. 由f ′(x )>0，得x <－1或x >2.所以函数f (x )的单调递增区间是(－∞，－1)，(2，＋∞). (2)由(1)知f (x )极大值＝f (－1)＝－13－12＋2－2＝－56， f (x )极小值＝f (2)＝83－2－4－2＝－163，由数形结合，可知要使函数g (x )＝f (x )－2m ＋3有三个零点， 则－163<2m －3<－56，解得－76<m <1312.所以m 的取值范围为⎝ ⎛⎭⎪⎫－76，1312.4.已知函数f (x )的定义域为[－1，4]，部分对应值如下表：f (x )的导函数y ＝f ′(x )的图象如图所示.当1<a <2时，函数y ＝f (x )－a 的零点的个数为( )A.1B.2C.3D.4解析 根据导函数图象，知2是函数的极小值点，函数y ＝f (x )的大致图象如图所示.由于f (0)＝f (3)＝2，1<a <2，所以y ＝f (x )－a 的零点个数为4. 答案 D5.设函数f (x )＝ln x ＋m x (m >0)，讨论函数g (x )＝f ′(x )－x3零点的个数. 解 函数g (x )＝f ′(x )－x 3＝1x －m x 2－x3(x >0)， 令g (x )＝0，得m ＝－13x 3＋x (x >0). 设h (x )＝－13x 3＋x (x >0)，所以h ′(x )＝－x 2＋1＝－(x －1)(x ＋1).当x ∈(0，1)时，h ′(x )>0，此时h (x )在(0，1)内单调递增；当x ∈(1，＋∞)时，h ′(x )<0，此时h (x )在(1，＋∞)内单调递减.所以当x ＝1时，h (x )取得极大值h (1)＝－13＋1＝23. 令h (x )＝0，即－13x 3＋x ＝0，解得x ＝0(舍去)或x ＝ 3. 作出函数h (x )的大致图象(如图)，结合图象知：①当m >23时，函数y ＝m 和函数y ＝h (x )的图象无交点.②当m ＝23时，函数y ＝m 和函数y ＝h (x )的图象有且仅有一个交点. ③当0<m <23时，函数y ＝m 和函数y ＝h (x )的图象有两个交点.综上所述，当m >23时，函数g (x )无零点；当m ＝23时，函数g (x )有且仅有一个零点；当0<m <23时，函数g (x )有两个零点.6.(2018·江苏卷改编)若函数f (x )＝2x 3－ax 2＋1(a ∈R )在区间(0，＋∞)内有且只有一个零点，求f (x )在[－1，1]上的最大值与最小值的和. 解 f ′(x )＝6x 2－2ax ＝2x (3x －a )(a ∈R )， 当a ≤0时，f ′(x )>0在(0，＋∞)上恒成立， 则f (x )在(0，＋∞)上单调递增，又f (0)＝1， 所以此时f (x )在(0，＋∞)内无零点，不满足题意. 当a >0时，由f ′(x )>0得x >a 3，由f ′(x )<0得0<x <a3，则f (x )在⎝ ⎛⎭⎪⎫0，a 3上单调递减，在⎝ ⎛⎭⎪⎫a 3，＋∞上单调递增，又f (x )在(0，＋∞)内有且只有一个零点，所以f ⎝ ⎛⎭⎪⎫a 3＝－a 327＋1＝0，得a ＝3，所以f (x )＝2x 3－3x 2＋1，则f ′(x )＝6x (x －1)， 当x ∈(－1，0)时，f ′(x )>0，f (x )单调递增， 当x ∈(0，1)时，f ′(x )<0，f (x )单调递减. 则f (x )max ＝f (0)＝1，f (－1)＝－4，f (1)＝0，则f (x )min ＝－4，所以f (x )在[－1，1]上的最大值与最小值的和为－3.7.已知函数f (x )＝ax ＋ln x ，其中a 为常数. (1)当a ＝－1时，求f (x )的单调递增区间；(2)当0<－1a <e 时，若f (x )在区间(0，e)上的最大值为－3，求a 的值； (3)当a ＝－1时，试推断方程|f (x )|＝ln x x ＋12是否有实数根. 解 (1)由已知可知函数f (x )的定义域为{x |x >0}， 当a ＝－1时，f (x )＝－x ＋ln x (x >0)，f ′(x )＝1－xx (x >0)； 当0<x <1时，f ′(x )>0；当x >1时，f ′(x )<0. 所以f (x )的单调递增区间为(0，1).(2)因为f ′(x )＝a ＋1x (x >0)，令f ′(x )＝0，解得x ＝－1a ； 由f ′(x )>0，解得0<x <－1a ；由f ′(x )<0，解得－1a <x <e.从而f (x )的单调递增区间为⎝ ⎛⎭⎪⎫0，－1a ，递减区间为⎝ ⎛⎭⎪⎫－1a ，e ，所以，f (x )max ＝f ⎝ ⎛⎭⎪⎫－1a ＝－1＋ln ⎝ ⎛⎭⎪⎫－1a ＝－3.解得a ＝－e 2.(3)由(1)知当a ＝－1时，f (x )max ＝f (1)＝－1， 所以|f (x )|≥1.令g (x )＝ln x x ＋12，则g ′(x )＝1－ln x x 2. 当0<x <e 时，g ′(x )>0； 当x >e 时，g ′(x )<0.从而g (x )在(0，e)上单调递增，在(e ，＋∞)上单调递减. 所以g (x )max ＝g (e)＝1e ＋12<1， 所以，|f (x )|>g (x )，即|f (x )|>ln x x ＋12，所以，方程|f (x )|＝ln x x ＋12没有实数根.。

导数隐零点问题处理的8大技巧(附30道经典题目)导数隐零点问题处理的8大技巧如下：1.分类讨论：对于含参数的零点问题，常常需要根据参数的不同取值范围进行分类讨论。

2.构造函数：利用导数研究函数的单调性，进而研究不等式恒成立问题。

3.分离参数：通过分离参数将参数与变量分开，转化为求最值问题。

4.数形结合：利用数形结合思想，将函数图像与x轴的交点问题转化为求函数的最值问题。

5.转化与化归：将复杂问题转化为简单问题，将陌生问题转化为熟悉问题。

6.构造法：通过构造新的函数或方程，将问题转化为已知的问题进行求解。

7.放缩法：通过对不等式进行放缩，将问题转化为易于处理的形式。

8.判别式法：通过引入判别式，将方程问题转化为二次方程的判别式问题。

以下是30道经典题目，以供练习：1.已知函数f(x)=x3−3x2+5，则f(x)的单调递增区间为( )A.(−∞,1)和(2,+∞)B.(−∞,−1)和(1,+∞)C.(−∞,−1)和(2,+∞)D.(−∞,2)和(1,+∞)2.已知函数f(x)=x3−3x2+5，则f(x)在区间[−2,3]上的最大值是____．3.已知函数f(x)=x3+ax2+bx+c在x=1和x=−21时取极值．(1)求a，b的值；(2)求函数极值．4. 已知函数f(x)=x3−3ax2+4，若x∈[0,2]时，f(x)的最大值为417，求实数a的取值范围．5. 已知函数f(x)=ln x−mx+m有唯一的零点，则实数m的取值范围是____．6. 已知函数 f(x) = x^3 - 3ax^2 + 3x + 1，若 x ∈ [0,1] 时，f(x) ≤ f(0) 恒成立，则 m 的取值范围是 _______．7. 已知函数 f(x) = ax^3 + bx^2 - 3x (a、b ∈ Z) 在 x = ±1 和x = ±2 时取极值．(1) 求 f(x) 的解析式；(2) 求 f(x) 的单调区间和极值；8. 已知函数 f(x) = x^3 + ax^2 + bx + c 在 x = ±1 和 x = ±3时取极值．(1) 求 a，b 的值；(2) 求 f(x) 的单调区间和极值．1.已知函数 f(x) = x^3 - 3x^2 + 4 在 [0,3] 上的最大值和最小值分别为 M, N，则 M + N = _______．2.设f(x)=x3−3x2+4，则f(−x)+f(x)的值等于____3.已知函数f(x)=x3−3x2+4，则f(x)在(−3,2)上的最大值是____．4.已知函数f(x)=x3−3x2+4，则f(x)在区间[−1,3]上的最大值是____．5.已知函数f(x)=x3−3ax2+bx+c在x=±1时取极值，且函数y=f(x)图象过原点．(1) 求函数y=f(x)的表达式；(2) 求函数的单调区间和极值；14. 已知函数 f(x) = x^3 - 3ax^2 + bx 在 x = -1 和 x = 3 时取极值．(1) 求 a，b 的值；(2) 求 f(x) 在区间 [-2,4] 上的最大值和最小值．15. 已知函数 f(x) = ax^3 + bx^2 + c 在 x = ±1 和 x = ±2 时取极值．(1) 求 a，b 的值；(2) 若 f(x) 的最大值为 8，求 c 的值．16. 已知函数 f(x) = ax^3 + bx^2 + c 在 x = ±1 和 x = ±√2 时取极值，且 f(-2) = -4．(1) 求 a，b，c 的值；(2) 求 f(x) 在区间 [-3,3] 上的最大值和最小值．17. 已知函数 f(x) = x^3 - 3ax^2 + b (a > 0)，若 f(x) 在区间[-1,0] 上是减函数，则 a 的取值范围是 _______．18. 若关于 x 的方程 x^3 - 3ax + a^3 = 0 有实根，则实数 a 的取值范围是 _______．19. 若关于 x 的方程 x^3 - ax^2 + b = 0 有三个不同的实根，则 a，b 应满足的条件是 _______．20. 若关于 x 的方程 x^3 - ax^2 + b = 0 有三个不同的实根，则 b应满足的条件是 _______．1.函数 f(x) = x^3 - 3x^2 + 4 在区间 [-1,3] 上的最大值和最小值分别为 _______．2.已知函数 f(x) = x^3 - 3x^2 + 4，若实数 x，y 满足 f(x) +3x^2 ≤ f(y) + 3y^2，则 x + y 的取值范围是 _______．3.已知函数 f(x) = x^3 - 3x^2 + 4，若实数 x，y 满足 f(x) ≤f(y) + 3，则 x + y 的取值范围是 _______．4.若关于 x 的方程 x^3 - ax^2 + b = 0 有三个不同的实根，则a，b 应满足的条件是 _______．5.已知函数 f(x) = x^3 - 3ax^2 + b 在 x = -1 和 x = 3 时取极值．(1) 求 a，b 的值；(2) 求 f(x) 在区间 [-3,3] 上的最大值和最小值．26. 若关于 x 的方程 x^3 - ax^2 + b = 0 有三个不同的实根，则 b 应满足的条件是 _______．27. 若关于 x 的方程 x^3 - ax^2 + b = 0 有两个不同的实根，则 a，b 应满足的条件是 _______．28. 若关于 x 的方程 x^3 - ax^2 + b = 0 有两个不同的实根，则 a，b 应满足的条件是 _______．29. 若关于 x 的方程 x^3 - ax^2 + b = 0 有两个相等的实根，则 a，b 应满足的条件是 _______．30. 若关于 x 的方程 x^3 - ax^2 + b = 0 有三个相等的实根，则 a，b 应满足的条件是 _______．。

导数中的零点问题解决方法解决零点问题，需要采用数形结合思想，根据函数的图像或者趋势图像找出符合题意的条件即可，因此用导数判断出单调性作出函数图像或趋势图像至关重要。

一、能直接分离参数的零点题目此类问题较为简单，分离之后函数无参数，则可作出函数的准确图像，然后上下移动参数的值，看直线与函数交点个数即可。

例1.已知函数(),()ln a f x x g x x x =+=，若关于x 的方程2()()2g x f x e x =-只有一个实数根，求a 的值。

解析：22()ln ()22g x x f x e a x ex x x =-⇒=-+，令2ln ()2x h x x ex x=-+，'21ln ()22x h x x e x-=-+，令'()0h x =，则x e = 当0x e <<时，'()0h x >，()h x 单调递增；当x e >时，'()0h x <，()h x 单调递 减，2max 1()()h x h e e e ==+ —注意这里()h x 的单调性不是硬解出来的，因为你会发现'()h x 的式子很复杂，但是如果把()h x 当成两个函数的和，即2ln (),()2x m x n x x ex x==-+，此时(),()m x n x 的单调性和极值点均相同，因此可以整体判断出()h x 的单调性和极值点。

所以21a e e=+（注意：有一个根转化为图像只有一个交点即可） 二、不能直接分离参数的零点问题（包括零点个数问题）这里需要注意几个转化，以三次函数为例，若三次函数有三个不同的零点，则函数必定有两个极值点，且极大值和极小值之积为负数，例如()f x 在区间(0,1)上有零点，此时并不能确定零点的个数，只能说明至少有一个零点，若函数在区间上单调，只需要用零点存在性定理即可，但是若函数在区间上不单调，则意味着()f x 在区间(0,1)上存在极值点。

(1) 若函数f(x)在(a , a + 1)上有极值，求实数 a 的取值范围； ⑵若关于x 的方程f(x)= X 2— 2x + k 有实数解，求实数 k 的取值范围. ［方法演示］In x解：⑴因为 f ' (x)=— ~x 2",当 Ovxvl 时，f ' (x)>0 ；当 x>1 时，f ' (x)<0,所以函数 f(x) 在(0,1)上单调递增，在(1,+^)上单调递减，故函数 f(x)的极大值点为 x = 1,所以avlva + 1,即0<a<1，故所求实数a 的取值范围是(0,1).(2) 方程f(x)= x 2— 2x + k 有实数解， 即f(x) — x 2+ 2x = k 有实数解. 设 g(x)= f(x) — x 2 + 2x , 则 g ' (x)= 2(1 — x)—哼.x接下来，需求函数 g(x)的单调区间，所以需解不等式 g ' (x)>0及g ' (x)< 0,因而需解方程g ' (x)= 0.但此方程不易求解，所以我们可以先猜后解.可得 g ' (1) = 0，且当 0<x<1 时，g ' (x)>0，当 x>1 时，g ' (x)<0，所以函数 g(x)在(0,1) 上单调递增，在(1, +)上单调递减.所以 g(x)max = g(1) = 2•当 X T 0 时，g(X)T —8 ；当 + ^ 时，g(x)^ — ，所以函数 g(x)的值域是(—^, 2］,所以所求实数 k 的取值范围是(—^, 2］.［解题师说］当所求的导函数解析式中出现 In x 时，常猜x = 1;当函数解析式中出现e x 时，常猜x=0 或 x = In x.［应用体验］11 .函数f(x) = e +尹2— (2 + In 2)x 的最小值为 ________ . 解析：f ' (x)= e x + x — (2 + In 2).接下来，需求函数 f(x)的单调区间，所以需解不等式 f ' (x)>0及f ' (x)< 0,因而需解方程f ' (x) = 0.但此方程不易求解，所以我们可以先猜后解.易知f ' (x)是增函数，所以方程f ' (x) = 0至多有一个实数根，且可观察出此实数根就是In 2,所以函数f(x)在(—^, In 2)上是减函数，在(In 2, +)上是增函数，三招妙解导数零点问题［典例］设 f(x) = 1 + In x所以f(x)min= f(In 2) = 2 —2In 2 —*n22.［典例］(2015全国卷)设函数f(x)= e-aln x.⑴讨论f(x)的导函数f' (x)零点的个数；2(2)证明：当a>0 时，f(x)> 2a+ aln .a［方法演示］解：⑴法一：f' (x)= 2e2x- x(x>0) •当a w 0时，f' (x)>0, f' (x)没有零点.当a>0 时，设u(x)= e2x, v(x)=--,因为u(x)= e2x在(0,+s)上单调递增，v(x)=-旦在(0,+s)上单调递增，所以f' (x)在(0,+s)上单调递增.a 1又f' (a)>0，当b满足0<b<4且b<4时，f(b)<°,所以当a>0时，f' (x)存在唯一零点.法二：f' (x)= 2e2x-a(x>0).令方程f' (x)= 0，得a= 2xe2x(x>0).因为函数ax)= 2x(x>0), h(x)= e2x(x>0)均是函数值为正值的增函数，所以由增函数的定义可证得函数u(x)= 2xe2x(x>0)也是增函数，其值域是(0 ,+^).由此可得，当a w 0时，f' (x)无零点；当a>0时，f' (x)有唯一零点.(2)证明：由⑴可设f' (x)在(0, + g)上的唯一零点为x o.当x € (0, x°)时,f' (x)<0 ;当x € (x°,+ g)时，f' (x)>0.所以f(x)在(0, x°)上单调递减，在(X0,+g)上单调递增，当且仅当x= X。

导函数零点问题一．方法综述导数是研究函数性质的有力工具，其核心又是由导数值的正、负确定函数的单调性．应用导数研究函数的性质或研究不等式问题时，绕不开研究()f x 的单调性，往往需要解方程()0f x '＝.若该方程不易求解时，如何继续解题呢？在前面专题中介绍的“分离参数法”、“构造函数法”等常见方法的基础上，本专题举例说明“三招”妙解导函数零点问题.二．解题策略类型一 察“言”观“色”，“猜”出零点【例1】【2020·福建南平期末】已知函数()()21e x f x x ax =++. （1）讨论()f x 的单调性；（2）若函数()()21e 1x g x x mx =+--在[)1,-+∞有两个零点，求m 的取值范围. 【分析】（1）首先求出函数的导函数因式分解为()()()11e xf x a x x =++'+，再对参数a 分类讨论可得； （2）依题意可得()()21e xg x m x =+'-，当0m 函数在定义域上单调递增，不满足条件；当0m >时，由（1）得()g x '在[)1,-+∞为增函数，因为()01g m '=-，()00g =.再对1m =，1m ，01m <<三种情况讨论可得.【解析】（1）因为()()21x f x x ax e =++，所以()()221e xf x x a x a ⎡⎤=+++⎣⎦'+， 即()()()11e xf x a x x =++'+. 由()0f x '=，得()11x a =-+，21x =-.①当0a =时，()()21e 0x f x x =+'，当且仅当1x =-时，等号成立.故()f x 在(),-∞+∞为增函数.②当0a >时，()11a -+<-，由()0f x >′得()1x a <-+或1x >-，由()0f x <′得()11a x -+<<-；所以()f x 在()(),1a -∞-+，()1,-+∞为增函数，在()()1,1a -+-为减函数.③当0a <时，()11a -+>-，由()0f x >′得()1x a >-+或1x <-，由()0f x <′得()11x a -<<-+；所以()f x 在(),1-∞-，()()1,a -++∞为增函数，在()()1,1a --+为减函数.综上，当0a =时，()f x 在为(),-∞+∞增函数；当0a >时，()f x 在()(),1a -∞-+，()1,-+∞为增函数，在()()1,1a -+-为减函数；当0a <时，()f x 在(),1-∞-，()()1,a -++∞为增函数，在()()1,1a --+为减函数.（2）因为()()21e 1x g x x mx =+--，所以()()21e x g x m x =+'-， ①当0m 时，()0g x '，()g x 在[)1,-+∞为增函数，所以()g x 在[)1,-+∞至多一个零点.②当0m >时，由（1）得()g x '在[)1,-+∞为增函数.因为()01g m '=-，()00g =.（ⅰ）当1m =时，()00g '=，0x >时，()0g x '>，10x -<<时，()0g x '<；所以()g x 在[)1,0-为减函数，在[)0,+∞为增函数，()()min 00g x g ==.故()g x 在[)1,-+∞有且只有一个零点.（ⅱ）当1m 时，()00g '<，()()210m g m e m m '=+->，()00,x m ∃∈，使得()00g x '=， 且()g x 在[)01,x -为减函数，在()0,x +∞为增函数.所以()()000g x g <=，又()()()22221e 1110m g m m m m m =+-->+--=， 根据零点存在性定理，()g x 在()0,x m 有且只有一个零点.又()g x 在[)01,x -上有且只有一个零点0.故当1m 时，()g x 在[)1,-+∞有两个零点.（ⅲ）当01m <<时，()01g m -'=-<，()00g '>，()01,0x ∃∈-，使得()00g x '=，且()g x 在[)01,x -为减函数，在()0,x +∞为增函数.因为()g x 在()0,x +∞有且只有一个零点0，若()g x 在[)1,-+∞有两个零点，则()g x 在[)01,x -有且只有一个零点.又()()000g x g <=，所以()10g -即()2110e g m -=+-，所以21e m -， 即当211em -<时()g x 在[)1,-+∞有两个零点. 综上，m 的取值范围为211em -< 【指点迷津】1.由于导函数为超越函数，无法利用解方程的方法，可以在观察方程结构的基础上大胆猜测.一般地，当所求的导函数解析式中出现ln x 时，常猜x ＝1；当函数解析式中出现e x时，常猜x ＝0或x ＝ln x .2.例题解析中灵活应用了分离参数法、构造函数法【举一反三】 【2020·山西吕梁期末】已知函数221()ln ()x f x a x a R x-=-∈. （1）讨论()f x 的单调性；（2）设()sin x g x e x =-，若()()()()2h x g x f x x =-且()y h x =有两个零点，求a 的取值范围. 【解析】（1）()f x 的定义域为(0,)+∞，1()2ln f x x a x x =--， 21()2f x x '=+2221a x ax x x-+-=， 对于2210x ax -+=，28a ∆=-，当[a ∈-时，()0f x '≥，则()f x 在(0,)+∞上是增函数.当(,a ∈-∞-时，对于0x >，有()0f x '>，则()f x 在(0,)+∞上是增函数.当)a ∈+∞时，令()0f x '>，得04a x <<或4a x >，令()0f x '<，得44a a x <<，所以()f x 在，)+∞上是增函数，在(44a a 上是减函数.综上，当(,a ∈-∞时，()f x 在(0,)+∞上是增函数；当)a ∈+∞时，()f x 在(0,)4a -，()4a ++∞上是增函数，在(44a a 上是减函数. （2）由已知可得()cos x g x e x '=-， 因为0x >，所以e 1x >，而c o s 1x ≤，所以cos 0x e x ->，所以()0g x '>，所以()sin xg x e x =-在()0+∞，上单调递增. 所以()()00g x g >=.故()h x 有两个零点，等价于()2y f x x =-=1aInx x--在()0+∞，内有两个零点. 等价于1ln 0a x x--=有两根， 显然1x =不是方程的根， 因此原方程可化为()1ln 01x x x x a-=>≠且， 设()ln x x x φ=，()ln 1x x φ='+，由()0x φ'>解得11x e<<，或1x > 由()0x φ'<解得10x e <<， 故()ln x x x φ=在10e ⎛⎫ ⎪⎝⎭，上单调递减，在()1,1,1,e ⎛⎫+∞ ⎪⎝⎭上单调递增.其图像如下所示：所以()min 11x e eφφ⎛⎫==- ⎪⎝⎭， 所以110e a-<-<， 所以a e >. 类型二 设而不求，巧“借”零点 【例2】【2015高考新课标1，文21】设函数()2ln x f x e a x =-.（I ）讨论()f x 的导函数()f x '的零点的个数；（II ）证明：当0a >时()22lnf x a a a ≥+. 【解析】（I ）()f x 的定义域为0+，，2()=20x a f x e x x . 当0a时,()0f x ，()f x 没有零点； 当0a 时，因为2x e 单调递增，a x 单调递增，所以()f x 在0+，单调递增.又()0f a ,当b 满足04a b 且14b 时，(b)0f ,故当0a 时，()f x 存在唯一零点. （II ）由（I ），可设()f x 在0+，的唯一零点为0x ，当00x x ，时，()0f x ;当0+x x ，时，()0f x .故()f x 在00x ，单调递减，在0+x ，单调递增，所以当0x x 时，()f x 取得最小值，最小值为0()f x . 由于0202=0x a e x ，所以00022()=2ln 2ln 2a f x ax a a a x a a . 故当0a 时，2()2ln f x a a a. 【指点迷津】本例第(2)问的解题思路是求函数()f x 的最值．因此需要求()0f x '＝的根．但是2()=20x af x e x 的根无法求解．故设出()0f x '＝的根为0x ，通过证明f (x )在(0，0x )和(0x ，＋∞)上的单调性知()min f x ＝()000222a f x ax aln x a＝＋＋，进而利用基本不等式证得结论，其解法类似解析几何中的“设而不求”．【举一反三】 【2020·江西赣州期末】已知函数2()x f x e ax x =--（e 为自然对数的底数）在点(1,(1))f 的切线方程为(3)y e x b =-+.（1）求实数,a b 的值；（2）若关于x 的不等式4()5f x m >+对于任意(0,)x ∈+∞恒成立，求整数m 的最大值. 【解析】（1）令2()x f x e ax x =--，则()21x f x e ax '=--，得：(1)e 1f a =--，(1)e 21f a '=--，由题得：(1)e 21e 31(1)e 1e 31f a a f a b b ⎧=--=-=⎧⇒⎨⎨=--=-+=⎩'⎩（2）根据题意，要证不等式4()5f x m >+对于任意恒成立，即证(0,)x ∈+∞时，4()5f x -的最小值大于m ， 令244()()()2155x x g x f x e x x g x e x '=-=---⇒=--， 记()()21()2x xh x g x e x h x e ''==--⇒=-，当(0,ln 2)x ∈时，()0h x '<；当x (ln 2,)∈+∞时，()0h x '>，故()h x 即()g x '在(0,ln 2)上单调递减，在(ln 2,)+∞上单调递增， 又(0)0g '=，(ln 2)12ln 20g '=-<，且(1)30g e '=-<，323402g e ⎛⎫'=-> ⎪⎝⎭， 故存在唯一031,2x ⎛⎫∈ ⎪⎝⎭，使()00g x '=， 故当()00,x x ∈时，0g x ；当()0,x x ∈+∞时，()0g x '>；故()g x 在()00,x 上单调递减，在()0,x +∞上单调递增，所以()02min 0004()5x g x g x e x x ==--- 一方面：()014(1)5g x g e <=- 另一方面：由()00g x '=，即00210x e x --=，得()022*********x g x e x x x x =---=-++ 由031,2x ⎛⎫∈ ⎪⎝⎭得：()0111205g x -<<，进而()011140205g x e -<<-<， 所以1120m <- ，又因为m 是整数，所以1m -，即max 1m =-. 类型三 二次构造（求导），避免求根 【例3】【2020重庆巴蜀中学月考】已知函数()()21ln 12f x x a x =+-.（1）当1a =-时，求()f x 的单调增区间；（2）若4a >，且()f x 在()0,1上有唯一的零点0x ，求证：210e x e --<<.【分析】（1）求出()'f x ，令()'0f x ≥，解不等式可得单调递增区间；（2）通过求()f x 的导函数，可得()f x 在()0,1上有两个极值点，设为1x ，2x ，又由()f x 在()0,1上有唯一的零点0x 可得0110,2x x ⎛⎫=∈ ⎪⎝⎭，所以有()()()200020001ln 10210f x x a x g x ax ax ⎧=+-=⎪⎨⎪=-+=⎩，消去a ，可得0002ln 10x x x -+=，记()00002ln 1t x x x x =-+，010,2x ⎛⎫∈ ⎪⎝⎭，研究其单调性，利用零点存在性定理可得结果.【解析】（1）由已知()f x 的定义域为0x >，当1a =-时，()()21ln 12f x x x =--， 则()()2111'x x x xf x x -++=--=， 令()'0f x ≥且0x >，则102x +<≤， 故()f x在10,2⎛ ⎝⎦上单调递增；（2）由()()21ln 12f x x a x =+-， 有()()2111'ax f x ax a x x x-+=+-=，记()21g x ax ax =-+，由4a >，有()()001011110242110a g g a a g >⎧⎪=>⎪⎪⎪⎛⎫=-+<⎨ ⎪⎝⎭⎪⎪=>⎪⎪⎩， 即()f x 在()0,1上有两个极值点，设为1x ，2x ，不妨设12x x <，且1x ，2x 是210ax ax -+=的两个根， 则121012x x <<<<， 又()f x 在()0,1上有唯一的零点0x ，且当0x +→时，()f x →-∞，当1x =时，()10f =， 所以得0110,2x x ⎛⎫=∈ ⎪⎝⎭， 所以()()()200020001ln 10210f x x a x g x ax ax ⎧=+-=⎪⎨⎪=-+=⎩，两式结合消去a ，得0001ln 02x x x --=， 即0002ln 10x x x -+=，记()00002ln 1t x x x x =-+，010,2x ⎛⎫∈ ⎪⎝⎭， 有()00'2ln 1t x x =+，其在10,2⎛⎫ ⎪⎝⎭上单调递增，所以()001'2ln 12ln 11ln 402t x x =+<+=-< 则()00'2ln 10t x x =+<在10,2⎛⎫⎪⎝⎭上恒成立， 即()0t x 在10,2⎛⎫ ⎪⎝⎭上单调递减，又222212*********e t e e e e e t e e e ⎧-⎛⎫=--+=< ⎪⎪⎝⎭⎪⎨-⎛⎫⎪=-=> ⎪⎪⎝⎭⎩， 由零点存在定理，210ex e --<<. 【指点迷津】当导函数的零点不易求时，可以通过进一步构造函数，求其导数，即通过“二次求导”，避免解方程而使问题得解.如上面例题，从题目形式来看，是极其常规的一道导数考题，第(3)问要求参数b 的范围问题，实际上是求g (x )＝x (ln x ＋x －x 2)极值问题，问题是g ′(x )＝ln x ＋1＋2x －3x 2＝0这个方程求解不易，这时我们可以尝试对h (x )＝g ′(x )再一次求导并解决问题．所以当导数值等于0这个方程求解有困难，考虑用二次求导尝试不失为一种妙法．这种方法适用于研究函数的单调性、确定极（最）值及其相关参数范围、证明不等式等.【举一反三】【2020·云南昆明一中期末】已知函数2()(1)x x f x eax e =-+⋅，且()0f x . （1）求a ；（2）证明：()f x 存在唯一极大值点0x ，且()0316f x <. 【解析】（1）因为()()ee 10x xf x ax =--≥,且e 0x >,所以e 10x ax --≥, 构造函数()e 1x u x ax =--,则()'e xu x a =-,又()00u =, 若0a ≤,则()'0u x >,则()u x 在R 上单调递增,则当0x <时,()0u x <矛盾,舍去；若01a <<,则ln 0a <,则当ln 0a x <<时,'()0u x >,则()u x 在(ln ,0)a 上单调递增,则()()ln 00u a u <=矛盾,舍去；若1a >,则ln 0a >,则当0ln x a <<时,'()0u x <,则()u x 在(0,ln )a 上单调递减,则()()ln 00u a u <=矛盾,舍去；若1a =,则当0x <时,'()0u x <,当0x >时,'()0u x >,则()u x 在(,0)-∞上单调递减,在(0,)+∞上单调递增,故()()00u x u ≥=,则()()e 0xf x u x =⋅≥,满足题意；综上所述,1a =.（2）证明:由（1）可知()()2e 1e x xf x x =-+⋅,则()()'e2e 2xxf x x =--,构造函数()2e 2xg x x =--,则()'2e 1xg x =-,又()'g x 在R 上单调递增,且()'ln20g -=,故当ln2x <-时,)'(0g x <,当ln 2x >-时,'()0g x >, 则()g x 在(,ln 2)-∞-上单调递减,在(ln 2,)-+∞上单调递增,又()00g =,()2220e g -=>,又33233332223214e 16e 022e 2e 8e 2e g --⎛⎫-=-==< ⎪⎝⎭+, 结合零点存在性定理知,在区间3(2,)2--存在唯一实数0x ,使得()00g x =, 当0x x <时,()'0f x >,当00x x <<时,()'0f x <,当0x >时,()'0f x >, 故()f x 在()0,x -∞单调递增,在()0,0x 单调递减,在()0,∞+单调递增,故()f x 存在唯一极大值点0x ,因为()0002e 20xg x x =--=,所以00e 12xx =+, 故()()()()0022200000011e 1e 11112244x x x x f x x x x ⎛⎫⎛⎫=-+=+-++=-+ ⎪ ⎪⎝⎭⎝⎭,因为0322x -<<-,所以()201133144216f x ⎛⎫<--+< ⎪⎝⎭.三．强化训练1.【2020·安徽合肥二中月考】已知函数() 01ln 0x x e x f x xe x x x -⎧-≤=⎨--->⎩，，，则函数()()()()F x f f x ef x =-的零点个数为（ ）（e 是自然对数的底数） A ．6 B ．5C ．4D ．3【答案】B【解析】0x ≤时，()xf x e -=-是增函数，(0)1f =-，0x >时，()1ln x f x xe x x =---，11()(1)1(1)()xx f x x e x e x x'=+--=+-，显然10x +>， 由1xe x=，作出xy e =和1(0)y x x=>的图象，如图，x y e =是增函数，1y x =在0x >是减函数它们有一个交点，设交点横坐标为0x ，易得0011x e x =>，001x <<， 在00x x <<时，1xe x <，()0f x '<，0x x >时，1xe x>，()0f x '>， 所以()f x 在0(0,)x 上递减，在0(,)x +∞上递增，0()f x 是()f x 的极小值，也是在0x >时的最小值．001x e x =，001x x e =，0001ln ln x x x ==-，即00ln 0x x +=，00000()1ln 0x f x x e x x =---=， 0x →时，()f x →+∞，x →+∞时，()f x →+∞．作出()f x 的大致图象，作直线y ex =，如图，0x >时y ex =与()f x 的图象有两个交点，即()0f x ex -=有两个解12,t t ，120,0t t >>．0x <时，()x f x e -=-，()x f x e '-=，由11()xf x e e -'==得1x =-，而1x =-时，(1)y e e =⨯-=-，(1)f e -=-，所以直线y ex =与()x f x e -=-在(1,)e --处相切．即0x ≤时方程()0f x ex -=有一个解e -．()(())()0F x f f x ef x =-=，令()t f x =，则()()0F x f t et =-=，由上讨论知方程()0f t et -=有三个解：12,,e t t -(120,0t t >>)而()f x e =-有一个解，1()f x t =和2()f x t =都有两个解，所以()0F x =有5个解， 即函数()F x 有5个零点．故选B ． 2．【2020江苏盐城期中】已知函数，若函数存在三个单调区间，则实数的取值范围是__________. 【答案】【解析】函数，若函数存在三个单调区间即0有两个不等实根，即有两个不等实根，转化为y=a 与y=的图像有两个不同的交点令，即x=，即y=在（0，）上单调递减，在（，+∞）上单调递增。

导数零点问题解题方法
一、不定积分求导数
1、首先要找到函数的原函数表达式：通过求导将函数原函数表达式带
入不定积分解析；
2、可以把函数分解成多项式简化解析过程，然后再求出各项求和得到
函数的原函数表达式；
3、利用反代的方法，根据函数的原函数表达式求得函数的导数；
4、如果函数原函数表达式不明确，亦可通过拉格朗日方法求导数解决。

二、图解法
1、首先在图像的横轴上取某个点作为参考点，观察左右坐标两边函数
有无十字交点；
2、如果有十字交点，说明这个点运动时X坐标是不变的，且该点应为
函数的零点；
3、如果求解的是函数的导数，需要把函数以十字交点两点为原点，重
新建立一个图象；
4、再对这个新图象进行分析，从图象中观察函数的曲线，从而解出函数的导数零点。

三、斜截式法
1、将函数的绝对值大于零的点用斜线连接起来，形成斜截线；
2、用斜截线代替函数曲线，从而可以推算出函数的零点及零点处的函数切线斜率；
3、它是一种比较粗略的解决方案，当函数曲线较复杂时，效果不是很好。

四、数值法
1、将函数设置初值和步长，运用循环语句求函数的极值点：比较前后两点的函数值的大小，当函数值变化符号变化时，则此时所在点便是函数的零点。

2、确定一定区间后，可以运用不定积分法与理论解求导比较所求函数的零点的准确性；
3、如果此法在大量求穷使用插值表、计算机等技术，获得更精确的解决方案。

导数大题零点问题解题技巧
导数大题零点问题的解题技巧主要包括以下几个方面：
1. 确定函数的单调性：通过求导数并判断导数的正负，可以确定函数的单调性。

如果函数在某区间内单调递增或递减，那么该区间内函数的值域就是连续的，因此在这个区间内函数最多只有一个零点。

2. 利用零点存在定理：如果函数在区间端点的函数值异号，即 f(a)f(b)<0，则函数在这个区间内至少有一个零点。

3. 构造函数：通过构造函数，可以将问题转化为求函数的最值问题，从而找到函数的零点。

4. 结合图像：通过画出函数的图像，可以直观地观察函数的零点位置和个数。

5. 转化问题：将问题转化为其他形式，例如转化为求函数的最值问题、不等式问题等，从而简化问题。

在解题过程中，要注意以下几点：
1. 确定函数的定义域和值域，确保函数的连续性和可导性。

2. 注意函数的奇偶性和周期性，这些性质可能会影响函数的零点位置和个数。

3. 注意函数的极值点和拐点，这些点可能是函数的零点或拐点。

4. 注意题目中的隐含条件，例如函数在某点的导数值、函数在某区间的单调性等。

5. 注意计算精度和误差控制，避免计算错误导致答案不准确。

导数与函数零点问题解题方法归纳导函数零点问题一、方法综述导数是研究函数性质的有力工具，其核心是由导数值的正负确定函数的单调性。

应用导数研究函数的性质或研究不等式问题时，绕不开研究$f(x)$的单调性，往往需要解方程$f'(x)=0$。

若该方程不易求解时，如何继续解题呢？在前面专题中介绍的“分离参数法”、“构造函数法”等常见方法的基础上，本专题举例说明“三招”妙解导函数零点问题。

二、解题策略类型一：察“言”观“色”，“猜”出零点例1】【2020·福建南平期末】已知函数$f(x)=x+ax+\frac{1}{e^{2x}}$1）讨论$f(x)$的单调性；2）若函数$g(x)=x+\frac{1}{e^{-mx}-1}$在$[-1,+\infty)$有两个零点，求$m$的取值范围。

分析】1）首先求出函数的导函数因式分解为$f'(x)=(x+a+1)(x+1)e^{-2x}$，再对参数$a$分类讨论可得：①当$a=0$时，$f'(x)=(x+1)e^{-2x}$，当且仅当$x=-1$时，等号成立。

故$f(x)$在$(-\infty,+\infty)$为增函数。

②当$a>0$时，$-10$得$x-1$，由$f'(x)<0$得$-a-1<x<-1$；所以$f(x)$在$(-\infty,-a-1)$，$(-1,+\infty)$为增函数，在$-a-1,-1$为减函数。

③当$aa+1$，由$f'(x)>0$得$x>-a-1$或$x<-1$，由$f'(x)<0$得$-1<x<-a-1$；所以$f(x)$在$(-\infty,-1)$，$-a-1,+\infty$为增函数，在$-1,-a-1$为减函数。

综上，当$a=0$时，$f(x)$在$(-\infty,+\infty)$为增函数；当$a>0$时，$f(x)$在$(-\infty,-a-1)$，$(-1,+\infty)$为增函数，在$-a-1,-1$为减函数；当$a<0$时，$f(x)$在$(-\infty,-1)$，$-a-1,+\infty$为增函数，在$-1,-a-1$为减函数。

导数与函数的零点问题解析在数学中，导数和函数的零点是非常重要的概念和问题。

导数可以描述函数的变化率，而函数的零点则表示函数在某一点上取值为零的情况。

在本文中，我们将对导数与函数的零点进行详细的解析和讨论。

一、导数的定义与作用导数是描述函数变化率的指标，可以用来衡量函数在某一点上的斜率或变化速度。

它定义为函数在某一点上的极限，即导数等于函数在该点处的切线斜率。

对于一个函数f(x)，它在点x处的导数可以通过以下公式计算得出：f'(x) = lim(h→0) [f(x+h) - f(x)] / h导数的概念对于理解函数的性质和行为非常重要，它可以帮助我们分析函数的增减性、凸凹性以及局部极值等特征。

通过导数，我们可以得出函数在各个点的斜率，从而推断函数的曲线形状和趋势。

二、函数的零点与解析函数的零点是指函数在某个点上的取值为零的情况。

换句话说，函数的零点是使得函数等于零的自变量的值。

寻找函数的零点在数学和实际问题中都具有重要的意义。

为了找到函数的零点，我们可以利用导数的概念和性质进行分析。

根据导数的定义，我们知道当函数在某一点的导数为零时，函数在该点可能存在极值或拐点。

因此，我们可以采用导数为零的点作为起点，通过求解函数的导数方程来找到函数的零点。

具体而言，我们可以按照以下步骤来解析函数的零点问题：1. 找到函数的导数方程。

2. 求解导数方程，得到导数为零的所有解。

3. 使用解析工具或数值逼近法，确定解的精确值或近似值。

4. 检验解是否满足函数为零的条件。

通过以上步骤，我们可以较为准确地求解函数的零点，从而揭示函数的性质和特征。

函数的零点问题在数学、经济、物理等领域具有广泛的应用，如寻找方程的根、求解最优化问题等。

三、解析与数值求解的比较在解析函数的零点问题时，我们依赖于函数的导数和解析工具的应用。

通过解析方法可以获得函数零点的精确解，这对于研究函数的性质和行为非常重要。

然而，对于一些复杂的函数和方程，解析求解可能变得非常困难甚至不可能。

2020题型一 利用导数讨论函数零点的个数 【题型要点解析】对于函数零点的个数的相关问题，利用导数和数形结合的数学思想来求解．这类问题求解的通法是：(1)构造函数，这是解决此类题的关键点和难点，并求其定义域； (2)求导数，得单调区间和极值点； (3)画出函数草图；(4)数形结合，挖掘隐含条件，确定函数图象与x 轴的交点情况进而求解．1.已知f (x )＝ax 3－3x 2＋1(a >0)，定义h (x )＝max{f (x )，g (x )}＝⎩⎪⎨⎪⎧f (x )，f (x )≥g (x )，g (x )，f (x )<g (x ).(1)求函数f (x )的极值；(2)若g (x )＝xf ′(x )，且存在x ∈[1,2]使h (x )＝f (x )，求实数a 的取值范围； (3)若g (x )＝ln x ，试讨论函数h (x )(x >0)的零点个数．【解】 (1)∈函数f (x )＝ax 3－3x 2＋1，∈f ′(x )＝3ax 2－6x ＝3x (ax －2)，令f ′(x )＝0，得x 1＝0或x 2＝2a，∈a >0，∈x 1<x 2，列表如下：∈f (x )的极大值为f (0)＝1，极小值为f ⎪⎭⎫⎝⎛a ＝8a 2－12a 2＋1＝1－4a 2. (2)g (x )＝xf ′(x )＝3ax 3－6x 2，∈存在x ∈[1,2]，使h (x )＝f (x )，∈f (x )≥g (x )在x ∈[1,2]上有解，即ax 3－3x 2＋1≥3ax 3－6x 2在x ∈[1,2]上有解， 即不等式2a ≤1x 3＋3x 在x ∈[1,2]上有解．设y ＝1x 3＋3x ＝3x 2＋1x 3(x ∈[1,2])，∈y ′＝－3x 2－3x 4<0对x ∈[1,2]恒成立，∈y ＝1x 3＋3x 在x ∈[1,2]上单调递减，∈当x ＝1时，y ＝1x 3＋3x 的最大值为4，∈2a ≤4，即a ≤2.(3)由(1)知，f (x )在(0，＋∞)上的最小值为f ⎪⎭⎫⎝⎛a 2＝1－4a 2， ∈当1－4a 2>0，即a >2时，f (x )>0在(0，＋∞)上恒成立，∈h (x )＝max{f (x )，g (x )}在(0，＋∞)上无零点．∈当1－4a2＝0，即a ＝2时，f (x )min ＝f (1)＝0.又g (1)＝0，∈h (x )＝max{f (x )，g (x )}在(0，＋∞)上有一个零点． ∈当1－4a2<0，即0<a <2时，设φ(x )＝f (x )－g (x )＝ax 3－3x 2＋1－ln x (0<x <1)， ∈φ′(x )＝3ax 2－6x －1x <6x (x －1)－1x <0，∈φ(x )在(0,1)上单调递减．又φ(1)＝a －2<0，φ⎪⎭⎫ ⎝⎛e 1＝a e3＋2e 2－3e 2>0，∈存在唯一的x 0∈⎪⎭⎫⎝⎛1,1e ，使得φ(x 0)＝0，(∈)当0<x ≤x 0时，∈φ(x )＝f (x )－g (x )≥φ(x 0)＝0， ∈h (x )＝f (x )且h (x )为减函数． 又h (x 0)＝f (x 0)＝g (x 0)＝ln x 0<ln 1＝0， f (0)＝1>0，∈h (x )在(0，x 0)上有一个零点； (∈)当x >x 0时，∈φ(x )＝f (x )－g (x )<φ(x 0)＝0， ∈h (x )＝g (x )且h (x )为增函数，∈g (1)＝0，∈h (x )在(x 0，＋∞)上有一零点；从而h (x )＝max{f (x )，g (x )}在(0，＋∞)上有两个零点，综上所述，当0<a <2时，h (x )有两个零点；当a ＝2时，h (x )有一个零点； 当a >2时，h (x )无零点．题组训练一 利用导数讨论函数零点的个数 已知函数f (x )＝ln x －12ax ＋a －2，a ∈R .(1)求函数f (x )的单调区间；(2)当a <0时，试判断g (x )＝xf (x )＋2的零点个数． 【解析】 (1)f ′(x )＝1x －a 2＝2－ax2x(x >0)．若a ≤0，则f ′(x )>0，∈函数f (x )的单调递增区间为(0，＋∞)；若a >0，当0<x <2a 时，f ′(x )>0，函数f (x )单调递增，当x >2a 时，f ′(x )<0，函数f (x )单调递减，综上，若a ≤0时，函数f (x )的单调递增区间为(0，＋∞)；若a >0时，函数f (x )的单调递增区间为⎪⎭⎫ ⎝⎛a 2,0，单调递减区间为⎪⎭⎫ ⎝⎛∞+a 2.(2)g (x )＝x ln x －12ax 2＋ax －2x ＋2，g ′(x )＝－ax ＋ln x ＋a －1.又a <0，易知g ′(x )在(0，＋∞)上单调递增， g ′(1)＝－1<0，g ′(e)＝－a e ＋a ＝a (1－e)>0， 故而g ′(x )在(1，e)上存在唯一的零点x 0， 使得g ′(x 0)＝0.当0<x <x 0时，g ′(x )<0，g (x )单调递减；当x >x 0时，g ′(x )>0，g (x )单调递增， 取x 1＝e a ，又a <0，∈0<x 1<1，∈g (x 1)＝x 1)2221(ln 111x a ax x +-+-＝e a⎪⎭⎫ ⎝⎛+-+-a a e a ae a 2221， 设h (a )＝a －12a e a ＋a －2＋2e a ，(a <0)，h ′(a )＝－12a e a －12e a －2e a ＋2，(a <0)，h ′(0)＝－12，h ″(a )＝e －a －e a ＋e －a －12a e a >0，∈h ′(a )在(－∞，0)上单调递增，h ′(a )<h ′(0)<0， ∈h (a )在(－∞，0)上单调递减，∈h (a )>h (0)＝0， ∈g (x 1)>0，即当a <0时，g (e a )>0.当x 趋于＋∞时，g (x )趋于＋∞，且g (2)＝2ln2－2<0. ∈函数g (x )在(0，＋∞)上始终有两个零点． 题型二 由函数零点个数求参数的取值范围 【题型要点解析】研究方程的根(或函数零点)的情况，可以通过导数研究函数的单调性、最大值、最小值、变化趋势等，并借助函数的大致图象判断方程根(函数零点)的情况，这是导数这一工具在研究方程中的重要应用．已知函数f (x )＝mxln x ，曲线y ＝f (x )在点(e 2，f (e 2))处的切线与直线2x ＋y ＝0垂直(其中e为自然对数的底数)．(1)求f (x )的解析式及单调减区间；(2)若函数g (x )＝f (x )－kx 2x －1无零点，求k 的取值范围．【解析】 (1)函数f (x )＝mx ln x 的导数为f ′(x )＝m (ln x －1)(ln x )2，又由题意有：f ′(e2)＝12∈m 4＝12∈m ＝2，故f (x )＝2xln x.此时f ′(x )＝2(ln x －1)(ln x )2，由f ′(x )≤0∈0<x <1或1<x ≤e ，所以函数f (x )的单调减区间为(0,1)和(1，e]．(2)g (x )＝f (x )－kx 2x －1∈g (x )＝x ⎪⎭⎫ ⎝⎛--1ln 2x kx x ，且定义域为(0,1)∈(1，＋∞)，要函数g (x )无零点，即要2ln x ＝kxx －1在x ∈(0,1)∈(1，＋∞)内无解，亦即要k ln x －2(x －1)x ＝0在x ∈(0,1)∈(1，＋∞)内无解．构造函数h (x )＝k ln x －2(x －1)x ∈h ′(x )＝kx －2x2.∈当k ≤0时，h ′(x )<0在x ∈(0,1)∈(1，＋∞)内恒成立，所以函数h (x )在(0,1)内单调递减，h (x )在(1，＋∞)内也单调递减.又h (1)＝0，所以在(0,1)内无零点，在(1，＋∞)内也无零点，故满足条件；∈当k >0时，h ′(x )＝kx －2x 2∈h ′(x )＝22x k x k ⎪⎭⎫ ⎝⎛-， (i)若0<k <2，则函数h (x )在(0,1)内单调递减，在⎪⎭⎫⎝⎛k 2,1内也单调递减，在⎪⎭⎫ ⎝⎛+∞,2k 内单调递增，又h (1)＝0，所以在(0,1)内无零点；易知h ⎪⎭⎫ ⎝⎛k 2<0，而h (e 2k )＝k ·2k －2＋2e2k>0，故在⎪⎭⎫⎝⎛+∞,2k 内有一个零点，所以不满足条件；(ii)若k ＝2，则函数h (x )在(0,1)内单调递减，在(1，＋∞)内单调递增．又h (1)＝0，所以x ∈(0,1)∈(1，＋∞)时，h (x )>0恒成立，故无零点，满足条件；(iii)若k >2，则函数h (x )在⎪⎭⎫ ⎝⎛k 2,0内单调递减，在⎪⎭⎫⎝⎛1,2k 内单调递增，在(1，＋∞)内单调递增，又h (1)＝0，所以在⎪⎭⎫⎝⎛1,2k 及(1，＋∞)内均无零点． 又易知h ⎪⎭⎫⎝⎛k 2<0，而h (e －k )＝k (－k )－2＋2e k ＝2e k －k 2－2，又易证当k >2时，h (e －k )>0，所以函数h (x )在⎪⎭⎫ ⎝⎛k 2,0内有一零点，故不满足条件．综上可得：k 的取值范围为：k ≤0或k ＝2.题组训练二 由函数零点个数求参数的取值范围 已知函数f (x )＝ln x －ax (ax ＋1)，其中a ∈R . (1)讨论函数f (x )的单调性；(2)若函数f (x )在(0,1]内至少有1个零点，求实数a 的取值范围． 【解析】(1)依题意知，函数f (x )的定义域为(0，＋∞)， 且f ′(x )＝1x－2a 2x －a＝2a 2x 2＋ax －1－x ＝(2ax －1)(ax ＋1)－x，当a ＝0时，f (x )＝ln x ，函数f (x )在(0，＋∞)上单调递增；当a >0时，由f ′(x )>0，得0<x <12a，由f ′(x )<0，得x >12a ，函数f (x )⎪⎭⎫⎝⎛a 21,0上单调递增， 在⎪⎭⎫⎝⎛+∞,21a 上单调递减． 当a <0时，由f ′(x )>0，得0<x <－1a ，由f ′(x )<0，得x >－1a，函数f (x )在⎪⎭⎫ ⎝⎛-a 1,0上单调递增，在⎪⎭⎫⎝⎛+∞-,1a 上单调递减． (2)当a ＝0时，函数f (x )在(]0，1内有1个零点x 0＝1；当a >0时，由(1)知函数f (x )在⎪⎭⎫ ⎝⎛a 21,0上单调递增，在⎪⎭⎫⎝⎛+∞,21a 上单调递减． ∈若12a ≥1，即0<a ≤12时，f (x )在(0,1]上单调递增，由于当x →0时，f (x )→－∞且f (1)＝－a 2－a <0知，函数f (x )在(0,1]内无零点；∈若0<12a <1，即当a >12时，f (x )在⎪⎭⎫ ⎝⎛a 21,0上单调递增，在⎥⎦⎤⎝⎛1,21a 上单调递减，要使函数f (x )在(0,1]内至少有1个零点，只需满足f ⎪⎭⎫⎝⎛a 21≥0，即ln 12a ≥34， 又∈a >12，∈ln 12a <0，∈不等式不成立．∈f (x )在(0,1]内无零点；当a <0时，由(1)知函数f (x )在⎪⎭⎫ ⎝⎛-a 1,0上单调递增，在⎪⎭⎫⎝⎛+∞-,1a 上单调递减． ∈若－1a ≥1，即－1≤a <0时，f (x )在(0,1]上单调递增，由于当x →0时，f (x )→－∞，且f (1)＝－a 2－a >0，知函数f (x )在(0,1]内有1个零点；∈若0<－1a <1，即a <－1时，函数f (x )在⎪⎭⎫ ⎝⎛-a 1,0上单调递增，在⎥⎦⎤⎝⎛-1,1a 上单调递减，由于当x →0时，f (x )→－∞，且当a <－1时，f ⎪⎭⎫⎝⎛-a 1＝ln ⎪⎭⎫⎝⎛-a 1<0，知函数f (x )在(0,1]内无零点．综上可得a 的取值范围是[－1,0]．题型三 利用导数证明复杂方程在某区间上仅有一解 【题型要点解析】证明复杂方程在某区间上有且仅有一解的步骤： (1)在该区间上构造与方程相应的函数； (2)利用导数研究该函数在该区间上的单调性； (3)判断该函数在该区间端点处的函数值的符号； (4)作出结论．已知函数f (x )＝(x 2－2x )ln x ＋ax 2＋2.(1)当a ＝－1时，求f (x )在点(1，f (1))处的切线方程；(2)当a >0时，设函数g (x )＝f (x )－x －2，且函数g (x )有且仅有一个零点，若e －2<x <e ，g (x )≤m ，求m 的取值范围．【解析】 (1)当a ＝－1时，f (x )＝(x 2－2x )ln x －x 2＋2，定义域为(0，＋∞)，∈f ′(x )＝(2x －2)ln x ＋x －2－2x ＝(2x －2)ln x －x －2.∈f ′(1)＝－3，又f (1)＝1，f (x )在(1，f (1))处的切线方程3x ＋y －4＝0.(2)令g (x )＝f (x )－x －2＝0，则(x 2－2x )ln x ＋ax 2＋2＝x ＋2，即a ＝1－(x －2)·ln xx ，令h (x )＝1－(x －2)·ln xx，则h ′(x )＝－1x 2－1x ＋2－2ln x x 2＝1－x －2ln xx 2.令t (x )＝1－x －2ln x ，t ′(x )＝－1－2x ＝－x －2x ，∈t ′(x )<0，t (x )在(0，＋∞)上是减函数， 又∈t (1)＝h ′(1)＝0，所以当0<x <1时，h ′(x )>0， 当x >1时，h ′(x )<0，所以h (x )在(0,1)上单调递增， 在(1，＋∞)上单调递减，∈h (x )max ＝h (1)＝1.因为a >0，所以当函数g (x )有且仅有一个零点时，a ＝1.g (x )＝(x 2－2x )ln x ＋x 2－x ，若e －2<x <e ，g (x )≤m ，只需g (x )max ≤m ， g ′(x )＝(x －1)(3＋2ln x )，令g ′(x )＝0得x ＝1，或x ＝e －32，又∈e －2<x <e∈函数g (x )在(e －2，e －32)上单调递增，在(e －32，1)上单调递减，在(1，e)上单调递增，又g (e －32)＝－12e －3＋2e －32，g (e)＝2e 2－3e ，∈g (e －32)＝－12e －3＋2e －32<2e －32<2e<2e ⎪⎭⎫ ⎝⎛-23e ＝g (e)，即g (e －32)<g (e)，g (x )max ＝g (e)＝2e 2－3e ，∈m ≥2e 2－3e .题组训练三 利用导数证明复杂方程在某区间上仅有一解 已知y ＝4x 3＋3tx 2－6t 2x ＋t －1，x ∈R ，t ∈R .(1)当x 为常数时，t 在区间⎥⎦⎤⎢⎣⎡32,0变化时，求y 的最小值φ(x )；(2)证明：对任意的t ∈(0，＋∞)，总存在x 0∈(0,1)，使得y ＝0.【解析】 (1)当x 为常数时，设f (t )＝4x 3＋3tx 2－6t 2x ＋t －1＝－6xt 2＋(3x 2＋1)t ＋4x 3－1，f ′(t )＝－12xt ＋3x 2＋1.∈当x ≤0时，由t ∈⎥⎦⎤⎢⎣⎡32,0知f (t )>0，f (t )在⎥⎦⎤⎢⎣⎡32,0上递增，其最小值φ(x )＝f (0)＝4x 3－1；∈当x >0时，f (t )的图象是开口向下的抛物线，其对称轴为直线；t ＝－3x 2＋1－12x ＝3x 2＋112x ，若⎩⎪⎨⎪⎧x >0，3x 2＋112x ≤13，即13≤x ≤1，则f (t )在⎥⎦⎤⎢⎣⎡32,0上的最小值为 φ(x )＝f ⎪⎭⎫⎝⎛32＝4x 3＋2x 2－83x －13.若⎩⎪⎨⎪⎧x >0，3x 2＋112x >13，即0<x <13或x >1，则f (t )在⎥⎦⎤⎢⎣⎡32,0上的最小值为φ(x )＝f (0)＝4x 3－1.综合∈∈，得φ(x )＝⎩⎨⎧4x 3－1，x <13或x >1，4x 3＋2x 2－83x －13，13≤x ≤1.(2)证明：设g (x )＝4x 3＋3tx 2－6t 2x ＋t －1，则g ′(x )＝12x 2＋6tx －6t 2＝12(x ＋t )⎪⎭⎫ ⎝⎛-2t x 由t ∈(0，＋∞)，当x 在区间(0，＋∞)内变化时，g ′(x )，g (x )取值的变化情况如下表：∈当t2≥1，即t ≥2时，g (x )在区间(0,1)内单调递减，g (0)＝t －1>0，g (1)＝－6t 2＋4t ＋3＝－2t (3t －2)＋3≤－4(3－2)＋3<0.所以对任意t ∈[2，＋∞)，g (x )在区间(0,1)内均存在零点，即存在x 0∈(0,1)，使得g (x 0)＝0.∈当0<t 2<1，即0<t <2时，g (x )在⎪⎭⎫ ⎝⎛2,0t 内单调递减，在⎪⎭⎫ ⎝⎛1,2t 内单调递增，若t ∈(0,1)，则g ⎪⎭⎫⎝⎛2t ＝－74t 3＋t －1≤－74t 3<0，g (1)＝－6t 2＋4t ＋3≥－6t ＋4t ＋3＝－2t ＋3≥1>0，所以g (x )在⎪⎭⎫⎝⎛1,2t 内存在零点；若t ∈(1,2)，则g (0)＝t －1>0，g ⎪⎭⎫ ⎝⎛2t ＝－74t 3＋t －1<－74×13＋2－1<0，所以g (x )在⎪⎭⎫⎝⎛2,0t 内存在零点．所以，对任意t ∈(0,2)，g (x )在区间(0,1)内均存在零点，即存在x 0∈(0,1)，使得g (x 0)＝0， 综合∈∈，对任意的t ∈(0，＋∞)，总存在x 0∈(0,1)，使得y ＝0.【专题训练】1．已知函数f (x )＝xln x＋ax ，x >1.(1)若f (x )在(1，＋∞)上单调递减，求实数a 的取值范围； (2)若a ＝2，求函数f (x )的极小值；(3)若方程(2x －m )ln x ＋x ＝0，在(1，e]上有两个不等实根，求实数m 的取值范围． [解析] (1)f ′(x )＝ln x －1ln 2x ＋a ，由题意可得f ′(x )≤0在(1，＋∞)上恒成立，∈a ≤1ln 2x －1ln x＝221ln 1⎪⎭⎫⎝⎛-x －14.∈x ∈(1，＋∞)，∈ln x ∈(0，＋∞)， ∈当1ln x －12＝0时，函数t ＝221ln 1⎪⎭⎫ ⎝⎛-x －14的最小值为－14，∈a ≤－14. 故实数a 的取值范围为⎥⎦⎤ ⎝⎛∞-41,(2)当a ＝2时，f (x )＝xln x ＋2x ，f ′(x )＝ln x －1＋2ln 2x ln 2x，令f ′(x )＝0，得2ln 2x ＋ln x －1＝0， 解得ln x ＝12或ln x ＝－1(舍)，即x ＝e 12.当1<x <e 12时，f ′(x )<0，当x >e 12时，f ′(x )>0，∈f (x )的极小值为f (e 12)＝e 1212＋2e 1e ＝4e 12.(3)将方程(2x －m )ln x ＋x ＝0两边同除以ln x 得(2x －m )＋x ln x ＝0，整理得xln x＋2x ＝m ，即函数g (x )＝xln x ＋2x 的图象与函数y ＝m 的图象在(1，e]上有两个不同的交点．由(2)可知，g (x )在(1，e 12)上单调递减，在(e 12，e]上单调递增，g (e 12)＝4e 12，g (e)＝3e ，在(1，e]上，当x →1时，x ln x →＋∞，∈4e 12<m ≤3e ，故实数m 的取值范围为(4e 12，3e]．2．已知f (x )＝2x ln x ，g (x )＝x 3＋ax 2－x ＋2.(1)如果函数g (x )的单调递减区间为⎪⎭⎫⎝⎛-1,31，求函数g (x )的解析式； (2)在(1)的条件下，求函数y ＝g (x )的图象在点P (－1，g (－1))处的切线方程； (3)已知不等式f (x )≤g ′(x )＋2恒成立，若方程a e a －m ＝0恰有两个不等实根，求m 的取值范围．【解】 (1)g ′(x )＝3x 2＋2ax －1，由题意知，3x 2＋2ax －1<0的解集为⎪⎭⎫⎝⎛-1,31， 即3x 2＋2ax －1＝0的两根分别是－13，1，代入得a ＝－1，∈g (x )＝x 3－x 2－x ＋2. (2)由(1)知，g (－1)＝1，∈g ′(x )＝3x 2－2x －1，g ′(－1)＝4，∈点P (－1,1)处的切线斜率k ＝g ′(－1)＝4，∈函数y ＝g (x )的图象在点P (－1,1)处的切线方程为y －1＝4(x ＋1)，即4x －y ＋5＝0.(3)由题意知，2x ln x ≤3x 2＋2ax ＋1对x ∈(0，＋∞)恒成立，可得a ≥ln x －32x －12x 对x ∈(0，＋∞)恒成立．设h (x )＝ln x －32x －12x，则h ′(x )＝1x －32＋12x 2＝－(x －1)(3x ＋1)2x 2，令h ′(x )＝0，得x ＝1，x ＝－13(舍)，当0<x <1时，h ′(x )>0；当x >1时，h ′(x )<0， ∈当x ＝1时，h (x )取得最大值，h (x )max ＝h (1)＝－2， ∈a ≥－2.令φ(a )＝a e a ，则φ′(a )＝e a ＋a e a ＝e a (a ＋1)， ∈φ(a )在[－2，－1]上单调递减，在(－1，＋∞)上单调递增，∈φ(－2)＝－2e －2＝－2e 2，φ(－1)＝－e －1＝－1e ，当a →＋∞时，φ(a )→＋∞，∈方程a e a －m ＝0恰有两个不等实根，只需－1e <m ≤－2e 2.3．设函数f (x )＝x 3＋ax 2＋bx ＋c .(1)求曲线y ＝f (x )在点(0，f (0))处的切线方程；(2)设a ＝b ＝4，若函数f (x )有三个不同零点，求c 的取值范围； (3)求证：a 2－3b >0是f (x )有三个不同零点的必要而不充分条件．【解析】 (1)由f (x )＝x 3＋ax 2＋bx ＋c ，得f ′(x )＝3x 2＋2ax ＋b .因为f (0)＝c ，f ′(0)＝b ，所以曲线y ＝f (x )在点(0，f (0))处的切线方程为y ＝bx ＋c .(2)当a ＝b ＝4时，f (x )＝x 3＋4x 2＋4x ＋c ， 所以f ′(x )＝3x 2＋8x ＋4. 令f ′(x )＝0，得3x 2＋8x ＋4＝0， 解得x ＝－2或x ＝－23.f (x )与f ′(x )在区间(－∞，＋∞)上的情况如下：所以，当c >0且c －3227<0时，存在x 1∈(－4，－2)，x 2∈⎪⎭⎫ ⎝⎛--3,2，x 3∈⎪⎭⎫⎝⎛-0,3，使得f (x 1)＝f (x 2)＝f (x 3)＝0.由f (x )的单调性知，当且仅当c ∈⎪⎭⎫⎝⎛2732,0时，函数f (x )＝x 3＋4x 2＋4x ＋c 有三个不同零点．(3)证明：当Δ＝4a 2－12b <0时，f ′(x )＝3x 2＋2ax ＋b >0，x ∈(－∞，＋∞)，此时函数f (x )在区间(－∞，＋∞)上单调递增，所以f (x )不可能有三个不同零点．当Δ＝4a 2－12b ＝0时，f ′(x )＝3x 2＋2ax ＋b 只有一个零点，记作x 0. 当x ∈(－∞，x 0)时，f ′(x )>0，f (x )在区间(－∞，x 0)上单调递增； 当x ∈(x 0，＋∞)时，f ′(x )>0，f (x )在的区间(x 0，＋∞)上单调递增． 所以f (x )不可能有三个不同零点．综上所述，若函数f (x )有三个不同零点，则必有Δ＝4a 2－12b >0. 故a 2－3b >0是f (x )有三个不同零点的必要条件．当a ＝b ＝4，c ＝0时，a 2－3b >0，f (x )＝x 3＋4x 2＋4x ＝x (x ＋2)2只有两个不同零点，所以a 2－3b >0不是f (x )有三个不同零点的充分条件．因此a 2－3b >0是f (x )有三个不同零点的必要而不充分条件．。

导数与零点问题解题技巧
1. 嘿，你想知道怎么通过导数来巧妙找到函数的零点吗？就像在一片迷雾中找到那关键的线索！比如求函数f(x)=x³-3x+2 的零点，咱通过求导找到极值点，就能逐步逼近零点啦，是不是很神奇？
2. 哇哦，注意啦！导数可是解决零点问题的一把利器呀！好比你找宝藏有了精确的地图。

像对于函数 g(x)=e^x-x-1，用导数不就能轻松分析它零点的情况嘛！
3. 嘿呀，有没有觉得导数和零点问题之间像是有一条神秘的纽带呀！就像侦探和线索一样。

比如分析函数 h(x)=sinx+x 在某个区间的零点，导数能帮大忙呢！
4. 哎呀，学会这些解题技巧那可真是太棒啦！简直像是掌握了绝世武功。

想想函数i(x)=lnx+x²，用导数去攻克零点问题，多有成就感！
5. 天呐，导数与零点问题的结合简直妙不可言！就如同给你一双慧眼。

拿函数 j(x)=x^4-4x² 来说，导数能让我们快速看清零点的分布呢。

6. 哇塞，这些解题技巧你可不能错过呀！这就好比游戏里的通关秘籍。

像是函数 k(x)=x+cosx ，利用导数去求解零点，厉害吧！
7. 嘿，你知道用导数解决零点问题能带来多大的乐趣吗？那可比发现新大陆还让人兴奋！好比函数l(x)=x³/3-x²+2x 的零点求解。

8. 总之，导数与零点问题解题技巧真的超有用的啦！你一定要好好掌握哦！就像拥有了一把打开数学难题大门的钥匙！不管遇到什么函数，都能轻松应对！。

函数与导数之零点问题一．考情分析零点问题涉及到函数与方程，但函数与方程是两个不同的概念,但它们之间有着密切的联系,方程f (x )＝0的解就是函数y ＝f (x )的图像与x 轴的交点的横坐标,函数y ＝f (x )也可以看作二元方程f (x )－y ＝0通过方程进行研究.就中学数学而言,函数思想在解题中的应用主要表现在两个方面：①是借助有关初等函数的性质,解有关求值、解(证)不等式、解方程以及讨论参数的取值范围等问题：②是在问题的研究中,通过建立函数关系式或构造中间函数,把所研究的问题转化为讨论函数的有关性 质,达到化难为易,化繁为简的目的.许多有关方程的问题可以用函数的方法解决,反之,许多函数问题也可以用方程的方法来解决.函数与方程的思想是中学数学的基本思想,也是各地模考和历年高考的重点.二．经验分享1.确定函数f (x )零点个数(方程f (x )＝0的实根个数)的方法：(1)判断二次函数f (x )在R 上的零点个数，一般由对应的二次方程f (x )＝0的判别式Δ＞0，Δ＝0，Δ＜0来完成；对于一些不便用判别式判断零点个数的二次函数，则要结合二次函数的图象进行判断．(2)对于一般函数零点个数的判断，不仅要用到零点存在性定理，还必须结合函数的图象和性质才能确定，如三次函数的零点个数问题．(3)若函数f (x )在[a ，b ]上的图象是连续不断的一条曲线，且是单调函数，又f (a )·f (b )＜0，则y ＝f (x )在区间(a ，b )内有唯一零点．2.导数研究函数图象交点及零点问题利用导数来探讨函数)(x f y =的图象与函数)(x g y =的图象的交点问题，有以下几个步骤： ①构造函数)()()(x g x f x h -=； ②求导)('x h ；③研究函数)(x h 的单调性和极值（必要时要研究函数图象端点的极限情况）； ④画出函数)(x h 的草图，观察与x 轴的交点情况，列不等式；⑤解不等式得解.探讨函数)(x f y =的零点个数，往往从函数的单调性和极值入手解决问题，结合零点存在性定理求解.三、题型分析（一）确定函数的零点与方程根的个数问题例1.【四川省成都七中2020届高三上半期考试，理科数学，12】函数)(x f 是定义在R 上的偶函数，周期是4，当[]2,0∈x 时，3)(2+-=x x f ，则方程0log )(2=-x x f 的根个数为（ ）A.3B.4C.5D.6 【答案】C【解析】)(x f 是定义在R 上的偶函数，周期是4，当[]2,0∈x 时，3)(2+-=x x f ，根据性质我们可以画出函数图像，方程0log )(2=-x x f 的根个数转化成⎩⎨⎧==x y x f y 2log )(的交点个数，有图像可以看出，一共有5个交点，ABCDE.其中我x=8处是要仔细看图，是易错点。

导数与函数的零点问题考点与题型归纳且f(1)=0，所以当x≥1时，f(x)≥XXX成立。

2)解：由题可知，x－－f(x)＝x3－2ex2＋tx，即f(x)＝x－－x3＋2ex2－tx。

设g(x)=f'(x)=1-2x+2ex-t，求g(x)的零点。

当x1时，g(x)>0.所以f(x)在[0,1)上是单调减函数，在(1,＋∞)上是单调增函数。

又因为f(0)=0，当x→＋∞时，f(x)→＋∞，所以方程x－－f(x)=x3－2ex2＋tx的根有且只有一个。

给定函数$f(x)=e^x-ax^2$，其中$a>0$。

1) 当$a=1$时，证明对于$x\geq 0$，有$f(x)\geq 1$。

证明：当$a=1$时，$f(x)\geq 1$等价于$(x^2+1)e^{-x}-1\leq 0$。

设$g(x)=(x^2+1)e^{-x}-1$，则$g'(x)=-e^{-x}(x^2-2x+1)=-e^{-x}(x-1)^2$。

当$x\neq 1$时，$g'(x)<0$，因此$g(x)$在$(0,1)$上单调递增，在$(1,+\infty)$上单调递减。

而$g(0)=0$，因此对于$x\geq 0$，有$g(x)\leq 0$，即$f(x)\geq 1$。

2) 若$f(x)$在$(0,+\infty)$只有一个零点，求$a$。

设$h(x)=1-ax^2e^{-x}$。

由于$f(x)$在$(0,+\infty)$只有一个零点，因此$h(x)$在$(0,+\infty)$只有一个零点。

i) 当$a\leq \frac{1}{e}$时，$h(x)>0$，因此$h(x)$没有零点。

ii) 当$a>\frac{1}{e}$时，$h'(x)=a(x-2)e^{-x}$。

当$x\in(0,2)$时，$h'(x)0$。

因此$h(x)$在$(0,2)$上单调递减，在$(2,+\infty)$上单调递增。

导数专题：利用导数研究函数零点的4种常见考法一、函数零点问题常规求解步骤：第一步：将问题转化为函数的零点问题，进而转化为函数的图象与x 轴（或y=k）在某区间上的交点问题；第二步：利用导数研究该函数在此区间上的单调性、极值、端点值等性质，进而画出其图象；第三步：结合图象判断零点或根据零点分析参数。

二、利用导数确定函数零点的常用方法1、图象法：根据题目要求画出函数的图象，标明函数极（最）值的位置，借助数形结合的思想分析问题（画草图时注意有时候需要使用极限）；2、利用函数零点存在定理：先用该定理判定函数在某区间上有零点，然后利用导数研究函数的单调性、极值（最值）及区间端点值的符号，进而判断函数在该区间上零点的个数。

三、利用函数的零点求参数范围的方法1、分离参数（a=g(x)）后，将原问题转化为y=g(x)的值域（最值）问题或转化为直线y=a 与y=g(x)的图象的交点个数问题（优先分离、次选分类）求解；2、利用函数零点存在定理构造不等式求解；3、转化为两个熟悉的函数图象的位置关系问题，从而构建不等式求解。

四、导函数的零点不可直接求时的应对策略1、“特值试探法”：当导函数的零点不可求时，可尝试利用特殊值试探，此时特殊值的选取应遵循一下原则：①当含有ln x 的函数中，通常选取k x e =，特别的，选当0k =时，1x =来试探；②在含有x e 的函数中，通常选取ln x k =，特别的，选取当1k =时，0x =来试探，在探得导函数的一个零点后，结合导函数的单调性，确定导函数在零点左右的符号，进而确定原函数的单调性和极值，使问题得到解决。

2、“虚设和代换法”：当导函数()f x '的零点无法求出显性的表达式时，我们可以先证明零点的存在，再虚设为0x ，接下来通常有两个方向：①由0()0f x '=得到一个关于0x 的方程，再将这个关于0x 的方程的整体或局部代入0()f x ，从而求得0()f x ，然后解决相关的问题；②根据导函数()f x '的单调性，得出0x 两侧导函数的正负，进而得出原函数的单调性和极值，使问题得解。