2020年高中数学(人教版必修5)配套练习：1.2 应用举例 第2课时

§ 1.2应用举例(二).2.利用正、余弦定课时目标 1.利用正、余弦定理解决生产实践中的相关高度的问题理及三角形面积公式解决三角形中的几何胸怀问题．1．仰角和俯角：与目标视野在同一铅垂平面内的水平视野和目标视野的夹角，目标视线在水平线 ____方时叫仰角，目标视野在水平线____方时叫俯角．(如下图 )2．已知△ ABC 的两边 a、 b 及其夹角C，则△ ABC 的面积为 ________．一、选择题1．从 A 处望 B 处的仰角为α，从B处望A处的俯角为β，则α与β的关系为() A．α >β B ．α＝βC．α <β D ．α＋β＝ 90°2．设甲、乙两楼相距20 m，从乙楼底望甲楼顶的仰角为60°，从甲楼顶望乙楼顶的俯角为 30°，则甲、乙两楼的高分别是 ()40A． 20 3 m，33mB． 10 3 m,20 3 mC． 10(3－ 2) m,203 m1520D. 2 3 m，3 3 m3．如图，为测一树的高度，在地面上选用 A 、B 两点，从 A 、 B 两点分别测得望树尖的仰角为 30°， 45°，且 A 、 B 两点之间的距离为 60 m，则树的高度为()A． 30＋ 30 3 m B． 30＋ 153mC． 15＋ 30 3m D ．15＋ 33m4．从超出海平面 h 米的小岛看正东方向有一只船俯角为30°，看正南方向一只船俯角为 45°，则此时两船间的距离为 ()A． 2h 米 B. 2h 米C. 3h 米 D ． 22h 米5．在某个地点测得某山岳仰角为θ，对着山岳在平行地面上行进600 m 后测仰角为原来的 2 倍，持续在平行地面上行进2003m 后，测得山岳的仰角为本来的 4 倍，则该山岳的高度是 ()A． 200 m B． 300 mC． 400 m D． 100 3 m6．平行四边形中， AC ＝ 65，BD ＝17，周长为18，则平行四边形面积是() A． 16B． 17.5C． 18D． 18.53二、填空题7．甲船在 A 处察看乙船，乙船在它的北偏东60°的方向，两船相距 a 海里，乙船正向北行驶，若甲船是乙船速度的3倍，则甲船应取方向 __________ 才能追上乙船；追上时甲船行驶了 ________海里．8．△ ABC 中，已知 A ＝ 60°，AB ∶ AC ＝ 8∶5，面积为 10 3，则其周长为 ________．9．已知等腰三角形的底边长为6，一腰长为 12，则它的内切圆面积为 ________．10．某舰艇在 A 处测得遇险渔船在北偏东45°，距离为 10 n mile 的 C 处，此时得悉，该渔船沿北偏东105°方向，以每小时 9 n mile 的速度向一小岛凑近，舰艇时速21 n mile ，则舰艇抵达渔船的最短时间是______小时．三、解答题11．如下图，在山顶铁塔上 B 处测得地面上一点 A 的俯角为α，在塔底 C 处测得 A 处的俯角为β已.知铁塔BC部分的高为h，求山高CD.12．已知圆内接四边形ABCD 的边长 AB ＝ 2，BC＝ 6， CD＝ DA ＝ 4，求圆内接四边形ABCD 的面积．能力提高13．如下图，为认识某海疆海底结构，在海平面内一条直线上的A、B、C三点进行丈量．已知 AB ＝ 50 m ，BC ＝ 120 m，于 A 处测得水深 AD ＝ 80 m，于 B 处测得水深 BE ＝200 m，于 C 处测得水深 CF＝ 110 m，求∠ DEF 的余弦值．14．江岸边有一炮台高30 m，江中有两条船，由炮台顶部测得俯角分别为45°和 30°，并且两条船与炮台底部连成30°角，求两条船之间的距离．1．丈量底部不行抵达的建筑物的高度问题．因为底部不行抵达，这种问题不可以直接用解直角三角形的方法解决，但常用正弦定理和余弦定理，计算出建筑物顶部到一个可到达的点之间的距离，而后转变为解直角三角形的问题．2．丈量角度就是在三角形内利用正弦定理和余弦定理求角的正弦值或余弦值，再依据需要求出所求的角．§ 1.2 应用举例 (二)答案知识梳理11．上下2.2absin C作业设计1． B 2．A[h＝ 20tan 60 ＝°20 3(m)． h403(m)． ]甲 乙＝ 20tan 60 －°20tan 30 ＝°31＝ PB60×＝ 303．A[ 在△ PAB 中，由正弦定理可得60 ，PB ＝ 2 ，－3sin 30 ° sin 15 °sin 15 °h ＝PBsin 45 ＝°(30＋ 30 3)m.]4. A [如下图，BC ＝ 3h ， AC ＝h ，∴ AB ＝ 3h 2＋ h 2＝ 2h.]5． B [ 如下图， 600 · sin 2＝ 200θ 3· sin 4，θ∴ cos 2 θ＝3，∴ θ＝ 15°，∴ h ＝ 200 3·sin 4＝θ300 (m) ． ] 26．A[ 设两邻边 AD ＝ b ， AB ＝ a ，∠ BAD ＝α，则 a ＋b ＝ 9， a 2＋ b 2－ 2abcos α＝ 17， a 2＋ b 2－ 2abcos(180 °－ α)＝65.解得： a ＝ 5， b ＝ 4， cos α＝ 35或 a ＝ 4， b ＝ 5， cos α＝ 35，∴ S＝ ab sin＝α16.]7．北偏东 30°3a分析如下图，设到C 点甲船追上乙船，乙到 C 地用的时间为 t ，乙船速度为 v ，则 BC ＝ tv ，AC ＝ 3tv ， B ＝ 120°，BCAC由正弦定理知 sin ∠ CAB ＝sin B ，∴1 ＝ 3 ， sin ∠ CAB sin 120°∴ sin ∠ CAB ＝ 1，∴∠ CAB ＝ 30°，∴∠ ACB ＝30°， 2∴ BC ＝AB ＝ a ，∴ AC 2＝ AB 2＋BC2－ 2AB ·BCcos 120°＝ a 2＋ a 2－ 2a 2·－ 1＝ 3a 2，∴ AC ＝ 3a.28． 20分析1 3k 2＝10 3.设 AB ＝ 8k ， AC ＝ 5k ， k>0，则 S ＝ AB ·AC ·sin A ＝ 102∴ k ＝1， AB ＝ 8， AC ＝ 5，由余弦定理：222 221 BC ＝AB＋ AC－ 2AB ·AC ·cos A ＝ 8 ＋ 5－ 2×8×5× ＝ 49.2∴ BC ＝7，∴周长为 AB ＋ BC ＋ CA ＝ 20.27 π 9. 5分析不如设三角形三边为a ，b ，c 且 a ＝ 6， b ＝ c ＝ 12，由余弦定理得：222222＝7，cos A ＝ b ＋ c － a ＝ 12 ＋12 － 62bc 2×12×12 8 ∴ sin A ＝1－ 7 2＝ 15.881 1 3 15由 (a ＋ b ＋ c) ·r ＝ bcsin A 得 r ＝5.22∴ S2 27π内切圆＝ πr＝5.210.3分析设舰艇和渔船在 B 处相遇，则在△ ABC 中，由已知可得：∠ ACB ＝120°，设舰艇抵达渔船的最短时间为t ，则 AB ＝ 21t ， BC ＝9t ，AC ＝ 10，则 (21t) 2＝ (9t) 2＋ 100－2×10×9tcos 120 ，°解得 2或 t ＝－5t ＝ 312(舍 )．11．解 在△ ABC 中，∠ BCA ＝ 90°＋β，∠ ABC ＝ 90°－ α，∠ BAC ＝ α－ β，∠ CAD ＝ β.依据正弦定理得：AC＝BC，sin∠ ABC sin∠ BAC即AC＝BC，－－∴AC＝BCcos α＝hcos α.－－在 Rt△ACD中， CD ＝ACsin ∠ CAD ＝ ACsin β＝hcosα sin β－.即山高 CD 为hcosα sin β－.12．解连结 BD ，则四边形面积S＝ S△ABD＋ S△CBD＝1A B·AD·sin A ＋1B C·CD·sin C.22∵A ＋ C＝ 180°，∴ sin A＝ sin C.1∴S＝2(AB ·AD ＋ BC·CD)·sin A ＝16sin A.由余弦定理：在△ ABD 中， BD 2＝22＋42－2×2×4cos A＝ 20－16cos A ，在△ CDB 中， BD 2＝ 42＋ 62－ 2×4×6cos C＝ 52－ 48cos C，∴20－16cos A＝ 52－ 48cos C.1又 cos C＝－ cos A，∴ cos A＝－2.∴ A＝ 120 °.∴四边形 ABCD的面积 S＝ 16sin A ＝ 8 3.13．解作 DM∥AC 交 BE 于 N，交 CF于 M.DF＝MF 2＋DM 2＝302＋ 1702＝ 10 298(m)，DE＝DN 2＋ EN 2＝502＋ 1202＝ 130(m) ，EF＝－2＋BC 2＝902＋ 1202＝150(m) ．在△ DEF 中，由余弦定理的变形公式，得22－ DF222－ 10216DE ＋EF＝130 ＋150×298 cos∠ DEF＝2DE·EF ＝65.2×130 ×15016即∠ DEF 的余弦值为65.14．解如下图：∠CBD ＝ 30°，∠ ADB ＝30°，∠ ACB ＝45°∵ AB ＝30，∴BC＝30，30BD ＝＝30 3.tan 30°在△ BCD 中，CD2＝ BC2＋ BD 2－ 2BC·BD·cos 30 °＝ 900，∴ CD＝30，即两船相距30 m.。

精品“正版”资料系列，由本公司独创。

旨在将“人教版”、”苏教版“、”北师 大版“、”华师大版“等涵盖几乎所有版本的教材教案、课件、导学案及同步练习和 检测题分享给需要的朋友。

本资源创作于2020年8月，是当前最新版本的教材资源。

包含本课对应 内容，是您备课、上课、课后练习以及寒暑假预习的最佳选择。

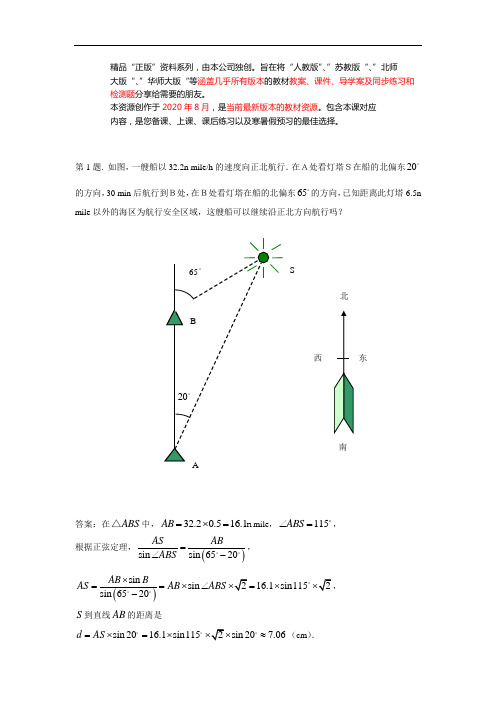
第1题. 如图，一艘船以32.2n mile/h 的速度向正北航行．在Ａ处看灯塔Ｓ在船的北偏东20的方向，30 min 后航行到Ｂ处，在Ｂ处看灯塔在船的北偏东65的方向，已知距离此灯塔6.5n mile 以外的海区为航行安全区域，这艘船可以继续沿正北方向航行吗？答案：在ABS △中，32.20.516.1AB =⨯=n mile ，115ABS ∠=， 根据正弦定理，()sin sin 6520AS ABABS =∠-， ()sin sin 16.1sin1152sin 6520AB B AS AB ABS ⨯==⨯∠=⨯⨯-，S 到直线AB 的距离是sin 2016.1sin1152sin 207.06d AS =⨯=⨯⨯⨯≈（cm ）．南 6520所以这艘船可以继续沿正北方向航行．第2题. 如图，在山脚A 测得出山顶P 的仰角为a ，沿倾斜角为β的斜坡向上走a 米到B ，在B 处测得山顶P 的仰角为γ，求证：山高()()sin sin sin -a a h a γβγ-=．答案：在ABP △中，180+ABP γβ∠=-，()()()180- 180-180+ =-BPA ABPαβαβγβγα∠=--∠=---．在ABP △中，根据正弦定理，()()()()sin sin sin -sin 180+αsin -sin -AP ABABP APBAP AP αγαγβγβγα=∠∠=-⨯=ＡＱ αβaBγＣ所以山高为()()sin sin -sin sin -h AP ααγβαγα==．第3题. 测山上石油钻井的井架BC 的高，从山脚A 测得65.3AC =m ，塔顶B 的仰角α是2525'．已知山坡的倾斜角是1738'，求井架的高BC ．答案：在ABC △中，65.3AC =m ，=25251738747BAC αβ'''∠=--=，90=9017387222ABC β''∠=--=，根据正弦定理，sin sin AC BCABC BAC=∠∠()sin 65.3sin 7479.3m sin sin 7222AC BAC BC ABC '∠==≈'∠井架的高约为9.3m ．Ａ βα DＢＣ(6739)第4题. 如图，货轮在海上以35n mile / h 的速度沿着方位角（从指北方向顺时针转到目标方向线的水平角）为148的方向航行．为了确定船位，在B 点观察灯塔A 的方位角是126，航行半小时后到达Ｃ点，观察灯塔A 的方位角是78．求货轮到达Ｃ点时与灯塔A 的距离（精确到１ n mile ）．答案：在ABC △中，BC ＝350.517.5⨯=n mile ，14812612ABC ∠=-=，()78180148110ACB ∠=+-=，1801101258BAC ∠=--=，根据正弦定理，sin sin AC BCABC BAC=∠∠， sin 17.5sin124.29sin sin 58BC ABC AC BAC ∠==≈∠（nmile ）．货轮到达Ｃ点时与灯塔的距离是约4.29n mile ．第5题. 轮船A 和轮船B 在中午12时离开海港C ，两艘轮船的航行方向之间的夹角为120，轮船A 的航行速度是25 n mile/h ，轮船B 的航行速度是15 n mile/h ，下午2时两船之间的距离是多少？答案：70 n mile ．第6题. 如图，已知一艘船从30 n mile/h 的速度往北偏东10的A 岛行驶，计划到达A 岛后停留10 min 后继续驶往B 岛，B 岛在A 岛的北偏西60的方向上．船到达Ｃ处时是上午10时整，此时测得B 岛在北偏西30的方向，经过20 min 到达Ｄ处，测得B 岛在北偏西45的方向，如果一切正常的话，此船何时能到达B 岛？78126BA3045 60BA20 min答案：在BCD △中，301040,BCD ∠=+=1801804510125BDC ADB ∠=-∠=--=，130103CD =⨯=（n mile ）， 根据正弦定理，sin sin CD BD CBD BCD =∠∠，()10sin 40sin 18040125BD=∠--， 10sin 40sin15BD ⨯=．在ABD △中，451055ADB ∠=+=，1806010110BAD ∠=--=， 1801105515ABD ∠=--=．根据正弦定理， sin sin sin AD BD ABABD BAD ADB==∠∠∠， 就是sin15sin110sin 55AD BD AB==， sin1510sin 406.84sin 70sin110BD AD ==≈（n mile ）．sin 5510sin 40sin 5521.65sin110sin15sin 70BD AB ==≈(n mile)．如果这一切正常，此船从Ｃ开始到Ｂ所需要的时间为：6.8421.65206010306086.983030AD AB +++⨯+≈+⨯≈（min ） 即约１小时26分59秒．所以此船约在11时27分到达Ｂ岛．第7题. 一架飞机在海拔8000m 的高度飞行，在空中测出前下方海岛两侧海岸俯角分别是2739和，计算这个海岛的宽度．答案：约5821.71m ．第8题. 一架飞机从A 地飞到B 到，两地相距700km ．飞行员为了避开某一区域的雷雨云层，从机场起飞后，就沿与原来的飞行方向成21角的方向飞行，飞行到中途，再沿与原来的飞行方向成35夹角的方向继续飞行直到终点．这样飞机的飞行路程比原来路程700km 远了多少？答案：在ABC △中，700AB =km ，1802135124ACB ∠=--=， 根据正弦定理，700sin124sin 35sin 21AC BC==， 700sin 35sin124AC =，700sin 21sin124BC =，700sin 35700sin 21786.89sin124sin124AC BC +=+≈（km ），所以路程比原来远了约86.89km ．8000m27 39P 700km21BC35第9题. 为测量某塔的高度，在A ，B 两点进行测量的数据如图所示，求塔的高度．答案：在21.418.6 2.8ABT ATB ∠=-=△中，，9018.6ABT ∠=+，15AB =（m ）．根据正弦定理，sin 2.8cos18.6AB AT=，15cos18.6sin 2.8AT ⨯=． 塔的高度为15cos18.6tan 21.4tan 21.4114.05sin 2.8AT =≈（m ）．第10题. A ，B 两地相距2558m ，从A ，B 两处发出的 两束探照灯光照射在上方一架飞机的机身上（如图），飞机离 两个探照灯的距离是多少？飞机的高度是多少？答案：飞机离A 处控照灯的距离是4801.53m ， 飞机离B 处探照灯的距离是4704.21m ， 飞机的高度是约4574.23m ．A72.3 76.5B第11题. 一架飞以326km/h 的速度，沿北偏东75的航向从城市A 出发向城市B 飞行，18min 以后，飞机由于天气原因按命令改飞另一个城市C ，问收到命令时飞机应该沿什么航向飞行，此时离城市C 的距离是多少？答案：AE =3261897.860⨯=km ， 在ACD △中，根据余弦定理：222cos66AC AD CD AD CD =+- 2257110257110cos66=+-⨯⨯ 101.235=根据正弦定理：sin sin AD ACACD ADC=∠∠， sin 57sin 66sin 0.5144101.235AD ADC ACD AC ∠∠==≈，30.96ACD ∠≈，13330.96102.04ACB ∠≈-=．在ABC △中，根据余弦定理：222cos AB AC BC AC BC ACB =+-∠22101.2352042101.235204cos102.04=+-⨯⨯245.93≈，222cos 2AB AC BC BAC AB AC +-∠=222245.93101.2352042245.93101.235+-=⨯⨯0.5847≈，54.21BAC ∠=．在ACE △中，根据余弦定理：222cos CE AC AE AC AE EAC +-∠22101.23597.82101.23597.80.5487=+-⨯⨯⨯90.75≈，222cos 2AE EC AC AEC AE EC +-∠=．22297.890.75101.2350.4254297.890.75+-≈≈⨯⨯，64.82AEC ∠=，()180180757564.8210.18AEC -∠--=-=．所以，飞机应该以南偏西10.18的方向飞行，飞行距离约90.75km ．第12题. 飞机的航线和山顶在同一个铅垂平面内，已知飞机的高度为海拔20250m ，速度为1000km/h ，飞行员先看到山顶的俯角为1830'，经过150s 后又看到山顶的俯角为81，求山顶的海拔高度（精确到1m ）．答案：飞行在150秒内飞行的距离是150100010003600d =⨯⨯m ， 根据正弦定理，()sin18.5sin 8118.5d x=-，这里x 是飞机看到山顶的俯角为81时飞机与山顶的距离．飞机与山顶的海拔的差是：C DB A E1830'81()sin18.5tan81tan8114721.64sin 8118.5d x =≈-(m)，山顶的海拔是2025014721.645528-≈m ．第13题. 一个人在建筑物的正西A 点，测得建筑物顶的仰角是α，这个人再从A 点向南走到B 点，再测得建筑物顶的仰角是β，设A，B 间的距离是a ． ．答案：设建筑物的同度是h ，建筑物的底部是C ， 则tan tan h h AC BC αβ==，． ABC △是直角三角形，BC 是斜边，所以222tan tan b h a αβ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭，222211tan tan a h βα⎡⎤⎛⎫⎛⎫=-⎢⎥⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦， 222222tan tan tan tan a h αβαβ=-2222222sin sin sin cos cos sin a αβαβαβ=- ()()222sin sin sin sin a αβαβαβ=--． 所以，h =．α ABDCβah。

1.2 应用举例学习目标：1．通过回顾正弦定理、余弦定理的表达式及文字语言的叙述，进—步熟悉正、余弦定理的内容，作用及所解三角形的类型．能够联系勾股定理、三角形面积定理及三角形内角和公式等有关三角形问题灵活地解三角形．2．善于利用分类讨论的思想、先易后难、逐层推进的思想解决一些繁、难三角形问题，把对学生的思维训练贯穿整节课的始终．重点难点重点：灵活选用正弦定理、余弦定理并结合面积公式进行有关的三角形中的几何计算．难点：利用正、余弦定理进行边角互化及正弦、余弦定理与三角形有关性质的综合应用.知识点：三角形的面积公式问题导思：如图，△ABC中，边BC、CA、AB上的高分别记为h a，h b和h c.1．你能用△ABC 的边角分别表示h a ，h b ，h c 吗？ 答：h a ＝b sin C ＝c sin B .h b ＝c sin A ＝a sin C .h c ＝b sin A ＝a sin B .2．你能用边a 与高h a 表示△ABC 的面积吗？答：S △ABC ＝12ah a ＝12ab sin C ＝12ac sin B .三角形面积公式已知△ABC 中，a ，b ，c 所对的角分别为A ，B ，C ，其面积为S ，则S ＝ ＝ ＝ . 12ab sin C 12bc sin A 12ca sin B类型1：三角形中的面积计算例1：在△ABC中，已知∠C＝120°，AB＝23，AC＝2，求△ABC的面积．解：由正弦定理AB sin C ＝AC sin B， ∴sin B ＝AC sin C AB ＝2sin 120°23＝12. 因为AB >AC ，所以∠C >∠B ，∴∠B ＝30°，∴∠A ＝30°.所以△ABC 的面积S ＝12AB ·AC ·sin A ＝12·23·2·sin 30°＝ 3.变式训练1：在△ABC中，∠A＝60°，AB＝2，且△ABC的面积S△ABC＝32，则边BC的长为________．【解析】由S △ABC ＝32，得12AB ·AC sin A ＝32， 即12×2AC ×32＝32，∴AC ＝1.由余弦定理得BC 2＝AB 2＋AC 2－2AB ·AC ·cos A ＝22＋12－2×2×1×12＝3. ∴BC ＝ 3.【答案】 3类型2：三角形中的证明问题例2：在△ABC中，求证：a(sin B－sin C)＋b(sin C－sin A)＋c(sin A－sin B)＝0.解：由正弦定理asin A＝bsin B＝csin C，则a sin B＝b sin A，a sin C＝c sin A，b sin C＝c sin B，所以左边＝a sin B－a sin C＋b sin C－b sin A＋c sin A－c sin B ＝(a sin B－b sin A)＋(b sin C－c sin B)＋(c sin A－a sin C)＝0＋0＋0＝0＝右边，所以原式成立．变式训练2：在△ABC中，内角A，B，C的对边分别为a，b，c.已知cos A－2cos Ccos B＝2c－ab.求证sin Csin A＝2.证明：由正弦定理，设a sin A ＝b sin B ＝c sin C＝k ， 则2c －a b ＝2k sin C －k sin A k sin B ＝2sin C －sin A sin B， 所以cos A －2cos C cos B ＝2sin C －sin A sin B， 即(cos A －2cos C )sin B ＝(2sin C －sin A )cos B .化简可得sin(A ＋B )＝2sin(B ＋C )，又∠A ＋∠B ＋∠C ＝π，所以sin C ＝2sin A ，因此sin C sin A＝2.类型3：三角形中的综合问题例3：△ABC 的内角A 、B 、C 所对的边分别为a 、b 、c ，若a 、b 、c 成等比数列且cos B ＝35.(1)求cos Asin A ＋cos Csin C 的值；(2)设BA →·BC →＝3，求a ＋c 的值．解：(1)由已知b 2＝ac ，及正弦定理得sin 2B ＝sin A sinC ，由cos B ＝35，则sin B ＝45.cos A sin A ＋cos C sin C ＝sin C cos A ＋cos C sin A sin A sin C＝sin (A ＋C )sin A sin C ＝sin B sin A sin C ＝1sin B ＝54.(2)由BA →·BC →＝3，得ac cos B ＝3，ac ＝3cos B ＝5，由余弦定理：b 2＝a 2＋c 2－2ac ×35， 得ac ＝a 2＋c 2－65ac ， a 2＋c 2＋2ac ＝215ac ＝21， ∴(a ＋c )2＝21.∴a ＋c ＝21.变式训练3：△ABC中，∠A、∠B、∠C的对边分别为a、b、c，且2b·cos A＝c·cos A＋a·cos C，(1)求∠A的大小；(2)若a＝7，b＋c＝4，求△ABC的面积．解：(1)由已知条件得2cos A sin B ＝sin A cos C ＋cos A sin C ＝sin(A ＋C )＝sin B .又∵sin B ≠0，∴cos A ＝12. 又∵0°<∠A <180°，∴∠A ＝60°.(2)由余弦定理得7＝b 2＋c 2－2bc ·cos 60°＝b 2＋c 2－bc ＝(b ＋c )2－3bc ， 将b ＋c ＝4代入，得bc ＝3.故△ABC 面积为S ＝12bc sin A ＝334.课堂小结：1．对于三角形中的几何计算问题，首先要把所求的量转化到三角形中，然后选用正弦定理、余弦定理解决．求三角形的面积的问题，先观察已知什么，尚缺什么，用正弦定理和余弦定理算出需要的元素，就可以求出三角形的面积．证明三角恒等式的关键是用正、余弦定理实现边角转化．2．许多问题既可用正弦定理也可用余弦定理解决，甚至可以两者兼用，当一个公式求解受阻时要及时考虑其他公式列式．3．解三角形问题除了应用正、余弦定理外，也经常用到内角和定理以及三角变换公式中的平方关系、两角和与差的正、余弦公式等.当堂检测：1．在△ABC 中，∠A ＝60°，AB ＝1，AC ＝2，则S △ABC 的值为( )A ．12B ．32C ．3D ．2 3【解析】S △ABC ＝12AB ·AC sin A ＝sin 60°＝32.【答案】B2．△ABC中，若∠A＝60°，b＝16，此三角形的面积S＝2203，则a的值为()A．20 6 B．25C．55 D．49【解析】由12bc sin A＝2203，∴c＝55.又a2＝b2＋c2－2bc cos A＝2 401.∴a＝49. 【答案】D3．边长为a的等边三角形的高为________．【解析】高h＝a sin 60°＝3 2a.【答案】3 2a4．已知△ABC 中，AB ＝3，BC ＝13，AC ＝4，求AC 边上的高． 解：设AC 边上的高为h ，由余弦定理知cos B ＝32＋(13)2－162×3×13＝1313，∴sin B ＝23913， ∴S ＝12×3×13×23913＝332×2＝3 3. 又S ＝12×4×h ，∴2h ＝33，∴h ＝332， ∴AC 边上的高为332.5．在△ABC 中，内角A 、B 、C 的对边分别为a 、b 、c ，cos A ＝13，a ＝3，探究△ABC 的面积S 的最大值．解：∵cos A＝13，∴sin A＝223，由正弦定理得b＝asin A·sin B＝364sin B，c＝asin A·sin C＝364sin C，∴bc＝(364)2sin B sin C＝278·12[cos(B－C)－cos(B＋C)]，又∵cos(B ＋C )＝－cos A ＝－13， ∴bc ＝2716[cos(B －C )＋13]≤94，∴S ＝12bc sin A ≤324. 故△ABC 的面积S 的最大值为324.。

1.2 应用举例
知识1：基线的概念
线段
基线长度精确度
高
：测量中的有关概念知识2
水平面
水平宽度
目标
垂直
类型1：求两点间可视但不可到达的距离问题
类型2：求两点均不可到达的距离问题
类型3：求底部不可到达的物体的高度问题
课堂小结：
1．解决实际测量问题一般要充分认真理解题意，正确作出图形，从中抽象出一个或几个三角形，把实际问题中的条件和所求转
换成三角形的已知和未知的边、角，然后解三角形，得到实际
问题的解．
2．运用正弦定理、余弦定理解决实际问题要依以下步骤进行(1)分析：理解题意，弄清已知与未知，画出示意图(一个或几个三角形)；
(2)建模：根据已知条件与求解目标，把已知量与待求量尽
可能地集中在有关三角形中，建立一个解三角形的数学模型；
(3)求解：利用正弦定理、余弦定理有序地解这些三角形，
求得数学模型的解；
(4)检验：检验上述所求的解是否符合实际问题，从而得出
实际问题的解．
【答案】B
【答案】D。

学习目标 1.会运用测仰角(或俯角)解决一些有关底部不可到达的物体高度测量的问题.2.会用测方位角解决立体几何中求高度问题.3.进一步培养学习数学、应用数学的意识．知识点一 测量仰角(或俯角)求高度问题思考 如图，AB 是底部B 不可到达的一个建筑物，A 为建筑物的最高点，如果能测出点C ，D 间的距离m 和由C 点，D 点观察A 的仰角，怎样求建筑物高度AB ？(已知测角仪器的高是h )答案 解题思路是：在△ACD 中，AC sin β＝msin(α－β).所以AC ＝msin βsin(α－β)，在Rt △AEC 中，AE ＝AC sin α，AB ＝AE ＋h .梳理 问题的本质如图，已知∠AEC 为直角，CD ＝m ，用α、β、m 表示AE 的长，所得结果再加上h .知识点二 测量方位角求高度思考 如图，一辆汽车在一条水平的公路上向正西行驶，到A 处时测得公路北侧远处一山顶D 在西偏北15°的方向上，行驶5km 后到达B 处，测得此山顶在西偏北25°的方向上，仰角为8°，怎样求此山的高度CD?答案 先在△ABC 中，用正弦定理求BC ＝5sin15°sin10°，再在Rt △DBC 中求DC ＝BC tan8°.梳理 问题本质是：如图，已知三棱锥D －ABC ，DC ⊥平面ABC ，AB ＝m ，用α、β、m 、γ表示DC 的长．类型一 测量仰角(或俯角)求高度问题 命题角度1 仰角例1 如图所示，D ，C ，B 在地平面同一直线上，DC ＝10m ，从D ，C 两地测得A 点的仰角分别为30°和45°，则A 点离地面的高AB 等于( )A ．10mB ．53mC ．5(3－1) mD ．5(3＋1) m答案 D解析 方法一 设AB ＝x m ，则BC ＝x m. ∴BD ＝(10＋x )m.∴tan ∠ADB ＝AB DB ＝x 10＋x ＝33.解得x ＝5(3＋1)m.所以A 点离地面的高AB 等于5(3＋1)m. 方法二 ∵∠ACB ＝45°，∴∠ACD ＝135°， ∴∠CAD ＝180°－135°－30°＝15°. 由正弦定理，得AC ＝CDsin∠CAD ·sin∠ADC＝10sin15°·sin30°＝206－2.∴AB ＝AC sin45°＝5(3＋1)m.反思与感悟 (1)底部可到达，此类问题可直接构造直角三角形．(2)底部不可到达，但仍在同一与地面垂直的平面内，此类问题中两次观测点和所测垂线段的垂足在同一条直线上，观测者一直向“目标物”前进．跟踪训练1 某登山队在山脚A 处测得山顶B 的仰角为35°，沿倾斜角为20°的斜坡前进1000m 后到达D 处，又测得山顶的仰角为65°，则山的高度为________m ．(精确到1m)答案 811解析 如图，过点D 作DE ∥AC 交BC 于E ，因为∠DAC ＝20°， 所以∠ADE ＝160°，于是∠ADB ＝360°－160°－65°＝135°. 又∠BAD ＝35°－20°＝15°， 所以∠ABD ＝30°. 在△ABD 中，由正弦定理，得AB ＝ADsin∠ADB sin∠ABD ＝1000×sin135°sin30°＝10002(m)．在Rt △ABC 中，BC ＝AB sin35°≈811(m)． 所以山的高度约为811m. 命题角度2 俯角例2 如图，在山顶铁塔上B 处测得地面上一点A 的俯角α＝54°40′，在塔底C 处测得A 处的俯角β＝50°1′.已知铁塔BC 部分的高为27.3m ，求出山高CD .(精确到1m)解 在△ABC 中，∠BCA ＝90°＋β，∠ABC ＝90°－α，∠BAC ＝α－β，∠BAD ＝α. 根据正弦定理，BC sin(α－β)＝ABsin(90°＋β)，所以AB ＝BCsin(90°＋β)sin(α－β)＝BCcos βsin(α－β).解Rt △ABD ，得BD ＝AB sin ∠BAD ＝BCcos βsin αsin(α－β).将测量数据代入上式，得BD ＝27.3cos50°1′sin54°40′sin(54°40′－50°1′)＝27.3cos50°1′sin54°40′sin4°39′≈176.5(m)．CD ＝BD －BC ≈176.5－27.3≈149(m)．答 山的高度约为149m.反思与感悟 利用正弦、余弦定理来解决实际问题时，要从所给的实际背景中，进行加工、提炼，抓住本质，抽象出数学模型，使之转化为解三角形问题．跟踪训练2 江岸边有一炮台高30m ，江中有两条船，船与炮台底部在同一水面上，由炮台顶部测得俯角分别为45°和30°，而且两条船与炮台底部连线成30°角，则两条船相距_____m. 答案 30解析 设两条船所在位置分别为A 、B 两点，炮台底部所在位置为C 点， 在△ABC 中，由题意可知AC ＝30tan30°＝303(m)，BC ＝30tan45°＝30(m)，C ＝30°，AB 2＝(303)2＋302－2×303×30×cos30°＝900，所以AB ＝30(m)．类型二 测量方位角求高度问题例3 如图所示，A 、B 是水平面上的两个点，相距800m ，在A 点测得山顶C 的仰角为45°，∠BAD ＝120°，又在B 点测得∠ABD ＝45°，其中D 点是点C 到水平面的垂足，求山高CD.解 由于CD ⊥平面ABD ，∠CAD ＝45°，所以CD ＝AD . 因此只需在△ABD 中求出AD 即可，在△ABD 中，∠BDA ＝180°－45°－120°＝15°， 由AB sin15°＝ADsin45°，得AD ＝AB·sin45°sin15°＝800×226－24＝800(3＋1)(m)．即山的高度为800(3＋1) m.反思与感悟 此类问题特点：底部不可到达，且涉及与地面垂直的平面，观测者两次观测点所在直线不经过“目标物”，解决办法是把目标高度转化为地平面内某量，从而把空间问题转化为平面内解三角形问题． 跟踪训练3 如图，为测得河对岸塔AB 的高，先在河岸上选一点C ，使C 在塔底B 的正东方向上，测得点A的仰角为60°，再由点C 沿北偏东15°方向走10m 到位置D ，测得∠BDC ＝45°，则塔AB 的高是( )A ．10mB ．102mC ．103mD ．106m答案 D解析 在△BCD 中，CD ＝10m ，∠BDC ＝45°， ∠BCD ＝15°＋90°＝105°，∠DBC ＝30°， 由正弦定理， 得BC sin∠BDC ＝CDsin∠DBC ，BC ＝10sin45°sin30°＝102(m)．在Rt △ABC 中，tan60°＝ABBC，AB ＝BC ×tan60°＝106(m)．1．一架飞机在海拔8000m 的高度飞行，在空中测出前下方海岛两侧海岸俯角分别是30°和45°，则这个海岛的宽度为________m ．(精确到0.1m) 答案 5856.4解析 宽＝8000tan30°－8000tan45°＝5856.4(m)．2．甲、乙两楼相距20米，从乙楼底望甲楼顶的仰角为60°，从甲楼顶望乙楼顶的俯角为30°，则甲、乙两楼的高分别是________________． 答案 203米、4033米解析 甲楼的高为20tan60°＝20×3＝203(米)， 乙楼的高为203－20tan30°＝203－20×33＝4033(米)． 3．为测量某塔的高度，在A ，B 两点进行测量的数据如图所示，求塔的高度．解 在△ABT 中，∠ATB ＝21.4°－18.6°＝2.8°， ∠ABT ＝90°＋18.6°，AB ＝15(m)． 根据正弦定理，15sin2.8°＝ATcos18.6°，AT ＝15×cos18.6°sin2.8°.塔的高度为AT ×sin21.4°＝15×cos18.6°sin2.8°×sin21.4°≈106.19(m)．1．在研究三角形时，灵活根据两个定理可以寻找到多种解决问题的方案，但有些过程较繁琐，如何找到最优的方法，最主要的还是分析两个定理的特点，结合题目条件来选择最佳的计算方式．2．测量底部不可到达的建筑物的高度问题．由于底部不可到达，这类问题不能直接用解直角三角形的方法解决，但常用正弦定理和余弦定理，计算出建筑物顶部到一个可到达的点之间的距离，然后转化为解直角三角形的问题．40分钟课时作业一、选择题1．为了测某塔AB 的高度，在一幢与塔AB 相距20m 的楼顶处测得塔顶的仰角为30°，塔基的俯角为45°，那么塔AB 的高为( ) A ．20⎝ ⎛⎭⎪⎫1＋33m B ．201＋32m C ．20(1＋3) m D ．30m答案 A解析 塔的高度为20tan30°＋20tan45°＝20⎝ ⎛⎭⎪⎫1＋33(m)，故选A. 2．在某个位置测得某山峰仰角为θ，对着山峰在地面上前进600m 后测得仰角为2θ，继续在地面上前进2003m 以后测得山峰的仰角为4θ，则该山峰的高度为( ) A ．200mB ．300mC ．400mD ．1003m 答案 B解析 方法一 如图，△BED ，△BDC 为等腰三角形，BD ＝ED ＝600m ，BC ＝DC ＝2003m.在△BCD 中， 由余弦定理可得cos2θ＝6002＋(2003)2－(2003)22×600×2003＝32，∴2θ＝30°，4θ＝60°. 在Rt △ABC 中，AB ＝BC sin4θ＝2003×32＝300(m)， 故选B.方法二 由于△BCD 是等腰三角形， 12BD ＝DC cos2θ， 即300＝2003cos2θ. cos2θ＝32，0°＜2θ＜90°，2θ＝30°，4θ＝60°. 在Rt △ABC 中，AB ＝BC ·sin4θ＝2003×32＝300(m)， 故选B.3．已知两座灯塔A ，B 与海洋观察站C 的距离相等，灯塔A 在观察站C 的北偏东40°，灯塔B 在观察站C 的南偏东60°，则灯塔A 在灯塔B 的( )A ．北偏东10°B ．北偏西10°C ．南偏东10°D ．南偏西10°答案 B解析 如图，因为△ABC 为等腰三角形， 所以∠CBA ＝12(180°－80°)＝50°，60°－50°＝10°，故选B.4．从高出海平面h 米的小岛看正东方向有一只船俯角为30°，看正南方向有一只船俯角为45°，则此时两船间的距离为( )A ．2h 米B.2h 米C.3h 米D ．22h 米答案 A解析如图所示，BC＝3h，AC＝h，∴AB＝3h2＋h2＝2h(米)．5．某人在C点测得某塔在南偏西80°，塔顶仰角为45°，此人沿南偏东40°方向前进10m到D，测得塔顶A的仰角为30°，则塔高为( )A．15m B．5mC．10m D．12m答案 C解析如图，设塔高为h，在Rt△AOC中，∠ACO＝45°，则OC＝OA＝h.在Rt△AOD中，∠ADO＝30°，则OD＝3h.在△OCD中，∠OCD＝120°，CD＝10，由余弦定理，得OD2＝OC2＋CD2－2OC·CD cos∠OCD，即(3h)2＝h2＋102－2h×10×cos120°，∴h2－5h－50＝0，解得h＝10或h＝－5(舍)．即塔高为10m.6．要测量底部不能到达的东方明珠电视塔的高度，在黄浦江西岸选择甲、乙两观测点，在甲、乙两点分别测得塔顶的仰角分别为45°，30°，在水平面上测得电视塔与甲地连线及甲、乙两地连线所成的角为120°，甲、乙两地相距500m，则电视塔在这次测量中的高度是( )A．1002m B．400mC．2003m D．500m答案 D解析 由题意画出示意图，设高AB ＝h ，在Rt △ABC 中，由已知BC ＝h ， 在Rt △ABD 中， 由已知BD ＝3h ， 在△BCD 中，由余弦定理BD 2＝BC 2＋CD 2－2BC ×CD ×cos ∠BCD ，得3h 2＝h 2＋5002＋h ×500，解得h ＝500(m)(负值舍去)．故选D. 二、填空题7.如图所示为一角槽，已知AB ⊥AD ，AB ⊥BE ，并测量得AC ＝3mm ，BC ＝22mm ，AB ＝29mm ，则∠ACB ＝________.答案3π4解析 在△ABC 中，由余弦定理，得 cos ∠ACB ＝32＋(22)2－(29)22×3×22＝－22.因为∠ACB ∈(0，π)，所以∠ACB ＝3π4.8.如图，测量河对岸的塔高AB 时，可以选与塔底B 在同一水平面内的两个测点C 与D ，测得∠BCD ＝15°，∠BDC ＝30°，CD ＝30米，并在点C 测得塔顶A 的仰角为60°，则塔高AB ＝________米．答案 15 6解析 在△BCD 中，∠CBD ＝180°－15°－30°＝135°.由正弦定理，得BC sin∠BDC ＝CDsin∠CBD，所以BC ＝30sin30°sin135°＝15 2.在Rt △ABC 中，AB ＝BC tan ∠ACB ＝152×tan60° ＝156(米)．9．如图，A 、B 、C 、D 都在同一个与水平面垂直的平面内，B 、D 为两岛上的两座灯塔的塔顶．测量船于水面A 处测得B 点和D 点的仰角分别为75°，30°，于水面C 处测得B 点和D 点的仰角均为60°，AC ＝0.1km.若AB ＝BD ，则B 、D 间的距离为________km.答案32＋620解析 在△ABC 中，∠BCA ＝60°， ∠ABC ＝75°－60°＝15°，AC ＝0.1km ， 由正弦定理，得AB sin∠BCA ＝ACsin∠ABC，所以AB ＝0.1sin60°sin15°＝32＋620(km)，又因为BD ＝AB ，所以BD ＝32＋620(km)．三、解答题10．如图，在山脚A 测得山顶P 的仰角为α，沿倾斜角为β的斜坡向上走a 米到B ，在B 处测得山顶P 的仰角为γ，求证：山高h ＝asin αsin(γ－β)sin(γ－α).证明 在△ABP 中，∠ABP ＝180°－γ＋β， ∠BPA ＝180°－(α－β)－∠ABP＝180°－(α－β)－(180°－γ＋β)＝γ－α. 在△ABP 中，根据正弦定理，AP sin∠ABP ＝AB sin∠APB， 即AP sin(180°－γ＋β)＝a sin(γ－α)， AP ＝a×sin (γ－β)sin(γ－α)， 所以山高h ＝AP sin α＝asin αsin(γ－β)sin(γ－α). 11．某人在塔的正东沿着南偏西60°的方向前进40m 后，望见塔在东北，若沿途测得塔的最大仰角为30°，求塔高．解 如图所示，设AE 为塔，B 为塔正东方向一点，沿南偏西60°行走40m 到达C 处，即BC ＝40，∠CAB ＝135°，∠ABC ＝30°，∠ACB ＝15°.在△ABC 中，AC sin∠ABC ＝BC sin∠CAB， 即AC sin30°＝40sin135°， ∴AC ＝20 2.过点A 作AG ⊥BC ，垂足为G ，此时仰角∠AGE 最大，在△ABC 中，由面积公式知12×BC ×AG ＝12×BC ×AC ×sin ∠ACB . ∴AG ＝AC×CB×sin∠ACB BC＝202×40×sin15°40＝202sin15°，∴AG ＝202sin(45°－30°)＝202(22×32－22×12) ＝10(3－1)．在Rt △AEG 中，∵AE ＝AG tan ∠AGE ，∴AE ＝10(3－1)×33＝10－1033， 所以塔高为(10－1033)m. 12．为保障高考的公平性，高考时每个考点都要安装手机屏蔽仪，要求在考点周围1千米处不能收到手机信号，检查员抽查青岛市一考点，在考点正西3千米有一条北偏东60°方向的公路，在此处检查员用手机接通电话，以每小时12千米的速度沿公路行驶，问最长需要多少分钟检查员开始收不到信号，并至少持续多长时间该考点才算合格？解 如图所示，考点为A ，检查开始处为B ，设检查员行驶到公路上C ，D 两点之间时收不到信号，即公路上C ，D 两点到考点的距离为1千米．在△ABC 中，AB ＝3(千米)，AC ＝1(千米)，∠ABC ＝30°，由正弦定理，得sin ∠ACB ＝sin30°AC ×AB ＝32， ∴∠ACB ＝120°(∠ACB ＝60°不合题意)，∴∠BAC ＝30°，∴BC ＝AC ＝1(千米)．在△ACD 中，AC ＝AD ＝1，∠ACD ＝60°，∴△ACD 为等边三角形，∴CD ＝1(千米)．∵BC 12×60＝5， ∴在BC 上需5分钟，CD 上需5分钟．∴最长需要5分钟检查员开始收不到信号，并持续至少5分钟才算合格．。

1.2 应用举例(二)一、基础达标1．为了测某塔AB 的高度，在一幢与塔AB 相距20 m 的楼顶处测得塔顶的仰角为30°，塔基的俯角为45°，那么塔AB 的高为( )A ．20⎝ ⎛⎭⎪⎫1＋33 mB ．20⎝⎛⎭⎪⎫1＋32 m C ．20(1＋3) m D ．30 m答案 A解析 如图，h ＝20tan 30°＋20tan 45°＝20⎝⎛⎭⎪⎫1＋33(m)，故选A. 2．在某个位置测得某山峰仰角为θ，对着山峰在地面上前进600 m 后测得仰角为2θ，继续在地面上前进200 3 m 以后测得山峰的仰角为4θ，则该山峰的高度为( )A ．200 mB ．300 mC ．400 mD ．100 3 m答案 B解析 法一 如图，△BED ，△BDC 为等腰三角形，BD ＝ED ＝600，BC ＝DC ＝200 3.在△BCD 中，由余弦定理可得cos 2θ＝6002＋(2003)2－(2003)22×600×2003＝32，∴2θ＝30°，4θ＝60°.在Rt △ABC 中，AB ＝BC ·sin 4θ＝2003×32＝300，故选B. 法二 由于△BCD 是等腰三角形，12BD ＝DC cos 2θ，即300＝2003cos 2θ.cos2 θ＝32，2θ＝30°，4θ＝60°.在Rt △ABC 中，AB ＝BC ·sin 4θ＝2003×32＝300，故选B.3．一架飞机在海拔8 000 m 的高度飞行，在空中测出前下方海岛两侧海岸俯角分别是30°和45°，则这个海岛的宽度为________．答案 5 856.4 m解析 宽＝8 000tan 30°－8 000tan 45°＝5 856.4(m)．4．为测量某塔的高度，在A ，B 两点进行测量的数据如图所示，求塔的高度．解 在△ABT 中，∠ATB ＝21.4°－18.6°＝2.8°，∠ABT ＝90°＋18.6°，AB ＝15(m)．根据正弦定理，AB sin 2.8°＝AT cos 18.6°，AT ＝15×cos 18.6°sin 2.8°.塔的高度为AT ·tan 21.4°＝15·cos 18.6°sin 2.8°·tan 21.4°≈114.05(m)． 所以塔的高度为114.05 m.5．如图，某货轮在A 处看灯塔B 在货轮的北偏东75°，距离为12 6 n mile ，在A 处看灯塔C 在货轮的北偏西30°，距离为8 3 n mile ，货轮由A 处向正北航行到D 处时，再看灯塔B 在货轮的南偏东60°.求：(1)A处与D处的距离；(2)灯塔C与D处的距离．解(1)在△ABD中，∠ADB＝60°，B＝45°，由正弦定理得AD＝AB sin B sin∠ADB＝126×2 232＝24 (n mile)．所以A处与D处的距离为24 n mile.(2)在△ADC中，由余弦定理得CD2＝AD2＋AC2－2AD·AC cos 30°，解得CD＝8 3 n mile.即灯塔C与D处的距离为8 3 n mile.二、能力提升6．某人在C点测得某塔在南偏西80°，塔顶仰角为45°，此人沿南偏东40°方向前进10 m到D，测得塔顶A的仰角为30°，则塔高为() A．15 m B．5 m C．10 m D．12 m答案 C解析如图，设塔高为h，在Rt△AOC中，∠ACO＝45°，则OC＝OA＝h.在Rt△AOD中，∠ADO＝30°，则OD＝3h.在△OCD中，∠OCD＝120°，CD＝10，由余弦定理得OD2＝OC2＋CD2－2OC·CD cos ∠OCD，即(3h)2＝h2＋102－2h×10×cos 120°，∴h2－5h－50＝0，解得h＝10或h＝－5(舍)．7．要测量底部不能到达的东方明珠电视塔的高度，在黄浦江西岸选择甲、乙两观测点，在甲、乙两点分别测得塔顶的仰角分别为45°，30°，在水平面上测得电视塔与甲地连线及甲、乙两地连线所成的角为120°，甲、乙两地相距500 m，则电视塔在这次测量中的高度是()A．100 2 m B．400 mC．200 3 m D．500 m答案 D解析由题意画出示意图，设高AB＝h，在Rt△ABC中，由已知BC＝h，在Rt△ABD中，由已知BD＝3h，在△BCD中，由余弦定理BD2＝BC2＋CD2－2BC·CD·cos ∠BCD得，3h2＝h2＋5002＋h·500，解之得h＝500 m．故选D.8．如图，在山脚A测得出山顶P的仰角为α，沿倾斜角为β的斜坡向上走a米到B，在B处测得山顶P的仰角为γ，求证：山高h＝a sin αsin(γ－β)sin(γ－α).解 在△ABP 中，∠ABP ＝180°－γ＋β，∠BP A ＝180°－(α－β)－∠ABP ＝180°－(α－β)－(180°－γ＋β)＝γ－α.在△ABP 中，根据正弦定理， AP sin ∠ABP ＝AB sin ∠APB ，AP sin (180°－γ＋β)＝αsin (γ－α)，AP ＝α×sin (γ－β)sin (γ－α)所以山高为h ＝AP sin α＝a sin αsin (γ－β)sin (γ－α).9．如图，A 、B 、C 、D 都在同一个与水平面垂直的平面内，B 、D 为两岛上的两座灯塔的塔顶．测量船于水面A 处测得B 点和D 点的仰角分别为75°，30°，于水面C 处测得B 点和D 点的仰角均为60°，AC ＝0.1 km.试探究图中B ，D 间距离与另外哪两点间距离相等，然后求B ，D 的距离(计算结果精确到0.01 km ，2≈1.414，6≈2.449).解 在△ABC 中，∠DAC ＝30°，∠ADC ＝60°－∠DAC ＝30°，∴CD ＝AC ＝0.1， 又∠BCD ＝180°－60°－60°＝60°，故CB 是△CAD 底边AD 的中垂线，∴BD ＝BA ，在△ABC 中，AB sin ∠BCA ＝AC sin ∠ABC， 即AB ＝AC sin 60°sin 15°＝32＋620.因此，BD ＝32＋620≈0.33 km ，故B ，D 的距离约为0.33 km.三、探究与创新10．为保障高考的公平性，高考时每个考点都要安装手机屏蔽仪，要求在考点周围1千米处不能收到手机信号，检查员抽查青岛市一考点，在考点正西约1.732千米有一条北偏东60°方向的公路，在此处检查员用手机接通电话，以每小时12千米的速度沿公路行驶，问最长需要多少分钟检查员开始收不到信号，并至少持续多长时间该考点才算合格？解如图所示，考点为A，检查开始处为B，设公路上C，D两点到考点的距离为1千米．在△ABC中，AB＝3≈1.732(千米)，AC＝1(千米)，∠ABC＝30°，由正弦定理sin ∠ACB＝sin 30°AC·AB＝3 2，∴∠ACB＝120°(∠ACB＝60°不合题意)，∴∠BAC＝30°，∴BC＝AC＝1(千米)，在△ACD中，AC＝AD，∠ACD＝60°，∴△ACD为等边三角形，∴CD＝1(千米)．∵BC12×60＝5，∴在BC上需5分钟，CD上需5分钟．所以最长需要5分钟检查员开始收不到信号，并持续至少5分钟才算合格．。

正、余弦定理在实际中的应用5．如右图，从气球A 测得济南全运会东荷、西柳两个场馆B ，C 的俯角分别为α，β，此时气球的高度为h ，则两个场馆B ，C 间的距离为( )A.h sin αsin βsin α－βB.h sin β－αsin αsin βC.h sin αsin βsin α－β D.h sin βsin αsin α－β解析：在Rt △ADC 中，AC ＝hsin β，在△ABC 中，由正弦定理，得BC ＝AC sin β－αsin α＝h sin β－αsin αsin β.答案：B6．一艘轮船从A 出发，沿南偏东70°的方向航行40海里后到达海岛B ，然后从B 出发，沿北偏东35°的方向航行了402海里到达海岛C .如果下次航行直接从A 出发到C ，此船航行的方向和路程(海里)分别为( )A ．北偏东80°，20()6＋2B ．北偏东65°，20()3＋2C ．北偏东65°，20()6＋2D ．北偏东80°，20()3＋2解析：由题可知∠ABC ＝105°，在△ABC 中，AB ＝40，BC ＝402， 所以AC 2＝AB 2＋BC 2－2AB ·BC ·cos ∠ABC ＝402＋()4022－2×40×402cos ()60°＋45°＝3 200＋1 6003，所以AC ＝20()6＋2.BCsin ∠BAC ＝AC sin ABC ⇒sin ∠BAC ＝AC ·sin ABC BC ＝22，所以∠BAC ＝45°，所以下次航行直接从A 出发到C ，航向为北偏东65°，故选C.答案：C7．如图，为测量山高MN ，选择A 和另一座山的山顶C 为测量观测点．从A 点测得M 点的仰角∠MAN ＝60°，C 点的仰角∠CAB ＝45°以及∠MAC ＝75°；从C 点测得∠MCA ＝60°.已知山高BC ＝100 m ，则山高MN ＝________ m.得水深CF ＝110 m ，求∠DEF 的余弦值．解：作DM ∥AC 交BE 于点N ，交CF 于点M ，作FH ∥AC 交BE 于点H . 由题中所给数据，得DF ＝MF 2＋DM 2＝302＋1702＝10298， DE ＝DN 2＋EN 2＝502＋1202＝130， EF ＝EH 2＋FH 2＝902＋1202＝150.在△DEF 中，由余弦定理，得cos ∠DEF ＝DE 2＋EF 2－DF 22×DE ×EF ＝1302＋1502－102×2982×130×150＝1665.10．一只船以20海里/时的速度向正东航行，它在A 点时测得灯塔P 在船的北偏东60°方向，2小时后船到达B 点时测得灯塔P 在船的北偏东45°方向，求：(1)船在B 点时与灯塔P 的距离；(2)已知以P 点为圆心，55海里为半径的圆形水域内有暗礁，那么此船继续向正东航行，有无触礁的危险？解：如图，在△ABP 中，依题意，知AB ＝20×2＝40，∠PAB ＝30°，∠ABP ＝135°，所以∠APB ＝15°.由正弦定理得BP sin30°＝ABsin15°，解得BP ＝20(6＋2)．(2)过P 点作PD ⊥AB ，D 为垂足，在Rt △BPD 中，PD ＝22BP ＝203＋20<55. 故船在B 点时与灯塔相距20(6＋2)海里，继续航行有触礁的危险．B 组 能力提升11．一货轮航行到M 处，测得灯塔S 在货轮的北偏东15°方向上，与灯塔S 相距20 n mile ，随后货轮按北偏西30°的方向航行3 h 后，又测得灯塔在货轮的东北方向，则货轮的速度为( )A.106＋23 n mile/h B.106－23 n mile/hC.106＋33 n mile/hD.106－33n mile/h解析：如图，在△MNS 中，MS ＝20，∠NMS ＝45°，∠SNM ＝105°，∠MSN ＝30°.在△MNS 中，由正弦定理， 得MS sin ∠MNS ＝MNsin ∠MSN.∴MN ＝20sin30°sin105°＝106＋24＝10(6－2)．∴货轮的速度为106－23n mile/h.答案：B12．甲船在岛B 的正南A 处，AB ＝10 n mile ，甲船自A 处以4 n mile/h 的速度向正北航行，同时乙船以6 n mile/h 的速度自岛B 出发，向北偏东60°方向驶去，则两船相距最近时经过了________ min.解析：设甲、乙两船行驶x h 后，分别位于C 、D 处，CD ＝y ，如图所示．在△CBD 中，y 2＝(10－4x )2＋(6x )2－2(10－4x )·6x ·cos120°＝28x 2－20x ＋100＝28⎝ ⎛⎭⎪⎫x －20562＋6757，所以当x ＝2056 h ，即x ＝2056×60＝1507min 时，y 2min ＝6757. 答案：1507。

第2课时角度、面积问题学习目标1.能把方向角等角度条件转化为解三角形的条件，解决航海等角度问题.2.掌握用两边及其夹角表示的三角形面积公式．知识点一 角度问题测量角度问题主要是指在海上或空中测量角度的问题，如确定目标的方位，观察某一建筑物的视角等．解决它们的关键是根据题意和图形及有关概念，确定所求的角在哪个三角形中，该三角形中已知哪些量，需要求哪些量．通常是根据题意，从实际问题中抽象出一个或几个三角形，然后通过解这些三角形得到所求的量，从而得到实际问题的解． 知识点二 用两边及其夹角表示的三角形面积公式一般地，三角形面积等于两边及夹角正弦乘积的一半,即S △ABC ＝12ab sin C ＝12bc sin A ＝12ac sin B .思考1 S △ABC ＝12ab sin C 中，b sin C 的几何意义是什么？答案 BC 边上的高．思考2 如何用AB ，AD ，角A 表示▱ABCD 的面积？ 答案 S ▱ABCD ＝AB ·AD ·sin A .1．仰角是视线与视线在水平面的射影的夹角．(√)2．在处理方向角时，两个正北方向线视为平行．(√)3．航海问题中，所求结果中的角度通常要化为方向角或方位角．(√)4．△ABC的面积S＝14R abc(其中R为△ABC外接圆半径)．(√)题型一角度问题例1如图，在海岸A处发现北偏东45°方向，距A处(3－1)海里的B处有一艘走私船．在A处北偏西75°方向，距A处2海里的C处的我方缉私船奉命以10 3 海里/时的速度追截走私船，此时走私船正以10海里/时的速度，从B处向北偏东30°方向逃窜．问：缉私船沿什么方向行驶才能最快截获走私船？并求出所需时间．解设缉私船应沿CD方向行驶t小时，才能最快截获(在D点)走私船，则CD＝103t，BD＝10t，在△ABC 中，由余弦定理，有 BC 2＝AB 2＋AC 2－2AB ·AC cos A＝(3－1)2＋22－2(3－1)·2·cos 120°＝6. ∴BC ＝ 6.又∵BC sin A ＝ACsin ∠ABC， ∴sin ∠ABC ＝AC ·sin A BC ＝2·sin 120°6＝22，又∠ABC ∈(0°，60°)，∴∠ABC ＝45°， ∴B 点在C 点的正东方向上， ∴∠CBD ＝90°＋30°＝120°， 在△BCD 中，由正弦定理得BD sin ∠BCD ＝CDsin ∠CBD，∴sin ∠BCD ＝BD ·sin ∠CBD CD ＝10t ·sin 120°103t ＝12.又∵∠BCD ∈(0°，60°)，∴∠BCD ＝30°， ∴缉私船沿北偏东60°的方向行驶．又在△BCD 中，∠CBD ＝120°，∠BCD ＝30°， ∴∠CDB ＝30°，∴BD ＝BC ，即10t ＝ 6. ∴t ＝610小时≈15分钟． ∴缉私船应沿北偏东60°的方向行驶，才能最快截获走私船，大约需要15分钟．反思感悟 解决航海问题先根据条件，画出示意图，然后把方向角、速度、时间等条件转化为三角形的角、边，化为解三角形问题．跟踪训练1 甲船在A 点发现乙船在北偏东60°的B 处，乙船以每小时a 海里的速度向北行驶，已知甲船的速度是每小时3a 海里，问甲船应沿着什么方向前进，才能最快与乙船相遇？ 解 如图所示．设经过t 小时两船在C 点相遇，则在△ABC 中， BC ＝at 海里， AC ＝3at 海里， B ＝90°＋30°＝120°， 由BC sin ∠CAB ＝ACsin B，得sin ∠CAB ＝BC sin B AC ＝at ×sin 120°3at ＝323＝12，∵0°<∠CAB <60°，∴∠CAB ＝30°， ∴∠DAC ＝60°－30°＝30°，∴甲船应沿着北偏东30°的方向前进，才能最快与乙船相遇．题型二 用两边夹角表示三角形面积命题角度1 求三角形面积例2 在△ABC 中，已知BC ＝6，A ＝30°，B ＝120°，则△ABC 的面积为( ) A ．9 B ．18 C ．9 3 D ．18 3 答案 C解析 由正弦定理得AC sin B ＝BC sin A ，∴AC ＝BC ·sin B sin A ＝6×sin 120°sin 30°＝6 3.又∵C ＝180°－120°－30°＝30°，∴S △ABC ＝12AC ·BC ·sin C ＝12×63×6×12＝9 3.反思感悟 求三角形面积，主要用两组公式(1)12×底×高． (2)两边与其夹角正弦的乘积的一半．选用哪组公式，要看哪组公式的条件已知或易求．跟踪训练2 在△ABC 中，已知AB →·AC →＝tan A ，当A ＝π6时，△ABC 的面积为 ．答案 16解析 ∵AB →·AC →＝|AB →||AC →|cos A ＝tan A ， ∴|AB →||AC →|＝sin A cos 2A ，∴S △ABC ＝12|AB →||AC →|sin A＝12sin 2A cos 2A ＝12tan 2A ＝16. 命题角度2 涉及三角形面积的条件转化例3 在△ABC 中，内角A ，B ，C 的对边分别是a ，b ，c ，若sin B ＝2sin A ，且△ABC 的面积为a 2sin B ，则cos B ＝ . 答案 14解析 由sin B ＝2sin A 及正弦定理，得b ＝2a ，由△ABC 的面积为a 2sin B ， 得12ac sin B ＝a 2sin B ，即c ＝2a ， ∴cos B ＝a 2＋c 2－b 22ac ＝a 24a 2＝14.反思感悟 表示三角形面积，即使确定用两边夹角，还要进一步选择好用哪两边夹角． 跟踪训练3 已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，面积S ＝14(a 2＋b 2－c 2)，则角C 为( )A ．135°B ．45°C ．60°D ．120° 答案 B解析 ∵S ＝14(a 2＋b 2－c 2)＝12ab sin C ，∴a 2＋b 2－c 2＝2ab sin C ，∴c 2＝a 2＋b 2－2ab sin C ．由余弦定理c 2＝a 2＋b 2－2ab cos C ，得sin C ＝cos C . 又C ∈(0°，180°)，∴C ＝45°.三角形中的建模问题典例 如图，A ，B ，C 三地有直道相通，AB ＝5 千米，AC ＝3千米，BC ＝4 千米．现甲、乙两警员同时从A 地出发匀速前往B 地，经过t 小时，他们之间的距离为f (t )(单位：千米)．甲的路线是AB ，速度为5千米/时，乙的路线是ACB ，速度为8千米/时．乙到达B 地后原地等待．设t ＝t 1时乙到达C 地．(1)求t 1与f (t 1)的值；(2)已知警员的对讲机的有效通话距离是3千米．当t 1≤t ≤1时，求f (t )的表达式，并判断f (t )在[t 1,1]上的最大值是否超过3.说明理由． 解 (1)由题意可得t 1＝AC v 乙＝38，设此时甲运动到点M ，则AM ＝v 甲t 1＝5×38＝158，∴f (t 1)＝MC ＝AC 2＋AM 2－2AC ·AM ·cos A＝32＋⎝⎛⎭⎫1582－2×3×158×35＝3418. (2)当t 1≤t ≤78时，乙在CB 上的Q 点，设甲在P 点，∴QB ＝AC ＋CB －8t ＝7－8t ，PB ＝AB －AP ＝5－5t ， ∴f (t )＝PQ ＝QB 2＋PB 2－2QB ·PB ·cos B ＝(7－8t )2＋(5－5t )2－2(7－8t )(5－5t )×45＝25t 2－42t ＋18，当78<t ≤1时，乙在B 点不动，设此时甲在点P ， ∴f (t )＝PB ＝AB －AP ＝5－5t ，∴f (t )＝⎩⎨⎧25t 2－42t ＋18，38≤t ≤78，5－5t ，78<t ≤1，∴当38≤t ≤1时，f (t )∈⎣⎡⎦⎤0，3418，故f (t )的最大值没有超过3.[素养评析] 本题是关于对讲机有效通话距离的实际问题．其解决完整经历了数学建模的全过程：在实际情境中提出问题(警员能否在行动过程中保持通话)，分析问题．建立模型⎝⎛⎭⎪⎪⎫f (t )＝⎩⎨⎧25t 2－42t ＋18，38≤t ≤78，5－5t ，78<t ≤1，计算求解．最终解决实际问题．1．在△ABC中，A，B，C所对的边分别为a，b，c，其中a＝4，b＝3，C＝60°，则△ABC 的面积为()A．3 B．3 3 C．6 D．6 3答案 B解析S△ABC＝12ab sin C＝12×4×3×sin 60°＝3 3.2.如图所示，在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°，向山顶前进100 m到达B处，又测得C对于山坡的斜度为45°，若CD＝50 m，山坡对于地平面的坡度为θ，则cos θ等于()A.32 B.22 C.3－1 D.2－1答案 C解析 在△ABC 中，由正弦定理得AB sin 30°＝ACsin 135°，∴AC ＝100 2.在△ADC 中，AC sin (θ＋90°)＝CDsin 15°，∴cos θ＝sin(θ＋90°)＝AC ·sin 15°CD＝3－1.3．已知三角形的面积为14，其外接圆的面积为π，则这个三角形的三边之积为( )A ．1B ．2 C.12 D ．4答案 A解析 设三角形外接圆的半径为R ，则由πR 2＝π，得R ＝1，∵S △＝12ab sin C ＝abc 4R ＝abc 4＝14，∴abc ＝1.4．某船开始看见一灯塔在南偏东30°方向，后来船沿南偏东60°的方向航行45 km 后，看见该灯塔在正西方向，则这时船与灯塔的距离是 km. 答案 15 3解析 设灯塔位置为A ，船的初始位置为O ，船的终止位置为B ， 由题意知∠AOB ＝30°，∠OAB ＝120°，则∠OBA ＝30°， 所以由正弦定理，得AB ＝153， 即此时船与灯塔的距离是15 3 km.1．各种测量问题本质上是把不能或不易直接测量的量转化为用能直接测量的量表示．而在三角形测量中易获得的数据方向角等多以铅垂线、正南正北为始边，需要准确地转化为三角形的元素．2．(1)对于面积公式S ＝12ab sin C ＝12ac sin B ＝12bc sin A ，一般是已知哪一个角就使用哪一个公式．(2)与面积有关的问题，一般要用到正弦定理或余弦定理进行边和角的转化.一、选择题1．如图已知两座灯塔A ，B 与海洋观察站C 的距离相等，灯塔A 在观察站C 的北偏东40°，灯塔B 在观察站C 的南偏东60°，则灯塔A 在灯塔B 的( )A ．北偏东10°B ．北偏西10°C ．南偏东10°D ．南偏西10°答案 B解析 如题图，因为△ABC 为等腰三角形， 所以∠CBA ＝12(180°－80°)＝50°，60°－50°＝10°.所以灯塔A 在灯塔B 的北偏西10°.2．从A 处望B 处的仰角为α，从B 处望A 处的俯角为β，则α，β的关系为( ) A ．α>β B ．α＝β C ．α＋β＝90° D ．α＋β＝180°答案 B3.当太阳光与水平面的倾斜角为60°时，一根长为2 m 的竹竿如图所示放置，要使它的影子最长，则竹竿与地面所成的角是( )A ．15°B ．30°C ．45°D ．60° 答案 B解析 设竹竿与地面所成的角为α，影子长为x m. 由正弦定理，得2sin 60°＝x sin (120°－α)，∴x ＝433sin(120°－α)．∵30°<120°－α<120°，∴当120°－α＝90°，即α＝30°时，x 有最大值． 即竹竿与地面所成的角是30°时，影子最长．4．在△ABC 中，AB ＝3，BC ＝13，AC ＝4，则△ABC 的面积是( ) A ．3 3 B.332 C ．3 D.32答案 A解析 ∵cos A ＝AB 2＋AC 2－BC 22AB ·AC ＝9＋16－132×3×4＝12，∴sin A ＝32， S △ABC ＝12bc sin A ＝12×4×3×32＝3 3.5．在△ABC 中，内角A ，B ，C 所对的边分别是a ，b ，c ，若c 2＝(a －b )2＋6，C ＝π3，则△ABC的面积是( )A. 3B.932C.332 D ．3 3答案 C解析 由题意得c 2＝a 2＋b 2－2ab ＋6，由余弦定理可得c 2＝a 2＋b 2－2ab cos C ＝a 2＋b 2－ab ， ∴－2ab ＋6＝－ab ，即ab ＝6. ∴S △ABC ＝12ab sin C ＝332.6．(2018·全国Ⅲ)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .若△ABC 的面积为a 2＋b 2－c 24，则C 等于( ) A.π2 B.π3 C.π4 D.π6 答案 C解析 ∵S ＝12ab sin C ＝a 2＋b 2－c 24＝2ab cos C 4＝12ab cos C ， ∴sin C ＝cos C ，即tan C ＝1. 又∵C ∈(0，π)，∴C ＝π4.7.如图，两座相距60 m 的建筑物AB ，CD 的高度分别为20 m ，50 m ，BD 为水平面，则从建筑物AB 的顶端A 看建筑物CD 的张角为( )A ．30°B ．45°C ．60°D ．75° 答案 B解析 依题意可得AD ＝2010，AC ＝305， 又CD ＝50，所以在△ACD 中，由余弦定理得cos ∠CAD ＝AC 2＋AD 2－CD 22AC ·AD＝(305)2＋(2010)2－5022×305×2010＝ 6 0006 0002＝22，又0°<∠CAD <180°，所以∠CAD ＝45°， 所以从顶端A 看建筑物CD 的张角为45°.8．若钝角△ABC 的面积是12，AB ＝1，BC ＝2，则AC 等于( )A ．5 B. 5 C ．2 D ．1 答案 B解析 ∵钝角△ABC 的面积是12，AB ＝c ＝1，BC ＝a ＝2， ∴S ＝12ac sin B ＝12，即sin B ＝22.当B 为钝角时，cos B ＝－1－sin 2B ＝－22. 利用余弦定理，得AC 2＝AB 2＋BC 2－2AB ·BC cos B ＝1＋2＋2＝5，即AC ＝5； 当B 为锐角时，cos B ＝1－sin 2B ＝22， 利用余弦定理，得AC 2＝AB 2＋BC 2－2AB ·BC cos B ＝1＋2－2＝1，即AC ＝1，此时AB 2＋AC 2＝BC 2，即△ABC 为直角三角形，不合题意，舍去． 故AC ＝ 5. 二、填空题9．在△ABC 中，角A ，B ，C 的对边a ，b ，c 满足b 2＋c 2＝a 2＋bc ，且bc ＝8，则△ABC 的面积为 ． 答案 2 3 解析 因为b 2＋c 2＝a 2＋bc ，所以cos A ＝b 2＋c 2－a 22bc ＝12，所以A ＝π3，三角形面积S ＝12bc sin A＝12×8×32＝2 3. 10．已知三角形ABC 的三边分别为a ，b ，c ，面积S ＝a 2－(b －c )2，则cos A ＝ . 答案1517解析 S ＝a 2－(b －c )2＝a 2－b 2－c 2＋2bc ＝－2bc cos A ＋2bc ， ∵S ＝12bc sin A ，∴12bc sin A ＝2bc －2bc cos A .即4－4cos A ＝sin A .平方得17cos 2A －32cos A ＋15＝0. 即(17cos A －15)(cos A －1)＝0. 得cos A ＝1(舍)或cos A ＝1517.11.如图所示，位于A 处的信息中心获悉：在其正东方向相距40海里的B 处有一艘渔船遇险，在原地等待营救．信息中心立即把消息告知在其南偏西30°、相距20海里的C 处的乙船，现乙船朝北偏东θ的方向沿直线CB 前往B 处救援，则cos θ的值为 ．答案2114解析 如题图知，在△ABC 中，AB ＝40，AC ＝20，∠BAC ＝120°， 由余弦定理得BC 2＝AB 2＋AC 2－2AB ·AC ·cos 120°＝2 800， 所以BC ＝207， 由正弦定理得sin ∠ACB ＝AB BC ·sin ∠BAC ＝217，由∠BAC ＝120°知∠ACB 为锐角， 故cos ∠ACB ＝277.故cos θ＝cos(∠ACB ＋30°)＝cos ∠ACB cos 30°－sin ∠ACB sin 30°＝2114. 三、解答题12．甲船在A 处，乙船在A 的南偏东45°方向，距A 有9海里的B 处，并以20海里/时的速度沿南偏西15°方向行驶，若甲船以28海里/时的速度行驶，用多少小时能最快追上乙船？ 解 如图所示，设用t 小时甲船能追上乙船，且在C 处相遇．在△ABC 中，AC ＝28t ，BC ＝20t ，AB ＝9， ∠ABC ＝180°－45°－15°＝120°.由余弦定理得AC 2＝AB 2＋BC 2－2AB ·BC cos ∠ABC ， 即(28t )2＝92＋(20t )2－2×9×20t ×⎝⎛⎭⎫－12， 128t 2－60t －27＝0，∴t ＝34或t ＝－932(舍去)，∴甲船用34小时能最快追上乙船．13．在△ABC 中，内角A ，B ，C 所对的边分别是a ，b ，c .已知A ＝π4，b 2－a 2＝12c 2.(1)求tan C 的值；(2)若△ABC 的面积为3，求b 的值．解 (1)由b 2－a 2＝12c 2及正弦定理得sin 2B －12＝12sin 2C ，所以－cos 2B ＝sin 2C .由A ＝π4，得B ＋C ＝34π，则－cos 2B ＝－cos ⎝⎛⎭⎫32π－2C ＝sin 2C ＝2sin C cos C ，所以sin 2C ＝2sin C cos C ，又sin C ≠0，解得tan C ＝2. (2)由tan C ＝2，C ∈(0，π)，得sin C ＝255，cos C ＝55.因为sin B ＝sin(A ＋C )＝sin ⎝⎛⎭⎫π4＋C ， 所以sin B ＝31010.由正弦定理得c ＝b sin C sin B ＝223b ，又因为A ＝π4，12bc sin A ＝3，所以bc ＝62，故b ＝3.14．如图，四边形ABCD 中，B ＝C ＝120°，AB ＝4，BC ＝CD ＝2，则该四边形的面积等于( )A. 3 B．5 3 C．6 3 D．7 3答案 B解析连接BD，四边形面积可分为△ABD与△BCD两部分面积的和，由余弦定理，得BD＝23，S△BCD＝12BC×CD sin 120°＝3，∠ABD＝120°－30°＝90°，∴S△ABD＝12AB×BD＝4 3.∴S四边形ABCD＝3＋43＝5 3.15．为保障高考的公平性，高考时每个考点都要安装手机屏蔽仪，要求在考点周围1千米处不能收到手机信号，检查员抽查某市一考点，在考点正西 3 千米有一条北偏东60°方向的公路，在此处检查员用手机接通电话，以每小时12千米的速度沿公路行驶，问最长需要多少分钟检查员开始收不到信号，并至少持续多长时间该考点才算合格？解如图所示，考点为A，检查开始处为B，设检查员行驶到公路上C，D两点之间时收不到信号，即公路上C，D两点到考点的距离为1千米．在△ABC中，AB＝3千米，AC＝1千米，∠ABC＝30°，由正弦定理，得sin∠ACB＝sin 30°AC×AB＝32，∴∠ACB＝120°(∠ACB＝60°不合题意)，∴∠BAC＝30°，∴BC＝AC＝1 千米．在△ACD中，AC＝AD＝1千米，∠ACD＝60°，∴△ACD为等边三角形，∴CD＝1千米．∵BC12×60＝5，∴在BC上需5分钟，CD上需5分钟．∴最长需要5分钟检查员开始收不到信号，并持续至少5分钟才算合格．。

1.2 应用举例5分钟训练(预习类训练,可用于课前)1.在△ABC 中，∠A ∶∠B ∶∠C=1∶2∶3 ，则a ∶b ∶c 等于（ ） A.1∶3∶2 B.1∶2∶3 C.2∶3∶1 D.3∶2∶1 解析：由已知得A=30°,B=60°,C=90°，根据正弦定理可知有CcB b A a sin sin sin ==, a ∶b ∶c=sin30°∶sin60°∶sin90°=1∶3∶2.答案：A2.从A 处望B 处的仰角为α，从B 处望A 处的俯角为β，则α、β 的关系为（ ） A.α＞β B.α+β=90° C.α=β D.α+β=180° 解析：由仰角、俯角的定义可知α=β. 答案：C3.在△ABC 中，a=2,b=3,c=4，则cosC=___________，其形状是___________.解析：由余弦定理得cosC=413224322222222-=⨯⨯-+=-+ab c b a ＜0,C 是钝角，故其形状是钝角三角形. 答案：41-钝角三角形 4.在△ABC 中，∠A ∶∠B=1∶2，a ∶b=1∶3，则∠A=___________,∠B=___________, ∠C=___________. 解析：由已知及正弦定理得31sin sin ==B A b a ，又B=2A ， ∴A A A A A A cos 21cos sin 2sin 2sin sin 31===,cosA=23,A=6π,B=3π,C=2π.答案：6π 3π 2π10分钟训练(强化类训练，可用于课中)1.若三角形的三个角的比是1∶2∶3，最大的边是20，则这个三角形的面积为（ ） A.350 B.1003 C.253 D.100 解析：由已知得A=30°,B=60°,C=90°，根据正弦定理可知有CcB b A a sin sin sin ==，a ∶b ∶c=sin30°∶sin60°∶sin90°=1∶3∶2，最小边为10. 答案：A2.边长为5、7、8的三角形的最大角与最小角的和是（ ）A.90°B.120°C.135°D.150°解析：本题只要先确定边长为7这边所对的内角，然后由三角形内角和定理，从而可求得最大角与最小角的和.设边长为7的边对应的角为B ，则cosB=21852785222=⨯⨯-+，∴B=60°． ∴A+C=120°．答案：B3.如右图，为测量障碍物两侧A 、B 间的距离，用a 、b 分别表示角A 、B 的对边，则下列给定四组数据中，测量时应当测的数据为（ ）A.a ，b ，∠AB.a ，∠A ，∠BC.b ，∠A ，∠BD.a ，b ，∠C 解析：由正余弦定理及生活实际容易得知. 答案：D4.甲船在岛B 的正南方A 处，AB=10千米，甲船以每小时4千米的速度向正北航行，同时乙船自B 出发以每小时6千米的速度向北偏东60°的方向驶去，当甲、乙两船相距最近时，它们所航行的时间是（ ）A.7150分钟 B.715分钟 C.21.5分钟 D.2.15分钟 解析：AC 2=(10-4t)2+(6t)2-2×(10-4t)×6t×cos120°=28t 2-20t+100=28(t-145)2+7725故当t=145小时，即t=145×60=7150分钟时，甲乙两船距离最近. 答案：A5.已知一个平行四边形的两条邻边的长分别为2、3，且其中的一个内角为30°，则这个平行四边形的面积为___________. 解析：本题可以围绕着平行四边形的面积公式来考虑，或者连结其对角线将原平行四边形分成两个全等的三角形，从而由三角形的面积公式来求得结果，S=2×3sin30°=3. 答案：36.一树干被台风吹断折成与地面成30°角，树干底部与树尖着地处相距20米，求树干原来的高度.解析：根据题意画出如图示意图，问题转化到Rt △ABC 中，BC=20，B=30°，tan30°=BCAC,AC=BCtan30°=20×332033=，∴AB=2AC, AC+AB=3AC=320(米).答案：即树干原来的高度为320米. 30分钟训练(巩固类训练，可用于课后)1.某人朝正东方向走了x km 后，向右转150°，再向前走了3 km ，结果他离出发点恰好为3 km ，那么x 的值是（ ）A.3B.23C.3或23D.3 解析：由题意画出示意图，设出发点为A ，则由已知可得AB=x 千米，BC=3千米，∠ABC=180°-150°=30°. AC=3，∴CABBCAC ∠=︒sin 30sin . ∴CAB ∠=sin 3213,∴sin ∠CAB=23. ∴∠CAB=60°或∠CAB=120°.当∠CAB=60°时，∠ACB=180°-30°-60°=90°.x=32千米;当∠CAB=120°，∠ACB=180°-120°-30°=30°.∴x=AC=3千米.答案：C2.如右图，B 、C 、D 三点在地面同一直线上，DC=a ，从C 、D 两点测得A 点的仰角分别是β、α(α＜β)，则A 点离地面的高AB 等于（ ）A.)cos(sin sin αββα-a B.)sin(sin sin αββα-aC.)sin(cos sin αββα-a D.)cos(cos cos αββα-a解析：在Rt △ABC 与Rt △ADC 中， tan β=BC AB ，tan α=BDAB,BC=ABcot β, BD=ABcot α，DC=BD-BC=AB(cot α-cot β)=a ， AB=)sin(sin sin cos cot αββαβα-=-a a .答案：B3.(2006高考全国卷Ⅰ，文12)用长度分别为2、3、4、5、6（单位：cm ）的5根细木棒围成一个三角形（允许连接，但不允许折断），能够得到的三角形的最大面积为（ ） A.58cm 2 B.106cm 2 C.553cm 2 D.20 cm 2 解析：用2、5连接，3、4连接各为一边，第三边长为6组成三角形，此三角形面积最大，面积为106cm 2.答案：B4.如右图，已知|F 1|=20 N ，|F 2|=30 N,|F 3|=40 N ，三力互成120°的角，求合力的大小.解：如下图，F 1、F 2的合力的大小|F|2=|F 1|2+|F 2|2-2|F 1||F 2|cos60°=700 N.∴F≈26.46 N ，合力的大小为|F 3|-|F|=13.54 N.5.甲、乙两人去测大河两岸A 、B 两点的距离（如右图）.当他们到达A 处时才发觉只带了测角仪，甲转身要回去拿工具.乙看见A 处那根24米长的电杆，忙说：“不用去了，能测出来.”甲用疑惑的目光望着乙.你能帮甲想一个办法吗？解：在A 点测得∠CAB ，在C 点测得∠BCA ， 然后可求得∠B=180-（∠CAB+∠BCA ）， 根据正弦定理∵)sin()180sin(sin sin C A AC C A AC B AC C AB +=--︒==∴AB=)sin(sin C A C+×AC, 带入实验数据即可求得A 、B 两点的距离. 解：在△ABC 中，∠B=152°-122°=30°，∠C=180°-152°+32°=60°，∠A=180°-30°-60°=90°，BC=235， ∴AC=43530sin 235=︒. 所以货轮与灯塔间的距离为354海里．6.如右图，货轮在海上以35海里/小时的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为152°的方向航行．为了确定船位，在B 点处观测到灯塔A 的方位角为122°．半小时后，货轮到达C 点处，观测到灯塔A 的方位角为32°．求此时货轮与灯塔之间的距离．7.在△ABC 中，a 、b 、c 分别是∠A 、∠B 、∠C 的对边长. 求证：Ac b Ab c C B cos cos cos cos --=. 证法一：由正弦定理得AC C A AB B A AC R B R A B R C R A c b A b c cos sin )sin(cos sin )sin(cos sin 2sin 2cos sin 2sin 2cos cos -+-+=--=--CBC A B A cos cos cos sin cos sin ==.证法二：由余弦定理得CBabcabacbcabcabcbcabcacbcbbcacbbcAcbAbccoscos222222coscos222222222222222222=-+-+=-+-+=-+⨯--+⨯-=--.8.甲船在A点发现乙船在北偏东60°的B处，乙船以每小时a海里的速度向北行驶，已知甲船的速度是3a海里/小时，甲船沿着什么方向前进，才能最快与乙船相遇?解：设甲船在C处追上乙船，并设所用的时间为t时，由已知得∠ABC=120°，BC=at，AC=at3.由正弦定理得BACBCABCAC∠=∠sinsin即BACatat∠=︒sin120sin3，∴sin∠BAC=21，即∠BAC=30°.∴甲船沿着北偏东30°方向前进，才能最快与乙船相遇.9.在山坡上有一棵垂直的大树.试一试：不用爬树怎样可测出大树的高度.解：在山坡上有一棵垂直的大树，通过“标准步”及简易测角工具，计算出大树的高度，具体步骤为：（1）把每一步跨度基本相同的跨步方式称为标准步，每个人可用“标准步”走若干步（例如20步），反复几次，量出每次所走距离，并计算几次走动中每步的平均距离就能获得自己的“标准步”.（2）可用量角器加指针作为简易测角工具.具体操作步骤：从大树底部A向下跨a步“标准步”到了B，用简易测角工具测得∠ABP=α，再向上跨了b步“标准步”到了C(a＞b)，测得∠ACP=β,该同学测出自己眼睛至脚底的高度大约是h cm，每步“标准步”跨度约为l cm,∴PA=)sin(cossin2)(sinsin2222αβαβαββ--+-abab这样就可知这棵大树的高度，PD=PA·l+h.10.在一个正三角形中画一条分割线（可以是直线、折线或曲线），把这个正三角形的面积两等分．（1）试设想各种画分割线的方法，并比较各条分割线的长短；（2）在你所画出的所有分割线中，哪一种最短？这是不是所有可能的分割线中最短的？证明你的结论.解：（1）图1、图2是容易想到的两种分法，分别计算分割线的长度（设正三角形的边长为1），得AD=23≈0.866 0(图1)；DE=22≈0.707 1(图2).图3这种分割线是否一定比图2的分割线长？答案是肯定的，以下证明这一点．如图3，设AD=m,AE=n, 则21mnsin60°=2143⨯,得mn=21. 于是DE 2=m 2+n 2-2mncos60°=m 2+n 2-mn≥2mn -mn=mn=21. 当且仅当m=n=22时等号成立，这说明DE min =22． 图4的情形一般被认为不可能是最短的，但计算验证一下又何妨？图4设AD=AE=AF=m ，由条件得:2×21m 2sin30°=83，故m 2=43． 于是DF 2=2m 2-2m 2cos30°=(23-)m 2=4332-. 因此，分割线的长为DF+EF=2DF=332-≈0.681 3＜0.707 1. 这是一个令人咋舌的结论，用圆弧来分割是否会最短呢? 如图5，不难计算=123π≈0.673 4．图5（2）图5中为最短的分割线，证明如下：如图6，将六个全等的正三角形拼成一个正六边形，六段分割线形成一个封闭的图形．问题转化为：给定面积，画一个周长最短的封闭图形，显然圆的周长最短．图6。