03第三章 动量与角动量作业答案
- 格式:doc
- 大小:537.00 KB
- 文档页数:5
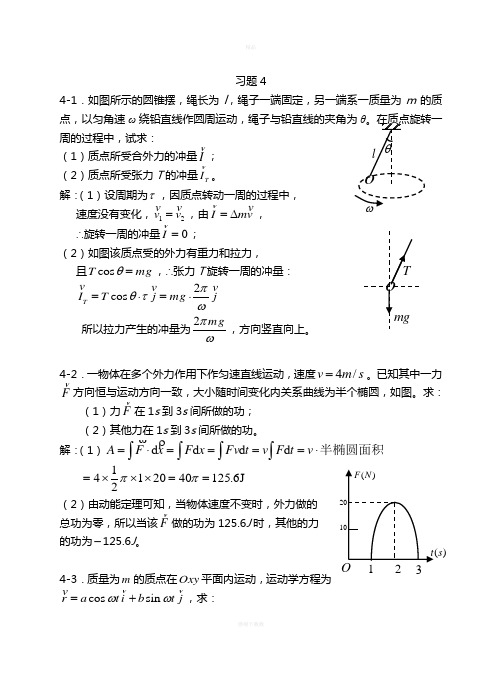
)s 习题44-1.如图所示的圆锥摆,绳长为l ,绳子一端固定,另一端系一质量为m 的质点,以匀角速ω周的过程中,试求:(1)质点所受合外力的冲量I v ;(2)质点所受张力T 的冲量T I v。
解:(1)设周期为τ,因质点转动一周的过程中, 速度没有变化,12v v =v v,由I mv =∆vv, ∴旋转一周的冲量0I =v;(2)如图该质点受的外力有重力和拉力, 且cos T mg θ=,∴张力T 旋转一周的冲量:2cos T I T j mg j πθτω=⋅=⋅v v v所以拉力产生的冲量为2mgπω,方向竖直向上。
4-2.一物体在多个外力作用下作匀速直线运动,速度4/v m s =。
已知其中一力F v方向恒与运动方向一致,大小随时间变化内关系曲线为半个椭圆,如图。
求:(1)力F v在1s 到3s 间所做的功;(2)其他力在1s 到3s 间所做的功。
解:(1)半椭圆面积⋅====⋅=⎰⎰⎰⎰v t F v t Fv x F x F A d d d d ρϖJ 6.12540201214==⨯⨯⨯=ππ(2)由动能定理可知,当物体速度不变时,外力做的 总功为零,所以当该F v做的功为125.6J 时,其他的力 的功为-125.6J 。
4-3.质量为m 的质点在Oxy 平面内运动,运动学方程为cos sin r a t i b t j ωω=+v v v,求:(1)质点在任一时刻的动量;(2)从0=t 到ωπ/2=t 的时间内质点受到的冲量。
解:(1)根据动量的定义:P mv =v v,而d r v dt==v v sin cos a t i b t j ωωωω-+v v , ∴()(sin cos )P t m a t i b t j ωωω=--v v v ;(2)由2()(0)0I mv P P m b j m b j πωωω=∆=-=-=v v v v v v ,所以冲量为零。


第三章 动量定理及动量守恒定律(思考题与习题解答)(一)思考题3.1试表述质量的操作型定义。
解答,kgv v m m 00 ∆∆=式中kg 1m 0=(标准物体质量) 0v∆:为m 与m0碰撞m0的速度改变 v∆:为m 与m0碰撞m 的速度改变这样定义的质量,其大小反映了质点在相互作用的过程中速度改变的难易程度,或者说,其量值反映了质量惯性的大小。
这样定义的质量为操作型定义。
3.2如何从动量守恒得出牛顿第二、第三定律,何种情况下牛顿第三定律不成立? 解答,由动量守恒)p p (p p ,p p p p 22112121 -'-=-'+='+' ,p p 21 ∆-=∆t p t p 21∆∆-=∆∆取极限dt p d dtp d 21 -= 动量瞬时变化率是两质点间的相互作用力。
,a m )v m (dt d dt p d F 111111=== ,a m )v m (dt d dt p d F 222222 ===21F F -=对于运动电荷之间的电磁作用力,一般来说第三定律不成立。
(参见P63最后一自然段) 3.3在磅秤上称物体重量,磅秤读数给出物体的“视重”或“表现重量”。
现在电梯中测视重,何时视重小于重量(称作失重)?何时视重大于重量(称作超重)?在电梯中,视重可能等于零吗?能否指出另一种情况使视重等于零? 解答,①电梯加速下降视重小于重量; ②电梯加速上升视重大于重量;③当电梯下降的加速度为重力加速度g 时,视重为零; ④飞行员在铅直平面内的圆形轨道飞行,飞机飞到最高点时,gR v ,0mg R v m N ,N mg R v m 22==-=+=飞行员的视重为零3.4一物体静止于固定斜面上。
(1)可将物体所受重力分解为沿斜面的下滑力和作用于斜面的正压力。
(2)因物体静止,故下滑力mg sin α与静摩擦力N 0μ相等。
α表示斜面倾角,N 为作用于斜面的正压力,0μ为静摩擦系数。


第3章动量守恒定律和能量守恒定律习题一选择题3-1 以下说法正确的是[ ](A)大力的冲量一定比小力的冲量大(B)小力的冲量有可能比大力的冲量大(C)速度大的物体动量一定大(D)质量大的物体动量一定大解析:物体的质量与速度的乘积为动量,描述力的时间累积作用的物理量是冲量,因此答案A、C、D均不正确,选B。
3-2 质量为m的铁锤铅直向下打在桩上而静止,设打击时间为t∆,打击前锤的速率为v,则打击时铁捶受到的合力大小应为[ ](A)mvmgt+∆(B)mg(C)mvmgt-∆(D)mvt∆解析:由动量定理可知,F t p mv∆=∆=,所以mvFt=∆,选D。
3-3 作匀速圆周运动的物体运动一周后回到原处,这一周期内物体[ ] (A)动量守恒,合外力为零(B)动量守恒,合外力不为零(C)动量变化为零,合外力不为零, 合外力的冲量为零(D)动量变化为零,合外力为零解析:作匀速圆周运动的物体运动一周过程中,速度的方向始终在改变,因此动量并不守恒,只是在这一过程的始末动量变化为零,合外力的冲量为零。
由于作匀速圆周运动,因此合外力不为零。
答案选C。
3-4 如图3-4所示,14圆弧轨道(质量为M)与水平面光滑接触,一物体(质量为m)自轨道顶端滑下,M与m间有摩擦,则[ ](A )M 与m 组成系统的总动量及水平方向动量都守恒,M 、m 与地组成的系统机械能守恒(B )M 与m 组成的系统动量不守恒, 水平方向动量守恒,M 、m 与地组成的系统机械能不守恒(C )M 与m 组成的系统动量不守恒, 水平方向动量不守恒,M 、m 与地组成的系统机械能守恒(D )M 与m 组成系统的总动量及水平方向动量都守恒,M 、m 与地组成的系统机械能不守恒解析:M 与m 组成的系统在水平方向上不受外力,在竖直方向上有外力作用,因此系统水平方向动量守恒,总动量不守恒,。
由于M 与m 间有摩擦,m 自轨道顶端滑下过程中摩擦力做功,机械能转化成其它形式的能量,系统机械能不守恒。

第三章 动量和角动量【例题精讲】例3-1 一颗子弹在枪筒里前进时所受的合力大小为 t F 31044005⨯-= (SI) 子弹从枪口射出时的速率为 300 m/s .假设子弹离开枪口时合力刚好为零,则子弹在枪筒中所受力的冲量I = ;子弹的质量m = 。
0.6 N·s 2 g例3-2一质量为1 kg 的物体,置于水平地面上,物体与地面之间的静摩擦系数μ 0=0.20,滑动摩擦系数μ=0.16,现对物体施一水平拉力F =t+0.96(SI),则2秒末物体的速度大小v = 。
2秒末物体的加速度大小a = 。
0.89 m/s 1.39 m/s 2例3-3 质量分别为m A 和m B (m A >m B )、速度分别为A v ϖ和B v ϖ(v A > v B )的两质点A 和B ,受到相同的冲量作用,则 (A) A 的动量增量的绝对值比B 的小。
(B) A 的动量增量的绝对值比B 的大。
(C) A 、B 的动量增量相等。
(D) A 、B 的速度增量相等。
[ C ]例3-4 一人用恒力F ϖ推地上的木箱,经历时间∆ t 未能推动木箱,此推力的冲量等于多少?木箱既然受了力F ϖ 的冲量,为什么它的动量没有改变?【答】推力的冲量为t F ∆ϖ。
动量定理中的冲量为合外力的冲量,此时木箱除受力F ϖ外还受地面的静摩擦力等其它外力,木箱未动说明此时木箱的合外力为零,故合外力的冲量也为零,根据动量定理,木箱动量不发生变化。
例3-5 如图,用传送带A 输送煤粉,料斗口在A 上方高h =0.5 m 处,煤粉自料斗口自由落在A 上.设料斗口连续卸煤的流量为q m =40 kg/s ,A 以v=2.0 m/s 的水平速度匀速向右移动.求装煤的过程中,煤粉对A 的作用力的大小和方向。
(不计相对传送带静止的煤粉质重)【解】 煤粉自料斗口下落,接触传送带前具有竖直向下的速度gh 20=v 设煤粉与A 相互作用的∆t 时间内,落于传送带上的煤粉质量为 t q m m ∆=∆ 设A 对煤粉的平均作用力为f ϖ,由动量定理写分量式:0-∆=∆v m t f x )(00v m t f y ∆--=∆ 将 t q m m ∆=∆代入得 v m x q f =, 0v m y q f = ∴ 14922=+=y x f f f Nf ϖ与x 轴正向夹角为α = arctg (f x / f y ) = 57.4° 由牛顿第三定律煤粉对A 的作用力f ′= f = 149 N ,方向与图(b)中f ϖ相反。
第三次作业(第三章动量与角动量)[B ]4.(自测提高2)质量为20 g 的子弹,以400 m/s 的速率沿图 3-17所示的方向射入一原来静止的质量为980 g 的摆球中,摆线长度 不可伸缩。
子弹射入后开始与摆球一起运动的速率为 (A) 2 m/s. (B) 4 m/s. (C) 7 m/s . (D) 8 m/s. 【提示】相对于摆线顶部所在点,系统的角动量守恒: mv 2l sin 30° = (M +/H )/V其中〃2为子弹质量,肱为摆球质量,/为摆线长度。
解得:V=4 m/s (解法二:系统水平方向动量守恒:mv 2 sin 30° = (M + m)V )一、选择题 [A ] 1.(基础训练2) 一质量为〃?。
的斜而原来静止于水平光滑平面上,将一质量为所的 木块轻轻放于斜面上,如图3-11所示。
如果此后木块能静止于斜面上,则斜面将 (A)保持静止. (B)向右加速运动. (C)向右匀速运动. (D)向左加速运动. mo【提示】设m°相对于地面以V 运动。
依题意,m 静止于斜面上,跟着图 3-11mo-起运动。
根据水平方向动量守恒,得:m.V + mV=0所以V=0, 斜而保持静止。
[C ]2.(基础训练3)如图3-12所示,圆椎摆的摆球质量为〃,速率 为“圆半径为R,当摆球在轨道上运动半周时,摆球所受重力冲量的大 小为(A) 2mv. (B) ^(2mv)2 +(mgTlR/v)2(C) TtRmg/ v(D) 0.r_2【提示】|/G | =Jmgdt[C ]3.(日测提高1)质量为〃?的质点,以不变速率〃沿图3.16中 正三角形ABC 的水平光滑轨道运动。
质点越过A 角时,轨道作用于质 点的冲量的大小为图 3.16(A) mv. (B) yflmv . (C) V3mv . (D) 2m v.【提示】根据动量定理I= ]fdtG=y/imv= mv 2 -mv l ,如图。
作业3 动量与角动量1、4 m /s . 2.5 m /s .2、2m v 指向正西南或南偏西453、211m m +∆t F 21211m t F t F ∆++∆m m 4、4.7 N·s 与速度方向相反5、 100 m/s 3分6、 356 N·s 3分160 N·s 2分7、 m v 0 2分竖直向下 2分 三、计算题1、解:由动量定理知质点所受外力的总冲量 I =12v v vm m m -=∆)(由A →BA B Ax Bx x m m m m I v v v v --=-=cos45°=-0.683 kg·m·s -1 1分I y =0- m v Ay = - m v A sin45°= - 0.283 kg·m·s -1 1分I =s N 739.022⋅=+y x I I 2分方向:==11/tg θθxy I I 202.5° (θ 1为与x 轴正向夹角) 1分.2、解:由题给条件可知物体与桌面间的正压力mg F N +︒=30sin 1分物体要有加速度必须 N F μ≥︒30cos 2分即 mg t μμ≥-)3(5, 0s 256.0t t =≥ 1分物体开始运动后,所受冲量为 ⎰-︒=tt t N F I 0d )30cos (μ)(96.1)(83.30202t t t t ---=t = 3 s, I = 28.8 N s 2分则此时物体的动量的大小为 I m =v速度的大小为 8.28==mIv m/s 2分3、解:(1) 因穿透时间极短,故可认为物体未离开平衡位置.因此,作用于子弹、物体系统上的外力均在竖直方向,故系统在水平方向动量守恒.令子弹穿出时物体的水平速度为v '有 m v 0 = m v +M v 'v ' = m (v 0 - v )/M =3.13 m/s 2分 T =Mg+M v 2/l =26.5 N 2分(2) s N 7.40⋅-=-=∆v v m m t f (设0v方向为正方向) 2分负号表示冲量方向与0v方向相反. 2分。
大学物理上册第3章习题解答第3章角动量定理和刚体的转动一、内容提要1、质点的角动量定理⑴质点对于某一定点的角动量和角动量定理:角动量L r mv =? 角动量定理 dL M dt=⑵质点对于z 轴的角动量和角动量定理:角动量z L r mv τ⊥=? 角动量定理 zz dL M dt=2、质点系的角动量定理刚体的转动惯量和定轴转动定理⑴质点系的角动量定理 i i iidM L dt =∑∑ ⑵刚体的转动惯量 2z iiiI r m =∑ 或2zI r dm =?⑶刚体的定轴转动定理 z z zd M I I dtωβ== 3、刚体的定轴转动动能定理⑴力矩的功z A M d θ=?⑵刚体的转动动能 212k z E I ω=⑶刚体的定轴转动动能定理 22211122z z z A M d I I θωω==-?4、角动量守恒定律⑴质点的角动量守恒定律:若0M =,则21L L = ⑵刚体的对轴角动量守恒定律:刚体对轴的角动量也可写为2z izizL r m I ωω=?=∑,若0iziM =∑,则0z z I I ωω=,即有0ωω=二、习题解答3.1 一发动机的转轴在7s 内由200/min r 匀速增加到3000/min r . 求:(1)这段时间内的初末角速度和角加速度. (2)这段时间内转过的角度和圈数. (3)轴上有一半径为2.0=r m 的飞轮, 求它边缘上一点在7s 末的切向加速度、法向加速度和总加速度.解:(1)初的角速度1200220.9/60rad s πω?=≈ 末的角速度230002314/60rad s πω?=≈角加速度231420.941.9/7rad s t ωβ?-==≈?(2)转过的角度为2211120.9741.97117622t t rad θωβ=+=?+??=117618622 3.14n r θπ===? (3)切向加速度241.90.28.38/a r m s τβ==?=法向加速度为:22423140.2 1.9710/n a r m s ω==?=?总的加速度为:421.9710/a m s ===?3.3 地球在1987年完成365次自转比1900年长14.1s. 求在1900年到1987年间, 地球自转的平均角加速度.解:平均角加速度为0003652365287T t T a t T ππωω??--+?==212373036523652 1.140.9610/8787(3.1510)t rad s T ππ-≈=-=-3.4一人手握哑铃站在转盘上, 两臂伸开时整个系统的转动惯量为22kgm . 推动后, 系统以15/min r 的转速转动. 当人的手臂收回时, 系统的转动惯量为20.8kgm . 求此时的转速.解:由刚体定轴转动的角动量守恒定律,1122I I ωω=121221537.5/min 0.8I r I ωω==?=3.5 质量为60kg , 半径为0.25m 的匀质圆盘, 绕其中心轴以900/min r 的转速转动. 现用一个闸杆和一个外力F 对盘进行制动(如图所示), 设闸与盘之间的摩擦系数为4.0. 求:(1)当100F N =, 圆盘可在多长时间内停止, 此时已经转了多少转?(2)如果在2s 内盘转速减少一半, F 需多大?图3-5 习题1.4图解:(1)设杆与轮间的正压力为N ,10.5l m =,20.75l m =,由杠杆平衡原理得121()F l l Nl +=121()F l l N l +=闸瓦与杆间的摩擦力为: 121()F l l f N l μμ+== 匀质圆盘对转轴的转动惯量为212I mR =,由定轴转动定律,M I β=,有 ()122112F l l R mR l μβ+-= 21212()40/3F l l rad s mRl μβ+=-=-停止转动所需的时间: 0900200607.06403t s πωβ--===- 转过的角度201532332.762t t rad rad θωβπ?=+=?≈532n θπ==圈(2)030ωπ=,在2s 内角速度减小一半,知0227.5/23.55/rad s rad s tωωβπ-=-=-=-()1222112F l l R mR l μβ+-= 112600.250.5(23.55)1772()20.4 1.25mRl F N l l βμ-=-=-≈+??3.6 发动机带动一个转动惯量为250kgm 的系统做定轴转动. 在0.5s 内由静止开始匀速增加到120/min r 的转速. 求发动机对系统施加的力矩.解:由题意,250I kgm =,00ω=,120/min 4/r rad s ωπ==系统角加速度为:20825.12/rad s t tωωωβπ-?====?? 由刚体定轴转动的转动定理,可知M I β=5025.121256M Nm =?=3.7一轻绳绕于半径为R 的圆盘边缘, 在绳端施以mg F =的拉力, 圆盘可绕水平固定光滑轴在竖直平面内转动. 圆盘质量为M , 并从静止开始转动. 求:(1)圆盘的角加速度及转动的角度和时间的关系. (2)如以质量为m 的物体挂在绳端, 圆盘的角加速度及转动的角度和时间的关系又如何?解:(1)由刚体转动定理可知:M I β= 上题可知: M FR mgR ==212I MR =代入上式得2mgMRβ=, 2212mg t t MRθβ==(2)对物体受力分析'mg F ma -= 'F R I β= a R β=,212I MR =由上式解得22mgMR mR β=+22122mg t t MR mRθβ==+3.8某冲床飞轮的转动惯量为32410kgm ?. 当转速为30/min r 时, 它的转动动能是多少?每冲一次, 其转速下降10/min r . 求每冲一次对外所做的功.解:由题意,转速为:()030/min /r rad s ωπ== 飞轮的转动动能为:232411410 1.9721022E I J ωπ===? 第一次对外做功为:22011122A I I ωω=- 1220/min 3r πω==()2422222301011111515410 3.14 1.0910*******A I I I I J ωωωωπ=-=-=?==?3.9半径为R , 质量为M 的水平圆盘可以绕中心轴无摩擦地转动. 在圆盘上有一人沿着与圆盘同心, 半径为R r <的圆周匀速行走, 行走速度相对于圆盘为v . 设起始时, 圆盘静止不动, 求圆盘的转动角速度.解:设圆盘的转动角速度为2ω,则人的角速度为12vrωω=-,圆盘的转动惯量为212MR ,人的转动惯量为2mr ,由角动量守恒定律, 222212v mr MR r ωω??-=即22222mrvmr MRω=+3.10 两滑冰运动员, 质量分别为60kg 和70kg , 他们的速率分别为7/m s 和6/m s , 在相距1.5m 的两平行线上相向滑行. 当两者最接近时, 互相拉手并开始绕质心做圆周运动. 运动中, 两者间距离保持m 5.1不变. 求该瞬时:(1)系统的总角动量. (2)系统的角速度.(3)两人拉手前后的总动能.解:⑴ 设1m 在原心,质心为c r70 1.50.87060c r m ?=≈+120.8, 1.50.810.7c r r m r m ===-=21112226070.870607630./J m v r m v r kg m s =+=??+??=⑵ 系统的转动惯量为: 222221122600.8700.772.7I m r m r kgm =+=?+?=6308.66/72.7J rad s I ω==≈ 222201122111160770627302222E m v m v J =+=??+??=221172.78.66272622E I J ω==??≈3.11半径为R 的光滑半球形碗, 固定在水平面上. 一均质棒斜靠在碗缘, 一端在碗内, 一端在碗外. 在碗内的长度为c , 求棒的全长.解:棒的受力如图所示本题属于刚体平衡问题,由于碗为光滑半球形,A 端的支持力沿半径方向,而碗缘B 点处的支持力方向不能确定,两个支持力和重力三者在竖直平面内。
第三次作业(第三章动量与角动量)一、选择题[A]1.(基础训练2)一质量为m0的斜面原来静止于水平光滑平面上,将一质量为m的木块轻轻放于斜面上,如图3-11(A) 保持静止.(B) 向右加速运动.(C) 向右匀速运动.(D) 向左加速运动.【提示】设m0相对于地面以V运动。
依题意,m静止于斜面上,跟着m0一起运动。
根据水平方向动量守恒,得:m V mV+=所以0V=,斜面保持静止。
[C]2.(基础训练3)如图3-12所示,圆锥摆的摆球质量为m,速率为v,圆半径为R,当摆球在轨道上运动半周时,摆球所受重力冲量的大小为(A) 2m v.(B) 22)/()2(vv Rmgmπ+(C) v/Rmgπ(D) 0.【提示】22TGTI mgdt mg==⨯⎰,而vRTπ2=[C ]3.(自测提高1)质量为m的质点,以不变速率v沿图3-16正三角形ABC的水平光滑轨道运动。
质点越过A点的冲量的大小为(A) m v.(B) .(C) .(D) 2m v.【提示】根据动量定理2121ttI fdt mv mv==-⎰,如图。
得:21I mv mv∴=-=[ B] 4.(自测提高2)质量为20 g的子弹,以400 m/s的速率沿图3-17所示的方向射入一原来静止的质量为980 g的摆球中,摆线长度不可伸缩。
子弹射入后开始与摆球一起运动的速率为(A) 2 m/s.(B) 4 m/s.(C) 7 m/s .(D) 8 m/s.【提示】相对于摆线顶部所在点,系统的角动量守恒:2sin30()mv l M m lV︒=+其中m为子弹质量,M为摆球质量,l为摆线长度。
解得:V=4 m/s(解法二:系统水平方向动量守恒:2sin30()mv M m V︒=+)图3-11图3-17二、填空题1、(基础训练7)设作用在质量为1 kg 的物体上的力F =6t +3(SI ).如果物体在这一力的作用下,由静止开始沿直线运动,在0到2.0 s 的时间间隔内,这个力作用在物体上的冲量大小I=18N s ⋅.【提示】2222(63)(33)18I Fdt t dt t t N s ==+=+=⋅⎰⎰2.(基础训练8)静水中停泊着两只质量皆为0m 的小船。
第一只船在左边,其上站一质量为m 的人,该人以水平向右速度v从第一只船上跳到其右边的第二只船上,然后又以同样的速率v 水平向左地跳回到第一只船上。
此后, (1) 第一只船运动的速度为v1=02m v m m -+ 。
(2) 第二只船运动的速度为v2=02m v m 。
(水的阻力不计,所有速度都相对地面而言)【提示】以地面为参考系,水平方向动量守恒。
(1)人与第一只船:第一跳: 010mvi m v i '-= ,第二跳:0101()mvi m v i m m v i '--=+联立求解,得:102mviv m m -=+(2)人与第二只船:第一跳:02()mvi m m v i '=+ ,第二跳:0202()m m v i mvi m v i '+=-+联立求解,得:202mviv m =3.(自测提高6) 质量为m 的小球自高为y 0处沿水平方向以速率v 0抛出,与地面碰撞后跳起的最大高度为21y 0,水平速率为21v 0,如图3-19所示。
(1)地面对小球的竖直冲量的大小为( ; (2)地面对小球的水平冲量的大小为012mv . 【提示】小球在与地面碰撞前后,动量发生了改变,根据动量定理:21I mv mv =-,在竖直方向和水平方向的分量式分别为:21((1y y y I mv mv =-==+ (注意1y v 为负的) 02100122x x x v I mv mv m mv mv =-=-=-故它们的大小分别为:(1y I =+ 012x I m v =4.(自测提高8)两球质量分别为m 1=2.0 g ,m 2=5.0 g ,在光滑的水平桌面上运动。
用直角坐标OXY 描述其运动,两者速度分别为i 101=v cm/s ,)0.50.3(2j i+=v cm/s .若碰撞后两球合为一体,则碰撞后两球速度v 的大小v =__6.14cm/s__,v与x 轴的夹角α=35.5 ︒.【提示】系统的动量守恒:112212()m v m v m m v +=+ ,解得:()3525 /77v i j cm s =+,y 21y 图3-19大小为:()6.14 /v cm s ==;方向:25arctan 35.535α︒⎛⎫== ⎪⎝⎭5(自测提高9)如图3-20所示,质量为m 的小球,自距离斜面高度为h 处自由下落到倾角为30°的光滑固定斜面上。
设碰撞是完全弹性的,则小球对斜面的冲量的大小为,方向为 垂直斜面向下 。
【提示】分析小球。
碰撞中内力很大,故小球重力可以忽略。
斜面对小球的冲量21I mv mv =-小球完全弹性碰撞,动能不变,∴21v v v ===x 方向:0=x F , 0x I =,210x x mv mv -=,∴碰撞前后的速度与斜面法向的夹角相等,如图所示。
y 方向:21y y y I mv mv =- ,cos30(cos30)y I mv mv ︒︒=--=;斜面对小球的冲量大小为I == 斜面向上。
根据牛顿第三定律,小球对斜面的冲量 I I '=-,所以,I ' 方向垂直斜面向下。
6、(自测提高10)在光滑的水平面上,一根长L =2 m 的绳子,一端固定于O 点,另一端系一质量m =0.5 kg 的物体。
开始时,物体位于位置A ,OA 间距离d =0.5 m ,绳子处于松弛状态,如图3-21所示。
使物体以初速度v A =4 m/s 垂直于OA 向右滑动。
设以后的运动中物体到达位置B ,此时物体速度的方向与绳垂直,则此时刻物体对O点的角动量的大小L B =21/kg m s ⋅,物体速度的大小v =1/m s .【提示】物体在运动过程中对O 点的角动量守恒。
位置A 和位置B 的角动量应相等B A A L L mv d ==21/kg m s =⋅ , B B L mv l =,得:v =v B =1/m s三、计算题1.(基础训练15)质量为m 的小球与桌面相碰撞,碰撞前、后小球的速率都是v ,入射方向和出射方向与桌面法线的夹角都是α,如图3-15所示。
若小球与桌面作用的时间为∆t ,求小球对桌面的平均冲力。
解:分析小球。
由动量定理210()tN mg dt mv mv ∆+=-⎰N为桌面对小球的作用力,mg为小球所受重力。
即 []()co s (c o s )2c o s N m g t m v m v j m v jααα-∆=--=, 忽略重力,则 2cos mv N j t α≈∆故小球对桌面的平均冲力为2cos 'mg N N j tα=-=-∆。
图3-20图3-20图3-21图3-152.(自测提高14)一质量为m 的匀质链条,长为L ,手持其上端,使下端离桌面的高度为h 。
现使链条自静止释放落于桌面,试计算链条落到桌面上的长度为l 时,桌面对链条的作用力。
解:取x 轴向下为正。
设t 时刻,落在桌面上的部分链条长为l ,质量为l m , 则有 l m m l l Lλ==(mL λ=为链条的质量线密度)此时在空中的链条的速度大小为:v =在dt 时间内,有dm vdt λ=链条元落在桌面上。
设桌面对链条元的作用力为1f,对链条元应用动量定理,得()100 f dt dm v vdt v iλ=-⋅=-,21 vdt f v i v i dtλλ=-=-另外,桌面对已落在桌面上的链条的作用力为2 l f m g i =-;所以,桌面对整根链条的作用力为 ()1232 m l h g f f f i L+=+=-,方向向上。
3、(自测提高15)如图所示,水平地面上一辆静止的炮车发射炮弹,炮车质量为M ,炮身仰角为α,炮弹质量为m ,炮弹刚出口时,相对于炮身的速度为u ,不计地面摩擦。
(1) 求炮弹刚出口时,炮车反冲速度的大小;(2) 若炮筒长为l ,求发炮过程中炮车移动的距离。
解:(1) 以炮弹与炮车为系统,以地面为参考系,水平方向动量守恒。
设炮车相对于地面的速度为i V x,则有0)cos (=++i V i u m i MV x xαmM mu V x +-=αcos即炮车向后退。
(2) 以u (t )表示发炮过程中任一时刻炮弹相对于炮身的速度,则该瞬时炮车的速度应为 mM t mu t V x +-=αcos )()(积分求炮车后退距离 ⎰=∆tx t t V x 0d )(⎰+-=t t t u m M m0d cos )(α αcos l mM mx +-=∆即向后退了mM ml +αcos 的距离。
x附加题:(自测提高13)有一水平运动的皮带将砂子从一处运到另一处,砂子经一竖直的静止漏斗落到皮带上,皮带以恒定的速率v 水平地运动。
忽略机件各部位的摩擦及皮带另一端的其它影响,试问:(1) 若每秒有质量为q m =d M /d t 的砂子落到皮带上,要维持皮带以恒定速率v 运动,需要多大的功率?(2) 若q m =20 kg/s ,v =1.5 m/s ,水平牵引力多大?所需功率多大?解:(1) d t 时间内,有d M=q m d t 的砂子落到皮带上,速率为v ,根据动量定理,皮带作用在砂子上的力F的冲量为:d d v d 0d v F t M M M =-⋅=⋅ ∴ d d m M F q t ==⋅v v由牛顿第三定律,砂子对皮带的作用力'F F =-.由于皮带匀速运动,所需的水平牵引力为'''F F F =-=,因此,所需供给的功率为:2''m m P F F q q =⋅=⋅=⋅= v v v v v(2) 当q m =d M/d t = 20 kg/s ,v =1.5 m/s 时,水平牵引力大小为 F "=v q m =30 N 所需功率为 P= v 2q m = 45 W。