初中几何经典例题及解题技巧

人教版初一数学几何图形初步典型例题及答题技巧单选题1、如图，小林利用圆规在线段CE上截取线段CD，使CD=AB．若点D恰好为CE的中点，则下列结论中错误．．的是（）CD D．CE=2ABA．CD=DE B．AB=DE C．CE=12答案：C解析：根据线段中点的性质逐项判定即可．解：由题意得：D是线段CE的中点，AB=CD∴CD=DE，即选项A正确；AB=1CE=CD=DE,即B、D正确，C错误．2故答案为C．小提示：本题考查了尺规作图和线段中点的性质，其中正确理解线段中点的性质是解答本题的关键．2、下列判断正确的有（）（1）正方体是棱柱，长方体不是棱柱；（2）正方体是棱柱，长方体也是棱柱；（3）正方体是柱体，圆柱也是柱体；（4）正方体不是柱体，圆柱是柱体．A．1个B．2个C．3个D．4个答案：B解析：根据棱柱的定义：有两个面平行，其余面都是四边形，并且相邻的两个四边形的公共边都互相平行；柱体的定义：一个多面体有两个面互相平行且相同，余下的每个相邻两个面的交线互相平行，进行判断即可．解：（1）正方体是棱柱，长方体是棱柱，故此说法错误；（2）正方体是棱柱，长方体也是棱柱，故此说法正确；（3）正方体是柱体，圆柱也是柱体，故此说法正确；（4）正方体是柱体，圆柱是柱体，故此说法错误．故选B．小提示：本题主要考查了棱柱和柱体的定义，解题的关键在于能够熟练掌握相关定义．3、可以近似看作射线的是（）A．绷紧的琴弦B．手电筒发出的光线C．孙悟空的金箍棒D．课桌较长的边答案：B解析：根据直线、线段、射线的基本特征进行判断即可．A.绷紧的琴弦可看作线段，故本选项不符合题意；B.手电筒发出的光线可以看作射线，故本选项符合题意；C.孙悟空的金箍棒可以看作线段，故本选项不符合题意；D.课桌较长的边可以看作线段，故本选项不符合题意．故选：B．小提示：本题考查了几何图形的初步认识，掌握直线、线段、射线的基本特征是解题的关键．4、给出下列各说法：①圆柱由3个面围成，这3个面都是平的；②圆锥由2个面围成，这2个面中，1个是平的，1个是曲的；③球仅由1个面围成，这个面是平的；④正方体由6个面围成，这6个面都是平的．其中正确的为（）A．①②B．②③C．②④D．③④答案：C解析：根据圆柱、圆锥、正方体、球，可得答案．解：①圆柱由3个面围成，2个底面是平面，1个侧面是曲面，故①错误；②圆锥由2个面围成，这2个面中，1个是平面，1个是曲面，故②正确；③球仅由1个面围成，这个面是曲面，故③错误；④正方体由6个面围成，这6个面都是平面，故④正确；故选：C．小提示：本题考查了认识立体图形，熟记各种图形的特征是解题关键．5、永定河，“北京的母亲河”．近年来，我区政府在永定河治理过程中，有时会将弯曲的河道改直，图中A，B 两地间的河道改直后大大缩短了河道的长度．这一做法的主要依据是（）A．两点确定一条直线B．垂线段最短C．过一点有且只有一条直线与已知直线垂直D．两点之间，线段最短根据线段的性质分析得出答案．由题意中改直后A ，B 两地间的河道改直后大大缩短了河道的长度，其注意依据是：两点之间，线段最短， 故选：D ．小提示：此题考查线段的性质：两点之间线段最短，掌握题中的改直的结果是大大缩短了河道的长度的含义是解题的关键．6、已知∠α=60°32′，则∠α的余角是（ ）A ．29°28′B ．29°68′C ．119°28′D ．119°68′答案：A解析：根据余角的定义、角度的四则运算即可得．∵和为90°的两个角互为余角，且∠α=60°32′，∴∠α的余角为90°−∠α=90°−60°32′=29°28′，故选：A ．小提示：本题考查了余角、角度的四则运算，熟练掌握余角的定义是解题关键．7、如图，BC =12AB ，D 为AC 的中点，DC =3cm ，则AB 的长是( )A ．72cmB ．4cmC ．92cmD ．5cm先根据已知等式得出AB与AC的等量关系，再根据线段的中点定义可得出AC的长，从而可得出答案．∵BC=12AB∴AC=AB+BC=AB+12AB=32AB，即AB=23AC∵D为AC的中点，DC=3cm ∴AC=2CD=6cm∴AB=23AC=23×6=4(cm)故选：B．小提示：本题考查了线段的和差倍分、线段的中点定义，掌握线段的中点定义是解题关键．8、下列四个图中，是三棱锥的表面展开图的是（）A．B．C．D．答案：B解析：根据三棱锥是由四个三角形组成，即可求解解：A是四棱柱，故该选项不正确，不符合题意；B是三棱锥，故该选项正确，符合题意；C是四棱锥，故该选项不正确，不符合题意；D是三棱柱，故该选项不正确，不符合题意；故选B．小提示：．本题考查了三棱锥的侧面展开图，解题的关键是掌握三棱锥是由四个三角形组成．填空题9、单位换算：56°10′48″＝_____°．答案：56.18解析：先将48″换算成“分”，再将“分”换算成“度”即可．）′＝0.8′，解：48×（160）°＝0.18°，则10.8×（160故56°10′48″＝56.18°，所以答案是：56.18．小提示：本题考查度、分、秒的换算，掌握换算方法是正确计算的前提．10、将如图所示的平面展开图折叠成正方体后，“爱”的对面的汉字是_____．答案：家解析：正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．解：正方体的表面展开图，相对的面之间一定相隔一个正方形，“我”字对面的字是“丽”，“爱”字对面的字是“家”，“美”字对面的字是“乡”．所以答案是：家．小提示：本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．11、用度、分、秒表示：37.68°=______．答案：37°40′48″解析：进行度、分、秒的转化运算，注意以60为进制．1°=60′，1′=60′′．解：37.68°=37°+0.68×60′=37°+40.8′=37°+40′+0.8×60′′=37°+40′+48′′=37°40′48′′故答案为37°40′48″小提示：考查了度分秒的换算，掌握1°=60′，1′=60′′是解题的关键12、将两个三角尺的直角顶点重合为如图所示的位置，若∠AOD=108°，则∠COB=_________．答案：72°.解析：由∠AOB=∠COD=90°，∠AOC=∠BOD，进而∠AOC=∠BOD=108°-90°=18°，由此能求出∠BOC．解：∵∠AOB=∠COD=90°，∴∠AOC=∠BOD，又∠AOD=108°，∴∠AOC=∠BOD=108°-90°=18°，∴∠BOC=90°-18°=72°．所以答案是：72°．小提示：本题考查的是角的和差，两锐角的互余，掌握以上知识是解题的关键．13、如图所示，∠AOC=90°，点B，O，D在同一直线上，若∠1=26°，则∠2的度数为______．答案：116°解析：由图示可得，∠1与∠BOC互余，结合已知可求∠BOC，又因为∠2与∠COB互补，即可求出∠2的度数．解：∵∠1=26°，∠AOC＝90°，∴∠BOC＝64°，∵∠2＋∠BOC＝180°，∴∠2＝116°．所以答案是：116°．小提示：此题考查了余角和补角的知识，属于基础题，关键是掌握互余的两角之和为90°，互补的两角之和为180°． 解答题14、已知OD 、OE 分别是∠AOB 、∠AOC 的角平分线．（1）如图1，OC 是∠AOB 外部的一条射线．①若∠AOC ＝32°，∠BOC ＝126°，则∠DOE ＝ °；②若∠BOC ＝164°，求∠DOE 的度数；（2）如图2，OC 是∠AOB 内部的一条射线，∠BOC ＝n °，用n 的代数式表示∠DOE 的度数．答案：（1）63；（2）∠DOE ＝82°；（3）∠DOE ＝12n °解析：（1）根据角平分线的定义，和角的和差关系，可找到∠BOC 和∠DOE 的度数，代入数据即可；（2）根据角平分线的定义，和角的和差关系，可找到∠BOC 和∠DOE 的度数，代入数据即可．解：（1）∵OD 、OE 分别是∠AOB 、∠AOC ，∴∠AOD ＝12∠AOB ，∠AOE ＝12∠AOC ，∴∠DOE ＝∠AOD +∠AOE ＝12（∠AOB +∠AOC ）＝12∠BOC ，∵∠BOC ＝126°，∴∠DOE ＝63°，所以答案是：63．（2）由①可知，∠DOE ＝12∠BOC ，∵∠∠BOC ＝164°，∴∠DOE ＝82°．（3）∵OD 、OE 分别是∠AOB 、∠AOC ，∴∠AOD ＝12∠AOB ，∠AOE ＝12∠AOC ， ∴∠DOE ＝∠AOD ﹣∠AOE ＝12（∠AOB ﹣∠AOC ）＝12∠BOC ，∵∠BOC ＝n °，∴∠DOE ＝12n °． 小提示：本题主要考查角平分线的定义，角的和差计算，根据图形，找到角之间的关系，是解题关键．15、如图，已知点C 为AB 上一点，AC=15cm ，CB=23AC ，若D 、E 分别为AC 、AB 的中点，求DE 的长．答案：DE =5cm解析：根据条件可求出AB 与CD 的长度，利用中点的性质即可求出AE 与AD 的长度，从而可求出答案． 解：∵AC =15 cm ，CB =23AC ，∴CB =10 cm ，AB =15+10=25 cm ．又∵E 是AB 的中点，D 是AC 的中点，∴AE =12AB =12.5 cm ．∴AD =12AC =7.5 cm ，∴DE =AE ﹣AD =12.5﹣7.5=5 cm ．小提示：本题考查了两点间的距离，解题的关键是熟练运用线段之间的熟练关系，本题属于基础题型．11。

初中几何试题及答案解析在初中数学的学习过程中，几何部分是培养学生空间想象能力和逻辑思维能力的重要环节。

下面是一份初中几何试题及其答案解析，旨在帮助学生巩固几何知识，提高解题能力。

试题一：已知一个等腰三角形的底边长为6cm，底边上的高为4cm，求等腰三角形的周长。

解析：首先，我们需要利用勾股定理来求出等腰三角形的腰长。

设等腰三角形的腰长为a，底边的一半为3cm（因为底边长为6cm）。

根据勾股定理，我们有：\[ a^2 = 3^2 + 4^2 \]\[ a^2 = 9 + 16 \]\[ a^2 = 25 \]\[ a = 5 \text{ cm} \]所以，等腰三角形的腰长为5cm。

那么，三角形的周长就是底边加上两条腰的长度：\[ \text{周长} = 6 \text{ cm} + 5 \text{ cm} + 5 \text{ cm} = 16 \text{ cm} \]答案：等腰三角形的周长为16cm。

试题二：一个圆的半径为5cm，求该圆的面积。

解析：圆的面积公式为 \( A = \pi r^2 \)，其中 \( r \) 是圆的半径。

将半径 \( r = 5 \text{ cm} \) 代入公式，我们得到：\[ A = \pi \times 5^2 \]\[ A = \pi \times 25 \]\[ A = 25\pi \text{ cm}^2 \]答案：该圆的面积为 \( 25\pi \text{ cm}^2 \)。

试题三：一个直角三角形的两条直角边长分别为3cm和4cm，求斜边的长度。

解析：根据勾股定理，直角三角形的斜边长度 \( c \) 可以通过两条直角边的长度 \( a \) 和 \( b \) 计算得出，公式为 \( c =\sqrt{a^2 + b^2} \)。

将 \( a = 3 \text{ cm} \) 和 \( b = 4\text{ cm} \) 代入公式，我们得到：\[ c = \sqrt{3^2 + 4^2} \]\[ c = \sqrt{9 + 16} \]\[ c = \sqrt{25} \]\[ c = 5 \text{ cm} \]答案：斜边的长度为5cm。

初中数学几何模型大全+经典题型(含答案) 初中数学几何模型大全及经典题型（含答案）全等变换平移：平行线段平移形成平行四边形。

对称：以角平分线、垂线或半角作轴进行对称，形成对称全等。

旋转：相邻等线段绕公共顶点旋转形成旋转全等。

对称半角模型通过翻折将直角三角形对称成正方形、等腰直角三角形或等边三角形。

旋转全等模型半角：相邻等线段所成角含1/2角及相邻线段。

自旋转：通过旋转构造相邻等线段的旋转全等。

共旋转：通过寻找两对相邻等线段构造旋转全等。

中点旋转：将倍长中点相关线段转换成旋转全等问题。

模型变形当遇到复杂图形找不到旋转全等时，先找两个正多边形或等腰三角形的公共顶点，围绕公共顶点找到两组相邻等线段，分组组成三角形证全等。

几何最值模型对称最值：通过对称进行等量代换，转换成两点间距离及点到直线距离。

旋转最值：找到与所要求最值相关成三角形的两个定长线段，定长线段的和为最大值，定长线段的差为最小值。

剪拼模型通过中点的180度旋转及平移改变图形的形状，例如将三角形剪拼成四边形或将矩形剪拼成正方形。

正方形的边长可以通过射影定理来求解。

假设正方形的边长为x，那么正方形的对角线长为x√2.将正方形分成两个等腰直角三角形，可以得到等腰直角三角形的斜边长为x√2/2.因此，根据射影定理，可以得到等腰直角三角形的高为x/2，进而得到正方形的边长为x=x√2/2.通过平移和旋转，可以将一个正方形变成另一个正方形。

这可以通过旋转相似模型来实现。

例如，两个等腰直角三角形可以通过旋转全等来实现形状的改变，而两个有一个角为300度的直角三角形可以通过旋转相似来实现形状的改变。

更一般地，两个任意相似的三角形可以通过旋转成一定角度来实现旋转相似，其中第三边所成夹角符合旋转“8”字的规律。

在相似证明中，需要注意边和角的对应关系。

相等的线段或比值在证明相似时可以通过等量代换来构造相似三角形。

另外，从三垂线到射影定理的演变，再到内外角平分线定理，需要注意它们之间的相同和不同之处。

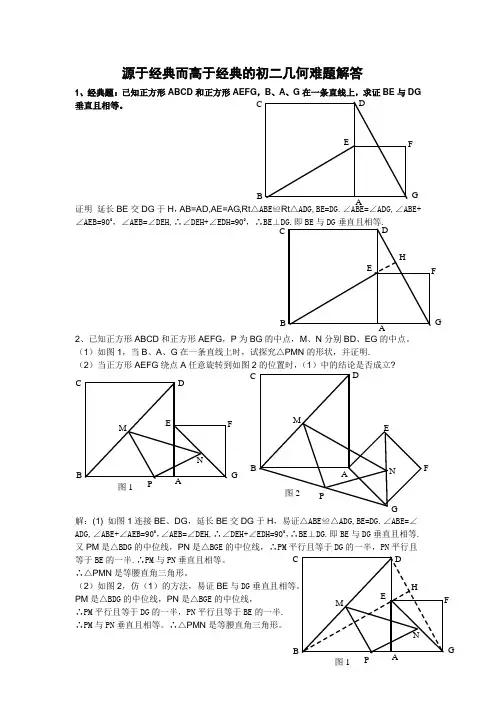
源于经典而高于经典的初二几何难题解答1、经典题：已知正方形ABCD 和正方形AEFG ，B 、A 、G 在一条直线上，求证BE 与DG垂直且相等。

证明 延长BE 交DG 于H ，AB=AD,AE=AG,Rt △ABE ≌Rt △ADG,BE=DG.∠ABE=∠ADG,∠ABE+∠AEB=900，∠AEB=∠DEH,∴∠DEH+∠EDH=900，∴BE ⊥DG.即BE 与DG 垂直且相等.2、已知正方形ABCD 和正方形AEFG ，P 为BG 的中点，M 、N 分别BD 、EG 的中点。

（1）如图1，当B 、A 、G 在一条直线上时，试探究△PMN 的形状，并证明. （2）当正方形AEFG 绕点A 任意旋转到如图2的位置时，（1）中的结论是否成立?解：(1) 如图1连接BE 、DG ，延长BE 交DG 于H ，易证△ABE ≌△ADG,BE=DG.∠ABE=∠ADG,∠ABE+∠AEB=900，∠AEB=∠DEH,∴∠DEH+∠EDH=900，∴BE ⊥DG.即BE 与DG 垂直且相等. 又PM 是△BDG 的中位线，PN 是△BGE 的中位线，∴PM 平行且等于DG 的一半，PN 平行且等于BE 的一半.∴PM 与PN 垂直且相等。

∴△PMN 是等腰直角三角形。

（2）如图2，仿（1）的方法，易证BE 与DG 垂直且相等。

PM 是△BDG 的中位线，PN 是△BGE 的中位线，∴PM 平行且等于DG 的一半，PN 平行且等于BE 的一半. ∴PM 与PN 垂直且相等。

∴△PMN 是等腰直角三角形。

N图1 D M E CPBA F G P 图2 A D M E N CB F G图1HD MEC PBAFGND E C B AF G H D E C B AF G说明：本题的第（2）小题也可看成以△ABG 边AB 、AG 向外作正方形ABCD 和 正方形AEFG 。

可得以上结论。

3、分别以任意四边形ABCD 的各边向外作正方形ABEF 、AGHD 、DIJC 、CKLB 。

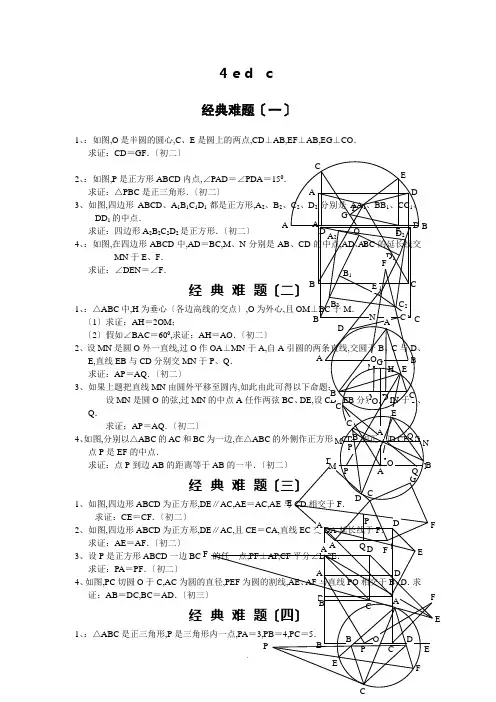
4e d c经典难题〔一〕1、：如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO．求证：CD＝GF．〔初二〕求证：△PBC是正三角形．3、如图,四边形ABCD、A1B1C1DD1的中点．求证：四边形A2B2C2D24、：如图,在四边形ABCD中,ADMN于E、F．求证：∠DEN＝∠F．1、：△ABC中,H〔1〕求证：AH＝2OM；〔2〕假如∠BAC＝600,求证：2、设MN是圆O外一直线,过OE,直线EB与CD分别交MN求证：AP＝AQ．〔初二〕3、如果上题把直线MN设MN是圆O的弦,过Q．求证：AP＝AQ．4、如图,分别以△ABC的AC和点P是EF的中点．求证：点P到边AB1、如图,四边形ABCD为正方形求证：CE＝CF．〔初二〕2、如图,四边形ABCD为正方形求证：AE＝AF．〔初二〕3、设P是正方形ABCD一边求证：PA＝PF．〔初二〕4、如图,PC切圆O于C,AC证：AB＝DC,BC＝AD．1、：△ABC是正三角形,P求：∠APB 的度数．〔初二〕2、设P 是平行四边形ABCD 内部的一点,且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．〔初二〕 3、设ABCD 为圆内接凸四边形,求证：AB ·CD ＋AD ·BC ＝AC ·BD ．〔初三〕 4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P,且 AE ＝CF ．求证：∠DPA ＝∠DPC ．〔初二〕经典难题〔五〕1、设P 是边长为1的正△ABC 内任一点,L ＝PA ＋PB ＋PC,求证：≤L ＜2．2、：P 是边长为1的正方形ABCD 内的一点,求PA ＋PB ＋PC 的最小值．3P 为正方形ABCD 内的一点,并且PA ＝a,PB ＝2a,PC ＝3a,求正方形的边长．4、如图,△ABC 中,∠ABC ＝∠ACB ＝800,D 、E 分别是AB 、AC 上的点,∠DCA ＝300,∠EBA ＝200,求∠BED 的度数． 经典难题〔一〕1.如如下图做GH ⊥AB,连接EO.由于GOFE 四点共圆,所以∠GFH ＝∠OEG,即△GHF ∽△OGE,可得EO GF=GO GH=COCD,又CO=EO,所以CD=GF 得证. 2. 如如下图做△DGC 使与△ADP 全等,可得△PDG 为等边△, △DGC ≌△APD ≌△CGP,得出PC=AD=DC,和∠DCG=∠PCG ＝150 所以∠DCP=300 ,从而得出△PBC 是正三角形3.如如下图连接BC 1和AB 1分别找其中点F,E.连接C 2F 与A 2E 连接EB 2并延长交C 2Q 于H 点,连接FB 2并延长交A 2Q 于G 点,由A 2E=12A 1B 1=12B 1C 1= FB 2 ,EB 2=12AB=12BC=F C 1 ,又∠GFQ+∠Q=900和∠GE B 2+∠Q=900,所以∠GE B 2=∠GFQ 又∠B 2FC 2=∠A 2EB 2 ,可得△B 2FC 2≌△A 2EB 2 ,所以A 2B 2=B 2C 2 , 又∠GFQ+∠HB 2F=900和∠GFQ=∠EB 2A 2 , 从而可得∠A 2B 2 C 2=900 , 同理可得其他边垂直且相等,从而得出四边形A 2B 2C 2D 2是正方形.4.如如下图连接AC 并取其中点Q,连接QN 和QM,所以可得∠QMF=∠F,∠QNM=∠DEN 和∠QMN=∠QNM,从而得出∠DEN ＝∠F.经典难题〔二〕APC B P A DCB CBDAFPD E CBAAP CBA CB P D E D CB A A CBP D1.<1>延长AD 到F 连BF,做OG ⊥AF,又∠F=∠ACB=∠BHD,可得BH=BF,从而可得HD=DF,又AH=GF+HG=GH+HD+DF+HG=2<GH+HD>=2OM<2>连接OB,OC,既得∠BOC=1200,从而可得∠BOM=600,所以可得OB=2OM=AH=AO,得证.3.作OF ⊥CD,OG ⊥BE,连接OP,OA,OF,AF,OG ,AG,OQ.由于22AD AC CD FD FD AB AE BE BG BG,由此可得△ADF ≌△ABG ,从而可得∠AFC=∠AGE.又因为PFOA 与QGOA 四点共圆,可得∠AFC=∠AOP 和∠AGE=∠AOQ, ∠AOP=∠AOQ,从而可得AP=AQ.4.过E,C,F 点分别作AB 所在直线的高EG,CI,FH.可得PQ=2EGFH.由△EGA ≌△AIC,可得EG=AI,由△BFH ≌△CBI,可得FH=BI. 从而可得PQ=2AI BI=2AB,从而得证. 经典难题〔三〕1.顺时针旋转△ADE,到△ABG ,连接CG . 由于∠ABG=∠ADE=900+450=1350从而可得B,G,D 在一条直线上,可得△AGB ≌△CGB. 推出AE=AG=AC=GC,可得△AGC 为等边三角形. ∠AGB=300,既得∠EAC=300,从而可得∠A EC=750. 又∠EFC=∠DFA=450+300=750. 可证：CE=CF.2.连接BD 作CH ⊥DE,可得四边形CGDH 是正方形.由AC=CE=2GC=2CH,可得∠CEH=300,所以∠CAE=∠CEA=∠AED=150, 又∠FAE=900+450+150=1500,从而可知道∠F=150,从而得出AE=AF.3.作FG ⊥CD,FE ⊥BE,可以得出GFEC 为正方形.令AB=Y ,BP=X ,CE=Z ,可得PC=Y-X . tan ∠BAP=tan ∠EPF=X Y =Z Y XZ,可得YZ=XY-X 2+XZ,即Z<Y-X>=X<Y-X> ,既得X=Z ,得出△ABP ≌△PEF , 得到PA ＝PF ,得证 .经典难题〔四〕1. 顺时针旋转△ABP 600 ,连接PQ ,如此△PBQ 是正三角形.可得△PQC 是直角三角形.所以∠APB=1500 .2.作过P 点平行于AD 的直线,并选一点E,使AE ∥DC,BE ∥PC. 可以得出∠ABP=∠ADP=∠AEP,可得：AEBP 共圆〔一边所对两角相等〕. 可得∠BAP=∠BEP=∠BCP,得证.3.在BD 取一点E,使∠BCE=∠ACD,既得△BEC ∽△ADC,可得： BE BC =ADAC,即AD •BC=BE •AC, ① 又∠ACB=∠DCE,可得△ABC ∽△DEC,既得AB AC =DEDC,即AB •CD=DE •AC, ② 由①+②可得: AB •CD+AD •BC=AC<BE+DE>= AC ·BD ,得证.4.过D 作AQ ⊥AE ,AG ⊥CF ,由ADE S=2ABCDS=DFCS,可得：2AE PQ =2AE PQ,由AE=FC. 可得DQ=DG,可得∠DPA ＝∠DPC 〔角平分线逆定理〕.经典难题〔五〕1.〔1〕顺时针旋转△BPC 600 ,可得△PBE 为等边三角形.既得PA+PB+PC=AP++PE+EF 要使最小只要AP,PE,EF 在一条直线上, 即如如下图：可得最小L=；〔2〕过P 点作BC 的平行线交AB,AC 与点D,F. 由于∠APD>∠ATP=∠ADP,推出AD>AP ① 又BP+DP>BP ② 和PF+FC >PC ③ 又DF=AF ④由①②③④可得：最大L< 2 ； 由〔1〕和〔2〕既得：≤L ＜2 .2.顺时针旋转△BPC 600 ,可得△PBE 为等边三角形.既得PA+PB+PC=AP+PE+EF 要使最小只要AP,PE,EF 在一条直线上, 即如如下图：可得最小PA+PB+PC=AF.既得213(1)42= 23=4232=2(31)2= 231)=622.3.顺时针旋转△ABP 900 ,可得如如下图：既得正方形边长L = 2222(2)()22a = 522a .4.在AB 上找一点F,使∠BCF=600 ,连接EF,DG,既得△BGC 为等边三角形,可得∠DCF=100 , ∠FCE=200 ,推出△ABE ≌△ACF , 得到BE=CF , FG=GE .推出 ： △FGE 为等边三角形 ,可得∠AFE=800 , 既得：∠DFG=400① 又BD=BC=BG ,既得∠BGD=800 ,既得∠DGF=400② 推得：DF=DG ,得到：△DFE ≌△DGE , 从而推得：∠FED=∠BED=300 .。

完整版)初中数学几何模型大全+经典题型(含答案)通过将倍长中点相关线段进行旋转变换，可以构造出旋转全等模型。

这种模型的特点是，将相邻等线段所成角的一半旋转后拼接在一起，形成对称全等。

同时，也可以通过将两个等腰三角形或正多边形的夹角进行变化，来构造出模型变形。

如果遇到复杂图形找不到旋转全等，可以先找到两个正多边形或等腰三角形的公共极点，然后围绕公共极点找到两组相邻等线段，分组组成三角形证全等。

幂定理可以用等线段、等比值、等乘积进行代换，从而将两个数之间的比值转换成乘积。

在相似证明中，常用的辅助线是平行线，根据题目条件来确定比值并做出相应的平行线。

题目一：在半圆中，圆心为O，圆上有点C、E，CD垂直于AB，EF垂直于AB，EG垂直于CO。

证明CD等于GF。

题目二：在正方形ABCD内部，点P满足∠PAD＝∠PDA＝15度。

证明△PBC是正三角形。

题目三：在图中，ABCD、A1B1C1D1都是正方形，A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点。

证明A2B2C2D2是正方形。

题目四：在四边形ABCD中，AD＝BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F。

证明∠DEN＝∠F。

题目五：在△ABC中，H为垂心，O为外心，且OM垂直于BC于M。

1）证明AH等于2OM；2）如果∠BAC等于60度，证明AH等于AO。

1.设P为正三角形ABC内任意一点，连接PA,PB,PC，由三角形不等式可得PA+PB>AB。

PB+PC>BC。

PC+PA>CA。

将三式相加得到2PA+2PB+2PC>AB+BC+CA=3，即PA+PB+PC>3/2.又由于P到三角形三边的距离不超过1，所以PA+PB+PC<3，综上可得1.5≤PA+PB+PC<3，即所求不等式成立。

2.设P为正方形ABCD内任意一点，连接PA,PB,PC,PD。

由于正方形四边相等，所以PA+PC=2，PB+PD=2.又由于P到四边的距离不超过1，所以PA+PB+PC+PD<4.将前两式相加得到PA+PB+PC+PD=2(PA+PB)/2+2(PC+PD)/2≥2√(PA·PB)+2√(PC·P D)。

七年级数学第四章几何图形初步典型例题及答题技巧单选题1、一个几何体由大小相同的小立方块搭成，从上面观察这个几何体，看到的形状如图所示，其中小正方形中的数字表示在该位置小立方块的个数，则从正面看该几何体的形状图为（）A．B．C．D．答案：A解析：由已知条件可知，从正面看有3列，每列小正方形数目分别为4，2，3，据此可得出图形．解：根据所给出的图形和数字可得：从正面看有3列，每列小正方形数目分别为4，3，2，则符合题意的是：故选：A．小提示：本题考查了从不同方向看几何体等知识，能正确辨认从正面、上面、左面（或右面）观察到的简单几何体的平2、下列各角中，是钝角的是（ ）．A ．14周角B ．23平角C ．平角D ．14平角答案：B解析：直接利用角的定义逐项分析即可得出答案．解：A. 14周角= 14×360°=90°，不是钝角，不合题意； B. 23平角=23×180°=120°，是钝角，符合题意；C. 平角=180°，不是钝角，不合题意；D. 14平角=14×180°=45°，不是钝角，不合题意． 故选：B小提示：此题主要考查了角的概念，正确掌握平角、周角、钝角的概念是解题关键．3、已知∠AOB =30°，如果用10倍的放大镜看，这个角的度数将（ ）A ．缩小10倍B ．不变C ．扩大10倍D ．扩大100倍答案：B解析：根据角是从同一点引出的两条射线组成的图形．它的大小与图形的大小无关，只与两条射线形成的夹角有关系，直接判断即可．解：角的大小只与角的两边张开的大小有关，放大镜没有改变顶点的位置和两条射线的方向，所以用10倍放大镜观察这个角还是30度．小提示：本题考查了角的概念．解题关键是掌握角的概念：从同一点引出的两条射线组成的图形叫做角，明确角的大小只与角的两边张开的大小有关．4、如图所示，∠COD的顶点O在直线AB上，OE平分∠COD，OF平分∠AOD，已知∠COD＝90°，∠BOC＝α，则∠EOF的度数为（）A．90°+αB．90°+α2C．45°+αD．90°﹣α2答案：B解析：先利用∠COD＝90°，∠BOC＝α，求出∠BOD的度数，再求出∠AOD的度数，利用角平分线，分别求出∠FOD和∠EOD的度数，相加即可．解：∵∠COD＝90°，∠BOC＝α，∴∠BOD＝90°-∠BOC＝90°-α，∴∠AOD＝180°-∠BOD＝90°+α，∵OF平分∠AOD，∴∠DOF=12∠AOD=45°+12α，∵OE平分∠COD，∴∠DOE=12∠COD=45°，∴∠EOF=∠FOD+∠DOE=90°+α；2故选：B．小提示：本题考查了角平分线的计算，解题关键是准确识图，弄清角之间的和差关系．5、观察下列图形，其中不是正方体的表面展开图的是（）A．B．C．D．答案：B解析：利用正方体及其表面展开图的特点解题．解：A、C、D均是正方体表面展开图；B、是凹字格，故不是正方体表面展开图．故选：B．小提示：本题考查了正方体的展开图，熟记展开图的11种形式是解题的关键，利用不是正方体展开图的“一线不过四、田凹应弃之”（即不能出现同一行有多于4个正方形的情况，不能出现田字形、凹字形的情况）判断也可．6、下列事实可以用“经过两点有且只有一条直线”来说明的是（）A．从王庄到李庄走直线最近B．在正常情况下，射击时要保证瞄准的一只眼睛在准星和缺口确定的直线上，才能射中目标C．向远方延伸的铁路给我们一条直线的印象D．数轴是一条特殊的直线答案：B解析：根据两点确定一条直线进而得出答案．在正常情况下，射击时要保证瞄准的一只眼在准星和缺口确定的直线上，才能射中目标，这说明了两点确定一条直线的道理．故选B.小提示：此题主要考查了直线的性质，利用实际问题与数学知识联系得出是解题关键．7、如图是一个正方体的平面展开图，把展开图折叠成正方体后，“红”字的面的对面上的字是（）A．传B．国C．承D．基答案：D解析：正方体的平面展开图中，相对面的特点是必须相隔一个正方形，据此作答．解：正方体的表面展开图，相对的面之间一定相隔一个正方形，则：“传”与“因”是相对面，“承”与“色”是相对面，“红”与“基”是相对面．故选：D．小提示：本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．8、如图，是一个几何体的表面展开图，则该几何体中写“英”的面相对面上的字是( )A．战B．疫C．情D．颂答案：B解析：正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．解：正方体的表面展开图，相对的面之间一定相隔一个正方形，“战”与“情”是相对面，“疫”与“英”是相对面，“颂”与“雄”是相对面．故选：B．小提示：本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手分析是解题的关键．填空题9、下列语句表示的图形是（只填序号）①过点O的三条直线与另条一直线分别相交于点B、C、D三点：_____．②以直线AB上一点O为顶点，在直线AB的同侧画∠AOC和∠BOD：_______．③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点：_________．答案：（3）（2）（1）解析：解：观察图形，根据所给的信息可得：①过点O的三条直线与另一条直线分别相交于点B、C、D三点的图形为（3）；②以直线AB上一点O为顶点，在直线AB的同侧画∠AOC和∠BOD的图形为（2）；③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点的图形为（1）．所以答案是：（3）；（2）；（1）．小提示：本题考查了直线、射线与线段的知识，注意掌握三者的特点，给出图形应该能判断出是哪一个．10、一个直角三角形的两条直角边的长分别为3厘米和4厘米，绕它的直角边所在的直线旋转所形成几何体的体积是_____立方厘米．（结果保留π）答案：12π或16π解析：根据题意可得绕它的直角边所在的直线旋转所形成几何体是圆锥，再利用圆锥的体积公式进行计算即可．解：绕它的直角边所在的直线旋转所形成几何体是圆锥，π×32×4=12π，①当绕它的直角边为3cm所在的直线旋转所形成几何体的的体积是：13π×42×3=16π，②当绕它的直角边为4cm所在的直线旋转所形成几何体的的体积是：13所以答案是：12π或16π．小提示：此题主要考查了点、线、面、体，关键是掌握圆锥的体积公式，注意分类讨论．11、如图，将甲、乙、丙、丁四个小正方形中的一个剪掉，使余下的部分不能围成一个正方体，则剪掉的这个小正方形是________答案：丁解析：能围成正方体的“一四一”，“二三一”，“三三”，“二二二”的基本形态要记牢．解题时，据此即可判断答案．解：将如图所示的图形剪去一个小正方形，使余下的部分不能围成一个正方体，编号为甲乙丙丁的小正方形中剪去的是丁，所以答案是：丁.小提示：本题考查了展开图折叠成正方体的知识，解题关键是根据正方体的特征，或者熟记正方体的11种展开图，只要有“田”，“凹”字格的展开图都不是正方体的表面展开图．12、如图，∠AOC=∠BOD=90°，∠AOB=70°，在∠AOB内画一条射线OP得到的图中有m对互余的角，其中∠AOP=x°，且满足0<x<50，则m=_______．答案：3或4或6解析：分三种情况下：①∠AOP＝35°，②∠AOP＝20°，③0＜x＜50中的其余角，根据互余的定义找出图中互余的角即可求解．∠AOB =35°时，∠BOP=35°①∠AOP＝12∴互余的角有∠AOP与∠COP，∠BOP与∠COP，∠AOB与∠COB，∠COD与∠COB，一共4对；②∠AOP＝90°-∠AOB =20°时，∴互余的角有∠AOP与∠COP，∠AOP与∠AOB，∠AOP与∠COD，∠COD与∠COB，∠AOB与∠COB，∠COP与∠COB，一共6对；③0＜x＜50中35°与20°的其余角，互余的角有∠AOP与∠COP，∠AOB与∠COB，∠COD与∠COB，一共3对．则m＝3或4或6．所以答案是：3或4或6．小提示：本题考查了余角和补角：如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角．13、已知∠A＝20°18'，则∠A的余角等于__．答案：69°42′解析：根据互为余角的两个角之和为90°解答即可．解：∵∠A＝20°18'，∴∠A的余角为90°﹣20°18′＝69°42′．所以答案是：69°42′．小提示：本题考查余角定义，熟知互为余角的两个角之和为90°是解答的关键．解答题14、如图，线段AB=8cm,C是线段AB上一点，M是AB的中点，N是AC的中点．（1）AC=3cm，求线段CM、NM的长；（2）若线段AC=m，线段BC=n，求MN的长度（m<n用含m,n的代数式表示）．答案：（1）CM=1cm，NM=2.5cm；（2）12n解析：（1）求出AM长，代入CM=AM-AC求出即可；分别求出AN、AM长，代入MN=AM-AN求出即可；（2）分别求出AM和AN，利用AM-AN可得MN．解：（1）∵AB=8cm，M是AB的中点，∴AM=12AB=4cm，∵AC=3cm，∴CM=AM−AC=4−3=1cm；∵AB=8cm，AC=3cm，M是AB的中点，N是AC的中点，∴AM=12AB=4cm，AN=12AC=1.5cm，∴MN=AM−AN=4−1.5=2.5cm；（2）∵AC=m，BC=n，∴AB=AC+BC=m+n，∵M是AB的中点，N是AC的中点，∴AM =12AB =12(m +n)，AN =12AC =12m ，∴MN =AM −AN =12(m +n)−12m =12n ． 小提示：本题考查了两点之间的距离，线段中点的定义的应用，解此题的关键是求出AM 、AN 的长．15、已知：如图，点C 在线段AB 上，点M 、N 分别是AC 、BC 的中点．(1)若线段AC ＝6，BC ＝4，求线段MN 的长度；(2)若AB ＝a ，求线段MN 的长度；(3)若将(1)小题中“点C 在线段AB 上”改为“点C 在直线AB 上”，(1)小题的结果会有变化吗?求出MN 的长度． 答案：（1）5cm ；（2）12a ；（3）1或5． 解析：（1）由点M 、N 分别是AC 、BC 的中点．可知MC =3，CN =2，从而可求得MN 的长度．（2）由点M 、N 分别是AC 、BC 的中点，MN =MC +CN =12（AC +BC ）=12AB ．（3）由于点C 在直线AB 上，所以要分两种情况进行讨论计算MN 的长度．解：（1）∵ AC ＝6，BC ＝4，∴ AB ＝6+4＝10，又∵ 点M 是AC 的中点，点N 是BC 的中点，∴ MC ＝AM ＝12AC ，CN ＝BN ＝12BC ，∴ MN ＝MC +CN ＝12AC +12BC ＝12（AC +BC ）＝12AB ＝5（cm ）．（2）由（1）中已知AB ＝10cm 求出MN ＝5cm ，分析（1）的推算过程可知MN ＝12AB ，故当AB＝a时，MN＝12a，从而得到规律：线段上任一点把线段分成的两部分的中点间的距离等于原线段长度的一半．（3）分类讨论：当点C在点B的右侧时，如图可得：MN=MC−NC=12AC−12BC=12(AC−BC)=12×(6−4)=1；当点C在线段AB上时，如（1）；当点C在点A的左侧时，不满足题意．综上可得：点C在直线AB上时，MN的长为1或5．小提示：本题考查线段计算问题，涉及线段中点的性质，分类讨论的思想，属于基础题型．。

初中数学经典几何题及答案1.题目：已知直角三角形的两条直角边分别为3cm和4cm，求斜边的长度。

解答：根据勾股定理，直角三角形中斜边的平方等于两直角边的平方和。

所以斜边的长度为√(3^2 + 4^2) = √(9 + 16) = √25 = 5cm。

2.题目：已知一个正方形的边长为6cm，求其对角线的长度。

解答：正方形的对角线可以看作是两个相等的直角三角形的斜边，所以可以使用勾股定理来计算对角线的长度。

正方形的边长为6cm，所以直角三角形的直角边为6cm，斜边即为对角线的长度。

所以对角线的长度为√(6^2+ 6^2) = √(36 + 36) = √72 ≈ 8.49cm。

3.题目：已知一个梯形的上底长为8cm，下底长为12cm，高为5cm，求梯形的面积。

解答：梯形的面积可以通过上底和下底的平均值乘以高来计算。

所以梯形的面积为(8 + 12) × 5 ÷ 2 = 20cm²。

4.题目：已知一个等边三角形的边长为10cm，求其面积。

解答：等边三角形的面积可以通过边长的平方乘以根号3再除以4来计算。

所以等边三角形的面积为(10^2 × √3) ÷ 4 = (100 × √3) ÷ 4 ≈ 43.30cm²。

5.题目：已知一个长方形的长为8cm，宽为5cm，求其周长。

解答：长方形的周长可以通过将长和宽分别乘以2再相加来计算。

所以长方形的周长为(8 × 2) + (5 × 2) = 16 + 10 = 26cm。

6.题目：已知一个圆的半径为6cm，求其面积。

解答：圆的面积可以通过半径的平方乘以π（约等于3.14）来计算。

所以圆的面积为6^2 × 3.14 ≈ 113.04cm²。

7.题目：已知一个正五边形的边长为4cm，求其周长。

解答：正五边形的周长可以通过边长乘以5来计算。

所以正五边形的周长为4 × 5 = 20cm。

初中几何证明技巧及经典试题证明两线段相等1. 两全等三角形中对应边相等。

2.同一三角形中等角对等边。

3.等腰三角形顶角的平分线或底边的高平分底边。

4.平行四边形的对边或对角线被交点分成的两段相等。

5.直角三角形斜边的中点到三顶点距离相等。

6.线段垂直平分线上任意一点到线段两段距离相等。

7.角平分线上任一点到角的两边距离相等。

8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。

*9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。

*10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。

11.两前项(或两后项)相等的比例式中的两后项(或两前项)相等。

*12.两圆的内(外)公切线的长相等。

13.等于同一线段的两条线段相等。

证明两个角相等1.两全等三角形的对应角相等。

2.同一三角形中等边对等角。

3.等腰三角形中，底边上的中线(或高)平分顶角。

4.两条平行线的同位角、内错角或平行四边形的对角相等。

5.同角(或等角)的余角(或补角)相等。

*6.同圆(或圆)中，等弦(或弧)所对的圆心角相等，圆周角相等，弦切角等于它所夹的弧对的圆周角。

*7.圆外一点引圆的两条切线，圆心和这一点的连线平分两条切线的夹角。

8.相似三角形的对应角相等。

*9.圆的内接四边形的外角等于内对角。

10.等于同一角的两个角相等。

证明两条直线互相垂直1.等腰三角形的顶角平分线或底边的中线垂直于底边。

2.三角形中一边的中线若等于这边一半，则这一边所对的角是直角。

3.在一个三角形中，若有两个角互余，则第三个角是直角。

4.邻补角的平分线互相垂直。

5.一条直线垂直于平行线中的一条，则必垂直于另一条。

6.两条直线相交成直角则两直线垂直。

7.利用到一线段两端的距离相等的点在线段的垂直平分线上。

8.利用勾股定理的逆定理。

9.利用菱形的对角线互相垂直。

*10.在圆中平分弦(或弧)的直径垂直于弦。

S△ACD ，则 S 四边形 EFGO＝S 阴影－S△ACD 。四边形 EFGO 的面积为：880 －1500÷2＝130（平方厘米）。
练一练 7： 如图 19 所示，已知平行四边形 EFGH 的底是 8 厘米，高是 6 厘 米，阴影部分的面积是 16 平方厘米，求四边形 ABCD 的面积。
八、两次求差法 两次求差法是指根据图形之间相容相斥的原理，通过两次求差求出面积的方 法。 例 8 如图 20，长方形 ABCD 的长是 6 厘米，宽是 4 厘米，求阴影部分的面积。
分析与解：通过作辅助线，可以将三角形 ABC 平均分成 16 个完全一样的小 三角形（如图 11 所示），阴影部分为其中 3 个小三角形，即阴影部分的面积占 三角形 ABC 的面积的。阴影部分的面积为：48×＝9（平方分米）。
练一练 4： 如图 12 所示，长方形 ABCD 的长是 10 厘米，宽是 6 厘米，E、F 分别是 AB 和 AD 的中点，求阴影部分的面积。
七、等量代换法 等量代换法是指根据题目中图形之间面积相等的关系，以此代彼，相互替换， 从而求出面积的方法。 例 7 如图 18，长方形 ABCD 的面积为 1500 平方厘米，阴影部分的面积为 880 平方厘米，求四边形 EFGO 的面积。
分析与解：在长方形 ABCD 中，△ABF 与△DBF 同底（即 BF 的长）、等高（即 长方形的宽），所以 S△ABF＝ S△DBF 。若从这两个三角形中同时减去△BEF， 则剩下的图形面积相等，即：S△ABE＝S△DEF 。这样 S 阴影＝S 四边形 EFGO＋
分析与解：通过仔细观察图形，我们可以发现：在大圆中，与阴影Ⅰ、阴影 Ⅱ、阴影Ⅲ面积相等的图形均有 4 个，其中阴影 1 个，空白 3 个。要求阴影部分 的面积，就相当于把大圆的面积平均分成 4 份，求其中一份的面积，列式为： 3.ቤተ መጻሕፍቲ ባይዱ4×（20÷2）2÷4＝78.5（平方厘米）。

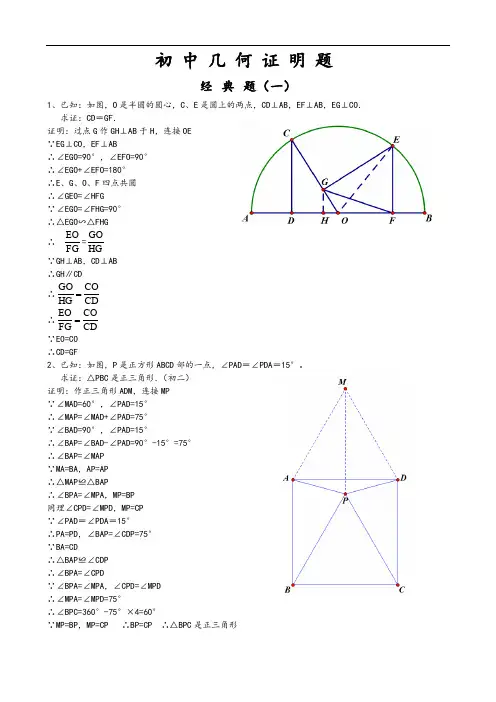
初中几何证明题经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ． 求证：CD ＝GF ．证明：过点G 作GH ⊥AB 于H ，连接OE ∵EG ⊥CO ，EF ⊥AB∴∠EGO=90°，∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ，CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知：如图，P 是正方形ABCD 部的一点，∠PAD ＝∠PDA ＝15°。

求证：△PBC 是正三角形．（初二） 证明：作正三角形ADM ，连接MP ∵∠MAD=60°，∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°，∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ，AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ，MP=BP 同理∠CPD=∠MPD ，MP=CP ∵∠PAD ＝∠PDA ＝15°∴PA=PD ，∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ，∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ，MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ． 求证：∠DEN ＝∠F ．证明:连接AC ，取AC 的中点G,连接NG 、MG ∵CN=DN ，CG=DG ∴GN ∥AD ，GN=21AD ∴∠DEN=∠GNM ∵AM=BM ，AG=CG ∴GM ∥BC ，GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ． （1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二） 证明：（1）延长AD 交圆于F ，连接BF ，过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ，BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2（GH+DH ）=2GD 又AD ⊥BC ，OM ⊥BC ，OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM （2）连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ，OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由（1）知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线，过O 作OA ⊥MN 于A ，自A 引圆的两条割线交圆O 于B 、C 及D 、E ，连接CD并延长交MN 于Q ，连接EB 并延长交MN 于P. 求证：AP ＝AQ ．证明：作点E 关于AG 的对称点F ，连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ，PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ． 求证：AP ＝AQ ．（初二）证明：作OF ⊥CD 于F ，OG ⊥BE 于G ，连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ，∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN ， ∴OA ⊥MN 又OG ⊥BE ，∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°，OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ，点O 是DF 的中点，在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQOP ⊥BC求证：BC=2OP （初二）证明：分别过F 、A 、D 作直线BC 的垂线，垂足分别是L 、M 、N ∵OF=OD ，DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形 ∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°，BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ． 求证：CE ＝CF ．（初二）证明：连接BD 交AC 于O 。

初中解析几何题型及解题方法解析几何是初中数学中的一个重要部分，主要涉及直线、圆、抛物线、双曲线等图形的性质和特点。

以下是一些常见的初中解析几何题型及解题方法：1. 求直线的方程题型描述：给定直线上两点或一点及斜率，要求求出直线的方程。

解题方法：+ 两点式：$\frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1}$+ 点斜式：$y - y_1 = m(x - x_1)$2. 求圆的方程题型描述：给定圆上的三点或两点及半径，要求求出圆的方程。

解题方法：$(x - h)^2 + (y - k)^2 = r^2$，其中 $(h, k)$ 是圆心，$r$ 是半径。

3. 直线与圆的位置关系题型描述：给定直线和圆的方程，要求判断直线与圆的位置关系（相交、相切、相离）。

解题方法：计算圆心到直线的距离，与半径比较。

4. 求抛物线的方程题型描述：给定抛物线上的两点或一点及焦点，要求求出抛物线的方程。

解题方法：标准方程为 $y = ax^2 + bx + c$。

如果知道焦点和准线，则可以求出 $a$ 和 $b$ 的值。

5. 求最值问题题型描述：在给定的图形中，求某一点的坐标或某条线段的长度，使得该值最大或最小。

解题方法：使用配方法、顶点式、导数等方法求最值。

6. 实际应用题题型描述：给定生活中的实际问题，如最短路径、最大面积等，要求用解析几何知识求解。

解题方法：建立数学模型，转化为几何问题，然后使用解析几何的知识求解。

在解决解析几何问题时，除了掌握上述方法外，还需要培养自己的空间想象能力和逻辑推理能力。

同时，多做练习题也是提高解题能力的有效途径。

八年级经典几何题一、三角形全等类。

题1：如图，在△ABC中，AB = AC，AD是BC边上的中线，求证：△ABD≌△ACD。

解析：1. 在△ABD和△ACD中：- 已知AB = AC（题目所给条件）。

- 因为AD是BC边上的中线，所以BD = CD（中线的定义）。

- AD = AD（公共边）。

2. 根据SSS（边 - 边 - 边）全等判定定理，可得△ABD≌△ACD。

题2：已知：如图，点B、E、C、F在同一直线上，AB = DE，AC = DF，BE = CF。

求证：∠A = ∠D。

解析：1. 因为BE = CF，所以BE+EC = CF + EC，即BC = EF。

2. 在△ABC和△DEF中：- AB = DE（已知）。

- AC = DF（已知）。

- BC = EF（已证）。

3. 根据SSS全等判定定理，△ABC≌△DEF。

4. 所以∠A = ∠D（全等三角形的对应角相等）。

二、等腰三角形性质类。

题3：等腰三角形的一个角是70°，求它的另外两个角的度数。

解析：1. 当70°角为顶角时：- 因为等腰三角形两底角相等，设底角为x。

- 根据三角形内角和为180°，则2x+70° = 180°。

- 2x = 180° - 70° = 110°，解得x = 55°。

- 所以另外两个角都是55°。

2. 当70°角为底角时：- 则另一个底角也是70°，顶角为180°-70°×2 = 180° - 140° = 40°。

- 所以另外两个角是70°和40°。

题4：已知等腰三角形ABC中，AB = AC，AD⊥BC于D，若∠BAD = 30°，求∠C的度数。

解析：1. 因为AB = AC，AD⊥BC，根据等腰三角形三线合一的性质，AD是∠BAC的平分线。

初中解析几何解题技巧与实例讲解解析几何是数学的一个重要分支，也是初中数学的一部分。

在学习解析几何时，同学们常常会遇到一些难题，需要一些技巧和方法来解决。

本文将介绍一些初中解析几何解题的技巧，并给出一些实例讲解，帮助同学们更好地掌握解析几何的应用。

一、直线与坐标在解析几何中，直线是一个重要的概念。

通过给定的条件，我们可以确定直线的方程或性质。

下面通过两个实例来说明解析几何中直线的解题技巧：实例1：已知点A(2，3)和点B(5，7)，求线段AB的中点坐标。

解析：线段的中点坐标可以通过x坐标和y坐标的平均值来确定。

根据题意，点A的坐标是(2，3)，点B的坐标是(5，7)。

所以线段AB的中点坐标为：[(2+5)/2，(3+7)/2]，即中点的坐标为(3.5，5)。

实例2：已知直线的斜率为1/2，且经过点(4，3)，求直线的方程。

解析：直线的方程可以通过斜率和截距来确定。

根据题意，直线的斜率为1/2，经过点(4，3)。

斜率为1/2说明直线上的任意两点横坐标的差和纵坐标的差的比值都是1/2。

现在取直线上的一点为(x，y)，则有(x-4)/(y-3)=1/2。

通过解这个方程可以得到直线的方程。

二、直角三角形与勾股定理直角三角形是解析几何中常见的一个概念，其中最重要的定理就是勾股定理。

下面通过两个实例来说明直角三角形的解题技巧：实例1：已知直角三角形的两条直角边长度分别为3和4，求斜边的长度。

解析：根据勾股定理，直角三角形的斜边的平方等于两条直角边的平方和。

所以斜边的长度等于√(3^2+4^2)=5。

实例2：已知直角三角形的斜边长度为5，一直角边长度为3，求另一直角边的长度。

解析：根据勾股定理，直角三角形的斜边的平方等于两条直角边的平方和。

所以另一直角边的长度等于√(5^2-3^2)=4。

三、圆与圆的相交解析几何中考察的另一个重要概念是圆与圆的相交。

通过确定圆心和半径，我们可以确定圆的性质与位置关系。

下面通过一个实例来说明圆与圆的相交的解题技巧：实例：已知圆A的圆心为(2，3)，半径为4；圆B的圆心为(5，7)，半径为3，求圆A和圆B的交点坐标。

初中几何经典题型共享,化异为同,迅速找到突破口!在初中数学中，几何是一个重要的部分，而几何题型中又有一些经典的题型，对于学生来说，能够熟练掌握这些经典题型是非常关键的。

本文将共享一些初中几何经典题型，并提供一些化异为同的方法，帮助学生迅速找到题目的突破口。

一、相似三角形的题型相似三角形在初中数学中是一个非常重要的概念，而与相似三角形相关的题型也是很常见的。

在解决相似三角形的题目时，我们可以采用化简、观察、找规律的方法快速找到突破口。

1. 根据比例关系求解当题目给出两个相似三角形的边长比例时，我们可以利用这个比例关系来求解其他未知边长。

比如题目给出一个大三角形ABC和一个小三角形DEF，并告诉我们AB与DE的比例为2:1，BC与EF的比例为3:2，我们就可以利用这个比例关系求出AC与DF的比例，从而得出未知边长。

2. 利用相似三角形的性质求解相似三角形有很多性质，比如对应角相等、对应边成比例等。

在解题过程中，我们可以利用这些性质来进行推导和求解。

当题目给出两个三角形相似时，我们可以利用对应角相等的性质来得出一些结论，进而找到解题的方法。

3. 观察图形找出等边和等角有时候，题目中的相似三角形可能隐藏着一些等边和等角的信息，我们可以通过观察图形，找出这些信息，然后利用这些信息来解题。

通过观察图形，我们可以找到一些直接的相等关系，从而快速找到题目的突破口。

二、平行线和角的关系题型平行线和角的关系也是初中几何中的一个重要内容，而与平行线和角的关系相关的题型也是比较常见的。

在解决这类题目时，我们可以采用化异为同的方法，将题目中的信息转化为相似的形式，从而快速找到解题的突破口。

1. 利用平行线的性质找角题目中常常会涉及到一些平行线的性质，比如同位角相等、内错角相等等。

在解题时，我们可以利用这些性质来找出一些角的关系，从而推导出一些结论。

通过化异为同，我们可以将题目中的信息转化为相似的形式，从而更容易找到解题的方法。

数学几何是初中数学的一个重要部分，也是学生们比较容易感到困惑的一个知识点。

通过典型例题的学习，可以帮助学生掌握数学几何的解题方法，提高他们的解题能力。

下面就一些典型的数学几何例题进行详细讲解，希望能够对广大学生有所帮助。

【例题一】已知直角三角形ABC中，∠B=90°，AB=5cm，BC=12cm，求AC的长度。

解题思路：1. 根据勾股定理，直角三角形的斜边长度可以通过其两条直角边的长度求得。

2. AC的长度即为三角形ABC的斜边长度，可以使用勾股定理求解。

具体步骤：1. 根据勾股定理，AC的长度可以通过AB和BC的长度求得，即AC²=AB²+BC²。

2. 代入数据，得到AC²=5²+12²=25+144=169。

3. 开平方，得到AC=√169=13cm。

AC的长度为13cm。

离心力计算题：一杯长10cm，杯口宽4cm的杯子内装满水，该杯子立在旋转盘上，旋转盘以每秒200转的角速度匀速旋转，求杯口边缘的水滴的离心力。

解题思路：1. 离心力是一个物体在旋转运动时产生的一种惯性力，可以通过公式计算得出。

2. 对于杯口边缘的水滴，可以看作是在旋转盘上做匀速圆周运动，因此可以利用离心力的公式进行计算。

具体步骤：1. 离心力的公式为F=mω²r，其中m为物体的质量，ω为角速度，r 为旋转半径。

2. 首先计算出水滴的质量，然后根据旋转盘的角速度和杯子的半径计算出离心力的大小。

这里就不再罗列具体计算步骤，具体计算过程略。

最后得出水滴的离心力为XXX。

【例题三】已知矩形ABCD中，AB=8cm，BC=6cm，P是AB的中点，E是BC 上一点，使得PE⊥AB，求PE的长度。

解题思路：1. 首先利用矩形的性质和垂直平分线的性质进行分析。

2. 利用相似三角形的性质，通过比较辅助线的长度来求解PE的长度。

具体步骤：1. 由矩形的性质可知，AD=BC=6cm，同时由垂直平分线的性质可知，PE=EC，且PE⊥AB。

1.证明线段相等或角相等两条线段或两个角相等就是平面几何证明中最基本也就是最重要得一种相等关系。

很多其它问题最后都可化归为此类问题来证。

证明两条线段或两角相等最常用得方法就是利用全等三角形得性质,其它如线段中垂线得性质、角平分线得性质、等腰三角形得判定与性质等也经常用到。

例1. 已知:如图1求证:DE ＝DF分析:由∆ABC 连结CD,易得CD = 证明:连结CDAC BC A BACB AD DBCD BD AD DCB B A AE CF A DCB AD CD=∴∠=∠∠=︒=∴==∠=∠=∠=∠=∠=90，，，，∴≅∴=∆∆ADE CDFDE DF说明:在直角三角形中,作斜边上得中线就是常用得辅助线;在等腰三角形中,作顶角得平分线或底边上得中线或高就是常用得辅助线。

显然,在等腰直角三角形中,更应该连结CD,因为CD 既就是斜边上得中线,又就是底边上得中线。

本题亦可延长ED 到G,使DG ＝DE,连结BG,证∆EFG 就是等腰直角三角形。

有兴趣得同学不妨一试。

例2. 已知:如图2所示,AB ＝CD,AD ＝BC,AE ＝CF 。

求证:∠E ＝∠FAB CD BC AD AC CA ABC CDA SSS B DAB CD AE CF BE DF===∴≅∴∠=∠==∴=，，，∆∆()在∆BCE 与∆DAF 中,BE DF B D BC DA BCE DAF SAS E F=∠=∠=⎧⎨⎪⎩⎪∴≅∴∠=∠∆∆()说明:利用三角形全等证明线段求角相等。

常须添辅助线,制造全等三角形,这时应注意: (1)制造得全等三角形应分别包括求证中一量; (2)添辅助线能够直接得到得两个全等三角形。

2.证明直线平行或垂直在两条直线得位置关系中,平行与垂直就是两种特殊得位置。

证两直线平行,可用同位角、内错角或同旁内角得关系来证,也可通过边对应成比例、三角形中位线定理证明。

证两条直线垂直,可转化为证一个角等于90°,或利用两个锐角互余,或等腰三角形“三线合一”来证。