第八章 -结构力学
- 格式:ppt
- 大小:2.25 MB
- 文档页数:91





潍坊学院机电系讲稿专用纸如车轮上的点P的运动,如果以地面作为参考系,点的轨迹是旋轮线,而如果以小车作为参考系,点的轨迹则是一个圆。
相对于地面是直线运动,相对于旋转的工件,是,因此,车刀在工件的表面上切出螺旋线。
在实际问题中,往往不仅要知道物体相对地球的运动,而且有时要知道被观察物体相对于地面运动着的参考系的运动情况。
例如在运动着的飞机、车船上观察飞机、车船潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸动系上与动点相重合的点相对于定系的速度、加速度称为牵连速度、牵连加速度。
6. 动点和动系的选择基本原则:(1)动点对动系要有相对运动。
(2)动点的相对运动轨迹要明确、容易确定。
具体选择方法:(1)选择持续接触点为动点。
(2)对没有持续接触点的问题,一般不选择接触点为动点。
根据选择原则具体问题具体分析。
实例见PPT。
潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸内的绝对位移绕固定轴O limlim11M M MM '+='M M MMM M '+='11潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸在定系和动系中的矢径分别用r 和r ′表示。
k z j y i x r r ''+''+''+='r潍坊学院机电系讲稿专用纸和为未知量,暂设潍坊学院机电系讲稿专用纸当牵连运动是定轴转动时,动点的绝对加速度并不等于牵连加速度与相对加速之矢量和。
牵连运动是定轴转动时点的加速度合成定理和角加速度α 绕定系Oxyz 的轴z 转动;动系)分析动系的单位矢量k j i''',,对时间的一阶导数以角速度e ω绕定轴z 转动,则角速度矢e ω沿潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸0=r v ③ r e v//ω r e v⊥, 此时 e k a =ω2是由于牵连运动和相对运动的相互影响而产生的潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸。



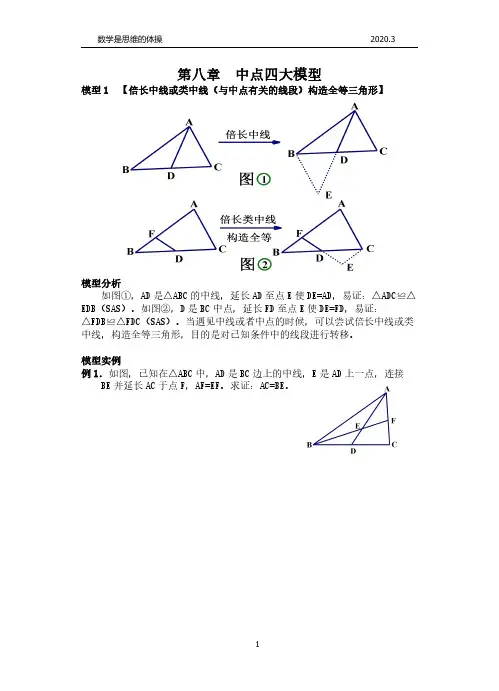
第八章中点四大模型模型1【倍长中线或类中线(与中点有关的线段)构造全等三角形】模型分析如图①,AD是△ABC的中线,延长AD至点E使DE=AD,易证:△ADC≌△EDB(SAS)。
如图②,D是BC中点,延长FD至点E使DE=FD,易证:△FDB≌△FDC(SAS)。
当遇见中线或者中点的时候,可以尝试倍长中线或类中线,构造全等三角形,目的是对已知条件中的线段进行转移。
模型实例例1.如图,已知在△ABC中,AD是BC边上的中线,E是AD上一点,连接BE并延长AC于点F,AF=EF。
求证:AC=BE。
热搜精练1.如图,在△ABC 中,AB=12,AC=20,求BC 边上中线AD 的范围。
2.如图,在△ABC 中,D 是BC 的中点,DM⊥DN,如果2222B M C N D M D N +=+。
求证:()22214A D AB AC =+。
模型2【已知等腰三角形底边中点,可以考虑与顶点连接用“三线合一”】模型分析等腰三角形中有底边中点时,常作底边的中线,利用等腰三角形“三线合一”的性质得到角相等或边相等,为解题创造更多的条件,当看见等腰三角形的时候,就应想到:“边等、角等、三线合一”。
模型实例例1.如图,在△ABC中,AB=AC-5,BC=6,M为BC的中点,MN⊥AC于点N,求MN的长度。
热搜精练1.如图,在△ABC中,AB=AC,D是BC的中点,AE⊥DE,AF⊥DF,且AE=AF。
求证:∠EDB=∠FDC。
2.已知Rt△ABC 中,AC=BC,∠C=90°,D 为AB 边的中点,∠EDF=90°,∠EDF 绕点D 旋转,它的两边分别交AC、CB(或它们的延长线)于E、F。
(1)当∠EDF 绕点D 旋转到DE⊥AC 于E 时(如图①),求证:12DEF CEF ABC S S S += ;(2)当∠EDF 绕点D 旋转到DE 和AC 不垂直时,在图②和图③这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,DEF S 、CEF S 、ABC S 又有怎样的数量关系?请写出你的猜想,不需证明。

【材料科学基础】必考知识点第⼋章2020届材料科学基础期末必考知识点总结第⼋章回复与再结晶第⼀节冷变形⾦属在加热时的组织与性能变化⼀回复与再结晶回复:冷变形⾦属在低温加热时,其显微组织⽆可见变化,但其物理、⼒学性能却部分恢复到冷变形以前的过程。
再结晶:冷变形⾦属被加热到适当温度时,在变形组织内部新的⽆畸变的等轴晶粒逐渐取代变形晶粒,⽽使形变强化效应完全消除的过程。
⼆显微组织变化(⽰意图)回复阶段:显微组织仍为纤维状,⽆可见变化;再结晶阶段:变形晶粒通过形核长⼤,逐渐转变为新的⽆畸变的等轴晶粒。
晶粒长⼤阶段:晶界移动、晶粒粗化,达到相对稳定的形状和尺⼨。
三性能变化1 ⼒学性能(⽰意图)回复阶段:强度、硬度略有下降,塑性略有提⾼。
再结晶阶段:强度、硬度明显下降,塑性明显提⾼。
晶粒长⼤阶段:强度、硬度继续下降,塑性继续提⾼,粗化严重时下降。
2 物理性能密度:在回复阶段变化不⼤,在再结晶阶段急剧升⾼;电阻:电阻在回复阶段可明显下降。
四储存能变化(⽰意图)1 储存能:存在于冷变形⾦属内部的⼀⼩部分(~10%)变形功。
弹性应变能(3~12%)2 存在形式位错(80~90%)点缺陷是回复与再结晶的驱动⼒3储存能的释放:原⼦活动能⼒提⾼,迁移⾄平衡位置,储存能得以释放。
五内应⼒变化回复阶段:⼤部分或全部消除第⼀类内应⼒,部分消除第⼆、三类内应⼒;再结晶阶段:内应⼒可完全消除。
第⼆节回复⼀回复动⼒学(⽰意图)1 加⼯硬化残留率与退⽕温度和时间的关系ln(x0/x)=c0t exp(-Q/RT)x0 –原始加⼯硬化残留率;x-退⽕时加⼯硬化残留率;c0-⽐例常数;t-加热时间;T-加热温度。
2 动⼒学曲线特点(1)没有孕育期;(2)开始变化快,随后变慢;(3)长时间处理后,性能趋于⼀平衡值。
⼆回复机理移⾄晶界、位错处1 低温回复:点缺陷运动空位+间隙原⼦缺陷密度降低(0.1~0.2Tm)空位聚集(空位群、对)异号位错相遇⽽抵销2 中温回复:位错滑移位错缠结重新排列位错密度降低(0.2~0.3Tm)亚晶粒长⼤3 ⾼温回复:位错攀移(+滑移)位错垂直排列(亚晶界)多边化(亚(0.3~0.5Tm)晶粒)弹性畸变能降低。
理论力学8章作业题解8-2 半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
如曲柄OA 以匀角加速度a 绕O 轴转动,且当运动开始时,角速度00=w ,转角0=j 。
求动齿轮以中心A为基点的平面运动方程。
解:图示,A 轮平面运动的转角为=A j ∠C 3AC 2=j +∠CAC 2由于弧长CC 1=CC 2,故有 ∠CAC 2=r R /j ,所以22/t rr R r r R r R A a j j j j +=+=+=A 轮平面运动方程为ïïîïïíì+=+=+=+=+=22212212)sin()()sin()()cos()(cos )(tr r R t r R r R y t r R r R x A A A a j a j a j8-6两刚体M ,N 用铰C 连结,作平面平行运动。
已知AC=BC=600mm ,在题附图所示位置s mm v s mm v B A /100,/200==,方向如图所示。
试求C 点的速度。
解:由速度投影定理得()()0==BC C BC B v v 。
则v C 必垂直于BC 连线,v C 与AC 连线的夹角为30°。
由()()AC A AC C v v = 即得:s mm v v A C /200== ,方向如题4-6附图示。
解毕。
8-9 图所示为一曲柄机构,曲柄OA 可绕O 轴转动,带动杆AC 在套管B 内滑动,套管B 及与其刚连的BD 杆又可绕通过B 铰而与图示平面垂直的水平轴运动。
已知:OA =BD =300mm ,OB =400mm ,当OA 转至铅直位置时,其角速度ωo =2rad/s ,试求D 点的速度。
C 12Aj C解 (1)平面运动方法: 由题可知:BD AC w w =确定AC 杆平面运动的速度瞬心。
套筒中AC 杆上一点速度沿套筒(为什么?)s rad IAOA IA v A AC /72.00=´==w w , s mm BD BD v AC BD D /216=´=´=w w D 点加速度如何分析?关键求AC 杆角加速度(=BD 杆角速度) 基点法,分析AC 杆上在套筒内的点(B’):(1) tA B n A B A B a a a a ¢¢¢++=r r r r大小:× ∠ ∠ × 方位:× ∠ ∠ ∠ 再利用合成运动方法:动点:套筒内AC 杆上的点B’,动系:套筒。